Abstract
We describe the development of a non-invasive method for quantitative tissue temperature measurements using Broadband diffuse optical spectroscopy (DOS). Our approach is based on well-characterized opposing shifts in near-infrared (NIR) water absorption spectra that appear with temperature and macromolecular binding state. Unlike conventional reflectance methods, DOS is used to generate scattering-corrected tissue water absorption spectra. This allows us to separate the macromolecular bound water contribution from the thermally induced spectral shift using the temperature isosbestic point at 996 nm. The method was validated in intralipid tissue phantoms by correlating DOS with thermistor measurements (R = 0.96) with a difference of 1.1 ± 0.91 °C over a range of 28–48 °C. Once validated, thermal and hemodynamic (i.e. oxy- and deoxy-hemoglobin concentration) changes were measured simultaneously and continuously in human subjects (forearm) during mild cold stress. DOS-measured arm temperatures were consistent with previously reported invasive deep tissue temperature studies. These results suggest that DOS can be used for non-invasive, co-registered measurements of absolute temperature and hemoglobin parameters in thick tissues, a potentially important approach for optimizing thermal diagnostics and therapeutics.
1. Introduction
Temperature-dependent changes in near-infrared (NIR) water absorption spectra have been well characterized (Collins 1925, Otal et al 2003). As temperature increases, the water peak around 970 nm blue-shifts, narrows and increases in intensity (Collins 1925, Kelly et al 1995, Libnau et al 1994, McCabe et al 1970, Merritt 2005), providing a sensitive spectral signature of temperature. Since tissue is primarily composed of water (typically ~60–70%), tissue water spectra can potentially reveal tissue temperature. However, at depths greater than the NIR transport scattering length in tissues (e.g. ≥1 mm), multiple light scattering obscures temperature-dependent water spectral shifts, impairing reliable spectral measurements of tissue temperature.
Broadband diffuse optical spectroscopy (DOS) acquires scattering-separated absorption spectra, typically from 650 to 1000 nm. In this work, we employ a type of DOS that combines broadband frequency-domain photon migration (FDPM) with steady-state (SS) reflectance spectroscopy (Tromberg et al 1993, Bevilacqua et al 2000, Cerussi et al 2006). This approach provides high resolution, quantitative absorption spectra, which are needed to characterize temperature-dependent changes associated with the water absorption features. DOS absorption spectra are used to quantify major tissue NIR chromophores including oxy- and deoxy-hemoglobin, lipid and water at centimeter depths. By measuring scattering-corrected absorption changes in the 970 nm water peak, additional information regarding the disposition of tissue water can be obtained. This includes the bound water fraction (Chung et al 2008) and, as we demonstrate in this paper, tissue temperature.
DOS measurements of temperature, hemodynamic and metabolic parameters are co-localized. As a result, this non-invasive technique could potentially be employed to optimize dosimetry during thermotherapies, enhancing therapeutic outcome and reducing damage to normal tissues. Thermal therapies are widely used in medicine, spanning from cryosurgery to hyperthermia and thermal ablation. Non-invasive imaging methods that measure and map subsurface tissue temperature can be difficult and expensive to employ (e.g. MRS), and implantable sensors may perturb energy deposition and tissue temperature distribution. Methods such as hyperthermia utilize heat to remove tumors by killing cells directly or sensitizing them to chemotherapy agents and/or radiation (Kim and Hahn 1979, Rieke and Pauly 2008, Seegenschmiedt et al 1995, Thomsen 1991, Vargas et al 2004). In order to remove a tumor using hyperthermia, heat in the range of 43–50 °C is applied for an extended period, in some cases hours (Vargas et al 2004). Vargas et al showed that tumor necrosis fraction is determined by peak tumor temperature as well as the thermal dose, and a 2.6 °C difference in the peak tumor temperature can result in a 50% difference in the tumor necrosis. Thus, absolute temperature measurements could be used to optimize dosimetry while co-localized tissue functional parameters such as oxy- and deoxy-hemoglobin report on the biologic effects of therapy.
In this work we validate our approach for quantifying temperature in multiple-scattering intralipid phantoms and compare DOS temperature calculations to simultaneous thermistor measurements. Our results show a correlation between non-invasive optical measurements and invasive thermal measurements (R = 0.96, average difference = 1.1 ± 0.91 °C, in 28–48 °C). In addition, we demonstrate the potential for broadband DOS to measure absolute temperature and hemodynamic parameters in vivo in human subjects during mild cold stress.
2. Background theory
A pronounced water absorption peak appears in the NIR around 970 nm. This peak is due to the combination of the first harmonic of the O–H symmetric stretch vibration and the fundamental anti-symmetric stretch vibration from hydrogen bound O–H (Bayly et al 1963). The characteristics of this peak are sensitive indicators of the local environment of water molecules.
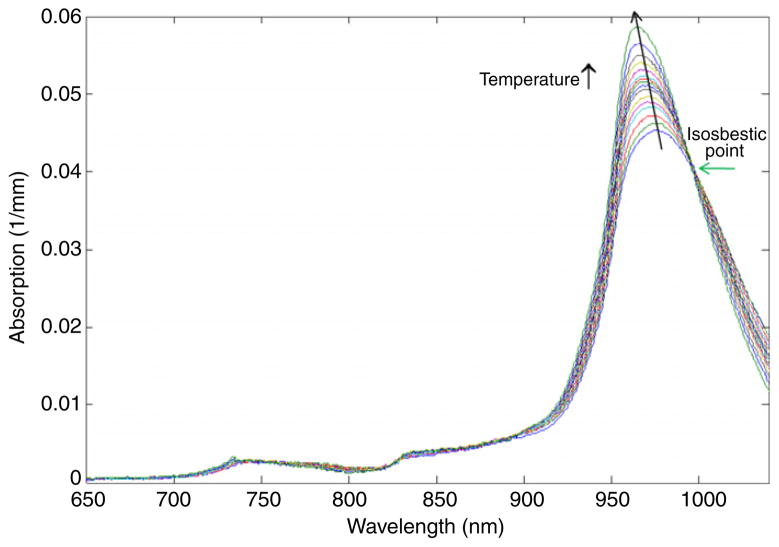
The spectral features of water absorption depend upon the temperature and water binding state. As temperature increases, the fraction of hydrogen-bound water molecules is reduced, causing the 970 nm water peak to increase in intensity, narrow in bandwidth and shift to higher energy (i.e. blue-shift), as shown in figure 1 (Kelly et al 1995, Libnau et al 1994, McCabe et al 1970, Merritt 2005). Walrafen (1967) explained that these changes are from a shift in the equilibrium between hydrogen-bound and -unbound (free) water molecules. Hydrogen bonding between water and macromolecules such as proteins causes further spectral broadening and red shifting of the 970 nm water peak (Pimentel and McClellan 1960, Chung et al 2008). These two competing effects (i.e. red and blue-shifts of the peak) complicate the proper interpretation of the water local environment. However, there is also an isosbestic point with respect to temperature in the water absorption spectrum at 996 nm (figure 1, Buijs and Choppin 1963, Walrafen 1967, Hollis 2002, Merritt 2005). As a result, the absorption coefficient at 996 nm can be used to account for macromolecular bound water effects independent of tissue temperature. Once the bound water correction is determined, the best fit to the temperature-dependent pure water spectra yields the absolute temperature of the measured tissue volume.
Figure 1.
Pure water absorption spectra measured as a function of temperature (15–65 °C). The water peak around 970 nm increases in intensity, narrows in width and blue-shifts in wavelength as temperature increases. An isosbestic point at 996 nm is observed.
3. Materials and methods
3.1. Instrumentation
Broadband DOS employed in this study combines multi-frequency, frequency domain photon migration (FDPM) with broadband steady-state (SS) spectroscopy in order to acquire continuous NIR absorption and scattering spectra in turbid media (Jakubowski et al 2009). Multi-frequency FDPM separates the effects of absorption from scattering in tissues using model-based analysis (Fishkin and Gratton 1993, Tromberg et al 1993). Models include a P1 approximation to the transport equation in the semi-infinite (for in vivo measurements) or infinite (for phantoms) geometry using an extrapolated boundary condition (Fishkin et al 1996, Haskell et al 1994). The SS component enables the acquisition of continuous absorption spectra of more than 1000 wavelengths from 650 to 998 nm for phantoms and 1013 nm for in vivo tissues (B&W Tek, Newark, DE, model 611a and 611b, respectively). Because the spectrometer is auto-calibrated, the absolute wavelengths are obtained for every measurement. Instrument response is determined using tissue-simulating phantoms with known scattering and absorption values for FDPM and spectraflect-coated integrating spheres with known reflectance values for SS measurements, as described in Cerussi et al (2006). Details of the broadband DOS system have been previously reported (Bevilacqua et al 2000, Cerussi et al 2006, Jakubowski et al 2009).
Measurements were performed by placing fixed source and detector optical fibers in the middle of intralipid phantoms (infinite geometry) or on a forearm (semi-infinite geometry) of a human subject. The multi-frequency (~400 frequencies from 50 to 300 MHz) swept FDPM data were acquired for 661, 681, 783, 806, 823 and 850 nm lasers (<20 mW power) for the phantoms and 658, 682, 785, 810, 830 and 850 nm lasers for the in vivo tissue measurements. The SS data (single tungsten–halogen lamp) for all wavelengths with 0.3–0.5 nm increments between 650 and 998 (phantoms) or 1013 nm (in vivo) were acquired in a total of ~6 s. The differences between the two systems were due to the availability of components at different times. The source–detector separation was 9 mm for phantom measurements and 20 mm for in vivo measurements. Model fits to SS and FDPM data were performed in order to recover absorption (μa) and reduced scattering (μ′s) values for all wavelengths between 650 and 998 nm as described in Bevilacqua et al (2000), Cerussi et al (2006), and Jakubowski et al (2009).
3.2. Spectral processing algorithm
The extinction coefficient spectra of major chromophores in tissues and phantoms (oxy- and deoxy-hemoglobin, water and lipid for tissues; water, lipid and nigrosin in phantoms) were used to recover the concentrations of these components from measured absorption spectra (Cerussi et al 2002, 2007, Cubeddu et al 2000, Pogue et al 2004, Quaresima et al 1998). For pure water, distilled water placed in a cuvette was measured using a spectrophotometer (Beckman DU 650) at various temperatures (Merritt 2005). Nigrosin (Sigma-Aldrich, St. Louis, MO, water soluble) was also measured with the spectrophotometer using a 511 mg l−1 stock solution. The lipid spectra were obtained from mammalian fat by van Veen et al (2005). For oxy- and deoxy-hemoglobin, we employed molar extinction coefficients of Zijlistra et al (2000). The measured absorption spectrum and extinction coefficient spectra provided needed information to solve nonnegative least-squares constraints problems (using ‘lsqnonneg’ in MATLAB®) to recover the concentrations of the major absorbers in phantoms and tissues mentioned above. A ‘water only’ tissue absorption spectrum was obtained by eliminating contributions from all non-water tissue absorbers. This was accomplished by subtracting hemoglobin (oxy- and deoxy-) and lipid extinction coefficient spectra, multiplied by their concentrations, from broadband tissue absorption spectra (Chung et al 2008). The ‘water only’ tissue absorption spectrum was normalized by multiplying the ratio of the water peak of a pure water spectrum to the measured water peak. The pure water spectrum used at this step was of the temperature that was measured using a thermistor for the phantoms or 33.5 °C for the forearm measurement.
In order to estimate temperature using the water absorption spectrum, we employed a two-step process. First, we corrected the tissue water spectra for the spectral shift and broadening caused by macromolecular binding using an iterative fitting algorithm and the isosbestic point of the pure water spectra. Then, the best-fit pure water spectrum at a specific temperature to the bound water corrected spectrum was used to calculate tissue temperature. These steps are explained in detail below.
Step 1. Bound effect correction
In order to determine the spectral shift in the absorption spectrum due to bound water, we fit the extinction coefficient spectrum for each tissue component to the absorption spectrum while correcting the water extinction coefficient spectrum using an iteration algorithm. A pure water extinction coefficient spectrum at the pre-measured (for phantoms) or assumed (for tissues) temperature is shifted using equation (1) (Merritt 2005):
| (1) |
where wpwl is the peak wavelength of the pure water spectrum, bws is the bound water shift defined as the peak-to-peak distance between the tissue water spectrum and the corrected pure water spectrum, and WL is the upper wavelength limit used for the bound water shift correction. It was found that above 935 nm the tissue water absorption spectrum was linearly shifted to higher wavelengths relative to the pure water spectrum; thus, 935 nm was used as the starting wavelength for the bound water shift calculation. The chromophore fit is then executed with the newly corrected pure water spectrum and a loop is entered in which the chromophore fit and the bound water shift calculation are performed until the bws in equation (1) changes by less than 0.1 nm. The calculated bws in equation (1) was used in order to blue-shift a normalized tissue water spectrum as the first step of bound water effect correction.
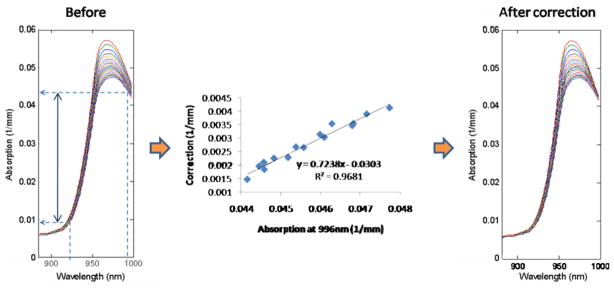
Although significant bound water shifting is accounted for using the above step, absorption values at the isosbestic point (996 nm, shown in figure 1) are not fully corrected. This may be due to uncertainties in our estimation of the temperature of pure water basis spectra with respect to tissue water. Additional correction is therefore performed on the normalized spectra by forcing an isosbestic point at 996 nm. We validated this procedure by determining the relationship between the normalized intensity at 996 nm and the correction amount using two intralipid phantoms with known temperature (28–48 °C with 3 ± 1.3 °C increment) and observed a linear relationship (y = 0.7238x − 0.0303, R2 = 0.9681) (figure 2). This equation was then used for the final blue-shifting of the tissue water spectrum in order to minimize the difference between measured and ideal spectra from 925 nm to 996 nm, where 925 nm is essentially independent of bound water effects. During the blue-shifting, the spectrum was extrapolated slightly if the upper limit of the spectrum was less than 998 nm.
Figure 2.
The relationship between the 996 nm water absorption value and the bound water effect correction. The water absorption spectra (left: normalized, bound water shift (bws) corrected; right: fully corrected for 996 nm isosbestic point) are from intralipid phantoms.
Step 2. Spectral fitting for absolute temperature determination
After the bound water effect corrections, the remaining tissue water spectrum was fit to a library of pure water spectra at different temperatures using a nonlinear least-squares curve-fitting algorithm (‘lsqcurvefit’ in MATLAB®). The temperature of the pure water spectrum that fits the tissue water spectrum with the lowest residuals was selected as the temperature of the measured tissue volume. For this fitting process, a spectral window from 940 to 995 nm was used because empirically we found it to be the most robust range for temperature fitting.
3.3. Phantom and human subjects measurements
Intralipid tissue phantoms were used for comparing broadband DOS and thermistor measurements of temperature. 600 ml of distilled water was mixed with 150 ml Intralipid (Intralipid® 20% I.V. emulsion, Fresenius Kabi, Uppsala, Sweden, distributed by Baxter, IL) and 5 ml nigrosin (Sigma-Aldrich, St Louis, MO) of 511 mg l−1 stock solution. Four of the intralipid phantoms were made and measured on different dates. A calibrated thermistor with ±0.2 °C accuracy (Newport, Santa Ana, CA) measured the temperature of the phantoms. The temperature in the middle of the phantom was measured simultaneously by the broadband DOS instrument and the thermistor. So as not to interfere with the optical measurement, the thermistor was placed about 5 mm longitudinally lower and 5 mm transversely away from the end of the detector fiber and the optical field of view. Phantom temperature was controlled using a hot plate placed underneath the phantom.
For in vivo tissue measurements, forearms (brachioradial muscles) of four healthy male subjects (20.5 ± 1.3 years) were measured continuously over a 70 min period. Ultrasound was used to measure adipose layer thicknesses, which ranged from 2 to 4 mm. The patient was lying in a supine position during the measurements. The arm was relaxed and put in a water tank that was lower than the bed height. The DOS probe was fixed onto the arm in order to maintain consistent contact with the tissue. The temperature of water in the tank was 37 ± 1 °C for the initial 5 min, decreased to 15 ± 1 °C for 30 min (cooling phase) and then increased to 37 ± 1 °C for 30 min (recovery phase) for three subjects. One of the subjects had a shorter cooling phase and recovery phase (20 min each). The temperature of water in the tank was monitored with a thermometer and kept constant by adding warm water or ice for the 37 ± 1 °C and 15 ± 1 °C water, respectively.
4. Results
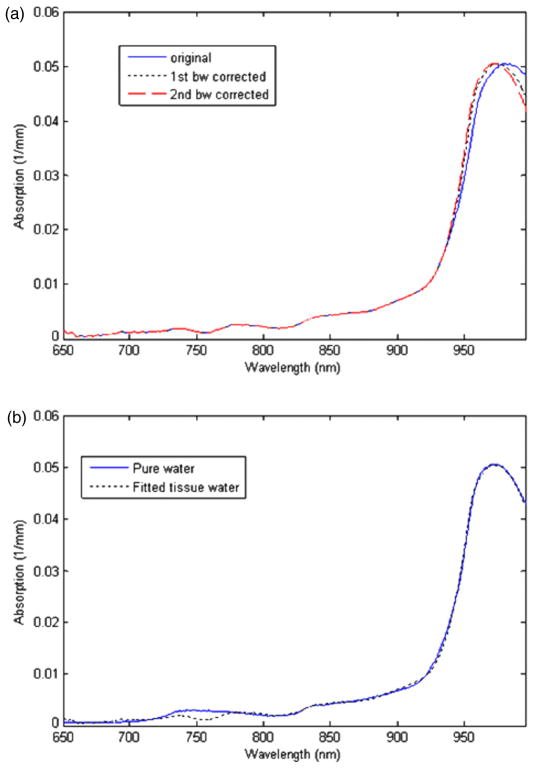
Representative bound water and temperature-corrected water spectra from a human subject (forearm muscle) are shown in figure 3. As a result of the first bound water shift correction, the water absorption spectrum was blue-shifted (‘first bw corrected’ in figure 3(a)). The calculated bws used for this blue-shift in Step 1 was 3–6 nm for the forearm measurements depending on the subject. The bws for the intralipid phantoms was 0 nm; thus, Step 1 was skipped. The value used for the blue-shift in Step 1 for a set of longitudinal measurements is the minimum bws obtained during the baseline or initial measurements. The ‘second bw corrected’ spectrum in figure 3(a) is the result of the additional optimization of the blue-shift. The additional shift resulted in the best fit to one of the temperature-dependent pure water spectra as shown in figure 3(b). The temperature of the best-fit pure water spectrum was assumed to be the average temperature of the measured volume.
Figure 3.
(a) Before and after first (fine dashed line) and second (coarse dashed line) bound water effect corrections. (b) Bound water corrected tissue water spectrum fit to a pure water spectrum at a specified temperature. The temperature of the best-fit pure water spectrum is the temperature of the measured tissue volume.
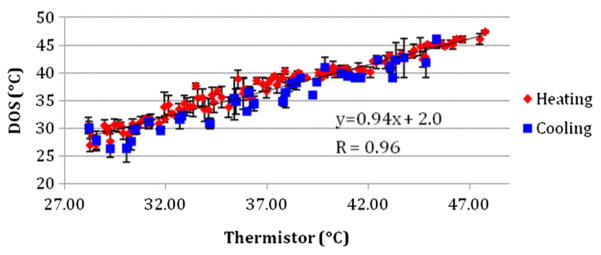
Temperature changes in the intralipid phantoms were monitored using both broadband DOS and a thermistor (figure 4). Temperature was measured in 0.27 ± 0.25 °C increments during the heating process in four phantoms and during the cooling process in two of them. No significant differences between heating and cooling measurements were observed. A high correlation between the thermistor and broadband DOS measured temperature was obtained (R = 0.96). The slope of the linear fit to the temperature from both techniques was 0.94. The overall mean difference between DOS and thermistor measurements was 1.1 ± 0.91 °C. The standard error of the DOS-measured temperature was 1.0 ± 0.74 °C.
Figure 4.
Comparison between DOS and thermistor temperature measurements during phantom heating and cooling. A high correlation (R = 0.96) is observed with a slope of 0.94.
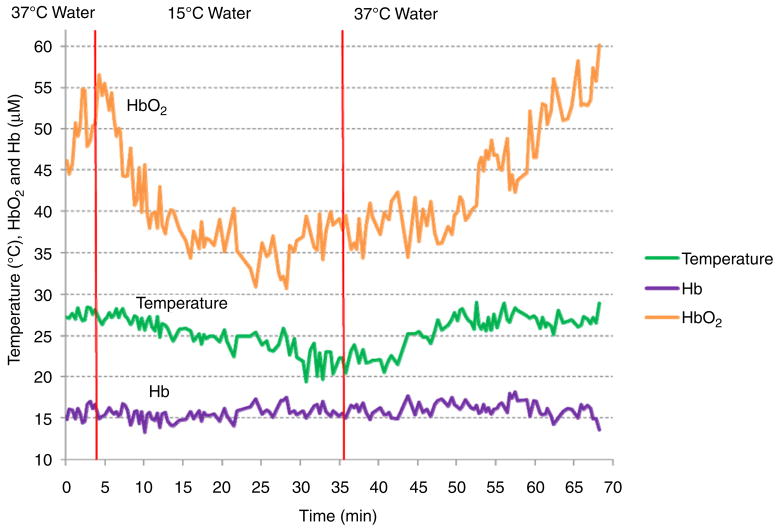
Thermal changes in the human forearm were measured longitudinally in four male subjects (age: 20.5 ± 1.3). In figure 5, one of the subject’s thermal and hemodynamic responses to environmental temperature changes are shown. During the 5 min baseline measurement, the temperature did not change significantly (27.6 ± 0.6 °C). Shortly after the arm was immersed in 15 °C water, arm temperature slowly decreased to 19.5 °C, about 8 °C lower than the baseline. Fifteen minutes after replacing the cold water with 37 °C water, the arm temperature recovered nearly to the initial values. In this subject, oxyhemoglobin, a sensitive indicator of tissue oxygen delivery, dropped significantly during cold stress. Deoxyhemoglobin, which reflects tissue oxygen consumption, did not change significantly. In all of the subjects, the baseline temperature during the first 5 min and the recovered temperature after the cold stress (last 5 min) were 27.6 ± 0.5 °C and 27.2 ± 0.3 °C, respectively (table 1). The minimum temperature during the cold stress was 22.8 ± 2.6 °C. The dynamic range of thermal response during the recovery was similar to the thermal dynamic range during the cold stress (0.63 ± 0.3 difference). The hemodynamic rate was different in all subjects in response to the environmental temperature changes.
Figure 5.
Non-invasive in vivo measurements of thermal and hemodynamic changes in forearm muscles in a human subject.
Table 1.
Thermal response to mild cold stress in four subjects (A, B, C and D, age: 20.5 ± 1.3). Baseline temperature during the first 5 min, the minimum temperature during the cold stress and recovered temperature after the cold stress are shown.
| Temperature (°C) | A | B | C | D |
|---|---|---|---|---|
| Baseline | 27.56 ± 0.60 | 28.15 ± 0.48 | 27.66 ± 0.53 | 27.00 ± 0.33 |
| Cold stress minimum | 19.46 | 22.30 | 25.35 | 24.15 |
| Recovered | 27.02 ± 0.80 | 27.08 ± 0.51 | 27.32 ± 0.56 | 27.57 ± 0.23 |
5. Discussion
We have described a method for absolute temperature measurements based on resolving water vibrational frequency shifts due to macro-molecular binding. Because this approach accounts for thermally induced changes in light scattering, protein denaturation/aggregation and/or changes in lipids and molecular complexes that typically occur with heating do not impact accuracy. The spectral changes are observed as shifts and broadening/narrowing of the water absorption peak at 970 nm as shown in figure 1. Because the method requires quantifying subtle changes in the NIR water absorption features, efficient separation of absorption from scattering and a high-resolution calibrated spectrometer are required.
The spectral processing algorithm separates counteracting bound water effects from temperature effects on the NIR water absorption spectrum. The bound water correction is based on our previous work (Chung et al 2008) where a bound water index (BWI) was introduced. The residual between a tissue water absorption spectrum and a pure water absorption spectrum was used to calculate the BWI, an index that represents both the water peak shift and its shape change. Those features were used to correct for the bound water effect on the water spectrum in this study. After the first correction using the fitting and iteration algorithm, the second correction using the pure water temperature isosbestic point at 996 nm completed the bound water effect correction (figures 2 and 3(a)). The absorption at 925 nm of normalized water absorption spectra was 0.0108 ± 0.0007 mm−1 in the intralipid phantoms and 0.0109 ± 0.0001 mm−1 in the in vivo forearm baseline measurements. Since the difference was negligible, the calibration equation derived using intralipid phantoms (figure 2) was employed for in vivo tissue temperature measurements. Finally, the corrected water spectra were fit to a library of pure water spectra at different temperatures to determine the temperature of the measured volume (figure 3(b)). At this step, we found that the library should have pure water spectra at least at every degree Celsius for accurate temperature determination. The discrepancy observed at 750 nm between the tissue water spectrum and pure water spectrum in figure 3 might be due to over-correction of lipid and deoxy-hemoglobin in the tissue water spectrum. However, this wavelength range does not affect the temperature measurement since only wavelengths above 935 nm were employed for temperature calculation.
The algorithm for calculating absolute temperature was tested and validated in several different intralipid phantoms during heating and cooling using simultaneous DOS and thermistor measurements (figure 4). Excellent correlation was observed (R = 0.96) with a slope near unity (0.94) indicating that the sensitivity of optical recordings is comparable to the thermistor. The average difference in the measured absolute temperature between the two techniques was 1.1 ± 0.91 °C. This difference was similar to the standard error of the broadband DOS system (1 ± 0.74 °C). Thus, the difference between the two systems might be due to instabilities of the DOS system, likely because the upper usable limit of our spectrometer was about 1000 nm. As a result, in some cases the spectrum was shortened to less than 998 nm after the blue-shift and we extended it using an extrapolation function in the MATLAB. Because the sensitivity of the spectrometer in this wavelength region is poor, the extrapolated portion can have greater error. Spectra with very large errors in the extrapolation were excluded using an exclusion criteria based on approximate second derivatives (‘diff’ function of the MATLAB) of the range 981–998 nm. Any spectra with second derivatives greater than 7 × 10−5 were excluded; however, many spectra with smaller but noticeable errors were included. When we used a different spectrometer with an upper limit of ~1010 nm for the in vivo measurement, this problem did not appear. Thus, a spectrometer with the highest possible spectral range is recommended for temperature determination.
Despite these factors, overall accuracy was ~1 °C regardless of whether we were monitoring heating or cooling. The scattering coefficients of our liquid phantom data were different during heating and cooling (for example, power law fit to μ′s versus wavelength: y = 16648x−1.225 for heating and y = 20485x−1.285 for cooling, data not shown), demonstrating that irreversible structural/macromolecular changes in the phantoms during heating did not impact accuracy. This is due to the fact that temperature was determined directly from scatter-corrected absorption spectra and therefore unaffected by scattering property changes. Other optical methods that are not model-based and do not correct for scattering properties may be subject to hysteresis effects during heating/cooling cycles (Belashev and Ternovoi 1996, Kakuta et al 2008).
In general, the accuracy and dynamic range of these DOS temperature measurements can be improved by including more precisely measured pure water extinction coefficient spectra in the library of water spectra at various temperatures and by expanding the pure water spectral library to include a broader temperature range and finer thermal resolution. The fact that this method relies on the quality and number of water spectra in the library is a potential weakness. However, since the peak wavelength of the water spectrum decreases linearly as the temperature increases (R = −0.95, 95% confidence interval: −0.98 and −0.91, p-value <2.2 × 10−16 in our water spectra library), we expect that if more precisely measured water spectra of higher and lower temperature are included in the library, both accuracy and dynamic range can be improved.
During in vivo tissue measurements, the initial temperature was about 28 °C, which is much lower than core body temperature (figure 5). This discrepancy is likely due to contributions from superficial tissues (i.e. skin and subcutaneous lipid) with thicknesses ranging from 2 to 5 mm in our subject population (Ducharme et al 1991). Forearm skin temperature has been measured in the range of 28.3–32°C depending on location (Montgomery and Williams 1976, Ducharme et al 1991). Although the forearm was immersed in 37 °C water for 5 min, the effect on tissue temperature was likely minor since approximately 20 min is required to achieve thermal equilibrium (Montgomery and Williams 1976, Ducharme and Tikuisis 1992).
The lowest tissue temperature measured (~20 °C) after the 30 min immersion in cold water agreed well with previously published studies that report ~20 °C measurements from an implanted multicouple probe in a forearm (Ducharme and Tikuisis 1992). When the cold water was replaced with the 37 °C bath, arm temperature eventually returned to baseline levels. The time required for the temperature decrease was about the same as recovery to the baseline. Although the arm was immersed for about 30 min in 37 °C water, the arm deep tissue temperature did not reach 37 °C. Thus, while the current DOS probe geometry (20 mm source–detector separation) has been shown to have the ~6–10 mm mean interrogation depth, the temperature sensitivity map is not precisely characterized and could be weighted to more superficial structures.
The baseline and recovered temperatures were similar in all four subjects before and after the mild cold stress (27.6 ± 0.5 °C and 27.2 ± 0.3°C, respectively). In three of the subjects, the temperature drop weakly correlated with an oxy-hemoglobin reduction (R = 0.55, 0.57 and 0.39, respectively in A, C and D). Oxy-hemoglobin changes are closely related to variations in blood delivery. Thus, the observed deep tissue temperature reductions during the cold stress may be accompanied by a decrease in vascular perfusion. In all subjects, the magnitude of the deoxy-hemoglobin change was smaller than the oxy-hemoglobin reduction (25.4 ± 8.7% compared to 52.9 ± 11.7%) suggesting that the rate of tissue oxygen utilization also decreases during cold stress although not much as the blood supply. During recovery, the deoxy- and oxy-hemoglobin concentration increased 36.9 ± 7.9% and 50.3 ± 15.8%, respectively, indicating re-perfusion and slightly increased metabolism.
In conclusion, we have developed a non-invasive optical method for absolute temperature measurements in thick tissues based on resolving opposing effects of water vibrational frequency shifts due to macromolecular binding. Unlike most reflectance methods for assessing temperature, this model-based approach accounts for thermally induced changes in light scattering and is essentially independent of denaturation of the test material. In tissue simulating intralipid phantoms, the difference between optical and conventional thermistor measurements was ~1 °C and no hysteresis was observed between heating and cooling. In in vivo tissue measurements, temperature and hemodynamic variations were measured simultaneously in response to a mild cold stress. Because temperature, hemodynamic and metabolic parameters are co-localized, this non-invasive technique could potentially be employed to optimize dosimetry during thermotherapies and enhance the information content of metabolic diagnostics such as cold stress. In addition, because DOS is compatible with diffuse optical tomography (DOT), this technique could lead to the development of new thermal contrast elements for thick tissue functional tomography.
Acknowledgments
This work was supported by the National Institutes of Health under grants P41-RR01192 (Laser Microbeam and Medical Program: LAMMP), U54-CA105480 and U54CA136400 (Network for Translational Research in Optical Imaging: NTROI), the Chao Family Comprehensive Cancer Center (P30-CA62203) and Chancellor’s Club for Excellence Fellowship of UC Irvine. Programmatic support was provided by the Beckman Foundation and the Medical Free Electron Laser program (MFEL). The authors thank Tim Quang and Kia Koko for assistance with measurement.
References
- Bayly JG, Kartha VB, Stevens WH. The absorption spectra of liquid phase H2O, Hdo and D2O from 0.7 μm to 10 μm. Infrared Phys. 1963;3:211–22. [Google Scholar]
- Belashev BZ, Ternovoi AN. Effect of optical temperature hysteresis. J Appl Spectrosc. 1996;63:573–6. [Google Scholar]
- Bevilacqua F, Berger AJ, Cerussi AE, Jakubowski D, Tromberg BJ. Broadband absorption spectroscopy in turbid media by combined frequency-domain and steady-state methods. Appl Opt. 2000;39:6498–507. doi: 10.1364/ao.39.006498. [DOI] [PubMed] [Google Scholar]
- Buijs K, Choppin GR. Near-infrared studies of structure of water.1. Pure water. J Chem Phys. 1963;39:2035–41. [Google Scholar]
- Cerussi A, Hsiang D, Shah N, Mehta R, Durkin A, Butler J, Tromberg BJ. Predicting response to breast cancer neoadjuvant chemotherapy using diffuse optical spectroscopy. Proc Natl Acad Sci USA. 2007;104:4014–9. doi: 10.1073/pnas.0611058104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cerussi A, Shah N, Hsiang D, Durkin A, Butler J, Tromberg BJ. In vivo absorption, scattering, and physiologic properties of 58 malignant breast tumors determined by broadband diffuse optical spectroscopy. J Biomed Opt. 2006;11:044005. doi: 10.1117/1.2337546. [DOI] [PubMed] [Google Scholar]
- Cerussi AE, Jakubowski D, Shah N, Bevilacqua F, Lanning R, Berger AJ, Hsiang D, Butler J, Holcombe RF, Tromberg BJ. Spectroscopy enhances the information content of optical mammography. J Biomed Opt. 2002;7:60–71. doi: 10.1117/1.1427050. [DOI] [PubMed] [Google Scholar]
- Chung SH, Cerussi AE, Klifa C, Baek HM, Birgul O, Gulsen G, Merritt SI, Hsiang D, Tromberg BJ. In vivo water state measurements in breast cancer using broadband diffuse optical spectroscopy. Phys Med Biol. 2008;53:6713–27. doi: 10.1088/0031-9155/53/23/005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins JR. Change in the infra-red absorption spectrum of water with temperature. Phys Rev. 1925;26:0771–9. [Google Scholar]
- Cubeddu R, D’Andrea C, Pifferi A, Taroni P, Torricelli A, Valentini G. Effects of the menstrual cycle on the red and near-infrared optical properties of the human breast. Photochem Photobiol. 2000;72:383–91. [PubMed] [Google Scholar]
- Ducharme MB, Tikuisis P. Forearm temperature profile during the transient phase of thermal-stress. Eur J Appl Physiol Occup Physiol. 1992;64:395–401. doi: 10.1007/BF00625057. [DOI] [PubMed] [Google Scholar]
- Ducharme MB, Vanhelder WP, Radomski MW. Cyclic intramuscular temperature-fluctuations in the human forearm during cold-water immersion. Eur J Appl Physiol Occup Physiol. 1991;63:188–93. doi: 10.1007/BF00233846. [DOI] [PubMed] [Google Scholar]
- Fishkin JB, Fantini S, VandeVen MJ, Gratton E. Gigahertz photon density waves in a turbid medium: theory and experiments. Phys Rev E. 1996;53:2307–19. doi: 10.1103/physreve.53.2307. [DOI] [PubMed] [Google Scholar]
- Fishkin JB, Gratton E. Propagation of photon-density waves in strongly scattering media containing an absorbing semi-infinite plane bounded by a straight edge. J Opt Soc Am A. 1993;10:127–40. doi: 10.1364/josaa.10.000127. [DOI] [PubMed] [Google Scholar]
- Haskell RC, Svaasand LO, Tsay TT, Feng TC, Mcadams MS. Boundary conditions for the diffusion equation in radiative transfer. J Opt Soc Am A. 1994;11:2727–41. doi: 10.1364/josaa.11.002727. [DOI] [PubMed] [Google Scholar]
- Hollis VS. PhDThesis. University College; London: 2002. Non-invasive monitoring of brain tissue temperature by near-infrared spectroscopy. [Google Scholar]
- Jakubowski D, Bevilaqua F, Merritt S, Cerussi A, Tromberg BJ. In: Biomedical Optical Imaging. Fujimoto JG, Farkas DL, editors. New York: Oxford University Press; 2009. pp. 330–55. [Google Scholar]
- Kakuta N, Arimoto H, Momoki H, Li FG, Yamada Y. Temperature measurements of turbid aqueous solutions using near-infrared spectroscopy. Appl Opt. 2008;47:2227–33. doi: 10.1364/ao.47.002227. [DOI] [PubMed] [Google Scholar]
- Kelly JJ, Kelly KA, Barlow CH. Tissue temperature by near-infrared spectroscopy. Proc SPIE. 1995;2389:818–28. [Google Scholar]
- Kim JH, Hahn EW. Clinical and biological studies of localized hyperthermia. Cancer Res. 1979;39:2258–61. [PubMed] [Google Scholar]
- Libnau FO, Kvalheim OM, Christy AA, Toft J. Spectra of water in the nearinfrared and midinfrared region. Vib Spectrosc. 1994;7:243–54. [Google Scholar]
- Mccabe WC, Subraman S, Fisher HF. Near-infrared spectroscopic investigation of effect of temperature on structure of water. J Phys Chem. 1970;74:4360–9. [Google Scholar]
- Merritt SI. PhDThesis. University of California; Irvine: 2005. Combination of broadband diffuse optical spectroscopy with magnetic resonance imaging. [Google Scholar]
- Montgomery LD, Williams BA. Effect of ambient-temperature on thermal profile of human forearm, hand, and fingers. Ann Biomed Eng. 1976;4:209–19. doi: 10.1007/BF02584515. [DOI] [PubMed] [Google Scholar]
- Otal EH, Inon FA, Andrade FJ. Monitoring the temperature of dilute aqueous solutions using near-infrared water absorption. Appl Spectrosc. 2003;57:661–6. doi: 10.1366/000370203322005355. [DOI] [PubMed] [Google Scholar]
- Pimentel GC, McClellan AL. The Hydrogen Bond. San Francisco, CA: Freeman; 1960. [Google Scholar]
- Pogue BW, Jiang SD, Dehghani H, Kogel C, Soho S, Srinivasan S, Song XM, Tosteson TD, Poplack SP, Paulsen KD. Characterization of hemoglobin, water, and NIR scattering in breast tissue: analysis of intersubject variability and menstrual cycle changes. J Biomed Opt. 2004;9:541–52. doi: 10.1117/1.1691028. [DOI] [PubMed] [Google Scholar]
- Quaresima V, Matcher SJ, Ferrari M. Identification and quantification of intrinsic optical contrast for near-infrared mammography. Photochem Photobiol. 1998;67:4–14. [PubMed] [Google Scholar]
- Rieke V, Pauly KB. MR thermometry. J Magn Reson Imaging. 2008;27:376–90. doi: 10.1002/jmri.21265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seegenschmiedt MH, Fessenden P, Vernon CC. Thermo-radiotherapy and Thermo-chemotherapy. Vol. 1. Berlin: Springer; 1995. [Google Scholar]
- Thomsen S. Pathological analysis of photothermal and photomechanical effects of laser–tissue interactions. Photochem Photobiol. 1991;53:825–35. doi: 10.1111/j.1751-1097.1991.tb09897.x. [DOI] [PubMed] [Google Scholar]
- Tromberg BJ, Svaasand LO, Tsay TT, Haskell RC. Properties of photon density waves in multiple-scattering media. Appl Opt. 1993;32:607–16. doi: 10.1364/AO.32.000607. [DOI] [PubMed] [Google Scholar]
- van Veen RLP, et al. Determination of visible near-IR absorption coefficients of mammalian fat using time- and spatially resolved diffuse reflectance and transmission spectroscopy. J Biomed Opt. 2005;10:054004. doi: 10.1117/1.2085149. [DOI] [PubMed] [Google Scholar]
- Vargas HI, Dooley WC, Gardner RA, Gonzalez KD, Venegas R, Heywang-Kobrunner SH, Fenn AJ. Focused microwave phased array thermotherapy for ablation of early-stage breast cancer: results of thermal dose escalation. Ann Surgical Oncol. 2004;11:139–46. doi: 10.1245/aso.2004.03.059. [DOI] [PubMed] [Google Scholar]
- Walrafen GE. Raman spectral studies of effects of temperature on water structure. J Chem Phys. 1967;47:114–26. [Google Scholar]
- Zijlistra WG, et al. Visible and Near Infrared Absorption Spectra of Human and Animal Haemoglobin: Determination and Application. Utrecht: VSP; 2000. [Google Scholar]