Imaged based estimation of food volume using circular referents in dietary assessment

Abstract

Measuring food volume (portion size) is a critical component in both clinical and research dietary studies. With the wide availability of cell phones and other camera-ready mobile devices, food pictures can be taken, stored or transmitted easily to form an image based dietary record. Although this record enables a more accurate dietary recall, a digital image of food usually cannot be used to estimate portion size directly due to the lack of information about the scale and orientation of the food within the image. The objective of this study is to investigate two novel approaches to provide the missing information, enabling food volume estimation from a single image. Both approaches are based on an elliptical reference pattern, such as the image of a circular pattern (e.g., circular plate) or a projected elliptical spotlight. Using this reference pattern and image processing techniques, the location and orientation of food objects and their volumes are calculated. Experiments were performed to validate our methods using a variety of objects, including regularly shaped objects and food samples.

1. Introduction

Accurate dietary assessment is an important procedure in both clinical and research studies of many diseases and disorders, such as obesity and diabetes (Franz et al., 2002; Mokdad et al., 2004; Knowler et al., 2009; Thompson and Subar, 2001). However, a major problem exists: the assessment is often inaccurate for individuals in a real life setting (Thompson and Subar, 2001; Wacholder, 1995; Trabulsi and Schoeller, 2001; Johansson et al., 1998). The self-reporting of food intake (e.g., food record, 24-h dietary recall and food frequency questionnaire) has been the primary method for acquiring information about consumed food and the portion size (Thompson and Subar, 2001; Wacholder, 1995; Trabulsi and Schoeller, 2001; Johansson et al., 1998; Goris and Westerterp, 1999; Goris et al., 2000; Most et al., 2003; Pietinen et al.,1988a,b; Chu et al., 1984; Martin et al., 2007). However, self-report methods are known to be biased, due to significant underreporting (Trabulsi and Schoeller, 2001; Johansson et al., 1998; Goris and Westerterp, 1999; Goris et al., 2000). In order to improve assessment accuracy, many portion-size measurement aids (PSMAs) have been developed (Posner et al., 1992; Faggiano et al., 1992; Kuehneman et al., 1994; Nelson et al., 1994; Lucas et al., 1995; Cypel et al., 1997; Godwin et al., 2006; Nelson and Haraldsdottir, 1998; Frobisher and Maxwell, 2003; Williamson et al., 2003; Turconi et al., 2005; Ershow et al., 2007; Foster et al., 2005; Martin et al., 2009). Common PSMAs include household measures (e.g., rulers), food models (real food samples or abstract models), and food photographs. While such PSMAs are useful in estimating portion size, they provide only a rough volumetric measure and are not always suitable or convenient in practice. Recently, camera-enabled cell phones and other mobile devices (e.g., iPad) have become very popular. These devices can be used to take food pictures conveniently, which can then be remotely transmitted to dietitians for dietary analysis (Kikunaga et al., 2007; Boushey et al., 2009; Zhu et al., 2010; Ngo et al., 2009).

Although digital images provide an excellent tool to document foods consumed, it is difficult to estimate food portion size from a single image without a dimensional referent, except in special cases (Du and Sun, 2006; Wang and Nguang, 2007). Accordingly, several approaches have been studied that include a dimensional referent in the field of view, such as a checkerboard (Boushey et al., 2009; Zhu et al., 2010; Subar et al., 2010; Sun et al., 2008, 2010a,b; Jia et al., 2009; Yue et al., 2010). However, it can be inconvenient and annoying for subjects constantly to have to remember to carry a checkerboard, and to place it beside the food when eating (Boushey et al., 2009; Zhu et al., 2010; Subar et al., 2010). Further, eating behavior changes when subjects are asked to document food intake. For example, they may reduce intake significantly, an effect frequently observed in obese subjects (Goris and Westerterp, 1999; Goris et al., 2000). In order to obtain objective data on food intake, we have developed a low-cost electronic device containing a miniature camera and a number of other sensors to record food intake automatically (Sun et al., 2008, 2009, 2010a,b). This device is designed to be almost completely passive to the subject, and thus hopefully not intrude on or alter the subject’s eating activities. This button-like device can be worn using a lanyard around the neck or attached to clothes using a pin or a pair of magnets (see Fig. 1). When utilized, it takes pictures of the scene in front of the subject at a pre-set rate (e.g., 2–4 s/frame). All the images are stored on a memory card. After the dietary study is complete (e.g., 1 week), the data are transferred to the dietitian’s computer for further analysis. Since images of the entire eating period are recorded (see Fig. 2), a pair of images can always be selected to represent each food item before and after eating (Fig. 2(a) and (d)). Once each food item is identified by the dietitian and its consumed volume is determined from the “before” and “after” images, our software system calculates calorie and nutrient values for each food using data available from the United States Department of Agriculture (USDA) Food and Nutrient Database for Dietary Studies (FNDDS) database (USDA, 2010). The energy intake during the study period can be accumulated and a detailed report on calorie and nutrient intake created for dietary assessment.

Fig. 1.

(a) Subject wearing the device; (b) electronic circuit board within the device.

Fig. 2.

Typical pictures before (a), during (b–c) and after eating (d).

In FNDDS, the conversion between measurable/observable volumes (e.g., cup, cubic inch, piece, slice, large/medium/small) and weight is available for most foods, such as cheeses, breads, vegetables and meats. For example, the weights of one cubic inch cheese and a cup of stewed pork chop are 17.3 and 134 g, respectively. Therefore the energy and nutrient contents of a specific food can be estimated based on its volume, as calculated from an image. In the current version of the FNDDS database, certain foods are listed without volumetric measures. In order to solve this problem, several research groups, including us, have been collaborating with USDA to conduct research on food density measures.

In the current study, we focus on image-based food volume estimation and present two novel methods for calculating food volume from a single image. Previous studies have shown that, under certain conditions, the elliptical image of a known circular object can provide sufficient information about the location and orientation of any planar object (Shin and Ahmad, 1989; Safaee-Rad et al., 1992). In our study, we have proposed two types of approaches based on the elliptical patterns extracted from a single input image (Jia et al., 2009; Yue et al., 2010). The first type is based on a circular object (e.g., a circular plate) which is commonly present during eating. We call the corresponding portion size estimation method the “plate method”. The second type is based on a conic spotlight projected by a light emitting diode (LED) installed on our wearable electronic device. We call this method the “LED method”. In either method, we first determine the location and orientation of an object plane by interactive elliptical pattern extraction and computation using our algorithms. Then, dimensional variables (e.g., length and thickness) are measured by selecting several feature points on the food image. The measured dimensions provide an estimate of food volume. In the following, we will describe our methods in detail and discuss our experimental results.

2. Methods

We model the camera using the pinhole model which is commonly utilized in photography (Sonka et al., 2007; Hartley and Zisserman, 2003). For simplicity, we assume that the camera has a fixed focal length, which is true in our wearable device and most cell phones; and that the physical image plane of the camera is perpendicular to its optical axis, which is almost universally true. Under these assumptions, the intrinsic parameters of the camera (e.g., the focal length) can be obtained either from manufacturer’s specifications or using a standard calibration procedure (Tsai, 1987). Based on the intrinsic parameters, the indices of each pixel in the digital image can be converted to the real-world coordinates in the image plane (Hartley and Zisserman, 2003; Sonka et al., 2007). For simplicity, we use the term “image” to refer to the image on the physical image plane. According to these assumptions, the relationship between the object plane (e.g., a table surface) and the image plane can be obtained by means of a perspective projection model. We describe this model with respect to the plate and LED methods separately in the following two sections.

2.1. Object location and orientation using the plate method

We first assume that the food item to be estimated is on an object plane in front of the subject, as in most dining environments. We further assume that the camera can be posed arbitrarily towards the food. The relationship between a circular object (e.g., dinning plate) on the object plane and its image is illustrated in Fig. 3(a).

Fig. 3.

Geometric model of the system and schematic diagrams of cone transformation. (a) Perspective relationship between circular object and its image: Origin O is the optical center of the camera and xyz defines the real word coordinate system where z is perpendicular to the image plane. (b) New coordinate system XYZ after applying cone transformation T: in this system, the cone is centralized. (c) New coordinate system X′Y′Z′ after applying another cone transformation: in this system, the object plane is parallel to the X′OY′ plane.

In this model, the image of a circular object becomes an ellipse/circle in the image plane under the pinhole model assumption. The equation of the ellipse is given by

$$a\prime x^2+2h\prime \mathit{\text{xy}}+b\prime y^2+2g\prime x+2f\prime y+d\prime =0.$$ (1)

Eq. (1) is known after fitting the boundary of the circle in the digital image. This boundary defines the base of a quadric cone. The equation of the cone in the three-dimensional coordinate system defined in Fig. 3(a) can be formulated in the following quadratic surface function (Safaee-Rad et al., 1992):

$$a\prime f^2{x}^2+2h\prime f^2\mathit{\text{xy}}+b\prime f^2{y}^2+2g\prime \mathit{\text{fxz}}+2f\prime \mathit{\text{fyz}}+d\prime z^2=0$$ (2)

where f is the focal length of the camera.

The object plane can be defined as:

$$\mathit{\text{lx}}+\mathit{\text{my}}+\mathit{\text{nz}}=\mathit{\text{constant}}$$ (3)

where (l, m, n) represents the norm of the plane with l² + m² + n² = 1. The intersection between the quadric cone and the object plane represents the boundary of the circular object. In order to simplify the expressions for (l, m, n), two cone transformations are utilized to centralize the quadric cone and then make the object plane parallel to the X′O′Y′ plane, see Fig. 3(b) and (c). After applying these transformations, the values of l, m, and n can be determined analytically (Safaee-Rad et al., 1992). Although there are four symmetrical solutions with respect to the origin of XYZ frame (Fig. 3(b)), it can be uniquely determined in our practical case since the wearable camera always takes pictures when the wearer is beside the food.

Under these given conditions, it has been shown (Safaee-Rad et al., 1992) that the solutions of l, m, n are:

$$[\begin{array}{ccc}\hfill l\hfill & \hfill m\hfill & \hfill n\hfill \end{array}]\prime =\mathbf{T}·[\begin{array}{ccc}\hfill L\hfill & \hfill M\hfill & \hfill N\hfill \end{array}]\prime$$ (4)

where L = 0, $M=\sqrt{\frac{{\lambda }_2-{\lambda }_1}{{\lambda }_2-{\lambda }_3}},N=\sqrt{\frac{{\lambda }_1-{\lambda }_3}{{\lambda }_2-{\lambda }_3}}$, λ₁, λ₂, λ₃ are the eigen values of matrix $\mathbf{Q}=\left[\begin{array}{ccc}\hfill a\prime f^2\hfill & \hfill h\prime f^2\hfill & \hfill g\prime f\hfill \\ \hfill h\prime f^2\hfill & \hfill b\prime f^2\hfill & \hfill f\prime f\hfill \\ \hfill g\prime f\hfill & \hfill f\prime f\hfill & \hfill d\prime \hfill \end{array}\right]\text{ and }\mathbf{T}=\left[\begin{array}{ccc}\hfill l_1\hfill & \hfill l_2\hfill & \hfill l_3\hfill \\ \hfill m_1\hfill & \hfill m_2\hfill & \hfill m_3\hfill \\ \hfill n_1\hfill & \hfill n_2\hfill & \hfill n_3\hfill \end{array}\right]·\left[\begin{array}{c}\hfill l_i\hfill \\ \hfill m_i\hfill \\ \hfill n_i\hfill \end{array}\right]$ are the three eigen vectors corresponding to the eigen values λ_i of Q in Eq. (3), i = 1, 2, 3.

Although the orientation of the object has been obtained, its location is still non-unique because parallel intersection planes of a conicoid are all similar (Bell, 1944), producing the same image on the image plane. However, if the size of the circular object is known, its location can be uniquely determined according to the geometry of perspective projection. For convenience, we apply another coordinate transformation, the equation of the intersection plane in the new coordinate system X′Y′Z′ becomes Z′ = p, see Fig. 3(c). Then, the vertical distance p between the origin O and the object plane is given by (Safaee-Rad et al., 1992):

$$p=\frac{C_{1}r}{\sqrt{C_2^2+C_3^2-C_1{C}_4}}$$ (5)

here r is the radius of the plate which must be provided, and C₁–C₄ are parameters calculated from the cone transformation:

$$\begin{array}{c}{C}_1={\lambda }_1{l}_1^2+{\lambda }_2{l}_2^2+{\lambda }_3{l}_3^2\hfill \\ C_2={\lambda }_1{l}_1{n}_1+{\lambda }_2{l}_2{n}_2+{\lambda }_3{l}_3{n}_3\hfill \\ C_3={\lambda }_1{m}_1{n}_1+{\lambda }_2{m}_2{n}_2+{\lambda }_3{m}_3{n}_3\hfill \\ C_4={\lambda }_1{n}_1^2+{\lambda }_2{n}_2^2+{\lambda }_2{n}_3^2\hfill \end{array}$$ (6)

2.2. Object location and orientation using the LED method

In this method, a narrow beam LED is positioned at the wearable device in a small distance from the camera. When the picture is taken, the LED produces a 16° conic spotlight into the field of view. The LED light can be either visible or invisible to the human eye, but must be visible to the camera. The LED light is selected carefully so that the spotlight in the cross-section perpendicular to the axis of the beam is as circular as possible.

In order to simplify the mathematic model of the measurement system using the LED as a referent, we assume that the optical axes of the camera and the light beam are in the same plane and parallel to each other. This assumption can be satisfied by carefully calibrating the wearable device. The resulting model is shown in Fig. 4. O and D are the optical centers of the camera lens and the LED, respectively, and β is the falloff angle of the LED cone. The spotlight is on the intersection plane between the camera and the LED cones.

Fig. 4.

Geometric model of measurement system using an LED: O and D are optical centers of the camera lens and LED, respectively, and β is the falloff angle of the LED cone. The elliptical spotlight is on the intersection plane (object plane) between the camera cone and the LED cones.

In this model, the equation of the camera cone in the coordinate system xyz can be derived in a similar way as that in Eq. (2), which can be written in the matrix form:

$$[\begin{array}{cccc}\hfill x\hfill & \hfill y\hfill & \hfill z\hfill & \hfill 1\hfill \end{array}]·{\mathbf{Q}}_{\mathbf{1}}·\left[\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \\ \hfill z\hfill \\ \hfill 1\hfill \end{array}\right]=0,\text{ where }{\mathbf{Q}}_{\mathbf{1}}=\left[\begin{array}{cccc}\hfill a\prime f^2\hfill & \hfill h\prime f^2\hfill & \hfill g\prime f\hfill & \hfill 0\hfill \\ \hfill h\prime f^2\hfill & \hfill b\prime f^2\hfill & \hfill f\prime f\hfill & \hfill 0\hfill \\ \hfill g\prime f\hfill & \hfill f\prime f\hfill & \hfill d\prime \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]$$ (7)

The norm of and z-distance of the object plane are, respectively, (l, m, n) and d₀ (see Fig. 4). Because (0, 0, d₀) is on the object plane, the plane equation is given by

$$\mathit{\text{lx}}+\mathit{\text{my}}+\mathit{\text{nz}}={\mathit{\text{nd}}}_0$$ (8)

$$\text{where }{l}^2+m^2+n^2=1.$$ (9)

In order to ease mathematical treatment, the following rotational transformation is applied (Safaee-Rad et al., 1992)

$$\begin{array}{c}\left[\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \\ \hfill z\hfill \\ \hfill 1\hfill \end{array}\right]=\mathbf{T}·\left[\begin{array}{c}\hfill x\prime \hfill \\ \hfill y\prime \hfill \\ \hfill z\prime \hfill \\ \hfill 1\hfill \end{array}\right],\text{ where}\hfill \\ \mathbf{T}=\left[\begin{array}{cccc}\hfill -\frac{m}{\sqrt{l^2+m^2}}\hfill & \hfill -\frac{\mathit{\text{nl}}}{\sqrt{l^2+m^2}}\hfill & \hfill l\hfill & \hfill 0\hfill \\ \hfill \frac{l}{\sqrt{l^2+m^2}}\hfill & \hfill -\frac{\mathit{\text{mn}}}{\sqrt{l^2+m^2}}\hfill & \hfill m\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sqrt{l^2+m^2}\hfill & \hfill n\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right],l\ne 0,m\ne 0.\hfill \end{array}$$ (10)

If l = m = 0, the object plane is perpendicular to the optical axis of the camera. In this case, it can be derived easily that the image of the spotlight is still a circle and the distance d₀ can be uniquely determined by the position of the circle in the image. The further the distance is, the closer the circle is to the center of the image.

Substituting (10) into (7) yields

$$[\begin{array}{cccc}\hfill x\prime \hfill & \hfill y\prime \hfill & \hfill z\prime \hfill & \hfill 1\hfill \end{array}]·\mathbf{T}\mathbf{\prime }·{\mathbf{Q}}_{\mathbf{1}}·\mathbf{T}·\left[\begin{array}{c}\hfill x\prime \hfill \\ \hfill y\prime \hfill \\ \hfill z\prime \hfill \\ \hfill 1\hfill \end{array}\right]=0$$ (11)

Under the new x′y′z′ coordinate systems, the object plane equation becomes

$$z\prime ={\mathit{\text{nd}}}_0$$ (12)

Substituting Eq. (12) into Eq. (11), we can obtain the equation of the elliptical spotlight on the object plane as the intersection between the object plane and the camera cone:

$$[\begin{array}{cccc}\hfill x\prime \hfill & \hfill y\prime \hfill & \hfill {\mathit{\text{nd}}}_0\hfill & \hfill 1\hfill \end{array}]·\mathbf{T}\prime ·{\mathbf{Q}}_{\mathbf{1}}·\mathbf{T}·\left[\begin{array}{c}\hfill x\prime \hfill \\ \hfill y\prime \hfill \\ \hfill {\mathit{\text{nd}}}_0\hfill \\ \hfill 1\hfill \end{array}\right]=0$$ (13)

Eq. (13) can be written in the form of a quadratic equation (detailed coefficients are listed in Appendix A):

$$x{\prime }^2+h_{1}x\prime y\prime +b_{1}y{\prime }^2+g_{1}x\prime +f_{1}y\prime +d_1=0$$ (14)

Besides the camera cone, there is another cone, called LED cone, in this model. The equation of the LED cone in the original coordinate system xyz can be derived easily:

$${(x-d)}^2+y^2-{\mathit{\text{tg}}}^2\beta ·z^2=0$$ (15)

Following the same procedure as Eqs. (7)–(13), the equation describing the intersection between the LED cone and the object plane with respect to the x′y′z′ coordinate system is given by

$$[\begin{array}{cccc}\hfill x\prime \hfill & \hfill y\prime \hfill & \hfill {\mathit{\text{nd}}}_0\hfill & \hfill 1\hfill \end{array}]·\mathbf{T}\prime ·{\mathbf{Q}}_{\mathbf{2}}·\mathbf{T}·\left[\begin{array}{c}\hfill x\prime \hfill \\ \hfill y\prime \hfill \\ \hfill {\mathit{\text{nd}}}_0\hfill \\ \hfill 1\hfill \end{array}\right]=0$$ (16)

$$\text{with }{\mathbf{Q}}_{\mathbf{2}}=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -d\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -{\mathit{\text{tg}}}^2\beta \hfill & \hfill 0\hfill \\ \hfill -d\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill d^2\hfill \end{array}\right].$$

This equation can be written as (see Appendix A for details)

$$x{\prime }^2+h_{2}x\prime y\prime +b_{2}y{\prime }^2+g_{2}x\prime +f_{2}y\prime +d_2=0$$ (17)

Since (14) and (17) represent the same ellipse on the object plane (see Fig. 4), the coefficients in these two equations should be the same, resulting in five equations, see Appendix A. We can solve these equations to obtain the information about the location and orientation of the object plane through iterative methods (Martinez, 1991) or optimization methods (Grosan and Abraham, 2008). However, it is generally very hard to obtain an analytical solution. Here we only consider a particular case where the plate is placed on a leveled surface, which is simple but common in our application. Let the relative rotation angle between camera and table be only in one direction. Under these assumptions, we define the sharp angle between the object plane and the optical axis of the camera to be θ. Then, the equations can be simplified and solved as (Appendix A):

$$d_0=\frac{\mathit{\text{fb}}\prime d}{(b\prime -a\prime )f·\mathit{\text{tg}}\theta +g\prime }$$ (18)

$$\theta =\mathit{\text{arctg }}\left(\frac{g\prime -\sqrt{{(g\prime )}^2-(a\prime -b\prime )(d\prime +{\mathit{\text{tg}}}^2\beta b\prime f^2)}}{(a\prime -b\prime )f}\right)\theta \in (0,\frac{\pi }{2})$$ (19)

The normalized orientation vector of the object plane is given by:

$$\{\begin{array}{c}l=\text{cos }\theta \hfill \\ m=0\hfill \\ n=\text{sin }\theta \hfill \end{array}$$ (20)

And the distance p between the origin O and the object plane is

$$p=d_0\text{ sin }\theta$$ (21)

2.3. Food volume estimation

In order to estimate the volume of food which can be determined using several dimensional measurements (e.g., length, width, height, and/or diameter), we must derive expressions for the distance of two arbitrary points that are either parallel to the object plane or perpendicular to it.

Fig. 5 shows the scheme of calculating the length DE which is on the object plane and the height FE which is perpendicular to the object plane. In Fig. 5(a), line AB is the perspective projection of DE in the observed image. We then define BC as a supplementary line which is parallel to DE in the plane ODE. For convenience, we represent A and B in the transformed X′Y′Z′ coordinate system specified by Eq. (10). Since, in this system, point C has the same coordinate value as the point B in the Z′-direction, and C is on the same line of OA whose equation is known, so |BC| can be calculated. With the known value of |BC|, length |DE| can be calculated from $|\mathit{\text{BC}}|/|\mathit{\text{DE}}|=z_1^{\prime }/p,\text{ where }{z}_1^{\prime }$ represents the Z′ coordinate of points B and C, and p is given by Eq. (5) or Eq. (21).

Fig. 5.

Schematic representation of length (left panel) and height (right panel) measurements.

The height FE can be derived in a very similar way, as shown in Fig. 5(b). Line EF is perpendicular to the plate plane with points E and F being on and off the plane, respectively. Let line HG be perspective projection of FE in the observed image. Draw a line GI parallel to EF and intersects line OF at point I. Since point H, G and line OH are known, |GI| is determined. Because ΔOIG and ΔOFE are similar, $|\mathit{\text{GI}}|/|\mathit{\text{EF}}|=z_2^{\prime }/p,\text{ where }{z}_2^{\prime }$ represent the Z coordinate of point G under X′Y′Z′. Thus, length |EF| is fully determined.

3. Experimental results

3.1. Experiment setup

We have conducted experiments to validate the feasibility of our food volume measurement methods. Four regularly shaped objects and six food replicas (Nasco, Fort Atkinson, Wisconsin) were utilized in our experiments (Fig. 6). The regularly shaped objects included a LEGO block, a small clip box, a large clip box and a golf ball. The food replicas included a piece of cornbread, a thin slice of onion, a whole hamburger, a glass of juice, a peach and an orange which were all realistically shaped and colored. These replicas represent three common shapes – prism, cylinder, cone and sphere. The ground truth for regular-shaped objects was measured by a micrometer. Since the volume of food replica provided by the manufacture is not accurate, the true volumes were the average over three measurements using the water displacement method. Each food replica was then modeled by a simple geometry shape, e.g., the cornbread was modeled by a prism with squared bottom, and the hamburger/onion was modeled by a cylinder. Under this assumption, the height of the food replica, except onion, was measured by a micrometer. The other dimensional information (length/radius) was then derived from the geometry model. For onion, the radius was measured while the height was derived because the top surface of the onion was not flat and not exactly parallel to the bottom. The radius peach/orange is calculated from the volume assuming its shape is a perfect sphere.

Fig. 6.

Samples used in experiment.

In order to achieve comparable data, our prototype device with a camera and an LED referent was fixed above a table and faced toward the sample (e.g., a block) on the table. Each sample was placed in four fixed locations on the table and one picture was taken for each location (see Fig. 7 for typical pictures). In this experiment, since the camera was fixed during the experiment, the LED spotlight was projected only once. In order to obtain a clear spotlight, white copy paper was placed on the table. Then, the location and orientation of the table was calculated and utilized to compute the volume of each sample. Circles printed on a paper were utilized as plates, making it easier to place different samples in the same location. The deformation of the big circles (16 cm in diameter) around the sample was utilized to estimate the food volume.

Fig. 7.

Each object (here a piece of cornbread) placed at four different locations (L1–L4) where the circular patterns represent hypothetical plates.

3.2. Determination of the object’s location and orientation

In our algorithm, the fitted parameter of the elliptical feature determines the location and orientation of the object plane. Currently these parameters are estimated by fitting eight manually-selected points on the border of the circular pattern or LED light pattern. The inaccuracy in the selection of points causes a certain error in the estimation of location and orientation. Since the boundary of the LED light pattern has a diffused region, ellipse fitting is not exact (see the left panel in Fig. 8). Thus, the variance in the estimated location and orientation from the 10 fitting results of the boundary points is larger for the LED method (see Table 1). In particular, the measured variance in the estimated angles was 1.8° for the LED method, while less than 0.3° for the plate method. Therefore, in the LED method, we used averaged location and orientation to compute food volume. In the plate method, only one fitting was required because the boundary was clear.

Fig. 8.

Ten fitting results for the LED spotlight (a) and plate (b). Only part of the image with the reference is shown.

Table 1.

Averaged location and orientation estimates of the object plane from 10 fitting results for the LED spotlight and circle patterns at four different locations.

	LED	Plate (L1)	Plate (L2)	Plate (L3)	Plate (L4)
Location (mm)	434.0 ± 4.3	−26.2 ± 3.1	42.3 ± 2.2	8.8 ± 2.2	−5.1 ± 1.7
	157.3 ± 0.6	−159.3 ± 1.3	−15.1 ± 0.8	−14.1 ± 0.7
	556.4 ± 1.8	572.2 ± 2.7	428.1 ± 1.2	409.1 ± 1.5
Orientation (°)	46.24 ± 1.80	0.90 ± 0.25	0.61 ± 0.18	0.35 ± 0.25	0.07 ± 0.23
	40.30 ± 0.27	40.16 ± 0.19	40.04 ± 0.13	40.78 ± 0.23
	40.7 ± 0.26	40.86 ± 0.19	41.00 ± 0.13	40.24 ± 0.23

3.3. Results of volume estimation

From each picture, we estimated the volume of the object using the following steps. First, a number of points were selected on the observed boundary of the circular pattern. Then, the best-fit ellipse was computed using the least-square algorithm based on the selected points to determine the location and orientation of the circular pattern. Next, a food model was selected for the object (e.g., a sphere model for an orange or a prism model for a piece of cornbread) and a number of point pairs that measure the length, width, height, and/or diameter of the object in the picture were manually selected at appropriate locations. Then, these dimensional measures in pixel units were automatically converted to real-world measures in the millimeter unit. Finally, the volume of the object was computed using the location and orientation calculated either from the LED reference or from the circular reference. Following this procedure, we were able to compare the difference between two references because all other factors were constant.

In order to quantify the measurement error, the Root Mean Square Error (RMSE) was used in this study. The RMSE was defined as, $\text{RMSE}=\sqrt{\frac{1}{n}{\displaystyle {\sum }_{j=1}^n}{\left(\frac{{\mathrm{V̂}}_j-V}{V}\right)}^2}\times 100\%$ where V̂_j is the estimated value, V is the ground truth and n is the number of images. The volumetric estimates of all test objects are shown in Fig. 9. The averaged RMSE values of the volumetric measures of all 10 samples were 12.01% and 29.01% for plate and LED methods, respectively. It can be seen that, in general, the estimated volume using the plate method was more accurate than the LED method.

Fig. 9.

Comparison of volume estimation using circular plate and LED methods.

The estimated results of dimensions (length, width, height, radius) are illustrated in Fig. 10. Most of the RMSE values in the dimensional estimates were below 10%. Larger errors were mainly in the height or diameter estimates. These indicated a practical difficulty since, usually, the height or diameter/radius cannot be well defined for foods without corners/edges or with only round edges, such as a hamburger, a peach or an orange. In the extreme case of onion slice, the estimated errors of the radius and height were both above 10%, but the error in volume estimation using the plate method was only 4.3%. The reason was found to be the over-estimation in radius and under-estimation in height.

Fig. 10.

Comparison of dimensional estimation using circular plate and LED methods.

In order to further improve estimation accuracy, it became necessary to explore the factors affecting the measurement results. In the following, we investigated two major factors using the plate method.

3.3.1. The sensitivity of volume estimation to object size

The picture of a LEGO block was further studied to test whether the estimation of a larger object leads to a larger error. There were eight stacks in this block, representing eight objects with different number of stacks (see Fig. 6). Fig. 11(a) indicates that the absolute measurement error increases as the size of the object increases, but this trend disappeared when divided by its true volume, i.e., when the relative error was compared (Fig. 11(b)). This suggested that the measurement error was independent of food size.

Fig. 11.

Volume estimation of a LEGO block using circular plate and LED methods.

3.3.2. Reliability of selecting paired points in the image

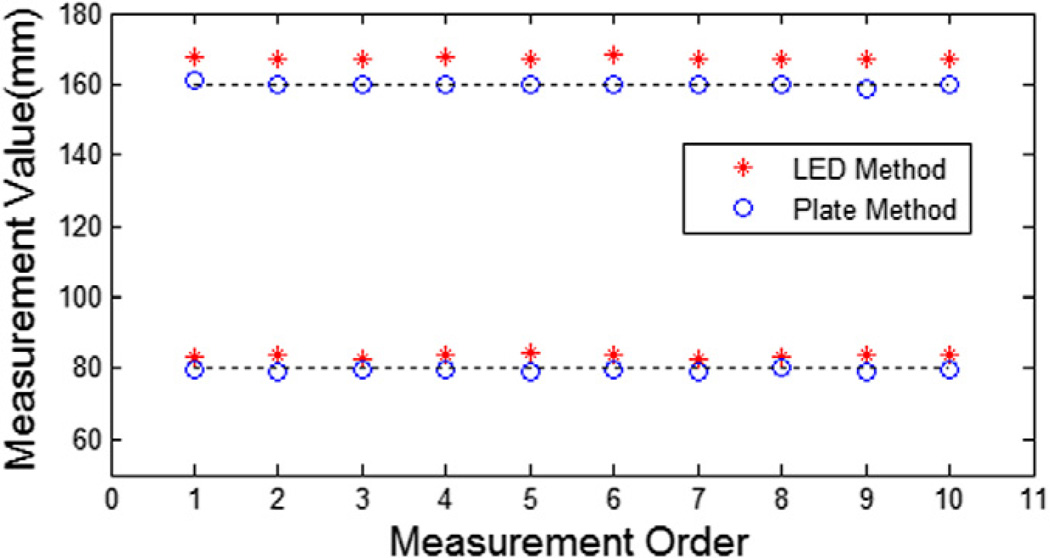
In order to study the error caused by paired point selection in the object plane, we performed an experiment where the ellipse parameters were kept constant. Two pairs of points on the white paper, representing the diameters of the small and big circles in Fig. 8(b) (80 and 160 mm, respectively), were selected from the image. The same points were selected 10 times. The length estimation results are shown in Fig. 12. The standard deviation of the relative error over the 10 estimations was below 1%. These results indicated that point pair selection did not affect the estimation accuracy significantly.

Fig. 12.

Stability and accuracy in length estimation.

4. Conclusions and discussion

In practical cases where our wearable device is utilized, a circular plate with known diameter may not always be available, such as in fast food restaurants. In contrast, the spotlight is always present in the image, since it is always projected by the wearable device. But the projected spotlight may be liable to distortion by the surface of the food or its container. Therefore, in this study we proposed two approaches, based on an elliptical pattern produced by a dining plate or an LED beam. The feasibility of these approaches has been examined experimentally using 10 test objects and food samples. The average error was 12.01% for the plate method and 29.01% for the LED method. These results demonstrate that food volume can be determined computationally from a single image, as long as one of these referents is present in the image. Further work is needed, however, to improve the accuracy of size estimations.

In our experiments, an ultra-bright LED was used to project the spotlight. Due to the diffraction effect when the light is projected onto a surface, the border of the ellipse observed in the image is blurred. The brightness of ambient light also affects the identification of the spotlight. As a result, errors in fitting the border of the spotlight in an image occur, and may result in a larger error in volume estimation using the LED method. Other types of structured lights, e.g., a circular laser beam, may be investigated in the future.

From the experimental results, we can see that the estimated volume is more accurate for the prism-like objects than cylindrical or spherical objects. This may be caused by the difficulty in selecting the pairs of points to represent the object’s height or diameter. We know that a circular object generally becomes an ellipse in the image unless the optical axis of the camera is perpendicular to the object, in which case the object image is circular. It is, therefore, usually difficult to select two points representing the true diameter of a circular/sphere object in its observed image. The difficulty of selecting points to represent an object’s height is also a problem, most notably for irregularly-shaped objects. The larger error in estimating the height of a hamburger was mainly due to this type of measurement ambiguity.

Occlusion is another problem in the current approach. Since we assume that the bottom of the food and the reference are in the same object plane, the bottom is known when the orientation and location of the object plane is determined. However, if the bottom is occluded, we have to assume that the upper surface of the model (e.g., prism) is parallel to its bottom by a distance (i.e., height). So the height of the object has to be estimated first in order to determine the plane that the upper surface locates. As a result, the estimation error will be even larger since the error in the height estimation will influence the dimensional estimation in the upper surface.

Because many foods are not regularly shaped and the ambiguity and occlusion in dimensional estimation are common in food pictures, alternative methods that do not use, or are less dependent on, the length measurement are desirable and warrant future investigation.

Although the two approaches proposed in this study are useful in estimating food volume from one single picture, a reference object is still necessary when applying either approach. Studies are being performed in our laboratory to remove this constraint. In addition, we are also conducting research on further improvement of the accuracy in food volume estimation by fitting food items with more flexible shapes. Finally, we would like to point out that food volume estimation is only one part of the system to determine food calories and nutritional contents. The accuracy of the volumetric and nutritional information in the food database also plays an essential role in the system. We expect the accuracy of the food database to improve continuously as the food volume measurement techniques advance.

Besides calculating energy intake from the food images, our system also estimates energy expenditure by integrating the multimedia data acquired by several sensors available in our wearable device (e.g., camera, GPS, light sensor, and accelerometer). We identify human activities (e.g., eating, walking, driving) and their durations from the automatically saved time stamps. A special physical activity database (Ainsworth et al., 2000) is then utilized to estimate the caloric expenditure. Thus, our device can provide a convenient, effective measure of energy balance between energy intake and expenditure, which is highly desirable in the study of obesity and related conditions.

Appendix A. Solution of the LED model

The intersection curve between the camera cone and the object plane can be obtained as:

$$x{\prime }^2+h_{1}x\prime y\prime +b_{1}y{\prime }^2+g_{1}x\prime +f_{1}y\prime +d_1=0$$ (A1)

where:

$$\begin{array}{c}{h}_1=\frac{2}{f(a\prime m^2-2h\prime \mathit{\text{ml}}+b\prime l^2)}(a\prime \mathit{\text{flmn}}-b\prime \mathit{\text{flmn}}+h\prime {\mathit{\text{fm}}}^{2}n-h\prime {\mathit{\text{fnl}}}^2-g\prime {\mathit{\text{ml}}}^2-g\prime m^3+f\prime l^3+f\prime {\mathit{\text{lm}}}^2)\hfill \\ b_1=\frac{1}{f^2(a\prime m^2-2h\prime \mathit{\text{ml}}+b\prime l^2)}[a\prime f^2{l}^2{n}^2+b\prime f^2{m}^2{n}^2+d\prime {(l^2+m^2)}^2+2h\prime f^2{\mathit{\text{mn}}}^{2}l-2\mathit{\text{fn}}(l^2+m^2)(g\prime l+f\prime m)\hfill \\ g_1=\frac{2{\mathit{\text{nd}}}_0\sqrt{l^2+m^2}}{f^2(a\prime m^2-2h\prime \mathit{\text{ml}}+b\prime l^2)}[-a\prime f^2{l}^{2}n-b\prime f^2{m}^{2}n+d\prime n(l^2+m^2)-2h\prime f^2\mathit{\text{mnl}}-g\prime {\mathit{\text{fn}}}^{2}l-f\prime {\mathit{\text{fn}}}^{2}m+(l^2+m^2)(g\prime \mathit{\text{fl}}+f\prime \mathit{\text{fm}})\hfill \\ f_1=\frac{2{\mathit{\text{nd}}}_0\sqrt{l^2+m^2}}{f(a\prime m^2-2h\prime \mathit{\text{ml}}+b\prime l^2)}\times [-a\prime \mathit{\text{fml}}+b\prime \mathit{\text{fml}}-h\prime {\mathit{\text{fm}}}^2-g\prime \mathit{\text{mn}}+h\prime {\mathit{\text{fl}}}^2+f\prime \mathit{\text{nl}}]\hfill \\ d_1=\frac{(l^2+m^2)d_0^2{n}^2}{f^2(a\prime m^2-2h\prime \mathit{\text{ml}}+b\prime l^2)}[a\prime f^2{l}^2+b\prime f^2{m}^2+2h\prime f^2\mathit{\text{ml}}+2g\prime \mathit{\text{fnl}}+2f\prime \mathit{\text{fmn}}+d\prime n^2\hfill \end{array}$$

And the intersection curve between the LED cone and the object plane is:

$$x{\prime }^2+h_{2}x\prime y\prime +b_{2}y{\prime }^2+g_{2}x\prime +f_{2}y\prime +d_2=0$$ (A2)

where

$$\begin{array}{c}{h}_2=0\hfill \\ b_2=n^2-{\mathit{\text{tg}}}^2\beta (l^2+m^2)\hfill \\ g_2=-\frac{2n}{\sqrt{l^2+m^2}}[{\mathit{\text{nd}}}_0(l^2+m^2)-\mathit{\text{dl}}+{\mathit{\text{tg}}}^2\beta (l^2+m^2){\mathit{\text{nd}}}_0]\hfill \\ f_2=\frac{2\mathit{\text{md}}}{\sqrt{l^2+m^2}}\hfill \\ d_2=n^2{d}_0^2{m}^2+n^2{d}_0^2{l}^2+d^2-2d_0\mathit{\text{dnl}}-{\mathit{\text{tg}}}^2\beta ·n^4{d}_0^2\hfill \end{array}$$

Since (A1) and (A2) and represent the same elliptical spotlight on the object plane, the coefficients in these two equations should be the same:

$$\{\begin{array}{c}{h}_1=h_2\hfill \\ b_1=b_2\hfill \\ g_1=g_2\hfill \\ f_1=f_2\hfill \\ d_1=d_2\hfill \end{array}$$ (A3)

Using (A3) and (9), we can solve for the location and orientation of the object plane. However, it is generally hard (if possible at all) to obtain a close-form solution of (A3) and (9). We have to rely on numerical approaches to solve these nonlinear simultaneous equations, e.g., through iterative methods (Martinez, 1991) or optimization methods (Grosan and Abraham, 2008). On the other hand, we can concentrate on a special case, which is simple but most commonly seen in our application: the dining table is horizontal, and the camera rotates in only one direction relative to the table. In this case, m = 0, $l=\sqrt{1-n^2}$ and the equations can be simplified as:

$$\begin{array}{c}(a\prime -b\prime )f^2{t}^2-2g\prime \mathit{\text{ft}}+d\prime +{\mathit{\text{tg}}}^2\beta b\prime f^2=0\hfill \\ (b\prime -a\prime )\mathit{\text{ft}}+g\prime -\mathit{\text{fb}}\prime \frac{d}{d_0}=0\hfill \end{array}$$ (A4)

where $t=\frac{n}{\sqrt{1-n^2}}$. If we define the sharp angle between the object plane and the optical axis of the camera as θ, $\theta \in (0,\frac{\pi }{2})$, then t = tgθ.

$$\mathit{\text{tg}}\theta =\frac{g\prime \pm \sqrt{{(g\prime )}^2-(a\prime -b\prime )(d\prime +{\mathit{\text{tg}}}^2\beta b\prime f^2)}}{(a\prime -b\prime )f}$$ (A5)

$$d_0=\frac{\mathit{\text{fb}}\prime d}{(b\prime -a\prime )f·\mathit{\text{tg}}\theta +g\prime }$$ (A6)

In our application, d₀ > 0, d > 0, and b′/a′ > 0. From (A6), we get:

$$\frac{\mathit{\text{fb}}\prime d}{(b\prime -a\prime )f·\mathit{\text{tg}}\theta +g\prime }>0,(b\prime -a\prime )f·\mathit{\text{tg}}\theta +g\prime >0.$$ (A7)

From (A5), we get:

$$(a\prime -b\prime )f·\mathit{\text{tg}}\theta -g\prime =\pm \sqrt{{(g\prime )}^2-(a\prime -b\prime )(d\prime +{\mathit{\text{tg}}}^2\beta b\prime f^2)}.$$ (A8)

Compare (A7) and (A8), only negative symbol is feasible in our application.

Therefore,

$$\mathit{\text{tg}}\theta =\frac{g\prime -\sqrt{{(g\prime )}^2-(a\prime -b\prime )(d\prime +{\mathit{\text{tg}}}^2\beta b\prime f^2)}}{(a\prime -b\prime )f}$$ (A9)