Sensitivity Enhanced Heteronuclear Correlation Spectroscopy in Multidimensional Solid-State NMR of Oriented Systems via Chemical Shift Coherences

Abstract

We present new sensitivity enhanced schemes for heteronuclear correlation spectroscopy (HETCOR) in solid-state NMR of oriented systems. These new schemes will enhance the sensitivity of the HETCOR by 40% for the two dimensional experiments (SE-HETCOR) and up to 180% for the 3D HETCOR- separated local field version (SE-PISEMAI-HETCOR). The signal enhancement is demonstrated for a single crystal of ¹⁵N N-acetylleucine and the integral membrane protein sarcolipin oriented in lipid bicelles. These new methods will significantly reduce the time needed to acquire multidimensional experiments for membrane proteins oriented in magnetically or mechanically aligned lipid bilayers as well as liquid crystalline materials.

INTRODUCTION

Anisotropic nuclear spin interactions such as chemical shift (CS or CSA) and dipolar coupling (DC) have been widely used to obtain structural information on oriented samples such as membrane peptides and proteins reconstituted in mechanically and magnetically aligned lipid bilayers.^1–18 Using amide ¹⁵N CS and ¹H-¹⁵N DC, it is possible to model the orientation of the peptide planes and the corresponding helical segments with respect to a fixed axis (B₀ or bilayer normal), determining the high-resolution structure and topology of the polypeptide backbone.¹⁹ When this method is combined with solution NMR restraints (i.e. distance and torsion angle restraints) derived from membrane proteins reconstituted in detergent micelles, it is possible to obtain the complete high-resolution structure and topology of both backbone and side chains for membrane proteins.^{9, 20} The two major methods utilized for measuring NMR anisotropic parameters (CS and DC) in oriented lipid membrane preparations are the separated local field (SLF)²¹ and heteronuclear correlation (HETCOR) experiments²². The most popular SLF experiment is the polarization inversion spin exchange at the magic angle or PISEMA²³, although several variants including SAMPI4²⁴ and HIMSELF²⁵ have been proposed to extract CS and DC from highly ordered samples. However, the low sensitivity of these pulse sequences has limited the applicability to only a few high-resolution structures of small membrane proteins. To address the sensitivity problem, we recently revisited the PISEMA experiment and designed a new pulse sequence (SE-PISEMA) with enhanced sensitivity. ²⁶ The SE-PISEMA utilizes a spin-echo sequence that allows one to recover the sine modulated dipolar coherences, which are lost in the conventional PISEMA experiment. With the SE-PISEMA, it is possible to reach a gain in sensitivity up to 40% (or a sensitivity enhancement factor of $\sqrt{2}$). We generalized the SE method to all the SLF experiments, demonstrating a remarkable gain in sensitivity for SE-SAMPI4 and SE-HIMSELF when applied to integral membrane proteins reconstituted in lipid bicelles.²⁷

Here, we report a new sensitivity-enhanced (SE) scheme for 2D-HETCOR and 3D-HETCOR-SLF experiments. The major difference in the SE schemes between the PISEMA and HETCOR experiments is that the former is achieved via single and multiple-quantum dipolar coherences, while the latter is obtained via chemical shift coherences. For the 2D SE-HETCOR, we attained an enhancement in signal-to-noise of 40% (sensitivity enhancement factor of $\sqrt{2}$). For the 3D experiment (SE-PISEMAI-HETCOR), we achieved a gain in signal-to-noise of 180% or a factor of $2\sqrt{2}$.

MATERIAL AND METHODS

Preparation of Sarcolipin in Lipid Bicelles

U-¹⁵N sarcolipin (SLN) was expressed and purified as previously described using a fusion construct (maltose binding protein-MBP) and affinity chromatography (amylose resin).^{28, 29} The protein was then cleaved from MBP using tobacco etch virus. All proteins were precipitated with trichloroacetic acid and then resuspended in methanol/chloroform/acetic acid (90/9/1, v/v/v). Due to the hydrophobic nature of SLN, this step gave sufficiently pure protein for NMR studies as previously utilized for other hydrophobic peptides. ^{28, 29} TBBPC (1-tetradecanoyl-2-(4-(4-biphenyl)butanoyl)-sn-glycero-3-PC) was synthesized from 1-dodecanoyl-2-BBPC and 1-myristoyl-2-hydroxy-sn-glycero-3-phosphocholine (Avanti Polar Lipids, Inc.) as described previously.^{30, 31} After synthesis, the product was purified using silica gel chromatography, giving a 60% final yield. SLN (2.5 mg in methanol) was added with TBBPC (36.5 mg in chloroform) and dried under N₂(g). The lipids/protein film was further dried overnight under vacuum/desiccant. The sample was then resuspended in 150 μl 20 mM Hepes (pH 7) and subjected to ~10 N₂(l)/60 °C cycles. To form the bicelles, 15 μl of 200 mg/ml 1,2-dihexanoyl-sn-glycero-3-phosphocholine (D6PC) was added to give a final molar ratio of 8/1 TBBPC/D6PC (q=8). The sample was then cycled between N₂(l)/60 °C several more times, and transferred to a 5 mm flat bottom sample holder (New Era Enterprises, Inc.).

Spectra Acquisition and Processing

All of the experiments were performed with a Varian VNMRS 700 MHz spectrometer, equipped with a low-E probe.³² HETCOR and SE-HETCOR experiments were acquired with 16 scans, 50 t₁ increments, a recycle delay of 5 s, an acquisition time of 10 ms and a temperature of 25 °C. The τ₁ and τ₂ periods are set to 80 μs and 100 μs respectively to satisfy the condition s_fslgcpτ₁ = s_wim24τ₂. The HETCOR spectra of sarcolipin were obtained by summing the data from two mixing times (τ₁=80, 160 μs, and τ₂=100, 200 μs). Experiments used a total of 1200 scans, 25 t₁ increments, a recycle delay of 4 s, an acquisition time 5 ms and a temperature of 10 °C. The 3D spectra using ¹⁵N NAL were acquired with a total of 8 scans and 32 t₁ and t₂ increments. During the τ period (120 μs), a WIM24 (Windowless isotropic mixing) pulse train is applied using 90° pulses of 5 μs.

All of the spectra were processed using NMRPipe software.³³ For the HETCOR and HETCOR-SLF experiment, the t₁ dimension was processed in States mode.³⁴ The t₁ dimension for the SE-HETCOR and SE-HETCOR-SLF as well as the t₂ points of SE-PISEMAI-HETCOR were processed in Rance-Kay mode.³⁵ The t₂ dimension for the HETCOR-SLF and SE-HETCOR-SLF, and the t₁ dimension of SE-PISEMAI-HETCOR were processed in Real mode. The data of HETCOR were zero filled to 128 and 2048 in t₁ and t₂ dimensions, respectively. A cosine-shifted sine bell window function was applied in t₁ and a 100 Hz exponential line broadening was applied in t₂. All of the 3D data were zero filled to 256 points in t₁ and t₂ dimensions, and 2048 in the t₃ dimension. Cosine-shifted sine bell window functions were applied in both t₁ and t₂, while for the t₃ dimension a 100 Hz exponential line broadening was applied. The SE processing (Rance-Kay mode) also increases the noise by a factor of $\sqrt{2}$. Hence the SE data was divided by $\sqrt{2}$ so that the RMS noise matches with its conventional counterpart. Therefore, the signal enhancement was a direct measure of sensitivity enhancement. All the pulse sequences were implemented with two-step phase cycling of the initial 90° pulse and receiver phases. During acquisition, SPINAL decoupling³⁶ was applied on the proton channel (I) for all pulse sequences, resulting in ¹⁵N (S) chemical shift evolution.

THEORETICAL BASIS

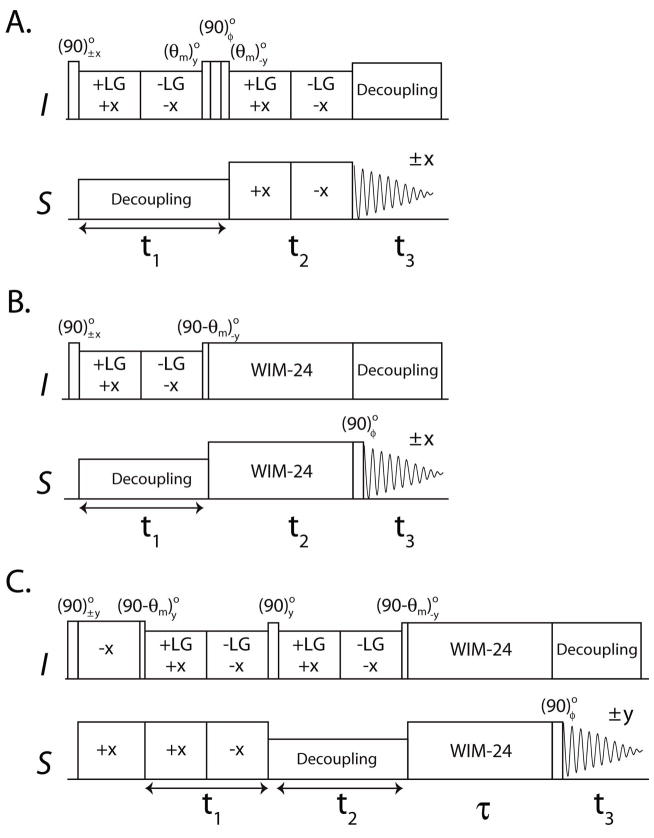
Figure 1 shows the commonly used 2D HETCOR experiment ³⁷ and the new sensitivity enhanced version (SE-HETCOR). Both the preparation and evolution periods of the two pulse sequences are identical. After an initial 90° pulse, the I spins are flipped in the transverse plane and a frequency switch Lee-Goldburg (FSLG) sequence³⁸ is applied for homonuclear decoupling of I spins (¹H). Simultaneously, a continuous wave (CW) irradiation is applied to S-spins (¹⁵N) that avoids the Hartmann-Hahn match condition and removes the heteronuclear DC. Since the I spin magnetization is aligned perpendicularly to the effective field direction of the FSLG sequence, it evolves under a scaled chemical shift Hamiltonian during t₁ evolution. In the HETCOR experiment, a (θ_m)_y(90)_φ(θ_m)_−y pulse train aligns the cosine or sine chemical shift components along the direction of the magic angle (θ_m = 54.7°),³⁷, which is then transferred to S spins using FSLG cross polarization (FSLG-CP) followed by S spin detection under I spin decoupling. The FSLG-CP or SEMA (spin exchange at the magic angle) scheme during the τ₁ period is obtained by FSLG on I spins synchronized with a 180° phase shifted RF field on the S spin channel with Hartmann-Hahn match. FSLG in our experiments is obtained by ramping the phase of the on-resonance ¹H RF field from 0° to 207.8° for +LG (+X) and 27.8° to 180° for –LG (−X) ³⁹. Quadrature detection along the F₁ dimension is achieved by the States method,³⁴ which requires at least two scans for each increment to form a complex t₁ signal. For an I-S spin system the effective Hamiltonians of FSLG and FSLG-CP are:

$$\begin{array}{l}{H}_{\mathit{FSLG}}=s_{\mathit{FSLG}}{\omega }_I{I}_z^{\prime }\\ H_{\mathit{FSLG}-CP}=s_{\mathit{FSLG}-CP}{\omega }_{IS}(I_x^{\prime }{S}_x^{\prime }+I_y^{\prime }{S}_y^{\prime })\end{array}$$

where

Figure 1.

2D HETCOR pulse sequences. A. Conventional experiment with φ = x, y B. New SE-HETCOR pulse sequence with φ = y, −y. θ_m is the magic angle (54.7°).

$$\begin{array}{l}{I}_x^{\prime }=e^{i{\theta }_m{I}_y}{I}_x{e}^{-i{\theta }_m{I}_y},I_y^{\prime }=I_y,I_z^{\prime }=e^{i{\theta }_m{I}_y}{I}_z{e}^{-i{\theta }_m{I}_y}\\ S_x^{\prime }=S_z,S_y^{\prime }=S_y,S_z^{\prime }=S_x\\ s_{\mathit{FSLG}}=0.58,s_{\mathit{FSLG}-CP}=0.82,\text{and}{\omega }_{IS}=2\pi D_{IS}\end{array}$$ (1)

D_IS is the heteronuclear dipolar coupling. The transformation of spin operators in eq. (1) are with respect to a doubly tilted rotating frame defined by the unitary operator U = e^−θ_mI_y e^−(π/2)S_y.

The final density matrix of the HETCOR experiment (Figure 1A) for an I-S spin system with two scans for each increment with φ = x, y is:

$$I_z\stackrel{{(90)}_x^o}{\to }-I_y\stackrel{H_{\mathit{FSLG}}(t_1)}{\to }-I_{y}cos(s_{\mathit{FSLG}}{\omega }_I{t}_1)+I_x^{\prime }sin(s_{\mathit{FSLG}}{\omega }_I{t}_1)\stackrel{{({\theta }_m)}_y{(90)}_{\phi }^o{({\theta }_m)}_{-y}^o}{\to }{I}_z^{\prime }{e}^{{is}_{\mathit{FSLG}}{\omega }_I{t}_1}\stackrel{H_{\mathit{FSLG}-CP}({\tau }_1)}{\to }\frac{1}{2}{S}_z^{\prime }{e}^{{is}_{\mathit{FSLG}}{\omega }_I{t}_1}[1-cos(s_{\mathit{FSLG}-CP}{\omega }_{IS}{\tau }_1)]\stackrel{t_2}{\to }\frac{1}{2}{S}_z^{\prime }{e}^{{is}_{\mathit{fs}lg}{\omega }_I{t}_1}[1-cos(s_{\mathit{FSLG}-CP}{\omega }_{IS}{\tau }_1)]e^{i{\omega }_S{t}_2}$$ (2)

The density matrix for the HETCOR is:

$${\rho }_{\mathit{HETCOR}}=\frac{1}{2}{S}_x{e}^{{is}_{\mathit{FSLG}}{\omega }_I{t}_1}[1-cos(s_{\mathit{FSLG}-CP}{\omega }_{IS}{\tau }_1)]e^{i{\omega }_S{t}_2}$$ (3)

In solution NMR, the SE scheme is obtained by detecting both cosine and sine chemical shift modulated components in a single scan.^{35, 40} To obtain the SE scheme in solids, we implemented WIM-24 pulse trains ⁴¹ on both I and S spins during the τ₂ period (Figure 1B). WIM-24 consists of twenty four 90° pulses with phases: −y, x, −y, −y, x, −y, y, x, y, y, x, y, −y, −x, −y, −y, −x, −y, y, −x, y, y, −x, y applied simultaneously on I and S spins.^{3, 4} This implementation results in the suppression of homonuclear dipolar coupling and chemical shift evolution, whereas the zero order average Hamiltonian takes the isotropic form:

$$\begin{array}{l}{H}_{\mathit{WIM}24}=s_{\mathit{WIM}24}{\omega }_{IS}(\overrightarrow{I}.\overrightarrow{\text{S}})\\ \text{where}{\text{s}}_{\text{WIM}24}=0.66\end{array}$$ (4)

Since the WIM-24 has an isotropic mixing Hamiltonian,⁴¹ both cosine and sine components simultaneously cross-polarize to the S spins. In the SE-HETCOR experiment, each t₁ increment requires at least two scans with final 90° pulse phase y and −y. In the first scan, the I spin magnetization evolves according to:

$$I_z\stackrel{{(90)}_x^o}{\to }-I_y\stackrel{H_{\mathit{FSLG}}(t_1)}{\to }-I_{y}cos(s_{\mathit{FSLG}}{\omega }_I{t}_1)-I_x^{\prime }sin(s_{\mathit{FSLG}}{\omega }_I{t}_1)\stackrel{{(90-{\theta }_m)}_{-y}^o}{\to }-I_{y}cos(s_{\mathit{FSLG}}{\omega }_I{t}_1)-I_{z}sin(s_{\mathit{FSLG}}{\omega }_I{t}_1)\stackrel{H_{\mathit{WIM}24}({\tau }_2)}{\to }-[S_{y}cos(s_{\mathit{FSLG}}{\omega }_I{t}_1)+S_{z}sin(s_{\mathit{FSLG}}{\omega }_I{t}_1)]\frac{1}{2}[1-cos(s_{\mathit{WIM}24}{\omega }_{IS}{\tau }_2)]\stackrel{{(90)}_y^o-t_2}{\to }-[S_{y}cos(s_{\mathit{FSLG}}{\omega }_I{t}_1)+S_{x}sin(s_{\mathit{FSLG}}{\omega }_I{t}_1)]\frac{1}{2}[1-cos(s_{\mathit{WIM}24}{\omega }_{IS}{\tau }_2)]e^{i{\omega }_S{t}_2}$$ (5)

In the second scan, a (90)°_−y pulse prior to t₂ gives rise to:

$$I_z\stackrel{{(90)}_x^o-t_1-{(90-{\theta }_m)}_y^o-{\tau }_2-{(90)}_{-y}^o-t_2}{\to }-[S_{y}cos(s_{\mathit{FSLG}}{\omega }_I{t}_1)-{\text{S}}_{x}sin(s_{\mathit{FSLG}}{\omega }_I{t}_1)]\frac{1}{2}[1-cos(s_{\mathit{WIM}24}{\omega }_{IS}{\tau }_2)]e^{i{\omega }_S{t}_2}$$ (6)

Addition and subtraction of eqs 5 and 6, respectively, gives the cosine and sine modulated chemical shift coherences of the t₁ evolution, which are 90° phase shifted during acquisition. Hence, a relative 90° zero-order phase correction is applied in both F₁ and F₂ dimensions. Note that the zero-order phase correction can also be applied before the Fourier transformation. ^{35, 40} The final density matrix of the SE-HETCOR is:

$${\rho }_{SE-\mathit{HETCOR}}=\frac{1}{\sqrt{2}}{S}_x{e}^{{is}_{\mathit{FSLG}}{\omega }_I{t}_1}[1-cos(s_{\mathit{WIM}24}{\omega }_{IS}{\tau }_2)]e^{i{\omega }_S{t}_2}$$ (7)

Since the SE processing increases the RMS noise by $\sqrt{2}$, the density matrix of SE-HETCOR is divided by $\sqrt{2}$ so that the RMS noise matches the conventional HETCOR given in eq 3. Unlike that of the SE-PISEMA experiment,²⁶ the density matrix for the SE-HETCOR experiment contains I spin chemical shift coherences during t₁, which are transferred to S spins via the isotropic mixing Hamiltonian (H_WIM24). Therefore, the theoretical $\sqrt{2}$ enhancement obtained by summing the sine and cosine modulated chemical shift coherences is uniform for all resonances within the spectrum. Note that in order to match the effective dipolar evolutions for the two experiments, we set the τ_i periods such that s_FSLG-CPτ₁ = s_WIM24τ₂. In both HETCOR and SE-HETCOR, the resultant intensities depend on the value of DC and τ_i, therefore, the τ_i values need to be chosen based on the range of DC values.

We also build the SE scheme into the 3D HETCOR-SLF experiment,⁴² which resolves the I spin CS, I-S DC, and S spin CS in F₁, F₂ and F₃ dimensions, respectively. In the original 3D HETCOR-SLF experiment (Figure 2A), the third dimension was achieved by allowing τ₁ in Figure 1A to evolve rather than be a fixed value as in the 2D SE-HETCOR experiment. We first built the SE scheme into the HETCOR-SLF pulse sequence (Figure 2B) by incrementing τ₂ (see Figure 1B) as t₂, with the S spin CS detected during t₃. For the HETCOR-SLF and SE-HETCOR-SLF experiments, the final density matrices can be written as:

$$\begin{array}{l}{\rho }_{\mathit{HETCOR}-\mathit{SLF}}=\frac{1}{2}{S}_x{e}^{{is}_{\mathit{FSLG}}{\omega }_I{t}_1}[1-cos(s_{\mathit{FSLG}-CP}{\omega }_{IS}{t}_2)]e^{i{\omega }_S{t}_3}\\ {\rho }_{SE-\mathit{HETCOR}-\mathit{SLF}}=\frac{1}{\sqrt{2}}{S}_x{e}^{{is}_{\mathit{FSLG}}{\omega }_I{t}_1}[1-cos(s_{\mathit{WIM}24}{\omega }_{IS}{t}_2)]e^{i{\omega }_S{t}_3}\end{array}$$ (8)

Figure 2.

3D HETCOR-SLF pulse sequences A. Conventional HETCOR-SLF with φ = x, y. B. SE-HETCOR-SLF and C. SE-PISEMAI-HETCOR with φ = y, −y. θ_m is the magic angle (54.7°).

As for the SE-HETCOR experiment, the theoretical sensitivity enhancement for SE-HETCOR-SLF over HETCOR-SLF is $\sqrt{2}$. The dipolar line widths of HETCOR-SLF and SE-HETCOR-SLF can be different due to different decoupling (SEMA and WIM24) schemes used during the t₂ evolution. Thus the $\sqrt{2}$ enhancement is based on the integrated peak intensities.

Notably, both the HETCOR-SLF and SE-HETCOR-SLF contain a constant term that does not oscillate during the t₂ evolution (eq 8). This is because in both of these sequences there is no polarization inversion period prior to t₂ evolution. Therefore only half of the initial magnetization contributes to an observed dipolar splitting with the remaining half giving a zero frequency peak in the F₂ dipolar plane. To recover this lost magnetization, we designed a new pulse scheme, switching the CS and the DC evolution periods (t₁ and t₂) in the HETCOR-SLF experiment, followed by a τ SE period (Figure 2C). The SE scheme is achieved by a WIM-24 pulse train during τ to transfer I spin cosine and sine CS components to the S spins, simultaneously. This new scheme (SE-PISEMAI-HETCOR) enables the insertion of a polarization inversion (PI) period prior to t₁, as in the PISEMA experiment.²³ The cross-polarization period followed by a (90 - θ_m)° pulse on I spins prepares the polarization inversion state (I′_z – S′_z) of an I-S spin pair that evolves as:

$$(I_z^{\prime }-S_z^{\prime })\stackrel{H_{\mathit{FSLG}-CP}(t_1)}{\to }(I_z^{\prime }-S_z^{\prime })cos(s_{\mathit{FSLG}-CP}{\omega }_{IS}{t}_1)-(2I_y^{\prime }{S}_x^{\prime }-2I_x^{\prime }{S}_y^{\prime })sin(s_{\mathit{FSLG}-CP}{\omega }_{IS}{t}_1)\stackrel{{(90)}_{\text{y}}^{\text{I}}}{\to }{I}_x^{\prime }+\dots \dots \stackrel{H_{\mathit{FSLG}}(t_2)}{\to }cos(s_{\mathit{FSLG}-cP}{\omega }_{IS}{t}_1)[I_x^{\prime }cos(s_{\mathit{FSLG}}{\omega }_I{t}_2)+I_{y}sin(s_{\mathit{FSLG}}{\omega }_I{t}_2)]\stackrel{{(90-{\theta }_{\text{m}})}_{\text{y}}^{\text{o}}}{\to }cos(s_{\mathit{FSLG}-CP}{\omega }_{IS}{t}_1)[I_{z}cos(s_{\mathit{FSLG}}{\omega }_I{t}_2)+I_{y}sin(s_{\mathit{FSLG}}{\omega }_I{t}_2)]\stackrel{H_{\mathit{WIM}24}(\tau )}{\to }cos(s_{\mathit{FSLG}-CP}{\omega }_{IS}{t}_1)[S_{z}cos(s_{\mathit{FSLG}}{\omega }_I{t}_2)+S_{y}sin(s_{\mathit{FSLG}}{\omega }_I{t}_2)]\stackrel{{(90)}_{\pm y}^o-t_3}{\to }cos(s_{\mathit{FSLG}-CP}{\omega }_{IS}{t}_1)[S_{x}cos(s_{\mathit{FSLG}}{\omega }_I{t}_2)\pm S_{y}sin(s_{\mathit{FSLG}}{\omega }_I{t}_2)]e^{i{\omega }_s{t}_3}$$ (9)

Note that during the t₂ period, the S spin coherences are dephased and become unobservable during t₃. Hence only the evolution of I spin coherence ( I′_x) is shown. The final density matrix with SE data processing is given by:

$${\rho }_{SE-\mathit{PISEMAI}-\mathit{HETCOR}}=\frac{1}{\sqrt{2}}[1-cos(s_{\mathit{WIM}24}{\omega }_{IS}\tau )][S_{x}cos(s_{\mathit{FSLG}-CP}{\omega }_{IS}{t}_1)e^{{is}_{\mathit{FSLG}}{\omega }_I{t}_2}{e}^{i{\omega }_S{t}_3}]$$ (10)

where the factor $\frac{1}{\sqrt{2}}$ compensates the $\sqrt{2}$ increase in noise which results from the data processing. 2 Unlike the 2D PISEMA experiment (which detects S spin dipolar coherence), the PISEMAI scheme in the 3D SE-PISEMAI-HETCOR pulse sequence detects the I spin dipolar coherence in the indirect dimension. In conventional 3D HETCOR-SLF and SE-PISEMAI-HETCOR the dipolar evolution is under SEMA spin lock, hence the dipolar line widths are identical.

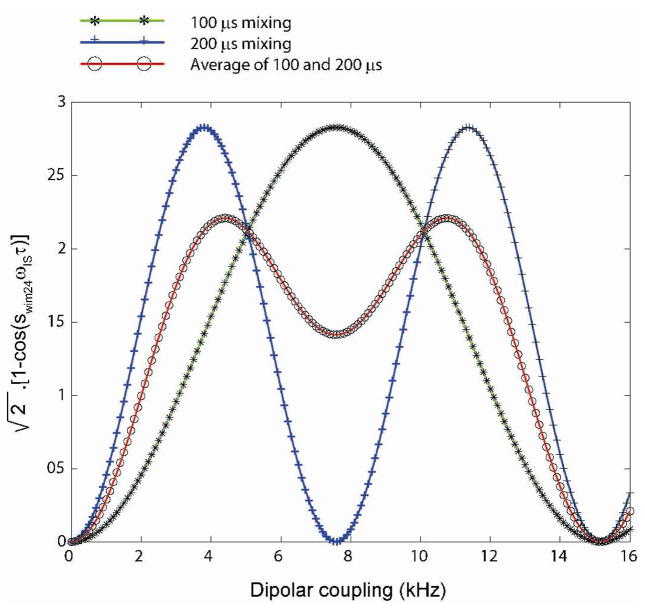
The resulting spectrum of SE-PISEMAI-HETCOR consists of a PISEMA spectrum in the F₁-F₃ dimensions and the HETCOR spectrum in the F₂-F₃ dimensions. In eq 10, the term [1−cos(s_WIM24 ω_IS τ)] ranges from 0 to 2. Thus, it is possible to obtain an enhancement factor up to $2\sqrt{2}$, depending on the value of D_IS and τ. The theoretical enhancement as a function of DC is reported in Figure 3 for τ = 100 and 200 μs. Note that when τ = 120 μs, sensitivity enhancement will be optimal for values D_IS values 3.2–9 kHz, which is typical of transmembrane peptides and proteins. For cytoplasmic domains (amphipathic helices absorbed on the membrane surfaces), the typical DC values range from 1.5 to 5 kHz, and one can use t = 200 μs. As for the 2D PISEMA experiment, the SE-PISEMAI-HETCOR experiment is performed separately for cytoplasmic and transmembrane domains of proteins, in order to optimize the CP contact time and ¹H offset. Thus, based on the region of interest (i.e. D_IS), one can optimize the value of t.

Figure 3.

Theoretical SE curves (eq. 10) for the SE-PISEMAI-HETCOR with mixing times τ of 100 and 200 μs. A wide range of dipolar couplings can be covered using a combination of two mixing times (average of 100 and 200 μs curves).

RESULTS

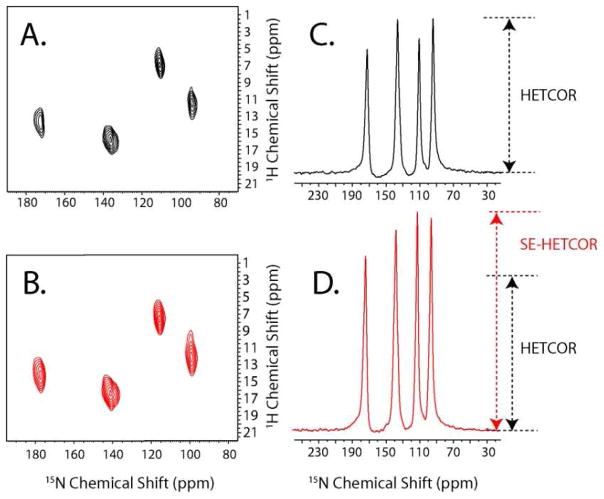
We tested the performance of the new pulse sequences on a single crystal of ¹⁵N N-acetylleucine (NAL). Figure 4 shows the spectra of HETCOR and SE-HETCOR. The SE obtained is given in Table 1. The theoretical sensitivity enhancement factor is $\sqrt{2}$. Similar to the SE-PISEMA experiment,²⁶ we detected slight deviations from this value in NAL probably due to: (a) differential relaxation times of the amide groups during τ₁ and τ₂, and (b) deviations of theoretical scaling factors s_FSLG-CP and s_WIM24.

Figure 4.

2D HETCOR spectra of ¹⁵N NAL single crystal. A. 2D spectrum obtained with the conventional HETCOR pulse sequence. B. 2D spectrum obtained with the SE-HETCOR experiment. The spectral widths of the F₁ dimension are scaled to compensate for the scaling factor (s_FSLG). A total of 16 scans and 50 t₁ increments were used, with a recycle delay of 5 s and an acquisition time of 10 ms. The effective fields during τ₁ (80 μs) and τ₂ (100 μs) periods are 50 and 61 kHz, respectively. To illustrate the SE, the sums of the F₁ cross sections (between 2 and 20 ppm) of (A) and (B) are given in (C) and (D).

Table 1.

Sensitivity enhancement factors of SE-HETCOR, SE-HETCOR-SLF and SE-PISEMAI-HETCOR over conventional HETCOR and HETCOR-SLF experiments for ¹⁵N resonances of NAL

15N Chemical Shift (ppm)	SE-HETCOR	SE-HETCOR-SLF	SE-PISEMAI-HETCOR
173	1.42	1.50	1.82 (2.42)
138	1.32	1.45	2.71 (2.79)
110	1.61	1.55	1.83 (2.30)
92	1.37	1.38	2.08 (2.60)

Theoretical enhancements for SE-HETCOR and SE-HETCOR-SLF experiments are $\sqrt{2}$, those for the SE-PISEMAI-HETCOR experiment are reported in parentheses.

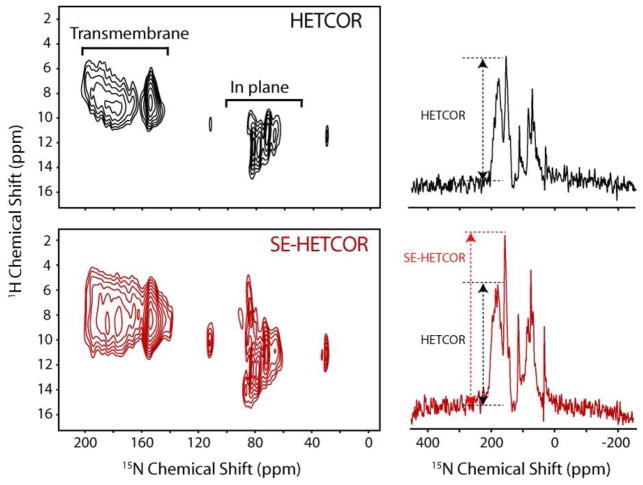
We also compare the SE-HETCOR and HETCOR methods with the integral membrane protein sarcolipin (SLN),⁴³ a 31-residue integral membrane protein, which was reconstituted in oriented TBBPC/D6PC (8/1) lipid bicelles (Figure 5). In both the experiments the resulting intensities are a function of DC and τ_i values (eqs 3 and 7). Sarcolipin has two sets of resonances corresponding to the transmembrane domain amides and to the cytoplasmic and luminal residue amides. The DC values range from 2–8 kHz. In order to cover both the regions, two τ_i values are needed. The spectra shown in Figure 5 were obtained by summing the data from two mixing times (τ₁=80, 160 μs, and τ₂=100, 200 μs). The sensitivity enhancement measured in the spectral regions ranging from 4–18 and 20–220 ppm of the SE-HETCOR spectrum over HETCOR is ~65%. The average enhancement is greater than the theoretical 40% due to the higher efficiency and less proton offset dependence of WIM24-CP over the FSLG-CP scheme.⁴⁴ For small DC values and large ¹H chemical shift dispersion, the FSLG-CP scheme performs poorly.⁴⁴ This is apparent for in plane residues of SLN, resonating around 60–120 ppm.

Figure 5.

2D HETCOR and SE-HETCOR spectra and corresponding slices taken at 10 ppm of U-¹⁵N labeled sarcolipin in aligned TBBPC/D6PC (8/1) bicelles. A. 2D spectrum obtained with the conventional HETCOR experiment (Figure 1A). B. 2D spectrum obtained using the SE-HETCOR experiment (Figure 1B). The spectra were obtained summing the data from two mixing times (τ₁=80, 160 μs, and τ₂=100, 200 μs). A total of 1200 scans, 25 t₁ increments, a recycle delay of 4 s and an acquisition time 5 ms was used.

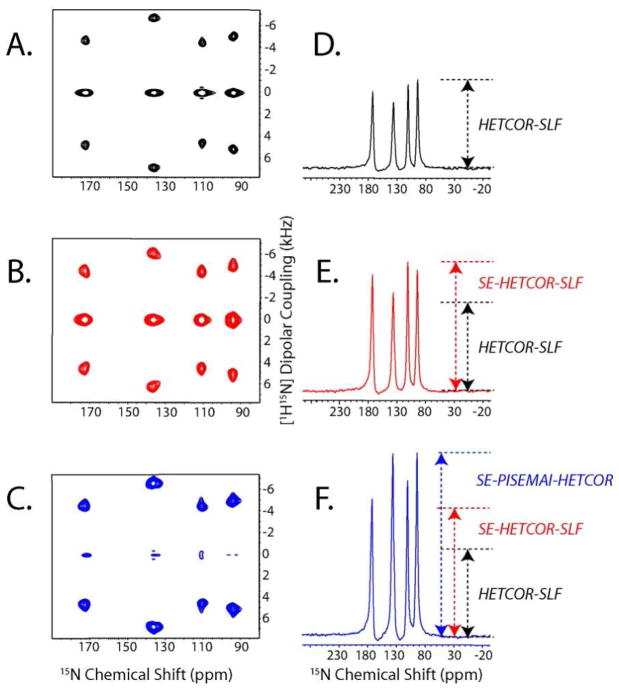
The 3D pulse sequences reported in Figure 2 were tested on a single crystal of ¹⁵N labeled NAL. The results are reported in Figures 6A–C, showing the sum of ¹H chemical shift planes from the HETCOR-SLF, SE-HETCOR-SLF and SE-PISEMAI-HETCOR 3D spectra, respectively. The zero-frequency peaks in Figure 6C are much weaker than those in Figure 6A and 6B. This indicates that the SE-PISEMAI-HETCOR performs better than the conventional HETCOR-SLF and SE-HETCOR-SLF experiments, with the PI period reducing the zero-frequency component of the magnetization and increasing the amplitude of the dipolar signal during the t₁ evolution.

Figure 6.

1D and 2D projections of the 3D spectra of ¹⁵N NAL single crystal. F₁ and F₂ dimensions are scaled to compensate for the scaling factors (s_FSLG, s_FSLG-CP, and s_WIM24). The 2D spectra in (A), (B), and (C) are obtained by summing the ¹H chemical shift planes (between 2 and 20 ppm) of the 3D HETCOR-SLF, SE-HETCOR-SLF, and SE-PISEMAI-HETCOR spectra, respectively. The 1D spectra in (D), (E) and (F) are obtained by summing the dipolar cross sections (3 and 7.5 kHz) of panels (A), (B) and (C), respectively. A total of 8 scans were used for 32 t₁ and t₂ increments. During the τ period (120 μs), a WIM24 pulse train is applied using 5 μs 90° pulses. Note that the zero frequency peaks in (A) and (B) are of opposite sign with respect to the dipolar peaks.

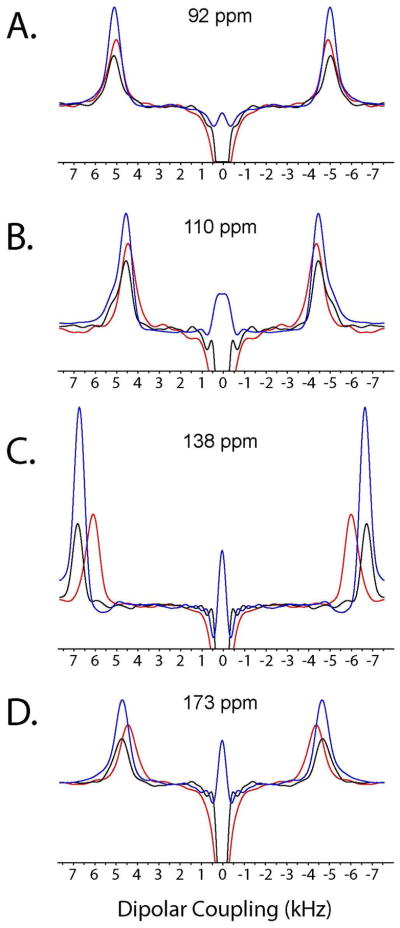
The dipolar line widths of HETCOR-SLF and SE-PISEMAI-HETCOR (Figure 7) are identical and slightly narrower with respect to the SE-HETCOR-SLF experiments. This is due to shorter relaxation (T_1ρ) during the WIM24 spin-lock and/or deviation from the theoretical scaling factor (0.82) of the SEMA spin-lock. For the SEMA block, the DC evolution is affected by proton offset and shows increased DC values. Note that for small dipolar couplings with large proton chemical shift dispersion (in plane residues of aligned membrane protein) WIM24 gives accurate DC values and narrower (or comparable) line widths with respect to the SEMA block. Since the slight deviations of dipolar line widths are dependent on the orientation of the membrane protein and acquisition conditions (¹H offset, pulse power, DC values, etc.), SE is measured by calculating the integrated intensities. The sensitivity enhancement of SE-HETCOR-SLF and SE-PISEMAI-HETCOR with respect to HETCOR-SLF are reported in Table 1. The average SE of SE-HETCOR-SLF is ~40%. For SE-PISEMAI-HETCOR the SE factor is greater than 1.8, with a maximum enhancement of ~2.7 for the amide resonance at 138 ppm. Finally, it is also possible to replace the PISEMA block of SE-PISEMAI-HETCOR with other SLF sequences.^{24, 44}

Figure 7.

The spectra in panels A–D are the dipolar cross-sections of the spectra reported in Figure 6. The traces from the HETCOR-SLF, SE-HETCOR-SLF and SE-PISEMAI-HETCOR spectra are colored in black, red, and blue, respectively. For the HETCOR-SLF and SE-PISEMAI-HETCOR spectra, the dipolar line widths (A–D) are 800 Hz, 565 Hz, 715 Hz, and 685 Hz, respectively. For SE-HETCOR-SLF, the dipolar line widths (A–D) are 890 Hz, 744 Hz, 774 Hz and 800 Hz, respectively.

CONCLUSIONS

In conclusion, we report a new heteronuclear correlation solid-state NMR experiment with sensitivity enhancement for aligned samples. While SE methods have been reported for magic angle spinning (MAS) experiments,^{45, 46} the implementation of these methods for solid-state NMR on oriented static samples is unprecedented. The 2D SE-HETCOR and 3D SE-HETCOR-SLF experiments can achieve a gain in signal to noise of 40% (or a sensitivity enhancement factor of $\sqrt{2}$). The redesigned 3D SE-PISEMAI-HETCOR can boost the signal by 180 % (a sensitivity enhancement factor of $2\sqrt{2}$). These methods can be incorporated in other double and triple resonance experiments.^{42, 47, 48} Taken with SE obtained with SLF experiments²⁶ and advancements in sample preparation⁴⁹ and probe hardware,³² these new SE experiments will dramatically improve the spectroscopy of membrane proteins and peptides as well as the characterization of liquid crystalline materials.