Abstract
Cardiac defibrillation, as accomplished nowadays by automatic, implantable devices (ICDs), constitutes the most important means of combating sudden cardiac death. While ICD therapy has proved to be efficient and reliable, defibrillation is a traumatic experience. Thus, research on defibrillation mechanisms, particularly aimed at lowering defibrillation voltage, remains an important topic. Advancing our understanding towards a full appreciation of the mechanisms by which a shock interacts with the heart is the most promising approach to achieve this goal. The aim of this paper is to assess the current state-of-the-art in ventricular defibrillation modeling, focusing on both numerical modeling approaches and major insights that have been obtained using defibrillation models, primarily those of realistic ventricular geometry. The paper showcases the contributions that modeling and simulation have made to our understanding of the defibrillation process. The review thus provides an example of biophysically based computational modeling of the heart (i.e., cardiac defibrillation) that has advanced the understanding of cardiac electrophysiological interaction at the organ level and has the potential to contribute to the betterment of the clinical practice of defibrillation.
Index Terms: Bidomain, computer modeling of the heart, defibrillation threshold, postshock activation, shock
I. Introduction
Cardiac fibrillation is the breakdown of the organized cardiac electrical activity driving the heart’s periodic pumping into disorganized self-sustained electrical activation patterns. A fibrillation episode results in the loss of cardiac output, and unless timely intervention takes place, death quickly ensues. The only known effective therapy for lethal disturbances in cardiac rhythm is defibrillation, the delivery of a strong electric shock to the heart. This technique, as accomplished nowadays by automatic, implantable devices (ICDs), constitutes the most important means of combating sudden cardiac death. Several multicenter clinical trials have provided consistent evidence that ICD therapy prolongs patient life. This convincing demonstration of efficacy has led to a nearly exponential growth, over the last decade, in the number of patients receiving implantable devices. Currently, around 0.2 million ICDs are implanted every year throughout the world.
Although ICD therapy has proved to be efficient and reliable in preventing sudden cardiac death [1], with success rates clearly superior to other therapeutic options such as pharmacological anti-arrhythmia therapy, defibrillation remains a painful experience, with thousands of patients also affected by high-voltage component ICD malfunctions and experiencing severe psychological distress [2]. Therefore, despite the impressive clinical success and efficacy of ICD devices, research on defibrillation mechanisms, particularly aimed at lowering defibrillation voltage, remains an important topic. Advancing our understanding towards a full appreciation of the mechanisms by which a shock interacts with the heart is the most promising approach to achieve this goal.
A. Experimental Approaches to Investigate Defibrillation Mechanismsa
The key to understanding the cardiac defibrillation process is to uncover those mechanisms by which electric current delivered to the heart by the shock traverses myocardial structures and interacts with the wavefronts underlying ventricular fibrillation. Elucidating the biophysical underpinnings of defibrillation mechanisms has been, however, a long and arduous process (see Dosdall et al. [3] for a recent review). These difficulties can be attributed to the lack of suitable experimental methodologies that allow researchers to observe electrical events occurring before, during and after shock delivery with sufficiently high spatiotemporal resolution. Early studies on defibrillation mechanisms relied on recordings of extracellular potentials following the defibrillation shock, since overwhelming electrical artifacts had prevented researchers from recording during and shortly after the shock.
Although these pioneering electrical mapping studies provided insights that laid the basis for understanding defibrillation mechanisms, such as the upper limit of vulnerability (ULV), there was no direct experimental evidence to prove the putative mechanisms. A major breakthrough occurred with the introduction of potentiometric dyes, which allowed recording of electrical events before, during and after shock delivery with high resolution. The ability of these optical mapping techniques to record optical fluorescence signals proportional to the transmembrane Vm voltage proved to be a major advantage. Unlike extracellularly recorded electric potentials, which integrate contributions of bioelectric activity in the vicinity of a recording site via the volume conductor in which the heart is immersed, recording Vm provides a direct measure of the shock-induced membrane responses. Although optical mapping techniques allow the visualization of shock-induced changes in membrane potential, these recordings are, however, confined to activity on the cardiac surfaces only. In a complex three-dimensional (3-D) anatomical structure such as the heart, shock-induced electrical events and postshock activity take place throughout the myocardial walls. Therefore, the restricted capability of current optical mapping techniques to detect events occurring in the depth of the wall that may not have any signature on the surfaces [4] poses a significant limitation, rendering investigations of defibrillation mechanisms by experimental means alone a challenging endeavor.
B. Role of Computer Modeling
The absence of experimental methodology for recording shock-induced membrane polarizations in 3-D has provided a major impetus to the theoretical and computational electrophysiology community to develop and refine computer models of the cardiac defibrillation process. Since there is insufficient direct experimental evidence to allow a direct verification of model predictions in the depth of the myocardium, results of computer models are being compared against optical maps recorded on the ventricular surfaces. Assuming that model formulations are a valid quantitatively correct representation of cardiac bioelectricity, models that correctly predict experimental observations at the surfaces are used to predict behavior inside the depth of the myocardial walls [5], [6].
In earlier computational studies of defibrillation mechanisms, monodomain (reaction-diffusion) representations of cardiac tissue electrical behavior were employed; these do not account explicitly for current flow in the extracellular space, and their suitability for simulating the process of defibrillation quickly turned out to be of limited value. Theoretical considerations based on the monodomain equations predicted shock-induced changes in transmembrane voltage, ΔVm, only along tissue boundaries and around conductive discontinuities in the heart, leaving the bulk of the myocardium essentially unaffected. The theoretical community subsequently adopted the more comprehensive bidomain model of the myocardium, which explicitly accounts for current flow in both the intracellular and interstitial domains. The bidomain model proved quickly to be an invaluable and powerful tool for studying defibrillation mechanisms, providing the sought after “missing link” [7] between externally applied electric field and membrane responses in the tissue bulk. Using the bidomain model, Sepulveda and coworkers [8] demonstrated in a seminal study that shock-induced changes in membrane potential (membrane polarization) can be much more complex than previously anticipated. Their simulation results suggested that the tissue response in the vicinity of a strong unipolar stimulus involved the simultaneous occurrence of both positive (depolarizing) and negative (hyperpolarizing) effects in close proximity, if the anisotropy ratios between intracellular and extracellular spaces comprising the myocardium are unequal, i.e., both spaces are anisotropic, but to a different degree. In the absence of unequal anisotropy ratios, as it is the case with monodomain models which inherently assume equal anisotropies, no polarizations of opposite polarity can occur (Fig. 1).
Fig. 1.
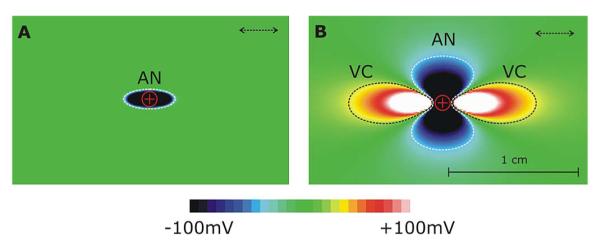
Unequal anisotropy ratios between the conductivities in the intracellular and extracellular spaces constitutes a necessary condition for the existence of bulk VEPs. (A) Unipolar anodal stimulus is delivered to the center of a tissue sheet of equal anisotropy ratios. Shock induced polarization of only one polarity (hyperpolarization) is observed and the tissue affected by the shock is limited by the immediate vicinity of the electrode. (B) Exact same shock delivered to tissue of unequal anisotropy ratios induced polarizations of both polarities and the area of tissue affected extends far beyond the electronic space constant. Dashed arrows indicate the longitudinal axis of myocyte orientation.
This prediction of the existence of “virtual electrodes” departed from the established view that tissue responses should only be depolarizing if the stimulus is cathodal, or hyperpolarizing if the stimulus is anodal. Optical mapping studies that followed convincingly confirmed these theoretical predictions [9]. Since, “virtual electrode polarization” (VEP) has been documented in experiments involving various stimulus configurations [10]-[14].
C. Objective of This Review
The aim of this paper is to assess the current state-of-the-art in ventricular defibrillation modeling, focusing on both numerical modeling approaches and the major insights that have been obtained using defibrillation models, primarily those of realistic ventricular geometry. The paper showcases the contributions that modeling and simulation have made to our understanding of the defibrillation process. The review thus provides an example of biophysically based computational modeling of the heart (i.e., ventricular defibrillation) that has advanced the understanding of cardiac electrophysiological interaction at the organ level and has the potential to contribute to the betterment of the clinical practice of defibrillation.
II. Computational Modeling of Defibrillation and Shock-Induced Arrhythmogenesis
The quest to unravel how shocks succeed in terminating ventricular fibrillation or re-initiate arrhythmia, as described above, has driven the technological aspects of computer simulations of 3-D bidomain activity. In order to be able to simulate electrical processes driven by the delivery of shocks to the ventricles, computational research has managed to overcome tremendous difficulties associated with obtaining solutions of very large systems of unknowns, involving stiff equations and computational meshes of irregular geometry. An overview of the computational approaches involved in conducting simulations of shock administration and postshock arrhythmogenesis is presented as follows.
A. Simulating Cardiac Bioelectric Activity at Tissue and Organ Level
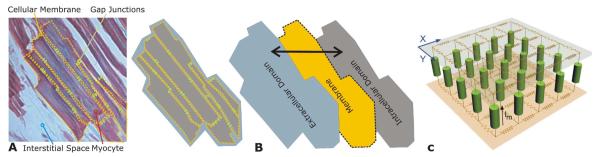
A building block in all computer models of cardiac biolelectric activity are the cardiac myocytes; the intracellular spaces of adjacent myocytes are interconnected by gap junctions [15]. The gap junction distribution over the cell is heterogeneous with a higher density at the intercalated discs located at cell ends (along the long axis of the cell) and a lower density along the lateral boundaries [16], [17]. As a consequence of the elongated cellular geometry and the directionally varying gap junction density, current flows more readily along the cells than transverse to them. The extracellular matrix consists of networks of collagen fibers which determine the passive mechanical properties of the myocardium. It is assumed that the preferred current flow directions are co-aligned between the two spaces, but that the conductivity ratios between the principal axes are unequal between the two domains [18]–[21]. As a consequence, direction and speed of propagation is constantly modified by interactions with discontinuous spatial variations in material properties at various spatial scales.
Typically, cardiac tissue is treated as a continuum, for which appropriate material parameters have to be determined that translate the discrete cellular matrix into an electrically analogous macroscopic representation. This is achieved by averaging material properties over suitable length scales such that both potential and current solutions for the homogenized and discrete representations match. A rigorous mathematical framework for this procedure is provided by the homogenization theory, the latter applied to the bidomain problem by several authors [22]–[25]. Homogenization is a two-step process where the intracellular and interstitial domain are homogenized in a first step and the two respective domains are spread out and overlapped to fill the entire tissue domain in the second. This concept of interpenetrating domains states that everywhere within the entire myocardial volume intracellular space, extracellular space and the cellular membrane coexist (Fig. 2).
Fig. 2.
(A) Cardiac tissue consists of discrete myocytes which are interconnected via gap junctions. (B) Discrete structures in the intracellular and extracellular spaces within the myocardium are homogenized to arrive at a continuum representation, the electrical properties at the discrete microscopic scale and at the continuous macroscopic scale match. Both homogenized domains are overlapped, separated by a membrane at each point in space (interpenetrating domains). (C) Discrete representation of both conductive domains, intra- and extracellular, and the membrane.
B. Governing Equations
The bidomain equations [26] describe the electrical behavior of cardiac tissue as a syncytium, where all tissue parameters are accounted for in an averaged sense. The domains of interest, intracellular and extracellular, and the cellular membranes, which physically separate the two domains, are distributed over the entire tissue volume. The bidomain equations state that currents enter the intracellular or extracellular spaces by crossing the cell membrane represent the sources for the intracellular potential, φi and the extracellular potential, φe
| (1) |
| (2) |
| (3) |
| (4) |
where σi and σe are the intracellular and extracellular conductivity tensors, respectively, β is the bidomain membrane surface to volume ratio, Im is the transmembrane current density, Istim is the current density of the transmembrane stimulus used to initiate an action potential, Ie is the current density of the extracellular stimulus (resulting from the shock), Cm is the membrane capacitance per unit area, Vm is the transmembrane potential, and Iion is the density of the total current flowing through the membrane ionic channels, pumps and exchangers, which depends on Vm and a set of state variables, η. At the tissue boundaries, electrical isolation is assumed, which is accounted for by imposing no-flux boundary conditions on φe and φi. If, however, cardiac tissue is surrounded by a conductive medium, such as blood in the ventricular cavities or a perfusing bath (Tyrode solution) in which the heart is submerged, then the Laplace equation has to be additionally solved
| (5) |
where σb is the isotropic conductivity of the surrounding conductive medium. For a description of model assumptions of the bidomain approach please refer to the comprehensive review by Henriquez [22].
For most applications the bidomain equations are recast into other forms by substituting (4) into (1) and (2) and executing algebraic transformations. Several ways to recast the bidomain equations have been proposed; a systematic overview of the different linear transformations is found in [27]. A widely used transformation is to add (1) and (2) and replace φi by Vm + φe [28]
| (6) |
| (7) |
which retains Vm and φe as the independent variables. For comparison of tissue and organ level simulations with experimental data this is advantageous since φe can be measured via electrical mapping, and optical mapping can be used to record optical signals Vopt ∝ Vm.
C. Computational Considerations
Large-scale computational studies employing the bidomain model in general, and defibrillation studies in particular, have remained a challenge even though computer speed and memory have dramatically increased. There are numerous factors which render any numerical solution of the bidomain equations computationally challenging. First, the upstroke of the action potential is very fast, lasting only ~1 ms. These fast transients translate into a steep propagating wavefront in space, where the depolarization wavefront extends only a few hundreds of μm. As a consequence, both spatially fine-grained computational grids and a high temporal resolution are required to faithfully capture wavefront propagation. Further, the discretized domain of interest has to be large enough to support reentrant wave propagation. With constraints on spatial discretization as mentioned above, the result is a large system, on the order of 0.1 to 100 million degrees of freedom. Finally, the maximum time step which can be taken to advance the solution of the bidomain equations in time is limited, either by stability [29] or accuracy constraints. Since the physiological processes of interest (postshock propagation) take place over seconds or minutes, temporal step size limits necessitate a large number of time steps, typically in the range from tens to hundreds of thousands.
Beyond the high computational load imposed by bidomain simulations in general, there are numerous additional methodological challenges which need to be addressed when using computer models for studying the delivery of defibrillation shocks. To model the effect of extracellularly applied fields, the use of unstructured grids for anatomically realistic heart models is mandatory since it allows smooth representation of the organ’s surfaces. Jagged boundaries, which inevitably form along organ surfaces when regular structured or block structured grids are employed, cause spurious polarizations upon delivery of a defibrillation-strength shock. Another difficulty is the use of state-of-the-art ionic models, which incorporate tens of state variables of ever increasing stiffness. These models are developed and tested within the normal physiological range of action potentials; however, during the shock transmembrane voltages may rise significantly beyond this range, even when ionic models are augmented with additional currents such as electroporation currents [30] or hypothetical potassium currents [31]. Moreover, due to the even faster transients in state variables enforced during shock onset, even smaller time steps may be required, making computations during the shock very burdensome. Typically, modifications are required to render an ionic model suitable for defibrillation studies [32], [33]. Finally, due to the nature of defibrillation, where shock success depends on a multitude of parameters such as shock strength and timing, pulse shape and polarity or electrode geometry and location, a large number of simulations is required to sweep the parameter space. For instance, a standard problem is to determine the window of vulnerability for a given electrode configuration, that is, for which range of shock strength and coupling intervals the tissue is vulnerable to arrhythmia induction. Such studies involve the construction of vulnerability grids where N timings and M shock strengths have to be tested. Therefore, a total of N × M shocks need to be computed and N × M simulations of postshock evolution need to be performed to determine arrhytmia inducibility for each combination.
D. Spatial Discretization
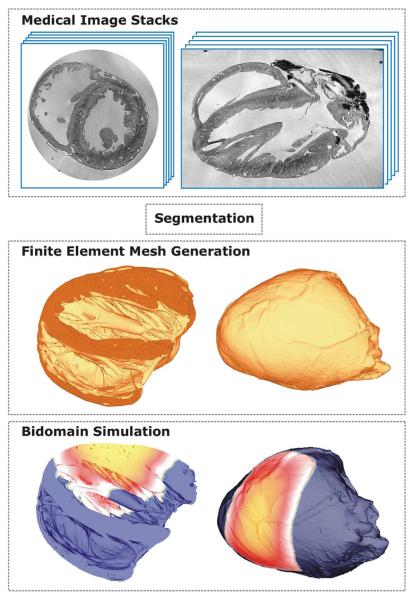
Various spatial discretization techniques have been applied to the cardiac bidomain problem, most notably the finite difference method (FDM) [34], [35], the finite volume method (FVM) [36], [37] and the finite element method (FEM) [38], [39], although other nonstandard techniques such as the interconnected cable model have been employed successfully as well [40], [41]. In general, FDM is easiest to implement, but the method does not accommodate complex boundaries as naturally as FEM or FVM do. Although suggestions were made to overcome this limitation by employing the phase-field approach [42] or other generalizations [43], [44], FDM loses its most appealing advantage, the ease of implementation. FEM and FVM are both very well suited for spatial discretizations of complex geometries with smooth representations of the boundaries, which is a key feature when polarization patterns induced via extracellularly applied currents are to be studied. Both FVM and FEM have been used to model electrical activity in anatomically realistic models of the atria [45]–[48] and the ventricles [4], [35], [49], [50]. Mesh generation requirements are similar for both techniques, that is, the domain of interest has to be tessellated into a set of nonoverlapping and conformal geometric primitives (Fig. 3).
Fig. 3.
Image-based mesh generation for constructing geometrically detailed models of cardiac anatomy. MR image stacks are segmented and fed into an image-based mesh generation algorithm which tesellates classified objects in the image stack into finite element meshes suitable for bidomain simulations.
With FVM, quadrilaterals in 2-D [36] and hexahedral elements in 3-D [37], [45] have been preferred, whereas with FEM, triangles and quadrilaterals were used in 2-D and tetrahedral [50] or hexahedral elements in 3-D [48], [51]. Typically, monolithic meshes consist of one element type only, but exception exist [52], [53], where hybrid meshes consisting of tetrahedra, hexahedra, pyramids and prisms were used. Furthermore, most FEM studies relied on the Galerkin FEM where linear test functions with tetrahedral elements [39], [54], [55], isoparametric trilinear test functions with hexahedral elements [51] or cubichermite hexahedral elements [38], [56] were employed.
Independently of the spatial discretization technique, the choice of space step h is of major importance. It has been known since early modeling studies that the solution of the bidomain equations depends, to a certain degree, h on, even with very fine spatial discretizations [57]. This sensitivity is attributed to the nonlinearity and stiffness of the reaction term resulting from the fast upstroke of the cardiac action potential. During propagation, a fast upstroke in time translates into a steep wavefront in space. Depending on tissue conductivity and cellular excitability, physiological conduction velocities range between 0.2–0.7 m/s within the myocardium, which translates an upstroke duration of 1 ms into a wavefront that extends 200–700 μm in space. Under pathological conditions, where tissue conductivity and/or excitability is reduced, conduction velocity may be substantially slower, resulting in wavefronts of spatial extent even below 100 μm. The spatial extent of a wavefront along a direction ζ is proportional to the space constant λζ
| (8) |
It has been shown that for sufficiently small effective discretizations, Hζ = λζ/hζ < 0.15, solutions converge with deviations in conduction velocity <1% [57]. In practice, a tradeoff has to be made between accuracy and computational tractability. In tissue and organ scale modeling studies a standard choice for h, or for an average discretization h̄ when unstructured grids are considered, is 250 μm, but finer [50] as well as coarser discretizations [4], [56] have been used as well. With very coarse discretizations, h > 500 μm, and physiologically realistic models of cellular dynamics, simulations deviate substantially from results obtained at finer resolutions. Conduction velocities at such coarse grids are underestimated to different degrees as a function of direction, leading to wavefront distortions [58], where even a conduction block might occur as a numerical side effect due to spatial undersampling.
E. Construction of Models of Cardiac Anatomy
As demonstrated in Section II, much of the mechanistic insight into the process of defibrillation was obtained using biophysically detailed realistic-geometry ventricular models (Fig. 4). In order to reconstruct cardiac anatomy, such information must be first obtained via various different imaging modalities, to then be processed and used in model construction. In the last few years, efforts have been focused towards developing techniques to construct 3-D computational cardiac models directly from noninvasive 3-D imaging modalities such as magnetic resonance (MR) [59]-[61]. The advent of stronger magnets and refined scanning protocols has significantly increased the resolution of anatomical MR scans, such that small mammalian hearts now can have MR voxel dimensions of ≈20 – 25 μm [50], [62]. An example of a high resolution anatomical MR scan of a rabbit heart with voxel resolution ≈25 μm isotropic is shown in Fig. 3. As a result of this increase in attainable resolution, anatomical MR imaging is now capable of providing a wealth of information regarding fine-scaled cardiac structural complexity. Such MR data is currently allowing accurate identification of microscopic features such as the coronary vasculature, extracellular cleft spaces and the free-running Purkinje system, as well as macroscopic structures such as trabeculations and papillary muscles. In addition, information regarding the organization of cardiomyocytes into cardiac fibers [63], as well as the laminar structure of the myocardial wall [64], is required to account for orthotropic tissue properties. Such data is unattainable with normal anatomical MR imaging, however the eigenaxes of the tissue can be estimated in 3-D using diffusion-tensor MR imaging (DT-MRI) [59]–[61].
Fig. 4.
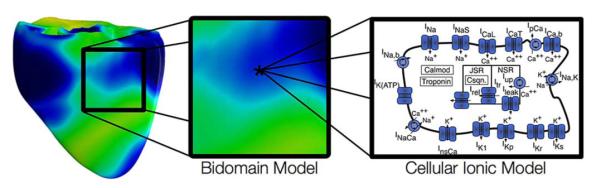
Biophysically detailed realistic-geometry bidomain ventricular model.
This information must then be processed and transformed into a usable format to facilitate the generation of anatomically detailed computational cardiac models. A first processing step is to faithfully extract the complex geometrical information present in the image stacks. This procedure, referred to as segmentation, involves labeling voxels based on their association with different regions, types of tissue, objects or boundaries within the image. Ideally, computational algorithms are employed, which automatically segment regions of interest within the image with little or no manual input. For generating a computational model it is necessary to discriminate those voxels in the MR data set which belong to cardiac “tissue” from those which represent nontissue or “background”, effectively translating a gray-scale MR image data set into a binary black/white (0/1) image mask.
In a final step, classified objects in the binarized image stacks are tesselated into finite element meshes. The construction of such meshes is a highly nontrivial task. Recent advances in image-based mesh generation techniques allow the direct construction of finite element meshes using segmented image stacks as input [52]. Although the exceptionally high resolution of such data sets currently being obtained can provide unprecedented insight regarding intact cardiac anatomical structure, faithfully transferring this information into a finite element mesh that is both of good quality and is computationally tractable, is a significant challenge. A widely used approach is based on a recently published image-based unstructured mesh generation technique [52] or its commercial implementation Tarantula (www.meshing.at, CAE-Software Solutions, Eggenburg, Austria). This method uses a modified dual mesh of an Octree applied directly to segmented 3-D image stacks. The algorithm operates fully automatically with no requirements for interactivity and generates accurate volume-preserving representations of arbitrarily complex geometries with smooth surfaces. The generated unstructured meshes are hybrid, hexahedral-dominant, boundary fitted, locally refined, conformal finite element meshes (see Fig. 3, middle panel). The smooth nature of the surfaces ensures general applicability of the generated meshes, in particular for studies involving the application of strong external stimuli, since the smooth, unstructured grids lack jagged boundaries that can introduce spurious currents due to tip effects. To reduce the overall computational load of the meshes, unstructured grids can be generated adaptively such that the spatial resolution varies throughout the domain. Fine discretizations with little adaptivity can be used to model the myocardium thus minimizing undesired effects of grid granularity on propagation velocity, while coarser elements that grow in size with distance from myocardial surfaces are generated to represent a surrounding volume conductor (e.g., tissue bath or torso for example). Using adaptive mesh generation techniques facilitates the execution of bidomain simulations with a minimum of overhead due to the discretization of the surrounding volume conductor.
F. Numerical Schemes for Solution of Bidomain Problem
Among the possible castings of the bidomain equations, the one presented as (6) and (7) is the most popular. In the most general case, where a conducting medium is in contact with the myocardium, the bidomain equations are written as
| (9) |
| (10) |
| (11) |
Numerically, the bidomain equations can be solved as a coupled system [39] or alternatively, operator splitting techniques are applied [65] to decouple the computing scheme into three components, an elliptic partial differential equation (PDE), a parabolic PDE, and a set of nonlinear ODEs. It has been shown that the decoupled scheme converges quickly against the coupled scheme by employing a Block Gauss-Seidel iteration [66]. However, in most studies the components are essentially treated as independent. Solutions are then found by leap-frogging between the decoupled components where either Vm in (9) or φe in (10) are considered as constant. In [39] it has been found that with small error tolerances the differences between coupled and decoupled approaches are negligible.
Discretizing the decoupled bidomain equations leads to a three-step scheme, which involves a solution of the parabolic PDE, the elliptic PDE and the nonlinear system of ODEs at each time step The inner loop of this scheme is given by
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
where the reaction and diffusion part of the parabolic PDE is split by employing a Strang or a Gudunov scheme [67], [68]. The parabolic portion (12) is solved either by choosing θ = 0.5, which results in a Crank-Nicholson scheme, or θ = 0.0, which results in an explicit forward Euler scheme. Depending on the choice of θ, the overall system is solved then either with a fully explicit or an implicit–explicit (IMEX) scheme. In the latter case, the linear system is solved in parallel. The ODE integration apporoach in (13)–(14) is based on the Rush-Larsen method [69], where an analytical solution is used to update the fast gating variables, ηf (τ and η∞ are functions of the rate coefficients that govern channel gating), and an explicit Euler step is employed to update all other slower state variables ηs, [70], [71].
Typically, additional Dirichlet boundary conditions have to be enforced for the elliptic PDE to eliminate the Nullspace; otherwise, the elliptic system is singular. This is usually achieved by adding a grounding electrode, i.e., choosing nodes in the mesh where φe is set to zero, which serves as the reference potential when simulating the shock, as is the case in a real physical defibrillation setup.
G. Linear Solvers
Although the PDEs are solved most efficiently with direct methods, this is possible for small grids only [39], [72]; otherwise, memory demands increase quickly which, in turn, significantly increases the required number of operations per solver step. Although direct methods have been implemented to run in parallel environments [73], [74], typically they are harder to parallelize due to the fine-grained parallelism, which is communication-intense. For large systems, iterative methods are mandatory.
When executing bidomain simulations on sequential computers, the main computational burden can be attributed to the solution of the elliptic problem and the set of ODEs. Typically, with simple ionic models, the elliptic problem contributes more than 90% to the overall workload, whereas with recent ionic models involving very stiff ODEs [75], [76], the ODE solution may even begin to dominate the computations. The parabolic problem is typically less of a concern. On coarser meshes, where time steps are limited by the ODEs, simple forward Euler steps can be employed to update Vm. In this case, the contributions of the diffusional component (PDE) and the local membrane component to changes in Vm can be updated separately, which renders the PDE linear. On finer grids, semi-implicit Crank-Nicholson schemes perform well. Even when relatively cheap iterative solvers are employed, the parabolic portion can be updated efficiently due to the diagonal dominance of the linear system.
For large systems, on the order of several hundreds of thousands of unknowns, parallel computing approaches are necessary to reduce execution times. The parallel computing context alleviates the problem of solving the set of ODEs. State variables in an ionic model do not diffuse, which qualifies the ODEs as an embarrassingly parallel problem. No communication between processors is required to update the state variable and thus the parallel scaling of the ODE portion is linear. The parabolic problem is efficiently solved in parallel as well. Either only a forward Euler step is required (essentially a matrix-vector product for which good scalability is expected), or the well-posed diagonally dominant linear system is solved efficiently with relatively cheap iterative methods, such as preconditioned conjugate-gradient (CG). Typically, with an incomplete LU (ILU) preconditioner for the iterative CG solver, the parabolic problem can be solved in less than 10 iterations.
The elliptic PDE is the most challenging problem. Standard iterative solvers like ILU-CG typically require several hundreds of iterations to converge, which makes this solution significantly more expensive than that of the parabolic system, although both systems share the same sparsity pattern. The parallel scaling of standard iterative solvers is fairly good [72]; for instance, a parallel ILU-CG solver, where the system is decomposed by a Block Jacobi preconditioner with ILU(0), i.e., an incomplete LU factorization with zero fill-in levels that preserves the sparsity pattern of the original matrix, used as a subblock preconditioner, exhibits good parallel scaling [72]. With fewer number of processors, ILU(N) with N levels of fill-in tends to be more efficient, however, with an increasing number of processors the efficiency of the preconditioning deteriorates since the preconditioner is applied to the main diagonal block only. This can be circumvented by employing overlapping block preconditioners such as additive Schwarz methods; however, they increase the communication burden, which, depending on the particular hardware, may be undesirable.
It has been demonstrated in several recent studies [72], [77], [78] that multilevel preconditioners for CG methods both significantly improve the overall performance and show reasonable parallel efficiency (better than 80%) for up to 128 processors. A generally applicable algebraic multigrid preconditioner (AMG) in conjunction with an iterative Krylov solver reduces the number of iterations per solver step by almost two orders of magnitude compared to ILU-CG. Although a single iteration with AMG is significantly more expensive than with ILU, the reduction in number of iterations clearly favors a multilevel approach. In [72], a speedup of 6 was reported. Using AMG-CG is, to date, the most efficient method for solving the elliptic portion of the bidomain equations. The method is particularly well suited for defibrillation studies since it is computationally efficient and handles unstructured grids straightforwardly.
While the modeling detail and simulation strategy presented in this section is general, the simulation results presented as follows were executed using two major simulation packages, MEMFEM [79] and CARP [80].
III. Contribution of Simulation Insights to Contemporary Understanding of Defibrillation Mechanisms
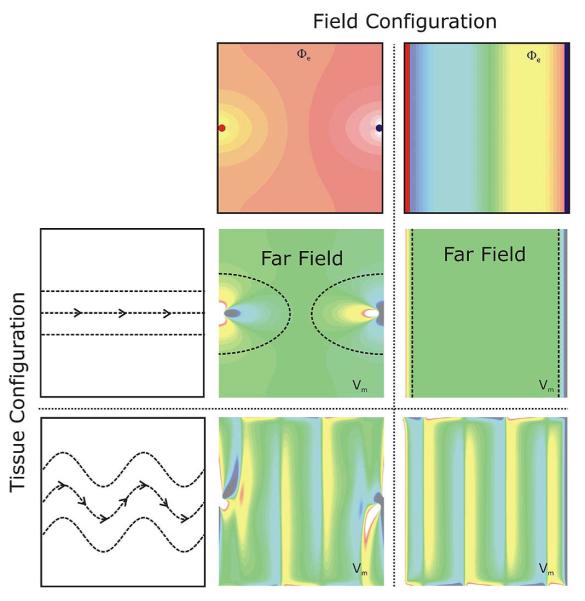
Conceptually, defibrillation can be considered to be a two-step process. Firstly, the applied shock drives currents that traverse the myocardium and cause complex polarization changes in transmembrane potential distribution [81]. Secondly, postshock active membrane reactions are invoked that eventually result either in termination of ventricular fibrillation in the case of shock success, or in reinitiation of fibrillatory activity in the case of shock failure. Using computer models to analyze the etiology of VEP patterns during the shock application phase revealed that the shape, location, polarity, and intensity of shock-induced VEP are determined by both the cardiac tissue structure as well as the configuration of the applied field [12], [81]–[83]. Based on theoretical considerations, VEPs can be classified either as “surface VEP”, which penetrates the ventricular wall over a few cell layers, or as “bulk VEP” where polarizations arise throughout the ventricular wall [84], [85]. Analysis of the bidomain equations revealed that a necessary condition for the existence of the bulk VEP is the presence of unequal anisotropy ratios in the myocardium. Sufficient conditions include either spatial nonuniformity in applied electric field [12], or nonuniformity in tissue architecture, such as fiber curvature [86], fiber rotation [87], fiber branching and anastomosis, and local changes in tissue conductivity due to resistive heterogeneities [88]–[90]. Fig. 5 provides a conceptual understanding of the dependence of the shock-induced VEPs on both the applied field and cardiac tissue structure. Fig. 6 then presents VEPs developed at the end of the defibrillation shock in a realistic model of the rabbit heart under various conditions (shock strengths, durations, waveforms, polarities, and timings of shock delivery).
Fig. 5.
An important insight learned from the bidomain model is that the etiology of VEPs is determined by both field configuration as well as tissue structure. Shown are shock-induced polarization patterns as a function of field and tissue configuration. Top panels: Extracellular potentials Φe, as induced by two point (left) and line electrodes (right). Red (blue) indicates cathodal (anodal) stimulus. Left panels: Two tissue structure configurations are shown, a homogeneous configuration with straight fibers (top), and a configuration where fiber orientation varies as a function of space (bottom). Fiber orientation is indicated by the dashed lines. Central panels: Shock-induced polarization patterns for all possible combinations between field and tissue configuration. In the case of plate electrodes with a homogeneous tissue structure only surface polarizations close to the electrode locations are observed; the bulk of the tissue remains essentially unaffected.
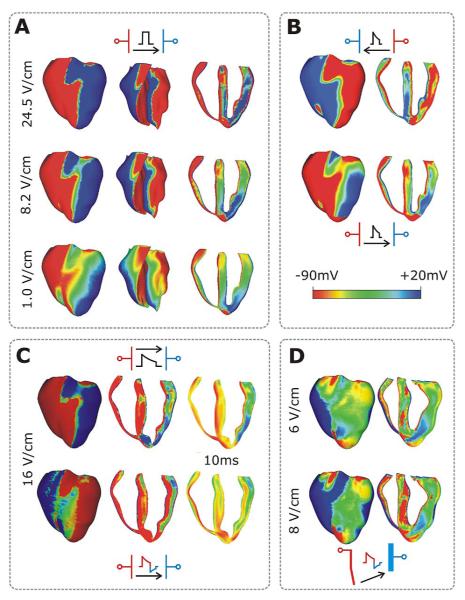
Fig. 6.
Transmembrane potential distribution at shock-end in the rabbit heart for various shock electrode configurations, waveforms, strengths, and polarities as indicated within each panel. Color scale is saturated, i.e., the transmembrane potentials above 20 mV and below 90 mV appear as 20 and 90 mV, respectively. (A) External shocks are monophasic, 4-ms long, and of strengths shown in the figure; they are applied at a coupling interval of 105 ms. For each case, the anterior epicardium and endocardium, and a transmural view of the ventricles are shown. Images are based on figures published in [94]. (B) External truncated-exponential monophasic shocks of reversed polarity and strength ~5 Vcm−1. Anterior epicardium and transmural views of the ventricles are shown. Images are based on figures published in [94]. (C) External truncated-exponential (62% tilt) monophasic and biphasic shocks are of 10 ms duration, coupling interval 220 ms, and of strengths shown in the figure. Anterior epicardium and transmural views of the ventricles are shown. Biphasic shock polarity reverses at 6 ms. In addition, the distribution of transmembrane potential 10 ms after shock-end is shown in a transmural view. (C) ICD-like electrode configuration delivers truncated-exponential (62% tilt) biphasic shocks of 10 ms duration at coupling interval 140 ms, and of strengths shown in the figure.
The cellular reaction to the shock depends on VEP magnitude and polarity as well as on the preshock state of the tissue. Action potential duration can be either extended (by positive VEP) or shortened (by negative VEP) to a degree that depends on VEP magnitude and shock timing, with strong negative VEP completely abolishing (de-exciting) the action potential, thus creating postshock excitable gaps. As demonstrated in bidomain modeling studies [4], [91], the postshock VEP pattern is also the major determinant of the origin of postshock activations. In those regions where shock-induced virtual anodes and cathodes are in close proximity, a “break” excitation at shock-end (i.e., at the “break” of the shock) can be elicited. The virtual cathode serves as an electrical stimulus eliciting a regenerative depolarization and a propagating wave in the newly created excitable area. Whether or not break excitations arise depends on whether the transmembrane potential gradient across the border spans the threshold for regenerative depolarization [92]. The finding of break excitations, combined with the fact that positive VEP can result in “make” excitations (where “make” refers to the onset of a shock) in regions where tissue is at or near diastole, resulted in a novel understanding of how a strong stimulus can trigger the development of new activations.
According to VEP theory, mechanisms for shock success or failure are multifactorial, depending mainly on the postshock distribution of Vm as well as timing and speed of propagation of the shock-induced wavefronts. Whether depolarization of the postshock excitable gap is achieved in time to block post-shock propagation critically depends on the number and conduction velocity of postshock activations, as well as on the available time window which is bounded by the instant at which refractory boundaries enclosing the excitable regions recover excitability. All factors depend, ultimately, on shock strength. Increasing shock strength results in higher voltage gradients across borders between regions of opposite polarity, leading to more break-excitations [92] which then traverse the postshock excitable gap earlier [34] and at a faster velocity [92], as well as extend tissue refractoriness to a larger degree [93].
In the shock failure episodes well below the ULV or the defibrillation threshold (DFT), arrhythmia is induced mostly right after the shock, initiated typically by a break excitation wave that reenters in the heart. However, numerous mapping studies, mostly electrical [95]–[102] but also some optical [103]–[105], have demonstrated that following failed defibrillation shocks or shocks applied during the vulnerable period, reentrant patterns were not always immediately observed. Although local activations were detected following strong shocks, these activations did not become global and quickly died [106]-[109]; the activations were followed by an electrically quiescent period termed the “isoelectric window”. The mechanisms underlying the origin of the first global postshock activations following the isoelectric window have also been the topic of much discussion and debate. Understanding the origins of the isoelectric window and the postshock activations is of great importance for uncovering the mechanisms of defibrillation failure.
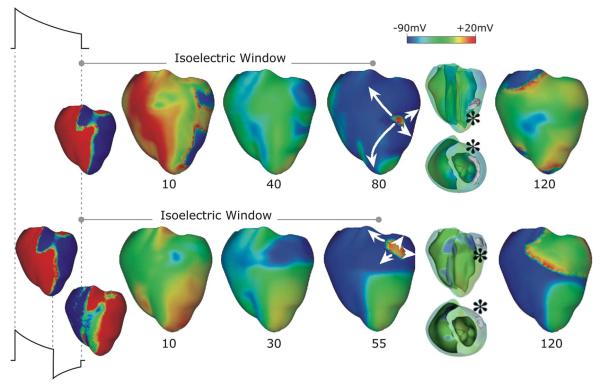
A recent 3-D simulation study proposed a new mechanism for the existence of the isoelectric window [4]. Fig. 7, top, presents an episode of earliest postshock activation following an isoelectric window in a 16-Vcm−1 monophasic shock. Formation of VEP, quick re-excitation, and synchronous repolarization take place sequentially. However, a wavefront which originated at a location deep within the wall remained submerged (transparent panel, wavefront indicated by *) until it made a breakthrough onto the epicardium, and then propagated, resulting in intramural reentry. In this example, the isoelectric window was nearly 80 ms. Fig. 7, bottom, presents an example of a postshock activation following an isoelectric window induced by 12-Vcm−1 biphasic shock. Here again, the wavefront originating 20 ms after shock-end (* in transparent view), which remained submerged for another 35 ms, made a breakthrough onto the epicardium, resulting in intramural scroll wave. In this case the isoelectric window was approximately 55 ms.
Fig. 7.
Monophasic (top) and biphasic (bottom) shock episodes resulting in isoelectric window and arrhythmia initiation in the rabbit heart. Progression of activity from VEP through initiation of intramural activation (transparent view with activation marked by *) to epicardial breakthrough followed by focal activation pattern and ultimately a reentry. Shocks are external of duration 10 ms (6/4 ms for the biphasic shock) and of strengths 16 (monophasic) and 12 (biphasic) Vcm−1 and are delivered at 220 ms coupling interval. Images based on figures published in [4].
The existence of the isoelectric window is explained by propagation of the postshock activations through intramural excitable areas (“tunnel propagation”), bounded by the long-lasting postshock depolarization of the surfaces. Such intramural postshock propagation is consistent with transmural plunge electrode recordings, demonstrating that the site of origin of the postshock activation was within the myocardium rather than on the surface [96], [102].
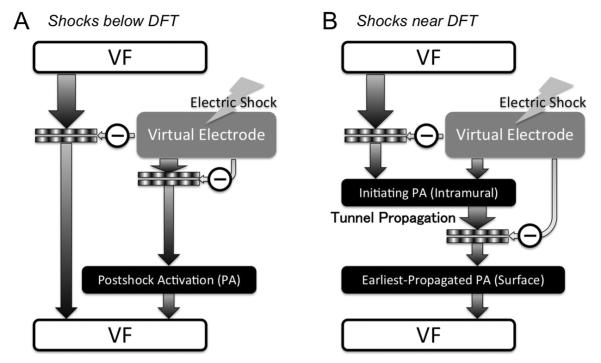
In a recent article by Constantino et al. [110], the new theory of tunnel propagation for near-ULV/DFT shocks was extended to explain the mechanisms responsible for the existence of isoelectric window following ICD shocks delivered to the fibrillating heart. The simulation results demonstrated that the nonuniform field created by ICD electrodes, combined with the fiber orientation and complex geometry of the ventricles, resulted in a postshock excitable region located always in the left ventricular (LV) free wall, regardless of preshock state. For near-ULV/DFT shocks, this excitable region was converted into an intramural tunnel (Fig. 8), through which either preexisting fibrillatory or shock-induced wavefronts propagated during the isoelectric window, emerging as breakthroughs on the LV epicardium. Interestingly, failed defibrillation for near-DFT shocks was found to not always be associated with termination of existing wavefronts and generation of new wavefronts by the shock, as previously believed; instead, wavefronts remained alive in the intramural postshock tunnel. Preshock activity within the LV played a significant role in shock outcome: a large number of preshock fibrillatory wavefronts resulted in an isoelectric window associated with tunnel propagation of pre-existing rather than shock-induced wavefronts. Furthermore, shocks were more likely to succeed if the LV excitable area was smaller. A schematic of the mechanisms of defibrillation failure for shocks well below the DFT and near it is presented in Fig. 9.
Fig. 8.
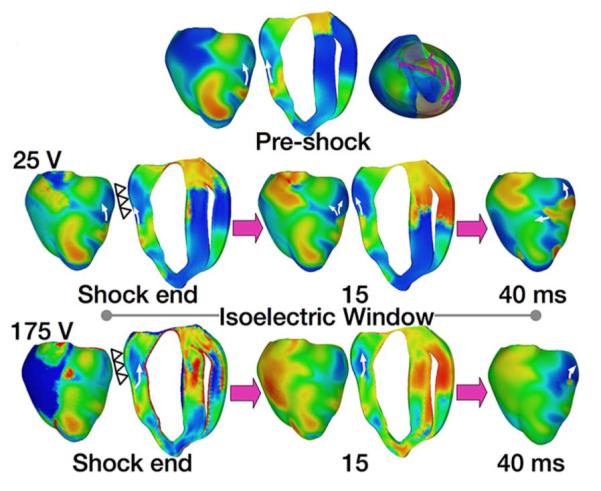
Tunnel propagation of activations following defibrillation shocks in the rabbit heart. Arrows indicate direction of propagation. Presented is the submerging of a preshock fibrillatory wavefront by a strong biphasic shock delivered from an ICD. Figure shows the model, the fibrillatory preshock state (with scroll-wave filaments, the organizing centers of reentry, shown in pink), and postshock transmembrane potential maps for two shock strengths at different postshock timings. In contrast to the 25-V shock, the near-DFT 175-V shock converted the left ventricular (LV) excitable area into an intramural excitable tunnel (see triangular arrows in shock-end panel) with no apparent propagation on the epicardium; the wavefront propagated in it until epicardial breakthrough following the isoelectric window. Images based on figures published in [110].
Fig. 9.
Mechanisms for shock failure, for shocks below (A) and near (B) the DFT.
Finally, ventricular defibrillation models have made signif-icant contributions to understanding the mechanisms of novel means of defibrillating the heart. The recent study by Tandri et al. [111] was based on the fact that sustained kilohertz-range alternating current (ac) fields have been known to block electrical conduction in nervous tissue; this conduction block is instantaneous and completely reversible upon cessation of the stimulus. Tandri et al. hypothesized that electric fields, such as those used for neural block, when applied to cardiac tissue, would similarly produce reversible block of cardiac impulse propagation and lead to successful defibrillation, and that this methodology could potentially be safer means for termination of life-threatening reentrant arrhythmias. The paper provided proof of the concept for conduction block in cardiac tissue during high-frequency ac field stimulation in cell monolayers and animal models (guinea pig and rabbit). Computer simulations using a bidomain rabbit heart model were used to dissect the underlying mechanisms. During field application over a broad frequency range (50 to 1000 Hz), the transmembrane potential of cells remained at a field-dependent, elevated (partially depolarized) voltage throughout the preparation, and pacing-initiated waves were completely blocked. The data revealed a previously unrecognized capacity for myocardial cells to be placed in an extended, yet immediately reversible, state of refractoriness by an applied electric field. The imposed refractory state blocked all wave propagation and resulted in termination of reentrant arrhythmias, without impairment of subsequent cellular electrical function or initiation of postshock fibrillatory activity. The recent efforts towards low-voltage defibrillation [112], [113] have also benefitted from insights obtained by ventricular modeling studies. Trayanova [114] demonstrated that small-scale virtual electrode polarization underlying the appearance of new wave-fronts following a repeated low-voltage field stimuli can arise not only from the coronary vasculature, but also from the presence of trabeculations on the endocardial surface.
IV. Limitations of Ventricular Models of Defibrillation
While ventricular defibrillation models represent the state-of-the-art in ventricular electrophysiological modeling since they require the solution of coupled partial differential equations describing current flow in both the intra- and extracellular spaces, as any modeling approach, they are associated with a number of limitations. The most significant one is the fact that the bidomain representation of the myocardium is a continuum representation, obtained by the process of homogenization as described in Section II of this review. For an extensive discussion on the limitations of the bidomain approximation, the reader is referred to [22] and [23]. Further limitation associated with the bidomain models of defibrillation is that while these multiscale models could incorporate membrane models of various cell and species, all membrane models have been developedbased of voltage clamp data under normal conditions. While efforts have been made to adapt existing membrane models and incorporate in them experimental data regarding cell behavior following defibrillation shocks [33], further experimental data and modeling developments are needed to fully describe the cell response to the shock. Finally, experimental data regarding the bidomain tissue conductivities is scarce and controversial. Because of this fact, ventricular models of defibrillation rely nowadays on matching the conduction velocities in the specific heart (or species) preshock with experimental data, rather than incorporating the reported in the literature bidomain conductivity values.
V. Conclusion
The information and examples presented in this review regarding the development, numerical aspects, and mechanistic insights provided by the 3-D models of shock-induced arrhythmogenesis and defibrillation underscore the achievements and power of realistic modeling and simulation in uncovering and understanding cardiac electrophysiology phenomena. Simulations of defibrillation are particularly useful in revealing shock-induced electrical behavior hidden within the cardiac wall, as demonstrated in this paper; insights into vulnerability and defibrillation, such as these presented here, cannot be achieved with experimental methodology alone. Supported by experimental observations of behavior during and after the shock over the cardiac surfaces, realistic whole-organ simulations have become invaluable in understanding the interaction of the applied electric field with the wavefronts of fibrillation. In addition to defibrillation, biophysically detailed realistic-geometry heart models are currently being employed and are expected to successfully contribute to the study of many other aspects of the mechanisms of arrhythmogenesis as well as to serve as a testbed for other potential anti-arrhythmia therapies.
Acknowledgment
N. Trayanova and G. Plank are cofounders of Cardiosolv, LLC. CardioSolv was not involved in this research.
This work was supported by the National Institutes of Health (NIH) under Award HL082729 (to N. Trayanova) and under Award HL103090 (to J. Constantino), by the National Science Foundation (NSF) under Award CBET-0933029 (to N. Trayanova), and by the Austrian Science Fund (FWF) under Grant SFB F3210-N18 (to G. Plank).
Biography

Natalia Trayanova is a Professor in the Department of Biomedical Engineering and the Institute for Computational Medicine at Johns Hopkins University, Baltimore, MD, and is the inaugural William R. Brody Faculty Scholar. She is the Editor of the book Cardiac Defibrillation—Mechanisms, Challenges and Implications, InTech Publishing, 2011.
Dr. Trayanova is the recipient of numerous awards, among which are the Excellence in Research and Scholarship Award (2005) and Outstanding Researcher Award (2002), and Fulbright Distinguished Research Award (2002). She has published extensively and has presented at a large number of international meetings. She is an Associate Editor of Frontiers in Computational Physiology and Medicine, served as Associate Editor of IEEE Transactions on Biomedical Engineering in the period 1997 to 2005, is on the Editorial Board of the journals Heart Rhythm and American Journal of Physiology (Heart and Circulatory System), and is an Area Editor of IEEE Reviews in Biomedical Engineering. She was the Vice-Chair in 2007 and the Chair in 2009 of the Gordon Research Conference on Cardiac Arrhythmia Mechanisms. She is a Fellow of the Heart Rhythm Society, American Heart Association, and American Institute for Medical and Biological Engineering.

Jason Constantino received the B.S. degree (summa cum laude) in biomedical engineering from Tulane University, New Orleans, LA, in 2006, and is currently working toward the Ph.D. degree in the Department of Biomedical Engineering, the Johns Hopkins University, Baltimore, MD.
His research interests include using computational modeling to uncover the mechanisms of defibrillation and to understand the relation between electrical and mechanical activity of the heart.

Takashi Ashihara received the M.D. and Ph.D. degrees from Shiga University of Medical Science, Otsu, Japan, in 1996 and 2002, respectively.
He is currently an Assistant Professor in the Department of Cardiovascular Medicine, Shiga University of Medical Science, Otsu, Japan. Prior to this, he was a Postdoctoral Research Fellow with the Department of Biomedical Engineering, Tulane University, New Orleans, LA, from 2002 to 2004, and an Assistant Professor (Researcher) with the Department of Physiology and Biophysics, Kyoto University Graduate School of Medicine, Kyoto, Japan, from 2004 to 2005. His research interests include clinical electrophysiology and computer simulations of cardiac arrhythmias.

Gernot Plank received the M.Sc. and Ph.D. degrees in electrical engineering from the Institute of Biomedical Engineering, Technical University of Graz, Austria, in 1996 and 2000, respectively.
Currently he is an Associate Professor with the Institute of Biophysics, Medical University of Graz, Austria, and Academic Fellow with the Oxford e-Research Centre, University of Oxford, U.K. Prior to that, he was a Postdoctoral Fellow with the Technical University of Valencia, Spain, from 2000 to 2002, the University of Calgary, AB, Canada, in 2003, and was a Marie Curie Fellow with Johns Hopkins University, from 2006 through 2008. His research interests include computational modelling of cardiac bioelectric activity, microscopic mapping of the cardiac electric field and defibrillation.
Contributor Information
Natalia Trayanova, Department of Biomedical Engineering and Institute for Computational Medicine, The Johns Hopkins University, Baltimore, MD 20218 USA.
Jason Constantino, Department of Biomedical Engineering and Institute for Computational Medicine, The Johns Hopkins University, Baltimore, MD 20218 USA.
Takashi Ashihara, Shiga University of Medical Science, Otsu 520–2192, Japan.
Gernot Plank, Institute of Biophysics, Medical University of Graz, Graz 8010, Austria.
REFERENCES
- [1].Bardy GH, Hofer B, Johnson G, Kudenchuk PJ, Poole JE, Dolack GL, Gleva M, Mitchell R, Kelso D. Implantable transvenous cardioverter-defibrillators. Circulation. 1993;87(4):1152–1168. doi: 10.1161/01.cir.87.4.1152. [DOI] [PubMed] [Google Scholar]
- [2].Maisel W. Pacemaker and ICD generator reliability: Meta-analysis of device registries. JAMA. 2006;295:1929–1934. doi: 10.1001/jama.295.16.1929. [DOI] [PubMed] [Google Scholar]
- [3].Dosdall D, Fast V, Ideker R. Mechanisms of defibrillation. Annu. Rev. Biomed. Eng. 2010;12:233–258. doi: 10.1146/annurev-bioeng-070909-105305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Ashihara T, Constantino J, Trayanova NA. Tunnel propagation of postshock activations as a hypothesis for fibrillation induction and isoelectric window. Circ. Res. 2008;102(6):737–745. doi: 10.1161/CIRCRESAHA.107.168112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Rodriguez B, Li L, Eason JC, Efimov IR, Trayanova N. Differences between left and right ventricular chamber geometry affect cardiac vulnerability to electric shocks. Circ. Res. 2005;97:168–175. doi: 10.1161/01.RES.0000174429.00987.17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Bishop MJ, Rodriguez B, Qu F, Efimov IR, Gavaghan DJ, Trayanova NA. The role of photon scattering in optical signal distortion during arrhythmia and defibrillation. Biophys. J. 2007;93(10):3714–3726. doi: 10.1529/biophysj.107.110981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Roth BJ, Krassowska W. The induction of reentry in cardiac tissue. The missing link: How electric fields alter transmembrane potential. Chaos. 1998;8(1):204–220. doi: 10.1063/1.166298. [DOI] [PubMed] [Google Scholar]
- [8].Sepulveda NG, Roth BJ, Wikswo JP., Jr. Current injection into a two-dimensional anisotropic bidomain. Biophys. J. 1989;55(5):987–999. doi: 10.1016/S0006-3495(89)82897-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Wikswo JP, Jr., Lin S-F, Abbas RA. Virtual electrodes in cardiac tissue: A common mechanism for anodal and cathodal stimulation. Biophys. J. 1995;69:2195–2210. doi: 10.1016/S0006-3495(95)80115-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Efimov IR, Cheng Y, Biermann M, Van Wagoner DR, Maz-galev TN, Tchou PJ. Transmembrane voltage changes produced by real and virtual electrodes during monophasic defibrillation shock delivered by an implantable electrode. J. Cardiovasc. Electrophysiol. 1997;8:1031–1045. doi: 10.1111/j.1540-8167.1997.tb00627.x. [DOI] [PubMed] [Google Scholar]
- [11].Efimov IR, Gray RA, Roth BJ. Virtual electrodes and deexcitation: New insights into fibrillation induction and defibrillation. J. Cardiovasc. Electrophysiol. 2000;11:339–353. doi: 10.1111/j.1540-8167.2000.tb01805.x. [DOI] [PubMed] [Google Scholar]
- [12].Knisley SB, Trayanova NA, Aguel F. Roles of electric field and fiber structure in cardiac electric stimulation. Biophys. J. 1999;77:1404–1417. doi: 10.1016/S0006-3495(99)76989-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Evans FG, Ideker RE, Gray RA. Effect of shock-induced changes in transmembrane potential on reentrant waves and outcome during cardioversion of isolated rabbit hearts. J. Cardiovasc. Electrophysiol. 2002;13:1118–1127. doi: 10.1046/j.1540-8167.2002.01118.x. [DOI] [PubMed] [Google Scholar]
- [14].Efimov IR, Aguel F, Cheng Y, Wollenzier B, Trayanova NA. Virtual electrode polarization in the far field: Implications for external defibrillation. Amer. J. Physiol. Heart Circ. Physiol. 2000;279:H1055–H1070. doi: 10.1152/ajpheart.2000.279.3.H1055. [DOI] [PubMed] [Google Scholar]
- [15].Desplantez T, Dupont E, Severs NJ, Weingart R. Gap junction channels and cardiac impulse propagation. J. Membr. Biol. 2007;218(1-3):13–28. doi: 10.1007/s00232-007-9046-8. [DOI] [PubMed] [Google Scholar]
- [16].Gourdie RG, Green CR, Severs NJ. Gap junction distribution in adult mammalian myocardium revealed by an anti-peptide antibody and laser scanning confocal microscopy. J. Cell. Sci. 1991;99(pt. 1):41–55. doi: 10.1242/jcs.99.1.41. [DOI] [PubMed] [Google Scholar]
- [17].Hoyt RH, Cohen ML, Saffitz JE. Distribution and three-dimensional structure of intercellular junctions in canine myocardium. Circ. Res. 1989;64(3):563–74. doi: 10.1161/01.res.64.3.563. [DOI] [PubMed] [Google Scholar]
- [18].Clerc L. Directional differences of impulse spread in trabecular muscle from mammalian heart. J. Physiol. 1976;255:335–346. doi: 10.1113/jphysiol.1976.sp011283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Roberts DE, Scher AM. Effect of tissue anisotropy on extracellular potential fields in canine myocardium in situ. Circ. Res. 1982;50(3):342–351. doi: 10.1161/01.res.50.3.342. [DOI] [PubMed] [Google Scholar]
- [20].Roth BJ. Electrical conductivity values used with the bidomain model of cardiac tissue. IEEE Trans. Biomed. Eng. 1997 Apr;44(4):326–328. doi: 10.1109/10.563303. [DOI] [PubMed] [Google Scholar]
- [21].Hooks DA, Trew ML, Caldwell BJ, Sands GB, LeGrice IJ, Smaill BH. Laminar arrangement of ventricular myocytes influences electrical behavior of the heart. Circ. Res. 2007;101(10):e103–e112. doi: 10.1161/CIRCRESAHA.107.161075. [DOI] [PubMed] [Google Scholar]
- [22].Henriquez CS. Simulating the electrical behavior of cardiac muscle using the bidomain model. Crit. Rev. Biomed. Eng. 1993;21:1–77. [PubMed] [Google Scholar]
- [23].Neu J, Krassowska W. Homogenization of syncytial tissue. Crit. Rev. Biomed. Eng. 1993;21(2):137–199. [PubMed] [Google Scholar]
- [24].Pennacchio M, Savare G, Franyone PC. Multiscale modeling for the bioelectric activity of the heart. SIAM J. Math. Anal. 2006;37(4):1333–1370. [Google Scholar]
- [25].Hand PE, Griffith BE, Peskin CS. Deriving macroscopic myocardial conductivities by homogenization of microscopic models. Bull. Math. Biol. 2009 doi: 10.1007/s11538-009-9421-y. [DOI] [PubMed] [Google Scholar]
- [26].Plonsey R. Bioelectric sources arising in excitable fibers (ALZA lecture) Ann. Biomed. Eng. 1988;16(6):519–546. doi: 10.1007/BF02368014. [DOI] [PubMed] [Google Scholar]
- [27].Hooke N, Henriquez CS, Lanzkron P, Rose D. Linear algebraic transformations of the bidomain equations: Implications for numerical methods. Math. Biosci. 1994;120(2):127–145. doi: 10.1016/0025-5564(94)90049-3. [DOI] [PubMed] [Google Scholar]
- [28].Pollard AE, Hooke N, Henriquez CS. Cardiac propagation simulation. Crit. Rev. Biomed. Eng. 1992;20(3-4):171–210. [PubMed] [Google Scholar]
- [29].Courant R, Friedrichs K, Lewy H. Über die partiellen Differenzengleichungen der mathematischen Physik. Mathematische Annalen. 1928;100(1):32–74. [Google Scholar]
- [30].DeBruin KA, Krassowska W. Electroporation and shock-induced transmembrane potential in a cardiac fiber during defibrillation strength shocks. Ann. Biomed. Eng. 1998;26:584–596. doi: 10.1114/1.101. [DOI] [PubMed] [Google Scholar]
- [31].Cheng DK-L, Tung L, Sobie EA. Nonuniform responses of transmembrane potential during electric field stimulation of single cardiac cells. Amer. J. Physiol. Heart Circ. Physiol. 1999;277:H351–H362. doi: 10.1152/ajpheart.1999.277.1.H351. [DOI] [PubMed] [Google Scholar]
- [32].Skouibine K, Trayanova NA, Moore PK. A numerically efficient model for simulation of defibrillation in an active bidomain sheet of myocardium. Math. Biosci. 2000;166:85–100. doi: 10.1016/s0025-5564(00)00019-5. [DOI] [PubMed] [Google Scholar]
- [33].Ashihara T, Trayanova N. Asymmetry in membrane responses to electrical shocks: Insight from bidomain simulations. Biophys. J. 2004;87:2271–2282. doi: 10.1529/biophysj.104.043091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Skouibine K, Trayanova NA, Moore P. Success and failure of the defibrillation shock: Insights from a simulation study. J. Cardiovasc. Electrophysiol. 2000;11:785–796. doi: 10.1111/j.1540-8167.2000.tb00050.x. [DOI] [PubMed] [Google Scholar]
- [35].Potse M, Dube B, Richer J, Vinet A, Gulrajani RM. A comparison of monodomain and bidomain reaction-diffusion models for action potential propagation in the human heart. IEEE Trans. Biomed. Eng. 2006 Dec;53(12, pt. 1):2425–2435. doi: 10.1109/TBME.2006.880875. [DOI] [PubMed] [Google Scholar]
- [36].Harrild DM, Henriquez CS. A finite volume model of cardiac propagation. Ann. Biomed. Eng. 1997;25(2):315–334. doi: 10.1007/BF02648046. [DOI] [PubMed] [Google Scholar]
- [37].Trew M, Le Grice I, Smaill B, Pullan A. A finite volume method for modeling discontinuous electrical activation in cardiac tissue. Ann. Biomed. Eng. 2005;33(5):590–602. doi: 10.1007/s10439-005-1434-6. [DOI] [PubMed] [Google Scholar]
- [38].Rogers JM, McCulloch AD. A collocation-Galerkin finite element model of cardiac action potential propagation. IEEE Trans. Biomed. Eng. 1994 Aug;41(8):743–757. doi: 10.1109/10.310090. [DOI] [PubMed] [Google Scholar]
- [39].Vigmond EJ, Aguel F, Trayanova NA. Computational techniques for solving the bidomain equations in three dimensions. IEEE Trans. Biomed. Eng. 2002 Nov;49(11):1260–1269. doi: 10.1109/TBME.2002.804597. [DOI] [PubMed] [Google Scholar]
- [40].Leon LJ, Roberge FA. Directional characteristics of action potential propagation in cardiac muscle. A model study. Circ. Res. 1991;69(2):378–395. doi: 10.1161/01.res.69.2.378. [DOI] [PubMed] [Google Scholar]
- [41].Wang S, Leon LJ, Roberge FA. Interactions between adjacent fibers in a cardiac muscle bundle. Ann. Biomed. Eng. 1996;24(6):662–674. doi: 10.1007/BF02684179. [DOI] [PubMed] [Google Scholar]
- [42].Fenton FH, Cherry EM, Karma A, Rappel WJ. Modeling wave propagation in realistic heart geometries using the phase-field method. Chaos. 2005;15(1):13502. doi: 10.1063/1.1840311. [DOI] [PubMed] [Google Scholar]
- [43].Buist M, Sands G, Hunter P, Pullan A. A deformable finite element derived finite difference method for cardiac activation problems. Ann. Biomed. Eng. 2003;31(5):577–588. doi: 10.1114/1.1567283. [DOI] [PubMed] [Google Scholar]
- [44].Trew ML, Smaill BH, Bullivant DP, Hunter PJ, Pullan AJ. A generalized finite difference method for modeling cardiac electrical activation on arbitrary, irregular computational meshes. Math. Biosci. 2005;198(2):169–189. doi: 10.1016/j.mbs.2005.07.007. [DOI] [PubMed] [Google Scholar]
- [45].Harrild D, Henriquez C. A computer model of normal conduction in the human atria. Circ. Res. 2000;87(7):E25–E36. doi: 10.1161/01.res.87.7.e25. [DOI] [PubMed] [Google Scholar]
- [46].Virag N, Jacquemet V, Henriquez CS, Zozor S, Blanc O, Vesin JM, Pruvot E, Kappenberger L. Study of atrial arrhythmias in a computer model based on magnetic resonance images of human atria. Chaos. 2002;12(3):754–763. doi: 10.1063/1.1483935. [DOI] [PubMed] [Google Scholar]
- [47].Vigmond EJ, Tsoi V, Kuo S, Arevalo H, Kneller J, Nattel S, Trayanova N. The effect of vagally induced dispersion of action potential duration on atrial arrhythmogenesis. Heart Rhythm. 2004;1(3):334–344. doi: 10.1016/j.hrthm.2004.03.077. [DOI] [PubMed] [Google Scholar]
- [48].Seemann G, Hoper C, Sachse FB, Dossel O, Holden AV, Zhang H. Heterogeneous three-dimensional anatomical and electrophysiological model of human atria. Philos. Transact. A. Math. Phys. Eng. Sci. 2006;364(1843):1465–1481. doi: 10.1098/rsta.2006.1781. [DOI] [PubMed] [Google Scholar]
- [49].Ten Tusscher KH, Hren R, Panfilov AV. Organization of ventricular fibrillation in the human heart. Circ. Res. 2007;100(12):e87–e101. doi: 10.1161/CIRCRESAHA.107.150730. [DOI] [PubMed] [Google Scholar]
- [50].Plank G, Burton R, Hales P, Bishop M, Mansoori T, Bernabeau M, Garny A, Prassl A, Bollensdorf C, Mason F, Rodriguez B, Grau V, Schneider J, Gavaghan D, Kohl P. Generation of histoanatomically representative models of the individual heart: Tools and application. Phil. Trans. Roc. Soc. 2009 doi: 10.1098/rsta.2009.0056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Munteanu M, Pavarino L, Scacchi S. A scalable Newton-Krylov-Schwarz method for the bidomain reaction-diffusion system. SIAM J. Sci. Comput. 2009 [Google Scholar]
- [52].Prassl AJ, Kickinger F, Ahammer H, Grau V, Schneider JE, Hofer E, Vigmond EJ, Trayanova NA, Plank G. Automatically generated, anatomically accurate meshes for cardiac electrophysiology problems. IEEE Trans. Biomed. Eng. 2009 May;56(5):1318–1330. doi: 10.1109/TBME.2009.2014243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Rocha BM, Kickinger F, Prassl AJ, Haase G, Vigmond EJ, Santos RW, Zaglmayr S, Plank G. A macro finite-element formulation for cardiac electrophysiology simulations using hybrid unstructured grids. IEEE Trans. Biomed. Eng. 2011 Apr;58(4):1055–1065. doi: 10.1109/TBME.2010.2064167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Franzone PC, Deuflhard P, Erdmann B, Lang J, Pavarino LF. Adaptivity in space and time for reaction-diffusion systems in electrocardiology. SIAM J. Sci. Comput. 2006;28(3):942–962. [Google Scholar]
- [55].Sundnes J, Nielsen BF, Mardal KA, Cai X, Lines GT, Tveito A. On the computational complexity of the bidomain and monodomain models of electrophysiology. Ann. Biomed. Eng. 2006;34(7):1088–1097. doi: 10.1007/s10439-006-9082-z. [DOI] [PubMed] [Google Scholar]
- [56].Saucerman JJ, Healy SN, Belik ME, Puglisi JL, Mc-Culloch AD. Proarrhythmic consequences of a KCNQ1 AKAP-binding domain mutation: Computational models of whole cells and heterogeneous tissue. Circ. Res. 2004;95(12):1216–1224. doi: 10.1161/01.RES.0000150055.06226.4e. [DOI] [PubMed] [Google Scholar]
- [57].Pollard AE, Burgess MJ, Spitzer KW. Computer simulations of three-dimensional propagation in ventricular myocardium. Effects of intramural fiber rotation and inhomogeneous conductivity on epicardial activation. Circ. Res. 1993;72(4):744–756. doi: 10.1161/01.res.72.4.744. [DOI] [PubMed] [Google Scholar]
- [58].Clayton RH, Bernus O, Cherry EM, Dierckx H, Fenton FH, Mirabella L, Panfilov AV, Sachse FB, Seemann G, Zhang H. Models of cardiac tissue electrophysiology: Progress, challenges and open questions. Prog. Biophys. Mol. Biol. 2011;104(1-3):22–48. doi: 10.1016/j.pbiomolbio.2010.05.008. [DOI] [PubMed] [Google Scholar]
- [59].Vadakkumpadan F, Rantner L, Tice B, Boyle P, Prassl A, Vigmond E, Plank G, Trayanova N. Image-based models of cardiac structure with applications in arrhythmia and defibrillation. J. Electrocardiol. 2009;42(2):157 e1–157 e10. doi: 10.1016/j.jelectrocard.2008.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Vigmond E, Vadakkumpadan F, Gurev V, Arevalo H, Deo M, Plank G, Trayanova N. Towards predictive modelling of the electrophysiology of the heart. Exp. Physiol. 2009;94(5):563–577. doi: 10.1113/expphysiol.2008.044073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Vadakkumpadan F, Arevalo H, Prassl A, Chen J, Kickinger F, Kohl P, Plank G, Trayanova N. Image-based models of cardiac structure in health and disease. Wiley Interdiscip Rev. Syst. Biol. Med. 2010;2:489–506. doi: 10.1002/wsbm.76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Burton R, Plank G, Schneider J, Grau V, Ahammer H, Keeling S, Lee J, Smith N, Gavaghan D, Trayanova N, Kohl P. 3-d models of individual cardiac histo-anatomy: Tools and challenges. Ann. NY Acad. Sci. 2006;1380:301–319. doi: 10.1196/annals.1380.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Streeter D, Spontnitz H, Patel D, Ross J, Sonnenblick E. Fiber orientation in the canine left ventricle during diastole and systole. Circ. Res. 1969;24:339–347. doi: 10.1161/01.res.24.3.339. [DOI] [PubMed] [Google Scholar]
- [64].LeGrice I, Smaill B, Chai L, Edgar S, Gavin J, Hunter P. Laminar structure of the heart: Ventricular myocyte arrangement and connective tissue architecture in the dog. Amer. J. Physiol. Heart Circ. Physiol. 1995;269:H571–H582. doi: 10.1152/ajpheart.1995.269.2.H571. [DOI] [PubMed] [Google Scholar]
- [65].Keener JP, Bogar K. A numerical method for the solution of the bidomain equations in cardiac tissue. Chaos. 1998;8(1):234–241. doi: 10.1063/1.166300. [DOI] [PubMed] [Google Scholar]
- [66].Pennacchio M, Simoncini V. Efficient algebraic solution of reaction-diffusion systems for the cardiac excitation process. J. Comp. Appl. Math. 2002;145:49–70. [Google Scholar]
- [67].Qu Z, Garfinkel A. An advanced algorithm for solving partial differential equation in cardiac conduction. IEEE Trans. Biomed. Eng. 1999 Sep;46(9):1166–1168. doi: 10.1109/10.784149. [DOI] [PubMed] [Google Scholar]
- [68].Sundnes J, Lines GT, Tveito A. An operator splitting method for solving the bidomain equations coupled to a volume conductor model for the torso. Math. Biosci. 2005;194(2):233–248. doi: 10.1016/j.mbs.2005.01.001. [DOI] [PubMed] [Google Scholar]
- [69].Rush S, Larsen H. A practical algorithm for solving dynamic membrane equations. IEEE Trans. Biomed. Eng. 1978 Apr;25(4):389–392. doi: 10.1109/TBME.1978.326270. [DOI] [PubMed] [Google Scholar]
- [70].Plank G, Zhou L, Greenstein JL, Cortassa S, Winslow RL, O’Rourke B, Trayanova NA. From mitochondrial ion channels to arrhythmias in the heart: Computational techniques to bridge the spatio-temporal scales. Philos. Trans. A. Math. Phys. Eng. Sci. 2008;366(1879):3381–3409. doi: 10.1098/rsta.2008.0112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Maclachlan MC, Sundnes J, Spiteri RJ. A comparison of nonstandard solvers for ODEs describing cellular reactions in the heart. Comput. Methods Biomech. Biomed. Engin. 2007;10(5):317–326. doi: 10.1080/10255840701259301. [DOI] [PubMed] [Google Scholar]
- [72].Plank G, Liebmann M, Weber dos Santos R, Vigmond EJ, Haase G. Algebraic multigrid preconditioner for the cardiac bidomain model. IEEE Trans. Biomed. Eng. 2007 Apr;54(4):585–596. doi: 10.1109/TBME.2006.889181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Li X, Demmel J. SuperLU DIST: A scalable distributed-memory sparse direct solver for unsymmetric linear systems. ACM Trans. Mathematical Software (TOMS) 2003;29(2):110–140. [Google Scholar]
- [74].Amestoy P, Duff IS, L’Excellent J-Y, Koster J. Mumps: A general purpose distributed memory sparse solver; PARA’00: Proc. 5th Int. Workshop Applied Parallel Computing, New Paradigms for HPC in Industry and Academia; London, U.K.. 2001; pp. 121–130. Springer-Verlag. [Google Scholar]
- [75].Iyer V, Mazhari R, Winslow RL. A computational model of the human left-ventricular epicardial myocyte. Biophys. J. 2004;87(3):1507–1525. doi: 10.1529/biophysj.104.043299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Cortassa S, Aon MA, O’Rourke B, Jacques R, Tseng HJ, Marban E, Winslow RL. A computational model integrating electrophysiology, contraction, and mitochondrial bioenergetics in the ventricular myocyte. Biophys. J. 2006;91(4):1564–1589. doi: 10.1529/biophysj.105.076174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].Weber dos Santos R, Plank G, Bauer S, Vigmond E. Parallel multigrid preconditioner for the cardiac bidomain model. IEEE Trans. Biomed. Eng. 2004 Nov;51(11):1960–1968. doi: 10.1109/TBME.2004.834275. [DOI] [PubMed] [Google Scholar]
- [78].Austin TM, Trew ML, Pullan AJ. Solving the cardiac bidomain equations for discontinuous conductivities. IEEE Trans. Biomed. Eng. 2006 Jul;53(7):1265–1272. doi: 10.1109/TBME.2006.873750. [DOI] [PubMed] [Google Scholar]
- [79].Trayanova NA, Eason JC, Aguel F. Computer simulations of cardiac defibrillation: A look inside the heart. Comp. Vis. Sci. 2002;4:259–270. [Google Scholar]
- [80].Vigmond EJ, Hughes M, Plank G, Leon LJ. Computational tools for modeling electrical activity in cardiac tissue. J. Electrocardiol. 2003;36(Suppl):69–74. doi: 10.1016/j.jelectrocard.2003.09.017. [DOI] [PubMed] [Google Scholar]
- [81].Sobie EA, Susil RC, Tung L. A generalized activating function for predicting virtual electrodes in cardiac tissue. Biophys. J. 1997;73(3):1410–1423. doi: 10.1016/S0006-3495(97)78173-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [82].Trayanova NA. Concepts of ventricular defibrillation. Phil. Trans. Roy. Soc. London A. 2001;359(1783):1327–1337. [Google Scholar]
- [83].Rodriguez B, Li L, Eason JC, Efimov IR, Trayanova NA. Differences between left and right ventricular chamber geometry affect cardiac vulnerability to electric shocks. Circ. Res. 2005;97(2):168–175. doi: 10.1161/01.RES.0000174429.00987.17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [84].Trayanova N, Skouibine K, Aguel F. The role of cardiac tissue structure in defibrillation. Chaos. 1998;8(1):221–233. doi: 10.1063/1.166299. [DOI] [PubMed] [Google Scholar]
- [85].Entcheva E, Trayanova NA, Claydon FJ. Patterns of and mechanisms for shock-induced polarization in the heart: A bidomain analysis. IEEE Trans. Biomed. Eng. 1999 Mar;46(3):260–270. doi: 10.1109/10.748979. [DOI] [PubMed] [Google Scholar]
- [86].Trayanova NA, Roth BJ, Malden LJ. The response of a spherical heart to a uniform electric field: A bidomain analysis of cardiac stimulation. IEEE Trans. Biomed. Eng. 1993 Aug;40(8):899–908. doi: 10.1109/10.245611. [DOI] [PubMed] [Google Scholar]
- [87].Entcheva E, Trayanova NA, Claydon F. Patterns of and mechanisms for shock-induced polarization in the heart: A bidomain analysis. IEEE Trans. Biomed. Eng. 1999 Feb;46(2):260–270. doi: 10.1109/10.748979. [DOI] [PubMed] [Google Scholar]
- [88].Fast VG, Rohr S, Gillis AM, Kléber AG. Activation of cardiac tissue by extracellular electrical shocks: Formation of ”secondary sources“ at intercellular clefts in monolayers of cultured myocytes. Circ. Res. 1998;82:375–385. doi: 10.1161/01.res.82.3.375. [DOI] [PubMed] [Google Scholar]
- [89].Fishler MG. Syncytial heterogeneity as a mechanism underlying cardiac far-field stimulation during defibrillation-level shocks. J. Cardiovasc. Electrophysiol. 1998;9:384–394. doi: 10.1111/j.1540-8167.1998.tb00926.x. [DOI] [PubMed] [Google Scholar]
- [90].Hooks DA, Tomlinson KA, Marsden SG, LeGrice IJ, Smaill BH, Pullan AJ, Hunter PJ. Cardiac microstructure: Implications for electrical propagation and defibrillation in the heart. Circ. Res. 2002;91:331–338. doi: 10.1161/01.res.0000031957.70034.89. [DOI] [PubMed] [Google Scholar]
- [91].Roth BJ. A mathematical model of make and break electrical stimulation of cardiac tissue by a unipolar anode or cathode. IEEE Trans. Biomed. Eng. 1995 Sep;42(9):1174–1184. doi: 10.1109/10.476124. [DOI] [PubMed] [Google Scholar]
- [92].Cheng Y, Mowrey KA, Van Wagoner DR, Tchou PJ, Efimov IR. Virtual electrode induced re-excitation: A mechanism of defibrillation. Circ. Res. 1999;85:1056–1066. doi: 10.1161/01.res.85.11.1056. [DOI] [PubMed] [Google Scholar]
- [93].Knisley S, Smith W, Ideker R. Prolongation and shortening of action potentials by electrical shocks in frog ventricular muscle. Amer. J. Physiol. Heart Circ. Physiol. 1994;266(6, pt. 2):H2348–H2358. doi: 10.1152/ajpheart.1994.266.6.H2348. [DOI] [PubMed] [Google Scholar]
- [94].Rodriguez B, Trayanova N. Upper limit of vulnerability in a defibrillation model of the rabbit ventricles. J. Electrocardiol. 2003;36(Suppl):51–56. doi: 10.1016/j.jelectrocard.2003.09.066. [DOI] [PubMed] [Google Scholar]
- [95].Zhou X, Daubert JP, Wolf PD, Smith WM, Ideker RE. Epicardial mapping of ventricular defibrillation with monophasic and biphasic shocks in dogs. Circ. Res. 1993;72:145–160. doi: 10.1161/01.res.72.1.145. [DOI] [PubMed] [Google Scholar]
- [96].Chen P-S, Shibata N, Dixon EG, Wolf PD, Danieley ND, Sweeney MB, Smith WM, Ideker RE. Activation during ventricular defibrillation in open-chest dogs: Evidence of complete cessation and regeneration of ventricular fibrillation after unsuccessful shocks. J. Clin. Invest. 1986;77:810–823. doi: 10.1172/JCI112378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [97].Chen P-S, Shibata N, Dixon EG, Martin RO, Ideker RE. Comparison of the defibrillation threshold and the upper limit of ventricular vulnerability. Circulation. 1986;73:1022–1028. doi: 10.1161/01.cir.73.5.1022. [DOI] [PubMed] [Google Scholar]
- [98].Shibata N, Chen P-S, Dixon EG, Wolf PD, Danieley ND, Smith WM, Ideker RE. Epicardial activation after unsuccessful defibrillation shocks in dogs. Amer. J. Physiol. Heart Circ. Physiol. 1988;255:H902–H909. doi: 10.1152/ajpheart.1988.255.4.H902. [DOI] [PubMed] [Google Scholar]
- [99].Usui M, Callihan RL, Walker RG, Walcott GP, Rollins DL, Wolf PD, Smith WM, Ideker RE. Epicardial sock mapping of following monophasic and biphasic shocks of equal voltage with an endocardial lead system. J. Cardiovasc. Electrophysiol. 1996;7:322–334. doi: 10.1111/j.1540-8167.1996.tb00533.x. [DOI] [PubMed] [Google Scholar]
- [100].Chattipakorn N, Fotuhi PC, Ideker RE. Prediction of defibrillation outcome by epicardial activation patterns following shocks near the defibrillation threshold. J. Cardiovasc. Electrophysiol. 2000;11:1014–1021. doi: 10.1111/j.1540-8167.2000.tb00174.x. [DOI] [PubMed] [Google Scholar]
- [101].Chattipakorn N, Rogers J, Ideker RE. Influence of postshock epicardial activation patterns on initiation of ventricular fibrillation by upper limit of vulneraibility shocks. Circulation. 2000;101:1329–1336. doi: 10.1161/01.cir.101.11.1329. [DOI] [PubMed] [Google Scholar]
- [102].Chattipakorn N, Fotuhi PC, Chattipakorn SC, Ideker RE. Three-dimensional mapping of earliest activation after near-threshold ventricular defibrillation shocks. J. Cardiovasc. Electrophysiol. 2003;14:65–69. doi: 10.1046/j.1540-8167.2003.02397.x. [DOI] [PubMed] [Google Scholar]
- [103].Chattipakorn N, Banville I, Gray RA, Ideker RE. Mechanism of ventricular defibrillation for near-defibrillation threshold shocks: A whole-heart optical mapping study in swine. Circulation. 2001;104:1515–1525. doi: 10.1161/hc3601.094295. [DOI] [PubMed] [Google Scholar]
- [104].Chattipakorn N, Banville I, Gray RA, Ideker RE. Effects of shock strengths on ventricular defibrillation failure. Cardiovasc. Res. 2004;61:39–44. doi: 10.1016/j.cardiores.2003.10.009. [DOI] [PubMed] [Google Scholar]
- [105].Wang NC, Lee M-H, Ohara T, Okuyama Y, Fishbein GA, Lin S-F, Karagueuzian HS, Chen P-S. Optical mapping of ventricular defibrillation in isolated swine ventricles: Demonstration of a postshock isoelectric window after near-threshold defibrillation shocks. Circulation. 2001;104:227–233. doi: 10.1161/01.cir.104.2.227. [DOI] [PubMed] [Google Scholar]
- [106].Moe GK, Harris AS, Wiggers CJ. Analysis of the initiation of fibrillation by electrographic studies. Amer. J. Physiol. Heart Circ. Physiol. 1941;134:473–492. [Google Scholar]
- [107].Shibata N, Chen P-S, Dixon EG, Wolf PD, Danieley ND, Smith WM, Ideker RE. Influence of shock strength and timing on induction of ventricular arrhythmias in dogs. Amer. J. Physiol. Heart Circ. Physiol. 1988;255:H891–H901. doi: 10.1152/ajpheart.1988.255.4.H891. [DOI] [PubMed] [Google Scholar]
- [108].Idriss SF, Wolf PD, Smith WM, Ideker RE. Effect of pacing site on ventricular fibrillation initiation by shocks during the vulnerable period. Amer. J. Physiol. Heart Circ. Physiol. 1999;227:H2065–H2082. doi: 10.1152/ajpheart.1999.277.5.H2065. [DOI] [PubMed] [Google Scholar]
- [109].Chattipakorn N, KenKnight BH, Rogers JM, Walker RG, Walcott GP, Rollins DL, Smith WM, Ideker RE. Locally propagated activation immediately after internal defibrillation. Circulation. 1998;97:1401–1410. doi: 10.1161/01.cir.97.14.1401. [DOI] [PubMed] [Google Scholar]
- [110].Constantino J, Long Y, Ashihara T, Trayanova N. Tunnel propagation following defibrillation with ICD shocks: Hidden postshock activations in the left ventricular wall underlie isoelectric window. Heart Rhythm. 2010;7(7):953–961. doi: 10.1016/j.hrthm.2010.03.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [111].Tandri H, Weinberg S, Chang K, Zhu R, Trayanova N, Tung L, Berger R. Reversible cardiac conduction block and defibrillation with high-frequency electric field. Sci. Translational Medicine. 2011;3(102):102 ra96–102ra96. doi: 10.1126/scitranslmed.3002445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [112].Ambrosi C, Ripplinger C, Efimov I, Fedorov V. Termination of sustained atrial flutter and fibrillation using low voltage multiple shock therapy. Heart Rhythm. 2010:101–108. doi: 10.1016/j.hrthm.2010.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [113].Luther S, et al. Low-energy control of electrical turbulence in the heart. Nature. 2011;475(7355):235–239. doi: 10.1038/nature10216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [114].Trayanova N. Atrial defibrillation voltage: Falling to a new low. Heart Rhythm. 2010:109–110. doi: 10.1016/j.hrthm.2010.10.037. [DOI] [PMC free article] [PubMed] [Google Scholar]