Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2001 May 8;98(10):5758–5763. doi: 10.1073/pnas.101113698

Cooperative enhancement of specificity in a lattice of T cell receptors

Cliburn Chan *,†, Andrew J T George †,‡,§, Jaroslav Stark *,†
PMCID: PMC33286  PMID: 11344310

Abstract

Two of the most important models to account for the specificity and sensitivity of the T cell receptor (TCR) are the kinetic proofreading and serial ligation models. However, although kinetic proofreading provides a means for individual TCRs to measure accurately the length of time they are engaged and signal appropriately, the stochastic nature of ligand dissociation means the kinetic proofreading model implies that at high concentrations the response of the cell will be relatively nonspecific. Recent ligand experiments have revealed the phenomenon of both negative and positive crosstalk among neighboring TCRs. By using a Monte Carlo simulation of a lattice of TCRs, we integrate receptor crosstalk with the kinetic proofreading and serial ligation models and discover that receptor cooperativity can enhance T cell specificity significantly at a very modest cost to the sensitivity of the response.

The T cell can recognize and respond appropriately to small numbers of its cognate ligand in the presence of up to a 10,000-fold excess of irrelevant antigens (mostly consisting of a wide diversity of self peptides) on the surface of an antigen presenting cell (APC; refs. 1 and 2). The T cell receptor (TCR) affinity for self peptide:MHC does not differ from that for foreign peptide:MHC by the same order of magnitude, suggesting that the number of TCRs engaged by self antigens will exceed the number engaged by foreign antigens at any one time. Because negative selection in the thymus during T cell maturation will remove autoreactive T cells, the self peptides presented on the APC will be seen with low affinity. However, T cells must retain some affinity for self antigens, because recognition of self molecules is necessary for naive T cell survival. The T cell, therefore, has a considerable challenge in being sensitive to small numbers of foreign antigens, yet specific enough to reliably distinguish infected and foreign cells from normal ones.

Recently, two important models have contributed greatly to our understanding of how this sensitivity and specificity are achieved. At the level of the individual TCR, kinetic models, in particular the kinetic proofreading model of McKeithan (3), explain how the TCR can reliably distinguish different ligands based on the duration of engagement (3–9). At the cellular level, the serial ligation model (10–12) shows how individual recognition events can be amplified by a single ligand serially engaging multiple different TCRs, resulting in a large gain in sensitivity.

Although the affinity of TCR for peptide:MHC is low (0.1–50 μM), it has been found that T cell activation does not necessarily correlate well with affinity (13, 14) but does so with the dissociation time of the ligand (15, 16). The kinetic proofreading model (3) explains this finding by suggesting that the ligand–receptor complex must pass through a series of intermediate stages before being activated fully. Dissociation of the ligand at any of the intermediate stages aborts the process. Other kinetic models allow intermediate stages (8) or alternative pathways (9) to generate negative signals. Alternative models for ligand discrimination at the receptor level include conformational change and architectural models (7), but the majority of data supports the kinetic models.

More recently, there has been experimental evidence for crosstalk between receptors, involving both positive and negative signaling (Fig. 1). Experimental evidence for a negative signal and evidence that it may spread to other receptors have been documented in dual specificity CD4+ T cell clones by using an antagonist ligand specific for only one of the TCRs (17, 18), although this result was not seen in similar experiments using CD8 + T cells. Germain and Štefanov́a (19) have suggested that this spreading inhibition of neighboring receptors is mediated by the recruitment of the phosphatase SHP-1, resulting in dephosphorylation and inactivation of lck kinase. This inhibition lasted for a significant duration, because the T cell remained inhibited when subsequently incubated with an APC-bearing agonist ligand. Similarly, Germain and Štefanov́a have documented a protection process that occurs when a receptor is activated fully by an agonist, mediated by the MAP kinase ERK-1, which seems to prevent SHP-1 binding to lck.

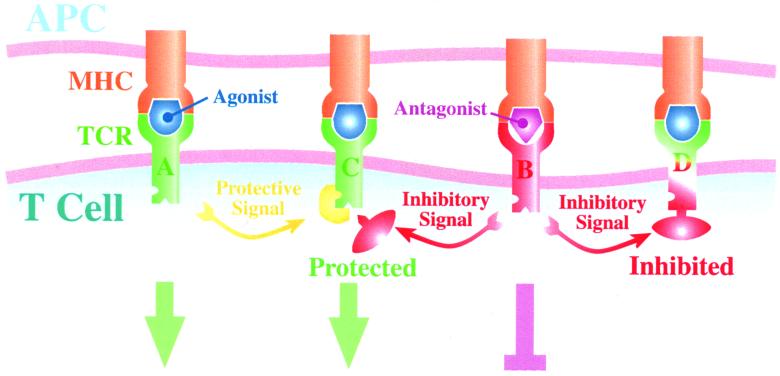
Figure 1.

Figure 1

Open in a new tab

Mechanism of action for spreading inhibition and protection. TCR A first binds to an agonist, which results in full downstream signaling. At the same time, protective molecules (e.g., ERK-1) are recruited to its neighbors (illustrated here by TCR C). Subsequently, TCR B binds to an antagonist, which results in partial downstream signaling. This incomplete activation results in the recruitment of inhibitory molecules (e.g., SHP-1) to its neighbors (illustrated here by TCRs C and D). TCR C is protected by ERK-1; thus SHP-1 fails to dock and has no effect, whereas TCR D is inhibited. Finally, both TCRs C and D bind to an agonist. This interaction results in full downstream signaling for TCR C, which is protected, but there is no downstream signal generated by TCR D, which is inhibited.

In this article, we integrate the kinetic and serial ligation models into a unified simulation and explore the implications of cooperative TCR signaling on sensitivity and specificity.

Methods

We simulate the TCRs at the T cell:APC interface with a square lattice of receptors (Fig. 2). Each individual TCR can exist in one of several basic states (empty, occupied, partially activated, and fully activated) at any one time (Fig. 3). In addition, TCRs are also unmodified, inhibited, or protected by means of the process of spreading inhibition and protection. Inhibited TCRs are incapable of further signaling, whereas protected TCRs behave like unmodified TCRs, except that they cannot be inhibited.

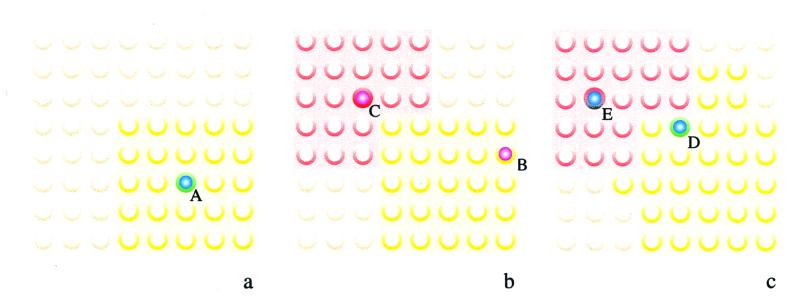
Figure 2.

Figure 2

Open in a new tab

Modeling spreading inhibition and protection in a lattice of TCR. In our model, TCR are arrayed in a lattice, initially in an unmodified state (light gold circles). In a, the example of TCR A binding to an agonist is shown. This interaction results in the protection of its neighboring receptors (yellow). In b, TCR C subsequently binds to an antagonist, resulting in spreading inhibition for its neighbors (red), except for receptors already protected. Binding of an antagonist to protected receptor B has no effect. In c, binding of an agonist to inhibited receptor E has no effect, whereas binding of an agonist to protected receptor D succeeds in signaling and extending the neighborhood of protected receptors.

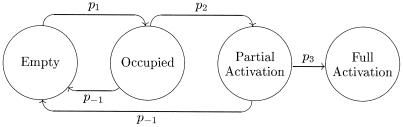
Figure 3.

Figure 3

Open in a new tab

Possible changes of state for simulated TCR. A TCR may exist in any of the states shown within circles, and arrows between circles represent possible state transitions with probability pi. In each simulation time step, a TCR has a probability of changing its state. An empty TCR may bind to a ligand and become occupied with probability p1 (0.1 s−1). An occupied TCR may become partially activated with probability p2, and a partially activated TCR may become fully activated with probability p3. The probability for these events is given by a sigmoid function of the duration of ligand binding, with thresholds of 3 and 5 sec, respectively. Dissociation of ligand occurs with probability p−1 and depends only on the koff. Dissociation before full activation results in the TCR reverting to the empty state, whereas fully activated TCRs are down-regulated. Partially and fully activated TCRs send inhibition and protection signals, respectively, to their neighbors, as illustrated in Figs. 1 and 2.

Most of the simulations were done with 2,500 receptors (50 by 50 matrix) and 10,000 ligands. We also have done simulations with up to 25,000 TCRs and 100,000 ligands, but scaling upward does not qualitatively affect the results.

Initially, all ligands are placed in a pool of free ligands. Ligands that bind to TCRs are removed from this pool and are replaced when they dissociate. Thus, serial ligation is incorporated automatically into the simulation. In the experiments described in this article, only two types of ligands are simulated. One represents the specific ligand and has a lower koff and is fewer in number than the other, which represents self ligands.

Initially, all receptors are in the empty state, without any protection or inhibition. The probability of encounter between ligand and TCR is set at 0.1 per sec, assuming that diffusion in the cell membrane is limiting. The threshold (defined as the time of ligand binding necessary for 50% of TCRs to change from one state to another) for partial activation is set at 3 sec after ligand engagement, and the threshold for full activation is set at 5 sec after partial activation, using the durations suggested by experiments with soluble receptors at 25°C (15). The simulations reported here were done with a neighborhood size of 25 receptors for spreading inhibition and protection. A maximum of 1% of total initial receptor number can be in an activated state at any one time, simulating some limiting resource or substrate (e.g., a limiting kinase or spatial constraints). We take the percentage of TCRs fully activated in 60 min as a measure of the strength of the signal received by the T cell.

Results

Poor Specificity in Absence of Signal Spread.

Running the simulation in the absence of any cooperativity (either inhibition or protection) allows us to test the predictions of a combined kinetic/serial ligation model of T cell signaling.

Because our measure of the strength of the signal received by the T cell is the total number of fully activated TCRs, there is an optimal koff (kopt) that results in the strongest signal to the T cell (Fig. 4). Ligands that are more avid than this optimum can fully activate TCRs but fail to ligate many TCRs serially. Ligands less avid than this optimum serially ligate multiple TCRs but often fail to bind long enough to result in full activation of the TCR. This result is in agreement with the prediction by Valitutti and Lanzavecchia (11), as well as with data by Hudrisier et al. (20); however, the result remains controversial, because other experiments fail to show a unimodal distribution about some optimum with improvements in TCR:peptide-MHC stability (21).

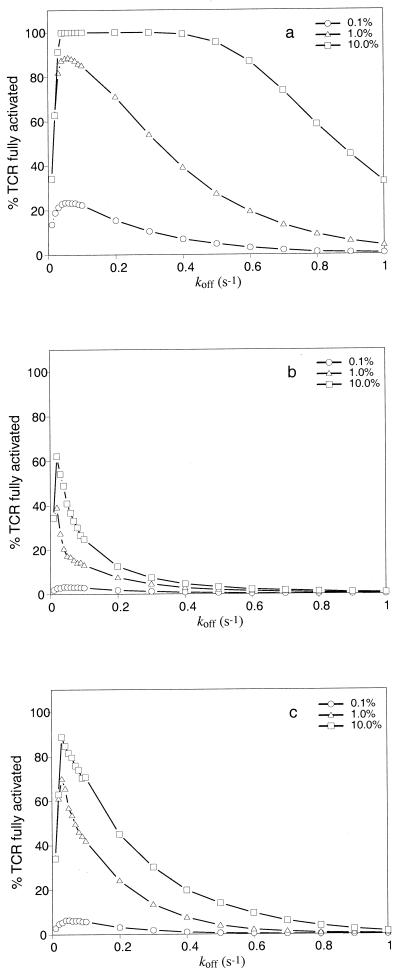
Figure 4.

Figure 4

Open in a new tab

Effects of receptor crosstalk on specificity and sensitivity. The figures show the percentage of TCRs fully activated by ligands with different koff. Ligand density is expressed as a fraction of the total, with the remainder being null ligands (koff = 5 s−1). a–c are for simulations without receptor crosstalk, with spreading inhibition only, and with both inhibition and protection, respectively. a shows that in the absence of inhibition or protection, there is a marked dependence on concentration, such that poor quality ligands with high density can result in fully activating many TCRs. In b, there is spreading inhibition, and now only ligands close to the kopt can fully activate significant numbers of TCRs. Ligands with high koff cannot fully activate many TCRs, even at densities of 10% of the total. c shows the tradeoff between specificity and sensitivity in the presence of spreading protection. At kopt, more TCRs are fully activated at each concentration level than in b, but the hump of the curve is slightly broader. An average of 10 experiments is shown.

An interesting result is that as the concentration of specific ligand increases, the graph shows a broad plateau over a large range of koff where signaling is maximal (Fig. 4a). For example, a ligand with a koff of 0.5 s−1, which would have fully activated only 3% of TCRs at a density of 0.1%, will fully activate close to 100% at a density of 10%. Obviously, in such a situation, specificity is very poor and concentration-dependent.

The problem arises because ligand dissociation from the TCR is a stochastic process. Even for low-affinity ligands, there is a small but finite probability that a ligand will bind for long enough to activate a TCR fully. As a result, as ligand density increases, even low-affinity ligands may result in a significant number of TCRs delivering a complete signal, limited only by MHC availability on the APC. This result suggests that partial agonists and possibly even antagonists can be converted to full agonists by increasing their concentrations, which is not seen experimentally (22).

These data highlight a problem with the serial ligation and kinetic proofreading models, which both assume that TCRs act independently. If this assumption is true, even if individual TCRs could time the duration of ligand binding exactly and without error (which can be modeled by using step functions for p2 and p3 in Fig. 3), the stochastic nature of ligand dissociation will mean that the T cell is still unable to discriminate between low concentrations of high-affinity ligands and high concentrations of low-affinity ligands (data not shown).

Spreading Inhibition Improves Recognition Specificity.

The T cell can improve ligand discrimination if the response of individual TCRs to ligand encounter depends on, to some extent, the previous responses of other TCRs after the engagement of ligands on the APC. Thus, the problem of poor specificity at high-ligand density disappears when spreading inhibition is introduced into the simulation. Fig. 4b shows that the peak of the graph is narrow in the presence of spreading inhibition. This improval in specificity remains true even at ligand densities as high as 10% of the total MHC peptide presented.

The reason for this finding is that ligands that have dissociation times faster than the optimal (i.e., larger koff) will often result in a TCR only progressing to a state of partial activation. Because inhibition then is spread to its nearest neighbors, there is an amplification of this negative effect, accounting for the sharp drop in efficacy of ligands with high koff.

In addition, there is a small shift of the peak of the curve to the left in the presence of spreading inhibition. In the absence of inhibition, the ligand that can serially ligate and result in full activation of the most TCRs is optimal. With inhibition however, the ligand must also bind slightly longer on average to minimize the chance of dissociating when a TCR is in a partially activated state.

It has been proposed that the spread of SHP-1 serves to shut down the signaling response (17). The data in Fig. 4 suggest that it may also serve to help the T cell discriminate between ligands with only slightly different koff, thus improving its specificity.

Altered Peptide Ligands.

In studies of altered peptide ligands for T cells, weak agonists, which can trigger a full set of effector responses if their concentration is increased, are often distinguished from partial agonists, which only trigger a subset of responses regardless of concentration. Spreading inhibition may explain the difference between these two types of agonists. Specifically, it is proposed that weak agonists are those with a smaller koff than the optimal, and therefore succeed in activating TCRs to give a complete signal but fail to ligate many receptors serially. Partial agonists, however, are proposed to have a koff intermediate between agonists and antagonists. Because of spreading inhibition, partial agonists will always result in fewer TCRs delivering a complete signal than full agonists. Therefore, based on the concept of hierarchical T cell response thresholds, such ligands will only trigger a subset of T cell effector functions, even at saturating densities.

In the moth-eaten (me) and viable moth-eaten (mev) mice, which have absolute or relative deficiency of active SHP-1, respectively, hyperresponsiveness to TCR stimulation can be shown in both thymocytes and mature T cells (23). Although this finding is expected from our model, an additional prediction is that high concentrations of peptides defined as partial agonists or even antagonists in wild-type mice may function as full agonists for SHP-1-deficient cells.

Thymocyte Development.

SHP-1 levels are low in thymocytes and increase during development (19). Therefore, in thymocytes, the graph resembles that in Fig. 4a. Because ligands with fast off rates can now deliver a significant signal, the T cell will recognize a broader range of peptide-MHC complexes (thus, thymocytes can be positively selected by weak self ligands, resulting in a large T cell repertoire). As the T cell matures and SHP-1 levels rise, the graph now resembles that in Fig. 4b. Now these same weak self ligands are in the partial agonist or antagonist category and can no longer fully activate the T cell. However, T cells that have high affinity for self ligands are likely to be deleted by negative selection. Such a mechanism would allow for the beneficial effect of positive selection for a large T cell repertoire, while minimizing the potential for autoimmunity, because the thresholds for T cell activation in the periphery and negative selection in the thymus are similar (24).

It has been observed that the T cell does not show a general decrease in sensitivity to all ligands with maturation; rather, sensitivity to the stronger ligand is maintained, whereas the response to the weaker ligand decreases several hundredfold (25). This result can be explained by the change with maturation from a fat to a narrow humped curve (because the peak of the hump stays at approximately the same koff), thus maintaining sensitivity to strong ligands, whereas weak ligands with higher koff rapidly fall off the peak as the curve becomes narrower.

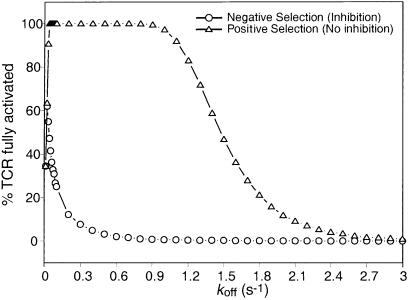
H2-Mα−/− mice lack a peptide exchange factor, and as a result, T cells from these animals are selected essentially on a single ligand (class II-associated invariant-chain peptide). Somewhat surprisingly, the animals have a reasonably diverse repertoire (26, 27). Our model demonstrates that in the absence of an inhibitory signal, high concentrations of a “poor” ligand can signal to the T cell (Fig. 2a). Therefore, our model predicts that a significant T cell repertoire can be selected positively by a single ligand present at a very high density (see Fig. 5). This prediction is in agreement with data suggesting that positive selection is promiscuous at high ligand densities (28, 29).

Figure 5.

Figure 5

Open in a new tab

Positive and negative selection on a single ligand. In this figure, we have modeled the signal that would be seen if the T cell encounters a single ligand presented at 100% density. This situation is analogous to what is seen in H2-Mα−/− mutant mice, where the majority of class II MHCs bear the CLIP peptide. As can be seen, in the absence of any inhibitory crosstalk between receptors (equivalent to positive selection occurring in the absence of SHP-1), a wide range of T cells with a very high koff (up to 50 × kopt) for the ligand will receive a significant signal, suggesting that positive selection would be reasonably effective at selecting a T cell repertoire. However, in the presence of inhibitory signaling, the window of koff that would result in strong signaling is much smaller. These conditions represent the situation seen during negative selection, suggesting that only a small proportion of the positively selected cells will be deleted. An average of 10 experiments is shown.

Spreading Protection Improves Sensitivity.

T cells are very sensitive, capable of responding to the presence of just 10 to 200 specific ligands on an APC. However, spreading inhibition results in a decrease in the maximum number of TCRs delivering a full signal (Fig. 4b). This decrease poses the obvious problem that small densities of foreign antigen may not result in enough TCRs giving a complete signal to activate the T cell.

One possible solution is to lower the threshold for T cell activation. Unfortunately, this solution also would raise the frequency of false positives. A better alternative, which takes into account the context in which a particular ligand is evaluated, is a system of positive cooperativity in the presence of agonist ligands.

Simulations incorporating both spreading inhibition and protection show that such a passive protective effect can restore sensitivity (Fig. 4c). There is a slight decrease in specificity, but this effect is minimal. The purpose of the protection offered by ERK-1 kinase, which prevents SHP-1 from inhibiting the src kinase lck (19), therefore seems to be to maintain the sensitivity of the system.

Varying the neighborhood sizes for inhibition and protection indicates that the tradeoff between sensitivity and specificity is a general principle. If the inhibition radius is larger than the protection radius, there is an increased specificity but lower sensitivity and vice versa (data not shown).

Reliability of Signaling in the Presence of Cooperativity.

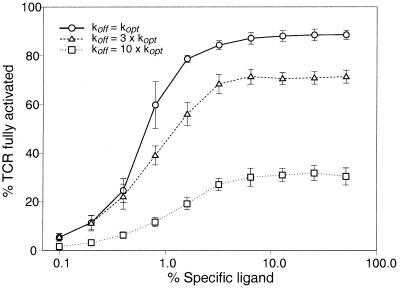
One criterion for a good sensor system is that it should consistently give the same results for similar inputs. In the presence of cooperativity, small random differences may be amplified, resulting in a system that gives inconsistent results. To test this possibility, we did multiple runs of the same simulation. The results summarized in Fig. 6 highlight that there are two different sources of variability that are biologically relevant.

Figure 6.

Figure 6

Open in a new tab

Robustness of ligand discrimination in the presence of receptor crosstalk. There are two sources of variability in the number of TCRs fully activated by ligand as discussed in the text. Runs of the same simulation with different random-number seeds were done to estimate the variability in numbers of TCRs that are fully activated. The results are expressed as the mean ± standard deviation of 25 experiments. There is a clear demarcation between optimal and suboptimal ligands that depends on the T cell activation threshold. For example, if the threshold for cell activation is set at a high value (e.g., 80% of TCR fully activated), the T cell can distinguish its optimal ligand from one whose koff varies by only a factor of 3. With less stringent thresholds (e.g., 40% of TCR fully activated), the T cell may be activated with high concentrations of this ligand but never by a ligand with a koff of 10 × kopt.

The first source is that, when loading APCs with a specific peptide, the actual number of molecules of the specific peptide presented on the cell surface will be distributed normally. The spread of this distribution alone can account for significant variability in the number of TCRs undergoing full activation, especially when the actual number of specific peptide:MHC complexes presented is low.

The second source of variability comes from the process of serial ligation, which introduces a random element to the number of productive encounters any particular ligand will have with TCRs. For ligands with a long dissociation time, there will be few opportunities to ligate TCRs serially; thus this effect is small. Conversely, for ligands with very short dissociation times, serial ligations hardly ever lead to the TCR delivering a complete signal; thus the effect on signaling is again small. It is for ligands with a koff close to kopt that the effect will be most pronounced. The variability arising from serial ligation amplifies the differences from initial specific ligand density, with the surprising result that the T cell will be most uncertain about its specific ligand near the kopt.

However, even with both sources of variability, the T cell is quite capable of distinguishing koff as little as 3 times larger than kopt and easily resolves koff which differ by a factor of 10 (Fig. 6).

Discussion

We have built our model on a kinetic interpretation of T cell signaling, because most of the experimental data support the concept that koff is the best predictor of ligand action (15, 16, 30). However, not all data are supportive of the kinetic model (14, 16), suggesting that other factors, possibly conformation, can be important. These factors are not directly addressed in our model. We have treated TCR activation as a quantal event in our simulation, assuming that each TCR gives the same signal after full activation. If TCR signaling was actually proportional to the duration a ligand stayed bound after full activation, the longer a ligand binds the stronger the signal. In such a case, the failure of ligands with a low koff to ligate a large number of TCRs serially would be compensated for by the increased signal strength (data not shown), and a peak at some kopt values would not be seen. Evidence for the quantal model comes from the fact that the T cell is activated at the same threshold number of the TCR regardless of the koff of the ligand (31).

Although ideally we should have used koff obtained at 37°C, most of the published data are for 25°C. Also, the limited data obtained at 37°C seem to be conflicting, with one report indicating an increase in binding time for agonists when compared with 25°C (32), and another showing a decrease (33). In addition, we have not included stabilization of the TCR–ligand interactions by coreceptors, which may significantly reduce the koff (34, 35). As discussed, this increase in stability will enhance the efficacy of kinetic proofreading (19) and may allow the T cell activation thresholds to be tuned (36, 37). It would not qualitatively change the results presented in this article. It should also be noted that the dissociation time of a few minutes described at 37°C (32) is not easily compatible with the activation of a large number of TCR by low concentrations of ligand, as seen in experiments supporting the serial ligation model. One possible resolution is that there is a high turnover of the ligand–TCR complex during formation of the immune synapse in the steps preceding stabilization of the final cluster (38).

Finally, we have also chosen to ignore the spatial and dynamic complexity of immune synapse formation (38, 39), which seems to be essential for the maintenance of a sustained signal to the T cell. If cooperativity between receptors is a very local event confined to small TCR clusters, then condensation of TCRs is unlikely to have much effect on crosstalk. However, if the inhibitory and protective signals are more extensive in their potential range, then their role will become more significant during synapse formation. Simulations where the radius of spreading is much larger or where the radii of spreading for inhibition and protection differ do not alter the qualitative results we present here, except for the tradeoff in sensitivity and specificity noted earlier.

An additional factor that may come into play when there is clustering of TCRs in the immune synapse is that TCR activation may be sustained by rapid rebinding of the same or different ligand (19). Our simulations show that the effect of this binding would be to enhance the signal from weak agonists, but there is no significant effect on strong agonists or very poor ligands (data not shown). The reason is intuitively obvious—strong agonists are fully capable of fully activating a TCR in the absence of rebinding, whereas even rebinding fails to push very poor ligands over the activation threshold. Again, the beneficial effects of spreading inhibition and protection are qualitatively unchanged.

Interestingly, Duke and Bray (40) have proposed recently that positive cooperativity among chemosensory receptors may enhance the sensitivity of Escherichia coli to attractants like aspartate across a wide range of concentration gradients, by using a similar sort of discrete Monte Carlo simulation. This model bears obvious resemblance to the spreading inhibition and protection discussed in this paper. An interesting possibility is that similar mechanisms to enhance signaling by receptor cooperativity may actually be quite common in nature (19).

Acknowledgments

We thank Ron Germain, Robert Lechler, and Mary Ritter for helpful discussions.

Abbreviations

TCR

T cell receptor

APC

antigen presenting cell

References

  • 1.Harding C V, Unanue E R. Nature (London) 1990;346:574–576. doi: 10.1038/346574a0. [DOI] [PubMed] [Google Scholar]
  • 2.Demotz S, Grey H M, Sette A. Science. 1990;249:1028–1030. doi: 10.1126/science.2118680. [DOI] [PubMed] [Google Scholar]
  • 3.McKeithan T W. Proc Natl Acad Sci USA. 1995;92:5042–5046. doi: 10.1073/pnas.92.11.5042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Germain R N, Levine E H, Madrenas J. The Immunologist. 1995;3:113–121. [Google Scholar]
  • 5.Jameson S C, Bevan M J. Immunity. 1995;2:1–11. doi: 10.1016/1074-7613(95)90074-8. [DOI] [PubMed] [Google Scholar]
  • 6.Sloan-Lancaster J, Allen P M. Curr Opin Immunol. 1995;7:103–109. doi: 10.1016/0952-7915(95)80035-2. [DOI] [PubMed] [Google Scholar]
  • 7.Madrenas J, Germain R N. Semin Immunol. 1996;8:83–101. doi: 10.1006/smim.1996.0011. [DOI] [PubMed] [Google Scholar]
  • 8.Rabinowitz J D, Beeson C, Lyons D S, Davis M M, McConnell H M. Proc Natl Acad Sci USA. 1996;93:1401–1405. doi: 10.1073/pnas.93.4.1401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Lord G M, Lechler R I, George A J T. Immunol Today. 1999;20:33–39. doi: 10.1016/s0167-5699(98)01379-6. [DOI] [PubMed] [Google Scholar]
  • 10.Valitutti S, Müller S, Cella M, Padovan E, Lanzavecchia A. Nature (London) 1995;375:148–151. doi: 10.1038/375148a0. [DOI] [PubMed] [Google Scholar]
  • 11.Valitutti S, Lanzavecchia A. Immunol Today. 1997;18:299–304. [PubMed] [Google Scholar]
  • 12.Itoh Y, Hemmer B, Martin R, Germain R N. J Immunol. 1999;162:2073–2080. [PubMed] [Google Scholar]
  • 13.Janeway C A. Immunol Today. 1995;16:223–225. doi: 10.1016/0167-5699(95)80163-4. [DOI] [PubMed] [Google Scholar]
  • 14.Sykulev Y, Vugmeyster Y, Brunmark A, Ploegh H L, Eisen H N. Immunity. 1998;9:475–483. doi: 10.1016/s1074-7613(00)80631-7. [DOI] [PubMed] [Google Scholar]
  • 15.Matsui K, Boniface J J, Steffner P, Reay P A, Davis M M. Proc Natl Acad Sci USA. 1994;91:12862–12866. doi: 10.1073/pnas.91.26.12862. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Lyons D S, Lieberman S A, Hamp J, Boniface J J, Chien Y, Berg L J, Davis M M. Immunity. 1996;5:53–61. doi: 10.1016/s1074-7613(00)80309-x. [DOI] [PubMed] [Google Scholar]
  • 17.Dittel B N, Štefanov́a I, Germain R N. Immunity. 1999;11:289–298. doi: 10.1016/s1074-7613(00)80104-1. [DOI] [PubMed] [Google Scholar]
  • 18.Robertson J M, Evavold B D. J Immunol. 1999;163:1750–1754. [PubMed] [Google Scholar]
  • 19.Germain R N, Štefanov́a I. Annu Rev Immunol. 1999;17:467–522. doi: 10.1146/annurev.immunol.17.1.467. [DOI] [PubMed] [Google Scholar]
  • 20.Hudrisier D, Kessler B, Valitutti S, Horvath C, Cerottini J, Luescher I. J Immunol. 1998;161:553–562. [PubMed] [Google Scholar]
  • 21.Davis M M, Chien Y-H. In: Fundamental Immunology. Allen W E, editor. Philadelphia: Lippincott; 1998. pp. 341–366. [Google Scholar]
  • 22.Bachmann M F, Mckall-Faienza K, Schmits R, Bouchard D, Beach J, Speiser D E, Mak T W, Ohashi P S. Immunity. 1997;7:549–557. doi: 10.1016/s1074-7613(00)80376-3. [DOI] [PubMed] [Google Scholar]
  • 23.Pani G, Fischer K, Mlinaric-Rascan I, Siminovitch K A. J Exp Med. 1996;184:839–852. doi: 10.1084/jem.184.3.839. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Mitchison N A, Katz D R, Chain B. Semin Immunol. 2000;12:179–183. doi: 10.1006/smim.2000.0229. [DOI] [PubMed] [Google Scholar]
  • 25.Lucas B, Štefanov́a I, Yasutomo K, Dautigny N, Germain R N. Immunity. 1999;10:367–376. doi: 10.1016/s1074-7613(00)80036-9. [DOI] [PubMed] [Google Scholar]
  • 26.Martin W D, Hicks G G, Mendiratta S K, Leva H I, Ruley H E, Van Kaer L. Cell. 1996;84:543–550. doi: 10.1016/s0092-8674(00)81030-2. [DOI] [PubMed] [Google Scholar]
  • 27.Ignatowicz L, Kappler J, Marrack P. Cell. 1996;84:521–529. doi: 10.1016/s0092-8674(00)81028-4. [DOI] [PubMed] [Google Scholar]
  • 28.Berg R E, Princiotta M F, Irion S, Moticka J A, Dahl K R, Staerz U D. Immunity. 1999;11:33–43. doi: 10.1016/s1074-7613(00)80079-5. [DOI] [PubMed] [Google Scholar]
  • 29.Irion S, Berg R E, Staerz U D. J Immunol. 2000;164:4601–4606. doi: 10.4049/jimmunol.164.9.4601. [DOI] [PubMed] [Google Scholar]
  • 30.Alam S M, Travers P J, Wung J L, Nasholds W, Redpath S, Jameson S C, Hogquist K A, Gascoigne N R J, Travers P J. Nature (London) 1996;31:616–621. doi: 10.1038/381616a0. [DOI] [PubMed] [Google Scholar]
  • 31.Viola A, Lanzavecchia A. Science. 1996;273:104–106. doi: 10.1126/science.273.5271.104. [DOI] [PubMed] [Google Scholar]
  • 32.Alam S M, Davies G M, Lin C M, Zal T, Nasholds W, Jameson S C, Hogquist K A, Gascoigne N R J, Travers P J. Immunity. 1999;10:227–237. doi: 10.1016/s1074-7613(00)80023-0. [DOI] [PubMed] [Google Scholar]
  • 33.Willcox B E, Gao G F, Wyer J R, Ladbury J E, van der Merwe P A. Immunity. 1999;10:357–365. doi: 10.1016/s1074-7613(00)80035-7. [DOI] [PubMed] [Google Scholar]
  • 34.Luescher I F, Vivier E, Layer A, Mahlou J, Godeau F, Malissen B, Romero P. Nature (London) 1995;373:353–356. doi: 10.1038/373353a0. [DOI] [PubMed] [Google Scholar]
  • 35.Garcia K C, Scott C A, Brunmark A, Carbone F R, Peterson P A, Wilson I A, Teyton L. Nature (London) 1996;384:577–581. doi: 10.1038/384577a0. [DOI] [PubMed] [Google Scholar]
  • 36.Grossman Z, Paul W E. Proc Natl Acad Sci USA. 1992;89:10365–10369. doi: 10.1073/pnas.89.21.10365. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Grossman Z, Singer A. Proc Natl Acad Sci USA. 1996;93:14747–14752. doi: 10.1073/pnas.93.25.14747. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Grakoui A, Bromley S K, Sumen C, Davis M M, Shaw A S, Allen P M, Dustin M L. Science. 1999;285:221–227. [PubMed] [Google Scholar]
  • 39.Monks C R F, Freiberg B A, Kupfer H, Sciaky N, Kupfer A. Nature (London) 1998;395:82–86. doi: 10.1038/25764. [DOI] [PubMed] [Google Scholar]
  • 40.Duke T A J, Bray D. Proc Natl Acad Sci USA. 1999;96:10104–10108. doi: 10.1073/pnas.96.18.10104. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES