The XAS Model of the Copper(II)-Imidazole Complex Ion in Liquid Aqueous Solution: A Strongly Solvated Square Pyramid

Abstract

Copper K-edge EXAFS and MXAN analyses were combined to evaluate the structure of the copper(II)-imidazole complex ion in liquid aqueous solution. Both methods converged to the same square pyramidal inner coordination sphere [Cu(Im)₄L_ax]²⁺, (L_ax indeterminate) with four equatorial nitrogens at: EXAFS, 2.02±0.01 Å, and; MXAN, 1.99±0.03 Å. A short axial N/O scatterer, (L_ax), was found at 2.12±0.02 (EXAFS) or 2.14±0.06 Å (MXAN). A second but very weak axial Cu-N/O interaction was found at 2.9±0.1 Å (EXAFS) or 3.0±0.1 Å (MXAN). In the MXAN fits, only a square pyramidal structural model successfully reproduced the doubled maximum of the rising K-edge XAS, specifically excluding an octahedral model. Both EXAFS and MXAN also found eight outlying oxygen scatterers at 4.2±0.3 Å that contributed significant intensity over the entire XAS energy range. Two prominent rising K-edge shoulders at 8987.1 eV and 8990.5 eV were found to reflect multiple scattering from the 3.0 Å axial scatterer and the imidazole rings, respectively. In the MXAN fits, the imidazole rings took in-plane rotationally staggered positions about copper. The combined (EXAFS and MXAN) model for the unconstrained cupric-imidazole complex ion in liquid aqueous solution is an axially elongated square pyramidal core, with a weak non-bonded interaction at the second axial coordination position and a solvation shell of eight nearest neighbor water molecules. This core square pyramidal motif has persisted through [Cu(H₂O)₅]²⁺, [Cu(NH₃)₄(NH₃,H₂O)]²⁺,^1,2 and now [Cu(Im)₄L_ax)]²⁺, and appears to be the geometry preferred by unconstrained aqueous-phase Cu(II) complex ions.

Introduction

Despite the plasticity in coordination number shown by Cu(II) in crystalline complexes^3,4 and in the gas phase,⁵ cupric complexes in liquid aqueous solution are typically represented as displaying a Jahn-Teller (JT) axially elongated octahedron.^6–12 Nevertheless, molecular dynamics simulations predicted a predominant square pyramidal core for aquated cupric ion,^13,14 which was corroborated using Minuit-XANES (MXAN) and EXAFS analysis of the [Cu(aq)]²⁺ K-edge XAS spectrum.^1,15,16 Despite the evidence from Linear Electric Field Effect (LEFE) EPR experiments reported more than 30 years ago,^17,18 topical reviews have only recently discussed the possible lack of centrosymmetry for dissolved cupric ion.^19,20

The biologically important interactions between transition metal ions and proteins invariably occur in water and are central to understanding diseases such as Parkinson’s and Alzheimer’s,^21,22 and other pathological states,²³ as well as universally critical to normal cellular function at all organismal scales.^24–27 Knowledge of the structure of transition metal aqua ions is central to the first steps of all these interactions. Aquated small-molecule complex ions are the simplest of all dissolved transition metal complexes, and so are also fundamental to excited state photophysics.²⁸ Likewise, empirical knowledge of atomic-scale structure of dissolved transition metal ions is core to any first principles calculation of the thermodynamic properties,²⁹ to testing and improving the theory supporting molecular dynamics simulations of aqua-ion behavior,³⁰ and to understanding electron transfer.^10,31 The structure of dissolved aquated transition metal complex ions at atomic resolution thus has direct import to fields as diverse as medical and biological chemistry, and chemical physics. We also note, however, that knowledge of solution structure is important for its own sake.³²

EXAFS and MXAN analyses have complementary strengths that can be combined to query the dominant structure of solvated ions in liquid media. In previous studies of the K-edge XAS spectrum of [Cu(aq)]²⁺, EXAFS analysis was able to exclude purely 4-coordinate models but could not distinguish between pentaaqua and hexaaqua coordination.^9,15 In contrast, MXAN analysis of the same K-edge XAS was able to exclude both regular and JT axially-elongated octahedral models for [Cu(aq)]²⁺, but could not distinguish between 4-coordinate D_2d and axially elongated 5-coordinate square pyramidal structures. However, the combination of EXAFS and MXAN analyses excluded all the possibilities except an equatorially distorted, axially elongated square pyramidal [Cu(H₂O)₅]²⁺ complex ion as the only structurally viable model for aquated Cu(II).^1,33

More recently, combined EXAFS and MXAN K-edge XAS analysis found that Cu(II) in liquid 4 M aqueous ammonia solution inhabited a similar square pyramidal core geometry, [Cu(NH₃)₅]²⁺.² A strongly localized but non-bonded axial solvent molecule about 3 Å from Cu(II) was also found to associate with dissolved [Cu(NH₃)₅]²⁺; an association apparently absent from dissolved [Cu(H₂O)₅]²⁺. Solution phase [Cu(NH₃)₅]²⁺ also uniquely supported a durable solvation shell of six waters at about 3.6 Å, which produced photoelectron back-scattering responsible for the prominent shoulders on the rising K-edge XAS.

Here the combined EXAFS and MXAN approach is extended to assess the structure of the dissolved aqueous Cu(II)-imidazole complex ion. A new structural model is derived.

Materials and Methods

The solution sample of cupric-imidazole complex ion was prepared by dilution of 0.50 mL of an aqueous 1.00 M stock solution of cupric perchlorate hexahydrate (Alfa Chemicals) containing 1.365 g (20 mmoles) of dissolved imidazole (Sigma Chemicals, >99%) to a total final volume of 5.0 mL and a final pH = 9.9. The complexation behavior of Cu(II) with imidazole is multifarious; see Figure S1 in the Supporting Information.³⁴ Solutions of 0.1 M Cu(II) with 4.0 M imidazole were unstable in the region of ~pH 4–7, and deposited crystals. Therefore, the experimental solution was made in a region of relative compositional stability that also ensured complete equatorial complexation of copper(II) (Figure S1). Doubly deionized water was used throughout.

X-ray absorption spectra were measured on SSRL 16-pole wiggler beam line 9-3, operating at 3 GeV and a wiggler field of 2.0 T. The beam line is equipped with a Rh-coated flat, bent, collimating and harmonic-rejecting pre-monochromator mirror, a Si[220] monochromator, and a Rh-coated toroidal focusing post-monochromator mirror. Data were collected as transmission spectra using nitrogen-filled ionization chambers as detectors.. The copper-imidazole solution was contained in a 2mm×2mm×20mm Teflon cell equipped with copper-free Kapton windows, while the experimental temperature was ambient and governed only by helium flow through the sample chamber. Two scans were measured and averaged. The two XAS scans were found superimposable, except for a trace of photo-reduction evident at 8983.3 eV in the second derivative of the rising edge energy region of the second scan. However, no discoloration of the sample solution was observed after XAS measurement. XAS spectra were energy calibrated against the first inflection on the rising K-edge of a copper foil XAS spectrum, measured concurrently, and assigned to 8980.3 eV. The XAS spectra of the crystalline copper(II)-tetraimidazole nitrate (CCDC Refcode IMCUCL) and sulfate (CCDC Refcode TIMZCU) complexes were reported previously.³⁵

Raw XAS data were processed using the program PROCESS within the EXAFSPAK program suite, which was written by Prof. Graham George, Department of Geological Sciences, University of Saskatchewan. Prior to EXAFS fitting, XAS spectra were splined and normalized using the local program PySpline,³⁶ which allows real-time evaluation of EXAFS spectrum Fourier transform as the knot points for the piece-wise polynomial spline are varied. For the EXAFS spectra discussed here, the spline knots were, (eV, [polynomial order]): 9025.4, [2]; 9168.4, [3]; 9443.1, [3]; 9649.4, and; E₀ = 9000.0 eV.

EXAFS spectra were fit over the k-range 2–13 Å⁻¹, based on models created using FEFF7 and using the EXAFSPAK program OPT. Coordinates for the FEFF7 input model were obtained from the crystal structure of [Cu(Im)₄(ClO₄)₂].³⁷ Separate FEFF7 muffin tin radii were distinguished for the two imidazole nitrogens, for three oxygens (two axial distances and one potential solvent scatterer), but only one was used for imidazole carbon. Coordination numbers were fixed at integer values during fits, while absorber-scatterer distances and mean square displacements (σ²) were allowed to float. The ΔE₀ value was varied as a common parameter for all individual scattering paths. The total number of fit parameters was thus 2n+1, where “n” is the number of scattering paths in a fit. The fit included Fourier transform features over the R-space range 0.5 Å- 4.0 Å, and so the EXAFS fit statistical degrees of freedom were ([2×Δk(Å⁻¹)×ΔR(Å)]÷π)+2 = 26,³⁸ while the total of fit variables never exceeded 23. The goodness-of-fit value minimized over the fitted k-range was

$$\text{F}={[\mathrm{\sum }{k}^6{({\chi }_{\mathit{exptl}}-{\chi }_{\mathit{calc}})}^2/\mathrm{\sum }{k}^6{({\chi }_{\mathit{exptl}})}^2]}^{1/2},$$

where “k” is the photoelectron wave vector, and “χ” is the calculated (calc) or experimental (exptl) data point.

The MXAN method has been described in detail,^16,39,40 and fits were carried out over the first 200 eV of the normalized K-edge XAS spectrum in the relative energy space E-E₀, where E₀=8990.00 eV. The muffin tin approximation was used for the atomic potentials, and the atomic radii were chosen according to the Norman criterion, with an optimized 3.4% contraction. Hydrogen atoms were not included in the fits, and the imidazoles were assumed to be perfectly rigid. Trans-equatorial absorber-scatterer distances were linked, as were the trans L_eq-Cu-L_ax θ-angles. The two axial distances were fit separately. The extraction of bond distances and angles followed the method previously described for the K-edge XAS of copper in liquid aqueous solution.^2,15,41 The function minimized during the MXAN fit was R_sq, defined as:

$$R_{sq}=n\frac{{\displaystyle \sum _{i=1}^m}{w}_i{[(y_i^{th}-t_i^{exp}){\epsilon }_i^{-1}]}^2}{{\displaystyle \sum _{i=1}^m}{w}_i},$$

where, “n” is the number of independent parameters, “m” is the number of data points, “ $y_i^{th}$” and “ $y_i^{exp}$” are the theoretical and experimental values of the absorption, respectively, “ε_i” is the error in each point of the experimental data set, and “w_i” is a statistical weight. When w_i = 1, the square residual function R_sq becomes the statistical χ² function. In this work, w_i = 1 was assumed and the experimental error ε = constant = 1.0 % of the main experimental edge jump over the whole data set. Statistical errors were calculated by the MIGRAD routine. MXAN also introduces a systematic error of 1–2% into the bond lengths that must be added to the MIGRAD statistical error. Atomic coordinates for the EXAFS and MXAN input files were derived from structural models constructed within the program CHEM 3D Pro (CambridgeSoft, Cambridge, MA). The CHEM 3D models were, in turn, based upon the known crystal structure of the complex [Cu(Im)₄(ClO₄)₂].³⁷

Results

Copper(II) exhibits six complexation steps with imidazole in aqueous solution.^34,42 The pH-dependent species distribution diagram of the XAS experimental solution is shown in Figure S1a in the Supporting Information. Visible absorption spectroscopic examination of this solution under conditions of varying pH (Figure S2 in the Supporting Information) was consistent with complexation past the tetraimidazole stage, indicating a stable composition when pH≥8.6. This result is predicted only by the K₁-K₆ distribution diagram (compare Figure S1 with Figure S2 in the Supporting Information). For the liquid solution-phase XAS experiment, the dissolved Cu(II) was required to be equatorially saturated by imidazole, and the species distribution to be insensitive to small mixing errors. These criteria are conjointly satisfied only in solutions of pH >8.5 (Figure S1a). The high imidazole-copper ratio ensured the absence of binuclear complex ions.⁴²

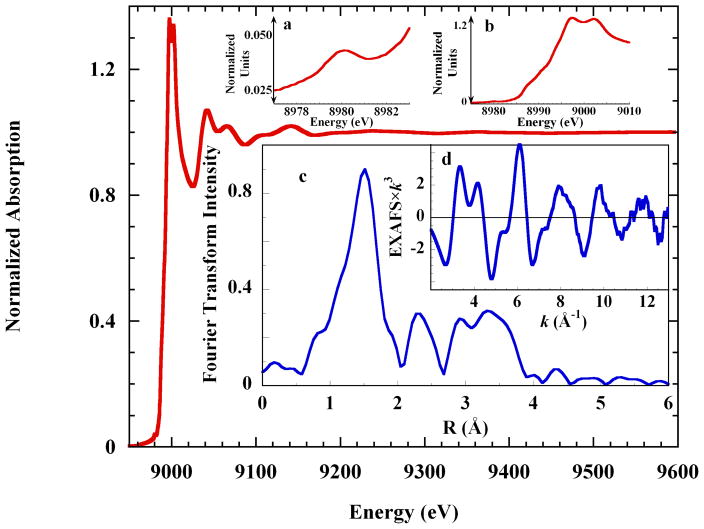
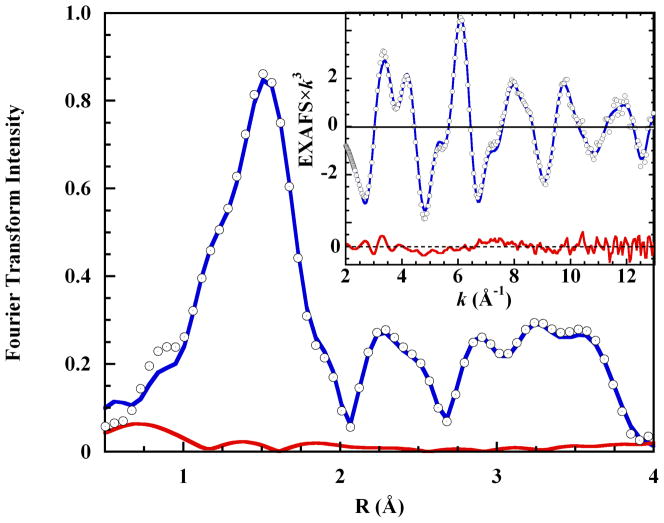
Figure 1 shows the K-edge XAS spectrum of 0.10 M cupric perchlorate in liquid aqueous 4 M imidazole solution, pH 9.9, along with the EXAFS spectrum and the Fourier transform of the EXAFS. The pre-edge energy region (inset a) exhibits the single low-intensity feature expected from a 1s→3d transition to the single 3d_x²-y² hole of tetragonal Cu(II). Shoulders occur on the rising K-edge at 8987.1 eV and 8990.5 eV and the intensity maximum is split. Complex beat patterns in the EXAFS spectrum (inset d) reflect the multiple shells of scatterers in the imidazole ring, which also contribute the intense Fourier features at R > 2 Å (inset c). These results are analogous to previous Kedge XAS studies of crystalline copper tetraimidazole.^43,44

Figure 1.

Cu K-edge XAS spectrum of 0.10 M Cu²⁺ in liquid 4 M aqueous imidazole solution. Insets: a. the pre-edge energy region; b. the rising edge region; c. the non-phase corrected Fourier transform of the EXAFS spectrum, and; d. the EXAFS spectrum.

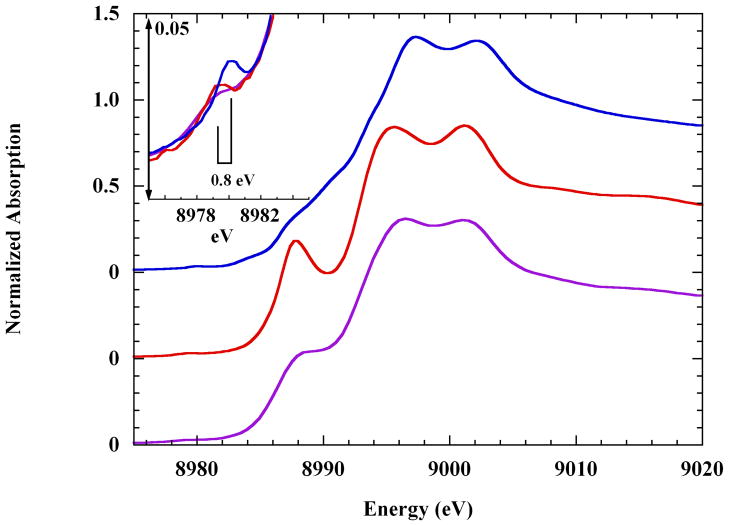
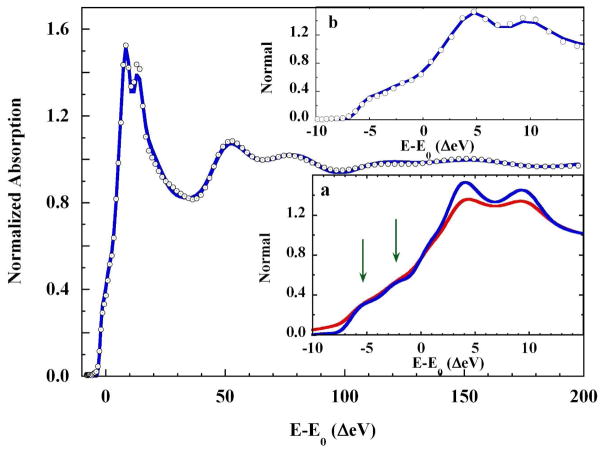
In Figure 2 are compared the rising K-edge XAS spectra of the dissolved copper-imidazole complex ion and the crystalline sulfate and dinitrate complexes. The latter two are axially elongated JT-octahedra (Cu-O_ax ≈ 2.6 Å), and the strong well-resolved rising K-edge shoulder they exhibit is much more intense than that of the dissolved complex ion. In contrast, the 1s→3d pre-edge transition of the dissolved complex is the most intense, and is shifted by about +0.8 eV (Figure 2 inset). Pseudo-Voigt fits yielded the energy positions and integrated intensities (in normalized absorption units, nau) of the relevant XAS 1s→3d transitions: sulfate, 8979.0 eV and 0.023 nau; nitrate, 8979.1 eV and 0.027 nau, and; solution complex, 8979.9 eV and 0.043 nau.⁴⁵

Figure 2.

Cu K-edge XAS spectra of copper(II)-tetra-imidazole, as: (top), the solution complex; (middle), the crystalline sulfate complex, and; (bottom), the crystalline dinitrate complex (see the Materials and Methods section). The latter two spectra have been offset by −0.50 and −1.0 normalized absorption units, respectively. Inset: the pre-edge energy region showing the 1s→3d transition of: ( ), the solution spectrum; ( ), the solid sulfate, and; ( ) the solid dinitrate. The space-bar shows the ~0.8 eV difference in the transition energies.

All three complexes share the same equatorial tetra-imidazole core,^34,46–48 and comparative visible spectroscopy has shown that the ligand field strength does not change much between the crystalline and solution phases.^48,49 Therefore, the differences found in the XAS spectrum of the dissolved complex ion must arise from something other than a changed equatorial ligand field.

EXAFS Fits were carried out over the range k=2–13 Å⁻¹, consistent with an inter-shell resolution of ±0.14 Å, and included separate potentials for all the heteroatom scatterers. No advantage was found in splitting the equatorial shell, and so all fits utilized four first shell nitrogens refined at a single distance. In fitting the imidazole rings, the scattering distances to the 2×C_α and the C_βN_β atom pairs were refined as two individual single shells.

All fits using the square pyramidal and octahedral models included the axial imidazoles which were indicated for the experimental solution (Figure S1a and Figure S2 in the Supporting Information). In the initial fits the equatorial imidazoles were treated as rigid bodies, using linked square planar best-fit distances to reduce the number of floated parameters. However, the fits including five or six imidazole ligands invariably failed. The failures manifested either as large internal σ² values or as physically unreasonable internal distances within the axial imidazoles. Alternatively, modeling the axial imidazoles as rigid bodies invariably caused the fit routine to exit.

It was decided, therefore, to disregard photoelectron scattering from the extended nucleus of any axial imidazole, and to model the axial ligands as single oxygen scatterers. However, the EXAFS phases and amplitudes of oxygen and nitrogen scatterers are very similar. Thus, even though the axial scatterers were modeled as oxygen the elemental identity is formally O/N indistinguishable.

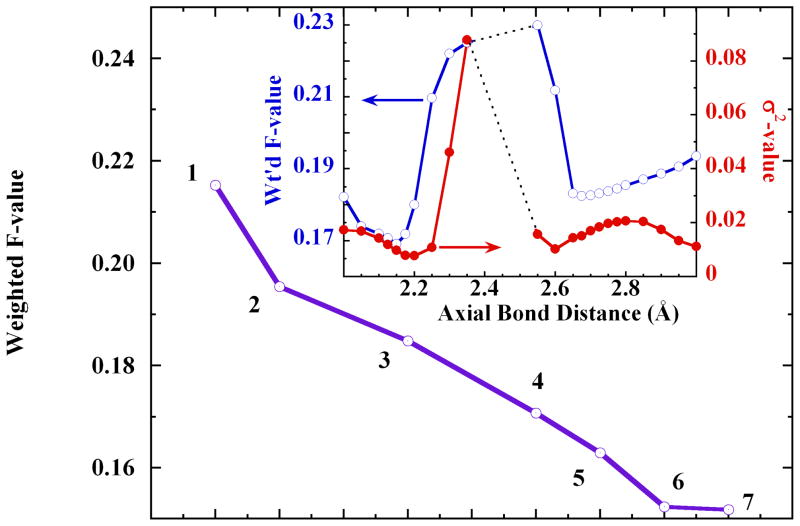
Exploring the Cu-axial scatterer distance produced two minima, near 2.15 Å and 2.70 Å, in the goodness-of-fit weighted F-value and in the Debye-Waller σ² (Figure 3 inset). In contrast, the analogous test using the Cu K-edge EXAFS of crystalline [Cu(Im)₄SO₄], produced only one minimum in weighted F-value, at 2.48 Å. The two minima in the solution-state fits implied the possibility of axial asymmetry in the dissolved cupric-imidazole complex ion. The fits shown in Figure 3 indicated that the models with ~2.15 Å axial bond distances produced better fits than those with ~2.7 Å axial distances. These test fits notably removed the JT-octahedral model with two long axial distances (Figure 3, fit #2) from further consideration, along with the trigonal-bipyramidal and purely square pyramidal models.

Figure 3.

The systematic improvement in the goodness-of-fit weighted F-value with model evolution: 1. axially elongated square pyramidal, O_ax=2.86 Å; 2. JT-octahedral, 2× O_ax=2.76 Å; 3. asymmetric octahedral, O_ax1=2.71 Å, O_ax2=2.85 Å; 4. axially short square pyramidal, O_ax=2.11 Å; 5. trigonal bipyramidal (Im_ax = 2.02 Å, O_ax = 1.99 Å); 6. axially elongated, split-axial square pyramidal, O_ax=2.13 Å, O_−z=2.86 Å; 7. short axial JT-octahedral, 2× O_ax=2.11 Å. The first shell imidazole and multiple scattering paths were identical throughout, with 4×Cu-N=2.02 Å. Inset: Double-y plot showing the changes in weighted F-value (○, left ordinate) and σ² value (●, right ordinate) with migration of the axial bond distance. The dotted lines at O_ax=2.35 Å–2.55 Å indicate a range within which the fits rapidly diverged.

The short-axial JT-octahedral model (2×O_ax=2.11 Å, weighted F= 0.1518) and the split-axial model (2×O_ax=2.13 Å, 2.86 Å; weighted F= 0.1524) yielded statistically equivalent fits, that were best overall.

In order to further test the short-axial JT-octahedral model, the two axial scatterers were slightly removed from the best fit distance of 2.11 Å (ΔR_axial = ±0.02 Å), and allowed to refine independently. In this event, the distances diverged strongly to produce an axially compressed asymmetric model, with one very short Cu-O_ax1=1.94 Å (σ² = 0.00808) and one longer Cu-O_ax2=2.22 Å (σ² = 0.00756). Although the weighted F-value (F = 0.1376) implied a best fit, this model was rejected on physico-chemical grounds, namely that a very short axial distance implies the presence of five strongly bound imidazole ligands, rather than the four strongly bound imidazole ligands that are known.³⁴ The importance of this result is that the short axial octahedral fit proved stable only when the two axial distances were constrained to be identical.

The stability of the short-axial octahedral model was then re-examined in an alternative manner: each of the two axial scatterers was set to exactly the original best-fit distance (2.11 Å) and σ² value (0.02263), and again independently floated. In this test, the axial scatterers refined to slightly unequal distances (2×O_ax=2.10 Å, 2.11 Å; σ² = 0.02260, 0.02250), with an unimproved weighted F = 0.1514. Taken together, these tests showed that the short-axial octahedral model resides in a narrow fit minimum of ΔR_axial< ±0.02 Å. The viability of the short-axial octahedral model is therefore an artifact of the constraint to identical axial distances. This outcome left the split-axial structure as the preferred EXAFS model.

Second Shell Solvation Structure

The fits to both the short axial JT-octahedral model and the split axial model fits were persistently improved when a distant shell of oxygen scatterers was added, consistent with solvating water molecules. Thus an 8-oxygen shell refining to 4.4 Å improved the octahedral model by ΔF=0.012 (weighted F = 0.1397). For the split axial model, the second shell of eight oxygen scatterers again refined to 4.4 Å and improved the fit by ΔF = 0.024 (weighted F = 0.1280). In each case, the solvation models improved the fit to the Fourier transform spectrum in a previously unfit region around R = 3.5–4 Å (see Figure S4 in the Supporting Information).

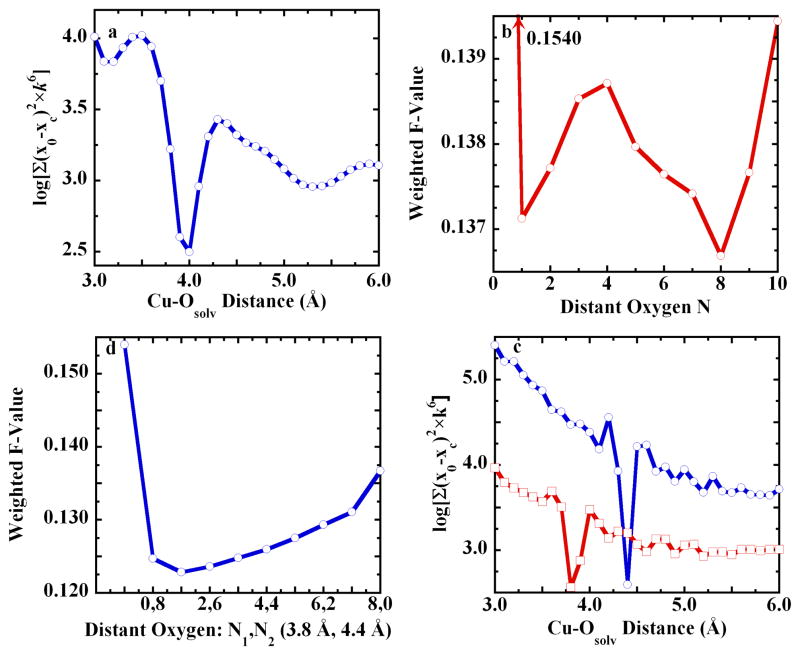
Figure 4 outlines the full discovery process for the solvation shell that completed the split axial model. A search of Cu-O_w distances revealed a pronounced minimum in weighted F-value at 4 Å (Figure 4a), with a subsequent minimum at eight such scatterers (Figure 4b). For eight scatterers, the search was expanded to include two shells. In this case, the prior best fit distance of 4 Å bifurcated into two separate minima at 3.8 Å and 4.4 Å (Figure 4c). Finally, the best overall fit was found when the outlying oxygen scatterers were asymmetrically distributed (1×O_w = 3.8 Å and 7×O_w=4.4 Å, weighted F = 0.1227), Figure 4d. However, the statistically indistinguishable fit with 2×O_w = 3.8 Å and 6×O_w=4.4 Å (weighted F = 0.1237) was chosen as the final second shell model, because a set of two nearer waters could be taken to reflect the asymmetry of the axial ligand distances (see below). Figure S5 and Figure S6 in the Supporting Information show the nearly equivalent improvement of the fits to the short-axial JT-octahedral model.

Figure 4.

Evidence for distant oxygen scatterers in the [Cu(Im)₄(O)_ax1(O)_ax2] split axial structural model: a. Unfit residual vs. distance for an oxygen scatterer, with a minimum at 4 Å. b. Weighted F-value vs. the number of outlying oxygen scatterers, which refined to 3.8 Å. c. Unfit residual vs. distance for two outlying shells of oxygen scatterers. The main shell was stepped from 3 Å to 6 Å in 0.1 Å units. At each 0.1 Å main shell step, the subordinate shell was stepped from 3 Å to 6 Å, in 0.1 Å units. For each trace, total simulations = 961: ( ), main shell at 3.8 Å, subordinate shell minimum = 4.4 Å, and; ( ), main shell at 4.4 Å, shell, subordinate shell minimum = 3.8 Å. d. Weighted F-value vs. distribution number for two outlying shells of oxygen scatterers, at 3.8 Å and 4.4 Å. The first point in “d” represents 0,0. The 8,0 fit duplicates the CN=8 fit in panel “b.”

In summary, all the purely square pyramidal models and both JT-octahedral models were excluded as viable candidates for the structure of the aqueous copper(II)-imidazole complex ion. Figure 5 exhibits the final fits to the EXAFS and the Fourier transform, representing the split axial structure with O_ax1 = 2.12 Å and O_ax2 = 2.87 Å, and shells of oxygen scatterers at 3.8 Å and 4.4 Å. The fit metrics appear in Table 1, and the fit components and the atomic scattering paths are shown in Figure S7 in the Supporting Information.

Figure 5.

(○), Fourier transform of the K-edge EXAFS spectrum of 0.10 M Cu(II) in aqueous 4 M imidazole solution; ( ), the final fit using the split axial model with eight outlying oxygen scatterers distributed into two shells (see Table 1 for the metrics), and; ( ), the fit residual. Inset: (○), the EXAFS spectrum; ( ), the final fit, and; bottom, ( ), the fit residual

Table 1.

EXAFS Metrics for Split Axial {[Cu(Im)₄(O_ax1)](O_ax2)}·8H₂O

CNa	R (Å)b	σ2×103
4 Neq	2.02±0.002	6.44
1 Oax short	2.12±0.01	13.4
1 Oax long	2.87±0.01	4.18
8 Cα	3.04±0.04	7.94
8 Cβ, Nβ	4.06±0.08	12.5
16 Neq-Cα msc	3.09±0.01	19.7
8 Neq-Nβ ms	4.38±0.13	13.8
16 Cα-Nβ ms	4.22±0.03	2.18
32 Cα-Neq(trans) msd	4.63±0.03	6.76
2 Ow	3.83±0.03	4.62
6 Ow	4.40±0.02	8.67
ΔE0 (eV)	−3.533
F-value	0.1237

^aCN=coordination number.

^buncertainty is the statistical error from the fit.

^c“ms” is multiple scattering. All other interactions are single scattering.

^dtriangular multiple scattering path 9; see Figure S7 in the Supporting Information.

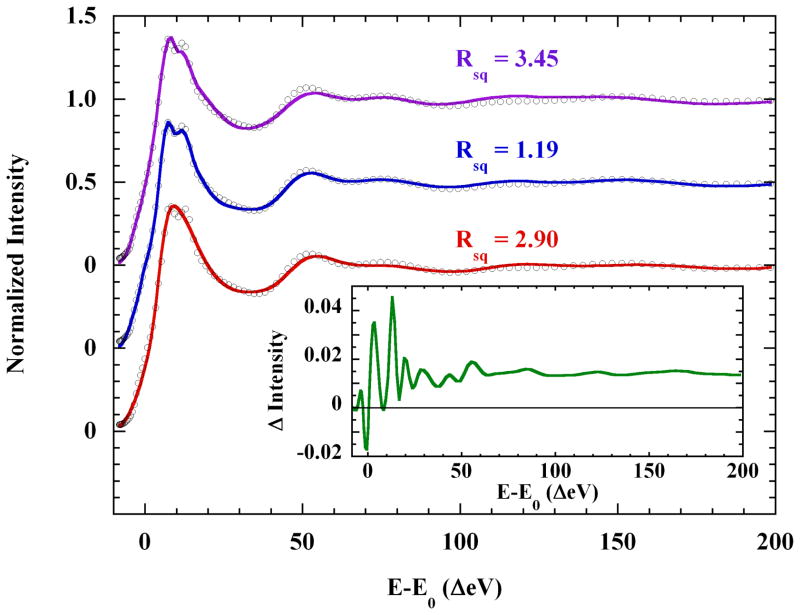
MXAN Fits were carried out over the range −8 eV to +200 eV in the E-E₀ scale (E₀=8990.00 eV), which includes the entire rising K-edge energy region. In all cases, axial ligands were represented by single oxygen scatterers. The basic square planar [Cu(Im)₄]²⁺, square pyramidal [Cu(Im)₄(O)]²⁺, and octahedral [Cu(Im)₄(O)₂]²⁺ models were first examined. The Cu-N_eq and Cu-O_ax distances and angles were refined during the fit until the error function, R_sq, was minimized (see the Materials and Methods section). The distances and angles in each set of trans copper ligands were linked and varied in concert. The imidazoles were treated as rigid bodies with fixed internal angles and distances, but were allowed to rotate freely about the Cu-N_eq bond. The results of these tests are shown in Figure 6, and Table 2. Relatively short axial distances were found in the best fits for both the square pyramidal and octahedral models, which corroborated the EXAFS fits described above.

Figure 6.

MXAN fits to the K-edge XAS of 0.10 M Cu(II) in 4 M aqueous imidazole solution, over the E-E₀ range −8 eV to 200 eV, with the following models: ( ), square planar [Cu(Im)₄]²⁺; ( ),axially elongated square pyramidal [Cu(Im)₄(H₂O)]²⁺ (offset −0.5 unit), and; ( ), axially elongated octahedral [Cu(Im)₄(H₂O)₂]²⁺ (offset −1.0 unit). Only the square pyramidal model reproduces both the rising edge shoulder and the split absorption maximum of the data. Inset: ( ), scattering contribution to the fitted XAS of the square pyramidal model, of four second shell equatorial solvent waters at 7.4±0.6 Å. See the text for discussion.

Table 2.

MXAN Metrics for the Basic Core Models

model	N1,2 (Å)	θ1,2	N3,4 (Å)	θ3,4	O+z	O−z	Rsq
Square plane	2.02	107.7	2.11	72.08	/	/	3.45
Square pyramid	1.97	100.9	2.04	106.8	2.23	/	1.19
Octahedron	1.92	105.3	2.02	104.1	2.16	2.16	2.90

The split maximum and structured rising edge present in the experimental XAS spectrum were reproduced using the square planar and square pyramidal models, but not the octahedral model (Figure 6). The square pyramidal fit was clearly superior below 100 eV, and especially in the XANES energy region (E-E₀ ≤50 eV) (see Figure S8 in the Supporting Information). In the higher energy region (E₀-E>100 eV), the octahedral and square pyramidal models did equivalently well and better than the square planar model. However, the poor reproduction of the rising edge and the relatively large R_sq (Figure 6) eliminated the octahedral model from further consideration. In contrast, the successful reproduction of the rising edge and the low fit R_sq is sufficient to definitively favor the core square pyramidal model.

Following this, an antipodal axial water was added to the square pyramid to test the EXAFS split-axial model. This water refined to an axial distance of 3.12 Å, while the original axial scatterer, previously at 2.23 Å, moved to a new best fit distance of 2.16 Å. Scattering from the new 3 Å oxygen reproduced a shoulder on the rising K-edge of the experimental XAS that had previously remained unfit (see Figure S9 in the Supporting Information). However, the original R_sq=1.19 increased to R_sq=1.88 reflecting a slightly poorer fit to the higher energy XAS region. Nevertheless, the rising edge shoulder was not reproduced by any other structural element, indicating a necessity for the 3 Å axial scatterer. As shown below, addition of the axial 3 Å scatterer lowered the fit R_sq only when the structural model was expanded to include a second shell of water molecules.

The first structural test for a solvation shell included four waters in the equatorial plane at 7 Å, bisecting the four equatorial Im-Cu-Im angles. The 7 Å distance avoided steric interactions with the equatorial imidazole ligands. Although scattering from inappropriately placed atoms can degrade an MXAN fit, this shell of waters improved the square pyramidal fit (R_sq = 1.19) to R_sq = 0.94, while the solvation waters adjusted to an average distance of 7.4±0.6 Å. Addition of a second axial oxygen to this solvated square pyramidal structure again refined to 3 Å, now yielding a further improved R_sq = 0.80. This 3 Å axial oxygen again reproduced the same shoulder on the rising K-edge (see Figure S9 in the Supporting Information).

The importance of this finding required a more critical examination. Therefore, MXAN fits were carried out on the XAS spectrum from which the core-hole broadening was removed. This method is described next, followed by an account of the results.

The intrinsic line widths of XAS spectra are a convolution of the widths of the electronic transitions to the local density of states, with added Lorentzian broadening due to the core-hole lifetime of the absorber. K-edge XAS spectra can be brought into sharper experimental relief by removal of the core hole broadening.⁵⁰ Sharper features in the rising edge energy region allow a stricter comparison between theory and experiment.

Removal of the core-hole width is based on the properties of the Fourier Transform (FT) and the convolution integral. In detail, one can write:

$${\mu }_{exp}=(m_{exp}^{no-ch}\ast L)(E)=\int {\mu }_{exp}^{no-ch}(E-\omega )L(\omega )d\omega ,$$ 1

where, μ_exp is the experimental absorption coefficient, E is XAS energy (in eV), L is the Lorentzian function associated with the copper core-hole width, ω is the energy variable of integration, and ${\mu }_{exp}^{no-ch}$ is the experimental absorption coefficient without the core-hole broadening. The FT of this integral is just the product of the individual FT’s of ${\mu }_{exp}^{no-ch}$ and the Lorentzian function L respectively. In this method, ${\mu }_{exp}^{no-ch}$ is readily derived by the back Fourier transform of the ratio between the FT of the absorption coefficient and the Lorentzian function. Thus,

$${\mu }_{exp}^{no-ch}={[FT]}^{-1}\left({\widehat{\mu }}_{exp}/\widehat{L}\right)$$ 2

where μ̂_exp is the Fourier transform of μ_exp, L̂ is the Fourier transform of the Lorentzian function, and [FT]⁻¹ indicates the back FT operation. This operation can be always done because the FT of a Lorentzian function behaves as an exponential.

The rising K-edge of the solution-phase copper(II)-imidazole complex as measured, i.e., μ_exp, and the identical XAS spectrum following removal of the core-hole broadening, i.e., ${\mu }_{exp}^{no-ch}$, are compared in Figure 7, inset a. Following deconvolution, the shoulders on the rising edge and the two features of the absorption maximum are more highly resolved. Figure 7 itself compares the deconvolved experimental XAS spectrum and the MXAN fit using the split axial model with 2×Cu-O_ax = 2.16 Å, 3.13 Å (R_sq = 1.69). The fit to the core hole deconvolved XAS gave the same core Cu-L metrics as the initial square pyramidal fit (Table 2), within statistical error. In Figure 7, inset b, the rising K-edge energy region of the deconvolved XAS spectrum and the fit to this spectrum are shown. The enhanced resolution allows a definitive conclusion that all the features in the XANES spectrum are fully reproduced.

Figure 7.

(○), Core-hole deconvolved K-edge XAS spectrum of 0.10 M Cu(II) in 4 M imidazole liquid aqueous solution and; ( ), the fit to the spectrum (R_sq = 1.69). Inset a: The rising edge region of: ( ), the K-edge spectrum of 0.1 M Cu(II) in 4 M imidazole liquid aqueous solution, and; ( ), the same spectrum with core-hole broadening removed. Arrows show the emergent delineation of the rising edge features when broadening is removed. The resolution of the K-edge maximum is also enhanced. Inset b: (○), the rising K-edge XAS spectrum deconvolved from core-hole broadening, and; ( ), the fit to the deconvolved XAS spectrum. The rising K-edge features are fully reproduced by this fit.

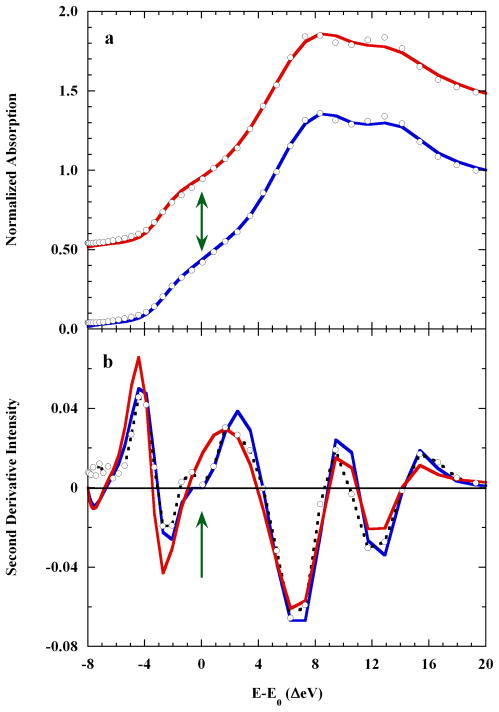
Figure 8a compares the fits to the core-hole deconvolved XAS, with or without the added 3.1 Å axial oxygen scatterer. The shoulder on the rising K-edge is fit only when this scatterer is present. In Figure 8b, the second derivative shows the new feature near E-E₀=0 eV. This feature was not reproduced in the MXAN fit using the octahedral model, nor was it reproduced using a model with two unequal but long axial distances (2.58 Å, 2.96 Å; fit not shown). Thus, only an axial scattering pair including both one short and one very long distance produced a complete description of the K-edge XAS spectrum of dissolved Cu(II)-imidazole.

Figure 8.

Panel a. A comparison of: (○), the K-edge XAS of 0.10 M copper(II) in 4 M imidazole liquid aqueous solution; ( ), the axially elongated (O_ax=2.17 Å) square pyramidal MXAN fit with a distal O_ax scatterer at 3.1 Å, and; ( ), the analogous fit (O_ax=2.28 Å) without the distal O_ax scatterer. Panel b. The second derivatives of: (-○-), the K-edge XAS spectrum of 0.10 M Cu(II) in 4 M aqueous imidazole; ( ) the axially elongated square pyramid with the distal scatterer, and; ( ), the axially elongated square pyramid alone. The arrows show where the 3.1 Å axial scatterer contributed a feature to the rising edge shoulder.

Finally, the first solvation shell was reappraised in light of the eight oxygen scatterers found during EXAFS analysis. An eight-water second shell was added, with each water molecule placed approximately in the middle of one of the eight triangular faces of the core split axial structure. Each of the two sets of four waters initially averaged 4.0±0.3 Å from the copper. In the course of the fit, the four waters near the 2.15 Å axial scatterer shifted their angular positions only slightly, but shifted radially across ±0.37 Å. Nevertheless, they ended the fit at the same average 4.0±0.3 Å distance from Cu(II) (range 3.63 Å–4.25 Å). In contrast, the four waters situated around the 3.0 Å axial scatterer finished at an average distance to Cu(II) of 4.5±0.1 Å (range 4.43 Å–4.64 Å).

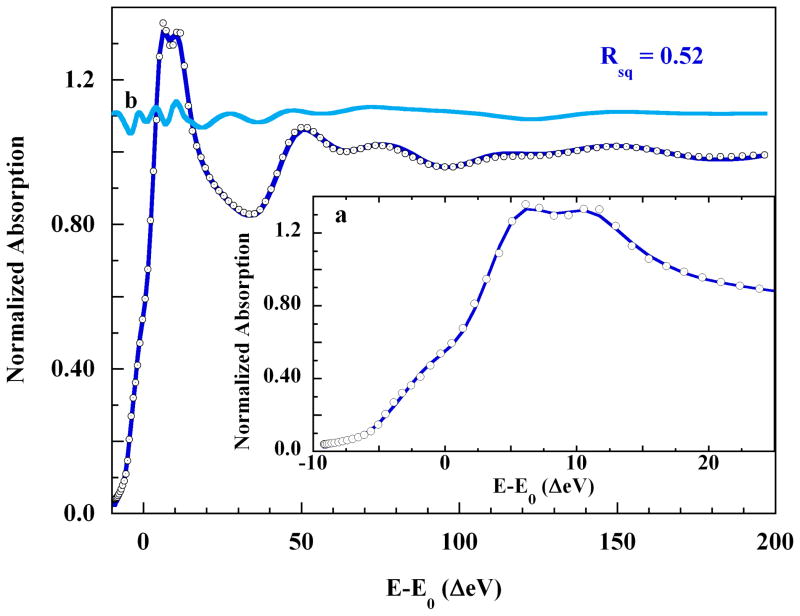
That is, these four Cu-OH₂ distances moved distally, reflecting interactions with a more distant axial scatterer. The final MXAN fit, R_sq = 0.52, is shown in Figure 9. All the major features of the XAS spectrum are well-reproduced by this model. The symmetry of the copper-ligand core is C_4v, and the four imidazoles are statistically within the equatorial plane. The build-up of the experimental XAS signal with successive shells of scatterers is shown in Figure S10 of the Supporting Information. The structure of the XANES is not fully developed until all the imidazole shells and the 3 Å axial scatterer are both present. This shell-by-shell reconstruction of the rising edge XAS explicitly demonstrates that scattering from distant atoms can produce strong features on the rising K-edge of an XAS spectrum, where they can mimic bound-state transitions. Therefore, multiple scattering from one-electron processes should always be eliminated before two-electron transitions are invoked to explain shoulders on the rising K-edges of open d-shell transition metal XAS spectra.^2,44,51 A complete theoretical discussion of this point can be found elsewhere.^41,51,52

Figure 9.

(○), the K-edge XAS of 0.10 M Cu(II) in 4 M aqueous imidazole, and; ( ), the MXAN fit using the split-axial pyramidal model and including eight distant solvent waters at 4.2±0.3 Å. Insets: a. Expansion of: (○), the rising edge energy region, and; ( ), the fit the rising edge. b. ( ), the contribution to the XAS intensity made by the eight-water solvation shell, plotted on the same scale and shifted vertically by 1.1 normalized units.

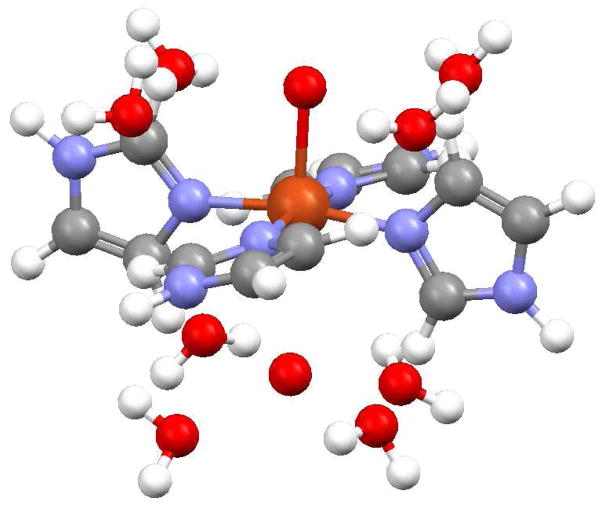
Figure 10 shows an illustration of the final XAS structural model, incorporating all the elements of the EXAFS and MXAN analyses. The final MXAN metrics are given in Table 3. The axial ligands are represented as bare oxygen scatterers but should be taken as indeterminate with respect to water or imidazole nitrogens. The rotational positions of the equatorial imidazole rings, as derived from the MXAN fits, are very similar to the positions found in crystalline [Cu(Im)₄SO₄] and [Cu(Im)₄(NO₃)₂]. A fit with the four equatorial rings disposed in a propeller conformation produced a poorer simulation of the experimental XAS spectrum.

Figure 10.

The XAS model of the square planar {[Cu(Im)₄(O_ax1)](O_ax2)}²⁺ complex ion and eight second shell solvent waters. The imidazole rings are staggered, approximately alternating between the xy- and yz-planes. The −z distant axial oxygen scatterer is directly below the copper. Only the proximal atoms of the axial scatterers could be detected. See the text for details.

Table 3.

MXAN Best Fit Models

model	N1,2 (Å)	θ1,2	N3,4 (Å)	θ3,4	O+z (Å)	O−z (Å)	Ow (Å)	Rsq
Square pyramid	1.97	100.9	2.04	106.8	2.23	---	---	1.19
Square pyr. + 4 Ow	1.98	107.8	2.09	72.09	2.34	---	7.4±0.6	0.89
Split axial	1.99	96.0	2.04	96.0	2.16	3.12	---	1.88
Split axial + 8 Ow	1.99	89.6	1.99	98.6	2.14	3.00	4.2±0.3	0.52

Errors in the metrics of the “final split axial + 4 O_w” model are: N_eq ±0.02 Å (ste), ±0.03 Å (sys); O_+z, ±0.11 Å (ste) ±0.03 Å (sys); O_−z, ±0.13 Å (ste) ±0.04 Å (sys); O_w, ±0.2 Å (ste)±0.1 Å (sys), where “ste” is statistical and “sys” is systematic. The tabulated uncertainty in O_w is the statistical spread in the eight fitted distances. The error in θ is ±3.9°.

Discussion

The central finding of this combined EXAFS and MXAN study is that in water solution dissolved Cu(II) forms an axially elongated square pyramidal complex ion with imidazole, rather than a JT-octahedron. In the equatorial region the four imidazole ligands could be assigned unambiguously at a net 2.00±0.02 Å. The identity of the axial ligands remained indeterminate, most likely due to the fast axial inversion and ligand exchange of Cu(II) (see below). Both methods of XAS analysis independently converged to this result. The axial copper-ligand distance of about 2.13 Å is relatively short compared to crystal structure analogues. Beyond the square pyramidal structure, an antipodal axial scatterer was found near 2.9 Å. This scatterer is too distant to be interpreted as a sixth copper ligand, and better described as constituting a strong solvent interaction. Further, both EXAFS and MXAN found evidence for a solvation shell of about eight water molecules near 4 Å from copper(II). The dissolved copper(II)-imidazole complex ion thus falls into the same square pyramidal structural regime as dissolved [Cu(H₂O)₅]²⁺ and [Cu(NH₃)₅]²⁺.^1,2,15

The greater intensity of the 1s→3d transition in the rising K-edge XAS of the dissolved Cu(II)-imidazole complex (Figure 2) now finds an explanation in the lack of centrosymmetry in this ion. Lower symmetry ligation environments allow more 4p mixing into transition metal 3d orbitals, and the intensities of transition metal 1s→3d pre-edge transitions are known to increase with 4p-3d mixing.^53,54

Relevant to the non-centrosymmetry of unconstrained Cu(II), recent structural and solution studies of Cu(II) coordination within the encapsulating ligand Me_ntricosaneN₆ (n=5,8),⁵⁵ have shown that ligand flexibility allows the choice between two proferred structural ground states. The Me_ntricosaneN₆ ligands provide six ammine nitrogens that can readily support the JT-octahedral coordination classically assigned to dissolved Cu(II) complex ions. However for dissolved [Cu(Me_ntricosaneN₆)]²⁺ (n=5,8), one ammine group dissociates and the predominant solution structure is square pyramidal. Nevertheless, this work found that interconversion between 5- and 6-coordinate [Cu(II)Me₈tricosaneN₆]²⁺ is facile, implying a small energetic barrier. Supporting this notion, recent calculations using density functional theory (DFT) evaluated the square pyramidal and JT-octahedral geometries for dissolved aqueous [Cu(aq)]²⁺ within a solvation model, finding the former to be the more stable but only by about 5.9 kJ-M^−1.56 Nevertheless, even this small energetic preference is enough to ensure that ~91% of [Cu(aq)]²⁺ exists as the square pyramidal [Cu(H₂O)₅]²⁺ complex ion in liquid aqueous solution at room temperature (300 K).

In the EXAFS and MXAN analyses of dissolved aqueous [Cu(H₂O)₅]²⁺ or [Cu(NH₃)₅)]²⁺, the axial ligands were small molecules that could be assigned with some confidence. However, the XAS case for [Cu(Im)₄]²⁺ is presently less clear. Figures S1 and S2 in the Supporting Information show that the experimental solution exhibited UV/vis spectroscopic behavior consistent only with the K₁-K₆ equilibrium scheme leading to [Cu(Im)₆]²⁺ as worked out by Sjöberg.^34,42 The calculated composition of the experimental XAS solution was thus 80% [Cu(Im)₆]²⁺, 18.6% [Cu(Im)₅]²⁺, and 1.4% [Cu(Im)₄]²⁺, neglecting any associated water molecules. Nevertheless, neither EXAFS nor MXAN analysis detected the extended structure of any axial imidazole groups, while very good fits were obtained when including axial oxygen scatterers only.

However, central to this apparent disparity is that the XAS experiment involved the liquid solution state. Solution phase Cu(II) complexes exhibit high inversion rates,^19,57–59 implying that the ~2.13 Å and ~2.9 Å axial scatterers may rapidly exchange distances even without dissociating. The usual axial Cu(II)-ligand bond is weak and has a relatively shallow potential well that, in aqueous solution, allows the Cu-L_ax distance to also undergo rapid low-energy fluctuations.^1,19,57–59 These axial inversions and fluctuations, in turn, can reduce the XAS backscattering intensity of any axial imidazole shells. In this context, the fifth and sixth imidazole equilibrium constants, K₅ = 10 M⁻¹ and K₆ = 2.5 M⁻¹, yield very small association free energies of ΔG₅ ≅ −5.8 kJ-M⁻¹ and ΔG₆ ≅ −2.3 kJ-M⁻¹ at 300K, approximating the strength of very weak hydrogen bonds.⁶⁰ These low stabilities are consistent with fast ligand exchange and large fluctuations in copper-ligand distance, and are entirely comparable in magnitude but opposite in sign to the 5.9 kJ-M⁻¹ required for the [Cu(H₂O)₅]²⁺+H₂O → [Cu(H₂O)₆]²⁺ conversion, calculated using DFT as noted above.

The fast axial solvolytic exchange rates of Cu(II) complexes,^19,57,61,62 can combine with internal dynamics to further attenuate any axial photoelectron back-scattering, making full resolution of the axial ligands difficult in liquid solution phase. Thus, even though oxygen atoms were sufficient to model the axial scatterers, this result is not unambiguous with respect to the complete identity of the axial ligands. Although it may be possible to interpret the progressive changes in Cu(II) UV/visible absorption spectra at high [Im] as reflecting something other than axial imidazole binding, such as, e.g., the emergence of a specific hydrogen bonding interaction between imidazole-nitrogen and an axial water, systematically induced by increasing [Im], such an alternative explanation is not made preferable by any existent data. The preferable explanation is presently the simpler one, namely that the changes detected using UV/vis spectroscopy reflect ligation of axial imidazoles, but that known solution dynamics renders them undetectable to XAS at the current level of data. An extended and higher resolution XAS data set may resolve this question.

It is important to note, however, that an inability to detect the extended structure of axial imidazole ligands does not translate into any ambiguity about the presence of proximate axial scatterers. The addition of axial scatterers to the EXAFS and MXAN structural models were critical and central to the production of a good fit to the data. This fact is demonstrated in Figure S3 in the Supporting Information (EXAFS), and Figure 6 and Figure S7 in the Supporting Information (MXAN), which show the poor fits obtained in the absence of these scatterers. From a physical-chemical perspective, a proximate atomic scatterer remains present whether the fluctuating axial ligand is water or imidazole. Four disparate axially dynamic structures are instantaneously present in solution, viz., {[Cu(Im)₄(Im_ax)_short](Im_ax)_long}²⁺, {[Cu(Im)₄(Im_ax)_short](H₂O_ax)_long}²⁺, {[Cu(Im)₄(H₂O_ax)_short](Im_ax)_long}²⁺, and {[Cu(Im)₄(H₂O_ax)_short](H₂O_ax)_long}²⁺. Assuming the discerned axial distances apply, then only the extended imidazole shells will suffer backscattering attenuation due to exchange. Two proximate atomic axial scatterers are always present and retain constant N/O identities.

Beyond the square pyramidal core, the distal ~3 Å axial distance is long compared to known crystallographic Cu(II) axial bond lengths,^3,63 and seems more indicative of strong solvation than of weak bonding. A similar 4-1-1 non-centrosymmetric structure has been found in crystalline Cu(OH)₂, which includes axial Cu-O distances of 2.356 Å and 2.915 Å.⁶⁴ Crystalline [Cu(NH₃)₄H₂O]SO₄ exhibits axial Cu-O interactions of 2.340 Å and 3.477 Å.⁶⁵

Both EXAFS and MXAN analyses provided evidence for a Cu-H₂O solvation shell of water molecules at the same 4.2 Å average distance. The number of waters in the final fits was set by EXAFS analysis, and the MXAN R_sq improved steadily with four, six, and eight waters in this shell. This 4.2 Å shell does not represent unfit weak scattering from shells of undetected axial imidazole ligands. An axial imidazole at 2.15 Å, for example, should produce a pair of more distant axial shells near 3.17 Å (C_α) and 4.36 Å (C_β-N_β). Likewise, an axial imidazole at 3.0 Å should produce analogous axial shells near 3.97 Å and 5.17 Å. None of these distances appeared in any of the fits. Further, in an MXAN fit, the calculated scattering from 8 dispersed water molecules would not fit the experimental XAS scattering features from localized axial imidazole shells. The situation is just as unambiguous in the EXAFS analysis, in that the solvent shell distances of 3.8 Å and 4.4 Å do not correspond to the C_α, C_β-N_β pairs of shells in undetected axial imidazole ligands at the extrapolated EXAFS distances of 3.14 Å and 4.33 Å, and 3.84 Å and 5.04 Å.

Aqueous solvation shells have previously been found around dissolved transition metals using EXAFS or scattering methods.^66–71 H/D neutron scattering revealed evidence for 7 waters of solvation about 4.5 Å from dissolved octahedral [Cr(H₂O)₆]^3+.71 However, only the combination of EXAFS and MXAN analysis has produced an empirical 3-dimensional structural model for a transition metal second shell hydration sphere.

The lack of centrosymmetry uniformly observed in dissolved Cu(II) complex ions implies that unconstrained copper(II) ion preferentially organizes itself into an axially elongated square pyramidal core complex ion; xy-coplanarity need not be present.¹ This consistency, in turn, removes the traditional structural rationale for the hypothesis of rack-induced bonding in blue copper protein active sites,^1,45 based as it was on the acceptance of a D₄h JT-octahedron as the ground state for unconstrained copper(II) complexes.^72–76

In rack-induced bonding theory, the structural stability of the protein forces the metal-ligand conformation to remain at the top of a negative thermodynamic gradient. Release would produce a spontaneous relaxation of the metal site to its true ground-state geometry, with the concomitant loss of energy appearing as an observable −ΔG_rackstrain. The structural identity of the apo- and holo-forms of blue copper proteins,^77–81 leads to the rack bonding theoretical prediction that the holo-protein should be thermodynamically less stable than the apo-protein, due to the +ΔG_rackstrain, directed back against the protein by the enforced high-energy conformation of the metal active site.¹ This result was absent from the protein folding experiments that should have revealed it, however, which falsifies the rack-bonding prediction.^1,82

An alternative version of the rack-induced bonding theory of blue copper proteins has been formulated, which suggests that a constraint imposed by the protein prevents the weak ~4.6 kcal-mol⁻¹ Cu(II)-S_Met bond from dissociating at physiological temperature.^76,83,84 However, the M121Q mutant of A. denitrificans azurin retains the entire wild-type (WT) H-bonding network,^85,86 but exhibits considerable flexibility specifically at the methionine locus.⁸⁷ This would seem to obviate a protein constraint at that site. The outer sphere F114A and F114N mutations of Ps. aer. Azurin again leave the WT H-bonding network entirely intact, and induce no significant structural modifications to the copper site. Nevertheless, these distant mutations significantly impact the Cu(II) redox potential (ΔE⁰′ = +54 mV and +98 mV, respectively),^88,89 decreasing the relative ground state stability of Cu(II) by 5.2 kJ-mol⁻¹ and 9.5 kJ-mol⁻¹, respectively, without any apparent energetic cost to the protein.

The backbone attachment of amino acids provides the protein equivalent of the chelate effect,⁹⁰ by preventing the translational diffusion of a ligand. In a metalloprotein active site, an appropriate ligand atom is thus always present near the coordinately unsaturated face of a bound metal ion. This protein chelate effect greatly increases the effective concentration of the ligand. For the blue copper site, a straight-forward statistical accounting of this effect (presented in the Supporting Information) predicts a spontaneous Cu(II)-SMet occupancy of at least 0.98 at 298 K, and again at no energetic cost to the protein. High occupancy thus requires only a small negative thermodynamic gradient favoring bond formation.

It is difficult to see how any theory of imposed rack-strain in blue copper proteins can survive all the disconfirmations. Rather, it seems clear that the structure and reactivity of the blue copper site is physically adjusted in ways far more subtle than by structural constraint.^{1,45,86,91–96} All these considerations apparently escaped a recent critical review of blue copper proteins.⁹⁷

Finally, the square pyramidal core structure repeatedly found for dissolved aqueous Cu(II) confirms the lack of centrosymmetry found earlier by Peisach and Mims for a series of dissolved Cu(II) complex ions.^17,18 Lack of centrosymmetry about unconstrained copper ion should impact the assessed magnitude of the Franck-Condon barrier to electron transfer involving this ion,^98–101 and may help explain the [Cu(H₂O)₅]²⁺/[Cu(aq)]⁺ self-exchange rate.^31,101 Extended solvent shells have thus far been found to attend aqueous Cu(II) complex ions other than the elementary pentaaqua ion. Clearly, after more than 60 years of study,^102–105 the structure of Cu(II) ion in water solution continues to provide surprises.