Physical Model for Self-Organization of Actin Cytoskeleton and Adhesion Complexes at the Cell Front

Abstract

Cell motion is driven by interplay between the actin cytoskeleton and the cell adhesions in the front part of the cell. The actin network segregates into lamellipodium and lamellum, whereas the adhesion complexes are characteristically distributed underneath the actin system. Here, we suggest a computational model for this characteristic organization of the actin-adhesion system. The model is based on the ability of the adhesion complexes to sense mechanical forces, the stick-slip character of the interaction between the adhesions and the moving actin network, and a hypothetical propensity of the actin network to disintegrate upon sufficiently strong stretching stresses. We identify numerically three possible types of system organization, all observed in living cells: two states in which the actin network exhibits segregation into lamellipodium and lamellum, whereas the cell edge either remains stationary or moves, and a state where the actin network does not undergo segregation. The model recovers the asynchronous fluctuations and outward bulging of the cell edge, and the dependence of the edge protrusion velocity on the rate of the nascent adhesion generation, the membrane tension, and the substrate rigidity.

Introduction

Biological cells spread and move on external substrates. Phenomenon of cell migration is of crucial importance for such fundamental processes as wound healing, morphogenesis, and cancer (1,2). Understanding of this phenomenon includes two equally important aspects: uncovering the related complex biology and revealing the physical forces, which determine the cell shape and movement.

Cell spreading and migration as well as the maintenance of the cell shape are determined by interactions between three structures: the cell plasma membrane, the cytoskeleton, and the extracellular matrix (2–4). The plasma membrane is a few nanometers thick elastic shell that forms the cell boundary and is based on a lipid bilayer (5,6). The cytoskeleton is an elaborate network of dynamic polymeric structures filling the cell interior (7). Among the cytoskeletal elements the polymers of the protein actin, called the actin filaments or F-actin, are the most abundant and play a major role in the cell mechanics (8). Actin cytoskeleton is dynamically associated with transmembrane adhesion receptors that mediate cell adhesion to the extracellular matrices (9–11).

The prevailing kind of cell locomotion along the substrates is the so-called crawling, which consists in directional generation of the cell surface protrusions and their attachment to the substrate followed by translocation of the cell body containing nucleus and other organelles (1,12,13). For many types of cells able to crawl along flat rigid substrates, the major type of protrusions is a flat thin (of a less than micron thickness) extension spreading along the substrate and referred to as lamellum, or lamella (14,15). Recent studies revealed a complex organization of the actin cytoskeleton in the lamellum. The most peripheral part of the lamellum, a 2–4 micron wide band immediately adjacent to the cell edge, is filled with a very dense gel-like network of actin filaments (16–18). This part, referred to as the lamellipodium, contains specific proteins regulating actin polymerization and depolymerization such as Arp2/3 complexes, WAVE, VASP, cofilin, and others (18–20). The more interior part of the lamellum referred to here as the lamellum proper or, simply, the lamellum is characterized by a severalfold lower density of the actin network, different actin organization, and different actin accessory proteins. In particular, it contains myosin II and tropomyosin (17,18,21). Formation of a distinct boundary between the lamellipodium and lamellum is a process of primary importance for the assembly of the entire actin cytoskeleton (22,23).

The mechanism of the actin network segregation into two domains of different structure and composition with a distinct boundary between them was a subject of theoretical modeling (23,24). In our previous work (23), we proposed that such boundary emerges due to interaction between the actin cytoskeleton and the adhesion complexes underneath the lamellipodium referred to as the nascent focal adhesions, which eventually grow in size. However, the interplay between mechanosensitivity of the adhesions, actin dynamics, and force generation was not addressed.

In this work we computationally analyze the self-consistent dynamics of the polymerizing and movable actin network on one hand and, on the other, of the system of mechanosensitive focal adhesions that emerge, grow, and disintegrate depending on their interactions with actin. The computational results reproduce the major higher order experimental observations on the dynamic organization of the lamellipodium, which include the adhesion accumulation in the proximity of the cell leading edge and the related development of the lamellipodium-lamellum boundary. They provide insight into why the lamellipodium-lamellum boundary tends to form in slow moving cell types rather than rapidly moving ones and account for such features of the cell leading edge behavior as its irregular local fluctuations and bulging in front of adhesions.

Phenomenological Background

Lamellipodium and lamellum

We consider the lamellipodium actin network as an isotropic gel (8,25) whose physical properties relevant for the present model are independent of its particular microstructure (26–29). The lamellipodium gel steadily polymerizes against the edge membrane and generates forces pushing the cell edge membrane forward (30,31). The membrane reacts by developing a contribution to the lateral tension that pushes back on the actin filaments and results in two main effects: movement of the actin gel from the membrane edge toward the cell interior, the phenomenon referred to as the actin retrograde flow (32–34), and generation of the elastic stresses within the gel.

Physical characteristics of the actin networks as a viscoelastic media have been thoroughly investigated (7,8,35). Crucial for this work is a hypothetical propensity of the lamellipodium gel to disintegrate in the regions of sufficiently strong stretching strains and stresses (23). This property of the gel has been earlier suggested to explain the formation of the wave-like lamellipodium boundary (23). Recently, it received indirect support from the discovered effects of myosin-II on disassembly of intracellular actin networks, which is most consistent with the enhanced breakage of the actin filaments by the myosin-driven stresses within the gel (36–38). It is also possible that stretching of the actin filaments in the direction of the stress (23) or bending of the filaments oriented in the perpendicular direction contribute to the actin depolymerization by ADF/cofilin (39–41).

The lamellum actin network is characterized by the presence of bundles of actin filaments, which include myosin molecules, exhibit an ATP-dependent contractility, and are referred to as the stress fibers. The space between the bundles is filled by a sparse network of actin filaments. In addition, the lamellum contains nonactin cytoskeleton elements such as microtubules and intermediate filaments. The lamellum network also undergoes a retrograde motion, which is, however, a few times slower than that of the lamellipodium actin and is fueled by the myosin driven contractility rather than the actin polymerization. Thus, the lamellipodium-lamellum boundary is characterized by an abrupt decrease of the actin density and of the velocity of the actin retrograde flow (16,18,22,24,33). Geometrically, this boundary has a characteristic shape of intersecting arcs delineated by thin actomyosin bundles (16,22,23).

Focal adhesions

Focal adhesions (FAs) are multicomponent protein complexes based on the membrane spanning integrin molecules, whose extracellular domains bind to the external substrate. The intracellular parts of the integrins are associated with a protein plaque that mediates a regulated link between the integrins and the actin network (9,42–44). Depending on the degree of maturation, FAs are classified as nascent FAs having submicron dimensions and mature elongated FAs of a few micron sizes (16,45,46).

The nascent adhesions are originated underneath the lamellipodium. The mature adhesions are found mainly at the lamellipodium-lamellum boundary, where they are located at the vertices between the apparent arcs, and in the lamellum at the tips the of stress fibers (16,45).

The cell adhesions exhibit a property of mechanosensing. Transformation of the nascent adhesions into mature ones and growth of the latter depends on the application to the adhesions of pulling forces (10,47). The mature adhesions enlarge in the direction of the force and eventually disassemble if the force is lifted (48,49). Several models have been suggested for the physics of the adhesion-dependent mechanosensitivity (50–52). According to the thermodynamic model based on the dependence of the chemical potential of the adhesion components on the stretching force, an adhesion assembles if the force exceeds a certain threshold level and disintegrates otherwise (52).

Interaction between actin and cell adhesions

The interaction between the actin cytoskeleton and the cell adhesions can be described by the molecular clutch hypothesis, according to which the system can switch between two basic types of behavior: slipping of the actin network with respect to the adhesion, and actin sticking to the adhesion (53,54). An intermediate behavior is the stick-slip motion, where the system repeatedly switches between sticking and slipping (55). Relevant for the overall retrograde flow of actin with respect to the substrate are the slipping and the stick-slip regimes. Experimental results along with theoretical modeling demonstrate the realization of these two regimes for different cell types and in different cell parts. The theory of nonlinear friction (56) applied to the actin-FA interaction (57) qualitatively predicts different relationships between the average actin velocity relative to the adhesions, v, and the average force with which the actin drags the adhesion, referred to as the traction force, f_trac (56,57). In the slipping regime predicted for low velocities, the traction force f_trac has to increase with increasing v. In the stick-slip regime, which is expected for large velocities, the traction force f_trac is predicted to decrease with increasing v (56,57). Experiments on epithelial cells showed that in the lamellipodium region the traction force decreases with the velocity, hence, inferring a stick-slip regime of the actin-adhesion interaction (58). For the lamellum, f_trac increased with v suggesting the slipping regime (58). Recent direct measurement of talin dynamics (59) is also consistent with the stick-slip mode of interactions between adhesions and the actin cytoskeleton.

Qualitative Essence of the Mechanism

Here, we suggest a mechanism for the self-organization of the cytoskeleton and FAs in the cell front, which involves two interrelated processes: segregation of the actin gel into the lamellipodium with a distinct boundary separating it from the lamellum, and segregation of the FA system into an array of dynamic nascent FAs underneath the lamellipodium and mature FAs located at the lamellipodium-lamellum boundary and close to it in the lamellum. The essence of the model is that the system's self-organization is based on four crucial properties of its components: the actin gel flow from the membrane toward the cell interior; the mechanosensitivity of the FAs (52); the disassembly of the actin gel upon stretching elastic stresses larger than a threshold value (23); and the stick-slip character of interaction between the retrogradely moving actin gel and the FAs (56,57). We numerically analyze the system's evolution during the retrograde movement of actin with respect to the FAs and show that the major factor driving this evolution is an uneven distribution of the actin-adhesion interaction force between the FAs located at different distances from the cell edge.

We start from an arbitrary distribution of nascent FAs under a uniformly moving actin gel, assuming that new nascent FAs emerge randomly in the course of the system evolution. Because of the stick-slip character of the actin-FA interaction, those FAs that are closer to the cell edge effectively offset the force that is exerted by the membrane on the FAs through the actin network and screen from this force the FAs that are located further away. As a result, the membrane-proximal FAs are subjected to a larger average force as compared to the membrane-distal FAs. Due to the mechanosensing property, the membrane-proximal FAs self-assemble and increase in size further reinforcing the screening effect, whereas the membrane-distal FAs disassemble and disappear. As was shown previously (23), the growing FAs produce stretching stresses within the adjacent portions of the actin gel and can drive the gel's disintegration, thereby generating the lamellipodium boundary with associated mature FA complexes. The new FAs, emerging and maturating between the lamellipodium boundary and the edge membrane, take over the stresses, leading to the advancement of the lamellipodium-lamellum boundary and protrusion of the cell edge.

However, as will be shown below, formation and advancement of the lamellipodium boundary depend on the system parameters such as the frequency of generation of the new nascent FAs, the membrane tension, and the effective sensing by the adhesions of the substrate rigidity.

Formulation of Physical Model

Actin gel

Geometrically, the lamellipodium actin gel is described as a two-dimensional band-shaped element (Fig. 1). One edge of the band underlies the membrane where a boundary condition of constant load is applied, whereas the opposite edge is unconstrained and, therefore, subject to a zero normal force. We apply the reflective boundary conditions to the two lateral sides of the band element, which means that the system properties and behavior beyond these boundaries are assumed to be the same as those of the modeled part of the gel. The initial width of the band is taken to be 10 μm, as a numerical approximation for an infinite gel. The actin gel is considered to be an elastic material (23) with a Young's modulus of 10 kPa (60,61) and a Poisson ratio of 0.4 (62). Before the initial calculation step, the actin gel is considered to be unstressed.

Figure 1.

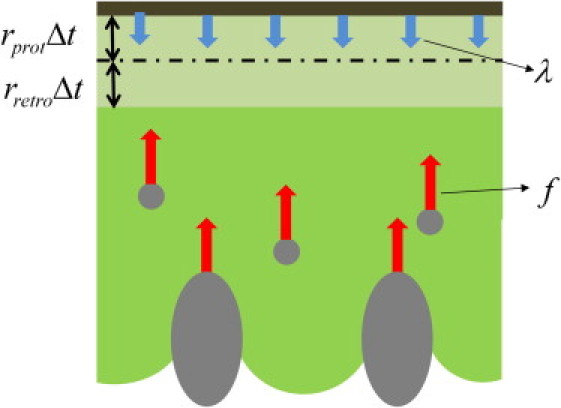
Schematic description of the system. At a discrete time step, the modeled components of the lamellipodium are the nascent and mature cell adhesions (gray circles and ellipsoids, respectively), the cell membrane (brown), and actin gel (green). Newly polymerized gel is shown in lighter green, with a dash-dot line indicating the position of the membrane before polymerization. Blue arrows designate force exerted on the gel by the cell membrane due to tension, whereas red arrows represent friction forces applied by the adhesions to the gel.

In general, application of a load to a cross-linked actin gel results in both elastic deformation, and a viscous flow of the gel (63). The time-dependant nature of the developed stresses and strains in the gel due to viscous effects is characterized by a long timescale corresponding to the typical binding time of the actin cross-linking proteins, and a short timescale corresponding to the time needed for stress equilibration within the gel. For the timescale relevant to this model, characterized by the ratio of the lamellipodium width and the actin retrograde velocity, the response of the gel to the load may be regarded as that of an isotropic elastic material. For a detailed treatment and justification of this assumption, see (23) and Appendix A in the Supporting Material.

The actin gel polymerization is localized to the membrane edge of the band. In general, the polymerization rate of each filament depends, according to the force-velocity relationship (30), on the load applied to the filament tip by the membrane tension γ. We assume that γ and the number of the polymerizing filament tips per unit length of the membrane edge are constant and, hence, so is the polymerization velocity r_pol. The latter is equal to the velocity of the gel elongation toward the edge membrane, under the assumption of negligible gel stretching-compression effects. The gel elongation gives rise to two kinds of motion with respect to the immobile substrate: protrusion of the membrane edge with a velocity r_prot (positive sign corresponding to the direction toward the cell front) and a retrograde motion of the bulk of the gel with a velocity r_retro (positive sign corresponding to the direction toward the cell interior) (Fig. 1), such that

$$r_{\mathit{pol}}=r_{\mathit{retro}}+r_{\mathit{prot}}.$$ (1)

Focal adhesions

Initially, nascent adhesions with a diameter of 0.1 μm are distributed underneath the actin gel, arranged in either a grid pattern or at random locations throughout the gel, and are set to be in the stick state. The formation of the new nascent adhesions is taken to be independent of the distribution of stresses in the system and the rate of their formation per unit area is denoted by r_form. Formation of focal adhesions is a multistage, hierarchical process, consisting of many sequential molecular events, including, besides interaction of integrin receptors with matrix ligands, several other potential rate-limiting stages. Thus, the parameter r_form depends both on the ligand density, and on intrinsic cell characteristics (64,65).

We model the mechanosensitive behavior of the adhesions according to the results of our previous model (23). The factor determining whether an adhesion grows or shrinks is the force f of interaction between the adhesion and the actin gel, which is related to the adhesion unit area and referred to below as the force density. We assume that if the force density exceeds a threshold value, f > f_th, the adhesion grows, whereas under smaller force densities, f < f_th, the adhesion shrinks and disintegrates. The rate with which the adhesion changes its size, r_FA, is taken to be

$$\begin{array}{l}{r}_{\mathrm{FA}}=r_{\mathit{grow}}\text{for}f>f_{\mathit{th}};\\ r_{\mathrm{FA}}=-r_{\mathit{shrink}}\text{for}f<f_{\mathit{th}};\\ r_{\mathrm{FA}}=0\text{for}f=f_{\mathit{th}},\end{array}$$ (2)

where r_grow and r_shrink are free parameters, taken in our model to be 0.02 and 0.01 μm/s, respectively. As the direction of the applied force largely determines the adhesion growth direction and, hence, the orientation of the adhesion, we model the FA as an elliptical object that elongates or shrinks with a velocity r_FA along the direction parallel to the applied force and a rate r_FA/2 in the perpendicular direction.

Actin-adhesion interaction

To model the stick-slip interaction, we consider individual adhesions as either fully attached to the gel, or completely disengaged from it. In the attached stick state, the actin gel is locally fixed to the adhesion, and has zero displacement relative to it. On the other hand, an adhesion in the detached slip state transmits no forces to the gel and, hence, offers no resistance to gel motion. Transition between stick and slip states is assumed to be a stochastic process, whose probability per unit time, p, is determined by the force density f according to

$$p\left(f\right)=\mathit{\omega }\left(\mathit{1}-e^{-\frac{f}{f^{\ast }}}\right),$$ (3)

where f^∗ is a characteristic critical force density; and ω is a characteristic frequency. Hence, the probability of the stick-slip transition vanished for zero force density, p(f = 0) = 0, and increases with the force density f, which means that the model does not account for a possibility of a catch-bond interactions between actin and FA (66).

Reattachment of the actin gel to the adhesion is considered to be force independent, and occurs within a characteristic time ω⁻¹.

Finally, to account for the gel disintegration under elastic stresses we follow the approach of our previous work (23), and assume that the disintegration occurs instantaneously if the stresses within the gel exceed a critical positive value, σ_crit = 40 Pa, determined in (23) by parameter fitting.

Sensing the substrate rigidity

Sensing rigidity of the external substrates influences multiple cellular properties such as morphology, motility, and differentiation (67–69). On the mechanical and structural levels, the substrate rigidity affects such factors as the cell generated traction forces and the dimensions of the mature focal adhesions (70). Here, we account for the effects of the substrate rigidity on the lamellipodium organization by assuming that the rigidity sensing is provided by the focal adhesions. Although theoretical models have been proposed for the effective cross talk between the focal adhesions and the substrate rigidity (50,51) (71) the underlying mechanisms have not been fully established. Therefore, we take a phenomenological approach based on the observation that adhesion growth is impaired on soft substrates (70). We assume that the substrate rigidity influences the threshold force density f_th determining the transition to the force-induced FA growth (Eq. 2). The softer the substrate, the larger the threshold force density. To account for this feature of the system, we take the force threshold force density to be $f_{\mathit{th}}=\alpha f^0$, where the coefficient α, referred to as the rigidity sensing parameter, equals α = 1 for infinitely rigid substrates and adopt larger values for softer substrates. The threshold force density for infinitely rigid substrates is taken $f^0=1000\mathrm{Pa}$.

Computational Procedure

To numerically analyze the time evolution of the system we present it as a series of discrete steps separated by a time interval τ_step. At each sequential step we perform the following changes to the system and the related computations.

• A strip of newly polymerized actin gel is added at the lamellipodium-membrane interface. The width of this strip is given by τ_step × r_pol.

• New nascent adhesions are added and randomly distributed throughout the system. The number of the new adhesions is N_new = τ_step × A_gel × r_form, where A_gel is the gel area.

• The membrane tension produces a pressure of λ = 300 pN/μm applied to the gel edge and directed perpendicularly to the gel-membrane interface.

• All adhesions that are colocalized with the actin gel (i.e., adhesions that are located inside the lamellipodium) are considered to be in the stick phase. This is equivalent to reversion of the adhesions to the stick phase within the characteristic time ω⁻¹ (discussed below).

• Using numerical finite-element techniques implemented by the commercial software package, COMSOL Multiphysics (see (23)), we calculate the distribution of the strains and stresses within the gel at this time step. This includes computation of the force density of interaction between the gel and each of the adhesions $f^{\left(n\right)}$.

• Each adhesion increases or decreases in size, depending on whether the corresponding force density $f^{\left(n\right)}$ is larger or smaller than the threshold value f_th. The change in each adhesion size, Δ⁽ⁿ⁾, is determined by ${\Delta }^{\left(n\right)}=r_{\mathrm{FA}}^{\left(n\right)}\times {\tau }_{\mathit{step}}$. The adhesions that shrink below the initial size of 0.1 μm are removed from the system.

• For each adhesion, we determine whether or not it undergoes a transition between the stick and slip states by stochastic choice according to the probability, p, and the force density, $f^{\left(n\right)}$(Eq. 3). The unknown parameters ω and f^∗ have to be found from fitting of the computation results to the observable values. To simplify the computations, we fix the frequency to be $\omega =1/{\tau }_{\mathit{step}}=0.2{\text{s}}^{-1}$. The corresponding fitted value of the critical force is f^∗ = 2000 Pa.

• The new distribution of the stresses within the gel following the evolution of the adhesions sizes and attachment to the gel is computed.

• Continuous regions of the gel for which the stress exceeds the critical value, σ > σ_crit, are considered as disintegrated and removed from the system. Small, enclosed regions of postcritical stress are excepted from the disintegration, because it is expected that they will refill due to local flow effects that are not included in the model. The contour of the new lamellipodium-lamellum interface is determined by the shape of the removed region of gel.

Results

Major regimes of the lamellipodium behavior

We found several typical regimes of the lamellipodium behavior depending on the values of the major system parameters such as the formation rate of the nascent adhesions, r_form, the membrane tension γ, and the rigidity sensing parameter α, which are determined by the cell types and states and by the characteristics of the external substrates.

Variation of the adhesion formation rate, r_form, which controls, effectively, the average adhesion density revealed three major regimes of the lamellipodium behavior. We present the results of r_form variation by fixing the values of the membrane tension, = 150 pN μm⁻¹, and of the rigidity sensing parameter α = 1. The results are presented in Fig. 2, Fig. 3, and Movies in the Supporting Material.

• Slow formation of nascent adhesions (r_form < 0.001 μm² s⁻¹), leading to low adhesion density, results in a formation of a stationary lamellipodium band of 2−4 μm width, with a lamellipodium-lamellum boundary represented by the typical arc shapes with mature adhesions at the arc intercepts (Fig. 2 A, Fig. 3 A, and Movie S1). The average protrusion rate of the edge membrane is zero in this case, so that the overall retrograde flow rate is equal, on average, to the actin polymerization rate.

• Intermediate rates (r_form ∼0.01 μm² s⁻¹) of nascent adhesion formation result in an advancing lamellipodium with a sharp lamellipodium-lamellum boundary (Fig. 2 B, Fig. 3 B, and Movie S2). In this case, the membrane edge moves forward because the emergence of new adhesions close to it drives the membrane protrusion. Subsequent to the edge membrane movement, the lamellipodium boundary leaps to a row of newly matured adhesions closer to the membrane, and, hence, advances after the membrane edge.

• High rate (r_form ∼0.1 μm² s⁻¹) of nascent adhesion formation results in a dense adhesion distribution. In that case, sufficient stretching stresses do not develop in the gel, and, subsequently, no gel disintegration occurs, and no lamellipodium-lamellum boundary forms (Movie S3 and Fig. 2 C, Fig. 3 C). The membrane protrusion rate is maximal in this case.

Figure 2.

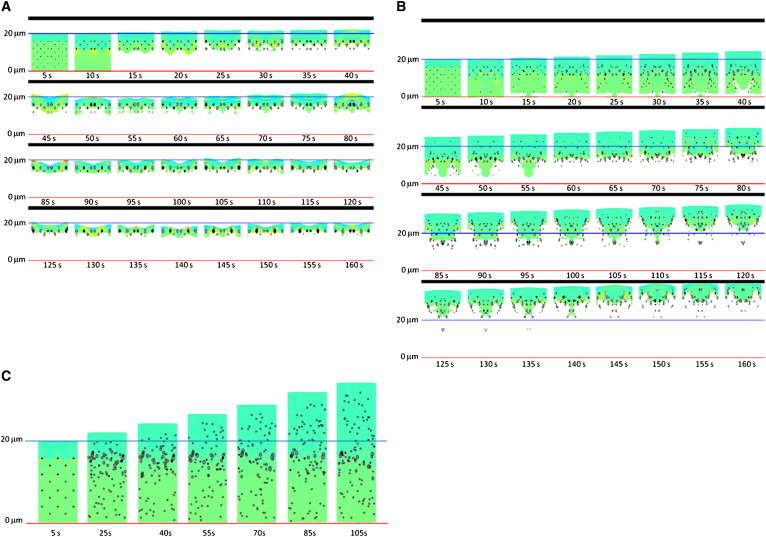
Self-assembly and organization of the lamellipodium. Individual images correspond to numerical results at discrete time steps of the simulation. Membrane edge (not indicated) is located at the top of each image, whereas the free edge is at the bottom. Initial state is a 10 μm wide band of gel, with an array of dot-like, R = 0.1 μm, adhesions. The values of all parameters except for the adhesion formation rate r_form are indicated in the text. (A) Simulation run with no formation of new adhesions, r_form = 0. (B) Simulation run with an adhesion formation rate of r_form = 0.01 s⁻¹μm⁻². A distinct lamellipodium is formed at time step T = 60s. (C) Simulation run with a high adhesion formation rate of r_form = 0.2 s⁻¹μm⁻². Color coding of the actin gel represents the local magnitude of the principal stress (see color bar in Fig. S2).

Figure 3.

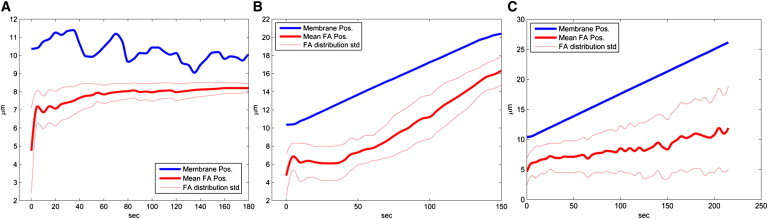
Time-varying, spatially averaged location of the cell edge (blue) and a time-varying average y-coordinate position of all the adhesions in each calculation step (red). The values of all parameters except for the adhesion formation rate r_form are indicated in the text. (A) No new adhesions formed, r_form = 0. (B) Intermediate adhesion formation rate, r_form = 0.01 s⁻¹μm⁻². (C) A high rate of adhesion formation, r_form = 0.2 s⁻¹μm⁻².

These three regimes have common general features such as the actin gel's retrograde motion and the adhesion evolution, but differ in the protrusion mode of the cell leading edge, the formation of the lamellipodium boundary, and in the steady-state distribution of the adhesions.

We varied the membrane tension in the experimentally relevant range between γ = 50 pN μm⁻¹ and γ = 300 pN μm⁻¹. The results are presented in the form of a phase diagram (Fig. S1). For small and intermediate formation rates of nascent adhesions (r_form < 0.05 μm² s⁻¹), variation of the membrane tension is found to determine the regime of the lamellipodium behavior (Fig. S1 D). Increase in membrane tension drives the system toward the stationary lamellipodium regime, whereas decrease in the tension drives the system to the regime of advancing lamellipodium with no lamellipodium-lamellum boundary formation. For high rates of nascent adhesion formation (r_form ∼0.1 μm² s⁻¹), the effect of the membrane tension was minimal (Fig. S1 D).

An additional effect of the membrane tension is on the lamellipodium width. The larger the tension, the narrower the lamellipodium (Fig. 3 C).

To simulate the effects of substrate rigidity on the dynamic regimes of the lamellipodium, the rigidity sensing parameter, α, relating efficiency of the adhesions' mechanosensitivity, was varied from α = 1 to α = 10. The results are presented in (Fig. S1, A and C). Increase of α corresponding to substrates with lower rigidity, stabilized the stationary regime of the lamellipodium, whereas low values of α, representing more rigid substrates, directed the system into the advancing lamellipodium regime. Taken together, the model predicts, in agreement with the literature data, that growing of substrate rigidity described by the decrease of the rigidity sensing parameter α accelerates the velocity of the cell crawling.

Adhesion dynamics

At each computational step, deformation of the newly polymerized strip of the actin gel by the force coming from the membrane tension results in a force applied by the gel to the adhesions in the stick state. As expected qualitatively, the closer the adhesion is to the edge membrane, the larger the force it experiences. If the force density acting on the adhesions closest to the edge membrane overcomes the critical value, f^∗, the probability of their detachment increases, which triggers a transition to the slip state, causing those adhesions to disengage from the gel. Consequently, the load applied by the membrane falls on the adhesions in the stick state located further away from the edge membrane, which in turn transition into the slip state and the load is transmitted further toward the cell interior. This cascade of the actin gel-adhesion interactions results in a time-averaged retrograde flow of the lamellipodial gel and the related evolution of the individual adhesions. Although the cascade of detachment events results, eventually, in transmission of the force to the adhesions further away from the membrane, until this occurs, the adhesion mechanosensitivity makes it more likely for the membrane-proximal adhesions to grow in size, whereas the membrane-distal adhesions have a larger probability to shrink and disappear. This results in a depletion of the membrane-distal adhesions, and maturation of the membrane-proximal ones.

Because the adhesion size is determined by the adhesion mechanosensitivity, increase in the rigidity sensing parameter α, simulating substrates with lower rigidity, strongly reduces the mean size of surviving adhesions (Fig. S1 C).

Cell edge dynamics

The shape and dynamics of the cell edge are determined by the interplay between two factors: the membrane tension, which promotes the edge retraction by pulling it backward in the direction of the cell interior, and the forces produced by the actin gel that support the edge protrusion by pushing it forward. Because the membrane tension is homogeneous throughout the membrane (72), the corresponding effective pulling force is equal at every point of the edge. In contrast, the pushing force is uneven along the edge. At every point in time, this force is larger at those edge points, which happen to be close to cell adhesions in the stick-state, and is lower in points that are remote from such adhesions. Because the adhesions are undergoing persistent generation, changes in their dimensions and transitions between the stick and slip states result in a time-varying distribution of the pushing force along the cell edge. A competition of a constant and homogeneous pulling force with an uneven and dynamic pushing force results in fluctuations in the edge shape and, in some cases, in spatial and temporal irregularities in the edge protrusion and retraction, as seen in Fig. 2 A and Fig. 3 A. Specifically, our computation revealed two characteristic regimes of the cell edge dynamics.

• Asynchronous fluctuations of the membrane edge (presented in Fig. 3 A), which are generated by stochastic transitions between the stick and slip states of the adhesions close to the cell edge. These fluctuations result from a combination of the edge protrusion and retraction events. The characteristic average frequency of these fluctuations is determined by the effective rate of the adhesion transition between the stick and slip states, ω, which is used as a fitting parameter in the model.

• Bulging of the membrane edge, which occurs when one or several adhesions are located in a small region of the lamellipodium close to the membrane, ahead of the rest of the adhesions in the system. Distinct bulges of the cell edge develop in this case right in front of the adhesions adjacent to the membrane (Fig. 4 A).

• The rate of protrusion of the membrane edge is shown to be inversely related to the membrane tension (Fig. S1 B). The reason for this is a competition between the forward movement of the cell leading edge fueled by the actin polymerization and its rearward movement driven by the effective load applied to the edge by the membrane tension.

Figure 4.

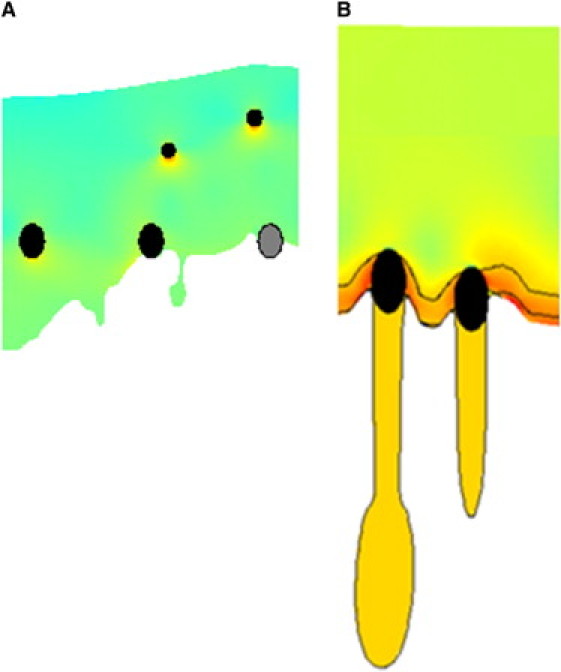
Morphological characteristics of the actin system. The membrane edge is located at the top of the figures (not indicated), and the free edge at the bottom. (A) Protrusion of the membrane edge in front of the adhesion sites. (B) Nondisintegrated actin tails forming from mature adhesions.

Inversely, an increase in the rate of formation of nascent adhesion results in a decreased probability for a cascade of stick-slip transitions, thereby providing a better resistance to the membrane load and an increase in the membrane edge protrusion rate.

Possible precursors of the stress fibers

As indicated by our earlier model, we find that, under the condition of the lamellipodium boundary formation, narrow regions of the actin gel originate from the mature adhesions decorating the boundary and extend toward the cell body (Fig. 4 B). Such actin tails are more likely to form if the adhesions are sparsely distributed. Although these actin tails predicted by the model are not stable, their subsequent incorporation of myosin and association with other elements of the actin cytoskeleton may lead to their evolution into stress fibers.

Discussion

We have presented a physical model for self-organization of the system of actin gel and cell adhesions in the front part of a cell. The model is based on three crucial features of the system components: the adhesion mechanosensitivity, the stick-slip character of the interaction between the adhesions and the moving actin gel, and a hypothetical propensity of the actin gel to disintegrate upon sufficiently strong stretching stresses. We have performed a self-consistent computation of the stresses that develop in the actin gel and the effective friction forces that are applied by the gel to the adhesions, and have analyzed the corresponding restructuring of both the gel and the adhesions. This resulted in three possible steady states of the system: a stationary state where the actin gel segregates into a lamellipodium with a distinct boundary separating it from the lamellum, but the cell edge and, hence, the lamellipodium, do not persistently move with respect to the substrate; a motile state where a lamellipodium with a distinct boundary forms and advances behind the moving cell edge; and the state where cell edge moves rapidly but the actin gel segregation into a lamellipodium and lamellum does not occur. In the first and second regimes, the dynamic nascent adhesions exist underneath the lamellipodium, whereas mature adhesions can be found only at the lamellipodium boundary and in the lamellum. In the third regime, the adhesions neither mature nor segregate and remain dispersed underneath the whole actin gel.

We have investigated how several key parameters influence the output state of the model characterized by the rates of cell edge protrusion and retrograde flow, the average adhesion size, and the lamellipodium thickness. We have chosen the nascent adhesion formation rate, the membrane tension, and the sensing of the substrate rigidity by the focal adhesions, as the most relevant parameters and presented their effects on the system state as phase diagrams (Fig. S1) and by Fig. 3.

• The effective density of the adhesions at the cell-substrate interface is regulated by several model parameters such as the rate of generation of the new nascent adhesions, and the mechanosensitivity of the adhesions. The higher the adhesion generation rate the larger the adhesion density. This effective adhesion density represents the characteristic length scale of the system. The stationary state of the system is stabilized at a relatively low adhesion density; a higher amount of adhesions results in the motile state, whereas a large adhesion density results in the state of fast movement of the cell edge without formation of the lamellipodium-lamellum boundary (Figs. 2 C and 3 C). The average adhesion sizes are decreased somewhat with an increase in the adhesion formation rate (Fig. S1 C), but this can be seen as a secondary, nonpronounced effect.

• The load applied by the membrane to the lamellipodium actin gel is due to the membrane tension. Low values of membrane tension result in higher protrusion rates and lower retrograde flow (Fig. S1, A and B). As the membrane tension increases, the protrusion rate decreases. High membrane tension acts in opposition to the effect of the adhesion density, and may stabilize the stationary state in a system with a higher rate of nascent adhesion formation. In addition, the membrane tension has a correlated effect on the size distribution of the adhesions in the lamellipodium, resulting in an increase in adhesion size for high membrane tension.

• The sensing of the substrate rigidity is implicitly included in the model via its effect on the critical force density resulting in the onset of the adhesion growth. Protrusion and spreading is seen to be more prominent in stiff substrates, indicated by a small rigidity sensing parameter. For higher values of the rigidity sensing parameter, describing softer substrates, the retrograde flow is increased (Fig. S1 A) and the protrusion are decreased. Substrate rigidity is seen to have a prominent effect on the distribution of adhesion sizes, with larger adhesions on stiffer substrates (Fig. S1 C).

All three steady states have been observed in live cells. The regime where the cell edge and the lamellipodium-lamellum boundary concertedly move forward is typical for the spreading cell (16). Another observation of the same study was the phenomenon of the cell edge bulging in front of mature adhesions (16). The effect of adhesion-substrate coupling efficiency on the dynamics of edge protrusion and retrograde flow has been recently observed (73).

Onset of the stationary regime occurs at the stage where the diameter of a spreading cell approaches its maximal value (74). Within this regime the cell edge often undergoes characteristic oscillations (74). In general, oscillations of the leading edges of migrating cells represent a common feature of the lamellipodial activity, which was studied beginning from the pioneering work (75) and still attracts the researcher attention (22). Some experimental evidence supported by theoretical modeling suggests that the oscillatory behavior of the cell leading edge is driven by the actomyosin contractility (74), or by periodic changes in the tension of the plasma membrane and the rate of F-actin assembly (76,77). Our finding of the cell edge undulations driven by the stick-slip interaction between the retrogradely moving actin gel and the dynamic focal adhesions does not require the assumption of variability in the membrane tension or actin dynamics, and provides a complementary mechanism for this complex phenomenon.

The third regime of the cell edge movement without formation of the lamellipodium-lamellum boundary has been observed in fast moving cells such as fish keratocytes, which are characterized by a large number of immature adhesions (78)