Anomalous Flexural Behaviors of Microtubules

Abstract

Apparent controversies exist on whether the persistence length of microtubules depends on its contour length. This issue is particularly challenging from a theoretical point of view due to the tubular structure and strongly anisotropic material property of microtubules. Here we adopt a higher order continuum orthotropic thin shell model to study the flexural behavior of microtubules. Our model overcomes some key limitations of a recent study based on a simplified anisotropic shell model and results in a closed-form solution for the contour-length-dependent persistence length of microtubules, with predictions in excellent agreement with experimental measurements. By studying the ratio between their contour and persistence lengths, we find that microtubules with length at ∼1.5 μm show the lowest flexural rigidity, whereas those with length at ∼15 μm show the highest flexural rigidity. This finding may provide an important theoretical basis for understanding the mechanical structure of mitotic spindles during cell division. Further analysis on the buckling of microtubules indicates that the critical buckling load becomes insensitive to the tube length for relatively short microtubules, in drastic contrast to the classical Euler buckling. These rich flexural behaviors of microtubules are of profound implication for many biological functions and biomimetic molecular devices.

Introduction

As one of the three major classes of cytoskeletal filaments, microtubules play essential roles in many biological functions of eukaryotic cells, such as providing mechanical strength to maintain cell shape (1,2), acting as guiding tracks for intracellular transport (3,4), and supporting the movement of chromosomes during mitosis (5,6). Most of these biological functions and even some molecular devices (7–9) rely on the unique mechanical properties of microtubules that are long, hollow cylinders made of typically 13 parallel protofilaments with outer diameter at ∼30 nm and inner diameter 20 nm (1).

The flexural rigidity of a slender molecular chain is usually measured by its persistence length, which is defined as the length over which the contour tangent remains strongly correlated during thermal fluctuation (1,2). In the past two decades, various experimental techniques have been employed to measure the persistence length of microtubules, such as optical tweezers (10–12), atomic force microscope (13,14), and analysis of thermally driven shape fluctuations (15,16). By utilizing a laser trapping technique and dark-field microscopy, Takasone et al. (17) inferred that the flexural rigidity of a microtubule is proportional to the square of its contour length and can be influenced by different deformation modes. Pampaloni et al. (18) confirmed that the persistence length of a microtubule depends on its contour length due to shear deformation between adjacent protofilaments. However, using all-atom molecular simulations, Sept and MacKintosh (19) pointed out that the actual shear modulus of microtubules is larger than that adopted in Pampaloni et al. (18) and speculated that the persistence length should be independent of the contour length. Recent experiments confirmed that the longitudinal bonds of microtubules are much stronger than the lateral bonds between adjacent protofilaments (20,21).

Due to these structural and material characteristics, orthotropic thin shell models have been adopted in the study of mechanical properties of microtubules (22–26). Although most experimental and theoretical studies on the flexural rigidity of microtubules have focused on comparing their bending behaviors with those of a stiff wormlike chain (WLC), only a few studies have approached the problem from the perspective of bending and buckling of a cylindrical shell. Recently, by using a simplified orthotropic shell model, Gao et al. (26) derived a closed form expression for the persistence length of a microtubule that depends on not only its material property but also its geometrical structure. This study provided feasible explanations for the seemingly contradictory experimental observations on the persistence length of microtubules. However, the analysis in Gao et al. (26) adopted a thin shell model with a number of questionable simplifications including omitting components of internal forces and moments of order (h/R) in the equilibrium equations, where R and h are the radius and thickness of the shell, respectively. To overcome these limitations, here we adopt a higher-order shell model to conduct a systematic investigation of the flexural behaviors of microtubules from the perspectives of bending, buckling, and statistical correlations of deformation in such tubular structures.

A Higher-Order Thin Shell Model

Governing equations

Microtubules are long, hollow cylindrical tubes assembled helically from tubulin dimers (1,2,27). Experiments have confirmed that the head-tail intraprotofilament contacts between tubulin dimers along the axial direction of the tube are much stronger than the circumferential interprotofilament contacts (18,27–29). Thus microtubules can also be viewed as hollow cylindrical tubes formed by (on average) 13 tubulin protofilaments assembled parallel to the tube axis (27). It is perhaps for this reason that the helicity of microtubule does not seem to play a significant role in its mechanical behavior, as shown by recent molecular mechanics models (30).

To model the tubular geometry and the anisotropic material properties along the axial and circumferential directions of microtubule, we consider an anisotropic elastic cylindrical shell, as shown in Fig. 1. A set of cylindrical coordinates (x, s, r) are placed at one end of the tube, where x is the axial coordinate, s is the circumferential arc length, and r is the radial coordinate. Let R be the radius of the midsurface of the shell, h the thickness, and L the length of the shell, and u(x, s), v(x, s), and w(x, s) be the longitudinal, circumferential, and radial displacements of the midsurface, respectively.

Figure 1.

Geometry and coordinate system of a microtubule.

The normal strains ε_x, ε_s along the x, s, directions and the shear strain ε_xs in the x-s plane at an arbitrary point of the shell are related to the midsurface displacements by (31)

$$\{\begin{array}{l}{\epsilon }_x=\frac{\partial u}{\partial x}-r\frac{{\partial }^{2}w}{\partial x^2},\\ {\epsilon }_s=\frac{\partial v}{\partial s}-\frac{Rr}{R+r}\frac{{\partial }^{2}w}{\partial s^2}+\frac{1}{R+r}w,\\ {\epsilon }_{xs}=\frac{R}{R+r}\frac{\partial u}{\partial s}+\frac{R+r}{R}\frac{\partial v}{\partial x}-\frac{2Rr+r^2}{R+r}\frac{{\partial }^{2}w}{\partial x\partial s}.\end{array}$$ (1)

The stress-strain relations of an orthotropic material are (26,31)

$$\{\begin{array}{l}{\sigma }_x=\frac{E_x}{1-{\mu }_x{\mu }_s}\left({\epsilon }_x+{\mu }_s{\epsilon }_s\right),\\ {\sigma }_s=\frac{E_s}{1-{\mu }_x{\mu }_s}\left({\epsilon }_s+{\mu }_x{\epsilon }_x\right),\\ {\tau }_{xs}=G{\epsilon }_{xs},\end{array}$$ (2)

where G is the shear modulus; E_x, E_s are Young's moduli, and μ_x, μ_s the Poisson ratios along the axial and circumferential directions of the microtubule, which are related as

$$E_x{\mu }_s=E_s{\mu }_x.$$ (3)

The internal forces and moments on a shell element shown in Fig. 2 can be expressed as (31)

$$\{\begin{array}{l}\left[N_x,S_x,M_x,M_{xs}\right]=\underset{-h/2}{\overset{h/2}{\int }}\left[{\sigma }_x,{\tau }_{xs},r{\sigma }_x,r{\tau }_{xs}\right]\frac{R+r}{R}dr,\\ \left[N_s,S_s,M_s,M_{sx}\right]=\underset{-h/2}{\overset{h/2}{\int }}\left[{\sigma }_s,{\tau }_{xs},r{\sigma }_s,r{\tau }_{xs}\right]dr,\end{array}$$ (4)

where we note that the ratio (R+r)/R in the first equation was neglected in the simplified shell model in Gao et al. (26). Substituting Eqs. 1 and 2 into Eq. 4, we obtain

$$\{\begin{array}{l}{N}_x=K_1\left[\frac{\partial u}{\partial x}+{\mu }_s\left(\frac{\partial v}{\partial s}+\frac{w}{R}\right)\right]-D_1\frac{{\partial }^{2}w}{R\partial x^2},\\ N_s=K_2\left[\frac{\partial v}{\partial s}-R\frac{{\partial }^{2}w}{\partial s^2}+{\mu }_x\frac{\partial u}{\partial x}+\text{ln}\left(\frac{2R+h}{2R-h}\right)\left(\frac{w}{h}+\frac{R^2}{h}\frac{{\partial }^{2}w}{\partial s^2}\right)\right],\\ S_x=K_3\left(\frac{\partial u}{\partial s}+\frac{\partial v}{\partial x}\right)+D_3\left(\frac{\partial v}{2R^2\partial x}-\frac{\partial w}{2R\partial x\partial s}\right),\end{array}$$ (5a)

$$\{\begin{array}{l}{S}_s=K_3\left[\frac{\partial v}{\partial x}-R\frac{{\partial }^{2}w}{\partial x\partial s}+\text{ln}\left(\frac{2R+h}{2R-h}\right)\left(\frac{R}{h}\frac{\partial u}{\partial s}+\frac{R^2}{h}\frac{{\partial }^{2}w}{\partial x\partial s}\right)\right]\\ M_x=D_1\left(\frac{{\mu }_s}{R}\frac{\partial v}{\partial s}+\frac{\partial u}{R\partial x}-\frac{{\partial }^{2}w}{\partial x^2}-{\mu }_s\frac{{\partial }^{2}w}{\partial s^2}\right)\\ M_s=K_2\left[1-\frac{R}{h}\text{ln}\left(\frac{2R+h}{2R-h}\right)\right]\left(w+R^2\frac{{\partial }^{2}w}{\partial s^2}\right)-D_2{\mu }_x\frac{{\partial }^{2}w}{\partial x^2},\end{array}$$ (5b)

$$\{\begin{array}{l}{M}_{xs}=D_3\left(\frac{\partial v}{R\partial x}-\frac{{\partial }^{2}w}{\partial x\partial s}\right)\\ M_{sx}=K_3\left[\left(R-\frac{R^2}{h}\text{ln}\left(\frac{2R+h}{2R-h}\right)\right)\frac{\partial u}{\partial s}+\left(R^2-\frac{R^3}{h}\text{ln}\left(\frac{2R+h}{2R-h}\right)\right)\frac{{\partial }^{2}w}{\partial x\partial s}\right]+\frac{D_3}{2}\left(\frac{\partial v}{R\partial x}-\frac{{\partial }^{2}w}{\partial x\partial s}\right),\end{array}$$ (5c)

$$K_1=\frac{E_{x}h}{1-{\mu }_x{\mu }_s},K_2=\frac{E_{s}h}{1-{\mu }_x{\mu }_s},K_3=Gh,$$ (6a)

$$D_1=\frac{E_x{h}^3}{12\left(1-{\mu }_x{\mu }_s\right)},D_2=\frac{E_s{h}^3}{12\left(1-{\mu }_x{\mu }_s\right)},D_3=\frac{G{h}^3}{6},$$ (6b)

where K₁, K₂, and K₃ are the generalized stretching stiffness, and D₁, D₂, and D₃ are the generalized bending stiffness. Experiments have shown that the effective bending stiffness is largely determined by the so-called “bridge” thickness that is smaller than the apparent thickness (28). Therefore, similar to carbon nanotubes (32–34), the effective bending stiffness of microtubule defined in Eq. 6b should be considered as an independent material constant (22–25). For this reason, the thickness h used in our model is not the actual thickness of a microtubule; rather, it should be regarded as a parameter for the effective bending stiffness in Eq. 6b.

Figure 2.

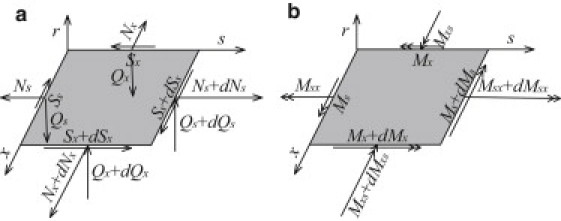
Internal forces and moments on a shell element used in the model: (a) shear and membrane forces; (b) moments and twists.

Bending

We consider the deformation of the tubular shell subjected to a distributed static radial load q(x, s) that is symmetrical about the x-r plane, namely q(x, s) = q(x, −s). The static equilibrium of shell elements shown in Fig. 2 requires

$$\{\begin{array}{l}\frac{\partial N_x}{\partial x}+\frac{\partial S_s}{\partial s}=0\\ \frac{\partial N_s}{\partial s}+\frac{\partial S_x}{\partial x}+\frac{\partial M_{xs}}{R\partial x}+\frac{\partial M_s}{R\partial s}=0\\ -\frac{N_s}{R}+\frac{{\partial }^2{M}_{sx}}{\partial x\partial s}+\frac{{\partial }^2{M}_x}{\partial x^2}+\frac{{\partial }^2{M}_{xs}}{\partial x\partial s}+\frac{{\partial }^2{M}_s}{\partial s^2}+q=0.\end{array}$$ (7)

Substituting Eq. 5 into Eq. 7 leads to

$$\{\begin{array}{l}{K}_1\frac{{\partial }^{2}u}{\partial x^2}+\lambda K_3\frac{{\partial }^{2}u}{\partial s^2}+\left(K_1{\mu }_s+K_3\right)\frac{{\partial }^{2}v}{\partial x\partial s}+\frac{K_1{\mu }_s}{R}\frac{\partial w}{\partial x}+K_{3}R\left(\lambda -1\right)\frac{{\partial }^{3}w}{\partial x\partial s^2}-\frac{D_1}{R}\frac{{\partial }^{3}w}{\partial x^3}=0\\ K_2\frac{{\partial }^{2}v}{\partial s^2}+\left(\frac{3D_3}{2R^2}+K_3\right)\frac{{\partial }^{2}v}{\partial x^2}+\left(K_3+K_2{\mu }_x\right)\frac{{\partial }^{2}u}{\partial x\partial s}+\frac{K_2}{R}\frac{\partial w}{\partial s}-\frac{3D_3+2D_2{\mu }_x}{2R}\frac{{\partial }^{3}w}{\partial x^2\partial s}=0\\ \frac{K_2{\mu }_x}{R}\frac{\partial u}{\partial x}-K_{3}R\left(1-\lambda \right)\frac{{\partial }^{3}u}{\partial x\partial s^2}-\frac{D_1}{R}\frac{{\partial }^{3}u}{\partial x^3}+\frac{K_2}{R}\frac{\partial v}{\partial s}-\frac{3D_3+2D_1{\mu }_s}{2R}\frac{{\partial }^{3}v}{\partial x^2\partial s}+\frac{\lambda K_2}{R^2}w-2K_2\left(1-\lambda \right)\frac{{\partial }^{2}w}{\partial s^2}+\left[D_1{\mu }_s+D_2{\mu }_x+\frac{3D_3}{2}-K_3{R}^2\left(1-\lambda \right)\right]\frac{{\partial }^{4}w}{\partial x^2\partial s^2}+D_1\frac{{\partial }^{4}w}{\partial x^4}-K_2{R}^2\left(1-\lambda \right)\frac{{\partial }^{4}w}{\partial s^4}=q,\end{array}$$ (8)

where λ = R ln[(2R + h)/(2R + h)]/h. Equation 8 contains higher-order terms compared to the equation used in Gao et al. (26).

To facilitate analytical solution, we adopt the following boundary conditions with simply supported tube ends:

$$\begin{array}{l}w\left(0,s\right)=w\left(L,s\right)=v\left(0,s\right)=v\left(L,s\right)=0,\hfill \\ {\frac{\partial u}{\partial x}|}_{x=0,L}=0,\hfill \\ {\frac{{\partial }^{2}w}{\partial x^2}|}_{x=0,L}=0.\hfill \end{array}$$ (9)

We expand q(x, s) into a Fourier series

$$q\left(x,s\right)=\sum _{m=0}^{\infty }\sum _{n=1}^{\infty }{q}_{m,n}\text{cos}\left(\frac{ms}{R}\right)\text{sin}\left(\frac{n\pi x}{L}\right),$$ (10)

where

$$q_{m,n}=\frac{2}{\pi RL}\underset{-\pi R}{\overset{\pi R}{\int }}\underset{0}{\overset{L}{\int }}q\left(x,s\right)\text{cos}\left(\frac{ms}{R}\right)\text{sin}\left(\frac{n\pi x}{L}\right)dxds.$$

We assume that the midsurface displacements u(x, s), v(x, s), and w(x, s) can be expressed as

$$\{\begin{array}{l}u\left(x,s\right)=\sum _{m=0}^{\infty }\sum _{n=1}^{\infty }{u}_{m,n}\text{cos}\left(\frac{ms}{R}\right)\text{cos}\left(\frac{n\pi x}{L}\right),\\ v\left(x,s\right)=\sum _{m=0}^{\infty }\sum _{n=1}^{\infty }{v}_{m,n}\text{sin}\left(\frac{ms}{R}\right)\text{sin}\left(\frac{n\pi x}{L}\right),\\ w\left(x,s\right)=\sum _{m=0}^{\infty }\sum _{n=1}^{\infty }{w}_{m,n}\text{cos}\left(\frac{ms}{R}\right)\text{sin}\left(\frac{n\pi x}{L}\right).\end{array}$$ (11)

Substituting Eqs. 10 and 11 into Eq. 8, and performing harmonic analysis, we have

$$v_{1,n}=\frac{q_{1,n}{b}_n}{a_n},w_{1,n}=\frac{q_{1,n}{c}_n}{a_n},$$ (12)

where

$$\{\begin{array}{l}{a}_n=2n^4{\pi }^4\lambda K_3{L}^4\left[\left(D_1+K_1{R}^2\right)\left(D_2+K_2{R}^2\right){\mu }_x{\mu }_s-K_2{R}^2\left(3D_1+K_1{R}^2\right)\right]+n^6{\pi }^6{R}^2{L}^2\left\{6D_1{K}_3^2{R}^2-\lambda K_3\left(3D_1+K_1{R}^2\right)\left(3D_3+2K_3{R}^2\right)-2D_1{K}_1{R}^2\left(K_2-K_3{\mu }_s\right)+2D_1{\mu }_x\left[K_2{R}^2\left(2K_3+K_1{\mu }_s\right)-D_2{K}_3\right]+2K_1{K}_3{R}^2\left(K_3{R}^2-D_2{\mu }_x\right)-2D_1^2\left[K_3{\mu }_s+K_2\left({\mu }_x{\mu }_s-1\right)\right]\right\}+n^8{\pi }^8{D}_1{R}^2\left(3D_3+2K_3{R}^2\right)\left(D_1-K_1{R}^2\right),\\ b_n=2\lambda K_2{K}_3{R}^2{L}^8+n^2{\pi }^2{R}^2{L}^6\left[2\lambda K_2{K}_3{R}^2{\mu }_x+\lambda K_3\left(3D_3+2K_3{R}^2+2D_2{\mu }_x\right)-2K_3{R}^2\left(K_3+K_2{\mu }_x\right)-2K_1{R}^2\left(K_3{\mu }_s+K_2{\mu }_x{\mu }_s-K_2\right)\right]+n^4{\pi }^4{R}^4{L}^4\left[K_1\left(3D_3+2D_2{\mu }_x\right)-2D_1\left(K_3+K_2{\mu }_x\right)\right],\\ c_n=-2\lambda K_2{K}_3{R}^2{L}^8+n^2{\pi }^2{R}^2{L}^6\left[2K_3{R}^2\left(K_3+K_2{\mu }_x\right)-\lambda K_3\left(3D_3+2K_3{R}^2\right)+2K_1{R}^2(K_3{\mu }_s+K_2{\mu }_x{\mu }_s-K_2)\right]-n^4{\pi }^4{K}_1{R}^4{L}^4\left(3D_3+2K_3{R}^2\right).\end{array}$$ (13)

Furthermore, we define the equivalent average lateral deflection of the tube as (26)

$$\tilde{w}\left(x\right)=\frac{1}{2\pi R}\underset{-\pi R}{\overset{\pi R}{\int }}\left[w\left(x,s\right)\text{cos}\left(\frac{s}{R}\right)-v\left(x,s\right)\text{sin}\left(\frac{s}{R}\right)\right]ds.$$ (14)

Substituting Eqs. 11 and 12 into Eq. 14 while using the orthogonality of trigonometric functions yields

$$\begin{array}{l}\tilde{w}\left(x\right)=\frac{1}{2\pi R}\sum _{n=1}^{\infty }\text{sin}\left(\frac{n\pi x}{L}\right)\underset{-\pi R}{\overset{\pi R}{\int }}\left[w_{1,n}{\text{cos}}^2\left(\frac{s}{R}\right)-v_{1,n}{\text{sin}}^2\left(\frac{s}{R}\right)\right]ds\\ =\frac{1}{2}\sum _{n=1}^{\infty }\left(w_{1,n}-v_{1,n}\right)\text{sin}\left(\frac{n\pi x}{L}\right)=\frac{R}{E_x}\sum _{n=1}^{\infty }{q}_{1,n}{d}_n\text{sin}\left(\frac{n\pi x}{L}\right),\end{array}$$ (15)

where

$$d_n=\frac{{\tilde{d}}_n}{{\hat{d}}_n}$$ (16)

and

$${\tilde{d}}_n=576{\alpha }_1{\alpha }_2{\beta }_2^8\left(1-{\alpha }_1{\mu }_x^2\right)\text{ln}\left(\frac{2+{\beta }_1}{2-{\beta }_1}\right)+24n^2{\pi }^2{\beta }_2^6\left(1-{\alpha }_1{\mu }_x^2\right)\{24{\alpha }_1{\beta }_1+{\alpha }_1{\alpha }_2{\mu }_x\left[12\text{ln}\left(\frac{2+{\beta }_1}{2-{\beta }_1}\right)-48{\beta }_1+{\beta }_1^2\text{ln}\left(\frac{2+{\beta }_1}{2-{\beta }_1}\right)\right]-6{\alpha }_2^2[4{\beta }_1-\left(4+{\beta }_1^2\right)\text{ln}\left(\frac{2+{\beta }_1}{2-{\beta }_1}\right)]\left(1-{\alpha }_1{\mu }_x^2\right)\}+24n^4{\pi }^4{\alpha }_2{\beta }_1{\beta }_2^4\left(12+5{\beta }_1^2\right)\left(1-{\alpha }_1{\mu }_x^2\right),$$

$${\hat{d}}_n=4n^4{\pi }^4{\alpha }_1{\alpha }_2{\beta }_1{\beta }_2^4\text{ln}\left(\frac{2+{\beta }_1}{2-{\beta }_1}\right)\left[36\left(4+{\beta }_1^2\right)-{\alpha }_1{\mu }_x^2{\left(12+{\beta }_1^2\right)}^2\right]-n^6{\pi }^6{\beta }_1{\beta }_2^2\times \left\{4{\alpha }_1{\beta }_1^3\left(12-{\beta }_1^2\right)\left(2{\alpha }_2{\mu }_x-1\right)+36{\alpha }_2^2\left(4+{\beta }_1^2\right)[4{\beta }_1-\left(4+{\beta }_1^2\right)\text{ln}\left(\frac{2+{\beta }_1}{2-{\beta }_1}\right)]\left(1-{\alpha }_1{\mu }_x^2\right)\right\}+n^8{\pi }^8{\alpha }_2{\beta }_1^4\left(4+{\beta }_1^2\right)\left(12-{\beta }_1^2\right),$$

and where α₁ = E_s/E_x, α₂ = G/E_x, β₁ = h/R, and β₂ = L/R. In the case of h << R << L, we can obtain d_n ≈ (α₂β⁴₂ + n²π²β²₂)/n⁴π⁴α₂β₁.

On the other hand, the statistical behaviors of semiflexible polymers can be described by the WLC model (26,35). Treating a microtubule with simply supported ends as a WLC under the same end restrictions, the ensemble-averaged deflection of the WLC should satisfy (26)

$$p{k}_{\text{B}}T{\partial }^4\frac{w_c\left(x\right)}{\partial x^4}=\tilde{q}\left(x\right),$$ (17)

where p is the effective persistence length of the microtubule, k_B Boltzmann's constant, T the temperature, w_c the deflection of the WLC, and

$$\tilde{q}\left(x\right)=\underset{-\pi R}{\overset{\pi R}{\int }}q\left(x,s\right)\text{cos}\left(\frac{s}{R}\right)ds=\pi R\sum _{n=1}^{\infty }{q}_{1,n}\text{sin}\left(\frac{n\pi x}{L}\right)$$ (18)

is the time-independent external load. It follows from Eqs. 17 and 18 that

$$w_c\left(x\right)=\frac{R{L}^4}{p{k}_{\text{B}}T}\sum _{n=1}^{\infty }\frac{q_{1,n}}{n^4{\pi }^3}\text{sin}\left(\frac{n\pi x}{L}\right).$$ (19)

Comparing the average deflection in Eq. 19 and that of the microtubule in Eq. 15 through relation

$$\underset{0}{\overset{L}{\int }}{\tilde{w}}^2\left(x\right)dx=\underset{0}{\overset{L}{\int }}{w}_c^2\left(x\right)dx,$$ (20)

we obtain an effective persistence length of the microtubule as

$$p=\frac{E_x{L}^4}{{\pi }^3{k}_{\text{B}}T}\sqrt{\frac{\sum _{n=1}^{\infty }{n}^{-8}{\eta }_n^2}{\sum _{n=1}^{\infty }{d}_n^2{\eta }_n^2}},$$ (21)

where η_n = q_{1, n}/q_1,1. Specifically, when the load has a sinusoidal distribution $q\left(x,s\right)=\hat{q}\left(s\right)\text{sin}\left(n\pi x/L\right)$, we have

$$p=\frac{E_x{L}^4}{n^4{\pi }^3{d}_n{k}_{\text{B}}T}.$$ (22)

As the tube length L tends to infinity, Eq. 22 behaves as

$$p_{\infty }=\underset{L->+\infty }{\text{lim}}p=\frac{\pi E_{x}h{R}^3\left[144\left(1-{\mu }_s{\mu }_x\right)-{\beta }_1^4{\mu }_s{\mu }_x+12{\beta }_1^2\left(3-2{\mu }_s{\mu }_x\right)\right]}{144\left(1-{\mu }_s{\mu }_x\right)k_{\text{B}}T}.$$ (23)

Equation 23 indicates that the persistence length of a microtubule approaches a constant value as its length increases. Noting that μ_s μ_x < 1/4, β₁ < 1/2, Eq. 23 can be reduced to the bending stiffness of an elastic beam p_∞k_BT ≈ πE_xhR³ ≈ E_xI, where I = π[(2R + h)⁴ – (2R − h)⁴]/64 ≈ πhR³ is the second moment of the hollow cylindrical cross-section area.

Equation 22 provides a closed-form formula for the persistence length of a microtubule of finite length, which can be reduced to the following in the case of h << R << L and G < E_s < E_x:

$$p\approx \frac{\pi E_{x}h{R}^3}{\left[k_{\text{B}}T\left(1+n^2{\pi }^2{\beta }_2^{-2}{\alpha }_2^{-1}\right)\right]}.$$ (24)

Buckling

For buckling of a cylindrical shell under an axial force P, we have the following governing equations (31)

$$\{\begin{array}{l}\frac{\partial N_x}{\partial x}+\frac{\partial S_s}{\partial s}-P\frac{{\partial }^{2}u}{\partial x^2}=0\\ \frac{\partial N_s}{\partial s}+\frac{\partial S_x}{\partial x}+\frac{\partial M_{xs}}{R\partial x}+\frac{\partial M_s}{R\partial s}-P\frac{{\partial }^{2}v}{\partial x^2}=0\\ -\frac{N_s}{R}+\frac{{\partial }^2{M}_{sx}}{\partial x\partial s}+\frac{{\partial }^2{M}_x}{\partial x^2}+\frac{{\partial }^2{M}_{xs}}{\partial x\partial s}+\frac{{\partial }^2{M}_s}{\partial s^2}-P\frac{{\partial }^{2}w}{\partial x^2}=0.\end{array}$$ (25)

For a simply supported tube, the boundary conditions are still given by Eq. 9. We consider solutions in the form

$$\{\begin{array}{l}u\left(x,s\right)=U\text{cos}\left(\frac{ms}{R}\right)\text{cos}\left(\frac{n\pi x}{L}\right),\\ v\left(x,s\right)=V\text{sin}\left(\frac{ms}{R}\right)\text{sin}\left(\frac{n\pi x}{L}\right),\\ w\left(x,s\right)=W\text{cos}\left(\frac{ms}{R}\right)\text{sin}\left(\frac{n\pi x}{L}\right),\end{array}$$ (26)

where n and m are integers. Equation 26 describes a buckling mode with n half-waves along the axial direction of the cylinder and 2m half-waves around its circumference. Substituting Eqs. 5 and 26 into Eq. 25 leads to

$$\left[\begin{array}{ccc}{B}_{11}+P{n}^2{\pi }^2/L^2& B_{12}& B_{13}\\ B_{21}& B_{22}+P{n}^2{\pi }^2/L^2& B_{23}\\ B_{31}& B_{32}& B_{33}+P{n}^2{\pi }^2/L^2\end{array}\right]\left[\begin{array}{c}U\\ V\\ W\end{array}\right]=0,$$ (27)

in which

$$\begin{array}{l}{B}_{11}=-\frac{n^2{\pi }^2{K}_1}{L^2}-\frac{\lambda m^2{K}_3}{R^2},B_{12}=B_{21}=\frac{nm\pi \left({\mu }_s{K}_1+K_3\right)}{LR},\\ B_{13}=B_{31}=\frac{n^3{\pi }^3{D}_1}{L^{3}R}+\frac{n\pi {\mu }_s{K}_1}{LR}+\frac{n{m}^2\pi \left(1-\lambda \right)K_3}{LR},\\ B_{22}=-\frac{n^2{\pi }^2\left(K_3+1.5D_3/R^2\right)}{L^2}-\frac{m^2{K}_2}{R^2},\\ B_{23}=B_{32}-\frac{m{K}_2}{R^2}-\frac{n^{2}m{\pi }^2\left(3D_3+2D_2{\mu }_x\right)}{2L^2{R}^2},\\ B_{33}=-\frac{n^4{\pi }^4{D}_1}{L^4}-\frac{\lambda K_2}{R^2}-\frac{2m^2\left(1-\lambda \right)K_2}{R^2}+\frac{m^4\left(1-\lambda \right)K_2}{R^2}-\frac{n^2{m}^2{\pi }^2\left[1.5D_3-\left(1-\lambda \right)K_3{R}^2+2D_1{\mu }_s\right)}{L^2{R}^2}.\end{array}$$

Setting the determinant of the coefficient matrix in Eq. 27 to zero yields the critical condition for buckling,

$$\frac{n^6{\pi }^6{P}^3}{L^6}+\frac{n^4{\pi }^4{P}^2\left(B_{11}+B_{22}+B_{33}\right)}{L^4}+\frac{n\pi P\left(B_{11}{B}_{22}+B_{11}{B}_{33}+B_{22}{B}_{33}-B_{12}{B}_{21}-B_{13}{B}_{31}-B_{23}{B}_{32}\right)}{L}+\left(B_{11}{B}_{22}{B}_{33}+B_{12}{B}_{31}{B}_{23}+B_{13}{B}_{21}{B}_{32}-B_{13}{B}_{22}{B}_{31}-B_{11}{B}_{23}{B}_{32}-B_{12}{B}_{21}{B}_{33}\right)=0,$$ (28)

from which one can determine the critical buckling load associated with a given buckling mode.

On the other hand, for an Euler-Bernoulli beam with bending stiffness EI and length L, the critical buckling load is n²π²EI/L². Taking pk_BT, with p given in Eq. 22, as the effective bending stiffness of a microtubule with length L, we can estimate the effective critical buckling load of the microtubule treated as an Euler-Bernoulli beam as

$$\tilde{P}=\frac{E_x{L}^2}{n^2\pi d_n},$$ (29)

where d_n is defined in Eq. 16.

Equations 28 and 29 give the critical buckling loads for a microtubule treated as a cylindrical shell and an Euler-Bernoulli beam, respectively. We will show later that these two types of critical buckling loads are quite different when the length of the microtubule is smaller than a threshold value, implying that only when the length of a microtubule is long enough will it behave like a linear polymer chain.

Results and Discussions

Based on the persistence length derived in Eqs. 21 and 22 and the buckling analysis described in the previous section, we have analyzed how the flexibility of microtubules can be influenced by their structural and material properties. For the numerical calculations in this section, we take T = 300 K as temperature, E_x = 1.4 GPa (16,22–25), E_s = 2 MPa (22–25,36), G = 6 KPa (18,36,37), and μ_x = 0.3 (22–25,36) as the material constants of microtubules, a summary of which is listed in Table 1, and R = 12.5 nm (22–25,36) and h = 2.7 nm (17,22–25,38) as the radius and thickness of microtubule, respectively.

Table 1.

Elastic coefficients of microtubules

Elastic coefficients	Experimental value (Ref.)	Model value
Longitudinal modulus Ex	∼1 MPa (13); 0.1–0.5 GPa (14); 0.5 ± 0.1 GPa (15); 0.8 GPa (28); 1.2–2.6 GPa (16); ∼7 GPa (10)	1.4 GPa
Circumferential modulus Es	1–4 MPa (22–25,36)	2 MPa
Shear modulus G	∼1 kPa (18,37); 1 kPa–1 MPa (36); 1.4 ± 0.1 MPa (14); 1.3–19 MPa (19,39)	6 kPa
Poisson's ratio μx	0.3 (22–25,36)	0.3

Simplified shell model versus rigorous shell model

In a previous study by Gao et al. (26), the dependence of persistence length on various factors including the material properties, contour length, and spatial mode of applied loading has been discussed. However, the persistence length expression from that study is based on a simplified shell model. Fig. 3 shows the comparison between the persistence length obtained from the simplified shell model by Gao et al. (26) under conditions h/R << 1 and E_s/E_x << R⁴/L⁴, the improved solutions given in Eq. 22, and the approximate solution in Eq. 24. Fig. 3 shows substantial deviations of the approximate solution in Eq. 24 or that in Gao et al. (26) from the more rigorous solution in Eq. 22. The simplified shell model by Gao et al. (26) appears to match our model when the tube length is very small, whereas the approximate solution in Eq. 24 works well when the tube length is large.

Figure 3.

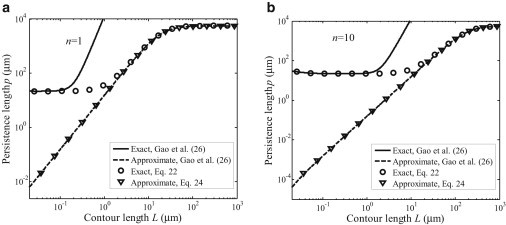
Comparison of the persistence length from a simplified shell model by Gao et al. (26) and the higher-order shell model presented in this article. The loading modalities are (a) n = 1 and (b) n = 10, respectively.

Persistence length influenced by contour length and loading configurations

Fig. 4 shows that the theoretical predictions of Eq. 22 are in reasonable agreement with the experimentally measured persistence length of microtubule (10,12,15–18). It can be seen from Fig. 4 a that our predictions agree quantitatively with the most recent experimental data by Pampaloni et al. (18). However, other experimental data shown in Fig. 4 b exhibit substantial scattering, which might be due to different measurement techniques or conditions. The persistence length of microtubules could be sensitive to various factors including the contour length, the shear modulus, the loading mode, the loading frequency, the boundary conditions, and the orientation of the material symmetry axis.

Figure 4.

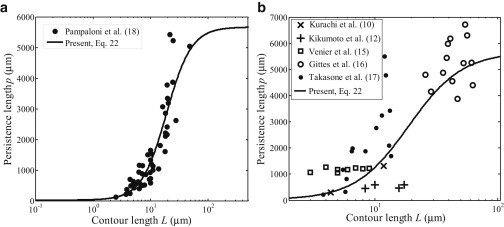
Comparison of the predicted persistence length based on Eq. 22 with experimental measurements by (a) Pampaloni et al. (18) and (b) others (10,12,15–17).

In addition, Eq. 21 shows clearly that the persistence length of a microtubule depends on its contour length and the deformation mode. The latter is related to the loading configurations through Eq. 19. Fig. 5 plots the predicted persistence length based on Eq. 21 under loads with different combinations of sinusoidal distribution functions,

$$q_1\left(x,s\right)=\tilde{q}\left(s\right)\text{sin}\left(\frac{\pi x}{L}\right),$$

$$q_2\left(x,s\right)=\tilde{q}\left(s\right)\sum _{n=1}^{100}\text{sin}\left(\frac{n\pi x}{L}\right),$$

$$q_3\left(x,s\right)=\tilde{q}\left(s\right)\text{sin}\left(\frac{2\pi x}{L}\right),\text{and}$$

$$q_4\left(x,s\right)=\tilde{q}\left(s\right)\sum _{n=2}^{100}\text{sin}\left(\frac{n\pi x}{L}\right).$$

Fig. 5 indicates that a range of tube lengths exists in which the persistence length strongly depends on the contour length and the loading configurations, as already pointed out by Gao et al. (26). On the other hand, we find that it is the distribution mode with the lowest spatial frequency that plays the dominant role in determining the length-dependency of the effective persistence length. This interesting property of loading mode shielding can be further illustrated in Fig. 6, which shows the persistence length as a function of tube length for loading function $q\left(x,s\right)=\tilde{q}\left(s\right)\text{sin}\left(\pi x/L\right)+{\eta }_{10}\tilde{q}\left(s\right)\text{sin}\left(10\pi x/L\right)$ with different values of the amplitude ratio η₁₀ between the two distribution modes sin(πx/L) and sin(10πx/L). Only when η₁₀ is ∼10³ does the distribution mode sin(10πx/L) start to play a role in the contour-length-dependence of persistence length (Fig. 6).

Figure 5.

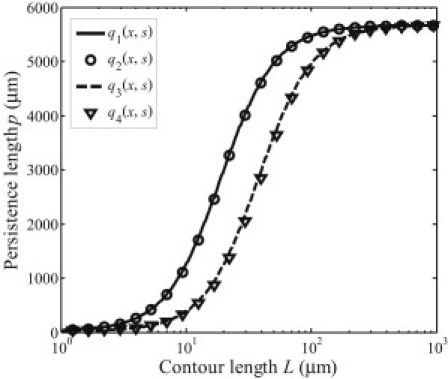
Persistence length as a function of contour length based on Eq. 21 under loads with different combinations of distribution modes.

Figure 6.

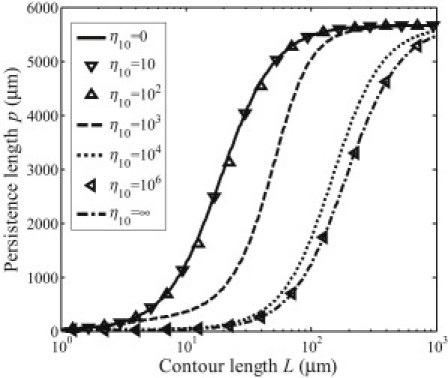
Persistence length from Eq. 21 under load $q\left(x,s\right)=\tilde{q}\left(s\right)\text{sin}\left(\pi x/L\right)+{\eta }_{10}\tilde{q}\left(s\right)\text{sin}\left(10\pi x/L\right)$.

Why does the lowest load distribution mode dominate the contour-length-dependence of persistence length?

To understand this, consider a simply supported beam of length L subjected to loads sin(πx/L) and sin(πx/L) + sin(10πx/L). In these two cases, the deformation energy of the beam are L⁵/4π⁴EI and 10,001 L⁵/40,000π⁴ EI, respectively, for which the relative difference in energy is only 0.01%. This clearly shows that the effect of higher-order load distribution modes can be strongly shielded by that of the lowest distribution mode in the contour-length dependence of the persistence length of microtubules.

Orientation correlation characteristics of microtubules

The WLC model in polymer physics is frequently used to describe the behavior of semiflexible polymers that may be regarded as a differentiable space curve of contour length L. Let r(s) be the radius vector at an arbitrary point along the WLC as a function of its contour distance s. The unit vector u(s) tangential to the curve at point s is given by u(s) ≡ ∂r/∂s with u² = 1. It can be shown that the orientation correlation function for the WLC decays exponentially as (40,41)

$$\langle \mathbf{u}\left(0\right)·\mathbf{u}\left(L\right)\rangle =e^{-L/p},$$ (30)

where p is the persistence length of the chain. The orientation correlation coefficient in Eq. 30 as a function of the ratio L/p describes the degree of correlation between the two chain ends, which allows the statistical behavior of linear polymer chains to be categorized into three different regimes, flexible (L/p >> 1), semiflexible (L/p ∼ 1), and rigid (L/p << 1). When a microtubule with length L is treated as a linear polymer chain, one can estimate its effective persistence length in terms of this contour length L by using Eq. 22.

Fig. 7 plots the ratio L/p as a function of L for microtubules. It can be seen that there exists a maximum value of L/p when L is equal to ∼1.5 μm. This means that a microtubule with length ∼1.5 μm would appear to have the lowest stiffness. It is interesting that a microtubule with length at ∼15 μm, the typical size of a cell (1), has the maximum thermal flexural rigidity.

Figure 7.

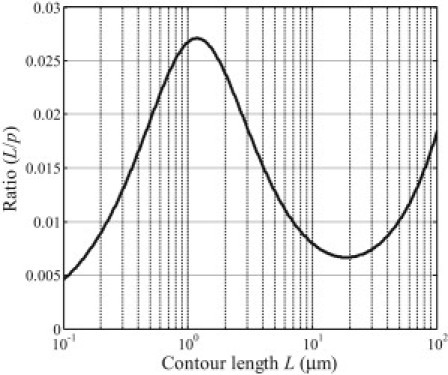
Thermal flexural rigidity ratio L/p of microtubules as a function of the contour length L.

As a key organizer of cell interior (1), the length-dependent flexural behavior of microtubules may have important implications in many biological functions: for example, the lowest stiffness at ∼1.5 μm may allow microtubules to efficiently search the intracellular space, so as to precisely position cell organelles by having them firmly bound to and moving together with microtubules. The mitotic spindle in animal cells consists of overlapping microtubules forming a central spindle and two asters (1,42). The center of the spindle is a meeting point for the antiparallel microtubules that grow from each spindle pole, whereas asters contain microtubules growing from a single pole outwards in all directions. During the cell cycle, the late anaphase (or Anaphase B, see Fig. 8) begins with the movement of spindle poles away from each other when chromatids are fully separated. The separation of sister centrosomes occurs through the following mechanisms (1,42):

• 1.The overlapping microtubules of the central spindle slide apart via molecular motors, with lengthening of the polar microtubules at the plus-ends. In this process, the size of the microtubules involved is comparable to that of the cell, and their high stiffness should be helpful in pushing the two spindle poles apart.
• 2.The astral microtubules interact with cell cortex via molecular motors, which pull the spindle poles apart. These microtubules at the cell periphery are usually shorter than those in the center of the spindle, and because they bear pulling forces, large stiffness seems unnecessary.

Figure 8.

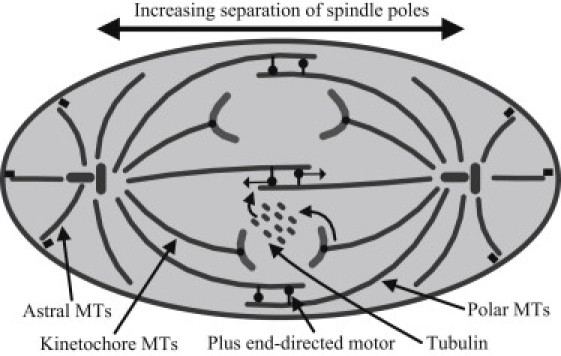
Schematic representation of late anaphase stage of the cell cycle.

Buckling of microtubules under axial compression

The flexural rigidity of microtubules can also be studied through buckling considerations. There have been many studies on the buckling behavior of microtubules by treating them as beams (43), shells (22,23), and beams with viscoelastic surroundings (44,45). Here we show that only when the length of a microtubule exceeds a certain value can a beam model be used to describe the buckling of microtubules. Equations 28 and 29 show the critical buckling loads and corresponding buckling modes based on the shell model and beam model, respectively. Fig. 9 plots the critical buckling loads as a function of the contour length and the corresponding buckling mode. It can be seen from Fig. 9 that, for sufficiently long microtubules, the critical buckling loads based on the shell model are consistent with those based on the beam model, and both appear to be in good agreement with experimental results (10,46). Interestingly, when the contour length is relatively small, the critical buckling load based on the shell model remains nearly constant and significantly smaller than that based on the beam model. By taking material constants E_x = 7 GPa (10), E_s = 1 MPa (22–24,36), G = 12 MPa (19,39), and μ_x = 0.3 (22–24,36), and thickness h = 2 nm (22–24,28), Fig. 10 plots the critical buckling loads and the corresponding buckling mode, with results showing that, for sufficiently long microtubules, the critical buckling loads and the number of axial half-waves for the shell model are consistent with those for the beam model. However, when the contour length is <∼1 μm, the critical buckling loads of the shell model become smaller than that of the beam model and the corresponding number of axial half-waves is larger than that associated with the first buckling mode for a microtubule with length <1 μm. Thus, the beam model for studying microtubule buckling is applicable only for sufficient long microtubules. These results may provide an alternative explanation of experimental observations that microtubules are usually highly curved in living cells (1,44,45).

Figure 9.

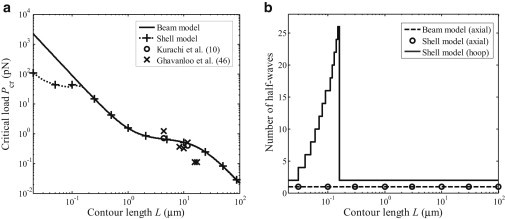
Critical buckling loads as a function of the contour length and the number of half-waves at buckling for a microtubule based on the shell model and the beam model: (a) critical buckling load and (b) number of half-waves at buckling.

Figure 10.

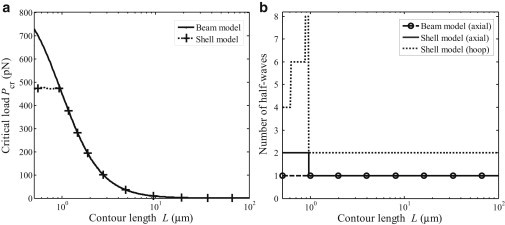
Critical buckling loads and the corresponding buckling mode for a microtubule based on the shell model and the beam model. Material parameters are E_x = 7 GPa (10), E_s = 1 MPa (22–24,36), G = 12 MPa (19,39), μ_x = 0.3 (22–24,36), and thickness h = 2 nm (22–24,28). (a) Critical buckling load and (b) number of half-waves at buckling.

Is the linear shell theory a limitation of the solution?

Because our objective is to link the behavior of microtubule, which is modeled as an orthotropic shell, to that of a wormlike chain, the persistence length has been determined by matching solutions in the small deformation (linear) limit. In this sense, a more accurate, nonlinear, elastic shell solution would not be appropriate for this objective.

On the other hand, we made a comparison between our linear solution and nonlinear, large deformation finite element simulations. Interestingly, as shown in Fig. 11, we found that the finite element method calculations of the bending deflection of the orthotropic shell (with material constants of microtubule listed in Table 1) deviate only slightly from our linear solution (by <10% up to very large deflection). In contrast, for an isotropic shell with Young's moduli E = 8 MPa and Poisson's ratio μ = 0.3, the difference between linear and nonlinear solutions increases rapidly as the deformation becomes larger.

Figure 11.

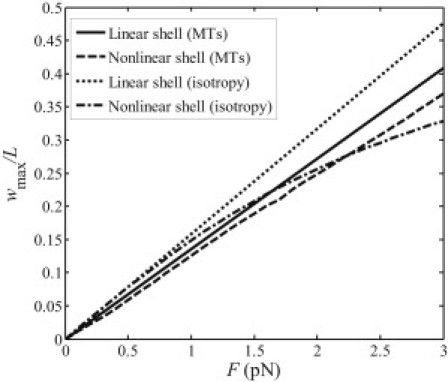
Comparison of the maximum deflections of an orthotropic microtubule and an isotropic microtubule calculated based on linear and nonlinear shell models.

Summary

We have used a higher-order continuum orthotropic thin shell model to study the flexural behaviors of microtubules by considering their effective bending, buckling, and the orientation correlation characteristics. Based on the proposed shell model, we have derived a more rigorous closed-form expression for the persistence length than that obtained previously by Gao et al. (26) based on a simplified shell model. In consistency with our previous analysis (26), this more rigorous study confirms that a range of tube lengths exists in which the persistence length of microtubules strongly depends on their contour length. It is shown that the effect of higher-order load distribution modes can be strongly shielded by the lowest-order load distribution mode in determining the contour-length dependence of the persistence length of microtubules. By studying the ratio between contour and persistence lengths that characterizes the thermal flexibility of the microtubule, we have shown that microtubules with length at ∼1.5 μm exhibit the lowest thermal flexural rigidity, whereas those with length at ∼15 μm exhibit the maximum thermal flexural rigidity. For the buckling of microtubules, we found that a range of tube lengths exists in which the first buckling mode is not the first wavemode of the structure, which is in drastic contrast to the classical Euler buckling of a rod. These anomalous flexural behaviors may provide a theoretical basis for understanding many biological functions that involve microtubules.