Multiple imputation of missing fMRI data in whole brain analysis

Abstract

Whole brain fMRI analyses rarely include the entire brain because of missing data that result from data acquisition limits and susceptibility artifact, in particular. This missing data problem is typically addressed by omitting voxels from analysis, which may exclude brain regions that are of theoretical interest and increase the potential for Type II error at cortical boundaries or Type I error when spatial thresholds are used to establish significance. Imputation could significantly expand statistical map coverage, increase power, and enhance interpretations of fMRI results. We examined multiple imputation for group level analyses of missing fMRI data using methods that leverage the spatial information in fMRI datasets for both real and simulated data. Available case analysis, neighbor replacement, and regression based imputation approaches were compared in a general linear model framework to determine the extent to which these methods quantitatively (effect size) and qualitatively (spatial coverage) increased the sensitivity of group analyses. In both real and simulated data analysis, multiple imputation provided 1) variance that was most similar to estimates for voxels with no missing data, 2) fewer false positive errors in comparison to mean replacement, and 3) fewer false negative errors in comparison to available case analysis. Compared to the standard analysis approach of omitting voxels with missing data, imputation methods increased brain coverage in this study by 35% (from 33,323 to 45,071 voxels). In addition, multiple imputation increased the size of significant clusters by 58% and number of significant clusters across statistical thresholds, compared to the standard voxel omission approach. While neighbor replacement produced similar results, we recommend multiple imputation because it uses an informed sampling distribution to deal with missing data across subjects that can include neighbor values and other predictors. Multiple imputation is anticipated to be particularly useful for 1) large fMRI data sets with inconsistent missing voxels across subjects and 2) addressing the problem of increased artifact at ultra-high field, which significantly limit the extent of whole brain coverage and interpretations of results.

1. Introduction

Missing data are a common problem in functional magnetic resonance imaging (fMRI) studies designed to examine activity across the brain. This is due in large part to susceptibility artifact and image acquisition parameters that result in incomplete brain coverage and spatial variation in acquired images, across subjects. Standard fMRI data analysis procedures involve the removal of voxels from group analyses even in cases where only one subject has missing voxel-wise data. These approaches can result in the exclusion of large brain regions (Figure 1A) that may be of theoretical interest and may produce Type II error at the boundary of excluded voxels. Removing voxels with missing data may also increase Type I error when spatial extent thresholds are used to establish significance, since fewer voxels in the analysis yield lower cluster size thresholds for significance. In this paper we examine the efficacy of missingness methods for group level univariate analysis of fMRI data (i.e., brain activity across subjects), with a focus on multiple imputation (Rubin, 1987). Multiple imputation techniques may also be applied to more complex missing fMRI data or statistical tests including individual differences analyses, single-subject datasets, multi-run datasets, meta-data, and multivariate analyses.

Figure 1.

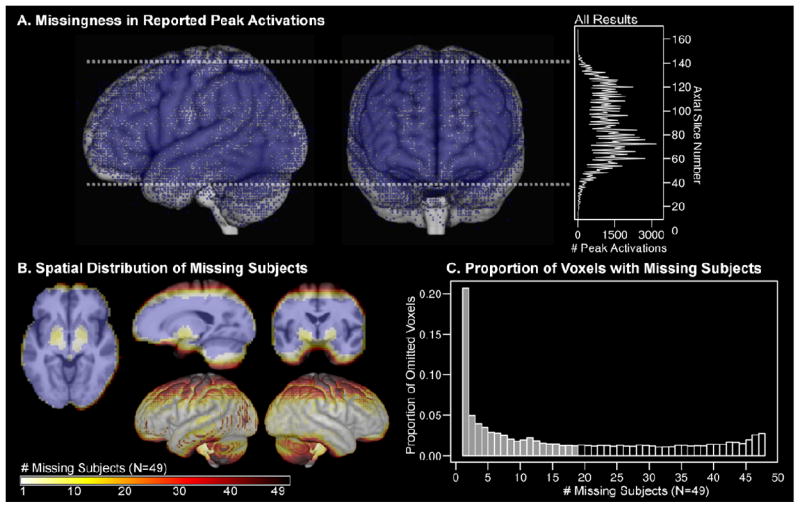
The standard approach in fMRI group statistics is to omit voxels that do not contain observations from all subjects. A) Due to common missingness mechanisms, omitted voxels would be predicted to coalesce into “blind spots” across many neuroimaging studies. A meta-result map was created in MNI space with 113,788 peak activations from 2,204 fMRI studies that were published from1996-2009, which make up the surface management system (SuMS) database (Dickson, Drury, and Van Essen, 2001). The resultant map demonstrates that peak activations (blue dots; rendered with infinite surface depth) are distributed most sparsely along typical bounding box edges (dashed white line), cortical boundaries, and frontal susceptibility artifact regions. The histogram shows the total number of peak activations for each axial slice in MNI space. B) Omitting partial datasets from analysis is costly to spatial coverage, especially along edge regions. Group data shown in B) and C) are from the speech recognition fMRI experiment analyzed in the current study (N=49). In cross sectional views, blue voxels contained non-missing data for every subject. The color scale indicates the number of subjects missing data for each voxel. Brighter colored voxels were missing data from few subjects. Darker colored voxels were missing data in a larger proportion of subjects. Most missing data occurred in regions at the boundary of the image acquisition bounding box and regions with susceptibility artifact, and correspond to missingness in A). C) The histogram shows the proportion of omitted voxels that were missing data from 1 and 48 subjects. More than 20% of those voxels were omitted as a result of missing data from only one subject. Half of the omitted voxels (11,748) were missing values from 18 or fewer subjects. There were 33,323 voxels with complete data from all subjects (N=49).

Multiple imputation is a principled “filling in” method that is widely used (Sterne et al., 2009), where multiple draws from the distribution of the observed data are used to estimate a set of plausible values for the missing data. Multiple versions of the data set are analyzed to provide an average parameter estimate and average within-imputation variance, which can be combined with the average between-imputation variance. Multiple random draws for a missing data point allow the imputed values to incorporate all sources of variability and uncertainty, which results in a more precise estimate of the standard error (Rubin, 1987). Moreover, multiple imputation performs well for small sample sizes (Barnes et al., 2006; Graham and Schafer, 1999) and when there is a high rate of missing data (Demirtas et al., 2008), thus making it an ideal method for many fMRI datasets.

Missing fMRI data can be missing completely at random (MCAR) because of random variations in the acquisition of brain images across subjects (e.g., field inhomogeneities) or small geometric differences in anatomy that must be normalized across subjects. Those examples are considered MCAR because the missingness mechanism is not related to or predictive of the missing values (i.e., missingness does not depend on the observed or unobserved data). Missing fMRI data can also be missing at random (MAR) because of predictable missingness when the probability of missing data is conditional on observed data but does not depend on unobserved data. For example, brain size or intracranial volume may predict missingness when the bounding box used to define the image acquisition space does not cover the entire brain in subjects with particularly large brains. If intracranial volume is included as a covariate in the multiple imputation analysis, then missing data outside of the acquisition space are considered MAR. Thus, MAR data can be filled in using observed data such as intracranial volume and other predictive variables such as scanner operator or motion parameters, in a regression based multiple imputation approach. The multiple imputation model can be further informed by imputing values based on the non-missing neighbor voxel values, which are typically strongly associated due to the resolution of the blood-oxygen-level dependent (BOLD) effect and Gaussian spatial smoothing that is often performed during preprocessing of fMRI data.

Another category of missingness involves selective missingness that can bias imputed test results. Data are considered missing not at random (MNAR) if the probability of missingness does depend on unobserved data or when missingness is related to comparisons or effects of interest (Rubin, 1973). For example, in an fMRI speech recognition experiment, subjects with head movement that occurred systematically during image acquisition (i.e., while data was collected) could translate a number voxels out of the current acquisition slice to another, without displacing the entire head measurably. Systematic head movement during image collection can therefore result in MNAR voxels, regardless of the inclusion of head size or motion estimates in an imputation analysis. We return to the issue of MNAR in subject and group level fMRI data in the Discussion.

While the application of imputation with fMRI data has not been studied extensively, there are some examples of imputation in the literature. These studies typically involve imputing missing fMRI runs where multiple scanning datasets were collected within a scanning session and subjects did not complete the entire session (Goldman et al., 2002; Strangman et al., 2008; Brown et al., 2011). The positron emission tomography literature offers examples of imputation (Higdon et al., 2004; Uijl et al., 2008) that are closely aligned with missingness in group level fMRI analyses. For example, linear regression imputation was performed to replace missing positron emission tomography data that were used to predict epilepsy surgery outcome (Uijl et al., 2008).

There have not, however, been efforts to leverage the spatial information in fMRI datasets that can be used to impute missing data across subjects and address the problem of missing data for group level fMRI analyses. In this study we compared 1) available case analysis, 2) randomly sampled neighbor-based imputation, and 3) regression based imputation approaches in a general linear model framework to determine the extent to which these methods quantitatively (effect size) and qualitatively (spatial coverage) increased the sensitivity of group analyses compared to the standard approach of excluding variables/brain regions with missing data. Missing data approaches were compared using a bootstrapping simulation of missing data and application to real missing data, which were both derived from a speech recognition fMRI experiment dataset. We demonstrate that multiple imputation provides a robust estimate of the original data and that it is less prone to Type I and Type II errors in comparison to the other missingness approaches across degrees of missingness and sample sizes.

2. Methods

2.1 Participants

Forty-nine adults age 19 to 85 years (M = 48.0, SD = 19.6; 24 female) participated in this study. All subjects reported American English to be their native language with a mean educational level of 16.1 (SD = 2.1) years and mean socioeconomic status of 51.2 (SD = 11.1; Hollingshead, 1975). The average degree of handedness assessed by the Edinburgh handedness questionnaire (Oldfield, 1971) was 70.8 (SD = 48.9, where 100 is maximally right handed and -100 is maximally left handed). Subjects provided written informed consent before participating in this Medical University of South Carolina Institutional Review Board approved study.

2.2 Materials and Procedures

The experiment was designed to detect differences in activity associated with word recognition. Subjects performed a word recognition task that included the presentation of 120 words, which were taken from a database of consonant-vowel-consonant words (Dirks et al., 2001) and presented with a multi-talker babble track (Bilger et al., 1984). The word stimuli were presented in 2 different signal to noise ratio conditions (+3 dB and +10 dB SNR), where SNR was manipulated by presenting words at 85 dB SPL or 92 dB SPL with the multi-talker babble presented at 82 dB SPL. Both conditions were balanced for word frequency and neighborhood density.

The word recognition task included 3 blocks of rest in quiet (30 volumes) during which no word was played, 2 blocks of rest in babble (30 volumes) during which only the babble track was played, and 24 blocks of word recognition in babble (4 to 6 trial blocks that alternated between +10 dB and +3 dB SNR conditions; 120 trials/volumes). The block length for word presentation varied to prevent subjects from predicting when the next block would begin. Quiet and babble rest trials were presented at the beginning and end of the experiment, and the third block of quiet rest occurred at the halfway point in the experiment.

Each 8.6 second trial (and image acquisition repetition time, TR) began with an image acquisition using a sparse sampling protocol. For rest trials, subjects were instructed to relax and view a rear projection screen through a coil-mounted 45 degree-angled mirror. On word recognition trials, a white cross-hair appeared in the center of the display at the beginning of the TR. The multi-talker babble track played continuously throughout these blocks. At 3.1 s into the TR, a word was presented with the babble. The cross-hair turned red at 4.1 s into the TR to cue subjects to repeat the word that they had heard. Subjects responded with the word “nope” if they could not identify the word so that a motor response would occur across trials. The cross-hair turned back to white at 6.1 s into the TR, indicating the end of the response period for that trial.

Eprime software (Psychology Software Tools, Pittsburgh, PA) was used to control the presentation and timing of each trial. One computer presented the word stimuli while a second presented the background babble stimuli. The stimuli from the two computers were mixed before being delivered to both ears via two MR-compatible insert ear phones (Sensimetrics, Malden, MA). Signal levels were calibrated for each scanning session using a precision sound level meter (Larson Davis 800B, Provo, UT).

2.3 Image acquisition and Preprocessing

The sparse sampling protocol was used to present stimuli and record responses in relative quiet, without scanner noise, and to provide time for subjects to stabilize their heads after responding (e.g., Eckert et al., 2008; Fridriksson et al. 2006; Harris et al., 2009). T2*-weighted functional images were acquired using a 32-channel head coil on a Siemens 3T scanner. A single shot echo-planar imaging (EPI) sequence covered the brain (32 slices with a 64 × 64 matrix, TR = 8.6 s, TE = 30 ms, slice thickness = 3.24 mm, and TA = 1647 ms). Functional images were composed of 3 mm isomorphic voxels. T1-weighed images also were collected to normalize the functional data using higher resolution anatomical information (160 slices with a 256 × 256 matrix, TR = 8.13 ms, TE = 3.7 ms, flip angle = 8°, slice thickness = 1 mm, and no slice gap).

SPM8 (http://www.fil.ion.ucl.ac.uk/spm) was used to realign and unwarp images, as well as smooth with an 8 mm Gaussian kernel. The Linear Model of the Global Signal method (Macey et al., 2004) was used to detrend the global mean signal fluctuations from these preprocessed images. Next, we used an algorithm described in Vaden et al. (2010) to identify time series fluctuations that exceeded 2.5 standard deviations from the mean voxel or volume intensity, in order to detect particularly noisy functional images. The two resultant signal outlier vectors produced by that algorithm were later submitted to the first level general linear model (GLM) as nuisance regressors. Two additional motion nuisance regressors (one for translational and one for rotational motion) were calculated using the Pythagorean Theorem from the six realignment parameters generated in SPM8 (Kuchinsky et al., in press; Wilke, 2012).

A first level fixed-effects analysis was performed for each subject’s functional data to estimate differences in activity associated with word recognition. The GLM contained one condition that represented the onsets and durations of word presentations (irrespective of SNR) and one condition that represented the onsets and durations of the babble background stimulus. The GLM also included the four nuisance regressors described above, two for head motion and two for signal outliers. Contrasts were derived in the individual-level analysis to examine the relative activation of listening to words versus an implicit baseline, which included the quiet rest trials. The resulting contrast images were then used to compare imputation methods and to perform group level statistical tests. It is important to note that we did not impute fMRI time series. We applied imputation methods to obtain contrast values within individual level maps that are normally derived using the convolved GLM that is fit to a functional time series. Individual level contrast values were missing as a result of 1) pseudo-random exclusion to simulate missingness in the bootstrap analyses or 2) missingness mechanisms such as bounding box edges, susceptibility artifacts, and geometric differences (additional details are presented below).

Study-specific template. The “Advanced Normalization Tools” (ANTS, version 1.5, www.picsl.upenn.edu/ANTS; Avants et al., 2011a) was used to create a study-specific structural template to ensure that the results of the individual level statistics were normalized to the study-specific average template space (e.g., Harris et al., 2009). An optimized average template was created using an algorithm that applied strong warping parameters, which maximized similarity among the normalized individual structural images (Avants and Gee, 2004). Each subject’s structural image was then normalized to the optimized average template using four successively smaller deformations. This second normalization stage allowed only large deformations of the individual structural images to approximate the template, followed by more restricted warps that resulted in finer-scale deformations. This two-template process was designed to reduce over-regularization errors that may otherwise appear in the transformed individual structural images and result from strong warping parameters. Individual contrast images were rigidly co-registered to their native space structural images and then spatially transformed into group-defined space using the combined parameters from the second, successive approximation method. Intracranial volume was calculated for each subject by summing native space probability maps for white matter, gray matter, and cerebrospinal fluid that were segmented using Atropos (Avants et al., 2011b) and used in multiple imputation analyses, as described below.

2.4 Implementing Missing Data Strategies

Several approaches were considered to deal with missingness, in a set of contrast images representing a comparison of listening to the speech stimuli and repeating them relative to an implicit baseline that included quiet resting periods when neither the words nor multi-talker babble was presented. For example, each subject’s contrast provided results demonstrating that temporal lobe regions activated in response to sound. For all bootstrap simulations and real missingness analyses, MATLAB scripts were written that called on SPM8 functions (http://www.fil.ion.ucl.ac.uk/spm) to import 3D contrast image files and then restructure the data into a large 2D matrix containing observed and missing contrast values in a single column. The data matrix also contained associated variable columns with rows that characterized each voxel (e.g., voxel ID number, xyz coordinates) or subject (subject ID, intracranial volume, head motion parameters, scanner operator). Custom R scripts (http://www.R-project.org) using MICE functions (van Buuren and Oudshoorn, 2011) were then used to impute data and perform statistical tests, and pool results where applicable. Group statistic results generated within R were then exported into 3D NIFTI format, using SPM8 functions. Precautions were taken at each step to ensure that data came from the same voxel locations that results were exported to (e.g., matrix voxel ID corresponded to voxels labeled with ID numbers in a 3D volume). Summary statistics at the whole brain level were computed using FMRISTAT (Worsley, 2006).

A group statistic is typically computed for voxels that contain contrast values from all subjects. In other words, a given voxel is only analyzed if every subject has a non-missing value for that voxel. The extent of shared brain coverage across subjects was determined by creating a normalized brain mask representing voxels where all 49 subjects had non-missing values. This mask provided baseline information about the number of voxels with non-missing values across all subjects and the number of voxels that were recovered by imputing missing values across subjects. Figure 1B demonstrates the spatial distribution of missing data as a function of the number of subjects that were missing data in each voxel location. Note that most of the missing data occurred at the edges of the bounding box that was used to define the space of acquisition and areas that were prone to susceptibility artifact. Figure 1C also demonstrates that a large number of voxels were missing values from just a few subjects. This indicates that over 20% of the omitted voxels in the standard analysis were excluded due to only one subject missing a value in that location, while values from the other 48 subjects were observed.

The following approaches were applied and results were compared for bootstrap simulated missingness (2-5, below) and real missingness (1-5, below), as it occurred in the fMRI dataset.

Missingness Approach 1: Subject Removal

Removing subjects with the most missing data was evaluated as a simple strategy for situations where removal of a single subject with considerable missing data could increase whole brain coverage across the remaining subjects. Indeed, Figure 1B shows that most of the omitted voxels occurred in regions where only one subject had missing data. We determined the extent to which a few subjects were consistently responsible for missing data, which would provide support for a subject removal strategy. Missing voxels within each subject’s contrast map were counted relative to the anatomically defined template space. Inclusion cost, or the number of omitted voxels that each subject was responsible for, was calculated by removing each subject’s data and counting the increase in non-missing (observed) values at the group level. Because the subject removal method was not a voxel-level approach, the results could not be directly compared to the other methods and was not included in the bootstrap simulations.

Missingness Approach 2: Available Case Analysis

This strategy involved analyzing all available non-missing values for each voxel, which meant that the number of subjects in each comparison varied across voxels. As a result, available case t-tests had varying df = 30 to df = 48. In order to compare results across voxels with different degrees of freedom, t-equivalent scores were calculated by submitting the observed p-values to the inverse cumulative t-distribution, which provided a t-score relative to 48 degrees of freedom. The variance of estimates from available case analyses were calculated on a voxel by voxel basis and is reported as the standard error of the mean (SE).

Missingness Approach 3: Mean Replacement

Mean replacement was performed within each voxel that was missing values from subjects, by substituting the mean non-missing value across subjects for the same contrast image voxel. This method was implemented by using the MICE function in R and specifying mean replacement as the method. After the missing contrast values were replaced, the SE and t-test were calculated from the imputed voxel dataset and the results were recorded for each voxel.

Missingness Approach 4: Multiple Imputation by Random Neighbor Replacement

Neighbor replacement of missing voxels was performed within a subject’s contrast map, by substituting each missing voxel with values from five randomly selected neighbor-voxels in an 18 mm or 24 mm radius sphere from the missing voxel. The 18 mm and 24 mm radius spheres were selected based on preliminary correlational analyses demonstrating that a smaller 12 mm sphere exhibited stronger correlations across voxels, but had an insufficient number of non-missing neighbor values for replacement (fewer than five) at the edge of the brain. Figure 2 presents the strength of correlation across subjects and within subjects for each neighborhood (sphere) size. Replacement for the 18 and 24 mm spheres provided for a comparison of replacement efficacy with increasing neighborhood size.

Figure 2.

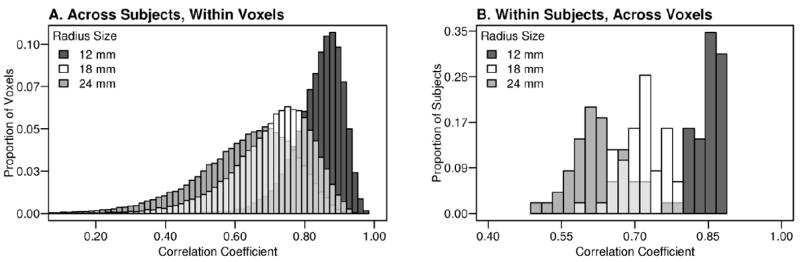
Correlation strength of neighbor voxels in contrast images varies with neighborhood (sphere) size. Contrast image voxel values from within 12 mm, 18 mm, and 24 mm radius spheres were correlated. Correlation tests performed across subjects between each voxel and the mean value of surrounding voxels within the sphere demonstrates stronger correlations for smaller neighborhoods at the group A) and individual level B).

Neighbor replacement was performed in two steps. The first step was to randomly draw five non-missing values from voxels within the 18 mm or 24 mm radius sphere that surrounded each missing voxel in that subject’s contrast map. In preliminary tests, increasing the number of neighbor replacements from five to ten did not change our results, but did increase the computational burden. The second step was to calculate the SE and t-test for each of those five imputed datasets and pool the results of those analyses. The result in each voxel (t-score, SE) reflected pooled results from five sampling distributions that included non-missing values and substituted missing subjects with their neighbor values, so this method was a simple form of multiple imputation. The neighbor replacement method was implemented the same way for simulated-missing data in the bootstrap experiment, and to impute real missing data from the word recognition experiment.

Missingness Approach 5: Multiple Imputation

When data are missing at random (MAR), multiple imputation is a reliable method for obtaining valid inference (Rubin, 1987). It produces imputations that reflect the uncertainty in the observed contrast image data. In the regression based imputation, our model included contrast values from a particular voxel as the outcome variable and covariates that are highly predictive of the missingness and that describe the special features of the study design (Schafer, 1999; Little and Rubin, 2002). The outcome variable (contrast value) had missing data, while the covariates did not. We implemented multiple imputation in three stages. In the first stage, m imputed versions of the missing data were created under a data model using methods that incorporate appropriate variability across the m imputations. In the second stage, the m versions of the complete data were analyzed using standard analysis techniques. In the third stage, the results were combined to produce the final inference (Rubin, 1987; Little and Rubin, 2002).

The imputation model is typically formulated as a joint distribution of the missing indicator, R, and the observed (Z and X) and missing variables (Y) where Z is represented by nuisance variables (e.g., scanner operator, intracranial volume, motion parameters, global mean voxel value) and X is represented by a predictor variable (e.g., neighbor voxel value). Thus, an imputation model was fitted using the observed data and imputed values were drawn by sampling from the posterior predictive distribution of the model. Let β̂, and Σ̂, be the set of estimated regression parameters and their corresponding covariance matrix from fitting the imputation model. In the m imputations, first a random draw, say b*, is taken from the posterior distribution commonly approximated by b*~MVN(β̂, Σ̂) (Rubin 1987). Then, imputations for y are drawn from the posterior predictive distribution of y using b* and the appropriate probability distribution. The MICE package for R allows the specification of different distributions that reflect different data types, i.e., normal, binomial, etc., for the outcome variable and each covariate (van Buuren and Oudshoorn, 2011). This incorporates all sources of variability and uncertainty in the imputed values, including prediction errors of the individual values and errors of estimation in the fitted coefficients of the imputation model (White et al., 2011). We included covariates (e.g., intracranial volume, variability in translation and rotational head movements) to increase the validity of the imputed data set (Rubin, 1996). These covariates were selected for inclusion in the imputation model based on our understanding of potential missingness mechanisms and because they were significantly associated with missingness (see Section 3.2, below).

The second step involved a standard analysis on each of the m complete data sets, which results in m different sets of model estimates. Consistent with Little and Rubin (2002) and van Buren et al. (2006), we observed that m = 5 imputations are typically sufficient to obtain consistent pooled results. The third and final stage is combining the m results. The combining procedure of the results from the multiple tests is done as follows. Let β̂₁,…, β̂_m and v(β̂₁) ,…, v(β̂_m) denote the m estimates and corresponding variances respectively. The arithmetic average of the estimates is denoted by $\overline{\beta }=\mathbf{\sum }_{i=1}^m{\widehat{\beta }}_i/m$, the arithmetic average of the variances is $\overline{v}=\mathbf{\sum }_{i=1}^{m}v({\widehat{\beta }}_i)/m$, and the variance of the β̂ estimates is $s=(1/(m-1))\mathbf{\sum }_{i=1}^m{({\widehat{\beta }}_i-\overline{\beta })}^2$. The final parameter estimates are given by β̂ = β̄ and var[β̂] = v̄ + (1+1/m)s. It has been shown that for a θ fraction of missing observations and m number of imputations, the efficiency of a multiple imputation estimator is (1 + θ / m)⁻¹ . For instance for θ = 0.5, the efficiency for m = 5, 10, 20 is 91, 95, and 98 percent, respectively (Schafer, 1999). Five imputed values were drawn from the estimated Gaussian distribution (van Buren et al., 2006). Using the five imputed datasets, the SE and t-test were calculated (N = 25 or 49, df = N - 1) and pooled for each voxel. Regression analyses were performed and pooled for the imputed datasets and each predictor from the imputation model.

Multiple imputation was implemented in MICE by fitting a regression model that estimated the distribution of values in each voxel that contains missing subjects, then generating values for missing subjects in m independent, simulated data sets that are drawn from the posterior predictive distribution conditioned by the observed data (White et al., 2011). The linear regression model used for multiple imputation in this study included the following six covariates: 1) average value for each subject’s contrast map (the outcome variables), variability in 2) translation and 3) rotational head movements, 4) average 18 mm radius sphere neighbors, and 5) scanner operator, and 6) intracranial volume. Because larger brains were more likely to have missing data at the edges of the bounding box than smaller brains, we used intracranial volume as a proxy measure for bounding box coverage during each subject’s functional data acquisition.

2.5 Bootstrap Simulations to Assess Bias in Imputation Results

We compared each imputation method described above using a bootstrap simulation for which sample size and the proportion of missing data were manipulated. The results using imputed data were then compared to results from a simulated-complete dataset. Although Monte-Carlo simulation could also be used for this kind of comparative study, resampling creates synthetic datasets that reflect the appropriate level of diversity and variability found in realistic populations (Efron and Tibshirani 1993, Marshall et al 2010). Simulated data were generated by resampling subject level statistical contrast maps (listen – implicit rest) from the word recognition fMRI experiment. Only voxels with complete data from all subjects (N=49) were included in the simulation. Voxels were the sampling unit in our bootstrapping approach (Belleca et al., 2009; Marshall et al., 2010) and contrast maps from each subject were pseudo-randomly selected with replacement to form 200 simulated-complete group level datasets with N = 25 and N = 49 individuals. After forming simulated-complete datasets, individual subjects were systematically removed to simulate 10%, 30%, and 50% proportions of missing subjects.

In order to simulate MAR data, each pseudo-randomly permuted list of subjects was first tested to determine whether simulated-missingness was predictable by performing a logistic regression to predict the missingness indicator (1=missing, 0=observed) at 10%, 30%, 50% proportion missing data, with covariates that were included in the imputation model: 1) intracranial volume, 2) translation and 3) rotation motion parameters, and 4) scanner operator. The permuted subject list was considered MAR and accepted for the simulation only if the covariates significantly (p<0.01) or perfectly (i.e., partial or complete separation) predicted the missingness indicator in a logistic regression analysis. Simulated-complete and missing lists were generated and logistic regression tests were performed until 200 subject lists of N=25 and N=49 were found that simulated MAR conditions. An average of 99 and 5,336 subject lists were formed, tested, and rejected, before finding each list of subjects for the N = 25 and N = 49 samples, respectively. For the N=25 subject lists, the missingness indicator was perfectly predicted with an average of 3.5 variables. The simulated-missingness indicator for the N=49 lists was perfectly predicted with an average of 3.2 covariates at 10% and 30% missing proportions and significantly predicted with an average of 1.3 covariates for datasets with 30% and 50% simulated-missingness. A bootstrap simulation study was also performed to demonstrate that multiple imputation could operate reasonably with MCAR data, which is described in Supplemental Figure 1.

Variances, t-statistics, and Type I and II error rates for each imputed data set were compared to the results of the simulated-complete data to examine the performance of each imputation method. First, we calculated efficiency as the ratio of variance in imputed datasets divided by variance in the simulated-complete dataset. When pooled across thousands of voxels and simulations, efficiency ratios that are substantially greater or less than one can indicate bias in the variance estimate and can also be used to make comparisons among the different missing data strategies. Second, we directly compared t-statistic results from the imputed and simulated-complete data, to measure the impact of missingness on hypothesis testing in relation to imputation method, sample size, and level of missingness. For each voxel in the N=49 simulations, p-values in the simulated-complete dataset were compared to p-values from the imputed datasets, to assess Type I and II error rates in the imputed results. A Family-wise Error corrected t-statistic threshold of p < .05 (t (48) = 5.29) was used to define significance. In addition to identifying important differences among imputation methods, the simulation experiments also demonstrate the importance of sample size and missing data proportion in obtaining imputed results that are representative of the sampling distribution.

The bootstrap simulations were performed on the Palmetto Cluster supercomputer at Clemson University to address the significant computational demands of applying 6 analyses × 2 sample sizes × 3 missing data proportions × 200 permutations × 33,323 voxels = 240 million voxel-level tests (without accounting for m imputations used for both neighbor replacement approaches and multiple imputation; Table 1).

Table 1. Summary of Methods.

Method summary of the bootstrap simulation and imputation of real missing cases. A) Variance (SEM) and t-statistic measures were collected from both the MAR and MCAR bootstrap simulations, and pooled from 200 permutations within each voxel for two sample sizes and three levels of simulated-missing data. Bootstrap simulations only included voxels with no missing data (33,323) and pseudo-randomly removed subjects from each permuted dataset to simulate missingness and allow direct comparisons with simulated-complete datasets. B) Imputation of real missing data began with an examination of the subject removal method, by counting the number of voxels that were gained by removing each subject. Each of the other measures was performed on 11,747 voxels that were missing between 1-18 cases, and pooled results were compared (indirectly) to the 33,323 complete data voxels. SEM and t-statistics were also collected for each voxel with real missing subjects.

A. MAR and MCAR Bootstrap Simulations	N = 25	N = 49
Simulated Missing Data Proportion	10%, 30%, 50%	10%, 30%, 50%
Missing Data Approach	# Missing Data Tests	# Missing Data Tests
Simulated-Complete Data (for comparisons)	3 × 200 × 33,323	3 × 200 × 33,323
Available Case Analysis	3 × 200 × 33,323	3 × 200 × 33,323
Mean Replacement	3 × 200 × 33,323	3 × 200 × 33,323
Multiple Imputation	3 × 200 × 33,323	3 × 200 × 33,323
Neighbor Replacement (18 mm)	3 × 200 × 33,323	3 × 200 × 33,323
Neighbor Replacement (24 mm)	3 × 200 × 33,323	3 × 200 × 33,323
Total MAR Analyses:	119,962,800	119,962,800
Total MCAR Analyses:	119,962,800	119,962,800
Total Bootstrap Analyses:	479,851,200

B. Imputation of Real Missing Cases
Missing Data Approach	# Missing Data Tests
Subject Removal	-
Available Case Analysis	11,747
Mean Replacement	11,747
Multiple Imputation	11,747
Neighbor Replacement (18 mm)	11,747
Neighbor Replacement (24 mm)	11,747
Total Analyses:	58,735

2.6 Evaluating Imputation in Real (Non-Simulated) Missing Subjects

In addition to bootstrap simulations to evaluate imputation methods, similar comparisons were made to examine the imputation methods when there was actual missing data in the subject contrast maps from the word recognition experiment. For these analyses, performance of the imputation methods was evaluated relative to each other and interpreted in the context of their relative performance when the missing data were known (simulation experiments described above).

In addition to comparing imputed variance and statistic results, the data were combined to form group statistic maps that revealed changes in the results when imputed data were included in the group level analysis. Group t-statistic maps were produced for 1) standard analysis, which omitted voxels with missing data, 2) available case analysis, 3) mean replacement, 4) multiple imputation with random neighbor replacement (18 mm or 24 mm), and 5) multiple imputation based on a regression model. Statistics for the standard analysis were calculated identically to the imputation strategies, including t-tests in R that were exported to 3D format, so they were directly comparable across voxels. Whole brain statistic summaries for all group statistic maps were produced using FMRISTAT (Worsley, 2006), with critical t-threshold of t (48) = 3.27, p = 0.001 (uncorrected), and cluster extent thresholding at p = 0.05 (Family Wise Error corrected). In order to compare multiple imputation and standard voxel omission approaches across statistical thresholds, we varied the critical t-thresholds so that p = 0.05 to 0.0001 (Family Wise Error corrected) and with cluster extent thresholding at p = 0.05 (Family Wise Error corrected). We predicted that multiple imputation would increase the size of significant clusters (an expansion of clusters into regions with imputed values) and the number of clusters (new results within regions with imputed values) across statistical thresholds, with no impact on the magnitude of peak voxel effects in regions significant with the standard voxel omission approach. Table 1 presents a summary of the experiments and analysis described above.

3. Results

3.1 MAR Simulation Results

The bootstrap simulations produced measures of variance (Figure 3), t-statistics (Figure 4), and Type I and II error counts (Figure 5) that characterized the performance of each missing data strategy relative to the simulated-complete datasets. For each strategy, variance estimates and t-statistics were pooled within each voxel across 200 permutations and across all voxels (33,323) for comparisons, which were then organized by sample size (N = 25, 49) and proportion of missing data (10%, 30%, 50%). Results comparing variance, t-score, and type of statistical errors across missing data strategies are presented below.

Figure 3.

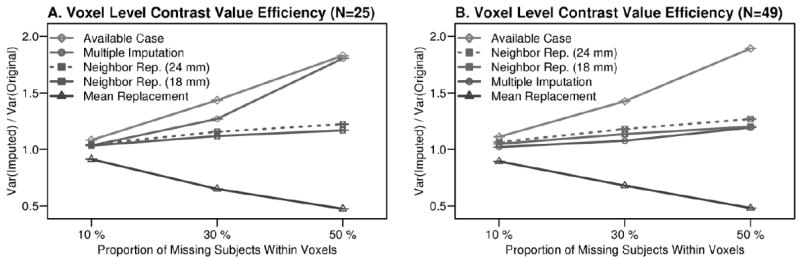
The bootstrap simulation demonstrated that available case analysis over-estimated variance while mean replacement over-estimated variance. Imputation error increased for those approaches with higher levels of missingness or smaller sample size. Multiple imputation performed best in the 10-30% missing range, although the regression model appeared to suffer from having too few degrees of freedom when N = 25 and missing = 50%. Multiple imputation preserved variability at the 50% missing point, when N = 49. Neighbor replacement appeared to preserve the original variability of simulated-complete data well, even for smaller sample sizes and high levels of missing data.

Figure 4.

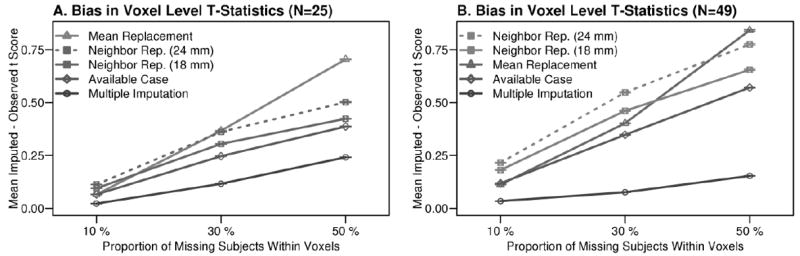
Bias in the t-statistic results for each missing data method was estimated by direct comparison with simulated-complete results. Specifically, the absolute value of difference in the imputed and observed t-statistic in small (N = 25) and large (N = 49) simulated datasets was pooled across voxels, as a function of proportions of missing data. Each method yielded increased t-statistic differences relative to the complete dataset when the proportion of missing subjects increased, although multiple imputation was less susceptible to that trend compared to the other methods as evidenced by its slope. Multiple imputation also provided the best approximation of the t-statistic obtained using simulated-complete datasets, which is demonstrated by the smallest t-statistic differences for multiple imputation compared to the other missingness strategies.

Figure 5.

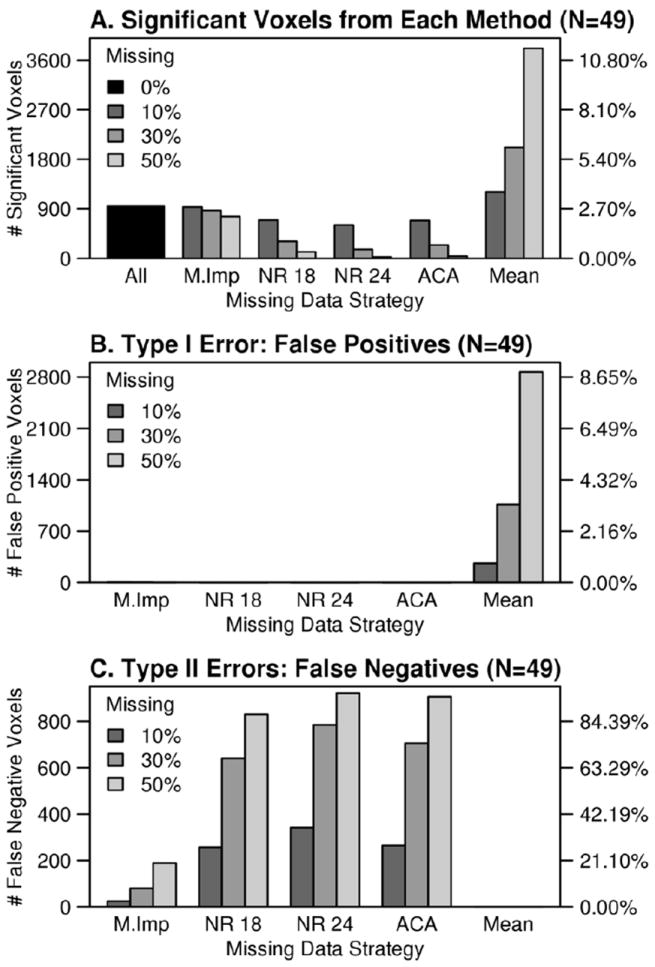
A) The number of significant voxels in simulated-complete results compared to imputed results (N=49). Missing data methods were abbreviated as follows: M.Imp = multiple imputation, ACA = available case analysis, NR 18 = neighbor replacement (18 mm), NR 24 = neighbor replacement (24 mm), Mean = mean replacement. The second y-axis in A) indicates the proportion of total voxels that were significant at the p<0.05 level (Family-Wise Error corrected) for each approach. B) Mean replacement showed a strong Type I error bias. The second y-axis in B) shows the proportion of the non-significant voxels in the simulated-complete results that survived an identical threshold after imputation. C) Type II error rates were calculated by counting voxels that were significant according to simulated-complete t-tests, but non-significant after missing data were imputed. The second y-axis in C) gives the proportion significant voxels in the simulated-complete results that were not significant in the imputed results.

Comparing variance in the simulated-complete datasets to each missing data approach showed that the available case analysis resulted in over-estimated variance, while the mean replacement approach under-estimated variance (Figure 3). Over-estimation by the available case and under-estimation by mean replacement analyses increased in magnitude as the proportion of missing data increased. The smallest differences in variance between simulated-complete and simulated-MAR data occurred with multiple imputation and neighbor replacement, particularly for the 10-30% missingness levels. These results were also observed for MCAR simulations (Supplementary Figure 1 A and B).

Available case t-statistics were consistently diminished due to variance inflation and t-equivalent calculations, which increased the absolute value of t-statistic differences shown in Figure 4. Mean replacement systematically over-estimated t-scores, as a result of reduced variance. Although neighbor replacement (18 mm, 24 mm) variances closely approximated true variance in the simulated-complete data (Figure 3), neighbor replacement under-estimated t-scores. Multiple imputation yielded smaller t-statistic differences compared to all of the other methods (Figure 4). As expected, when the missing data proportion increased from 10% to 50%, all of the missing data approaches yielded increased t-statistic differences compared to the simulated-complete data results. The MCAR bootstrapping simulations yielded similar results (Supplemental Figure 1 C and D).

There were qualitatively different types of error across the different missing data methods. When the voxels that were (on average) significant in the simulated-complete dataset were compared to each method, mean replacement yielded a high number of Type I errors (hundreds of false positive results). In contrast, available case analysis and neighbor replacement results were biased toward Type II errors (hundreds of false negative results). Multiple imputation resulted in the fewest Type I and II errors compared to all of the missing data approaches (Figure 5). The MCAR simulations revealed a similar pattern of results, although the false positive and negative error rates were slightly reduced (Supplemental Figure 1 E-G). Post-hoc analyses were used to demonstrate that coefficient bias in the imputation model was strongly associated with t-score under-estimation in Type II errors voxels (Supplementary Figure 2).

In summary, the simulation experiment demonstrated that multiple imputation provided the best approximation of variance, t-scores, and number of significant voxels based on simulated-complete datasets. Both the MAR and MCAR simulations also demonstrated high Type I and II error rates in the mean replacement and available case approaches, which stem from systematic under- or over-estimation of variances. The neighbor replacement approach was shown to approximate the variance of simulated-complete data, but nonetheless increased Type II errors with reduced t-scores.

3.2 Real Data Analysis Results

The standard practice of omitting voxels with missing data resulted in a group statistic map containing 33,323 voxels where all 49 subjects had non-missing values. More than 20% of the omitted voxels were missing data from one subject and 50% of the omitted voxels (11,748) were missing 18 or fewer subjects (Figure 1C). Imputation for 18 or fewer subjects expanded the group statistic map by 35%, largely along the edges of cortex, close to the boundaries of the image acquisition bounding box, and in regions with susceptibility artifact (Figure 1B).

Excluding Subjects with Missing Data

We examined the extent to which excluding subjects with the most missing data would limit the missingness problem. Figure 6 presents the number of voxels that would be added to the whole brain analysis with the exclusion of subjects with the most missing data. Removing a subject increases the number of voxels that can be analyzed by less than 500 voxels (~1.5 % of all voxels analyzed). When all 5 subjects with the most missing data were excluded, the group statistic map was expanded by 5% to include 35,101 voxels, while the df were reduced to 43. Thus, there was a modest gain in coverage by excluding subjects at the expense of reduced degrees of freedom and reduced power.

Figure 6.

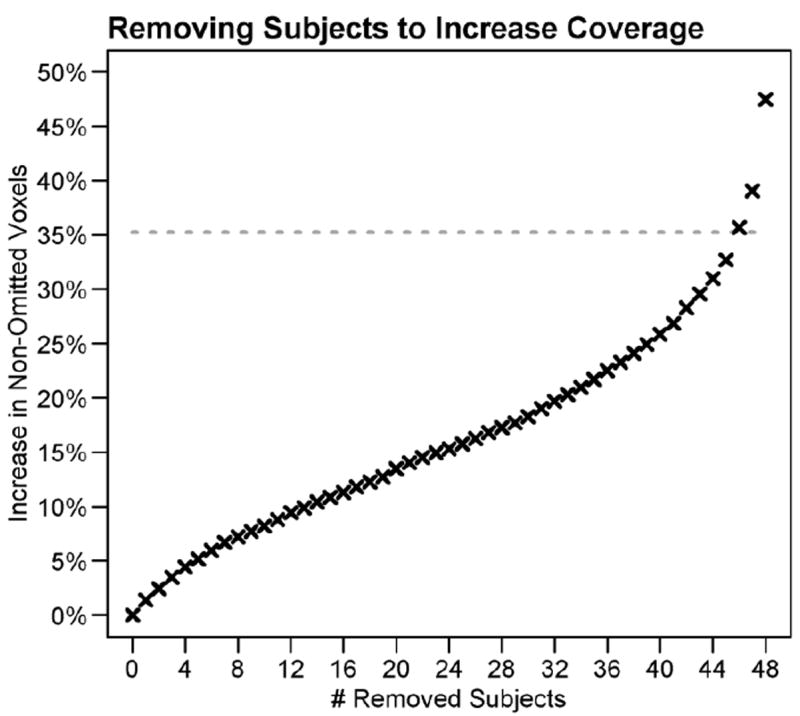
Increasing spatial coverage by removing subjects. Removing subjects increased spatial coverage in small increments in exchange for reduced degrees of freedom. Removing subjects with the most missing data resulted in increases of less than 460 voxels or 1.4%. Note that imputing values provides a 35% increase in voxels (dashed line).

Predicting Missingness

To examine the extent to which missing data were MAR, logistic regression was performed on the missingness indicator for non-missing (0) or missing subjects (1) for each voxel to determine the extent to which they were correlated with intracranial volume, MRI operator, and head movement measured in translation and rotation. Table 2 demonstrates that increased intracranial volume, different MRI operators, and the subject head motion during the experiment significantly predicted when a voxel was missing. Because the estimates in Table 2 were pooled across voxels, perfectly classified voxels were excluded from the pooled estimates to avoid (infinity values) inflating the pooled estimates. The logistic regression model perfectly predicted missingness for 4082 voxels, or 34.7% of the 11,747 voxels with missing data. Table 2 also presents the percent of voxels with missing subjects that were perfectly predicted by one (15.7%) or a combination of variables (19.1%) for each of the variables. Since we anticipate that missingness was not task or condition-dependent (MNAR), these results demonstrate that the missingness mechanisms in this dataset included MAR.

Table 2. Logistic Regression and Predicting Missingness.

All four variables were significantly correlated with the missing indicator for 7,665 voxels (65.3%). C-Sep: Percent of voxels with missing data that were perfectly predicted by the variable in combination with other variables. I-Sep: Percent of voxels with missing data that were perfectly predicted by that variable.

	Std. Estimate	95% LCI.	95% UCI.	Z-test	p-value	C-Sep.	I-Sep.
Intracranial Volume	0.80	0.76	0.84	42.27	< 0.001	13.7%	0.0%
MRI Operator	0.69	0.53	0.84	8.78	< 0.001	16.9%	13.6%
Translation	1.08	1.00	1.15	28.29	< 0.001	18.8%	1.1%
Rotation	-1.09	-1.17	-1.01	-26.13	< 0.001	18.6%	1.0%

Replacement Strategy Comparisons

Figure 7 presents the increase in whole brain coverage when imputation was performed for voxels that were missing 18 or fewer subjects, or 50% of all the missing data, combined across voxels and subjects. Again, analyzing these voxels with missing contrast values increased brain coverage 35.3%, especially in voxels at the edges of cortex and orbitofrontal regions that typically exhibit susceptibility artifact, but not for the most severely affected regions.

Figure 7.

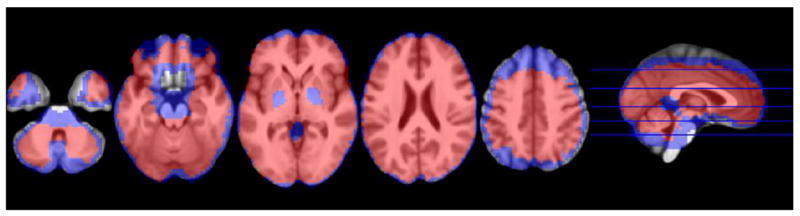
The extent of increased coverage with missing data replacement. Blue voxels were missing data from 18 or fewer subjects and were the focus of data-replacement strategies in the current study. Red voxels show complete voxel-wise data that were submitted to group level analyses under default analysis strategies, while blue would normally be ignored. Whole brain coverage increased by 35.3% following imputation, most notably at the edges of cortex.

Each imputation strategy was evaluated by comparing the mean variability and t-scores from the imputed voxel datasets. Figure 8 demonstrates a systematic increase in variability or t-test results for an increasing number of imputed voxels. Mean replacement reduced variability in imputed datasets and inflated t-scores, which were exaggerated with an increasing number of imputed values. Available case analysis increased variability and decreased t-scores with decreasing sample size. The results of mean replacement and available case analyses were consistent with the Type I and Type II errors in the bootstrap simulation results.

Figure 8.

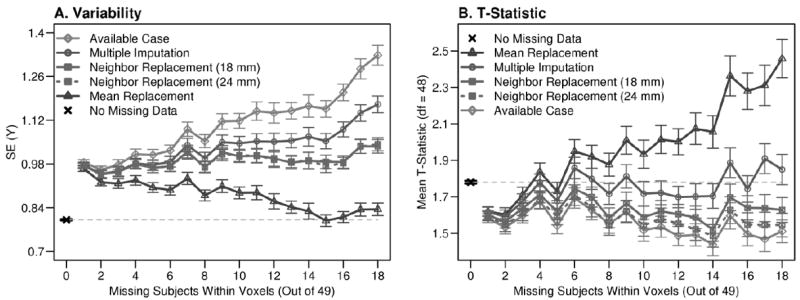
Results for each missing data replacement strategy by the amount of missing data. A) Variability was estimated using the SE for imputed and non-missing voxel datasets. Mean variability is organized by the number of missing subjects and error bars designate the SE of that estimate. B) Mean t-scores were also calculated across the imputed voxels, and are shown with SE error bars reflecting the variability in the t-scores. A systematic change in variability and t-scores was observed for the available case and mean replacement methods as the number of missing subjects increased, which is consistent with the biases demonstrated using the bootstrap simulation. The neighbor replacement and multiple imputation strategies yielded relatively stable results with respect to missingness.

Figure 8 shows that the neighbor replacement strategy provided stable variance estimates and elevated t-scores compared to the available case analysis. SE and mean t-score were not systematically related to missingness when data were imputed using this method, indicating less sensitivity to the proportion of missing data in estimating values from missing subjects, compared to other methods. Despite a modest mean t-score advantage for replacing data using the 18 mm versus the 24 mm radius sphere, there was relatively limited impact of sphere radius on the group results. In both cases, however, the mean t-score was lower for neighbor replacement compared to the standard omission approach.

Figure 8 further demonstrates that neighbor replacement and multiple imputation exhibited similar performance, until data were imputed for 6 (12%) or more subjects. The SE and average t-score increased with multiple imputation compared to neighbor replacement with increasing missing data. Note that the multiple imputation approach most closely approximated the mean t-score for voxels that did not have any missing data compared to the other imputation strategies.

Multiple imputation and neighbor replacement exhibited similar group results because the 18 mm radius sphere data were included as a covariate in the multiple imputation model. A linear regression was performed for each voxel that fitted the imputed data using the variables that were predictive of missingness (Table 2), as well as the global mean voxel intensity. Table 3 demonstrates that each variable uniquely predicted variation in voxel values, with the exception of the global mean voxel value. These results show that the variables predicted variation in voxel values, as well as the probability of missingness. These results also demonstrate why multiple imputation exhibited relatively better performance than the neighbor replacement approach. Intracranial volume, scanner operator, and head movement in translation and rotation provided additive predictive variance relative to neighbor voxel values.

Table 3. Evaluating Predictors Used in the Imputation Model.

	Std. Estimate	95% LCI.	95% UCI.	Z-test	p-value
Subject Mean	0.02	-0.002	0.03	1.72	0.09
Intracranial Volume	-0.12	-0.14	-0.11	-15.78	< 0.001
MRI Operator	-0.21	-0.25	-0.16	-9.02	< 0.001
Translation	0.72	0.65	0.79	20.71	< 0.001
Rotation	-0.57	-0.63	-0.50	-16.95	< 0.001
18mm Neighbor Average	4.63	4.58	4.68	193.07	< 0.001

Finally, whole brain statistics revealed the impact of imputation methods across brain regions. Analyses with missing data replacement using multiple imputation, in particular, yielded significant clusters that were on average 58% larger (97 more voxels) after multiple imputation compared to the standard voxel omission approach. Figure 9 shows that this increase in cluster size occurred at the edges of significant clusters that were identified with the standard missing data omission approach. The impact of multiple imputation was particularly evident for orbitofrontal regions affected by susceptibility artifact and supplementary motor cortex affected by bounding box placement during image acquisition. At the group level, multiple imputation and neighbor replacement results were nearly indistinguishable. Figure 9 shows that both the number of significant clusters and the number of significant voxels across the brain was greater for multiple imputation compared to the standard voxel omission approach across t-statistic thresholds. There were several clusters only detected by mean replacement (Supplemental Table 1), which could be attributed to the Type I error bias that was demonstrated using bootstrap simulations. Supplementary Table 1 presents summary cluster and peak voxel results for each of the missing data strategies. This table also shows that there was limited impact of imputation strategy on the magnitude of peak voxel effects, supporting our prediction that imputation would have limited effects on the magnitude of effects. Instead, multiple imputation yielded increases in the size of significant clusters and revealed new effects in previously omitted regions.

Figure 9.

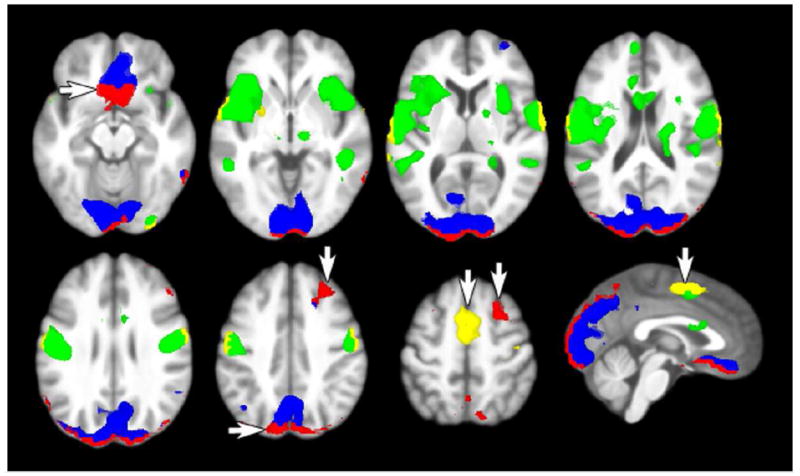
Multiple imputation increased the spatial extent of clusters that showed significant task-correlated activity and revealed otherwise hidden clusters that contained missing data. The standard analysis found positive (green) and negative (blue) task-correlated activity, but multiple imputation identified 57.9% more voxels per cluster (positive: yellow, negative: red) on average.

4. Discussion

A significant problem for whole brain fMRI studies involving large samples is the loss of brain coverage due to missing data (Figure 1). We have demonstrated that imputation can significantly increase brain coverage, in this study by 35% (from 33,323 to 45,071 voxels). As a result, imputing statistics in voxels that were missing subjects had a substantial impact on the spatial extent of significant effects. Significant clusters were 58% larger and added 97 voxels to each cluster on average compared to the standard omission approach. Multiple imputation, in particular, provided simulation and real missingness results that limited the risk of false positive and false negative errors in comparison to other missingness approaches.

The primary strategy for dealing with missing data in fMRI analyses is to omit voxels from analysis, even when just one or two subjects are missing data. The advantage of this omission approach is that degrees of freedom are constant across all comparisons, which simplifies the calculation of statistics across space. Unfortunately, this strategy tends to result in group statistic maps that are missing data along the outer edges of cortex. This is concerning given that BOLD effects can be pronounced in these regions, as demonstrated in our experiment in which subjects performed an aural word recognition task and exhibited significant effects in regions where missing values were imputed. For experiments in which cluster extent thresholding is used, the omission of these voxels could produce Type II error because cluster size may not survive a particular size threshold. More broadly, the omission of voxels leads to potential problems for readers interpreting negative results as it is not clear whether an effect might be present in omitted regions. For example, it is unclear whether the absence of anterior temporal, orbitofrontal, and cerebellar results from 2,204 fMRI studies in Figure 1A reflect omitted voxels or genuine negative findings. This is one reason for a call to present the anatomical space of group fMRI analyses (Poldrack et al., 2008).

An intuitive and simple solution for missingness is to remove individual subjects that contribute a large number of missing voxels within the group defined space. No single subject in our data set accounted for more than 500 missing voxels, however, limiting the effectiveness of this approach for our dataset where thousands of voxels were excluded across subjects because subjects had different missing voxels. Moreover, the removal of subjects who would impart the largest recovery of voxels was an inefficient strategy because spatial extent increases came at a loss to statistical power. Specifically, removing one subject from the group level test reduced the degrees of freedom in every voxel in the statistic map. For example, removing five subjects from our data set with the most missing data increased spatial coverage by 5% and reduced the degrees of freedom from 48 to 44. As a result of this loss of power, the sizes of significant clusters were reduced, a problem that was further compounded when the increased number of voxels were considered in the correction of multiple comparisons. Since removing subjects changes the population being studied, this strategy may introduce a selection bias unless the data are truly MCAR. This approach may be efficient in some data sets where one subject has very large susceptibility artifact, for example, but we anticipate that most studies will have the greatest percentage of missing data due to missing voxels across multiple subjects.

Available case analysis is a similarly intuitive missingness approach where all non-missing data within each voxel are analyzed, regardless of whether there were missing subjects. This is an unbiased strategy for data that are MCAR (Rubin, 1987), with the caveat of inflated variance and varying degrees of freedom for t tests across voxels. The majority of missing fMRI data is, however, unlikely to be MCAR (Table 2), which means that statistics performed on available cases may be biased by factors that contributed to missingness. Importantly, when we compared the results of available case analyses to other strategies, it was clear that this approach is susceptible to over-estimating variability in the data with increasing missing data (Figures 3A, 8A).

Mean replacement is commonly viewed as sub-optimal for dealing with missing data (Schafer and Graham, 2002) and we performed mean replacement to demonstrate why this approach should be avoided with fMRI data. The well-known flaw with mean replacement is that it reduces variance in a dataset. Although the mean is likely an accurate estimate for the mean of the missing data, it does not preserve the distribution of the values and under-estimates variability (Schafer and Graham, 2002). Our results for mean replacement show increased risk for false positives with increasing missing data across subjects (Figures 3B, 5B, 8B).

Neighbor replacement was considered as an alternative to the above approaches because the contrast of neighbor voxels tend to be highly correlated (Biswal et al., 1995; Cordes et al., 2000; Figure 2), due in part to the low resolution of fMRI data and spatial smoothing. Our implementation of neighbor replacement was to randomly draw values from among neighbors where neighbors were defined as falling within a sphere with an 18 mm or 24 mm radius from the missing voxel. We chose these relatively large neighborhoods because smaller neighborhoods/spheres were problematic for missing voxels at the edge of the brain. This is unfortunate because most missing voxels occur at cortical boundaries. Neighbor replacement performed well in comparison to the available case and mean replacement approaches, although white matter voxels in its sampling space may have led to the increased Type II bias observed in the bootstrapping simulation. Neighbor replacement compared more favorably for real missing voxels, which tended to occur along cortical edges and further from white matter distributions. Future studies will involve a more exhaustive evaluation of neighbor replacement methods including permutation (Nichols and Holmes, 2001) or using regional information to enhance this approach, particularly at the time series level of analysis.

Multiple imputation has an advantage over neighbor replacement because while it can incorporate neighbor information in a linear model to replace missing cases across subjects, additional variables can also be included in the model. Multiple imputation samples from an informed sampling distribution to replace missing subjects, which contrasts with the naïve sampling distribution resulting from neighbor replacement. We included intracranial volume, scanner operator, and head motion in the model because they are variables that could be included across research sites. Each was a significant predictor of voxel intensity across the brain (Table 3). Additional variables can be included in an imputation model that may be project specific where there is a known or predicted contributor of variance to voxels values. For example, medication dose or a behavioral measure may be included in the model even when that measure relates to a group outcome (Little and Rubin, 2002). In the current study, age would have enhanced the multiple imputation results as it significantly predicted voxels in our sample of 19-85 year olds (Z = 50.7, p < 0.001), but was not included to emphasize the value of multiple imputation using covariates that could be used across many different studies.

Multiple imputation most closely approximated complete data in both the bootstrap simulation and real missingness analyses, on the basis of variances, imputed t-statistics, and Type I or II error rates. This supports the premise that the imputed data were relatively unbiased with respect to missingness. This result is important in the context of the increased brain coverage (Figure 7), increased extent of significant effects that were obtained with multiple imputation (Figure 9), and increased number of significant clusters (Figure 10, Supplementary Table) obtained with multiple imputation in comparison to the standard voxel omission approach. The impact of multiple imputation may have been under-estimated by including voxels that represent white matter and CSF in the analyses. These voxels were included to avoid altering the size of clusters that extend into these regions. In general, the multiple imputation results from this study are similar to what would be predicted from other multiple imputation studies in which this method has been established as the most appropriate approach to the problem of missing data (Rubin, 1977; Gebregziabher and DeSantis 2010; Gebregziabher and Langholz, 2010).

Figure 10.

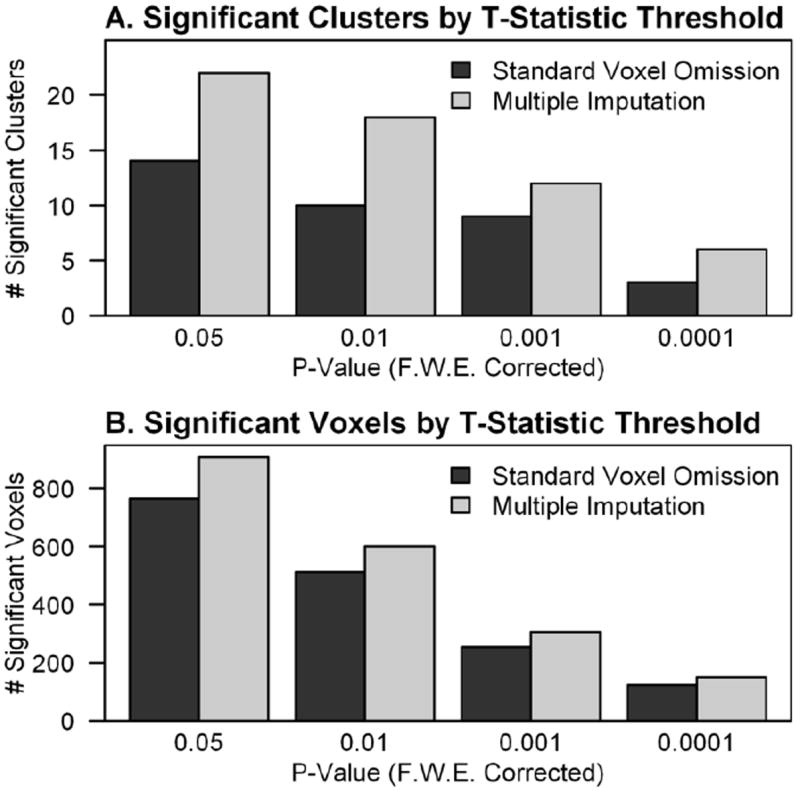
Multiple imputation yields A) more significant clusters and B) more significant voxels across multiple comparison corrected t-statistic thresholds than the standard voxel omission approach, despite the additional 11,748 comparisons that occurred with the multiple imputation approach.

The results of this study demonstrate that multiple imputation is an appropriate solution for missing fMRI contrast data, but several caveats should be considered. The multiple imputation method described here should be tested using other fMRI datasets to determine the extent to which our findings generalize to other functional imaging datasets. The current study used a relatively large sample size and data set acquired with a temporally sparse imaging protocol that may have limited the impact of motion artifact on missingness. The analysis of data sets with large amounts of head motion, especially in combination with continuous acquisition sequences, may benefit from using imputation methods to replace voxels that were missing portions of time series. In this context, multiple imputation may be particularly useful for pediatric and clinical populations that are more likely to have motion-related artifact. Empirical questions remain regarding the conditions in which multiple imputation is appropriate. For example, the results of this study apply specifically to the use of Random Field Theory for statistical testing (Worsley et al., 1996). We anticipate similar results with other forms of statistical testing (e.g., Nichols and Holmes, 2001; Hayasakaa and Nichols, 2003).

The proportion of missing subjects for which results can reliably be imputed and what constitutes sufficient study size for data replacement are outstanding questions. One limitation of the current study is that while our sample size (N=49) is not small in comparison to many fMRI studies, it is not sufficiently large to fully characterize the influence of sample size on multiple imputation. The results of our study are highly relevant for standard fMRI sample sizes however, because they demonstrate that stable results were observed when missing data were imputed for 10-30% missingness in the simulation analyses and for up to 37% missingness in the real dataset. Multiple imputation may require a larger number of imputations in datasets with smaller sample size or more missing data compared to the five imputations used in the current study (Schafer, 1999). With larger datasets, multiple imputation models may have more evidence to establish distribution estimates and therefore reduce statistical bias. Indeed, we view multiple imputation as an appropriate method for very large datasets where inconsistent missing voxels across many subjects is a significant problem.

This study was focused on contrast images from subjects that were used as dependent variables in group level analyses. Future work will examine the extent to which multiple imputation for individual subject time series data is useful for subject and group level comparisons. A key distinction between subject and group level imputation, besides the relative sample size and raw T2* values where neighbor replacement may be particularly useful, are the differences in missingness assumptions (Heitjan and Basu, 1996). Again, data that is MCAR is the most basic case of missingness where the probability of having missing data is unrelated to any characteristics of the missing data (Rubin, 1973). Much of the missing data in the present analysis were considered MAR, because the probability of missingness could be predicted by the covariates used in the imputation model (Table 2). Moreover, the imputed values could be predicted by information about the identity of the missing data (Rubin, 1973).

The contrast maps that were imputed in the current study had identical spatial extent regardless of the statistical comparison made for individual level data. Voxels that were missing contrast values representing activity during listening were also missing for every potential comparison. Put another way, the missing voxels within subject level contrast maps were unrelated to experimental conditions. In functional time series, however, data may be missing that is related to tasks or other comparisons of interest, raising the potential for imputation biased by non-representative data (e.g. resting activity as the basis for estimating listening activity). Data that are missing as a result of the same process that generated the effects of interest are considered MNAR (Rubin, 1973) and occur frequently in longitudinal or time series data. For example, trials with a speaking task may result in more head movement than resting trials – so missing data in voxel-level time series from a single subject may be MNAR with respect to task and the values imputed using data observed only in resting trials will be biased in estimating activity during speaking trials.

Similar concerns about data that are MNAR also apply to group level analysis with imputed data. For example, in the dataset that we used in the current study, a statistical comparison of male and female subjects may contain voxels with data that are MNAR, with respect to gender. Because males tend to have larger intracranial volumes than females on average, some voxels may be missing from all male subjects at the edge of the bounding box. In those voxels, multiple imputation would use non-missing values from females in order to fit its model and replace missing values from exclusively male subjects. In the imputed voxels where the pattern of missingness aligns with the variable of interest (gender), imputation would bias results to detect fewer significant differences between males and females. There is no agreed upon strategy for imputing MNAR data (Gebregziabher and DeSantis, 2010; Ibrahim and Molenberghs, 2009) and failing to distinguish instances of MNAR from MAR can result in biased inference.

5. Conclusion

Missing data can substantially reduce spatial coverage and detection of group level effects in fMRI data, even when voxels are only missing data from one subject. In comparison to the standard voxel omission approach, we compared several strategies for dealing with missing data in a group level analysis that included 1) subject removal, 2) available case analysis, 3) mean replacement, 4) neighbor replacement, and 5) multiple imputation. Consistent with the literature on missingness and imputation strategies for replacing missing data (e.g., Schafer, 1999 for review; Sinharay, Stern, Russell, 2001; van der Heijden et al., 2006), multiple imputation was demonstrated to be an effective strategy for missing fMRI data. We anticipate that multiple imputation will become an increasingly important tool for the neuroimaging community with the development of 1) large open-access data sets where inconsistent missing voxels across subjects will dramatically and negatively affect group results and 2) ultra-high field imaging experiments where susceptibility artifacts are a more significant problem. Missingness in these studies could be corrected with multiple imputation methods.

Supplementary Material

02

Supplemental Figure 1. A bootstrap simulation of MCAR data was performed for completeness and to demonstrate that multiple imputation could operate reasonably with data that were missing completely by chance. A logistic regression was used to constrain MCAR subject list generation, but the criterion was reversed from MAR; the missing indicators were not significantly predicted (p > 0.20) by the covariates for any sample size (N=25, 49) or proportion of missingness (10%, 30%, 50%). The results of the MCAR simulation were similar to the MAR simulation. Mean replacement and available case analyses systematically under-estimated and over-estimated variances, respectively (A, B), and resulted in biased t-scores (C, D). The simulated MCAR data were more likely to be normally distributed and the expected value was the mean, in contrast with simulated MAR data, which would explain why F) mean replacement resulted in slightly fewer false positives compared to MAR and G) available case analysis produced slightly fewer false negatives. Neighbor replacement methods (radii = 18 mm, 24 mm) performed well in approximating the variance of the simulated-complete datasets (A, B), but resulted in the most biased t-scores (C, D). Multiple imputation approximated the variance of the simulated-complete datasets well (A, B), produced the least biased t-scores (C, D), and resulted in the smallest number of false negatives and false positives compared to the other methods (E-G). The comparatively small differences in the multiple imputation results using simulated MAR and MCAR data was likely due to the inclusion of the mean neighbor sphere covariate, which introduced information about local contrast values from each missing subject to aid with estimation of missing values. The abbreviations used in (E-G) are identical to Figure 5.

03

Supplemental Figure 2. We performed regression analyses using the data from the A) MAR and B) MCAR bootstrapping simulations (N=49) to evaluate the association between regression coefficient bias and t-scores underestimated by multiple imputation (i.e., false negatives, Figs 5C and Sup Fig 1G). For each voxel where multiple imputation resulted in a Type II error, the covariates from the multiple imputation model were used in a linear regression model to predict either the simulated-complete contrast values or non-missing contrast values. The bias of each regression coefficient was calculated as the absolute difference between the coefficient based on simulated-complete and the simulated-missing dataset, averaged over 200 simulations. The mean under-estimation of the t-score was calculated for each voxel as the difference in t-scores from simulated-complete and simulated-missing datasets, averaged over 200 simulations. Coefficient bias was significantly correlated with under-estimation of the t-score, based on A) MAR or B) MCAR simulations. This demonstrates that missing data results in bias for some imputed t-scores, because multiple imputation uses regression to estimate missing values, although the occurrence is relatively low and depends on the extent of missingness.