The dynamics of sexual contact networks: effects on disease spread and control

Abstract

Sexually transmitted pathogens persist in populations despite the availability of biomedical interven tions and knowledge of behavioural changes that would reduce individual-level risk. While behavioural risk factors are shared between many sexually transmitted infections, the prevalence of these diseases across different risk groups varies. Understanding this heterogeneity and identifying better control strategies depends on an improved understanding of the complex social contact networks over which pathogens spread. To date, most efforts to study the impact of sexual network structure on disease dynamics have focused on static networks. However, the interaction between the dynamics of partnership formation and dissolution and the dynamics of transmission plays a role, both in restricting the effective network accessible to the pathogen, and in modulating the transmission dynamics. We present a simple method to simulate dynamical networks of sexual partnerships. We inform the model using survey data on sexual attitudes and lifestyles, and investigate how the duration of infectiousness changes the effective contact network over which disease may spread. We then simulate several control strategies: screening, vaccination and behavioural interventions. Previous theory and research has advanced the importance of core groups for the spread and control of STD. Our work is consistent with the importance of core groups, but extends this idea to consider how the duration of infectiousness associated with a particular pathogen interacts with host behaviors to define these high risk subpopulations. Characteristics of the parts of the network accessible to the pathogen, which represent the network structure of sexual contacts from the “point of view” of the pathogen, are substantially different from those of the network as a whole. The pathogen itself plays an important role in determining this effective network structure; specifically, we find that if the pathogen’s duration of infectiousness is short, infection is more concentrated in high-activity, high-concurrency individuals even when all other factors are held constant. Widespread screening programs would be enhanced by follow-up interventions targeting higher-risk individuals, because screening shortens the expected duration of infectiousness and causes a greater relative decrease in prevalence among lower-activity than in higher-activity individuals. Even for pathogens with longer durations of infectiousness our findings suggest that targeting vaccination and behavioural interventions towards high-activity individuals provides comparable benefits to population-wide interventions.

1 Introduction

Sexually transmitted infections (STIs) exact a staggering public health cost. Recent estimates indicate that there is an annual loss of over 80 million disability adjusted life years due to sexually transmitted infections each year; HIV is responsible for nearly 90% of this burden [22]. Biomedical (e.g. drugs, vaccines) and behavioural interventions (e.g. increasing condom use, reducing “high risk” sexual behaviour including partner exchange rates and concurrency) have been used to control the spread of specific STIs in communities with varying effectiveness [3]. The reasons for successes and failures of these interventions are often not well understood and efforts to improve the performance of existing control measures or to design novel methods for interrupting transmission require additional knowledge of STI dynamics.

Models of STI transmission have helped to elucidate the importance of “core” and “bridge” groups for the spread and persistence of these pathogens within communities, have been used to develop specific policy guidance about necessary levels of coverage and appropriate targeting of treatment and vaccination to control disease [23, 16, 4, 13] and have been used to investigate the effects of behavioural change in response to the presence of disease within the population [7, 18].

Behavioural data on the duration of relationships and the number of partners each person has at a particular point in time (their relationship concurrency) have been used to construct network models that account for the dynamic nature of sexual contacts. Models that reflect the time-dependent nature of these contacts often provide different insights than those based on static networks; accordingly, these dynamic network models, provided they more realistically encapsulate underlying behavioural patterns, may yield new insight into the spread of disease and better methods for controlling this spread [17, 27, 12, 28]. Most recently, Rocha et al [28] found that including temporal structure in networks substantially changes the size and timing of outbreaks, with highly variable outbreak sizes occurring when sexual networks are dynamic.

Research in this field has largely focused on understanding how individual sexual behaviours help to determine the contact networks over which STIs are transmitted. For example, the level of concurrency (the proportion of sexually active individuals with sexual partnerships overlapping in time) has been found to be a stronger indicator of the rate at which an infection will spread than the cumulative number of partners in a simulation model [26]. Concurrent partnerships have also been proposed as an explanation for racial disparities in HIV prevalence [27]. Different partnering behaviours (monogamy, serial monogamy or polygamy, relationship durations, etc.) result in the emergence of different network structures that in turn affect both the rate of spread of infection and the projected disease prevalence [11].

This can significantly complicate the task of modelling the spread of STIs. In a recent paper, Althaus et al compared three individual-based models of chlamydia spread that obtained widely differing results on the effectiveness of intervention [1]. Their work highlights the importance of relationship dynamics, which in individual-based models are often complicated, ad hoc and buried in supplementary material. They also comment on the fact that such models are “exceedingly difficult” to implement and contain a multitude of parameters.

In addition to the complex role played by the relationship patterns in sexual networks, the pathogen itself also shapes the transmission network. There are several studies highlighting the importance of whether the duration of infectiousness is sufficient to persist through gaps between relationships, thereby effectively linking successive partnerships into transmission chains [21, 9] but this does not inform further about the shape of the contact networks over which disease actually spreads. This “effective network” is shaped by an interplay between host behavioural factors and the natural history specific to each pathogen. The underlying contact network for a whole population, together with its dynamic behavioural 88 properties and traditional behavioural risk factors, is the same for most sexually transmitted infections. But the prevalence of pathogens in high- vs low-risk groups is often very different, even without clear differences in transmissibility. For example, Aral [2] et al compared gonorrhea and chlamydia prevalence in different activity groupings and found that while the burden of chlamydia was similar across groups, gonorrhea was concentrated among those reporting higher sexual activity.

Differences in the duration of infectiousness of a pathogen are known to lead to different patterns of epidemic spread. Garnett [16] finds that decreasing a pathogen’s duration of infectiousness leads to a contraction of the core group around its higher-risk members, and Blanchard [6] suggests that core groups are more important for sustaining transmission of pathogens with shorter durations. Wasserheit and Aral [29] make an important distinction between control of spreading STIs in the early phase of an epidemic and control later when duration has been reduced. It has also been seen that individuals are more at risk of infection by a particular pathogen if the gaps between their sexual partnerships are shorter than the pathogen’s duration of infectiousness [21]; this also affects the types of partnership which are more important for control purposes [9]. While there is a qualitative understanding of how networks affect the spread of sexually transmitted pathogens and of the role of duration of infectiousness, the extent to which different pathogens therefore effectively have access to different networks of individuals is not known.

Here we present a very simple approach to modelling dynamic sexual contact networks, using a minimal set of parameters. We use the resulting individual-based simulations to evaluate the role of the duration of infectiousness of a pathogen in shaping the effective network over which it may spread. We base our underlying contact network on survey data, and identify how individual-level risk factors for infection differ based on the properties of the pathogen. In particular, we consider the effect of a pathogen’s duration of infectiousness on which individuals in the network may become infected (i.e. the “reachable path of infection” [27]). By comparing the effective networks of pathogens with different durations of infectiousness, we are then able to assess how this parameter changes the network of individuals accessible to the pathogen. We then examine how the projected efficacy of interventions differs for pathogens with different durations of infectiousness and thus different reachable subnetworks.

2 Methods

The models described below were implemented in both R and C++.

2.1 Dynamic network

Our network model comprises extensions to the basic configuration model [25], in which we allow assortative mixing by activity level and use a specified distribution of accumulated degree over time to create an underlying dynamic network.

The network creation proceeds as follows: Each node (i) is assigned an “aggregate degree”, k_i, representing the number of contacts the node will have over the five year simulation period. We used data from the 2000 National Survey of Sexual Attitudes and Lifestyles (NATSAL) survey [19], collected in Britain from adults aged 16-44, to determine the k_i values (data show long tails in the distribution of k_i). These data are publicly available at the UK Data Archive (www.data-archive.ac.uk) [14].

Next, half the nodes are designated “relationship initiators” and each of these nodes, say j, is given k_j start times for its attempted relationships. Start times are selected uniformly between the start and end times of the simulation. Each initiator attempts to make links to non-initiators n who have not yet formed their k_n desired contacts. Partnerships are assigned in order of increasing start time. To incorporate the idea that partners are not chosen completely at random and that partners of like behaviors are more likely to be selected, we assumed a 70% probability that the end-node is required to have a “similar” (within 15%) k_i value to that of the start-node.

It remains to determine when partnerships end. To model the notion that highly active individuals probably have shorter partnerships than individuals with few relationships, the duration of an edge depends on the aggregate degree, or overall activity level, of the individuals that it links. In particular, each node has a preferred relationship duration d_i, which is exponentially distributed with a mean inversely proportional to the node’s degree, i.e. $\langle d_i\rangle =\frac{M}{\nu k\left(i\right)}$, where M is the simulation time period. The duration d_ij of an edge between nodes i and j is a weighted average of the preferred duration d_i of node i, and dj of node j: $d_{ij}=\frac{1}{4}{d}_i+\frac{3}{4}{d}_j$ where without loss of generality we take d_i < d_j. Partnership durations are in weeks.

This approach for calculating partnership durations was chosen for several reasons: individuals with higher overall activity have more rapid rates of partner exchange, this approach is simple, and it incorporates the fact that a relationship’s duration is related to the preferences of both individuals in the relationship. The parameter ν = 3 in the distribution was chosen to permit the investigation of dynamic networks that retain connectivity over the simulation time frame while leaving gaps between relationships that are in accordance with the data (see Figure 1). We constrain relationship duration d_i to be at least one week, i.e. the time resolution of the simulation.

Figure 1.

Comparison of model network attributes with survey data. A: Distribution of number of partners, for our model (circles) and NATSAL (National Survey of Sexual Attitudes and Lifestyles [19]) data (lines). B: Comparison of gap length distributions in our model and the NATSAL data. The gap length is defined as the time between the end of one relationship and the start of the next; negative gaps indicate concurrent relationships.

Overall, this method leads to the creation of a dynamic, bipartite (heterosexual) contact network whose aggregate contact distribution matches the survey data, which admits assortative mixing by activity level, and in which individuals with higher activity levels have shorter partnerships. We used 20,000 individuals and a simulation period of 260 weeks. We introduced a pathogen after a ‘burn-in’ period of 50 weeks, so that results reported here are taken from a time when the relationship dynamics are well established and the number of edges is approximately constant. The implementation in R is relatively slow but the C++ implementation runs take on the order of one minute on a standard desktop.

2.2 Networks accessible to a pathogen

We select a duration of infectiousness (D), a start time, and an initially infected node; we then extract the maximal accessible network for a pathogen starting at that site. The resulting reachable network can be viewed as the infected subgraph for a pathogen conferring no immunity (i.e. allowing continual reinfection) and which has a probability of transmission of 100% and constant duration of infectiousness D. (We refer to this maximal accessible network as a D-graph.) For example, if node A is infectious and near the end of his or her infectious period, but then makes contact with infectious node B, node B can reinfect A and thereby extend A’s infectious period. Our model is therefore a susceptible-infectious-susceptible (SIS) model where reinfection can extend the duration of infectiousness. Because the early stochastic behaviour of recruitment of new nodes to the reachable network depends on the degree of the start node, we examined 150 graphs for each of 11 D values, stratified by the degree of the starting node (making a total of 1650 simulations). The duration of infectiousness values were in the range 3 - 100 weeks, and starting nodes were randomly selected from within the network’s largest connected component. Of the 1650 simulations, there were 1013 that had infected nodes at the end time. Of these, 584 had more than 100 infected nodes at the end time. Mean degree and concurrency are reported for these 584 simulations, as the others had too small a reachable path for an infection to take hold.

2.3 Interventions

We explore the impact of interventions on the potential spread of pathogens with less than 100% transmission probability. Simulated interventions were chosen to reflect three control approaches: screening, vaccination, and behavioural modification. Screening was assumed to reduce the duration of infectiousness; the rigor of screening was varied, resulting in different effective durations of infectiousness. A vaccine preventing infection was introduced as either a random or preferential intervention: random vaccination was distributed uniformly among nodes whereas preferential vaccination was targeted at nodes with aggregate degree 10 or greater. A behavioural modification intervention was modelled as a proportionate reduction in the number of contacts that each individual made above a threshold value. This models an intervention targeted to highly active individuals, and assumes that it has some effect but does not completely prevent such individuals from making a large number of contacts.

For the vaccinations, 525 simulations were done (15 start nodes, 5 durations, 6 types of vaccination + one set with no vaccination), and the start nodes were picked from the 150 start nodes used for the non-intervention simulations. Simulations for which reachable networks did not die out for D=20 were chosen. For the behavioural intervention, an entirely new network was needed; these were created by choosing 5 random start nodes from the full network, 5 durations of infectiousness and 5 types of behaviour change, for a total of 150 simulations including the case with no intervention.

3 Results

We incorporated data on aggregate numbers of sexual contacts into the model, which therefore has similar aggregate degree to the NATSAL data but has fewer high-degree individuals, because of our assortativity requirement and the limited number of very high-degree nodes among the 20,000 simulated individuals (Figure 1a). The similarities between relationship gap lengths (Figure 1b) in the simulations and in the data emerge from the model’s dynamics; no parameter fitting was used. Relationship duration also broadly matches, with the model having a higher portion of relationships with duration less than 5 years. However, comparing relationship duration is challenging because of both the limitations on simulation time and, more substantively, the fact that the relationships that are active at the time of the survey have not reached their natural end [8, 10]. For these reasons it is useful to compare the durations of the second most recent relationship, which by definition has ended at the time of survey (or in the model, the time of sampling). Our model has a mean duration of the second most recent relationship of 19.16 weeks, while the comparable mean in the NATSAL data is 20.46 weeks. Furthermore, when we examine the duration of relationships that the model would create if simulation time were not limited (ie if relationships were not constrained to begin and end within the 5-year simulation period), the model predicts a higher portion of relationships of length greater than 5 years than are reported in the data (not shown). Mean durations are 53 weeks (NATSAL) and 52 weeks (model).

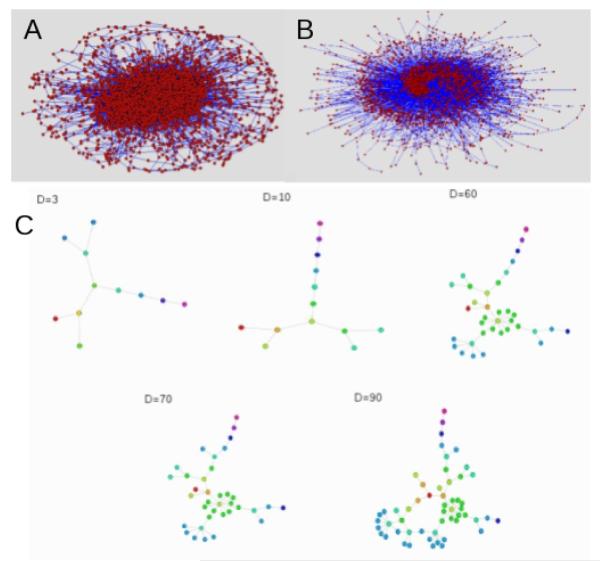
The algorithm produces dynamic contact networks that typically have a number of components of varying size; Figure 2 shows the largest connected component of the network (2A) and a large subnetwork accesible to a pathogen (2B). Figure 2C illustrates how the network accessible to the pathogen changes as the duration of infectiousness (D) increases.

Figure 2.

Plots of a model network and reachable subgraphs. A: The largest component of a contact network over five years. B: A large reachable subgraph initiated from a node with degree five, with duration of infectiousness 100 weeks. Of the subgraphs calculated, 48% contained at least 2000 nodes and 47% contained no more than 20 nodes, leaving only 5% in the range 20 - 2000. C: A small reachable subgraph showing the increase in size with increasing duration of infectiousness. Infection starts at the red node; nodes of the same colour are at the same number of links from the starting point. Plots were created using Pajek [5]. The degree of the originating node is 3.

3.1 How does a pathogen’s duration of infectiousness shape its reachable network?

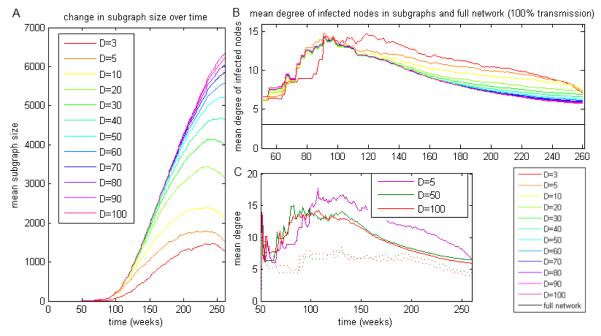
Pathogens with a shorter duration have access to smaller fractions of the overall networks than those with longer duration (Figure 3A), but these smaller subgraphs include individuals with a considerably higher mean activity level (Figure 3B). In general, the reachable subgraph includes individuals with higher activity level; the mean cumulative degree of nodes in the entire network is approximately 3, while the mean cumulative degree in the networks accessible to a pathogen is usually over 5 (in 88% of simulations; Figure 3B). The mean cumulative degree in the 584 simulations having more than 100 infected nodes at the end of the simulation was 7.8345, compared to 3.0705 for the full network. Recently, Rocha et al [28] used a dynamical model based on commercial sex workers and reported that there is a threshold duration of infectiousness of 31 ± 1 days such that infection can persist if the duration is longer than this. As in their work, we observe highly variable outbreak sizes, and evidence of threshold behaviour at D ~ 6 weeks (higher than their 31 days because we have modelled a general population and they have modelled commercial sex contacts).

Figure 3.

Degrees of nodes included in reachable subgraphs. The aggregated, rather than instantaneous, degrees are shown, so that the mean activities reported relate to overall activity level and not to the number of contacts in each particular week. Duration of infectiousness (D) values are given in weeks. A: Size of the network reachable to the pathogen over time, by duration of infectiousness. B: Mean activity of potentially infected nodes over time, for subgraphs with the same start position and start time. The mean activity in the network as a whole (black horizontal line) is much lower than the mean activity in any of the D-graphs. C: Mean activity of potentially infected nodes over time, for pathogens with 10% (dotted lines) and 50% (solid lines) transmission probability, at durations of 5, 50 and 100 weeks. The 10% transmission probability with short duration went extinct after a short time. The rise in mean activity soon after the pathogen is introduced corresponds to a rise in the subgraph’s size when the part of the entire network containing high-activity individuals is reached.

For pathogens with very short durations of infectiousness few individuals of any activity level will be included. In these cases, the reachable network will depend strongly on the characteristics of the start node. Beyond a threshold duration (determined by the network’s topology and by the natural history of the pathogen), we observe a phase transition where the majority of nodes, and virtually all those with a degree higher than 10, will be reachable (Figure 4C). Even in this situation, very low degree nodes are still unlikely to be in the reachable network. As duration is increased further, the proportion of low-activity individuals infected increases slightly, although most remain outside the reachable network even for large durations. The distribution of degree within the reachable networks is qualitatively similar to that of the whole network, although with a higher mean.

Figure 4.

Concurrency in the reachable network. Top: Network concurrency over time. While concurrency is higher in the reachable networks than in the whole population, it does not vary appreciably with duration of infectiousness. Middle: Proportion of concurrency groups infected for increasing duration of infectiousness. As duration of infectiousness increases, a higher proportion of polygamous and serially monogamous individuals are potentially exposed. Bottom: Proportion of nodes exposed to infection, stratified by degree, for increasing duration of infectiousness.

The dependence of the reachable path’s mean activity level on the pathogen’s duration of infectiousness means that the extent to which sexual activity level is a risk factor for infection depends on the pathogen itself. Risk is less highly concentrated in high-activity groups when the duration of infectiousness is longer.

The level of concurrency in a network at any particular time reflects the proportion of its nodes with an instantaneous degree at least 2 (i.e. an individual in more than one sexual relationship at a single time). Previous studies have shown that higher levels of concurrency result in faster spread of pathogens [15, 21, 26]. Figure 4A shows the level of concurrency over time for reachable networks of pathogens with different durations of infectiousness, and illustrates that typical reachable networks often have 5 to 6 times the concurrency of the full network. The concurrency in the full network is on average 0.0940. The mean concurrency of the 584 simulations having more than 100 nodes at the end time of the simulation was 0.2375, approximately 2.5 times larger than the concurrency of the whole network. For very long durations of infectiousness, however, concurrency declines slowly with time over the simulation. This is caused by the fact that individuals with concurrent partnerships are reached first. Subsequently, the infection reaches individuals with fewer or no concurrent partnerships, when the duration of infectiousness is long enough for infection to persist through gaps between relationships.

Figure 4B shows the proportion of “polygamous” nodes (nodes with at least one instance of concurrent edges over the five year simulation), serially monogamous nodes (nodes with more than one edge over the whole simulation, none of which are concurrent) and monogamous nodes (nodes with no more than one edge over the whole simulation) included in these subgraphs. The proportion of monogamous nodes in the reachable path of infection remains roughly constant with duration while the numbers of polygamous and serially monogamous nodes rise with duration. The risk of infection is much higher for serially monogamous nodes than for those that are completely monogamous, particularly if the length of time between relationships is less than the duration of infectiousness - in these cases, the partnerships can be considered as effectively concurrent [15].

3.2 How does a pathogen’s duration of infectiousness affect the efficacy of interventions?

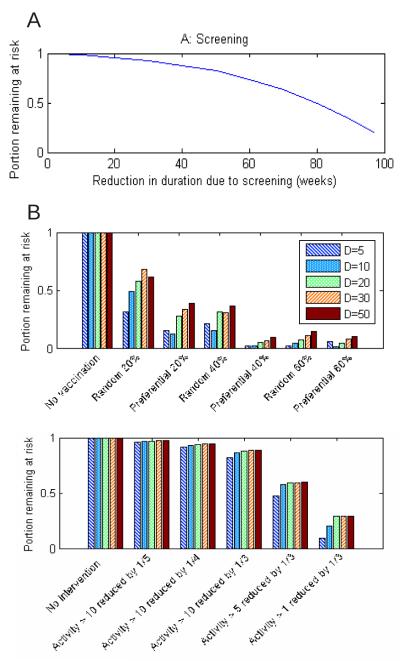
The projected impact of interventions is shown in Figure 5. Screening reduces the effective duration of infectiousness, and thus the size of the at-risk population. An additional consequence is that the screening causes a greater relative decrease in prevalence among lower-activity than in higher-activity individuals; for example, reducing the duration of infectiousness from 30 to 5 weeks results in the mean aggregate number of partners in the potentially exposed subgroup increasing by approximately 3. This quantitatively supports the idea that the performance of screening programs targeted at the general population could be enhanced if they were followed by targeted interventions aimed at the highest risk groups, as was suggested by Wasserheit and Aral [29].

Figure 5.

Effects of interventions, showing that a pathogen’s duration of infectiousness (and hence extent of concentration in high-risk groups) has little effect. A: Screening. An intervention modelling reducing the duration of infectiousness (from 100 weeks) by the amounts shown can reduce the size of the at-risk group (reachable subgraph). B: Vaccination. In some cases the subgraph collapsed due to disconnectedness, representing vaccination of an individual near the seed case (not plotted). This occurred in 6-9, 1-6, 0-7, 2 and 1 cases for durations D=5, 10, 20, 30 and 50 respectively. C: Behavioural intervention. Again, epidemic size was reduced to near 0 due to disconnectedness in approximately 1/5 of cases.

Preferential vaccination of higher-activity individuals (those with aggregate degree at least 10 over five years) is more effective in our model than random vaccination, and has considerable potential to stop epidemic spread entirely by breaking the connectivity of the network. One might expect that targeting highly active individuals would have a larger proportional effect for infections that are highly concentrated in core groups, and our simulations bear this out in showing a greater reduction with 20% preferential vaccination than 20% random vaccination for D=5 (Figure 5B). However, preferential vaccination gives nearly as much reduction for longer durations of infectiousness (D=10, 15, 20 in Figure 5B) even though risk is then not highly concentrated in highly active indivuals. This is because high-activity individuals are responsible for the rapid increase in the reachable subgraph’s size over time, so targeted vaccination has a comparable effect even for pathogens with longer durations. Accordingly, targeting highly active individuals may be more effective than distributing the same amount of vaccine more widely, even for diseases that are not typically concentrated among core groups.

Behavioural interventions that preferentially reduce the activity levels of higher-activity individuals produce benefits that are comparable to a more widespread intervention; this effect does not appear to be dependent on the duration of infectiousness (Figure 5C). While behavioural interventions are a natural way to reduce the spread of any STI, our simulations indicate that even when risk of infection is not particularly concentrated in high-risk groups, interventions specifically targeted at those groups may be as effective as interventions with a much wider focus such as mass media campaigns. In other words the best target group for receiving interventions may be far smaller than the group experiencing risk.

4 Discussion

We have developed a simple model for simulating dynamic networks, allowing for assortative mixing according to activity level, and allowing the use of any distribution for the accumulated degree over the timespan of the simulation. It requires only one parameter (although more can be used) to specify the relationship between activity level and relationship duration. A key advantage is that our method does not depend on a detailed model of partner exchange rates and relationship history, or ad-hoc divisions of relationships into “fast” and “slow” categories, yet it is able to represent the gap length and duration features of the NATSAL data realistically.

We have focused on the network accessible to the pathogen, rather than the network actually reached by a pathogen, because our intention was to study how the network structure over which disease spreads depends on the pathogen’s properties. However, we have also used a lower transmission rate and attained the same conclusions for networks of individuals actually infected in a specific transmission model. We have used a susceptible-infected-susceptible (SIS) model and allowed reinfection, as this is consistent with many sexually transmitted infections, so reinfection has played a role in shaping the reachable networks in our results. We acknowledge that simulating a vaccination programme in an SIS framework ignores the potential role of natural immunity conferred by infection and a full study of preferential vs random vaccination would be better suited by an SIR framework. However, there are a number of pathogens, such as human papilloma virus (HPV) with a number of distinct circulating variants, for which vaccines are available that target more than one type. As it is not always clear how type-specific natural immunity is, the SIS framework could serve as a ‘worstcase scenario’ for this kind of pathogen – vaccination providing better protection than is conferred by infection with any one type.

If the network were static, the part accessible to a pathogen would simply be the connected component to which the start node belongs. For dynamic networks, fewer individuals are accessible to the pathogen, since the order in which edges are traversed by the infection makes a difference. A pathogen with a short duration of infectiousness will only reach a subset of the nodes reached by one which is longer-lasting, as it will be less able to persist through gaps between relationships. Most importantly, the topological and dynamic properties of the reachable subgraph are different from those of the underlying population network.

For pathogens with shorter durations of infectiousness, risk of disease is primarily concentrated in a small group of individuals with high risk behaviours, whereas for a pathogen with a longer infectious period, the risk of infection will be more evenly distributed among the activity and concurrency classes. Accordingly, the extent to which traditional behaviour risk factors define the risk of exposure to a pathogen depends on the pathogen’s duration of infectiousness. While the intuition that increased frequency or concurrency of partnerships increases the risk of infection remains intact, our analysis supports the understanding that the natural history of the pathogen has a strong impact on the effect of these risk factors with risk rising more steeply with activity level for diseases with shorter duration of infectiousness.

The durations of infectiousness of gonorrhea and chlamydial infections have been estimated at 55 days and 10 months respectively [20, 24, 30]. Our model therefore predicts that chlamydial infection would be less closely linked to number of partners than infection by gonorrhea. This pattern is consistent with Aral et al.’s comparison of infection rate for these diseases, among subpopulations divided by activity level [2]. While their study found that the percentage of participants infected by chlamydia was approximately 24% for all activity level groupings (participants with one, two or more than three partners over a three month period), the percentage of participants infected by gonorrhea increased from 11.7% for those with one partner to 25.1% for those with three or more.

This expands the conventional view emphasizing the importance of sexual behaviour for an individual’s risk of infection, and has implications for both the spread of disease and its control. For example, a population-level screening program that acts to reduce the duration of infectiousness may also serve to “drive” infection into higher-risk groups, changing the overall distribution in the community [16]. The idea that this motivates phased intervention programs that leverage these potential changes in epidemiology was originally developed in [29], and discussed in [6]; our model provides a way to simulate and quantify the effects of such interventions in a simple, natural framework that does not require highly complex assumptions about host behaviour, length run times or tuning with large numbers of parameters.