Modeling nuclear blebs in a nucleoskeleton of independent filament networks

Abstract

Correlations between altered nuclear shape and disease are empirically observed, but the causes of nuclear dysmorphisms are poorly understood. The nucleoskeleton, which provides the majority of the mechanical stability of the nucleus, is composed primarily of intermediate filaments of lamin proteins. The nucleoskeleton forms a mostly-planar network between the inner nuclear membrane and chromatin. It is unclear if blebs and larger scale changes in nuclear morphology are consequences of reorganization of the nucleoskeleton alone or of other cellular processes. To test this, we computationally recapitulate the lamina network using a mechanical network model created as a network of Hookean springs. A- and B-type lamin filaments were distributed over a spherical surface into distinct networks linked to one another by lamin-associated proteins. Iterative force-based adjustment of the network structure, together with a stochastically modified Bell model of bond breakage and formation, simulates nucleoskeleton reorganization with blebs. The rate of bleb retraction into the nucleus depends on both initial size of the bleb and number of networks being deformed. Our results show that induced blebs are more stable when only one filament component is deformed or when the networks have no interconnections. Also, the kinetics of retraction is influenced by the composition of the bleb. These results match with our experiments and others.

Introduction

In metazoan nuclei, the nuclear envelope is lined by a structural nucleoskeleton composed primarily of type V intermediate filaments made of lamin proteins. A-type lamin networks are formed primarily from lamin A and lamin C, products of alternative splicing of the LMNA gene. A-type lamins appear to be responsible for mechanical stiffness of nuclei.^{1, 2} Nuclei in cells from lmna-null mouse cells are mechanically weak.² In diseases such as Hutchinson Gilford progeria syndrome (HGPS) an over accumulation of mutant lamin A at the nucleoskeleton stiffens nuclei.³ B-type lamin networks are formed from primarily lamins B1 and B2, encoded by separate genes.^{4, 5} B-type lamins are essential for life, and few mutations exist which alter levels of B-type lamins. The A- and B- filament networks assemble separately,⁶ have different membrane binding partners,⁷ and are mostly disconnected in the metaphase cell.⁸ It is unclear why cells have two independent, but juxtaposed, nucleoskeletal networks. We suggest that the independent networks may help maintain a consistent nuclear structure despite constant intracellular forces.

Nuclei deform significantly inside cells. In crawling cells, the nucleus deforms from intracellular force generation and as cells crawl between one another.⁹ Nuclei can deform permanently, such as blebbing during neutrophil nuclear segmentation associated with altered lamin levels.¹⁰ Transient nuclear blebs and dysmorphic shapes are also found during human embryonic stem cell differentiation.¹⁰ In both of these cases, nuclear blebs occur during fluctuations in lamin expression, either by a reduction or an addition of only A-type lamin filaments. The mechanisms of bleb formation or stabilization are not known, but recent evidence has suggested that blebs are not random. Nucleoskeleton blebs rich in lamin A/C but lacking lamin B2 contain active genes and polymerases, suggesting blebs form in preferred regions defined by space, mechanics or function.⁸ Interestingly, blebs, lobes and nuclear dysmorphisms have been used to describe both fragile nuclei such as in lmna-null^{2, 11} as well as stiffer nuclei such as in HGPS.^{3, 12}

To investigate the mechanical role of the double-network nucleoskeleton in bleb stabilization, we have produced a reductionist three-dimensional network of filaments with similar properties to lamin filaments. This nucleoskeleton model contains independent networks of A-type lamins and B-type lamins with interconnecting segments. Here, we have tested the resilience of the model nucleoskeleton to localized bleb formation. We have modeled the retraction of blebs which contain only one lamin network component (A-type filaments) or both lamin network components (A- and B-type filaments). When nucleoskeleton networks which contain both filament types are deformed, they retract together in a coordinated way that is easily modeled by an exponential decay. When only one lamin network component is deformed, the retraction is better modeled by a double exponential decay, and stable blebs result for large initial deformations. Thus, a disconnection of nucleoskeletal components results in increased bleb stability, as we have seen in experiments. We show here that reduction of the connector molecule nuclear αII-spectrin results in one-component nucleoskeleton blebs.¹³ Our results are also consistent with nuclei from patients with HGPS where A-type lamins are effectively increased at the nuclear envelope and pull away from B-type lamins to form a one-component bleb.¹²

Methods

Simulation

The Matlab computational model of the lamina nucleoskeleton explores the effects of filament arrangement on bleb behavior, and five matrix components were constructed. The three-dimensional structure of the A-type lamin protein network is stored in two matrices: one matrix for the coordinate values for potential lamin endpoints and one matrix for endpoints which are linked by lamin proteins. Similarly, two matrices encode the B-type lamin network. The fifth matrix contains the arrangement of linking proteins connecting the A- and B-type lamin networks. The simulation progresses through 4 stages: initialization, pre-equilibration, forming a bleb, and tracking bleb behavior.

Initiation

In initiation, the vertices for the independent networks are evenly distributed on a spherical shell. Spacing between the vertices is close to the contour length of the lamin proteins (Table 1), allowing connections to form. Proteins are added to the networks until there are no more viable options for placement. Whether additional proteins can be added is determined by the number of proteins connected to each vertex and the distance from each unfilled vertex to each other.

Table 1.

Physical properties of filaments used in the simulation

	Persistence length ξp (nm)	Contour length Lc (nm)	Number per network
Lamins	1000	50	3000
Connectors	50	100	1500

Pre-equilibration

To find an initial equilibrium state, the model is allowed to run for 2500 iterations, after which there was less than 1% change in diameter. After each iteration, the length of each protein, L_filament, is calculated. The difference in the actual length from the equilibrium contour length, L_c, is used to determine the force of the protein on neighboring vertices, F_bond, based on Hooke’s law. The spring constant for the filament, k_sp, is determined based on the contour length, L_c, and persistence length, ξ_p, of filaments.¹⁴

$$F_{\mathit{\text{bond}}}=-k_{\mathit{\text{sp}}}\mathrm{\Delta }x$$ equation 1

$$\Delta x=L_{\mathit{\text{filament,i}}}-L_c$$ equation 2

$$k_{\mathit{\text{sp}}}=\frac{3k_{B}T}{2L_c{\xi }_p}$$ equation 3

Physical properties of intermediate filaments made of lamin proteins are presented in Table 1, and the A- and B-filament networks are interconnected set by a small number of “connector” elements. These elements were set to be more than an order of magnitude less stiff and twice as long as lamin filaments. These could represent either force transmission through the nuclear membrane via inner-nuclear membrane lamin binding proteins or force transmission through large, repeat domain proteins which connect the A- and B-type lamins networks.^{13, 15, 16} These global connector elements are used to propagate global network forces as the distance between vertices changes. After vertices are moved in the direction of the applied forces, a new protein is placed into the model for each that was broken and iterated. By allowing the simulated nuclear network to reach an equilibrium point, later changes to size and shape can more readily be attributed to the bleb creation.

Forces are calculated at vertices based on the filaments which intersected at these points, and the maximum number of filaments per vertex is capped at 5, since the only observed structures of lamin networks observed have 4 per vertex.¹⁷ Only direct connections (immediate neighbors) are considered for the displacement of each vertex. To measure filament disconnection (breakage) at the vertices, we apply a modified Bell model of bond breakage¹⁸. Rather than find a mean lifetime for each bond based on applied force, we calculate a breakage probability for filaments at vertices. Since each iteration has no defined time interval, results are presented as iterations not absolute time. Forces on all nodes are then simultaneously calculated at each iteration for global distribution of force and resultant strain.

Bleb formation

A bleb was formed by identifying the vertex with the largest x-coordinate value (Figure 1). The distance from this vertex is calculated for all other vertices and a weighted probability is assigned to each based on this calculation. This probability determines whether a given vertex will be incorporated into the bleb. These vertices are shifted a predetermined, variable amount (reported in results as a % of nuclear radius) to form small, medium and large blebs. For the first condition tested, only vertices from the A-type lamin network were selected; for the second condition, vertices from both A-type and B-type lamin networks were selected.

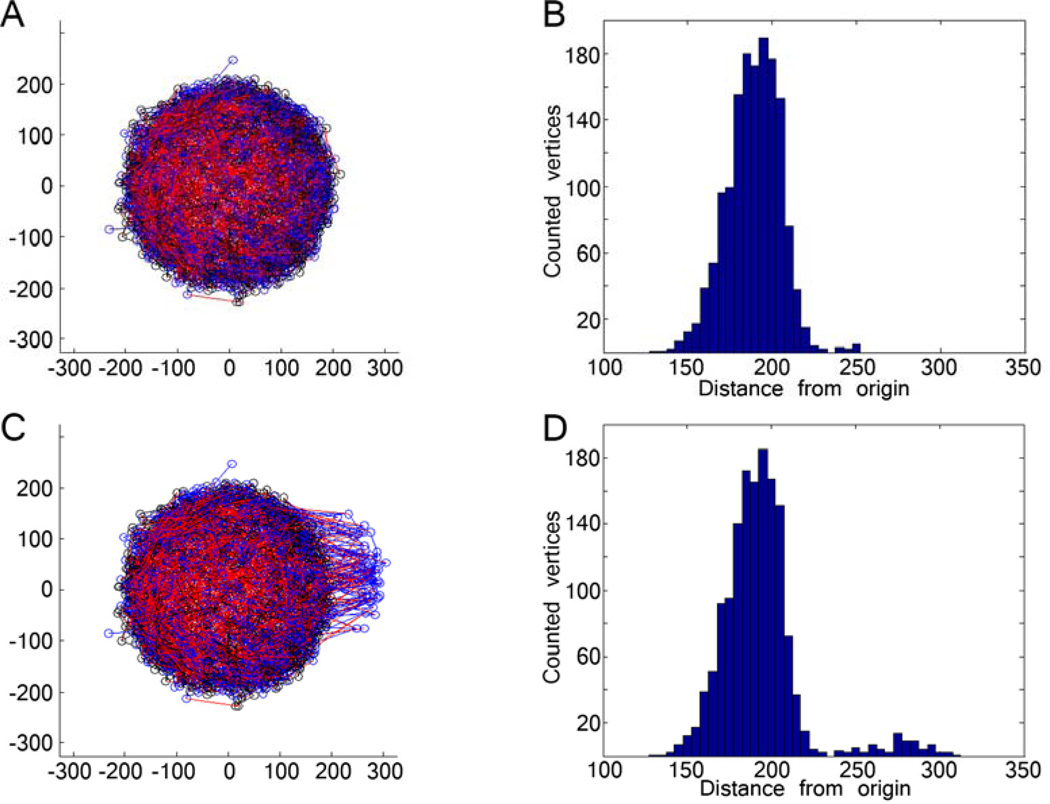
Figure 1. Creating a bleb on a simulated lamina network.

(A) A pre-equilibrated lamin network of 3000 A-type lamins (red) and 3000 B-type lamins (blue) interconnected with 1500 ‘connector’ molecules (black). (B) The histogram of vertices (represented as circles in A) represents the lamin distribution in the pre-equilibrated nucleus, and shows a normal distribution with some fluctuation. (C) Bleb induced by translocation of lamins by 50% of the nuclear radius. (D) The distribution of vertices shows a second mode distribution of vertices.

Tracking the bleb

The final stage of the simulation, studying bleb progression, uses the same mechanisms discussed for finding pre-equilibrium. 5000 iterations were determined to be sufficient (Supplemental Figure 1). “Bleb length” is determined as the rightmost region of lamin vertices still attached to the nuclear structure (see Supplemental Figure 2 for excluded datasets).

Cell culture and imaging

HeLa cells were cultured under standard condition and transfected with Polyfect transfection agent (Qiagen) and vectors for αII-spectrin shRNAmir (shRNAmir against SPTAN1; RHS1764-9695009 from Open Biosystems). G418 (500 µg/ml) was used to select shRNAmir-expressing cells. Cells were fixed and stained by indirect immunofluorescence using mouse monoclonal antibodies specific for either lamins A/C (Santa Cruz Biotechnology #SC-7292) and goat anti-lamin B (Santa Cruz Biotechnology #SC-6217, recognizes B1 and B2) with complementary antibodies and DAPI for DNA. Cells were imaged using Leica AF 6000 microscopy and a DFC 350 FXR2 camera controlled by Leica software. For live imaging, cells were cultured under microscope using CO₂-independent medium (Invitrogen 18045088) with 10% FBS and 1% pen-strep at 37°C in a climate controlled chamber.

Results and Discussion

Lamin filament properties

For the model, we used available data to determine mechanical properties of filaments (see Methods; Table 1). However, there is some uncertainty with these values. Filaments of lamin proteins are notoriously difficult to produce in vitro, which limits biophysical characterization. Purification of recombinant filaments leads to the formation of paracrystals with a 25 nm repeat structure.^{19, 20} Model systems including Xenopus oocytes show 10 nm think filaments with 50 nm inter-filament nodal spacing¹⁷ The paracrystal repeat of 25 nm also suggests a functional spacing on the order of 10’s of nm. More recent examination Xenopus oocytes has shown that filaments are 10 nm and range from 7 to16 nm in thickness, ²¹ but the length may be much longer. Since lamin filaments cannot be produced in vitro, the persistence length of lamin filaments is based on other intermediate filament structures.²² Vimentin and desmin have persistence lengths of 100–1000 nm.^{23, 24} We set the persistence length of lamin filaments to be ~1000 nm since lamins have substantially larger tail domains which could stabilize filaments.²⁵

Induced blebs retract back to the equilibrium structure at different rates

Blebs were induced in the A-type lamin network alone (red filaments only in Figure 1) or in both A-type and B-type (AB) lamin networks (red and blue filaments in Figure 1). Blebs were “induced” by moving vertices away from the equilibrated sphere (see Methods). After the bleb formation, the blebbed-sphere was allowed to reorganize to minimize the forces on the filaments. In both cases, by iterating the induced blebs relaxed back toward the core nuclear structure. Five initial bleb sizes (10, 25, 50, 75 and 100% of the initial radius of the nucleus) were tested for both single network deformation and double network deformation.

When only one network was deformed, and the other network remained at the initial configuration (A-only), the initial retraction occurred very quickly, an effect that was most evident for large initial deformations (Figure 2A). Deformation of both networks (both A- and B-networks) showed a slow, but steady retraction of the networks (Figure 2B). Retraction “kinetics” were measured by tracking bleb size as a function of iteration number. The retraction data (bleb size versus iteration number) was then fit with a single exponential decay, plotted with the raw data in Figure 2C and 2D. Data was fit to a single exponential equation

$$\mathit{\text{size}}(t)=\mathit{\text{size}}{(\mathit{0})}^{*}\text{exp}(-{\mathit{\text{decay}}}^{*}t)$$ equation 4

Single network retraction (A-only, Figure 2A) was poorly fit with a single exponential at short iteration times (Figure 2C, Table 2), particularly for larger initial blebs. By comparison, retraction of both A- and B-networks was well fit with a single exponential decay (Figure 2D, Table 2). A double exponential

$$\mathit{\text{size}}(t)\propto \text{exp}(-{{\mathit{\text{decay}}}_{\text{max}}}^{*}t)+\text{exp}(-{{\mathit{\text{decay}}}_{\text{min}}}^{*}t)$$ equation 5

fit the A-only data significantly better (Figure 2E, Table 2), especially at large initial bleb size. This may reflect a strong contribution from the A-only network retraction and a smaller contribution from inter-network force distribution and reorganization. Quality of fits are presented in Table 2. While double exponential fits improved both A-only and AB networks, the slight improvement in the AB-network reflects overfitting.

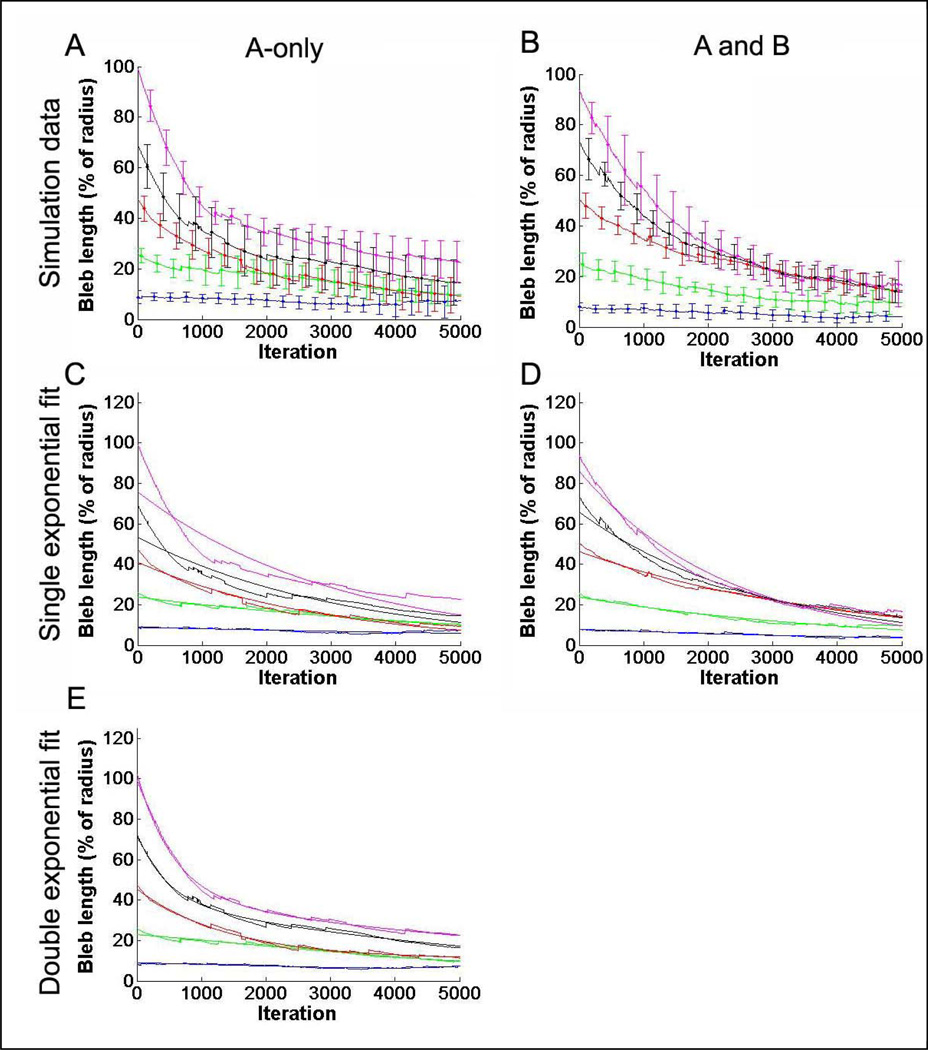
Figure 2. Tracking bleb dynamics over time shows different relaxation profiles based on networks involved.

(A) The mean of eight trials each for blebs of increasing initial size (y-axis) in systems where only the A-type lamin network was perturbed. Bleb sizes selected were 10%, 25%, 50%, 75% and 100% of the equilibrium nucleus radius. Larger blebs appeared to retract faster than smaller blebs at early times (iterations). Error bars represent standard deviation and are presented every 250 iterations for clarity. (B) Similar trials for blebs containing both A and B lamin networks show more gradual initial retraction. (C) Fits of a single exponential decay to data from blebs of A-type lamin networks show deviation for large blebs suggesting bimodal reorganization. (D) Fits of a single exponential decay to blebs containing both A- and B-networks shows strong correlation. (E) Double exponential fits to A-only data appear to capture the features better.

Table 2.

Quality of fits for single and double exponential fits based on r².

	A-only		A and B
initial bleb size (% of radius)	1 exponential fit (r2)	2 exponential fits (r2)	1 exponential fit (r2)	2 exponential fits (r2)
10	0.8546	0.9964	0.9727	0.9986
25	0.9002	0.9923	0.9750	0.9983
50	0.9457	0.9916	0.9858	0.9965
75	0.9614	0.9710	0.9639	0.9929
100	0.6805	0.8204	0.8322	0.8756

Kinetics of retraction

From plots of bleb size versus iteration, we calculated a decay constant for each simulated condition accordingly. We compared this decay constant to initial bleb size, which may provide insight into the “potential energy” of network blebs. We found that the retraction of both the AB-networks showed a relatively linear correlation in decay constant versus initial bleb size (Figure 3A, blue lines). This suggests that increasing the size of the bleb, or the potential energy of the bleb, results in increased retraction speed. This follows since the networks were individually modeled as integrated spring-like networks; thus the reorganization shows spring-like behavior wherein retraction speed, related to force, is a function of initial displacement.

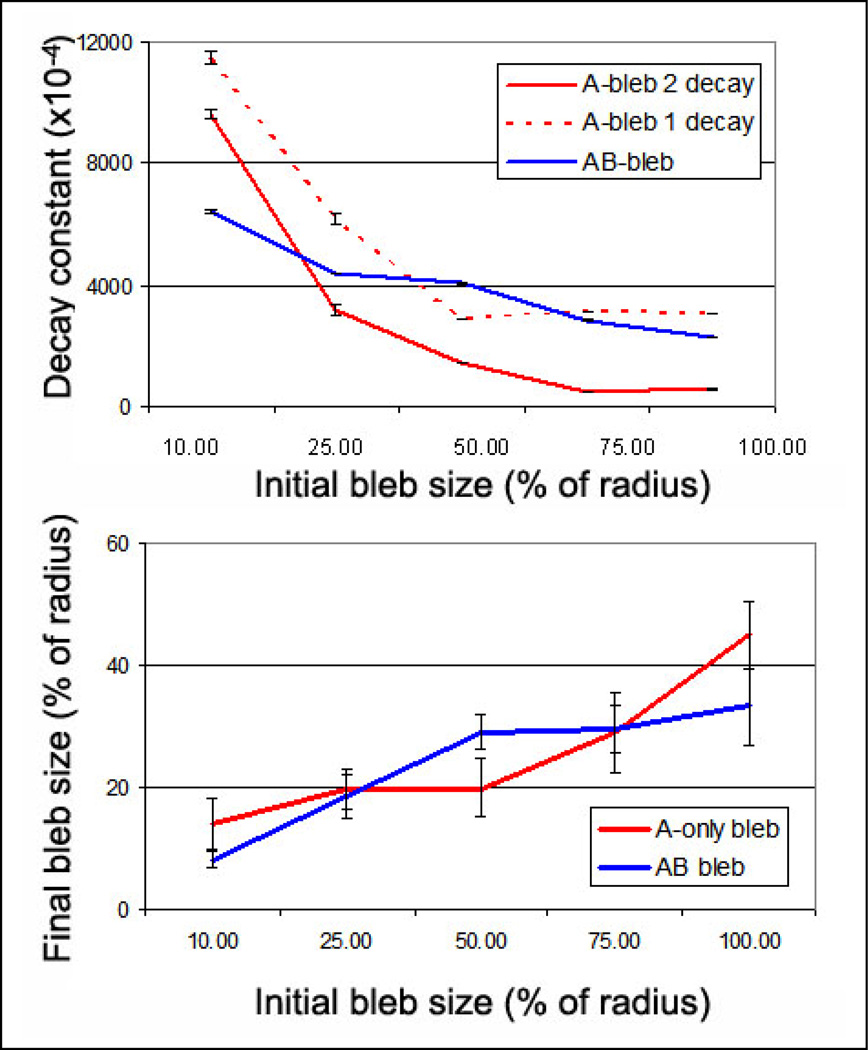
Figure 3. Quantification of bleb retraction based on initial bleb size shows different behavior for 1-component blebs versus 2-components.

(A) The decay constant, which is a single exponential fit of the retraction versus iteration from Figure 2, is plotted versus the initial bleb size and shows differential behavior in A-only and AB-lamin networks. AB network blebs show a relatively linear increase in decay constant with increasing bleb size (raw data as a solid line and approximate fit as a dashed line), suggesting that larger blebs retract faster. In contrast the A-only network bleb appeared to show fast retraction at small bleb size, and constant retraction at larger bleb size. We have plotted both the single-exponential fit and the double exponential fit (A-bleb 1 decay and A-bleb 2 decay, respectively) to show that the fitting does not affect the qualitative trend. (B) The decay constants are reflected in the final, equilibrium sizes of the blebs, wherein the “slow and steady” recession of the AB blebs produce smaller blebs at large initial blebs.

However, A-only networks appear to have different underlying phenomena which govern their retraction. As observed in the raw data, small blebs retract rather quickly to the equilibrium nucleus structure (Figure 2C,E). For small bleb size the decay constant of retraction agrees with this observation (Figure 3A, red lines, small initial bleb size). At higher initial bleb size, the decay constant plateaus (Figure 3A, red lines, larger initial bleb size). This may suggest that when the two networks (A- and B-) are significantly separated from one another the retraction of the distended network will relax more slowly since it is mechanically independent from the stable network. Given these competing effects, at very large induced bleb size, single network blebs (A-only blebs) will be larger than if both structural networks are involved (Figure 3B).

Limitations of the model

We assume that the lamina will attempt to reorganize to minimize forces on individual filaments which can extend and then will rupture. Thus, small perturbations will be dampened over the entire structure. Previous results have shown that model lamina networks deform elastically.²² Similarly, our results are based on a uniform elastic filament, which may be limited since some intermediate filament meshes can show viscoelastic behavior²⁶ possibly caused by structural transitions in the protein to allow additional extensions.²⁷ It is experimentally unclear if the energies to dissociate filaments from one another are stronger than inducing molecular transitions in the filaments.

Another limitation of the model is the interaction of filaments at each vertex. We have considered a summation of forces on each vertex, and forces then induce filament deformation or the probability of filament breakage from the vertex. We capped the number of filaments at each intersection at 5, based on observation¹⁷ and steric hindrance; interactions of 10 nm diameter filaments in 2D have spatial limitations. However, this assumption has not been thoroughly verified. Previous work has shown that multiple molecular bonds in parallel require larger forces to rupture collective bonding compared to any individual bond. Conversely, forces transmitted in series can cause lower apparent forces to rupture bonds than the stiffness would imply.²⁸ This integration of forces will be considered in future work, but given the limited number of possible bonds per vertex, the impact of this refinement on the global results is likely small.

While the number of filaments does not match the number found in a cell, we attempted to match the number density and maintained nucleus curvature significantly larger than the filament contour length to remove filament bending. Also, earlier studies have suggested that nuclear deformation, particularly under hyper-physiological stress, is limited by membrane components as much as the nucleoskeleton.²⁹

Comparison with experiment

Cells put large forces on the nucleus (Figure 4), and temporary induced blebs are expected frequently, including in interphase. The transmission of extracellular and subcellular forces to the nucleus has been observed for some time,³⁰ and likely results from the LINC complex, which physically interconnects the cytoskeletal networks with nucleoskeletal networks.^{31, 32} We hypothesized that the observed phenomena of reduced retraction of large, single network blebs may show itself in experimental conditions. We considered a condition wherein one network was altered such that it preferentially dilated one condition with loss of connector molecules.

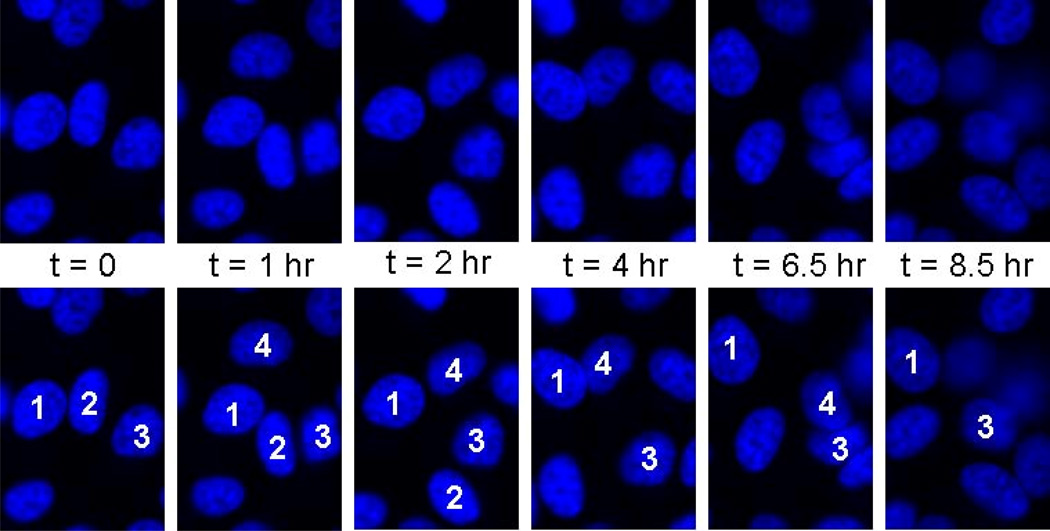
Figure 4. Live imaging of HeLa cell nuclei over many hours shows nuclear deformation.

Nuclei were labeled inside cells (using Hoechst 33342) and were imaged in live cells for up to 12 hours. Nuclei in cells within a confluent monolayer deform significantly from intracellular stress and extracellular forces over the time course of hours.

In Hutchinson Gilford progeria syndrome (HGPS), retention of a prenylation on a mutant lamin A (also called progerin) results in a hyper-association of the progerin with the nuclear membrane.^{3, 12} Ultimately, this results in numerous nuclear pathologies including dysmorphic nuclei. Previously, many studies have shown that the severe nuclear blebbing associated with HGPS involves only lamin A and progerin but not lamin B.¹²

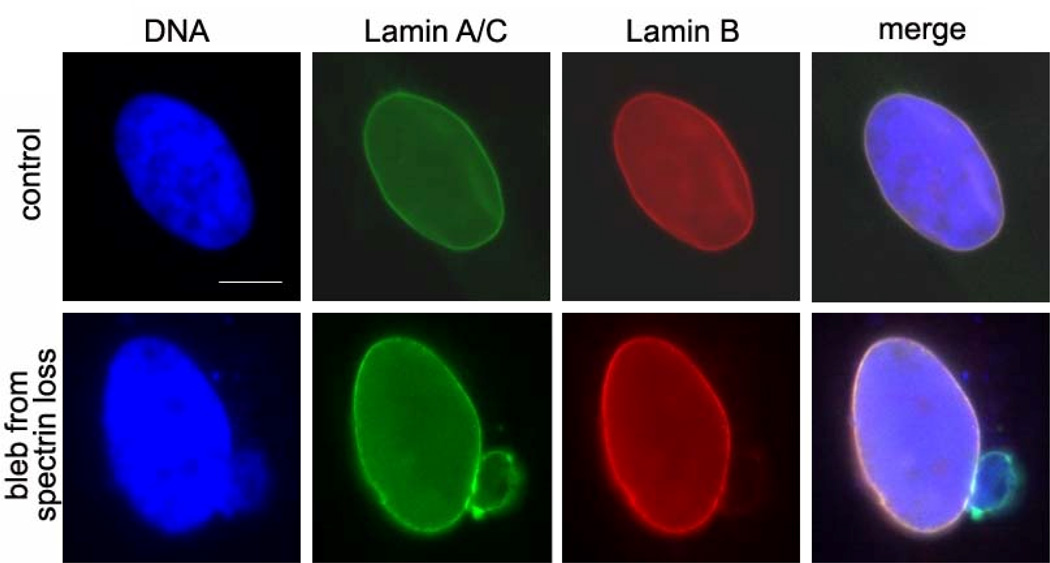
Similarly, reduction of αII-spectrin causes stable blebs of one network component (Figure 5). Recent works has shown large, repeat-domain, structural proteins in the nucleoskeleton including spectrin-like proteins and titin.^{13, 15, 16} Reduction of these connectors may promote easier distension between the two networks.

Figure 5. Experimental results show altered lamin components in nuclear blebs.

Nuclei in fixed cells are labeled with antibodies with lamin A/C (green) and lamin B (red) and DAPI for DNA (blue). Control nuclei in HeLa cells show spheroid morphology with aligning lamin filament networks. Reduction of αII-spectrin, which acts as a connector protein, produces lamin blebs which contain only one network component. Scalebar is 5 µm.

Conclusions

The mammalian nucleoskeleton is composed of independent A-type and B-type filament networks. There are numerous physiological and pathological examples wherein only one lamin network deforms into a bleb, and the other network remains with the central structure. To investigate this behavior and probe the mechanical utility of having A-type and B-type filament networks, we simulate the nucleoskeleton as an assembly of two independent but interconnected filaments networks with filament mechanical properties matched to measured values. By monitoring bleb retraction of a one-component network or two-component networks, we provide insight into large scale reorganization of nucleoskeletal structures. Retraction kinetics is different for these initial bleb conditions, and one-component blebs stabilize in the blebbed state whereas two-component blebs retract to the main nuclear body. Ultimately, we feel this model will lead to a better understanding of heterogeneous force distribution in discrete versus continuous to understand forces integrated over both small and long length scales.