Homophily and Contagion Are Generically Confounded in Observational Social Network Studies

Abstract

The authors consider processes on social networks that can potentially involve three factors: homophily, or the formation of social ties due to matching individual traits; social contagion, also known as social influence; and the causal effect of an individual’s covariates on his or her behavior or other measurable responses. The authors show that generically, all of these are confounded with each other. Distinguishing them from one another requires strong assumptions on the parametrization of the social process or on the adequacy of the covariates used (or both). In particular the authors demonstrate, with simple examples, that asymmetries in regression coefficients cannot identify causal effects and that very simple models of imitation (a form of social contagion) can produce substantial correlations between an individual’s enduring traits and his or her choices, even when there is no intrinsic affinity between them. The authors also suggest some possible constructive responses to these results.

Introduction: “If Your Friend Jumped Off a Bridge, Would You Jump too?”

We all know that people who are close to each other in a social network are similar in many ways: They share characteristics, act in similar ways, and similar events are known to befall them. Do they act similarly because they are close in the network, due to some form of influence that acts along network ties (or, as it is often suggestively put, “contagion”¹)? Or rather, are they close in the network because of these similarities, through the processes known as assortative mixing on traits, or more simply as homophily (McPherson, Smith-Lovin, and Cook 2001)? Suppose that there are two friends named Ian and Joey, and Ian’s parents ask him the classic hypothetical of social influence: “If your friend Joey jumped off a bridge, would you jump too?” Why might Ian answer “yes”?

1. because Joey’s example inspired Ian (social contagion/influence);

2. because Joey infected Ian with a parasite that suppresses fear of falling (biological contagion);

3. because Joey and Ian are friends on account of their shared fondness for jumping off bridges (manifest homophily, on the characteristic of interest);

4. because Joey and Ian became friends through a thrill-seeking club, whose membership rolls are publicly available (secondary homophily, on a different yet observed characteristic);

5. because Joey and Ian became friends through their shared fondness for roller-coasters, which was caused by their common thrill-seeking propensity, which also leads them to jump off bridges (latent homophily, on an unobserved characteristic);

6. because Joey and Ian both happen to be on the Tacoma Narrows Bridge in November 1940, and jumping is safer than staying on a bridge that is tearing itself apart (common external causation).

The distinctions between these mechanisms—and others that no doubt occur to the reader—are all ones that make causal differences. In particular, if there is any sort of contagion, then measures that specifically prevent Joey from jumping off the bridge (e.g., restraining him) will also have the effect of tending to keep Ian from doing so; this is not the case if contagion is absent. However, the crucial question is whether these distinctions make differences in the purely observational setting, since we are usually not able to conduct an experiment in which we push Joey off the bridge and see whether Ian jumps (let alone repeated trials.)

The goal of this article is to establish that these are, by and large, phenomena that are surprisingly difficult to distinguish in purely observational studies. More precisely, latent homophily and contagion are generically confounded with each other (see the second section), and any direct contagion effects cannot be nonparametrically identified from observational data.² To identify contagion effects, we need either strong parametric assumptions or strong substantive knowledge that lets us rule out latent homophily as a causal factor. It has been proposed that asymmetries in regression estimates that match asymmetries in the social network would let us establish direct social contagion; we show (see following section on “The Argument From Asymmetry”) as a corollary of our main result that this also fails.

We realize that many issues with unobservable characteristics exist in many observational study settings, not just in those that share our explicit focus on network phenomena, yet our investigations of social contagion are not driven by some animus; we are just as concerned for those investigations that ignore network structure when it is present. If contagion works along with homophily, we show that it confounds inferences for relationships between homophilous traits and outcome variables such as observed behaviors (third section). In particular, even when the true causal effect of the homophilous trait is zero, the trait can still act as a strong predictor of the outcome of interest merely through the outcome’s natural diffusion in a network (see “Simulation Model”).

We also realize that our main findings are negative and implicitly critical of much previous work. The fourth section suggests some possible constructive responses to our findings, while the fifth section concludes with some methodological reflections.

Notation, Terminology, Conventions

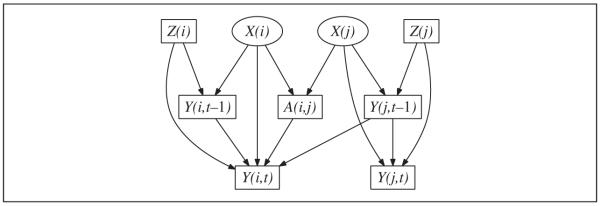
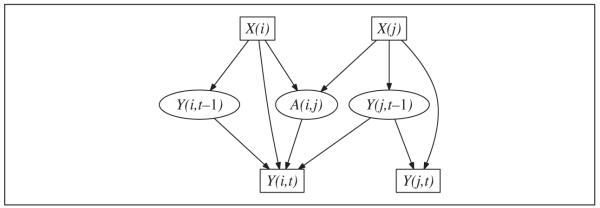
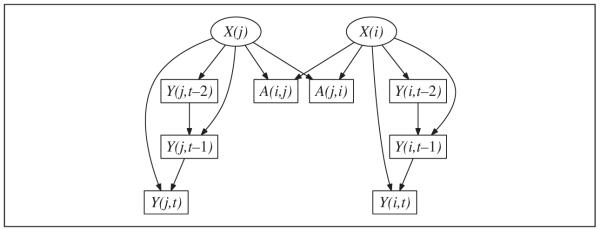
In our framework, the random variable X_i is a collection of unchanging latent traits for node i; similarly, Z_i is a collection of static observed traits. Both X and Z may be discrete, continuous, mixtures of both, and so on. The social network is represented by the binary variable A_ij, which is 1 if there is a (directed) edge from i to j—that is, i considers j to be a “friend”—and 0 otherwise. Time t advances in discrete steps of equal duration; this is inessential but avoids mathematical complications. Y_i(t) denotes a response variable for node i at time t; again, whether categorical, metric, or otherwise doesn’t matter. (We will sometimes write this as Y(i,t) or even Y_it, as typographically convenient, and likewise for other indices.) These variables are also listed in Figure 1, alongside a graphical representation of the prototypical process we are examining (Figure 2).

Figure 1.

Notational guide to terms used in this investigation

Figure 2.

Causal graph allowing for latent variables (X) to influence both manifest network ties A_ij and manifest behaviors (Y)

We conducted all simulations in R (R Development Core Team 2010). Our code is available from http://www.stat.cmu.edu/cshalizi/homophilyconfounding/.

How Homophily and Individual-Level Causation Look Like Contagion

The members of a social network often exhibit correlated behavior. When we speak of contagion or influence within networks, we imply that conditioning on all other factors, there will be a temporal relationship between the behavior of individual i at time t and any neighbors of i (potential js) at the previous time point. This is easiest to see when all other causes of adoption of a trait aside from the network itself are eliminated, such as person-to-person infectious diseases (M. S. Bartlett 1960; Ellner and Guckenheimer 2006; Newman 2002), though other examples include the spread of innovations (Rogers 2003).

More puzzling are situations such as the investigation of Christakis and Fowler (2007), where the behavior that apparently spreads through the network is “becoming obese,” as obesity is not normally thought of as an infectious condition,³ or the apparent spread of “happiness,” documented by Fowler and Christakis (2008). It is natural to ask how much of such “network autocorrelation”—the tendency of these behaviors to be correlated in individuals that are closely connected—is due to some direct influence of i’s neighbors on i’s behavior, as opposed to the effect of homophily, in which social ties form between individuals with similar antecedent characteristics, who may then behave similarly as a result.⁴

Social network scholars have long been concerned with this issue, under the label of “selection versus influence” or “homophily versus contagion” (Leenders 1995), usually with regard to manifest homophily but certainly not limited to it. To give just one example of a sophisticated recent attempt to divide the credit for network autocorrelation between homophily and contagion, consider Aral, Muchnik, and Sundararajan (2009). (The following remarks apply, with suitable changes, to many other high-quality studies, e.g., Anagnostopoulos, Kumar, and Mahdian 2008; Bakshy, Karrer, and Adamic 2009; Bramoullé, Djebbari, and Fortin 2009; Yang, Longini, and Halloran 2007.) They worked with a uniquely obtained data set with a clear outcome measure: the adoption of an online service over time, with users of an instant messaging service as the (extremely large) community of interest. To separate the effects of contagion from those of homophily, a large and rich table of covariates on an individual’s personal and network characteristics was assembled (with 46 covariates in total), and matched pairs were assembled using propensity score estimation (Rosenbaum and Rubin 1983) so that one member of the pair had, at one point, exposure to the online service through one (or more) of their network neighbors; assuming that these characteristic differences had then been teased out, the difference in the adoption rate would then reflect the total proportion of the adoption by contagion, allowing for an estimate of the proportion of association that is attributable to contagion, as opposed to the proportions caused by homophily, either secondary (in terms of the 46 observed network characteristics) or manifest (caused by two users becoming friends specifically due to their connection on the online service)—but notably, not latent homophily, which may still remain as a component of the so-called contagious proportion; this is due to the nature of propensity score matching, which can simplify the relationships between observed properties and the adoption of a “treatment” (in this case, network-localized exposure to the service); the effort may prove to be inadequate if any unobserved covariates have a part in both tie selection and in service adoption.

This brings us to our fundamental point: To attempt to assign strengths to influence or contagion as opposed to homophily presupposes that the distinction is identifiable, and there have been grounds to doubt this for some time. Manski (1993), in a well-known paper, considered the related problem of the identification of group effects: Supposing that an individual’s behavior depends on some individual-level predictors and on the mean behavior of the group to which they belong, can the degree of dependence on the group be identified? He showed that in general the answer is no, unless you make strong parametric assumptions, and perhaps not even then (since group effects can fail to be identified even in linear models). Indeed, this has been shown to cause difficulties in other social situations where this sort of phantom influence can be observed: Among others, Calvó-Armengol and Jackson (2009) note that estimating the apparent effect of parental influence on a child’s educational outcomes is confounded by the actions of the larger community. (See Blume et al. 2010 for a recent review of the group-effects literature.) However, this does not quite answer our questions, since Manski (1993) considered influence from the group average, rather than from individual members of the network neighborhood, and one could hope this would provide enough extra information for identification.

We now show that in fact, contagion effects are nonparametrically un-identifiable in the presence of latent homophily—that there is just no way to separate selection from influence observationally. Our proof involves some simple manipulations of graphical causal models; we refer the reader to standard references (Morgan and Winship 2007; Pearl 2009a, 2009b; Spirtes, Glymour, and Scheines 2001) for the necessary background.

Contagion Effects Are Nonparametrically Unidentifiable

We first assume that there is latent homophily present in the system: The network tie A_ij is influenced by the unobserved traits of each individual, X_i and X_j. We assume that the “past” observable outcome Y_i(t − 1) has a direct influence on the same outcome measured in the present, Y_i(t).⁵ We also assume that X_i directly influences Y_i(t) for all t, though possibly not to the same magnitude or mechanism at each time t.⁶ Finally, we assume that another individual’s prior outcome Y_j(t − 1) can directly influence Y_i(t) only if A_ij=1—that is, there must be an edge present for this direct influence to occur. We are indifferent as to whether the observable covariates Z_i have a direct influence on Y_i(·), or whether it is correlated with the latent covariates X_i. The upshot of these assumptions is the causal graph in Figure 2, examination of which should make it unsurprising that contagion, the direct influence of Y_j(t − 1) on Y_i(t), is confounded with latent homophily:

• Y_j(t − 1) is informative about X_j;

• X_j is informative about X_i when i and j are linked (A_ij = 1); and

• X_i is informative about Y_i(t).

Thus Y_i(t) depends statistically on Y_j(t − 1), whether or not there is a direct causal effect of contagion present.

While this argument would appear to be loosely assembled, it can be tightened up using the familiar rules for manipulating graphical causal models (Pearl 2009b; Spirtes et al. 2001). X_i d-separates Y_i(t) from A_ij. Since X_i is latent and unobserved, Y_i(t) ← X_i → A_ij is a confounding path from Y_i(t) to A_ij. Likewise Y_j(t − 1) ← X_j → A_ij is a confounding path from Y_j(t − 1) to A_ij. Thus, Y_i(t) and Y_j(t − 1) are d-connected when conditioning on all the observed (boxed) variables in Figure 2. Hence the direct effect of Y_j(t − 1) on Y_i(t) is not identifiable (Pearl 2009b:93-4).

This argument is not affected by adding conditioning on Y_i(t − 1) or Y_j(t), as that does not remove the confounding paths. Nor does adding conditioning on Z_i,Z_j remove the confounding. Nor is the situation helped by allowing A_ij, or indeed X, to vary over time, as is readily verified by drawing the appropriate graphs. Finally, adding a third individual to the graph would not help: Even if they were, say, assumed to be linked to i but not j or vice versa, Y_i(t) ← X_i → A_ij and Y_j(t − 1) ← X_j → A_ij would remain confounding paths.

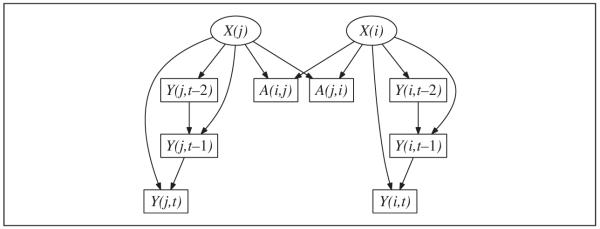
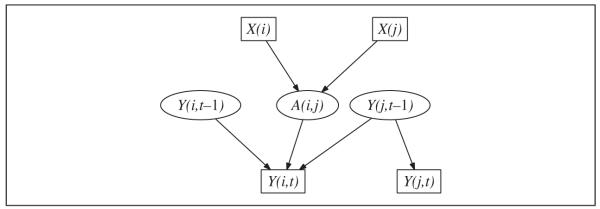
How then might we get identifiability? It may be that very stringent parametric assumptions would suffice, though we have not been able to come up with any that would suffice.⁷ Otherwise, we must keep X from being latent, or, more precisely, either the components of X that influence Y must be made observable (Figure 3a), or those parts of X that influence the social tie formation A (Figure 3b). In either case the confounding arcs go away, and the direct effect of Y_j(t − 1) on Y_i(t) becomes identifiable.⁸ It is noteworthy that the most successful attempts at explicit modeling that handle both homophily and influence, as found in the work of Leenders (2005) and Steglich, Snijders, and Pearson (2004), involve, all at once, strong parametric (exponential-family) assumptions, plus the assumption that observable covariates carry all of the dependence from X to Y and A; the latter is also implicitly assumed by the matching methods of Aral et al. (2009).

Figure 3.

Modifications of the causal graph shown in Figure 2, in which observable covariates (Z) convey enough information about X that contagion effects are unconfounded with latent homophily

Note: In panel a (left), Z carries all of the causal effect from X to the observable outcome Y; in panel b (right), Z carries all of the effect from X to the social network tie A.

Whether we face the unidentifiable situation of Figure 2 or the identifiable case of Figure 3 currently depends upon subject-matter knowledge rather than statistical techniques. It may be possible to adapt algorithms, such as those in Spirtes et al. (2001), to detect the presence of influential latent variables. Some new methodological work would be required, however, since all such algorithms known to us rely strongly on having a supply of independent cases, and social networks are of interest precisely because individuals, and even dyads, are not independent.

The Argument From Asymmetry

A clever argument for the presence of direct influence was introduced by Christakis and Fowler (2007). By focusing on unreciprocated directed edges—pairs (i,j) where A_ij = 1 but A_ji = 0, so that j’s prior outcome can be said to influence i’s present, but not i’s prior outcome on j’s present—one can consider the distributions of the outcomes conditional on their partner’s previous outcome, Y_i(t)|Y_j(t − 1) and Y_j(t)|Y_i(t − 1) (though other observable covariates [Z_i,Z_j] may also be conditioned on). An asymmetry here, revealed by the difference in the corresponding regression coefficients, might then be due to some influence being transmitted along the asymmetric edge, and not due to external common causes (e.g., a new fast food restaurant) or other behaviors attributable to latent characteristics.

This idea has considerable plausibility and has been picked up by a number of other authors (Anagnostopoulos et al. 2008; Bramoullé et al. 2009), who have shown that it works as a test for direct influence in some models. However, we show that the argument can break down if two conditions are met: first, the influencers (the j in the pair) differ systematically in their values of X from the influenced (the i), and second, different neighborhoods of X have different local (linear) relationships to Y. As previously mentioned, the most successful claims of simultaneous accounting of these phenomena require strong parametric assumptions, and our demonstration shows that even assumptions of linearity may be too strong for this sort of data.

To illustrate this claim, we present a toy model of a network with latent homophily on an X variable that controls an observable time series Y at multiple points, but with no direct influence between values of Y for different nodes. We present this as a multistep time series to approximate the scenario of Christakis and Fowler (2007), so that we can add the two most recent time steps of the alter’s expression into the regression.⁹ We also note that there is no “coupled evolution” of two nodes’ outcomes due to an exogenous common cause, one of the stated purposes of the asymmetry test. Despite the lack of direct interaction, it is possible to predict Y_i at time t from the value of Y at its neighbors for times t – 1 and t – 2, and these relations are asymmetric across unreciprocated edges.

First we present the formation of the network, which contains n individuals (nodes), and each node i has a scalar latent attribute X_i ~ u(0,1), which are generated independently. We generate an underlying undirected network (a potential friendship pool) where such an edge forms between i and j with probability equal to logit⁻¹(− 3|X_i – X_j|), so that edges are more likely to form between individuals with similar values of X. Each individual i then nominates their “declared” friendships from these neighbors, naming j with probability proportional to ∝ logit⁻¹(–|X_j – 0.5|)—individuals, whatever their own value of X, prefer to nominate acquaintances closer to the median value of that trait.¹⁰ For this demonstration, as in the data sets used in Christakis and Fowler (2007) and Fowler and Christakis (2008), each individual i declares one friend, though the results hold for greater numbers of nominations. This produces the sociomatrix/adjacency matrix A, where A_ij = 1 signifies that individual i has nominated j as a “friend.”

Second, we establish the time trends of the observable outcomes (Y_i(t = 0),Y_i(t = 1)):

• At time t = 0, we set $Y_i\left(0\right)={(X_i-0.5)}^3+\mathcal{N}(0,{\left(0.02\right)}^2)$, a nonlinear assignment of outcome attributes.

• For time t = 1, we set $Y_i\left(1\right)=Y_i\left(0\right)+0.4X_i+\mathcal{N}(0,{\left(0.02\right)}^2)$, so that the trend is greater for those individuals with higher values of the latent attribute.

• For time t = 2, we set $Y_i\left(2\right)=Y_i\left(1\right)+0.4X_i+\mathcal{N}(0,{\left(0.02\right)}^2)$, repeating the trend.

Figure 2 is the graphical model for the actual causal structure of our simulation at three time points.

We simulate a network of fixed size (n= 400) from this model and estimated the linear model

$$Y_i\left(2\right)=\alpha +{\beta }_1{Y}_i\left(1\right)+{\beta }_2\sum _j{A}_{ij}{Y}_j\left(1\right)+{\beta }_3\sum _j{A}_{ij}{Y}_j\left(1\right)+{\beta }_4\sum _j{A}_{ij}{Y}_j\left(0\right)+{\beta }_5\sum _j{A}_{ij}{Y}_j\left(0\right)+{∊}_i,$$

so that α represents the intercept term and β₁ represents the autocorrelation; β₂ is the effect of the nominee’s status at time t=1 on the nominator, and β₃ is the converse, the network effect if i was nominated by j, at time t=1; β₄ and β₅ are those same coefficients for the outcome at time t=0. This was replicated 5,000 times, with the latent variables, time series,=and network regenerated in each replication.

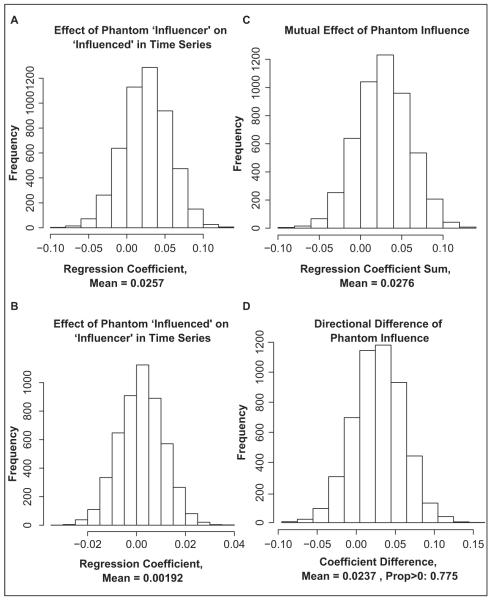
Figure 5 shows the results of these simulations. Figure 5a shows the magnitude of β₂, the coefficient of network influence; in 4,010 of these 5,000 trials is the estimate less than zero despite the lack of a direct connection, in line with the empirical results of Cohen-Cole and Fletcher (2008). This is also the case for Figure 5b, showing the apparent coefficient of a “reverse” network effect β₃, which is smaller in magnitude. Figure 5c shows the sum of the two effects; this demonstrates that the effect of a mutual tie, where A_ijA_ji=1, is determined by the sum of the one-way effects and is greater than the effect of a “named” tie, A_ij = 1, which is greater than the effect of a “naming” tie, A_ji=1. This is the result of the type that was cited in Christakis and Fowler (2007) and Fowler and Christakis (2008) but produced without any network interaction.¹¹

Figure 5.

Results for a toy model where a latent variable causes spurious timedependent network effects

Note: Clockwise from the top left: (a) the estimate for β₂, the effect in the expected direction of influence; (b) the estimate for β₂, the effect in the opposite direction of influence (from the namer to the named); (c) the sum of the estimated effects, indicating that the effect for a mutual tie (in which each respondent names the other) is greater than either the expected or opposite unreciprocated tie effect; (d) the normalized difference between directional effects is clearly greater than zero on balance (in roughly 77 percent of simulations), suggesting that the asymmetry in coefficient estimates can be produced without contagion and falsely detected by t tests on the difference.

Figure 5d shows the difference between the “sender” and “receiver” coefficients, which would be approximately Gaussian (for a t-distribution with 400 degrees of freedom) and centered at zero; if this were the case, a t test could be used to claim statistical significance in the difference between the two effects. It is evident from the histogram that this null distribution is not centered at zero, and about 77 percent of the sample values are positive, even though there is really no effect. Thus, latent homophilous variables can produce a substantial apparent contagion effect, including the asymmetry expected of actual contagion.

The parameter values in this model were not chosen to maximize either the apparent contagion effect or its asymmetry, merely to demonstrate their presence. As well, we note that controlling for additional past values of the property for each node reduces the imbalance in magnitude, while it still remains statistically significant; as we show in the section “Bounds,” this is not the end of the story if we cannot find a bound for this asymmetry.

In addition, it may seem unlikely that these conditions may exist on unobserved variables in the system, but this still places the burden on the investigator to pursue as many possible latent factors as may be present—an extremely onerous task in a multidecade observational study—or to work exclusively with experimental data, such as in the recent work of Fowler and Christakis (2010).

How Contagion and Homophily Look Like Causation at the Individual Level

We would be remiss if we gave the impression that it is only investigators who actually take network structure into account who have problems. In this section, we show that a very common kind of use of survey data, namely, that relating individuals’ choices (cultural, political, economic, etc.) to their long-term stable traits is also confounded in the presence of homophily and contagion (see Figure 6). Continuing the spirit of “Argument From Asymmetry,” we present another toy model in which regressions of choices on traits produce significant non-zero coefficients that are solely due to this confounding.¹²

Figure 6.

Typical situation in surveys linking cultural choices to social traits when homophily and influence exist

It should be emphasized that there is a long tradition within social science of distinguishing long-term, hard-to-change aspects of social organization and individuals’ place in it from more short-term, malleable aspects that show up in behavior and choices. As Ernest Gellner (1973) put it, “Social structure is who you can marry, culture is what you wear at the wedding.” The long-standing theoretical presumption, common to all the classical sociologists (even, in his own way, to Max Weber), and going back through them to Montesquieu if not beyond (Aron 1989), is that social structure explains culture, or that the latter reflects the former; in many versions, culture is an adaptation to social structure. This intuition is alive and well through the social sciences, the humanities, and among lay people. Many of these accounts have considerable plausibility, though since they conflict with each other they cannot all be true. However, aside from casual empiricism, the evidence for them consists largely of correlations between cultural choices and social positions, demonstrations that the superstructure can be predicted from the base. Famously, for instance, Bourdieu (1984) attempts to do this for survey data.

We do not wish to assert that social position is never a cause of cultural choices; like everyone else, we think that it often is. The issue, rather, is the evidence for such theories, and in particular for the magnitude of such effects.

Simulation Model

We work with what is, frankly, a toy model of contagion (though, see footnote 13). There are n individuals connected in an undirected social network. Each individual i has an observed trait X_i, which is an unchanging variable; in our examples, this will be binary. The network is homophilous on this trait, so that individuals with the same value of X are more likely to be connected. Individuals also have a time-varying choice variable Y_i(t), which again we will take to be binary. The initial choices, Y_i(0), are set by flipping a fair coin (i.e., an unbiased Bernoulli process), and are therefore independent of the traits X_i.

Choices evolve as follows: At each time t, we pick an individual I_t, uniformly at random from i ∈ {1,…,n}, independently of all prior events. This individual then picks a neighbor, again uniformly at random, J_t ∈ {j : A_Itj =1}, and either, with very high probability, copies their choice, so that Y_It(t) = Y_Jt (t − 1), or, with very low probability, assumes the opposite choice, for Y_It(t) = 1 – Y_Jt(t − 1); all other individuals retain their previous choices. This process repeats for each time step. Figure 7 shows the causal structure.

Figure 7.

Graphical model showing the causal structure of the model simulated in “Simulation Model” section (cf. Figure 6)

Note: Notice that here, the persistent traits X have no direct causal influence on the choices Y. As we show, however, diffusion of choices along homophilous ties creates states where Y can be predicted from X.

This random copying model is, of course, a drastic oversimplification of actual processes of transmission and influence, which have been extensively studied in social psychology and allied fields since the 1920s (F. C. Bartlett 1932; Friedkin 1998; Huckfeldt, Johnson, and Sprague 2004; Sperber 1996).¹³ However, not only is it adequate to demonstrate the existence of the phenomenon we are concerned with, its very abstraction helps indicate just how robust the problem is.

Probabilistically, the vector Y(t) is a Markov chain, specifically, a variant of the “voter model” of statistical mechanics on a graph (Liggett 1985; Sood and Redner 2005); the minor addition of low-frequency noise (doing the opposite of the selected neighbor) keeps the homogeneous configurations (where Y_i is constant over i) from being absorbing states, but has little influence on the medium-run behavior we are concerned with.

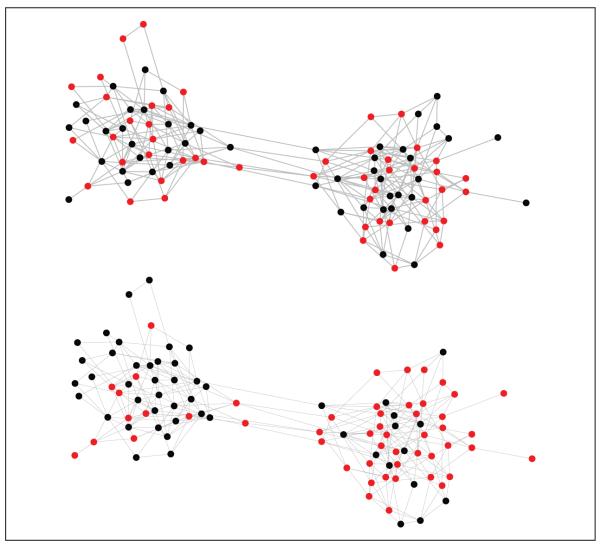
Figure 8 shows a typical evolution of this model. In the top image at the initial state of the system, there are two clusters based on social traits X, but the individual cultural choices (colors represent values of Y) are independent of these traits. The bottom image shows the same network and configurationafter 3,000 updates. Now, even by eye, it is clear that one of the choices has become associated with one of the social types.

Figure 8.

An illustration of the diffusion process on a network with homophilous ties; members of the left and right clusters have attribute values of 0 and 1, respectively

Note: Initially (top), there is very little detectable similarity between choices within each cluster; however, after a few hundred time steps (bottom), there is a clear association between trait and cluster caused entirely by the diffusion along homophilous ties.

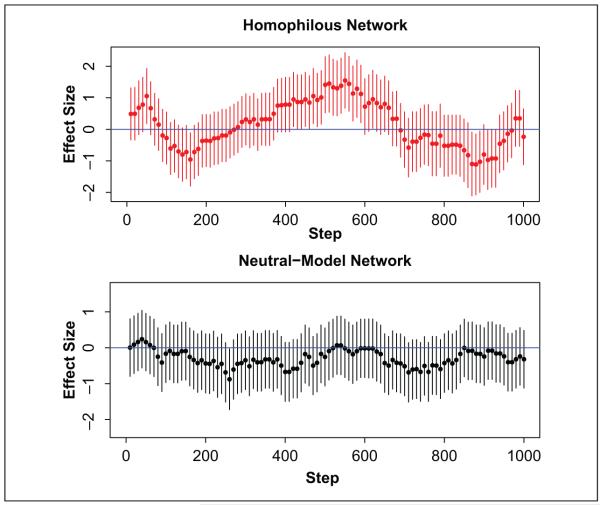
This can be confirmed more quantitatively by doing a logistic regression of choice on trait (Figure 9) at several points during the diffusion process. In this particular example, there are significant deviations in each direction. First, the association between trait 1 and color 1 is positive and significant, and remains so for several dozen iterations; then the diffusion reverses the association, which then becomes negative and significant. For comparison, a network with the same average degree but no homophilous tie formation is shown to undergo the same diffusion process but with no corresponding association between choice and trait.¹⁴

Figure 9.

Coefficient estimates for logistic regressions of choice on trait as functions of time.

Note: Error bars represent 95 percent confidence intervals on each run, independent of all others. Left: the evolution in a homophilous network; in this run of the simulation, the coefficient first becomes negative and statistically significant, then becomes positive and significant, purely due to diffusion along homophilous ties, before returning to a state of negative significance. Right: a corresponding series of estimates in a network where ties form independently of traits; deviations from neutrality are much smaller.

Intuitively, the copying process tends to make neighbors more similar to each other; Ian’s choice can be predicted from Joey’s choice. On regular lattices, this mechanism causes the voter model to self-organize into spatially homogeneous domains, with slowly shifting boundaries between them (Cox and Griffeath 1986). A similar process is at work here, only, owing to the assortative nature of the graph, neighbors tend to be of the same social type. Hence social type is an indirect cue to network neighborhood, and accordingly predicts choices.

To summarize, this “neutral” process of diffusion, together with homophily, is sufficient to create what looks like a causal connection between an individual’s social traits and cultural choice. This is because individuals’ choices are not independent conditional on their traits, as is generally assumed in, for example, survey research; diffusion creates the observed dependence.¹⁵

This demonstration shows that it is difficult to argue that, for example, being of type 0 is an indirect cause of picking the color black as opposed to red, since even within a single run of the model the association can be seen to reverse. Put another way, differences in social types are at most related to differences in choices, not to the actual content of those choices.

Constructive Responses

To sum up the argument so far, we have shown that latent homophily together with causal effects from the homophilous trait cannot be readily distinguished, observationally, from contagion or influence, and that this remains true even if there is asymmetry between “senders” and “receivers” in the network. We have also shown that the combination of homophily and contagion can imitate a causal effect of the homophilous trait. It requires little extra to see that contagion, plus a causal influence of the contagious trait, yields a network that contains the appearance of homophily. Thus, given any two of homophily, contagion, and individual-level causation, the third member of the triad seems to follow.

We realize that these results appear to wreck the hopes on which many observational studies of social networks have rested. It would be nice to think that something, nonetheless, could be salvaged from the ruins. The “easy” solution is to use expert knowledge of the system to identify all causally relevant variables, measure a sufficient set of them, and adjust for them appropriately (Morgan and Winship 2007; Pearl 2000; Spirtes et al. 2001). Since this is clearly a Utopian proposal, we sketch three constructive responses that may be possible when dealing with network data where the causal structure is imperfectly understood or incompletely measured. These are to randomize over the network, place bounds on unidentifiable effects, and use the division of the network into communities as a proxy for latent homophily.

Identifying Contagion From Non-Neighbors

The essential obstacle to identifying contagion in the setting of Figure 2 is that the presence or absence of a social tie A_ij between individuals i and j provides information on the latent variable X_i, whether we implicity include the tie by predicting Y_i(t) from the past values of neighbors Y_j(t − 1) or we explicitly add A_ij to the prediction model. In the language of graphical models, conditioning or selecting on A_ij “activates the collider” at that variable. This suggests that we would do better, in some circumstances, to construct a useful inference by deliberately not conditioning on the social network, thereby keeping the collider quiescent.¹⁶ We outline this method to demonstrate the possibility, rather than to advocate a new prescription for solving the problem.

We can conduct the following procedure over many repeated trials:

1. Divide the nodes into two groups, by assigning each node to one of two bins with equal probability; let these groups be labeled as J₁ and J₂.

2. Let Y_J1(t) be the vector-valued time series obtained by collecting each of the Y_i(t) for i ∈ J₁ into one object, and similarly for Y_J2(t).

3. Use some available mechanism to predict the time series for the first bin, Y_J1(t). from its lagged counterpart, Y_J2(t − 1), while controlling for the previous time point within the first half, Y_J1(t − 1).

By repeating this procedure, then averaging over all iterations (producing new partitions each time), there will be a non-zero predictive ability if and only if there is actual contagion or influence. We can see why one must average over multiple divisions as follows. Clearly, influence is possible between the two halves only if there are social ties linking them. However, there will generally exist some way of picking J₁ and J₂ so that there are no linking ties, and in the presence of homophily, those will tend to be divisions of the network into parts that are unusually dissimilar in their homophilous traits. If we restricted ourself to values of J₁ and J₂, which did have linking ties, we would once again be selecting on the homophilous trait and activating colliders.

This may not be a practical method, as the statistical power of this test may be very low—the data have very high dimension, and the method deliberately selects random predictors—but it will be non-zero.

Even the random-halves test will fail, however, if we add a direct causal effect of X_j on Y_i(t) (or one modulated by A_ij). We omitted such a link in Figure 2 and subsequently, on the assumption that causal effects between individuals must pass through observed behavior Y, but this is a nontrivial substantive hypothesis requiring rigorous justification.

Bounds

In the second and third sections, we saw that certain causal effects were not identifiable; that different causal processes could produce identical patterns of observed associations. As Manski (2007) emphasizes, even when parameters (e.g., the causal effect of Y_j(t − 1) on Y_i(t)) are observationally unidentifiable, the distribution of observations may suffice to bound the parameters. (With sampled data, the empirical distribution of observations generally provides estimators of those bounds.) Sometimes these bounds can be quite useful, even in the general nonparametric case.

We thus propose as a topic for future research placing bounds on the causal effect of Y_j(t − 1) on Y_i(t) in terms of observable associations, assuming the structure of Figure 2. If the bound on this effect excluded zero, that would show the observed association could not be due solely to homophily, but that some contagion must also be present.

If we keep the causal structure of Figure 5, assuming that the Y and X variables are all jointly Gaussian and all relations between continuous variables are linear¹⁷ would let us employ the usual rules for linear path diagrams (Spirtes et al. 2001). The standardized linear-model coefficient for regressing senders on receivers, namely, Y_i(t) on Y_j(t − 1), controlling for all other observables, turns out to be

$$\rho [X_j,Y_j(t-1)]\rho [X_i,X_j\mid A_{ij}=1]\rho [X_i,Y_i\left(t\right)]$$

where ρ[K,L] is the path coefficient between K and L (and ρ[K,L|M] is the path coefficient given the required condition M, rather than an observable that would be controlled for). Clearly, any standardized regression coefficient can be obtained here by adjusting path coefficients for unobserved variables X. Thus, a bound on the true causal effect cannot be based on the linear regression coefficient alone, but we hope it may still be possible to find a bound that uses more information about the pattern of associations.

It would also be valuable—and perhaps more tractable—to place limits on the magnitude of the association that could be generated solely by homophily. Parallel remarks apply to bounding the causal effect of X_i on Y_i(t) assuming the structure of Figure 6; we suspect, though merely on intuition, that this will be harder than bounding contagion effects.

Along these lines, it would be particularly interesting to bound the degree of asymmetry in regressions that can be generated in the absence of direct causal influence (as in “The Argument From Asymmetry”). Even though asymmetry as such can be produced in the absence of influence or contagion, it could be that by some standard, really big asymmetries can only plausibly be explained by influence, so that detecting such asymmetries would be evidence for influence. More exactly, if one can establish that in the absence of direct influence the degree of asymmetry can be at most α₀, and one finds an actual asymmetry of $\widehat{\alpha }>{\alpha }_0$, then the hypothesis of influence has passed a more or less severe test (Mayo 1996), the severity depending on the ease with which sampling fluctuations and the like can push the estimated asymmetry $\widehat{\alpha }$ over the threshold when the “true” asymmetry (in the population or ensemble) was below it.

Network Clustering

Since the problems we have identified stem from latent heterogeneity of a causally important trait, the solution would seem to be to identify, and then control for, the latent trait. “Homophily” means simply that individuals tend to choose neighbors that resemble them; this tendency will be especially pronounced if pairs of neighbors also have other neighbors in common, since these pairings will also be driven by homophily. This suggests that homophily, latent or manifest, will tend to produce a network built primarily of homogeneous clusters, also called, in this context, “communities” or “modules.” Inversely, such clusters will tend to consist of nodes with the same value of the homophilous trait.

The topic of community discovery—essentially, dividing graphs into homogeneous, densely interconnected clusters of nodes, with minimal connection between clusters—has been thoroughly explored in the recent literature (explicitly in Bickel and Chen 2009; Fortunato 2010; Girvan and Newman 2002; Newman and Girvan 2003; Porter, Onnela, and Mucha 2009; implicitly in much smaller clusters in Elwert and Christakis 2008). A natural idea would be to first establish the existence of these clusters, to note the memberships of each individual in the chosen model, call this estimate Ĉ_i, and to control for Ĉ_i when looking for evidence of contagion or influence.

By the arguments we have presented so far, such control-by-clustering will generally be unable to eliminate the confounding.¹⁸ However, in conjunction with the bounds approach mentioned earlier, conditioning on estimated community memberships might still noticeably reduce the confounding. On the other hand, misspecification of the block structure may make the problem worse—consider the cases where the generating mechanism may be a mixed-membership block model (Airoldi et al. 2008) or “role” model (Reichardt and White 2007) but communities are “discovered” assuming a simple modular network structure. Estimating the damage due to misspecification in this case is a goal of future research.

Conclusion: Toward Responsible Just-So Storytelling

We have seen that when there is latent homophily, contagion effects are unidentifiable, and even the presence of contagion cannot be distinguished observationally from a causal effect of the homophilous trait. Conversely, when contagion and homophily both exist, choices can be predicted from the homophilous trait, and so the effects of such traits on socially influenced variables are again observationally unidentifiable. These results raise barriers to many inferences social scientists would like to make. The barriers can be breached by assuming enough about the causal architecture of the process in question, though then the inferences stand or fall with those architectural assumptions; perhaps the bounding approach can squeeze an opening through them as well. Beyond these technical qualifications, what is the larger moral for social science?

Accounts of social contagion are fundamentally causal accounts, pointing to one of a number of mechanisms—imitation, persuasion, and so on—by which a belief or behavior spreads through a population. Similarity among individuals is explained by their belonging to common networks; differences by differences in their networks. This parallels the other great project of social science, which is to explain differences in cultural choices by location within the social structure, or, at a broader scale, by differences between social structures (Boudon 1989, Berger 1995; Lieberson 2000). The accounts that have connected social structure to behavior have typically been adaptationist or functionalist: The content or meaning of cultural choices serves the choosers’ interests, or their classes’ interests, or (far more nebulously) the interests of the system, or reflects their experiences in life, or rationalizes their positions in life, and so forth. At the very least, these are causal accounts: If social structure or social positions were different, the content of the choices would be different. Far more commonly, they really are adaptationist accounts: Choices fit to the objective circumstances. They accordingly follow the familiar pattern of the “Just-So” story (Kipling 1912/1974), with all their familiar problems. It would be intellectually irresponsible to accept such accounts, with their strong causal claims, without careful checking; but also irresponsible to simply dismiss them out of hand.

The example of biology suggests that a powerful way of doing such tests is to use “neutral models” (Gillespie 1998; Harvey and Pagel 1991), which biologists use to test claims that features of organisms are evolutionary adaptations; we note the similarity with the “null hypothesis” in general statistical hypothesis testing. A neutral evolutionary model should include all the relevant features of the evolutionary process except adaptive forces (e.g., natural or sexual selection). The expected behavior of the system is then calculated under the neutral model (i.e., the distribution of expected outcomes); if the data depart significantly from the predictions of the neutral model, this is taken as evidence of adaptation. Said another way, the neutral model as a whole is used as the null hypothesis, not just a generic regression model with some coefficients set to zero. For instance, a model might include mutation and genetic recombination but assume all organisms are equally likely to be parents of the next generation; all have equal fitness. Gene frequencies will change in such a model because of random fluctuations; some organisms become parents and have differing numbers of offspring. Indeed, we expect some genetic variants to go to fixation (to become universal) in the population and others to disappear entirely through the effects of repeated sampling.¹⁹ We are not aware of any studies in the sociology of culture or related fields employing formal neutral models; however, something similar to this is implicit in the arguments of Lieberson (2000)²⁰ and some other strands of recent work on “endogenous explanations of culture” (Kaufman 2004).

The point is not that accounts of causation and adaptation in social phenomena must be rejected; it is that they must be subjected to critical scrutiny, and that comparison to neutral models is a particularly useful form of critique. Our toy models produce the kind of phenomena that theories of contagion, or of adaptation and reflection, set out to explain. (It is only too easy to imagine crafting a historical narrative for Figure 8, explaining the deep forces that impelled the east to become red.) The best way forward for advocates of those theories may in fact be to craft better, more compelling neutral models than ours and show that even these cannot account for the data. Thus, they will support their theories not only by plausible just-so stories, but by compelling evidence.

Figure 4.

Graphical causal model for our simulation study in “The Argument From Asymmetry”

Note: Here, unlike Figure 2, there are no arrows from (Y_j(t – 2), Y_j(t − 1)) to Y_i(t)—the former outcomes for the “alter” are not, in reality, a cause of the latter for the “ego,” and the relationships of the Y_j and Y_i time series are symmetrical. As we show in the text, however, not only is Y_i(t) predictable from Y_j(t − 1), but the relationship is asymmetric when social network ties are unreciprocated, namely, A_ij = 1 but A_ji = 0.

Bios

Cosma Rohilla Shalizi is assistant professor of statistics, Carnegie Mellon University, and external faculty at the Santa Fe Institute.

Andrew C. Thomas is visiting assistant professor of statistics, Carnegie Mellon University.