Perceptual learning as improved probabilistic inference in early sensory areas

Abstract

Extensive training on simple tasks like fine orientation discrimination results in large improvements in performance, a form of learning known as perceptual learning. Previous neural models have argued that perceptual learning is the result of sharpening and amplification of tuning curves in early visual areas. However, these models are at odds with the conclusions of psychophysical experiments manipulating external noise, which argue for improved decision making, presumably in later visual areas. Here, we explore the possibility that perceptual learning for fine orientation discrimination is due to improved probabilistic inference in early visual areas. We show that this mechanism captures both the changes in response properties observed in early visual areas and the changes in performance observed in psychophysical experiments. We also suggest that sharpening and amplification of tuning curves may play only a minor role in improving performance, in comparison to the role played by the reshaping of inter-neuronal correlations.

Introduction

Extensive training on simple behavioral tasks like Vernier acuity or orientation discrimination leads to a gradual improvement in performance over several sessions, a form of learning known as perceptual learning ^1-3. This form of learning has been observed in a wide range of tasks and across many modalities, thereby suggesting that it represents a general mechanism by which humans and animals improve their performance in response to task demands ^4-9. While the behavioral consequences of such learning are well understood, there is debate in the literature as to the nature of the neural changes that underlie the observed behavioral changes.

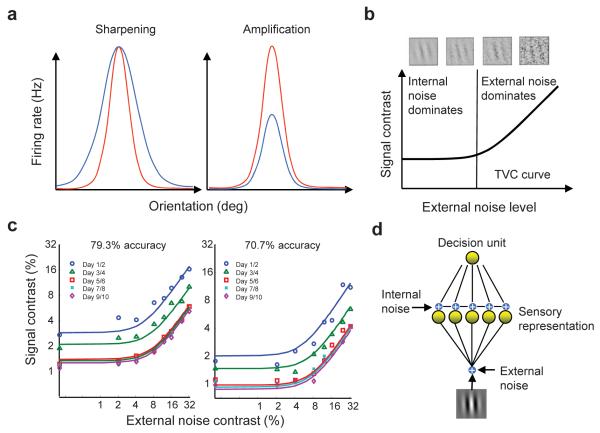
Perceptual learning is typically very specific both in terms of the task itself and in terms of the location of the stimulus ^{1, 10-12} (but see ^{13, 14}). For instance, in the visual domain, training on Vernier acuity does not transfer to other tasks like orientation discrimination or to the same Vernier shown at a different retinal location ². This specificity, particularly the specificity to retinal location, suggests that this form of learning engages early visual areas where retinotopy is reasonably well preserved ¹⁵. This is indeed consistent with single cell recordings which have revealed modifications in the response properties of cells in early and mid level visual areas like V1 and V4 after extensive training on orientation discrimination ^{8, 9, 16}. Two main types of changes have been reported: a sharpening and an amplification of tuning curves to orientation (Fig. 1a). Theoretical studies have argued that such changes could account for the observed behavioral improvement as both types of changes increase the slope of the tuning curves, thereby increasing the ability of single neurons to discriminate orientation ^{17, 18}. Moreover, at least one study has also proposed that perceptual learning leads to reduced internal noise through a lowering of the Fano factor of visual cells ¹⁶, a change that could also potentially explain the behavioral improvement.

Figure1.

Neural and behavioral correlates of perceptual learning. (a) An illustration of the two types of changes observed in the tuning curves of trained orientation-selective neurons. Each panel shows an illustration of a tuning curve before (blue) and after (red) learning. The x-axis represents orientation (in degrees) and the y-axis represents firing rate (in Hz). (b) The characteristic shape of a threshold-versus-contrast, or TVC curve, plotted on a log-log scale, showing the two major regimes. The x-axis represents the level of external noise added to the stimulus (example stimuli are shown in the top panel). The y-axis represents the signal contrast needed to elicit the specific level of performance. (c) Observed changes in TVC curves as a result of perceptual learning – the entire curve shifts downwards ²⁷. The axes are the same as in b. This finding of uniform shift is maintained at any level of performance (TVC curves for two levels of performance are shown here). The ratio of the TVC curves at the two levels of performance also stays constant across external noise levels ²⁷. (d) Standard model of perceptual learning. The image is preprocessed by a set of filters corrupted by noise. The noisy output of these filters is then fed into a single decision unit trained to optimize discrimination between two orientations.

Although these studies offer a potential neural mechanism for perceptual learning in a fine discrimination task, there are several open issues, and serious problems, with this perspective. First, the claim that tuning curve sharpening and amplification, or noise reduction, accounts for the observed behavioral improvement rests on the assumption that neural variability is independent before and after learning ^{17, 18}. This assumption is problematic because neural variability is correlated in vivo ^19-21 and these correlations will likely change before and after learning if learning is due to changes in connectivity, as is assumed in these models ^{17, 18}. This is all the more serious because, when correlations are taken into account, previous studies have shown that amplification and sharpening via lateral connections do not necessarily result in more informative neural representations, and therefore do not necessarily lead to behavioral improvements ^{22, 23}.

Second, it is unclear whether current neural theories could account for the impact of perceptual learning on what is known as a ‘threshold versus external noise contrast’, or TVC, curve, a comprehensive measure of human perceptual sensitivity that has been widely used to reveal observer characteristics in a wide range of auditory and visual tasks and changes of the perceptual limitations associated with cognitive, developmental, and disease processes ²⁴. A TVC curve shows the perceptual threshold (detection or discrimination threshold depending on the task) of a subject, as a function of the amount of external noise present in the stimulus (i.e., the noise injected in the image on every trial, see top of Fig. 1b). When plotted on a log-log scale, this curve takes on a characteristic shape (Fig. 1b). For low levels of external noise, the perceptual threshold stays relatively constant as external noise increases because internal noise dominates. For large values of external noise, on the other hand, the perceptual threshold increases linearly with the logarithm of the amplitude of the external noise because external noise is now the dominant source of variability.

Several experiments have shown that TVC curves change in a very specific manner during perceptual learning: the entire curve shifts down by a constant amount from one training session to the next (Fig. 1c) ^{4, 25-27}. As argued by some authors, such a uniform shift in TVC curves is consistent with a ‘late’ theory of perceptual learning ^{4, 24-28}. This conclusion relies on an engineering-inspired model containing two stages of processing: a sensory processing stage typically composed of a set of oriented spatial filters corrupted by additive and multiplicative noise, followed by a decision stage (Fig. 1d). In this class of models, the uniform shift in TVC curves is best explained by changes to the connections between the sensory representation and the decision stage, as opposed to a change in the early sensory representation ²⁹. Such results are consistent with a ‘late’ theory of perceptual learning, as cortical areas involved in decision making, such as the lateral intraparietal area (LIP) and the pre-frontal cortex (PFC), are late in the hierarchy of cortical processing. This is also consistent with a recent report documenting a change in the response properties of LIP neurons as an animal learns a motion discrimination task ^{30, 31}.

The problem with this conclusion, however, is that training on orientation discrimination leads to changes in the response of neurons in areas V1 and V4, two areas that are not thought to be implicated in decision making. Moreover, neurally inspired models that have been developed to capture the learning-induced changes in TVC curves assume noise sources, such as multiplicative and additive noise, that cannot easily be mapped onto neural variability ⁴. Indeed, while neuronal responses are known to be variable, this variability is neither additive nor multiplicative, but rather appears to exhibit properties that are close to the Poisson distribution ³².

In this paper, we show that all these perspectives can be reconciled when we consider a neural model of perceptual learning with realistic response statistics. In such a model, learning can be implemented in early visual areas in a manner that captures all the main features of the observed TVC curve changes, while also explaining the retinal specificity of learning. In addition, the model reveals that the key to learning is not to sharpen or amplify tuning curves, as these changes are neither sufficient nor necessary for learning. Instead, the key is to improve the efficiency of probabilistic inference in early cortical circuits by adjusting the feedforward weights in a manner that brings them closer to a matched filter. We show that at the neural level, this weight adjustment has only a minor impact on the shape of the tuning curves (as has been found in vivo), but leads to a large decrease in the magnitude of pairwise correlations.

Results

Template matching in primary visual cortex

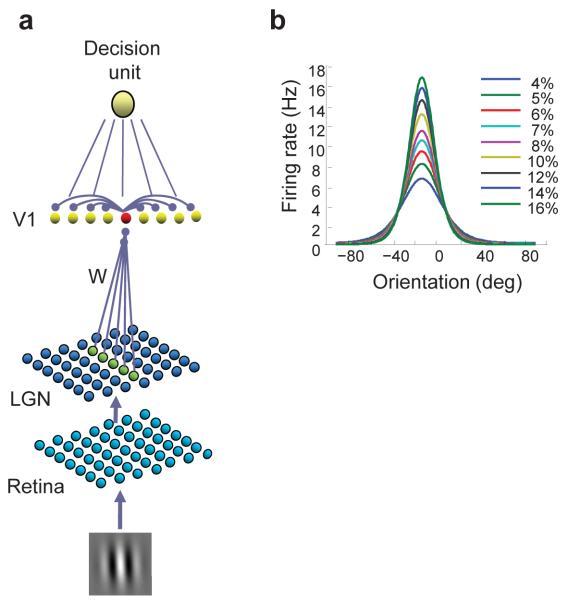
The neural architecture used in our simulations is illustrated in Figure 2a (see Supplementary Materials). Several aspects of the model are based on previous models of orientation discrimination, particularly the models in ³³ and ²². The model consists of three layers: retina, the Lateral Geniculate Nucleus (LGN) and V1. The retinal layer corresponds to grids of ON and OFF center ganglion cells modeled by difference-of-Gaussian filters. The output of each filter is passed through a smooth nonlinearity and used to drive the LGN cells, which generate Poisson spikes. The output spikes from the LGN cells are pooled using oriented Gabor function receptive fields, the orientations of which are uniformly distributed along a circle. The pooled output from the LGN cells is then used as input to the V1. The V1 stage represents an orientation hypercolumn – a set of neurons with receptive fields centered at the same spatial location but with different preferred orientations – of Linear Non-linear Poisson (LNP) neurons, coupled through lateral connections (see Online Methods). Importantly, the lateral connections are tuned to ensure that the resulting orientation tuning curves are contrast invariant. In other words, changing the contrast of the image only affects the gain of the cortical response (Fig. 2b), while keeping the width of the tuning curves constant, as has been reported in the primary visual cortex ³⁴. We constrained our parameter search to preserve contrast invariance in all the networks discussed in this paper.

Figure 2.

Network architecture. (a) A schematic of the neural architecture used to simulate orientation discrimination. (b) Cortical tuning curves in the simulated network are contrast invariant. This figure shows the tuning curve of cortical neurons in the network shown in Figure 3, after one session of training, when presented with stimuli of 9 different signal contrasts. The x-axis represents orientation (in degrees) and the y-axis represents firing rate (in Hz). The width of the tuning is roughly invariant to changes in contrast – only the amplitude of the tuning curve changes with a change in contrast. Similar results were obtained for the network before learning and after both sessions of training.

This model was used to simulate the orientation discrimination task used in ^{4, 27}. In those experiments, subjects were asked to report the orientation (clockwise or counterclockwise) of Gabor patches corrupted by pixel noise and oriented at either −12 or 12 deg from vertical (Fig. 1b). To model this task, we added a decision stage to our network in the form of a linear classifier. The linear classifier is equivalent to a decision unit whose activity is determined by the dot product of a weight vector with the population activity in the cortical layer (Fig. 2a). The weights were tuned to optimize classification performance in the pre-training condition, and were left untouched thereafter (see Online Methods). Network TVC curves were obtained using an analytical approach combined with numerical simulations. Specifically, we derived a lower bound on Fisher information in the cortical layer, as a function of specific network parameters such as the feedforward and recurrent connectivity, using our recent work on computing Fisher information in recurrent networks of spiking neurons ³⁵. We then used this expression to derive Fisher information in the decision unit. Finally, we numerically estimated TVC curves using the expression for Fisher information in the decision unit, taking advantage of the fact that Fisher information is inversely related to the discrimination threshold ¹⁹ (see Online Methods).

Since several neural models of early perceptual learning modify lateral connections ^{17, 18}, we first explored whether such changes could capture the main features of perceptual learning, such as the uniform shift of the TVC curves. Despite an extensive parameter search (see Supplementary Materials), this approach failed; sharpening tuning curves by adjusting lateral connections often resulted in worse performance, and in an upward shift of the TVC curve, because sharpening tuning curves often modified the correlations between neurons in a way that decreases Fisher information. In the few cases in which the TVC curves shifted downward, we could never find a configuration in which the curves shifted uniformly. Of course, given the size of the parameter space, we cannot rule out the possibility that there exists a solution based only on changes to the lateral connections that accounts for perceptual learning. However, we can conclude that changes to lateral connections that result in sharpening or amplification do not necessarily result in behavioral improvement, in contrast to what previous models suggest.

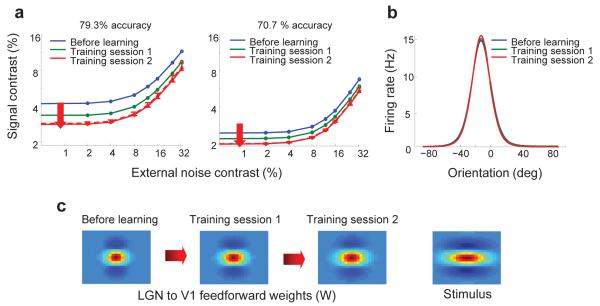
Next, we considered changes to feedforward connections, and found that this approach can indeed shift the TVC curves nearly uniformly (Fig. 3a; see Supplementary Table 1 for parameter values used). Importantly, the ratio of any two TVC curves, between training sessions, was approximately constant across external noise levels (with a maximum value of 1.26 and a minimum value of 1.23), as has been reported experimentally ²⁷. Moreover, the ratios of any two TVC curves, between criterion levels, were approximately constant across noise levels (1.81 ± 0.05 in the pre-training session, 1.63 ± 0.07 in training session I and 1.53 ± 0.08 in session II) and quantitatively similar to values observed experimentally ²⁷ (1.82 ± 0.51 on Day1/2, 1.67 ± 0.22 on Day3/4 and 1.27 ± 0.15 on Day 5/6). Crucially, in order to get these results, the spatial profile of the feedforward weights, between LGN and V1, had to be changed so as to match more closely the spatial profile of the stimulus (Fig. 3c). We repeated the simulations for three new sets of initial weights and found that the TVC curves always shifted uniformly as long as the weights were moved towards a matched filter (Supplementary Fig. S1). Our results were also robust to variability in the value of the final weights. Adding 10% of independent noise to the final weights resulted in variability in the TVC curves (error bars in Fig. 3a), but the shift remains close to uniform.

Figure 3.

Modeling perceptual learning using a realistic neural model of orientation discrimination. (a) Replicating the uniform shifts in TVC curves (Fig. 1b,c) using the neural model of orientation discrimination. These results were obtained by adjusting the feedforward connections between the LGN and V1 in a manner that moved them towards a matched filter for the stimulus. After training, we reran 10 new simulations with ±10% independent noise added to the final (training session 2) feedforward thalamo-cortical weights. The red dashed TVC curve represents the average TVC curve across the 10 runs and the error bars represent one standard deviation around the average values. It is clear that although there is variability in the TVC curve, for both performance criteria the qualitative results are robust to perturbations in the post-learning weights. (b) Tuning curves of cortical neurons from the network, demonstrating modest amplification and sharpening as a result of learning. The x-axis represents orientation (in degrees) and the y-axis represents firing rate (in Hz). (c) Moving the thalamo-cortical feedforward weights towards a matched filter. The rightmost panel shows the 2-D spatial profile of a stimulus. The leftmost panel shows the 2-D spatial profile of the feedforward weights before learning, the second panel from left shows the spatial profile of the feedforward weights after one training session and the panel second from the right shows the spatial profile of the feed-forward weights after two training sessions. Together these figures show the spatial profile of the thalamo-cortical feedforward connections moving towards the spatial profile of the stimulus, a manipulation which led to the changes in TVC curves shown in a.

These results show that it is possible to capture the main features of perceptual learning induced TVC curve changes, by adjusting the feedforward connectivity in early visual areas. This solution has the added advantage of capturing the specificity of perceptual learning to retinal location since it involves changing weights at a specific location on the retinotopic map.

The role of amplification and sharpening

The tuning curve of a trained cortical neuron before learning and after the first and second training sessions is shown in Figure 3b. The amplitude of the tuning curve grows slightly with training, and the width is slightly reduced, thereby revealing modest amounts of amplification and sharpening. These changes are consistent with neurophysiological recordings in animals trained on orientation discrimination, which have reported that the tuning curves in both V1 and V4 are sharpened and/or amplified during perceptual learning ^{8, 9, 16}. However, these effects were found to be small, particularly in V1. Indeed, some studies failed to find any significant sharpening or amplification ³⁶, while others found only a small amount of sharpening or amplification ^8,9, as is the case in our network.

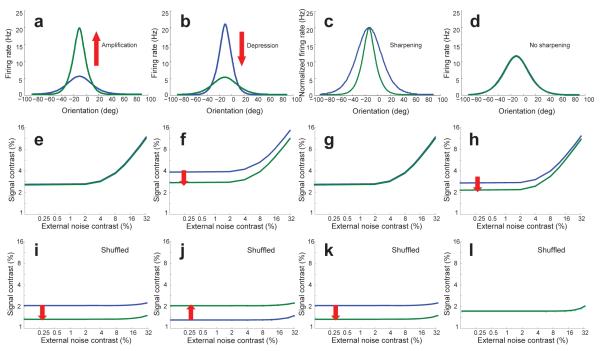
Nonetheless, the fact that the tuning curves in our model exhibit amplification and sharpening would appear to be consistent with conclusions from previous models that have invoked these mechanisms as the neural basis of perceptual learning ^{17, 18}. Yet, this would be misleading because, in our model, amplification and sharpening are neither sufficient nor necessary to account for perceptual learning. For instance, with appropriate choice of parameters, it is possible to find a network in which the tuning curves are amplified (Fig. 4a) but in which the TVC curve shows no shift (Fig 4e), corresponding to no change in performance and a lack of perceptual learning. This indicates that amplification is not sufficient for perceptual learning. The opposite scenario is illustrated in Figure 4b: this time, the tuning curves show depression, as opposed to amplification, but the TVC curve shifts downward (Fig. 4f) in line with changes observed during perceptual learning. This implies that amplification is not necessary for learning. Equivalent scenarios for sharpening are shown in Figure 4c,g and Figure 4d,h, thus establishing that sharpening, like amplification, is neither sufficient nor necessary for learning (see Supplementary Table 2 for parameter values used).

Figure 4.

Taking correlations into account demonstrates that amplification and sharpening are neither necessary nor sufficient for learning. (a,e,i) A demonstration that amplification is not sufficient for learning. Parameters in this network have been changed in a manner that led to amplification of the orientation tuning curves (a). At the level of TVC curves, the same change led to no improvement in performance – the TVC curve did not shift (e) – thereby showing that amplification is not sufficient for learning. Interestingly, single cell recordings in such a network would incorrectly conclude that learning did take place as illustrated by the drop of the TVC curve when computed with I_shuffled (see main text) (i). (b,f,j) Amplification is not necessary for learning. Learning can take place in a network (f) in which the gain of the tuning curve decreased during learning (b). (c,g,k) Sharpening is not sufficient for learning. This network shows no sign of learning (g) despite very significant sharpening of the tuning curves (c). (d,h,l) Sharpening is not necessary for learning. Learning can take place (h) even in the absence of any sharpening (d). All TVC curves were obtained for the 89% correct performance criterion.

These results demonstrate that single cell responses alone are insufficient to predict behavioral performance. To get a comprehensive neural theory of perceptual learning, one must also consider the correlations between cells.

The role of correlations

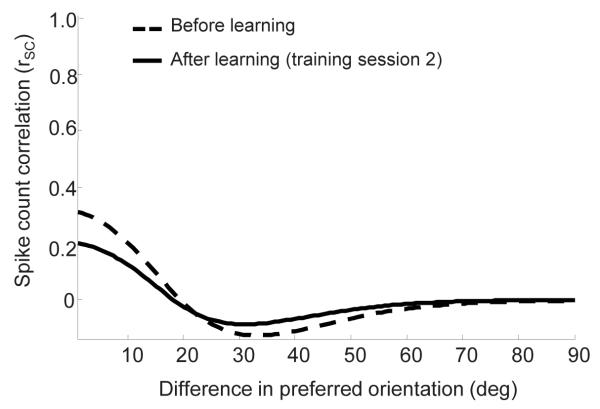
The pattern of correlations before and after learning is shown in Figure 5. The before learning correlations are within the range −0.1 to 0.4, which is consistent with the values reported in vivo ^{20, 37, 38}. Moreover, correlations tend to decrease with the difference in preferred orientations between pairs of cells, as is typically found in models of orientation selectivity and in vivo ^{20, 38}.

Figure 5.

The impact of perceptual learning on correlations. The dashed curve shows the correlation coefficients as a function of the difference in preferred orientation before learning. The correlation coefficients were computed using a similar procedure to that used in ³⁸, in response to a stimulus with 8% signal contrast. As has been reported in vivo, correlations are between 0.4 and −0.1, and their magnitude decreases as a function of orientation difference. The solid curve shows the correlations after learning took place. The main effect of perceptual learning is to reduce the magnitude of the correlations while preserving the overall pattern of correlations.

After learning, correlation coefficients show the same dependence on the difference in preferred orientation but the overall amplitude of the coefficients is reduced. It would be tempting to conclude that the increase in information is due to this general decrease in correlations, but one has to be cautious with such conclusions. Just as sharpening the tuning curve does not guarantee an increase in information, neither does a decrease in correlation coefficients. The increase in information is determined by a combination of a change in the pattern of correlations, and a change in the shape of the tuning curves.

To determine more quantitatively the contribution of correlations to the increase in Fisher information in our network, we used a metric that was recently proposed ²⁰. We compared the increase in information across training sessions for the network shown in Figure 3, against the change in information in a virtual population of neurons with the same change in correlations but with identical tuning curves across training sessions. This analysis revealed that correlations contribute to 70% of the increase in Fisher information, indicating that correlations are responsible for much of the performance improvement.

In addition, to illustrate the kind of errors that one would encounter by ignoring correlations, we plotted the TVC curves for all the networks we have described so far, but using an information theoretic quantity called I_shuffled, i.e., the Fisher information in a set of neurons with the same single cell response statistics as in the original data but without correlations ¹⁹. This is effectively the measure used in some previous models ^{17, 18} and in neurophysiological studies using single cell recordings.

This analysis revealed that the changes in TVC curves derived from I_shuffled do not necessarily reflect changes in the TVC curves derived from the true Fisher information (Fig. 4i–l). For instance, in Figure 4c,g,k, we consider a network in which the tuning curve sharpens as a result of training. As one would expect from previous work on population codes with independent noise, a sharpening of the tuning curves increases I_shuffled, which results in a downward shift of the TVC curve (Fig. 4k). Yet, the true TVC curve for this particular network does not shift during training, indicating no change in performance (Fig. 4g). In addition, one can see that the TVC curve derived from I_shuffled does not have the right profile; it remains basically flat over the range of external noise values tested (Fig. 4k). A different network is shown in Figure 4b,f,j, one in which the tuning curves are depressed as a result of training. Again, the shift in the TVC curve derived from I_shuffled differs from the shift in the true TVC curve: the TVC curve derived from I_shuffled shifts upward (Fig. 4j) while the true TVC curve shifts downward (Fig. 4f).

Finally, we also computed the TVC curves from I_shuffled for the network shown in Figure 3, in which we modify the feedforward connections. In this network, the TVC curves from I_shuffled move in the right direction, but the curves are much too flat compared to the real ones, and the amount by which they move is considerably less than the shift obtained with the true information (Fig. 6). Therefore, although the TVC curves derived from I_shuffled move in the right direction in this case, they still do not accurately reflect the TVC curves obtained from Fisher information.

Figure 6.

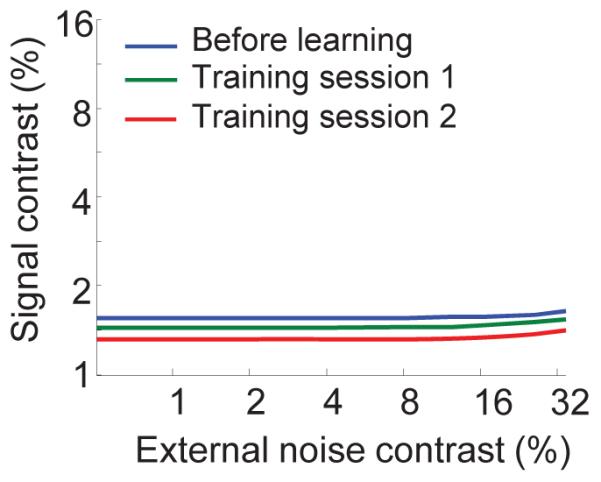
TVC curves for the network shown in Figure 3, computed from responses in which correlations have been removed through shuffling (using I_shuffled – see main text). The TVC curves still shift downward by a uniform amount, as was the case in Fig 3a. However, the magnitude of shift is significantly reduced and the TVC curves no longer show the characteristic linear increase in signal contrast as external noise level increases, at high levels of external noise. These curves were computed for 79.3% accuracy.

Subsampling neurons: how many does it take?

Our results suggest that the neural basis of perceptual learning can only be revealed by recording the tuning curves and correlations of all the neurons involved in the task, within a cortical area. However, such recordings are not currently available. Although, multi-electrode arrays make it possible to record from multiple neurons simultaneously, this technique can only record the responses from a small fraction of all the neurons present in a given cortical patch ^{38, 39}.

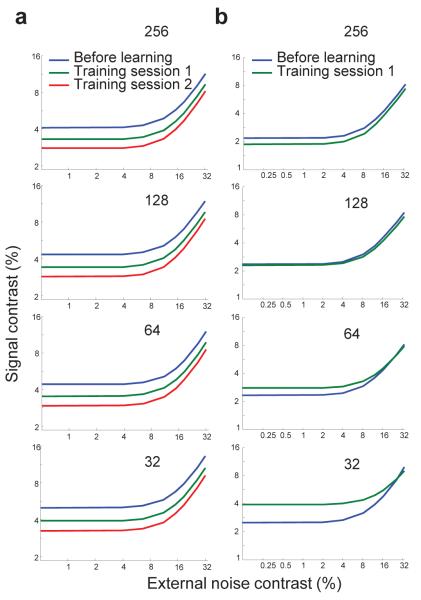
To determine whether the same conclusions would be reached in our simulated networks when recording from a smaller number of neurons, we derived the TVC curves from subsets of neurons. More specifically, we simulated each of the networks considered so far with 256 neurons in the cortical layer, but we computed information based only on the responses of a subset of randomly sampled cortical neurons. We then generated TVC curves based on this measure of information. The TVC curves derived for the network shown in Figure 3, based on the responses of 256, 128, 64 and 32 neurons are shown in Figure 7a. The results are qualitatively the same, even when we sample as little as 32 neurons.

Figure 7.

TVC curves obtained from subsets of neurons in the networks shown in Figure 3 (a) and Figure 4b,f,j (b). The plots in each panel were obtained by simulating the full network, but by computing the TVC curve based on the response of a randomly picked sample of neurons. The number of neurons in each subset is indicated on each panel and varies from 256 to 32. (a) TVC curves obtained by subsampling the network shown in Fig. 3. The results are qualitatively the same, even when we sample as little as 32 neurons. (b) TVC curves obtained by subsampling the network shown in Fig. 4b,f,j. With 256 neurons, the results are similar to the results obtained with the full network (Fig. 4f) while with only 32 neurons, the result starts mimicking the results obtained with I_shuffled (Fig. 4j). The upward shift of the TVC curve with learning, observed with 32 cells, is therefore an artifact of subsampling and does not reflect the behavior of the whole neuronal population. All TVC curves were obtained for the 79% correct performance criterion.

However, this does not hold for all networks, as can be seen with the TVC curves derived for the network shown in Figure 4b,f,j using subsets of varying size (Fig. 7b). In this network, training led to a depression of the tuning curve amplitude and the TVC curves derived from the true Fisher information with all 256 neurons shifted downward, indicating a performance improvement. In contrast, the TVC curves estimated from 32 neurons show the reverse trend: performance is degraded as a result of training (Fig. 7b).

These results suggest that, in some networks, when we only consider the responses of a subset of a population of cortical neurons, we may not retain all the qualitative results obtained by considering the entire population, even when we have enough data to accurately characterize the correlations (see Supplementary Fig. S2 for more examples). This in turn implies that a discrepancy between behavioral results and the information content of a subpopulation of neurons should not necessarily be taken as evidence that the recorded area does not play a role in learning.

Discussion

We explored the neural basis for the improvement in behavioral performance observed during perceptual learning in a fine discrimination task. Classical neural theories have argued that perceptual learning is mediated through a steepening – via amplification or sharpening – of the tuning curves of neurons in early sensory areas. Further, they have proposed that tuning curves are steepened through changes in the lateral connections between neurons in early cortical sites ^{17, 18}. Our analysis suggests a different picture: given the observed changes in TVC curves, learning can be explained by changes in the feedforward connections between the thalamus and the primary visual cortex. More specifically, the feedforward connections must be modified in a manner that moves them towards a matched filter for the stimulus. These modifications also result in modest changes in tuning curves, in line with what has been reported in vivo, and in a decrease in the magnitude of pairwise correlations. To our knowledge, this is the first neural theory of perceptual learning that is consistent with the mean change in neural response in early visual areas, with the response statistics of sensory neurons, and with the uniform downward shift in TVC curves documented with human observers.

One of the limitations of some previous theories of perceptual learning has been the assumption that neural variability remained the same before and after learning ^{28, 31}. Under this assumption, steepening tuning curves can indeed improve behavioral performance. In contrast, we have shown here that when learning induced changes in correlations are taken into account, steepening of tuning curves is neither necessary nor sufficient for learning. Therefore, the key to the neural basis of perceptual learning may have less to do with how tuning curves change and more to do with how the connectivity is adjusted to improve the inference performed by neural circuits. Such changes to neural connectivity can still have an impact on tuning curves, but it is the combination of the change in tuning curves and the change in correlations that ultimately determines the presence or absence of learning.

Although this paper focuses on changes in early sensory areas, our work is conceptually related to late theories of perceptual learning. In late theories of perceptual learning, neural processing is decomposed into two stages: a sensory processing stage followed by a read-out or decision stage. The read-out stage is typically formalized as a probabilistic inference stage, whose goal is to compute the probability distribution over possible choices given the sensory evidence ^{28, 31, 40}. During learning, the weights between the early and late areas are adjusted so as to bring the probability distribution over choices closer to the optimal posterior distribution that would be obtained by applying Bayes rule to the output of the early sensory stage, which in turn leads to a uniform shift in TVC curves. This perspective is in line with several neurophysiological and modeling results which strongly suggest that neurons in areas such as LIP encode probability distributions, or likelihood functions, over choices and actions ^{41, 42}.

Here, we argue that perceptual learning might be due to improved probabilistic inference induced by changes at the sensory processing stage rather than at the decision stage (at least in the case of orientation discrimination). This possibility has been ignored in the past, in part because it is not common to think of early visual areas as performing probabilistic inference. Instead, the responses of neurons in early sensory areas are typically modeled as noisy nonlinear filters encoding scalar estimates of variables like orientation. Recent theories ^{43, 44} have challenged this perspective and suggested that, even in early sensory areas, neural patterns of activity might in fact represent probability distributions or likelihood functions. This raises the possibility that learning in early visual areas involves an improvement in probabilistic inference which could in turn lead to a uniform shift in TVC curves. This is very much the logic that we have pursued here. Therefore, our solution is computationally very similar to the one proposed by late theories. Indeed, our model does not supersede previous models of late perceptual learning ^{28, 31, 40} but instead complements them by showing how similar results can be obtained by modifying population codes in early sensory areas. Our approach however has one significant advantage: it accounts for the fact that neural responses change in early and mid-level visual areas as a result of training on an orientation discrimination task ^{8, 9, 16}, an experimental observation that is difficult to reconcile with late theories.

Ultimately, whether perceptual learning involves early or late stages (or both) is likely to depend on the task, the sensory modalities involved, and the nature of the feedback and training received by subjects. For example, in the somatosensory and auditory systems, large changes have been reported in primary sensory cortices as a result of perceptual learning ^{6, 7}. In the visual system, on the other hand, while training on orientation discrimination seems to engage early and mid-level areas like V1 and V4 ^{8, 9, 16, 45}, training on other tasks like motion discrimination triggers changes in late areas like LIP ³⁰. Moreover, double training on contrast and orientation discrimination appears to trigger learning in both early and late areas, with nearly complete transfer of learning across trained locations ^{13, 14}. Our approach could be extended to all of these forms of learning, since none of what we have presented is specific to the LGN-V1 architecture used here.

Finally, although we have focused on perceptual learning here, our approach can be generalized to other domains such as adaptation or attention. In the case of attention, our approach (as well as our previous work, see ⁴⁶) would suggest that changes in correlations might play a critical role in the behavioral improvement associated with enhanced attention, perhaps more so than changes in tuning curves, which are typically the focus of single cell studies ^{47, 48}. Interestingly, it was recently reported ²⁰ that changes in correlations account for 86% of the behavioral improvement triggered by attention. Likewise, another recent study ³⁷ found that correlations play a critical role in adaptation. It will be important to investigate whether these neural changes can also account for the changes in TVC curves induced by attention or adaptation.

Appendix

Online Methods

Stimulus design

We generated stimulus displays that mimicked those used in the perceptual learning experiments of Dosher & Lu ⁴. The signals were Gabor patterns tilted θ^°_s to the right or left of vertical. Each stimulus image was created by assigning grayscale values to image pixels according to the following function:

$$Z(x,y,\theta )=Z_0\left(1.0+\left(c{e}^{-\left[\frac{C{x}^2}{2{\sigma }_x^2}+\frac{C{y}^2}{2{\sigma }_y^2}\right]}\cos \left(2\pi KCx\right)\right)\right)$$ (1)

where Cx = xcosθ + ysinθ; Cy = ycosθ − xcosθ; θ = rad(90±θ_s) and x and y are the horizontal and vertical co-ordinates respectively, K is the spatial frequency of the Gabor pattern,σ_x and σ_y are the standard deviation (extent) of the Gabor in the x and y directions respectively, Z₀ is the mean, or background, grayscale value for the image and c is the maximum contrast of the Gabor pattern as a proportion of the maximum achievable contrast. In all our experimental conditions, θ°_s was set to 12°, the spatial frequency K was set to 0.75 cycles/deg,σ_x was set to 0.4,σ_y was set to 0.4 and Z₀ was set to 126.22 which was the equivalent mean grayscale value used in Dosher & Lu’s studies ^{4, 27}. The maximum contrast of the Gabor, labeled the signal contrast, varied depending on the experimental condition.

Pixel gray levels for the external noise were drawn from a Gaussian distribution with mean zero and standard deviation depending on the experimental condition. As in Dosher & Lu’s studies, we used eight external noise levels in which the standard deviation of the external noise distribution was varied as a proportion of the maximum achievable contrast. The effective noise levels we used were: 0.005%, 2%, 4%, 8%, 12%, 16%, 25% and 33%. Each noise element included a single pixel and the noise gray level values were added to the stimulus gray level values on a pixel by pixel basis to generate the noise-injected image

Modeling orientation selectivity

We simulated the circuits involved in one orientation hypercolumn of primary visual cortex using a network model of spiking neurons subject to realistic variability. Several aspects of the model are based on previous models of orientation discrimination, particularly the models in ³³ and ²². The model consists of three layers: retina, LGN and V1. The retinal and LGN stages closely follow those described in ²², with one difference being that we only model the spatial receptive fields of retinal and LGN cells, owing to the temporally stationary nature of our stimuli. The retinal stage corresponds to grids of uncoupled, ON and OFF ganglion cells modeled by difference-of Gaussian filters. The output of each retinal filter is passed through a nonlinearity to produce an analog firing rate that accounts for stimulus contrast sensitivity. These firing rates are then used by the cells at the LGN stage to generate spikes according to a Poisson process.

The V1 stage represents a hypercolumn of orientation selective layer IV simple cells. It comprises 256 Linear, Non-Linear, Poisson (LNP) units which are coupled to each other through lateral connections. LNP units represent a mathematical description that provides a good model of integrate and fire neurons in the physiologically realistic high-noise limit ⁴⁹, while still being analytically tractable. The cortical simple cell receptive field structure is established through a segregation of ON and OFF LGN inputs into ON and OFF subfields, and is modeled using a Gabor function. Each cortical cell receives connections from all the LGN cells within a subfield boundary, with ON-subfields yielding connections from all ON-center LGN cells and OFF subfields yielding connections from all OFF-center LGN cells. We implement full lateral connectivity – every cell is coupled with every other cell in the cortical layer. Unlike previous models of orientation selectivity, the cortical layer in our model only includes excitatory neurons. We are nevertheless able to implement the full range of excitatory and inhibitory lateral connectivity to a given cell by allowing the strength of a recurrent connection between two cells to be either positive or negative. We model all the lateral connections as being inhibitory in polarity by making the baseline connection strength significantly negative. However, the pattern of connection strengths between neurons versus the difference in their preferred orientations is chosen so that the connection strengths form a “Mexican hat” function ³³, relative to baseline.

The parameters of the model are adjusted so that the response properties of individual cells in the cortical layer of our network closely match the response properties of V1 neurons in vivo. First, since we model cortical cells as LNP units, the variability of generated spikes is guaranteed to be of the Poisson form which is a good description of neural variability in vivo. Second, the response of cortical cells in our network shows the characteristic contrast-invariance that has been reliably demonstrated in orientation selective cells in the primary visual cortex ³⁴. Finally, units in the network are subject to realistic inter-neuronal correlations which arise from an interaction between the variability in the stimulus, the variability in neuronal firing and the pattern of network connections, and not from any artificial injection of variability.

In Dosher & Lu’s experiments, subjects were tasked with reporting the orientation of Gabor patches corrupted by pixel noise and oriented at either −12 or 12 degrees from vertical. To model this task, we added a decision stage to our network in the form of a linear classifier. The linear classifier is equivalent to a decision unit whose activity is determined by the dot product of a weight vector with the population activity in the cortical layer. The weights were tuned to optimize classification performance in the pre-training condition, and were left untouched thereafter.

Computing discrimination performance

We compute the orientation discrimination performance of our network, when presented with the noisy oriented Gabor stimuli (described above), by estimating Fisher information. Discrimination thresholds can be computed via Fisher information because Fisher information is inversely proportional to the discrimination threshold of an ideal observer, i.e., it directly predicts performance in discrimination tasks. Recently, we have derived an analytic expression for the linear Fisher information in a population of LNP neurons driven to a noise-perturbed steady state ³⁵. Linear Fisher information corresponds to the fraction of Fisher information that can be recovered by a locally optimal linear estimator. In practice, linear Fisher information has been found to provide a tight bound on total Fisher information, both in simulations ²² and in vivo ¹⁹. This expression can be written as follows:

$$I={\left(M{h}^{\prime }\right)}^T{[M{\Gamma }_{hh}{M}^T+D^{-1}G{D}^{-1}]}^{-1}\left(M{h}^{\prime }\right)$$ (2)

where M represents the matrix of thalamo-cortical feed-forward connections, h represents the mean input firing rates from the thalamus,Γ_hh represents the covariance matrix of the input firing rates from the thalamus, G is a diagonal matrix whose entries give the mean response of the LNP neurons and D is a diagonal matrix which gives the derivative, or slope, of the activation function G of the cortical neurons in steady state.

One point to note is that the expression in (2) is based on the assumption that the decoder used to read out the activity of the cortical layer is the optimal decoder for the specific network. However, in this study, we are interested in highlighting the changes in early response properties that could lead to the observed behavioral improvements, while keeping the decoder constant. Thus, based on prior work by Wu, Nakahara & Amari ⁵⁰, we derived another form of the expression in (2), for the Fisher information in our network using a fixed decoder, which takes the following form:

$$\begin{array}{c}I\left(W_{dec}\right)=\frac{{\left(W_{dec}^T{\mu }^{\prime }\right)}^2}{W_{dec}^T\Gamma W_{dec}}\hfill \\ \text{where}\hfill \\ {\mu }^{\prime }={(D^{-1}-W)}^{-1}M{h}^{\prime }\hfill \\ \Gamma ={(D^{-1}-W)}^{-1T}[M{\Gamma }_{hh}{M}^T+D^{-1}G{D}^{-1}]{(D^{-1}-W)}^{-1},\hfill \end{array}$$ (3)

and W_dec represents the pattern of connection weights from the cortical layer to the decision stage, i.e. the fixed decoder described earlier and W represents the matrix of cortical recurrent connections.

Deriving TVC curves

Using the expression in equation (3) allows us to compute the Fisher information, and hence the discrimination threshold, at the decision stage in response to a specific stimulus. In their experiment, Dosher & Lu used a staircase over signal contrast to generate a TVC curve which represents the signal contrast needed to elicit a specific level of performance (represented by percent correct performance), given a particular level of external noise. In our simulations of their experiment, we numerically obtain TVC curves using the analytic expression in (3). Specifically, we first compute the Fisher information at the decision stage using stimuli with a wide range of signal contrasts and a specific level of external noise. We used 15 signal contrast levels. They were: 1.25%, 1.5%, 2%, 2.5%, 3%, 3.5%, 4%, 5%, 6%, 7%, 8%, 10%, 12%, 14% and 16%. We then repeat this process with the eight levels of external noise used by Dosher & Lu. Finally, we compute an iso-information contour, for a value of information that is equivalent to the percent correct criterion used by Dosher & Lu (computed via Signal Detection theory) through the matrix of information generated by the previous two steps, to obtain a TVC curve. As a result of this process, we are able to generate equivalent TVC curves, or orientation discrimination performance curves, from our network as Dosher & Lu were able to generate for their human subjects.

I_shuffled

We denote as I_shufffled, the information available in an artificial data set in which the activity of the cortical units was shuffled across trials to remove all correlations across cells. This shuffling operation is analogous to making single-cell recordings and generating artificial population patterns of activity by grouping the activity of different cells collected under the same stimulus conditions. To compute I_shufffled for a given stimulus we only consider the diagonal elements of the cortical covariance matrix (i.e. we only consider the variance terms and assume no covariance) when computing the information at the decision stage using the analytic expression in (3). In order to then compute TVC curves based on I_shufffled, we use the same numerical approach as that used in computing TVC curves based on the true information (described above).

Subsampling neuronal populations

To quantify the results we would have obtained from our simulations had we only been able to record from a subset of the simulated cortical neurons, we also compute information based only on the responses of a subset of randomly sampled cortical neurons. To do this, we again simulate all of the networks considered in the main paper with the full 256 neurons in the cortical layer. However, when we compute information using the expression in (3), we only use the activities and the correlations derived from a randomly sampled subset of neurons, and the weights from these neurons to the decision stage, in computing the Fisher information at the decision stage. We then use the same numerical approach as that used in computing TVC curves based on the true information, to compute TVC curves based on the subsampled information. To quantify the effect of varying sample size, we repeat this process for a random sample of 128, 64 and 32 neurons.