Confidence intervals and bands for the binormal ROC curve revisited

Abstract

Two types of confidence intervals (CIs) and confidence bands (CBs) for the receiver operating characteristic (ROC) curve are studied: pointwise CIs and simultaneous CBs. An optimized version of the pointwise CI with the shortest width is developed. A new ellipse-envelope simultaneous CB for the ROC curve is suggested as an adaptation of the Working–Hotelling-type CB implemented in a paper by Ma and Hall (1993). Statistical simulations show that our ellipse-envelope CB covers the true ROC curve with a probability close to nominal while the coverage probability of the Ma and Hall CB is significantly smaller. Simulations also show that our CI for the area under the ROC curve is close to nominal while the coverage probability of the CI suggested by Hanley and McNail (1982) uniformly overestimates the nominal value. Two examples illustrate our simultaneous ROC bands: radiation dose estimation from time to vomiting and discrimination of breast cancer from benign abnormalities using electrical impedance measurements.

1. Introduction

The receiver operating characteristic (ROC) curve has been known for more than 30 years and is widely used in biomedical research to visually represent the trade-off between the sensitivity and specificity of a test. There are many excellent texts and review articles on the ROC curve. We refer the reader to papers [3,16,24,26] and books [21,28,36] for general discussion. The simplest and perhaps the most common ROC curve is when the two discriminating populations have normal distributions, termed the binormal ROC curve [15,24]. The remarkably robust features of the binormal ROC curve are well documented [14,32] and stem from the fact that the ROC curve is invariant to any monotonic transformation applied to the two discriminating populations.

Confidence interval (CI) should be distinguished from confidence band (CB) in the framework of the ROC curve: CI specifies the interval of values of the sensitivity given specificity with probability λ, but CB specifies the set of points in the unit square that the entire ROC curve belongs to with probability λ. Two types of CIs have been extensively discussed in the literature. Early authors starting from Bamber [2] developed CI for the area under the curve (AUC), which represents the overall discrimination power of the test. Much effort has been put into the construction of CB for the ROC curve in a nonparametric setting (see [12,18] among recent references). Several papers consider the situations when observations are subject to measurement error ([6,33] among them).

The topic of CI and CB for the binormal ROC curve is sparsely scattered through the literature. For example, in the major reference on the topic [23], the Working–Hotelling simultaneous CB is expressed in terms of Φ(a − bx), where Φ is the normal cumulative distribution function (cdf), but an additional and missing step is required to express a and b and their variances through the sample statistics. Likewise, we could not find a closed-form expression for the CI for the area under the binormal ROC curve.

The goal of the present work is to develop optimized (shortest width) CI and CB for the binormal ROC curve: (1) a CI for sensitivity, or pointwise CB, based on the delta method with the shortest width and (2) a simultaneous ellipse-envelope CB for the entire ROC curve as a modification of the Working–Hotelling approach.

The organization of the paper is as follows. In the next section, we introduce notation and give basic definitions in the framework of the binormal ROC curve. The optimized pointwise CI is discussed in Section 3. The CB as the confidence region that covers the entire ROC is discussed in Section 4. Statistical simulations for assessing the coverage probability for the CB and CI for the AUC are reported in Section 5. Section 6 offers two examples, and Section 7 concludes.

2. Basic concepts and definitions

To be specific, consider two populations of people: nondiseased (D₀) and diseased (D₁). We do not know in advance who is healthy and who is sick, but there is a test that aims to discriminate people based on the outcome of the test. For example, a high prostate-specific antigen (PSA) level or another biomarker may warn of prostate cancer. There are two types of errors: false positive (FP), or false alarm, and false negative (FN) when the disease is overlooked. There are two types of correct identification: true positive (TP), called sensitivity, and true negative, called specificity. The ROC curve represents the trade-off between TP and FP rates when the cut-off value of the test changes. In this paper, it is assumed that the distribution of the test's continuous outcome variable is normal, $\mathcal{N}({\mu }_0,{\sigma }_0^2)$, and the distribution in the diseased group is $\mathcal{N}({\mu }_1,{\sigma }_1^2)$. Without loss of generality, we assume that on average the nondiseased group has a smaller value of the test that, in terms of the general population, is expressed as μ₀ < μ₁.

Sensitivity, as the TP probability, is the probability that the test gave a value greater than the cut-off (c) in the diseased population. In the case of the normal distribution, sensitivity can be expressed through the cdf Φ as

$$T\left(c\right)=\Phi \left(\frac{{\mu }_1-c}{{\sigma }_1}\right).$$ (1)

The FP probability is the probability that the test gave a value greater than the cut-off (c) in the nondiseased population,

$$F\left(c\right)=\Phi \left(\frac{{\mu }_0-c}{{\sigma }_0}\right).$$ (2)

The binormal ROC curve can be represented on the unit square as the curve (F(c), T(c)) parametrized by c ∈ (−∞, ∞) or explicitly through the FP probability p = F(c) in a functional form as

$$R\left(p\right)=\Phi \left(\frac{{\mu }_1-{\mu }_0+{\sigma }_0{\Phi }^{-1}\left(p\right)}{{\sigma }_1}\right),p\in (0,1).$$ (3)

It is straightforward to see that the ROC curve starts at (0, 0), is an increasing function of p and ends at (1,1).

There is a special point on the ROC curve where the sum of the two errors, FP and FN, is minimal. Using the derivation rule of implicit functions, it is easy to show that this point on the ROC curve is where the tangent line has a 45° slope. The optimal cut-off value, c, is found from the quadratic equation

$$\frac{{({\mu }_0-c)}^2}{{\sigma }_0^2}-\ln {\sigma }_1^2=\frac{{({\mu }_1-c)}^2}{{\sigma }_1^2}-\ln {\sigma }_0^2$$ (4)

with the solution

$$c=\{\begin{array}{cc}\frac{({\mu }_0{\sigma }_1^2-{\mu }_1{\sigma }_0^2)+\sqrt{\begin{array}{c}\hfill {({\mu }_0{\sigma }_1^2-{\mu }_1{\sigma }_0^2)}^2-({\sigma }_1^2-{\sigma }_0^2)\hfill \\ \hfill ({\sigma }_1^2{\mu }_0^2-{\sigma }_0^2{\mu }_1^2+{\sigma }_0^2{\sigma }_1^2\ln ({\sigma }_0^2∕{\sigma }_1^2))\hfill \end{array}}}{{\sigma }_1^2-{\sigma }_0^2}\hfill & \mathrm{if}{\sigma }_0^2\ne {\sigma }_1^2,\hfill \\ \frac{1}{2}({\mu }_0+{\mu }_1)\hfill & \mathrm{if}{\sigma }_0^2={\sigma }_1^2.\hfill \end{array}\phantom{\}}$$ (5)

There is an interesting connection to discriminant analysis: if ${\sigma }_0^2\ne {\sigma }_1^2$, Equation (4) is the solution to the quadratic equationand if ${\sigma }_0^2={\sigma }_1^2$, Equation (5) is the solution to the standard discriminant analysis that minimizes the total misclassification error [22].

In reality, we do not know the true values of the mean and variance but estimate them from the outcome sample in the nondiseased group $\{x_i^0,i=1,\dots ,n_0\}$ and diseased group $\{x_i^1,i=1,\dots ,n_1\}$, where n₀ and n₁ are sample sizes in control and diseased groups. It is assumed that observations are independent within the group as well as between groups. Then, we estimate the ROC curve by replacing the true unknown values for $({\mu }_k,{\sigma }_k^2)$ with their unbiased sample estimates $({\stackrel{‒}{x}}_k,s_k^2),k=0,1$.

The AUC serves as=an indicator of the discrimination power of the test [2]. In the case of the binormal ROC curve, it admits a closed-form solution

$$\mathrm{AUC}=\Phi \left(\frac{{\mu }_1-{\mu }_0}{\sqrt{{\sigma }_0^2+{\sigma }_1^2}}\right),$$ (6)

assuming that μ₀ < μ₁, which implies that AUC > 0.5. Referring to the PSA example, the AUC can be interpreted as the overall proportion of the prostate cancer patients with a PSA greater than that of the normal controls. Alternatively, one can say that the AUC is the average sensitivity using control-test outcomes as cut-offs.

3. Pointwise CI

Let p be fixed and we want to construct a CI for R(p) specified by Equation (3) using the sample values for the mean and variance. Define the cut-off c = Φ⁻¹(p) and let

$$X_c=\frac{{\stackrel{‒}{x}}_1-{\stackrel{‒}{x}}_0+s_{0}c}{s_1},$$ (7)

where Φ⁻¹ is the inverse cdf. In order to construct a CI for the ROC curve, one needs to approximate var(X_c). Since the data have a normal distribution, using standard formulas, we obtain

$$\mathrm{var}({\stackrel{‒}{x}}_1-{\stackrel{‒}{x}}_0)=\frac{{\sigma }_0^2}{n_0}+\frac{{\sigma }_1^2}{n_1},\mathrm{var}\left(s_0^2\right)=\frac{2{\sigma }_0^4}{n_0-1},\mathrm{var}\left(s_1^2\right)=\frac{2{\sigma }_1^4}{n_1-1}.$$ (8)

For the normally distributed data, x̄₁ − x̄₀, $s_0^2$ and $s_1^2$ are mutually independent, so from the delta method [4], similar to what can be found in [35], we obtain

$$\mathrm{var}\left(X_c\right)=\frac{1}{{\sigma }_1^2}\left(\frac{{\sigma }_0^2}{n_0}+\frac{{\sigma }_1^2}{n_1}\right)+\frac{c^2{\sigma }_0^2}{2{\sigma }_1^2(n_0-1)}+\frac{{({\mu }_1-{\mu }_0+{\sigma }_{0}c)}^2}{2{\sigma }_1^2(n_1-1)}.$$

Hence, with fixed c, if α is the significance level, an approximate λ = 1 − α CI for R(p) is

$$\Phi \left(X_c\pm Z_{1-\alpha ∕2}\sqrt{\widehat{\mathrm{var}}\left(X_c\right)}\right),$$ (9)

where Z_1−α/2 is the (1 − α/2)th quantile (we use the hat over the variance to indicate that the sample estimates are used instead of the true unknown values). We expect that this CI will have the nominal coverage probability for large n₀ and n₁.

It is curious to note that the minimum var(X_c), or equivalently the minimum width of the CI, occurs at the cut-off value

$$c_{\min }=-\frac{n_0-1}{n_1+n_2-2}\frac{{\stackrel{‒}{x}}_1-{\stackrel{‒}{x}}_0}{s_0}.$$

That is, when the FP rate is less than 0.5.

We note that in our approach, the unbiased moment estimators for variances are used (Equation (8)), which allows us to derive the closed-form expression for the CI and its optimized version in finite samples; Hsieh and Turnbull [19] and Cai and Moskowitz [5] used an asymptotic approach with maximum-likelihood estimation. When the sample size in both samples gets large, the two approaches converge.

3.1 CI with the shortest width

When constructing the CI (9), we usually assume an equal-tail probability, which results in −Z_1–α/2 and Z_1–α/2. However, we are at liberty to take any quantiles so that the area under the density between these quantiles is equal to the specified confidence level, 1–α. We select those quantiles that minimize the width of the CI for the ROC curve after Φ transformation (on the probability scale), not before as in the standard approach. This idea is realized below.

In an optimized version, when c=Φ⁻¹(p) is fixed, we represent the estimate of the ROC curve similar to Equation (9) as Φ(a+bz), where $z\sim \mathcal{N}(0,1)$, and a = X_c and $b=\sqrt{\widehat{\mathrm{var}}\left(X_c\right)}$ are assumed constant. We note that under those assumptions, for any values z₁ < 0 and z₂ > 0 such that

$$\Phi \left(z_2\right)-\Phi \left(z_1\right)=\lambda ,$$ (10)

a CI (Φ(a + bz₂), Φ(a + bz₁)) will cover the true value of the ROC curve, namely Φ(a), with probability λ. Therefore, we can chose z₁ and z₂ such that the CI has the shortest width,

$$\Phi (a+b{z}_2)-\Phi (a+b{z}_1)=\min .$$

Expressing z₂ through z₁ using Equation (10), we reduce this optimization problem to a one-variable minimization problem (z = z₁):

$$H\left(z\right)\stackrel{\mathrm{def}}{=}\Phi (a+b{\Phi }^{-1}(\lambda +\Phi \left(z\right))-\Phi (a+bz)\Rightarrow \min$$ (11)

over −∞ < z < Φ⁻¹(α). Minimization of function H(z) is a trivial task using modern statistical packages such as SAS or R/S-Plus (note that z₁ and z₂ depend on c). It is easy to see that the width of this CI is less than the “standard” width, H(−Z_1−α/2) = Φ(a + bZ_1−α/2) − Φ(a − bZ_1−α/2).

3.2 The AUC CI

Typically, the λ-CI for theAUC curve given by formula (6) is computed as the transformation of the symmetric λ-CI of the argument with the standard error approximated using the delta method. Here, we apply the above idea of the shortest CI to the AUC with

$$X=\frac{{\stackrel{‒}{x}}_1-{\stackrel{‒}{x}}_0}{\sqrt{s_0^2+s_1^2}}.$$

Based on the mutual independence of four estimates by the delta method, using formulas (8), we obtain

$$\widehat{\mathrm{var}}\left(X\right)\simeq \frac{s_0^2∕n_0+s_1^2∕n_1}{s_0^2+s_1^2}+\frac{{({\stackrel{‒}{x}}_1-{\stackrel{‒}{x}}_0)}^2}{2{(s_0^2+s_1^2)}^3}\left(\frac{s_0^4}{n_0-1}+\frac{s_1^4}{n_1-1}\right).$$

Then, the CI for the AUC is the Φ transformation of the interval

$$X\pm Z_{1-\alpha ∕2}\sqrt{\widehat{\mathrm{var}}\left(X\right)}.$$ (12)

The shortest CI reduces to a one-variable minimization problem (11). Typically, the CI for the AUC computed on the ROC scale may lead to values outside the interval [0,1], while the Φ-transformed CI remains in the desired range. We compare the coverage probability for the AUC based on Equation (12) with that suggested earlier by Hanley and McNail [17] via statistical simulations.

4. Simultaneous CBs

The pointwise CI for the ROC curve gives the CI of the sensitivity given the FN rate, p. Instead, one may seek a confidence set on the unit square that covers the entire ROC curve with a prespecified probability, λ. This idea leads to the concept of the simultaneous CB as a special case of the confidence region routinely used in multivariate statistics [30]. We argue that CI for the ROC curve (the simultaneous CB) seems more natural than the pointwise CI since the curve is of interest. Two types of simultaneous CB are considered in this section: one is based on the original idea in [34] and another is based on the novel idea of the ellipse-envelope approach.

4.1 Working–Hotelling CBs

Ma and Hall [23] adopted the idea of Working and Hotelling [34], originally intended for regression lines, to construct a CB for the ROC curve. Working and Hotelling developed a CB for a linear regression y = a + b(x − x̄) with coaxial ellipses:

$$\frac{{(a-\alpha )}^2}{{\sigma }_a^2}+\frac{{(b-\beta )}^2}{{\sigma }_b^2}={\chi }^2\left(2\right),$$ (13)

where $b=\sum (y_i-\stackrel{‒}{y})(x_i-\stackrel{‒}{x})∕\sum {(x_i-\stackrel{‒}{x})}^2$ and $a=\stackrel{‒}{y}-b\stackrel{‒}{x}$ are the least squares estimates of the intercept α and slope β. Ma and Hall simply applied this approach to X_c as a linear function of c defined in Equation (7) with intercept a = (x̄₁ − x̄₀)/s₁ and slope b = s₀/s₁. The attractiveness of this approach is that the same pointwise CB is used but with a different (greater) confidence coefficient. Specifically, instead of Z_1−α/2 in Equation (9), we use $\sqrt{q_{\lambda ,2}}$, where q_λ,2 is the λth quantile of the chi-square distribution with two degrees of freedom. It is possible to prove that $Z_{1-\alpha ∕2}<\sqrt{q_{\lambda ,2}}$, which implies that these CBs are wider than the pointwise version. For example, for λ = 0.95, we have $\sqrt{q_{\lambda ,2}}=2.45$, while Z_1−α/2 = 1.96.

4.2 The ellipse-envelope CB

In the Working–Hotelling approach, variances ${\sigma }_a^2$ and ${\sigma }_b^2$ in Equation (13) are assumed fixed and known which is not true even for the linear regression. Now we modify the Working–Hotelling approach to account for the fact that, instead of the true variances, we use ${\widehat{\sigma }}_a^2$ and ${\widehat{\sigma }}_b^2$. This approach is illustrated with the binormal ROC curve.

Recall that the basis of our CB for the ROC curve is the function

$$\gamma \left(c\right)=\frac{\mu -c}{\sigma }$$

since the sensitivity (1) and the FN probability (2) are functions of γ(c). Letting $\widehat{\gamma }\left(c\right)=(\stackrel{‒}{x}-c)∕s$ from the delta method [4], we approximate

$$\begin{array}{cc}\hfill \mathrm{var}\left(\widehat{\gamma }\left(c\right)\right)& \simeq \frac{1}{s^2}\mathrm{var}\left(\widehat{\mu }\right)+\frac{{(\widehat{\mu }-c)}^2}{4s^6}\mathrm{var}\left(s^2\right)\hfill \\ \hfill & =\frac{1}{n}+\frac{{(\widehat{\mu }-c)}^2}{2(n-1)s^2}=\frac{1}{n}+\frac{{\widehat{\gamma }}^2\left(c\right)}{2(n-1)}.\hfill \end{array}$$

As with the Working–Hotelling approach, we define the λ confidence region for the pair (γ₁(c), γ₂(c)) as the interior of an ellipse in terms of x and y,

$$\frac{{(x-{\widehat{\gamma }}_1\left(c\right))}^2}{1∕n_1+{\widehat{\gamma }}_1^2\left(c\right)∕2(n_1-1)}+\frac{{(y-{\widehat{\gamma }}_2\left(c\right))}^2}{1∕n_2+{\widehat{\gamma }}_2^2\left(c\right)∕2(n_2-1)}=q_{\lambda ,2}.$$ (14)

The envelope to this system of ellipses specifies simultaneous bounds for the ROC curve. Note that when the terms with ${\widehat{\gamma }}_1^2\left(c\right)$ and ${\widehat{\gamma }}_2^2\left(c\right)$ in the denominator of Equation (14) are ignored, we arrive at the classic Working–Hotelling approach, as implemented by Ma and Hall for the ROC curve.

To find these bounds, we differentiate the above equation with respect to c and equate it to zero. This equation generates a pair of curves that are the lower and the upper bounds for the (γ₁(c), γ₂(c)) curve.

As we show in the appendix, the ellipse envelope is reduced to a polynomial equation of the fourth order. The simultaneous bounds for the ROC curve are obtained after transformations (1) and (2).

5. Statistical simulations

In this section, we describe statistical simulations to assess the coverage probability for: (1) the two methods of simultaneous bands, Ma and Hall (MA) and our ellipse envelope, ${\widehat{\lambda }}_{\mathrm{MH}}$ and ${\widehat{\lambda }}_{\mathrm{EE}}$, respectively, and (2) the CI for the AUC as developed previously in [17] (see also [21, p. 79]) compared with that following from Equation (12), ${\widehat{\lambda }}_{\mathrm{HM}}$ and ${\widehat{\lambda }}_{\left(12\right)}$ respectively. The results of simulations are presented in Table 1; R is used for simulations with 10,000 experiments. Five sample sizes for the two groups (n₀ and n₁) in the range of 50–1000 were used to see whether the coverage probability depends on the sample size. Two significance levels α = 0.05 and α = 0.25 corresponding to the nominal confidence levels λ_nom = 0.95 and λ_nom = 0.75 were used. Two scenarios for the means were used: μ₀ = 1, μ₁ = 3 (strong discrimination) and μ₀ = 1, μ₁ = 2 (weak discrimination). The standard deviations were in the range from 0.5 to 2.5. The chosen parameters yield a wide range of binormal ROC curves with the AUC from 0.634 to 0.998.

Table 1.

Coverage probabilities from statistical simulations for [23] and the ellipse-envelope CB, and the CI for the AUC using Equation (12) and [17].

Strong discrimination (μ0 = 1, μ1 = 3)								Weak discrimination (μ0 = 1, μ1 = 2)
Sample size		SD		CB ROC		CI AUC		Samplesize		SD		CB ROC		CI AUC
n0	n1	σ 0	σ 1	${\widehat{\lambda }}_{\mathrm{EE}}$	${\widehat{\lambda }}_{\mathrm{MH}}$	${\widehat{\lambda }}_{\left(12\right)}$	${\widehat{\lambda }}_{\mathrm{HM}}$	n0	n1	σ 0	σ 1	${\widehat{\lambda }}_{\mathrm{EE}}$	${\widehat{\lambda }}_{\mathrm{MH}}$	${\widehat{\lambda }}_{\left(12\right)}$	${\widehat{\lambda }}_{\mathrm{HM}}$
λnom = 0.95
50	20	0.5	0.5	0.90	0.83	0.97	0.99	50	20	0.5	0.5	0.89	0.81	0.96	0.97
100	50	0.5	0.5	0.92	0.84	0.97	1.00	100	50	0.5	0.5	0.92	0.82	0.96	0.98
300	100	1.0	1.5	0.93	0.82	0.98	0.99	300	100	1.0	1.5	0.93	0.81	0.96	0.98
500	150	1.0	2.0	0.93	0.81	0.98	0.99	500	150	1.0	2.0	0.93	0.81	0.96	0.99
1000	300	1.5	2.5	0.94	0.82	0.97	0.99	1000	300	1.5	2.5	0.94	0.82	0.95	0.98
λnom = 0.75
50	20	0.5	0.5	0.66	0.41	0.81	0.98	50	20	0.5	0.5	0.63	0.34	0.78	0.84
100	50	0.5	0.5	0.68	0.42	0.81	0.99	100	50	0.5	0.5	0.66	0.35	0.79	0.85
300	100	1.0	1.5	0.68	0.31	0.80	0.88	300	100	1.0	1.5	0.68	0.30	0.77	0.84
500	150	1.0	2.0	0.66	0.29	0.81	0.89	500	150	1.0	2.0	0.67	0.28	0.77	0.86
1000	300	1.5	2.5	0.68	0.29	0.78	0.86	1000	300	1.5	2.5	0.68	0.28	0.76	0.84

${\widehat{\lambda }}_{\mathrm{EE}}$, Ellipse-envelope CB coverage probability; ${\widehat{\lambda }}_{\mathrm{MH}}$, Ma and Hall [23] CB coverage probability; ${\widehat{\lambda }}_{\left(12\right)}$, CI coverage probability of AUC using Equation (12); ${\widehat{\lambda }}_{\mathrm{HM}}$, Hanley and McNail [17] CI coverage probability of AUC.

In all scenarios, the empirical coverage probability for the simultaneous CB was smaller than the nominal confidence level. However, while the EE method $\left({\widehat{\lambda }}_{\mathrm{EE}}\right)$ produced the ROC band that just slightly less frequently covered the true ROC curve compared with the desired confidence level, the coverage probability for the MH method $\left({\widehat{\lambda }}_{\mathrm{MH}}\right)$ was significantly less than the nominal one. The latter method had especially poor performance for the nominal coverage λ_nom = 0.75, the coverage probability was half in this case. Remarkably, the coverage probability for both methods remained fairly stable across the sample sizes, means and standard deviations, although for the EE method the coverage probability improved slightly when the sample size got larger due to asymptotics (this is clearly seen for the 95% CB).

In terms of the AUC, the coverage probability of our method $\left({\widehat{\lambda }}_{\left(12\right)}\right)$ based on the Φ transformation of the interval (12) was close to nominal, while the Hanley and McNail [17]CI $\left({\widehat{\lambda }}_{\mathrm{HM}}\right)$ significantly overestimated the AUC.

6. Examples

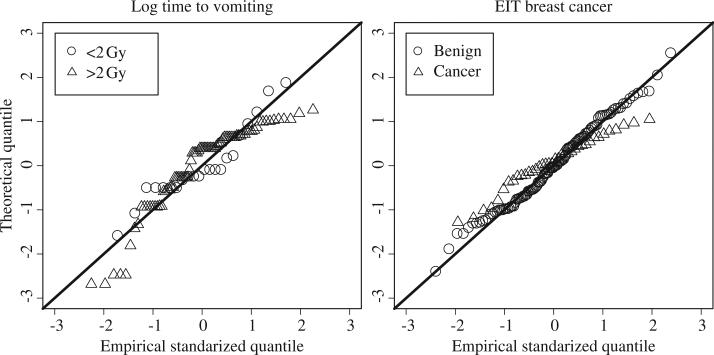
We illustrate CIs and CBs with two examples. In the first example, the original data are skewed to right, but after the log transformation makes them look quite normal. In the second example, as follows from a Q–Q plot, the transformation is not needed.

6.1 ROC curve for time to vomiting

Nuclear terrorism is one of today's dangers. In the case of a “dirty bomb” attack, one needs to get a rapid assessment of the radiation dose received by a large number of innocent individuals. It is well documented that victims typically vomit after receiving the radiation – the larger the dose, the sooner vomiting occurs [1]. Time to vomiting is a rapid self-evaluation technique that can be used for triage in the case of mass population involvement.

Several papers investigate the relationship between time to vomiting and the radiation dose received [11,27]. Here, we focus on assessing the sensitivity and specificity of time to vomiting when discriminating individuals who received less than 2 Gy and greater than 2 Gy of radiation, a widely accepted threshold for medical triage in the case of nuclear attack (Gy is a scale of radiation dose, 1 Gy = 100 rad): people who received less than 2 Gy do not require medical attention, but those who received greater than 2 Gy should undergo a thorough evaluation and possibly medical treatment [9].

We use the data on three radiological accidents that happened in the former USSR and the USA in the period 1956–2001 to illustrate the computation of sensitivity and specificity for the vomiting test (Figure 1). The majority of the cases came from the Chernobyl accident. For this example, the 0 group constitutes individuals who received < 2 Gy (n₀ = 24), and the 1 group received ≥ 2 Gy (n₁ = 84). We want to predict who received radiation > 2 Gy knowing how long after the accident the person vomited. We make a couple of comments: first, since more radiation leads to sooner vomiting, our decision rule is based on “<” not the “>”, as in the previous sections. The change of the inequality sign does not change the theory, but should be kept in mind at the interpretation stage. Second, before constructing the ROC curve and its confidence bounds, it is advantageous to take log₁₀ of the time to vomiting because the data are skewed to the right. Indeed, as follows from the Q–Q plot in Figure 2, the data in the two groups after the log transformation seem to follow the normal distribution, so that the binormal ROC curve is valid. For the group of individuals who received less than 2 Gy, ${\widehat{\mu }}_0=0.633$ and ${\widehat{\sigma }}_0=0.305$, and for individuals who received greater than 2 Gy, ${\widehat{\mu }}_1=0.115$ and ${\widehat{\sigma }}_1=0.455$ on the log₁₀ scale. Apparently, different cut-offs in time to vomiting lead to different FP and FN errors, so the ROC curve becomes a very valuable graphical technique to compare different scenarios of handling a large mass of people.

Figure 1.

Time-to-vomiting data as a function of the radiation dose received from three accidents, n = n₀ + n₁ = 108. The 2 Gy radiation dose divides people into two groups: those who are OK and those who should go through additional evaluation. The log scale seems appropriate for this data (Figure 2).

Figure 2.

Q–Q plots for the two examples – the distributions are fairly close to normal.

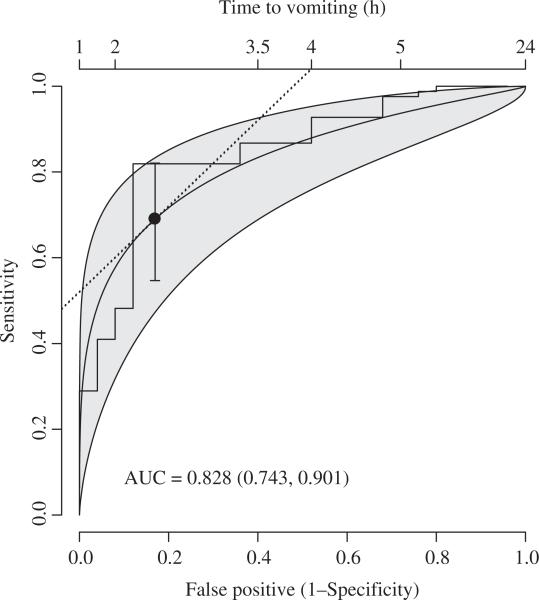
The ROC curve with its 95% ellipse-envelope CB (shaded area) is presented in Figure 3. The bold curve shows the binormal ROC (3) with sample means and standard deviations. The cut-off time to vomiting is shown on the top axis. For example, if the decision of 2 Gy is made based on the 2 h rule, 60% of victims will be identified correctly at the price of a 10% FP rate. The area under the ROC curve is 0.828, meaning that the probability that a randomly chosen pair of individuals can be truly discriminated based on time to vomiting is 0.828.

Figure 3.

Time-to-vomiting ROC curve as a 2 Gy discriminator with 95% CB and CI with the shortest width at the discriminant solution point (the step line is the empirical ROC curve).

The discriminant solution for the cut-off point minimizes the sum of FN and FP errors and corresponds to the point where the 45 degree straight line (dotted) touches the ROC curve. This solution gives c = 0.34 which corresponds to 10^0.34 = 2.2 h. We show the pointwise 95% CI with the shortest width at this point. Obviously, this interval lies within the simultaneous CB.

The shortest CI for the sensitivity given the specificity requires a univariate minimization defined in Equation (11). Assuming that the cut-off is 2 h after vomiting, which is equivalent to a FP rate of about 10%, the sensitivity lies in the interval (0.35, 0.7) with probability 95%. The standard 95% CI for the AUC is (0.736, 0.896) with Z = − 1.96, but the 95% CI with the shortest width is (0.743, 0.901) with z₁ = − 1.828 and z₂ = 2.138.

In summary, although time to vomiting is a simple measure for dose reconstruction, it is quite imprecise because it has large CBs. The ROC curve with its CB is an indispensable tool for government agencies when time to vomiting is used for radiation dose reconstruction in the case of nuclear terrorism.

6.2 Electrical impedance tomography breast cancer detection

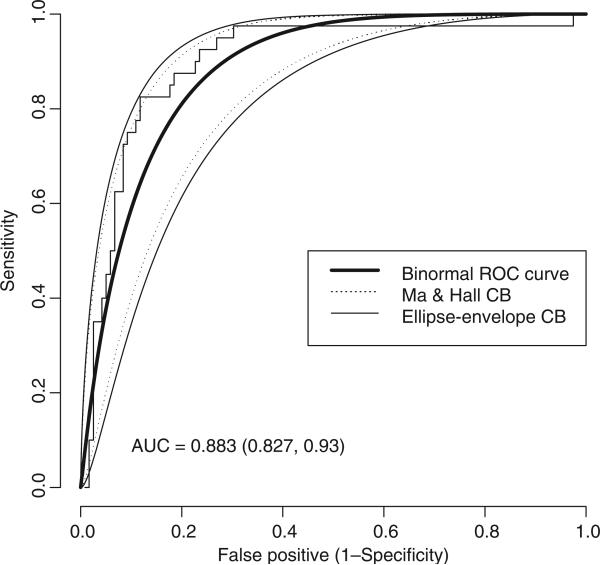
Traditional breast imaging techniques, such as mammography and ultrasound, tend to overlook breast cancer in young women. Radiologist's interpretations of images is essentially subjective and contribute to FP rates and decreases in sensitivity of malignant abnormality detection. Electrical impedance tomography (EIT) is an alternative physical model-based imaging modality aimed at reducing erroneous diagnosis by estimating electric properties of the breast, such as conductivity and permittivity, at specific suspicious locations of the breast [25,31]. Statistical estimation methods of electrical properties become dominating techniques in breast tissue classification and probability assessment of the malignancy [7]. Fundamental to breast cancer detection are calibration ex vivo studies when conductivity and permittivity are measured in excised breast tissues and used for calibration for in vivo exams [13]. We use ex vivo data presented in [20] to construct a binormal ROC curve to discriminate benign mass from a cancer tumour using 10 current frequencies (Figure 4; as follows from Figure 2, the distribution in the two groups is close to normal). The stepwise line depicts the empirical ROC curve based on 159 breast tissue samples; among them 119 are benign abnormalities classified as fibroadenoma, mastopathy and mammary gland, and 40 are carcinoma tumours. The bold line depicts the binormal ROC curve. Two simultaneous CBs are shown: our ellipse-envelope band is wider than that of Ma and Hall. This can be explained with our simulation results because the coverage probability of this method is consistently less than nominal.

Figure 4.

The binormal ROC curve for breast cancer discrimination based on the EIT measurements.

7. Conclusion and future work

The ROC curve is a well-established statistical concept that visually represents the trade-off between the sensitivity and specificity of a test. Although much work has been done on the construction of the CB for the nonparametric ROC curve, surprisingly little research and software is available for the simplest parametric, binormal, ROC curve. For example, we could not find a closed-form expression for the CI of the area under binormal ROC curve in the existing literature.

We have developed optimized (shortest width) CIs and CBs for the binormal ROC curve and demonstrated through simulations that coverage probabilities are much closer to the nominal level than for the existing methods. The R code along with the data on time to vomiting is available online at the author's webpage: www.dartmouth.edu/^~eugened.

While the binormal ROC curve has been criticized as being restrictive, we found that in real applications the data can be successfully normalized after an appropriate monotonic transformation, such as the log transformation. The existence of the normalizing transformation for the continuous random variable with density p(x) follows from the theory of ordinary differential equation (ODE). Indeed, if an increasing inverse transformation function is g(·) and ϕ is the density of the normal distribution, we have ϕ(x) = g′(x)p(g(x)), so that the transformation function obeys the ODE g′(x) = p(g(x))/ϕ(x), a nonlinear ODE of the first order. As follows from Picard's existence theorem [10], a normalizing monotonic transformation exists for any continuous random variable. Recall that nonparametric estimation of the ROC curve is not assumption free; for example, the choice of the width in the kernel density estimation significantly influences the ROC curve.

The performance of the considered CIs and CBs is questionable in small samples because the delta method was used for variance approximation. This suggests a direction for a future work on exact CIs and CBs that would assure the coverage probability equal, or close, to the nominal probability for all n₀ and n₁. A hint to the construction of an exact and possibly optimal CI is an observation that the CI (C₁, C₂) for the random variable of interest given by Equation (7) can be rewritten as

$$C_1{s}_1<{\widehat{\mu }}_1-{\widehat{\mu }}_0+s_{0}c<C_2{s}_1.$$

Since ${\widehat{\mu }}_1-{\widehat{\mu }}_0$, $s_0^2$ and $s_1^2$ are mutually independent with known distributions, there is a possibility to find C₁ < C₂ such that the probability of the above double inequality is at least λ and C₂ – C₁ = min. The construction of CIs and CBs for the binormal ROC curve is a practically urgent and theoretically challenging task.

Appendix. Derivation of the ellipse-envelope CB

Let

$$u=x-{\widehat{\gamma }}_0\left(c\right),v=y-{\widehat{\gamma }}_1\left(c\right)$$ (A1)

and

$$A_k={\left(\frac{1}{n_k}+\frac{{\widehat{\gamma }}_k^2\left(c\right)}{2(n_k-1)}\right)}^{-1},k=0,1.$$

After differentiating equation (14) with respect to c and setting the derivative to zero, we obtain the equation

$$\frac{2A_0}{{\sigma }_0}u-\frac{2A_0^2}{{\sigma }_0}{u}^2{\widehat{\gamma }}_0\left(c\right)+\frac{2A_1}{{\sigma }_1}v-\frac{2A_1^2}{{\sigma }_1}{v}^2{\widehat{\gamma }}_1\left(c\right)=0,$$

which, in combination with Equation (14), defines a couple of curves as functions of c.After some simplification, we come to a system of two equations for u and v:

$$\begin{array}{cc}\hfill A_0{u}^2+A_1{v}^2& =q_{\lambda ,2},\hfill \\ \hfill B_{0}u-D_0{u}^2+B_{1}v-D_1{v}^2& =0,\hfill \end{array}$$

where

$$B_k=\frac{A_k}{{\sigma }_k},D_k=\frac{{\widehat{\gamma }}_1\left(c\right)A_k^2}{{\sigma }_k(n_k-1)}.$$

After some algebra, one can find

$$\begin{array}{cc}\hfill v& =\eta ,\hfill \\ \hfill u& =\frac{(A_0{D}_1-D_0{A}_1){\eta }^2-A_0{B}_1\eta +D_0{q}_{\lambda ,2}}{B_0{A}_0},\hfill \end{array}$$

where η is a root of a fourth-order polynomial equation:

$$p_4{\eta }^4+p_3{\eta }^3+p_2{\eta }^2+p_1\eta +p_0=0$$

with coefficients defined as

$$\begin{array}{cc}\hfill p_4& =A_1^2{D}_0^2-2D_0{D}_1{A}_0{A}_1+A_0^2{D}_1^2,\hfill \\ \hfill p_3& =2D_0{A}_0{A}_1{B}_1-2A_0^2{D}_1{B}_1,\hfill \\ \hfill p_2& =A_0{A}_1{B}_2^2+2D_0{A}_1{D}_1{q}_{\lambda ,2}+B_1^2{A}_0^2-2D_0^2{A}_1{q}_{\lambda ,2},\hfill \\ \hfill p_1& =-2A_0{D}_0{B}_1{q}_{\lambda ,2},\hfill \\ \hfill p_0& =-B_0^2{A}_{0}q+D_0^2{q}_{\lambda ,2}^2.\hfill \end{array}$$

This polynomial has two real roots for each c that, from Equation (A1), determine a couple of curves x(c) and y(c) leading to the simultaneous lower and upper confidence bounds.