Bayesian Kernel Mixtures for Counts

Abstract

Although Bayesian nonparametric mixture models for continuous data are well developed, there is a limited literature on related approaches for count data. A common strategy is to use a mixture of Poissons, which unfortunately is quite restrictive in not accounting for distributions having variance less than the mean. Other approaches include mixing multinomials, which requires finite support, and using a Dirichlet process prior with a Poisson base measure, which does not allow smooth deviations from the Poisson. As a broad class of alternative models, we propose to use nonparametric mixtures of rounded continuous kernels. An efficient Gibbs sampler is developed for posterior computation, and a simulation study is performed to assess performance. Focusing on the rounded Gaussian case, we generalize the modeling framework to account for multivariate count data, joint modeling with continuous and categorical variables, and other complications. The methods are illustrated through applications to a developmental toxicity study and marketing data. This article has supplementary material online.

1. INTRODUCTION

Nonparametric methods for estimation of continuous densities are well developed in the literature from both a Bayesian and frequentist perspective. For example, for Bayesian density estimation, one can use a Dirichlet process (DP) (Ferguson 1973, 1974) mixture of Gaussians kernels (Lo 1984; Escobar and West 1995) to obtain a prior for the unknown density. Such a prior can be chosen to have dense support on the set of densities with respect to Lebesgue measure. Ghosal et al. (1999) show that the posterior probability assigned to neighborhoods of the true density converges to one exponentially fast as the sample size increases, so that consistent estimates are obtained. Similar results can be obtained for nonparametric mixtures of various non-Gaussian kernels using tools developed in Wu and Ghosal (2008).

In this article our focus is on nonparametric Bayesian modeling of counts using related nonparametric kernel mixture priors to those developed for estimation of continuous densities. There are several strategies that have been proposed in the literature for nonparametric modeling of count distributions having support on the non-negative integers $\mathcal{N}=\{0,\dots ,\infty \}$. The first is to use a mixture of Poissons

$$\mathrm{Pr}(Y=j\mid P)=\int \mathrm{Poi}(j;\lambda )dP\left(\lambda \right),j\in \mathcal{N},$$ (1)

with Poi(j; λ) = λ^j exp(−λ)/j! and P a mixture distribution. When P is chosen to correspond to a Ga(ϕ, ϕ) distribution on the Poisson rate parameter, one induces a negative-binomial distribution, which accounts for over-dispersion with the variance greater than the mean. Generalizations of (1) to include predictors and random effects within a log-linear model for λ are widely used. A review of the properties of Poisson mixtures is provided in Karlis and Xekalaki (2005).

As a more flexible nonparametric approach, one can instead choose a DP mixture of Poissons by letting P ~ DP(αP₀), with α the DP precision parameter and P₀ the base measure. As the DP prior implies that P is almost surely discrete, we obtain

$$\mathrm{Pr}(Y=j\mid \pi ,\lambda )=\sum _{h=1}^{\infty }{\pi }_h\mathrm{Poi}(j;{\lambda }_h),{\lambda }_h\sim P_0,$$ (2)

with π = {π_h} ~ Stick(α) denoting that the π are random weights drawn from the stick-breaking process of Sethuraman (1994). Krnjajic et al. (2008) recently considered a related approach motivated by a case control study. Dunson (2005) proposed an approach for nonparametric estimation of a non-decreasing mean function, with the conditional distribution modeled as a DPM of Poissons. Kleinman and Ibrahim (1998) proposed to use a DP prior for the random effects in a generalized linear mixed model. Guha (2008) recently proposed more efficient computational algorithms for related models. Chen et al. (2002) considered nonparametric random effect distributions in frequentist generalized linear mixed models.

On the surface, model (2) seems extremely flexible and to provide a natural modification of the DPM of Gaussians used for continuous densities. However, as the Poisson kernel used in the mixture has a single parameter corresponding to both the location and scale, the resulting prior on the count distribution is actually quite inflexible. For example, distributions that are under-dispersed cannot be approximated and will not be consistently estimated. One can potentially use mixture of multinomials instead of Poissons, but this requires a bound on the range in the count variable and the multinomial kernel is almost too flexible in being parametrized by a probability vector equal in dimension to the number of support points. Kernel mixture models tend to have the best performance when the effective number of parameters is small. For example, most continuous densities can be accurately approximated using a small number of Gaussian kernels having varying locations and scales. It would be appealing to have such an approach available also for counts.

An alternative nonparametric Bayes approach would avoid a mixture specification and instead let y_i ~ P with P ~ DP(αP₀) and P₀ corresponding to a base parametric distribution, such as a Poisson. Carota and Parmigiani (2002) proposed a generalization of this approach in which they modeled the base distribution as dependent on covariates through a Poisson log-linear model. Although this model is clearly flexible, there are some major disadvantages. To illustrate the problems that can arise, first note that the posterior distribution of P given iid draws yⁿ = (y₁, … , y_n)’ is simply

$$(P\mid {\mathbf{y}}^n)\sim \mathrm{DP}\left((\alpha +n)\left\{\alpha P_0+\sum _i{\delta }_{y_i}\right\}\right),$$

with δ_y a degenerate distribution with all its mass at y. Hence, the posterior is centred on a mixture with weight proportional to α on the Poisson base P₀ and weight proportional to n on the empirical probability mass function. There is no allowance for smooth deviations from the base.

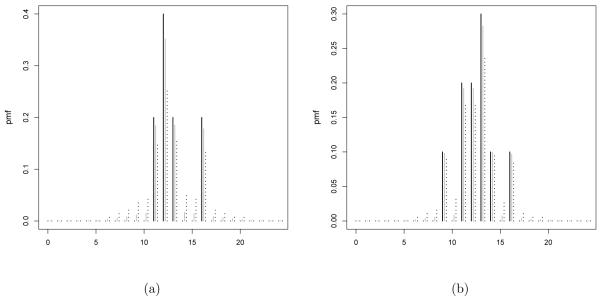
As a motivating application, we consider data from a developmental toxicity study of ethylene glycol in mice conducted by the National Toxicology Program (Price et al. 1985). As in many biological applications in which there are constraints on the range of the counts, the data are underdispersed having mean 12.54 and variance 6.78. A histogram of the raw data for the control group (25 subjects) is shown in Figure 1 along with a series of estimates of the posterior mean of Pr(Y = j) assuming y_i ~ P with P ~ DP(αP₀), α= 1 or 5, and $P_0=\mathrm{Poi}\left(\stackrel{‒}{y}\right)$ as an empirical Bayes choice. To illustrate the behavior as the sample size increases we take random subsamples of the data of size n_s ∈ {5, 10}. As Figures 1 and 2 illustrates, the lack of smoothing in the Bayes estimate is unappealing in not allowing borrowing of information about local deviations from P₀. In particular for small sample size as in Figure 2 the posterior mean probability mass function corresponds to the base measure with high peaks on the observed y. As the sample size increases, the empirical probability mass function increasingly dominates the base.

Figure 1.

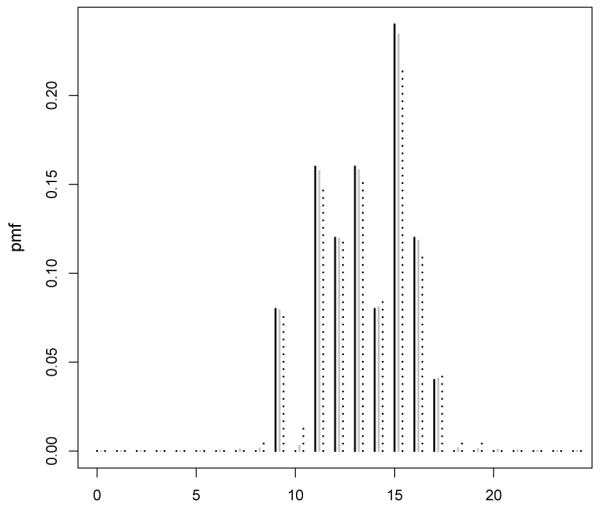
Histogram of the number of implantation per pregnant mouse in the control group (black line) and posterior mean of Pr(Y = j) assuming a Dirichlet process prior on the distribution of the number of implants with α = 1, 5 (grey and black dotted line respectively) and base measure $P_0=\mathrm{Poi}\left(\stackrel{‒}{y}\right)$.

Figure 2.

Histogram of subsamples (n = 5, 10) of the control group data on implantation in mice (black line) and posterior mean of Pr(Y = j) assuming a Dirichlet process prior on the distribution of the number of implants with α = 1, 5 (grey and black dotted line respectively) and base measure $P_0=\mathrm{Poi}\left(\stackrel{‒}{y}\right)$.

With this motivation, we propose a general class of kernel mixture models for count data, with the kernels induced through rounding of continuous kernels. Such rounded kernels are highly flexible and tend to have excellent performance in small samples. Methods are developed for efficient posterior computation using a simple data augmentation Gibbs sampler, which adapts approaches for computation in DPMs of Gaussians. Simulation studies are conducted to assess performance and the methods are applied to the developmental toxicity data and a marketing application.

2. UNIVARIATE ROUNDED KERNEL MIXTURE PRIORS

2.1 Rounding continuous distributions

In the univariate case, letting $y\in \mathcal{N}$ denote a count random variable, our goal is to specify a prior for the probability mass function p of this random variable. Following the philosophy of Ferguson (1973), nonparametric priors for unknown distributions should be interpretable, have large support and lead to straightforward posterior computation. We propose a simple approach that induces Π through first choosing a prior Π* for the density f of a continuous random variable $y^{\ast }\in \mathcal{Y}$ and then rounding $y^{\ast }\in \mathcal{Y}$ to obtain $y\in \mathcal{N}$. Here, $\mathcal{Y}$ is either the real line $\mathbb{R}$ or a measurable subset. As we will show, this approach clearly leads to all three of the desirable properties mentioned by Ferguson and additionally is easily generalizable to more complex cases involving multivariate modeling of counts jointly with continuous and categorical variables and nonparametric regression for counts.

Focusing first on the univariate case, let y = h(y*), where h(·) is a rounding function defined so that h(y*) = j if y* ∈ (a_j, a_j+1], for j = 0, 1, … , ∞, with a₀ < a₁ < … an infinite sequence of pre-specified thresholds that defines a disjoint partition of $\mathcal{Y}$. For example, when $\mathcal{Y}=\mathbb{R}$ one can simply choose $\mathbf{a}={\left\{a_j\right\}}_{j=0}^{\infty }$ as {−∞, 0, 1, 2, … , ∞}. The probability mass function p of y is p = g(f), where g(·) is a rounding function having the simple form

$$p\left(j\right)=g\left(f\right)\left[j\right]={\int }_{a_j}^{a_{j+1}}f\left(y^{\ast }\right)\mathrm{d}{y}^{\ast }j\in \mathcal{N}.$$ (3)

The thresholds a_j are such that $a_0=\min \{y^{\ast }:y^{\ast }\in \mathcal{Y}\}$, $a_{\infty }=\max \{y^{\ast }:y^{\ast }\in \mathcal{Y}\}$ and hence ${\int }_{a_0}^{a_{\infty }}f\left(y^{\ast }\right)\mathrm{d}{y}^{\ast }=1$.

Relating ordered categorical data to underlying continuous variables is quite common in the literature. For example, Albert and Chib (1993) proposed a very widely used class of data augmentation Gibbs sampling algorithms for probit models. In such settings, one typically lets a₀ = −∞ and a₁ = 0, while estimating the remaining k – 2 thresholds, with k denoting the number of levels of the categorical variable. A number of authors have relaxed the assumption of the probit link function through the use of nonparametric mixing. For example, Kottas et al. (2005) generalized the multivariate probit model by using a mixture of normals in place of a single multivariate normal for the underlying scores, with Jara et al. (2007) proposing a related approach for correlated binary data. Gill and Casella (2009) instead used Dirichlet process mixture priors for the random effects in an ordered probit model.

In the setting of count data, instead of estimating the thresholds on the underlying variables, we use a fixed sequence of thresholds and rely on flexibility in nonparametric modeling of f to induce a flexible prior on p. In order to assign a prior Π on the space of count distributions, it is sufficient under this formulation to specify a prior Π* on the space $\mathcal{L}$ of densities with respect to Lesbesgue measure on $\mathcal{Y}$. In Section 2.3, we demonstrate that the induced prior P ~ Π for the count probability mass function satisfies Ferguson’s desired properties of interpretability and large support.

2.2 Some examples of rounded kernel mixture prior

For appropriate choices of kernel, it is well known that kernel mixtures can accurately approximate a rich variety of densities, with Dirichlet process mixtures of Gaussians forming a standard choice for densities on $\mathbb{R}$. Hence, in our setting a natural choice of prior for the underlying continuous density corresponds to

$$\begin{array}{cc}\hfill & f(y^{\ast };P)=\int N(y^{\ast };\mu ,{\tau }^{-1})dP(\mu ,\tau ),\hfill \\ \hfill & P\sim \tilde{\Pi },\hfill \end{array}$$ (4)

where N(y; μ, τ⁻¹) is a normal kernel having mean μ and precision τ and $\tilde{\Pi }$ is a prior on the mixing measure P, with a convenient choice corresponding to the Dirichlet process DP(αP₀), with P₀ chosen to be Normal-Gamma. Let Π* denote the prior on f induced through (4) and let denote the resulting prior on p induced through (3) with the thresholds chosen as a₀ = −∞ and a_j = j – 1 for j ∈ {1, 2, … }.

Other choices can be made for the prior on the underlying continuous density, such as mixtures of log-normal, gamma or Weibull densities with a_j = j. However, we will focus on the class of DP mixtures of rounded Gaussian kernels for computational convenience and because there is no clear reason to prefer an alternative choice of kernel or mixing prior from an applied or theoretical perspective. This choice leads to all three of the desired Ferguson properties of a nonparametric prior.

2.3 Some properties of the prior

Let Π denote the prior on p defined in Section 2.2, with F denoting the cumulative distribution function corresponding to the density f. As p is a random probability mass function, it is of substantial interest to define the prior expectation and variance of p(j). In what follows we show that the prior mean and variance have a simple form under the proposed prior, leading to ease in interpretation and facilitating prior elicitation through centering on an initial guess for p. Clearly

$$\mathrm{E}\left\{p\right(j\left)\right\}=\mathrm{E}\left\{{\int }_{a_j}^{a_{j+1}}f(y^{\ast };P)d{y}^{\ast }\right\}=\mathrm{E}\left\{F\right(a_{j+1}\left)\right\}-\mathrm{E}\left\{F\right(a_j\left)\right\}.$$

One can express the expected value of F(a_j) marginalizing over the prior $P\sim \tilde{\Pi }$ as

$$\mathrm{E}\left\{F\right(a_j\left)\right\}=\int F(a_j;P)d\tilde{\Pi }\left(P\right)=\int {\int }_{-\infty }^{a_j}f(y^{\ast };P)d{y}^{\ast }d\tilde{\Pi }\left(P\right).$$

Assuming $\tilde{\Pi }=DP\left(\alpha P_0\right)$ with P₀ = N(μ; μ₀, κτ⁻¹)Ga(τ; ν/2,ν/2) we have

$$\mathrm{E}\left\{p\right(j\left)\right\}={\mathcal{T}}_{\nu }(a_{j+1};{\mu }_0,\kappa +1)-{\mathcal{T}}_{\nu }(a_j;{\mu }_0,\kappa +1)$$ (5)

where ${\mathcal{T}}_{\nu }(\cdot ;\xi ,\omega )$ is the cdf of a non central Student-t distribution with ν degrees of freedom, location ξ and scale ω. Hence, the expected probability of y = j is simply a difference in t cdfs having ν degrees of freedom, mean μ₀, and scale κ + 1. Setting μ₀ = 0 and κ = 1 for identifiability, the prior for p can be centered to have expectation exactly equal to an arbitrary pmf q chosen to represent one’s prior beliefs simply by moving around the thresholds; a simple iterative algorithm for choosing a to enforce E{p(j)} = q(j), for j = 0, 1, … is shown below. Although we can conceptually define an infinite sequence of thresholds, practically it is sufficient to define E{p(j)} = q(j), for j = 0, 1, … , J with ${\sum }_{j=0}^{J}q\left(j\right)=1-∊$ and let the remaining a_j for j = J + 1, … to be equispaced with unit step.

The variance can be computed along similar lines. Let F_D(a, b) = F(b) – F(a), Φ(a; ξ, ω) the cumulative distribution function of a normal with mean ξ and variance ω, Φ_D(a, b; χ, ω) = Φ(b; ξ, ω) – Φ(a; ξ, ω) and ${\mathcal{T}}_{D,\nu }(a,b;\xi ,\omega )={\mathcal{T}}_{\nu }(b;\xi ,\omega )-{\mathcal{T}}_{\nu }(a;\xi ,\omega )$,

$$\begin{array}{cc}\hfill \mathrm{Var}\left\{p\right(j\left)\right\}=& \mathrm{Var}\left\{F_D\right(a_j,a_{j+1}\left)\right\}\hfill \\ \hfill =& \mathrm{E}\left\{F_D{(a_j,a_{j+1})}^2\right\}-\mathrm{E}{\left\{F_D\right(a_j,a_{j+1}\left)\right\}}^2\hfill \\ \hfill =& \frac{1}{\alpha +1}\left[\mathrm{E}\left\{{\Phi }_D{(a_j,a_{j+1};\mu ,{\tau }^{-1})}^2\right\}-{\left\{{\mathcal{T}}_{D,\nu }\right(a_j,a_{j+1};{\mu }_0,\kappa +1\left)\right\}}^2\right].\hfill \end{array}$$ (6)

The expected value of the squared normal cdf is with respect to P₀ and can be computed numerically. The derivations are outlined in the supplemental materials.

In the presence of prior information on the random p, one can define the sequence of a_j iteratively in order to let E{p(j)} = q(j), where q is an initial guess for the probability mass function, defined for all j. Result (5), with μ₀ and κ fixed to 0 and 1, leads to define the thresholds iteratively as

$$\begin{array}{cc}\hfill a_0& =-\infty \hfill \\ \hfill a_1& ={\mathcal{T}}_{\nu }^{-1}\left(q\right(0);0,2)\hfill \\ \hfill a_2& ={\mathcal{T}}_{\nu }^{-1}\left(q\right(0)+q(1);0,2)\hfill \\ \hfill \cdots & \hfill \\ \hfill a_j& ={\mathcal{T}}_{\nu }^{-1}\left(\sum _{i=0}^{j-1}q\right(i);0,2)\hfill \end{array}$$

From the above, it is clear that the prior is interpretable to the extent that simple expressions exist for the mean and variance that can be used in prior elicitation. In addition, as we will show the prior has appealing theoretical properties in terms of large support and posterior consistency. Large Kullback-Leibler support of the prior Π is straightforward if we start from a prior Π* with such a property. Lemma 1, in fact, demonstrates that the mapping $g:\mathcal{L}\to \mathcal{C}$ maintains Kullback-Leibler neighborhoods and, as is formalised in Theorem 1, this property implies that the induced prior p ~ Π assigns positive probability to all Kullback-Leibler neighbourhoods of any $p_0\in \mathcal{C}$ if at least one element of the set g⁻¹(p₀) is in the Kullback-Leibler support of the prior Π*. By using conditions of Wu and Ghosal (2008), the Kullback-Leibler condition becomes straightforward to demonstrate for a broad class of kernel mixture priors Π*.

Lemma 1

Assume that the true density of a count random variable is p₀ and choose any f₀ such that p₀ = g(f₀). Let ${\mathcal{K}}_{∊}\left(f_0\right)=\{f:KL(f_0,f)<∊\}$ be a Kullback-Leibler neighbourhood of size ∊ around f₀. Then the image $g\left({\mathcal{K}}_{∊}\right(f_0\left)\right)$ contains values $p\in \mathcal{C}$ in a Kullback-Leibler neighbourhood of p₀ of at most size ∊.

Theorem 1

Given a prior Π* on ${\mathcal{L}}_{{\Pi }^{\ast }}\subseteq \mathcal{L}$ such that all $f\in {\mathcal{L}}_{{\Pi }^{\ast }}$ are in the Kullback-Leibler support of Π*, then all $p\in {\mathcal{C}}_{\Pi }=g\left({\mathcal{L}}_{{\Pi }^{\ast }}\right)$ are in the Kullback-Leibler support of Π.

Theorem 1 follows directly from Lemma 1, because for every $f\in {\mathcal{L}}_{{\Pi }^{\ast }}$ by Lemma 1 we have $\Pi \left({\mathcal{K}}_{∊}\right(p\left)\right)\ge \Pi \left(g\right({\mathcal{K}}_{∊}\left(f\right)\left)\right)={\Pi }^{\ast }\left({\mathcal{K}}_{∊}\right(f\left)\right)>0$.

A direct consequence of Theorem 1 is that, under the theory of Schwartz (1965), the posterior probability of any weak neighbourhood around the true data-generating distribution $p_0\in {\mathcal{C}}_{\Pi }$ converges to one with P_p0-probability 1 as n → ∞.

Theorem 2 points out that in the space of probability mass functions weak consistency implies strong consistency in the L₁ sense. This implies that the Kullback-Leibler condition is sufficient for strong consistency in modeling count distributions.

Theorem 2

Given a prior p ~ Π for a probability mass function $p\in \mathcal{C}$, if the posterior Π(·∣y₁, … , y_n) is weakly consistent, then it is also strongly consistent in the L₁ sense.

2.4 A Gibbs sampling algorithm

For posterior computation, we can trivially adapted any existing MCMC algorithm developed for DPMs of Gaussians with a simple data augmentation step for imputing the underlying variables. For simplicity in describing the details, we focus on the blocked Gibbs sampler of Ishwaran and James (2001), with $f\left(y^{\ast }\right)={\sum }_{h=1}^N{\pi }_{h}N(y^{\ast };{\mu }_h,{\tau }_h^{-1})$ with π₁ = V₁, π_h = V_h∏_l<h(1 − V_l), V_h independent Beta(1,α) and V_N = 1. Modifications to avoid truncation can be applied using slice sampling as described in Walker (2007) and Yau et al. (2010). The blocked Gibbs sampling steps are as follows:

Step 1 Generate each $y_i^{\ast }$ from the full conditional posterior

• Step 1a Generatge $u_i\sim U\left(\Phi (a_{y_i};{\mu }_{S_i},{\tau }_{S_i}^{-1}),\Phi (a_{y_i+1};{\mu }_{S_i},{\tau }_{S_i}^{-1})\right)$

• Step 1b Let $y_i^{\ast }={\Phi }^{-1}(u_i;{\mu }_{S_i},{\tau }_{S_i}^{-1})$

Step 2 Update S_i from its multinomial conditional posterior with

$$\mathrm{Pr}(S_i=h\mid -)=\frac{{\pi }_{h}p(y_i\mid {\mu }_h,{\tau }_h^{-1})}{\sum _{l=1}^N{\pi }_{l}p(y_i\mid {\mu }_l,{\tau }_l^{-1})},$$

where $p(j\mid {\mu }_h,{\tau }_h^{-1})=\Phi (a_{j+1}\mid {\mu }_h,{\tau }_h^{-1})-\Phi (a_j\mid {\mu }_h,{\tau }_h^{-1})$.

Step 3 Update the stick-breaking weights using

$$V_h\sim \mathrm{Be}\left(1+n_h,\alpha +\sum _{l=h+1}^N{n}_l\right)$$

Step 4 Update (μ_h, τ_h) from its conditional posterior

$$({\mu }_h,{\tau }_h^{-1})\sim \mathrm{N}({\widehat{\mu }}_h,{\widehat{\kappa }}_h{\tau }_h^{-1})\mathrm{Ga}({\widehat{a}}_{{\tau }_h},{\widehat{b}}_{{\tau }_h})$$

with ${\widehat{a}}_{{\tau }_h}=a_{\tau }+n_h∕2$, ${\widehat{b}}_{{\tau }_h}=b_{\tau }+1∕2\left({\sum }_{i:S_i=h}\right(y_i^{\ast }-{\stackrel{‒}{y}}_h^{\ast })+n_h∕(1+\kappa n_h\left){({\stackrel{‒}{y}}_h^{\ast }-{\mu }_0)}^2\right)$, ${\widehat{\kappa }}_h={({\kappa }^{-1}+n_h)}^{-1}$ and ${\widehat{\mu }}_h={\widehat{\kappa }}_h({\kappa }^{-1}{\mu }_0+n_h{\stackrel{‒}{y}}_h^{\ast })$.

2.5 Simulation study

To assess the performance of the proposed approach, we conducted a simulation study. Four different approaches for estimating the probability mass function were compared to our proposed rounded mixture of Gaussians (RMG): the empirical probability mass function (E), two Bayesian nonparametric approaches, with the first assuming a Dirichlet process prior with a Poisson base measure (DP) and the second using a Dirichlet process mixture of Poisson kernels (DPM-Pois), and lastly the maximum likelihood estimate under a Poisson model (MLE). Several simulations have been run under different simulation settings leading to qualitatively similar results. In what follows we report the results for four scenarios. The first simulation case, henceforth scenario (a), assumed the data were simulated as the floor of draws from the mixture of Gaussians given by 0.4N(25, 1.5) + 0.15N(20, 1) + 0.25N(24, 1) + 0.2N(21, 2), the second scenario (b), assumed a simple Poisson model with mean 12, the third (c) assumed the mixture of Poissons given by 0.4Poi(1) + 0.25Poi(3) + 0.25Poi(5) + 0.1Poi(13), while the last one (scenario (d)) assumed an underdispersed probability mass function, the Conway-Maxwell-Poisson distribution (Shmueli et al. 2005) with parameters λ = 30 and ν = 3.

For each case, we generated sample sizes of n = 10, 25, 50, 100, 300. Each of the five analysis approaches were applied to R = 1, 000 replicated data sets under each scenario. The methods were compared based on a Monte Carlo approximation to the mean Bhattacharya distance (BCD) and Kullback-Leibler divergence (KLD) calculated as

$$\begin{array}{cc}\hfill \mathrm{BCD}=& \frac{1}{R}\sum _{r=1}^R\left(\sum _{j=\max (0,\min (y)-B)}^{\max \left(y\right)+B}-\log \left(\sqrt{p\left(j\right){\widehat{p}}_r\left(j\right)}\right)\right),\hfill \\ \hfill \mathrm{KLD}=& \frac{1}{R}\sum _{r=1}^R\left(\sum _{j=\max (0,\min (y)-B)}^{\max \left(y\right)+B}p\left(j\right)\log \left(p\left(j\right)∕{\widehat{p}}_r\left(j\right)\right)\right),\hfill \end{array}$$

where we take the sums across the range of the observed data ± a buffer of 10.

In implementing the blocked Gibbs sampler for the rounded mixture of Gaussians, the first 1, 000 iterations were discarded as a burn-in and the next 10, 000 samples were used to calculate the posterior mean of $\widehat{p}\left(j\right)$. For the hyperparameters, as a default empirical Bayes approach, we chose ${\mu }_0=\stackrel{‒}{y}$, the sample mean, and κ = s², the sample variance, and a_τ = b_τ = 1. The precision parameter of the DP prior was set equal to one as a commonly used default and the truncation level N is set to be equal to the sample size of each sample. We also tried reasonable alternative choices of prior, such as placing a gamma hyperprior on the DP precision, for smaller numbers of simulations and obtained similar results. The values of p(j) for a wide variety of js were monitored to gauge rates of apparent convergence and mixing. The trace plots showed excellent mixing, and the Geweke (1992) diagnostic suggested very rapid convergence.

The DP approach used $\mathrm{Poi}\left(\stackrel{‒}{y}\right)$ as the base measure, with α = 1 or α ~ Ga(1, 1) considered as alternatives. For fixed α, the posterior is available in closed form, while for α ~ Ga(1, 1) we implemented a Metropolis-Hastings normal random walk to update log α, with the algorithm run for 10, 000 iterations with a 1, 000 iterations burn-in.

The blocked Gibbs sampler (Ishwaran and James 2001) was used for posterior computation in the DPM-Pois model, with the first 1,000 iterations discarded as a burn-in and the next 10,000 samples used to calculate the posterior mean $\widehat{p}\left(j\right)$. A gamma base measure with hyperparameters a = b = 1 was chosen within the DP while the precision parameter was fixed to α = 1.

The results of the simulation are reported in Table 1. The proposed method performs better, in terms of BCD and KLD, than the other methods when the truth is underdispersed and clearly not Poisson, as in the first scenario. As expected, when we simulated data under a Poisson model the MLE under a Poisson model and the DPM of Poissons performs slightly better than the proposed RMG approach in very small samples. However, even in modest sample sizes of n = 25, the RMG approach was surprisingly competitive when the truth was Poisson. Interesting, when the truth was a mixture of Poissons (third scenario) we obtained much better performance for the RMG approach than the DPM-Pois model. The ∞ recorded for the empirical estimation is due to the presence of p(j) exactly equal to zero if we do not observe any y = j.

Table 1.

Bhattacharya coefficient and Kullback-Leibler divergence from the true distribution for samples from the four scenarios

		Scenario (a)		Scenario (b)		Scenario (c)		Scenario (d)
n	Method	BCD	KLD	BCD	KLD	BCD	KLD	BCD	KLD
10	RMG	0.04	0.16	0.04	0.17	0.03	0.11	0.04	0.12
	E	0.24	∞	0.35	∞	0.39	∞	0.09	∞
	DP (α = 1)	0.14	0.68	0.19	0.9	0.16	1.14	0.06	0.25
	DP (α ~ Ga(1, 1))	0.11	0.47	0.11	0.49	0.12	0.87	0.05	0.22
	MLE	0.13	0.37	0.01	0.05	0.11	0.78	0.07	0.21
	DPM-Pois	0.26	0.69	0.09	0.29	0.15	0.43	0.26	0.67
25	RMG	0.02	0.08	0.02	0.08	0.02	0.06	0.02	0.06
	E	0.09	∞	0.14	∞	0.23	∞	0.03	∞
	DP (α = 1)	0.07	0.34	0.10	0.57	0.10	0.90	0.02	0.11
	DP (α ~ Ga(1, 1))	0.06	0.24	0.06	0.29	0.08	0.68	0.02	0.10
	MLE	0.13	0.36	0.01	0.02	0.11	0.76	0.06	0.20
	DPM-Pois	0.18	0.5	0.02	0.06	0.02	0.10	0.21	0.55
50	RMG	0.01	0.05	0.01	0.04	0.01	0.04	0.01	0.04
	E	0.04	∞	0.07	∞	0.17	∞	0.02	∞
	DP (α = 1)	0.03	0.16	0.06	0.33	0.06	0.69	0.01	0.06
	DP (α ~ Ga(1, 1))	0.03	0.12	0.04	0.18	0.05	0.54	0.01	0.05
	MLE	0.13	0.35	> 0.01	0.01	0.11	0.75	0.06	0.19
	DPM-Pois	0.16	0.44	0.03	0.09	0.12	0.28	0.19	0.51
100	RMG	0.01	0.03	0.01	0.02	> 0.01	0.02	0.01	0.03
	E	0.02	∞	0.03	∞	0.13	∞	0.01	∞
	DP (α = 1)	0.02	0.08	0.03	0.18	0.03	0.47	0.01	0.03
	DP (α ~ Ga(1, 1))	0.02	0.07	0.02	0.11	0.03	0.37	0.01	0.03
	MLE	0.13	0.35	>0.01	0.01	0.11	0.75	0.06	0.19
	DPM-Pois	0.54	1.41	>0.01	0.01	0.01	0.03	0.18	0.48
300	RMG	>0.01	0.01	>0.01	0.01	>0.01	0.01	>0.01	0.02
	E	0.01	∞	0.01	∞	0.10	∞	>0.01	∞
	DP (α = 1)	0.01	0.03	0.01	0.07	0.01	0.17	0.26	2.29
	DP (α ~ Ga(1, 1))	0.05	0.29	0.01	0.35	0.05	0.74	0.03	0.16
	MLE	0.13	0.35	>0.01	>0.01	0.10	0.74	0.06	0.19
	DPM-Pois	0.14	0.40	0.01	0.05	0.10	0.21	0.17	0.47

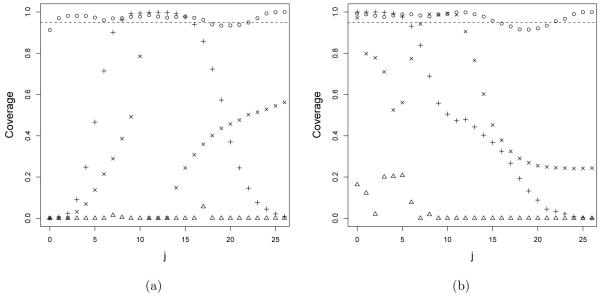
We also calculated the empirical coverage of 95% credible intervals for the p(j)s. These intervals were estimated as the 2.5th to 97.5th percentiles of the samples collected after burn-in for each p(j), with a small buffer of ±1e – 08 added to accommodate numerical approximation error. The plots in Figure 3 report the results with j on the x-axis for the second and third scenario and sample size n = 50. We found qualitatively similar results for other scenarios and sample sizes and we report a plot for each of them in the sumpplemental materials. The effective coverage of the credible intervals for p(j) for the RMG fluctuates around the nominal value for all the scenarios and sample sizes. However using the Dirichlet process prior we get an effective coverage that is either strongly less than the nominal levels, or much too high, due to too wide credible intervals. For DP-Pois, we obtain coverage close to the nominal level only at the values of j such that the true p(j) is high enough so that substantial numbers of observations fall at that value.

Figure 3.

Coverage of 95% credible intervals for p(j) under the (a) second and (b) third scenario. Points represent the RMG method, cross-shaped dots the DP with α = 1, triangles the DP with α ~ Ga(1, 1) and x-shaped dots the DPM of Poisson.

3. MULTIVARIATE ROUNDED KERNEL MIXTURE PRIORS

3.1 Multivariate counts

Multivariate count data are quite common in a broad class of disciplines, such as marketing, epidemiology and industrial statistics among others. Most multivariate methods for count data rely on multivariate Poisson models (Johnson et al. 1997) which have the unpleasant characteristic of not allowing negative correlation.

Mixtures of Poissons have been proposed to allow more flexibility in modeling multivariate counts (Meligkotsidou 2007). A common alternative strategy is to use a random effects model, which incorporates shared latent factors in Poisson log-linear models for each individual count (Moustaki and Knott 2000; Dunson 2000, 2003). A broad class of latent factor models for counts is considered by Wedel et al. (2003).

Copula models are an alternative approach to model the dependence among multivariate data. A p-variate copula C(u₁, … , u_p) is a p-variate distribution defined on the p-dimensional unit cube such that every marginal distribution is uniform on [0, 1]. Hence if F_j is the CDF of a univariate random variable Y_j, then C(F₁(y₁), … , F_p(y_p)) is a p-variate distribution for Y = (Y₁, … , Y_p) with F_js as marginals. A specific copula model for multivariate counts is recently proposed by Nikoloulopoulos and Karlis (2010). Copula models are built for a general probability distribution and can hence be used to model jointly data of diverse type, including counts, binary data and continuous data. A very flexible copula model that considers variables having different measurement scales is proposed by Hoff (2007). This method is focused on modeling the association among variables with the marginals treated as a nuisance.

We propose a multivariate rounded kernel mixture prior that can flexibly characterize the entire joint distribution including the marginals and dependence structure, while leading to straightforward and efficient computation. The use of underlying Gaussian mixtures easily allows the joint modeling of variables on different measurement scales including continuous variables, categorical and counts. In the past, it was hard to deal with counts jointly using such underlying Gaussian models unless one inappropriately treated counts as either categorical or continuous. In addition we can naturally do inference on the whole multivariate density, on the marginals or on conditional distributions of one variable given the others.

3.2 Multivariate rounded mixture of Gaussians

Each concept of Section 2 can be easily generalized into its multivariate counterpart. First assume that the multivariate count vector y = (y₁, … , y_p) is the transformation through a threshold mapping function h of a latent continuous vector y*. In a general setting we have

$$\begin{array}{cc}\hfill & \mathbf{y}=h\left({\mathbf{y}}^{\ast }\right)\hfill \\ \hfill & {\mathbf{y}}^{\ast }=(y_1^{\ast }\dots .,y_p^{\ast })\sim f\left({\mathbf{y}}^{\ast }\right)=\int {\mathrm{K}}_p({\mathbf{y}}^{\ast };\theta ,\Omega )d\mathrm{P}(\theta ,\Omega ),\hfill \\ \hfill & P\sim \tilde{\Pi },\hfill \end{array}$$ (7)

where K_p(·; θ, Ω) is a p-variate kernel with location θ and scale-association matrix Ω and $\tilde{\Pi }$ is a prior for the mixing distribution. The mapping h(y*) = y implies that the probability mass function p of y is

$$p(y_1=J_1,\dots ,y_p=J_p)=p\left(\mathbf{J}\right)=g\left(f\right)\left[\mathbf{J}\right]={\int }_{A_J}f\left({\mathbf{y}}^{\ast }\right)d{\mathbf{y}}^{\ast }\mathbf{J}\in {\mathcal{N}}^p$$ (8)

where $A_J=\{{\mathbf{y}}^{\ast }:a_{1,J_1}\le y_1^{\ast }<a_{1,J_1+1},\dots ,a_{p,J_p}\le y_p^{\ast }<a_{p,J_p+1}\}$ defines a disjoint partition of the sample space. Marginally this formulation is the same of that in (3).

Remark 1

Lemma 1 and Theorem 1 demonstrate that in the univariate case the mapping $g:\mathcal{L}\to \mathcal{C}$ maintains Kullback-Leibler neighborhoods and hence the induced prior Π assigns positive probability to all Kullback-Leibler neighbourhoods of any $p_0\in \mathcal{C}$. This property holds also in the multivariate case.

The true p₀ is in the Kullback-Leibler support of our prior, and hence we obtain weak and strong posterior consistency following the theory of Section 2, as long as there exists at least one multivariate density f₀ = g⁻¹(p₀) that falls in the KL support of the mixture prior for f described in (6). In the sequel, we will assume that K_p corresponds to a multivariate Gaussian kernel and $\tilde{\Pi }$ is DP(αP₀), with P₀ corresponding to a normal inverse-Wishart base measure. Wu & Ghosal (2008) showed that certain DP location mixtures of multivariate Gaussians support all densities f₀ satisfying a mild regularity condition. The size of the KL support of the DP location-scale mixture of multivariate Gaussians has not been formalized (to our knowledge), but it is certainly very large, suggesting informally that we will obtain posterior consistency at almost all p₀.

3.3 Out of sample prediction

Focusing on Dirichlet process mixtures of underlying Gaussians, we let the mixing distribution in (7) be P ~ DP(αP₀) with base measure P₀ = N_p(μ; μ₀, κ₀∑)Inv-W(∑; ν₀, S₀). To evaluate the performance, we simulated 100 data sets from two scenarios. The first is the mixture

$${\mathbf{y}}_i^{\ast }\sim \sum _{h=1}^3{\pi }_{h}N({\mu }_h,{\Sigma }_h),$$

with π = (π₁, π₂, π₃) = (0.14, 0.40, 0.46), μ₁ = (35, 82, 95), μ₂ = (−2, 1, 2.5), μ₃ = (12, 29, 37) and variance-covariance matrices

$${\Sigma }_1=\left(\begin{array}{ccc}\hfill 3\hfill & \hfill -0.6\hfill & \hfill 0.25\hfill \\ \hfill -0.6\hfill & \hfill 3\hfill & \hfill 0.7\hfill \\ \hfill 0.25\hfill & \hfill 0.7\hfill & \hfill 2\hfill \end{array}\right),{\Sigma }_2=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0.5\hfill & \hfill 0.4\hfill \\ \hfill 0.5\hfill & \hfill 1\hfill & \hfill -0.4\hfill \\ \hfill 0.4\hfill & \hfill -0.4\hfill & \hfill 0.7\hfill \end{array}\right),{\Sigma }_3=7.5\cdot {\Sigma }_2,$$

with the continuous observation floored and all negative values set equal to zero leading to a multivariate zero-inflated count distribution. The second scenario is a mixture of multivariate Poisson distributions (Johnson et al. 1997)

$$\pi \mathrm{mPoi}({\lambda }_1,{\lambda }_{01})+(1-\pi )\mathrm{mPoi}({\lambda }_2,{\lambda }_{02})$$

with λ₁ = (1, 8, 15), λ₂ = c(8, 1, 3), ${\lambda }_{01}^{-1}={\lambda }_{02}=2$ and π = 0.7.

The samples were split into training and test subsets containing 50 observations each, with the Gibbs sampler applied to the training data and the results used to predict y_i1 given y_i2 and y_i3 in the test sample. This approach modifies Müller et al. (1996) to accomodate count data.

The hyperparameters were specified as follows:

$$\begin{array}{cc}\hfill {\mu }_0\sim & N_3({\stackrel{‒}{\mathbf{y}}}^{\ast },\widehat{\mathbf{S}}),{\mathbf{S}}_0\sim \mathrm{InvWishart}(4,{\Psi }_0),\hfill \\ \hfill {\Psi }_0=& I_3,{\nu }_0=4,{\kappa }_0\sim \mathrm{Gamma}(0.01,0.01),\alpha =1\hfill \end{array}$$ (9)

with ${\stackrel{‒}{\mathbf{y}}}^{\ast }=(1-{\widehat{p}}_0){\stackrel{‒}{\mathbf{y}}}_{+}-{\stackrel{‒}{p}}_0{\stackrel{‒}{\mathbf{y}}}_{+}$, ${\widehat{p}}_0$ the proportion of zeros in the training sample, ${\stackrel{‒}{y}}_{+}$ the mean of the non-zero values and $\widehat{\mathbf{S}}=\mathrm{diag}(s_1,s_2,s_3)$ with s_j the empirical variance of y_ij, i = 1, … , n. The Gibbs sampler reported in the Appendix was run for 10, 000 iterations with the first 4, 000 discarded. We assessed predictive performance using the absolute deviation loss, which is more natural than squared error loss for count data. Under absolute deviation loss, the optimal predictive value for y_i1 corresponded to the median of the posterior predictive distribution.

We compare our approach with prediction under an oracle based on the true models, Poisson log-linear regressions fit with maximum likelihood, generalized additive models (GAM) (Hastie et al. 2001) with spline smoothing function and generalized latent trait model (GLTM) (Moustaki and Knott 2000; Dunson 2003) with Poisson responses. The generalized latent trait model assumed a single latent variable which was assigned a standard normal prior, while a vague normal prior with mean 0 and variance 20 was assigned to the factor loadings with one of them constrained to be positive for identifiability. The out of sample prediction was made taking the median of a MCMC chain of length 12, 000 after a burn in of 3, 000 iterations from the posterior predictive distribution of y_i1 in the test set. The results are reported in Table 2.

Table 2.

Mean absolute deviation errors for the prediction obtained with the rounded mixture of Gaussian prior (RMG), the Oracle prediction, the generalized additive Poisson model (GAM), the Poisson log-linear model (GLM) and the generalized latent trait model.

	Scenario 1	Scenario 2
RMG	2.44	1.42
oracle	1.36	1.28
GAM	2.72	1.55
GLM	5.34	1.98
GLTM	9.68	4.98

An additional gain of our approach is a flexible characterization of the whole predictive distribution of y_i1 given y_i2, y_i3 and not just the point prediction ${\widehat{y}}_{i1}$. In addition to median predictions, it is often of interest in applications to predict subjects having zero counts or counts higher than a given threshold q. Based on our results, we obtained much more accurate predictions of both y_i1 = 0 and y_i1 > q than either the log-linear Poisson model or the GAM approach when the true model is not a mixture of multivariate Poissons and prediction with similar degree of precision when the truth is a mixture of multivariate Poissons. As an additional competitor for predicting y_i1 = 0 and y_i1 > q, we also considered logistic regression, logistic GAM and a logistic latent trait model with the same prior specification as before fitted to the appropriate dichotomized data. Based on a 0-1 loss function that classified y_i1 = 0 if the probability (posterior for our Bayes method and fitted estimate for the logistic GLM and GAM) exceeded 0.5, we compute the misclassification rate out-of-sample in Table 3.

Table 3.

Misclassification rate out-of-sample based on the proposed method, GAM, generalized linear regressions, oracle and generalized latent trait models for samples under scenario 1 (S1) and scenario 2 (S2).

	RMG		GAM		GLM		Oracle		GLTM
		Mediana	0-1 Lossb	Poisson	Logistic	Poisson	Logistic	-	0-1 Lossb
S1	yi1 = 0	0.02	0.08	0.42	0.14	0.42	0.20	0.00	0.44
	yi1 > 20	0.02	0.10	0.02	0.40	0.08	0.30	0.00	0.50
	yi1 > 25	0.04	0.02	0.04	0.06	0.06	0.08	0.02	0.56
	yi1 > 35	0.06	0.06	0.06	0.08	0.06	0.14	0.06	0.48
S2	yi1 = 0	0.14	0.12	0.12	0.12	0.12	0.12	0.12	0.86
	yi1 > 10	0.16	0.12	0.16	0.12	0.16	0.12	0.12	0.50

^a= prediction based on posterior median,

^b= prediction based on 0-1 loss

4. APPLICATIONS

4.1 Application to developmental toxicity study

As a first application, we consider the developmental toxicity study mentioned in Section 1. Pregnant mice were assigned to dose groups of 0, 750, 1,500 or 3,000 mg/kg per day, with the number of implants measured for each mouse at the end of the experiment. Group sizes are 25, 24, 23 and 23, respectively. The scientific interest is in studying a dose response trend in the distribution of the number of implants. To address this, we first estimate the probability mass function within each group using the RMG methodology of Section 2. Trace plots showed rapid convergence and excellent mixing, with the Geweke (1992) diagnostic failing to show lack of convergence.

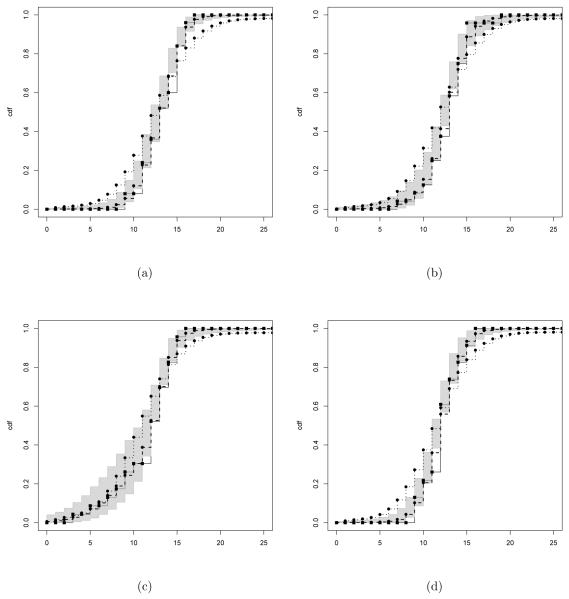
Figure 4 shows the estimated and empirical cumulative distribution functions in each group along with 95% pointwise credible intervals and the estimates from a DPM of Poissons analysis. Clearly, the DPM of Poissons provided a poor fit to the data and hence poor characterization of changes with dose, while the proposed RMG method provided an excellent fit for each group. To summarize changes in the distribution of the number of implants with dose, we estimated summaries of the posterior distributions for changes in each percentile between the control group and each of the exposed groups, with the results shown in Figure 5. In each of the dose levels, the exposure led to a stochastic decrease in the distribution of the number of implants, with an estimated decrease in the number of implants at each percentile (there is a minor exception at high percentiles in the 750 mg/kg group). The estimated posterior probabilities of a negative average change across the percentiles was 0.72, 0.99 and 0.94 in the 750, 1,500 and 3,000 mg/kg groups, respectively. These results were consistent with Mann-Whitney pairwise comparison tests that had p-values of 0.23, 0.04 and 0.06 for stochastic decreases in the low, medium and high dose groups. In contrast, likelihood ratio tests under a Poisson model failed to test any significant differences between the control and exposed groups.

Figure 4.

Posterior estimates for the cumulative distribution function for (a) the control group and (b)–(d) the dose groups. Black solid line for the empirical cumulative distribution function, dashed line for the RMG estimation and dotted for the DPM of Poisson. Gray shading for 95% posterior credible bands for the RMG

Figure 5.

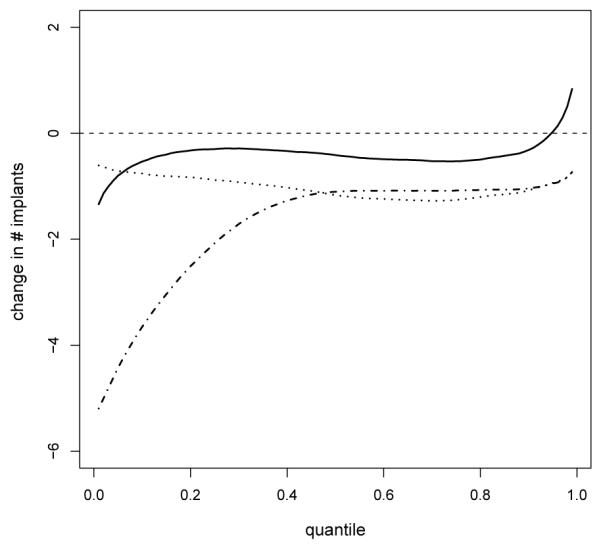
Posterior mean for the changes in the percentiles (x-axis) between the control group and 750 mg/kg (continuous line), 1,500 mg/kg (dash-dotted line) and 3,000 mg/kg (dotted line) dose groups.

4.2 Application to Marketing Data

Telecommunications companies every day store plenty of information about their customer behaviour and services usage. Mobile operators, for example, can store the daily usage stream such as the duration of the calls or the number of text and multimedia messages sent. Companies are often interested in profiling both customers with high usage and customers with very low usage. Suppose that at each activation a customer is asked to simply state how many text messages (SMS), multimedia messages (MMS) and calls they anticipate making on average in a month and the company wants to predict the future usage of each new customer.

We focus on data from 2, 050 SIM cards from customers having a prepayed contract, with a multivariate y_i = (y_i1, … , y_ip) available representing usage in a month for card i. Specifically, we have the number of outgoing calls to fixed numbers (y_i1), to mobile numbers of competing operators (y_i2) and to mobile numbers of the same operator (y_i3), as well as the total number of MMS (y_i4) and SMS (y_i5) sent. Jointly modeling the probability distribution f(·) of the multivariate y using a Bayesian mixture and assuming an underlying continuous variable for the counts, we focus on the forecast of y_i1, using data on y_i2, … , y_i5. Some descriptive statistics of the dataset show the presence of a lot of zeros for our response variable y₁. Such zero-inflation is automatically accommodated by our method through using thresholds that assign negative underlying $y_{ij}^{\ast }$ values to y_ij = 0 as described in Section 2.3. Excess mass at zero is induced through Gaussian kernels located at negative values.

We can model the data assuming the model in (7) with hyperparameters specifiedas in (9) and computation implemented as in Section 3.3. A training and test set of equal size are chosen randomly. Trace plots of y_i1 for different individuals exhibit excellent rates of convergence and mixing, with the Geweke (1992) diagnostic providing no evidence of lack of convergence.

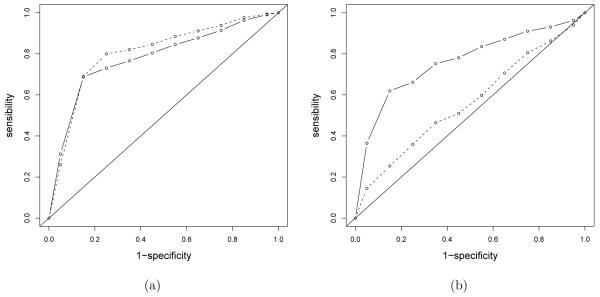
Our method is compared with Poisson GLM and GAM as in Section 3.3 and with a generalized latent trait model with prior as in Section 3.3. The out-of-sample median absolute deviation (MAD) value was 8.08 for our method, which is lower than the 8.76 obtained for the best competing method (Poisson GAM). The generalized latent trait model turns out to have a too restrictive structure with poor performance both computationally and in terms of prediction (MAD of 10.63). These results were similar for multiple randomly chosen training-test splits. Suppose the interest is in predicting customers with no outgoing calls and highly profitable customers. We predict such customers using Bayes optimal prediction under a 0-1 loss function. Using optimal prediction of zero-traffic customers, we obtained lower out-of-sample misclassification rates than the Poisson GAM, but had comparable results to logistic GAM as illustrated in the ROC curve in Figure 6 (a). Our expectation is that the logistic GAM will have good performance when the proportion of individuals in the subgroup of interest is ≈ 50%, but will degrade relative to our approach as the proportion gets closer to 0% or 100%. In this application, the proportion of zeros was 69% and the sample size was not small, so logistic GAM did well. The results for predicting highly profitable customers having more than 40 calls per month are consistent with this, as illustrated in Figure 6 (b). It is clear that our approach had dramatically better predictive performance.

Figure 6.

ROC curves for predicting customers having outgoing calls to fixed numbers equal to zero (a) or more than 40 (b). The continuous line is for our proposed approach and the dotted lines are for the logistic GAM. Both classifications are based on a 0-1 loss function that classify y_i1 = 0 or y_i1 > 40 if the posterior (estimated) probability is greater than 1/2.

5. DISCUSSION

The usual parametric models for count data lack flexibility in several key ways, and nonparametric alternatives have clear disadvantages. Our proposed class of Bayesian nonparametric mixtures of rounded continuous kernels provides a useful new approach that can be easily implemented in a broad variety of applications. We have demonstrated some practically appealing properties including simplicity of the formulation, ease of computation and straightforward joint modeling of counts, categorical and continuous variables from which is it possible to infer conditional distributions of response variables given predictors as well as marginal and joint distributions. The proposed class of conditional distribution models allows a count response distribution to change flexibly with multiple categorical, count and continuous predictors.

Our approach has been applied to a marketing application using a DP mixture of multivariate rounded Gaussians. The use of an underlying Gaussian formulation is quite appealing in allowing straightforward generalizations in several interesting directions. For example, for high-dimensional data instead of using an unstructured mixture of underlying Gaussians, we could consider a mixture of factor analyzers (Gorur and Rasmussen 2009). As an alternative we considered generalized latent trait models, which induce dependence through incorporating shared latent variables in generalized linear models for each response type. However, this strategy would rely on mixtures of Poisson log-linear models for count data, which restrict the marginals to be over-dispersed and can lead to a restrictive dependence structure as pointed out in the simulation and in the real data application. It also becomes straightforward to accommodate time series and spatial dependence structures through mixtures of Gaussian dynamic or spatially dependent models. In addition, we can easily adapt any method for density regression for continuous responses to include rounding such as dependent Dirichlet processes (MacEachern 1999, 2000), kernel stick-breaking processes (Dunson and Park 2008), or probit stick-breaking processes (Chung and Dunson 2009).

APPENDIX.

Proof of Lemma 1

Let f a general element of ${\mathcal{K}}_{∊}\left(f_0\right)$ and denote p = g(f) its image on $\mathcal{C}$, hence

$$KL(f_0,f)={\int }_{a_0}^{a_{\infty }}{f}_0\left(x\right)\log \left(\frac{f_0\left(x\right)}{f\left(x\right)}\right)\mathrm{d}x<∊.$$ (10)

If we discretizise the integral (10) in the infinite sum of integrals on disjoint subset of the domain of f we have

$$\sum _{h=0}^{\infty }{\int }_{a_h}^{a_{h+1}}{f}_0\left(t\right)\log \left(\frac{f_0\left(t\right)}{f\left(t\right)}\right)\mathrm{d}t<∊.$$

Using the condition (see Theorem 1.1 of Ghurye (1968))

$${\int }_A{g}_1\left(t\right)\mathrm{d}t\times \log \left(\frac{{\int }_A{g}_1\left(t\right)\mathrm{d}t}{{\int }_A{g}_2\left(t\right)\mathrm{d}t}\right)\le {\int }_A{g}_1\left(t\right)\log \left(\frac{g_1\left(t\right)}{g_2\left(t\right)}\right)\mathrm{d}t$$

for each $A\in \mathcal{A}$, countable family of disjoint measurable sets of $\mathcal{Y}$ and $g_1,g_2\in \mathcal{L}$, we get

$$p_0\left(j\right)\log \frac{p_0\left(j\right)}{p\left(j\right)}\le {\int }_{a_j}^{a_{j+1}}{f}_0\left(t\right)\log \left(\frac{f_0\left(t\right)}{f\left(t\right)}\right)dt$$

and hence

$$\sum _{j=0}^{\infty }{p}_0\left(j\right)\log \frac{p_0\left(j\right)}{p\left(j\right)}\le \sum _{a_0}^{a_{\infty }}{f}_0\left(x\right)\log \left(\frac{f_0\left(x\right)}{f\left(x\right)}\right)\mathrm{d}x<∊,$$

that gives the result.

Proof of Theorem 2

In $\mathcal{C}$ weak convergence of sequences implies pointwise convergence by definition. In addition, Schur’s property holds in $\mathcal{C}$ and hence weak convergence of sequences implies also strong convergence. Weak and strong metrics are hence topologically equivalent since p_n → p weakly iff p_n → p in L₁. Topologically equivalent metrics generate the same topology and this implies that the balls nest, i.e. that for any $p\in \mathcal{C}$ and radius r > 0, there exist positive radii r₁ and r₂ such that

$$S_{r_1}\left(p\right)\subseteq W_r\left(p\right)\text{and}{W}_{r_2}\left(p\right)\subseteq S_r\left(p\right)$$

where S_r(p) and W_r(p) are respectively strong and weak open neighborhoods of p of radius r. It follows that for any L₁ neigborhood S there exists a weak neighborhood W such that S^C ⊆ W^C. Hence the posterior probability of S^C is

$$\Pi (S^C\mid y_1,\dots ,y_n)\le \Pi (W^C\mid y_1,\dots ,y_n).$$

Since the right hand side of the last equation goes to zero with P_p0-probability 1, it follows that also

$$\Pi (S_r^C\mid y_1,\dots ,y_n)\to 0$$

with P_p0-probability 1 and this concludes the proof.

Multivariate Gibbs Sampler

For the multivariate rounded mixture of Gaussians we adopt the Gibbs sampler with auxiliary parameters of Neal (2000), and more precisely the Algorithm 8 with m = 1. The sampler iterates among the following steps:

Step 1 Generate each ${\mathbf{y}}_i^{\ast }$ from the full conditional posterior for j in 1, … , p

• Step 1a Generate $u_{ij}\sim U\left(\varphi (a_{y_{ij}-1};{\tilde{\mu }}_{i,j},{\tilde{\sigma }}_{i,j}^2),\Phi (a_{y_{i}j};{\tilde{\mu }}_{i,j},{\tilde{\sigma }}_{i,j}^2)\right)$, where

  $$\begin{array}{cc}\hfill & {\tilde{\mu }}_{i,j}={\mu }_{s_i,j}+{\Sigma }_{S_i,12}{\Sigma }_{S_i,22}^{-1}({\mathbf{y}}_{-j}^{\ast }-{\mu }_{S_i,-j})\hfill \\ \hfill & {\tilde{\sigma }}_{i,j}^2={\sigma }_{S_i,j}^2-{\Sigma }_{S_i,12}{\Sigma }_{S_i,22}^{-1}{\Sigma }_{S_i,21}\hfill \end{array}$$

  are the usual conditional expectation and conditional variance of the multivariate normal.

• Step 1b Let $y_{ij}^{\ast }={\Phi }^{-1}(u_{ij};{\tilde{\mu }}_{i,j},{\tilde{\sigma }}_{i,j}^2)$

Step 2 Update S_i as in Algorithm 8 of Neal (2000) with m = 1.

Step 3 Update (μ_h, ∑_h) from their conditional posteriors.