The use of classification trees for bioinformatics

Abstract

Classification trees are non-parametric statistical learning methods that incorporate feature selection and interactions, possess intuitive interpretability, are efficient, and have high prediction accuracy when used in ensembles. This paper provides a brief introduction to the classification tree-based methods, a review of the recent developments, and a survey of the applications in bioinformatics and statistical genetics.

Introduction

The rapid advent of technologies (such as microarrays, high-throughput sequencing, genotyping arrays, mass spectrometry and automated high resolution imaging acquisition techniques) has led to a dramatic increase in biomedical data. In order to transform the data explosion into useful scientific knowledge, novel bioinformatic approaches are required to face the challenge of the growing complexity (including the massive size) of the data. Machine learning, including supervised learning algorithms, are well suited for those data and has been applied to a variety of bioinformatic problems, including genome annotation [1-3], biomarker identification [4,5], protein function prediction [6], protein structure prediction [7], protein localization prediction [8,9], identification of protein interactions [10,11] and drug discovery researches [12,13].

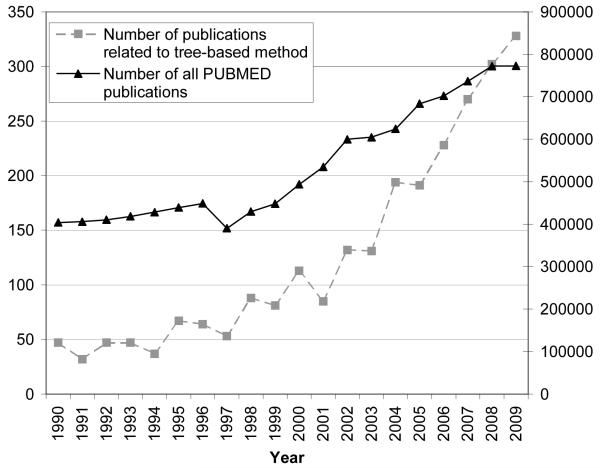
Tree-based methods such as decision trees are among the most popular machine learning algorithms applied in bioinformatics and statistical genetics. Figure 1 shows the increasing popularity of classification tree based approaches in biomedical research in the last two decades. This apparent success largely stems from the model simplicity and interpretability and its capability in handling high dimensional data with limited sample sizes (the large p and small n problem, where the number of variables, p, is much larger than the number of samples, n), which are common in bioinformatic and statistical genetic datasets.

Figure 1.

The annual number of publications related to classification tree or random forest in PUBMED between 1990 and 2009. The example query used for 1990 is: “classification tree”[All Fields] OR “decision tree”[All Fields] OR “random forest”[All Fields] AND “1990”[Entrez Date]

This review mainly focused on the application of tree and forest based approaches in bioinformatics areas. Interested readers could refer to large volume of published literatures for discussion on general tree and forest approaches [14-16] as well as its usage in other areas, such as pharmaceutical research [17]and business analysis [18]. Below, we first describe the tree-based approaches, including the basic recursive partitioning algorithm, followed by a discussion about ensemble approaches and tree-based variable importance measures. We then survey the applications of tree-based algorithms in the context of bioinformatics and statistical genetics. Finally, we provide links to common classification tree and ensemble software.

Classification tree

Almost all classification tree construction algorithms such as ID3 [19], C4.5 [20] and CART [21], employ a top-down heuristic search using recursive partitioning since the enumeration for all 2ⁿ possible partitions is essentially intractable. Starting from a of all heterogeneous set (in terms of the variation in the class label or outcome variable) of training samples (root node), each feature (or predictor) is evaluated using a statistic to determine how well it classifies the training samples by itself. The best feature is selected to split the training samples to descendant nodes, or daughter nodes. The whole process is recursively repeated to split the descendant nodes until some pre-specified stopping criterion is met. This search algorithm is greedy because it never backtracks to reconsider its previous choices. Usually the tree-growing step is followed by a bottom-up pruning step, which removes unessential subtrees to avoid overfitting.

Splitting a node

The critical step in tree growing is to select the best feature to split a node. Most algorithms evaluate the performance of a candidate feature in separating different class labels in the training samples. The concept of impurity is usually used. Two common choices of impurity within node t are entropy (where the reduction of entropy is also referred as information gain)

$$I_e\left(t\right)=-\sum _{j=1}^l{p}_j\left(t\right){\log }_2\left(p_j\left(t\right)\right),$$

and Gini index

$$I_G\left(t\right)=\sum _{j=1}^l{p}_j\left(t\right)(1-p_j\left(t\right)),$$

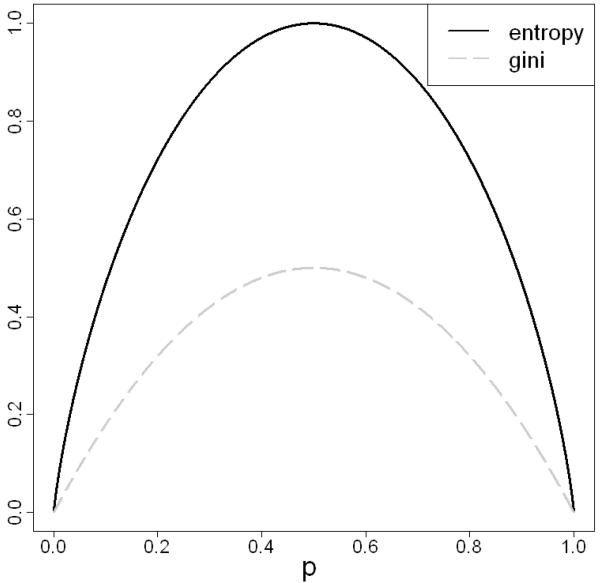
where we assume that there are l classes and p₁, p₂,…, p_l are the proportions of samples in the l classes, respectively. Figure 2 depicts the shapes of these two impurity functions for a binary response with the success probability of p.

Figure 2.

Impurity functions

Then, in binary trees, a feature and a split are chosen according to the following decrement in impurity:

$$\Delta (s,t)=I\left(t\right)-h\left(t_L\right)I\left(t_L\right)-h\left(t_R\right)I\left(t_R\right),$$

where s is a split of node t , h(t_L) and h(t_R) are the proportions of the samples in the left and right daughter nodes of node t, respectively. In addition to the two described above, there are families of splitting approaches proposed, many of which were discussed in [22] and [23].

Stop-splitting and Pruning

By recursively using the node splitting procedure, we usually end up with an overgrown tree (with too many descendant nodes), which produces a tree that overfits the training samples and is prone to random variations in the data. Two commonly employed strategies to overcome the overfitting is either to interrupt the tree growing by a stop-splitting criterion or to apply a pruning step on the overgrown tree, which removes some nodes to reach an optimal bias-variance tradeoff. The stop-splitting criterion could be either based on the node size, the node homogeneity or elaborate criterion based on statistical testing [20]. Pruning approaches include the use of independent validation (or called test) samples or cross-validation (a sample re-use approach) [14,21]. These approaches provide unbiased or nearly unbiased comparisons (in terms of misclassification errors) among the sub-trees that can be considered as the final tree.

Trees with multivariate ordinal responses

Most decision trees in use or developed deal with a single class label, but many biomedical studies collect multiple responses to determine the health condition of a study subject, and each response may have several ordinal levels. Often, these responses are examined one at a time and by dichotomizing the ordinal levels into a binary response, which may lead to loss of information. Zhang and Ye proposed a semi-parametric tree-based approach to analyzing a multivariate ordinal response [24]. The key idea is to generalize the within-node impurity to accommodate the multivariate ordinal response, which was achieved by imposing a “working” parametric distribution for the multivariate ordinal response when splitting a node. Their method produced some interesting insights into the “building related occupant sick syndromes.”

Classification Tree Based Ensembles

Although tree models are easy to interpret, single tree based analysis has its own limitations in analyzing large data sets. To name a few,

1. Similar to other stepwise models, the topology of a tree is usually unstable. A minor perturbation of the input training sample could result in a totally different tree model.

2. For ultra-high dimensional data such as a typical genomewide scan data, a single parsimonious model is not enough to reflect the complexity in the data set.

3. Tree based models are data-driven and it is difficult, if not impossible, to perform theoretical inference.

4. A single tree may have a relatively lower accuracy in prediction, especially compared to support vector machine (SVM) and artificial neural networks (ANN).

One approach to overcoming these limitations is to use forests, or ensembles of trees. This may improve the classification accuracy while maintaining some desirable properties of a tree, such as simplicity in implementation and good performance in “the large p and small n problem”. In the past few years, forest based approaches have become a widely used nonparametric tool in many scientific and engineering applications, particularly in high dimensional bioinformatic and genomic data analyses [25-28].

In the following, we briefly discuss several forest construction algorithms, followed by algorithms to estimate the variable importance.

Random forest (RF) construction

The random forest (RF) algorithm[29] is the most popular ensemble method based on classification trees. A random forest consists of hundreds or thousands of unpruned trees built from random variants of the same data. Although an individual tree in the forest is not a good model by itself, the aggregated classification has been shown to achieve much better performance than what a single tree may achieve.

To construct a RF with B trees from a training data set with n observations with k features, we employ the following steps:

1. A bootstrap sample is drawn from the training sample.

2. A classification tree is grown for the bootstrap sample. At each node, the split is selected based on a randomly selected subset of m_try (much smaller than k) features. The tree is grown to full size without pruning.

3. Steps 1 and 2 are repeated B times to form a forest. The ensemble classification label is made by a majority vote of all trees in the ensemble.

It may first seem counterintuitive that trees are grown to full length without post-pruning in RF. Using Strong Law of Large Numbers, Breiman showed that there is no overfitting in RF without pruning [29]. The ensemble prediction error converges as the number of trees increases and the accuracy depends on both the predictive strength of individual trees and the correlation among trees.

A practical decision to make in RF construction is the selection of m_try. Common choices are log (k) and $\sqrt{k}$, although their performance in high dimensional data has been debated. Genuer et al. [30] performed a careful investigation on the effects of m_try on RF performance in high dimensional problems. They found that while in most cases, a small m_try works well, but they also found that it needs to be sufficiently large in high dimensional problems to achieve good performance. In many situations, the optimal size of m_try is close to the number of variables, which is computationally prohibitive for most of the ultra-high dimensional data. To address these concerns, Amaratunga et al. [5] proposed an enriched random forest approach in gene expression analysis where the sampling probability is based on a monotonic function of the significance level of differential gene expression detections instead of selecting a subset of the genes with equal probability from all genes.

Forests construction for features with uncertainty

In practice, we tend to use or assume the observed features as if they are fixed without uncertainty. However, in genetic studies for complex diseases, it is of great interest to identify haplotypes that may be associated with a complex trait. A haplotype is a set of alleles in multiple loci on a homolog and those alleles are more likely to be transmitted together to the next generation if the loci are closer. However, haplotypes are not readily observed on a large scale by the current technology, and are usually inferred statistically with uncertainties.

In order to explicitly account for the uncertainties in the features, Chen et al. developed an approach called HapForest [31], which is a variant of forests. The major difference between the original RF method and this approach lies in the way of constructing the training data for individual trees. In the original RF, a bootstrap sample is used. In HapForest, each feature with uncertainties is taken as a multinomial random variable. Each training data set is generated according to the empirical distributions of the feature levels.

Deterministic forests

A major cause for the unstability of a single tree is that the number of training samples is not sufficiently large relative to the number of features. In ultra high dimensional data, the sample size is usually much smaller than the number of features, and as a result, many trees with similar structure and similar performance could be deduced from the same dataset. Zhang et al. proposed a method that combines these trees into a forest, which is called deterministic forest [32]. It has been shown that compared to a single tree model, the deterministic forest approach provides better classification rules, which are also more biologically interpretable than random forests. The construction of the deterministic forest is straightforward. Each tree in the forest is grown to a pre-specified depth and at each node, a pre-specified number of top splits are selected to grow the tree. For example, Zhang et al. selected 20 top splits for the root node and 3 splits for each of the two daughter nodes. In total, they generated a forest with 180 (20 by 3 by 3) trees [32].

Variable importance (VI)

Unlike most other classifiers, classification tree directly performs feature selection while a classification rule is built. In a classification tree, only a small portion of features from a potentially large feature set is used in the tree construction. By concentrating on the selected features, it is also computationally quick to evaluate the influence of the selected features, and set the influence of the non-selected to none. The concept of variable importance (VI) is precisely for the purpose of ranking the importance of the features. Due to the greedy nature of the tree construction, only one split variable is used at each node. Consequently, VI in single tree methods suffers from masking effects because when multiple features produce similar reductions of impurity at a specific node, all but one selected feature are masked and have zero VI. On the contrary, ensemble methods, which pool many trees together, alleviate the masking issue either directly (such as the deterministic forest approach) or indirectly through introducing randomness in the tree construction (the RF approach). Also, in most cases, an ensemble of trees is more difficult to interpret than a single tree. Thus, it is even more pressing to estimate the VI in a forest so that we can easily identify “important” features. In the following, we discuss several commonly used VI measures.

The two commonly used VI measures are Gini importance index and permutation importance index [33]. Gini importance index is directly derived from the Gini index when it is used as a node impurity measure. A feature’s importance value in a single tree is the sum of the Gini index reduction over all nodes in which the specific feature is used to split. The overall VI for a feature in the forest is defined as the summation or the average of its importance value among all trees in the forest.

Permutation importance measure is arguably the most popular VI used in RF. The RF algorithm does not use all training samples in the construction of an individual tree. That leaves a set of out of bag (oob) samples, which can be used to measure the forest’s classification accuracy. In order to measure a specific feature’s importance in the tree, we randomly shuffle the values of this feature in the oob samples and compare the classification accuracy between the intact oob samples and the oob samples with the particular feature permutated. It is noteworthy that in standard classification problems where p ⪡ n , the choice of m_try affects the magnitude of the VI scores, but little on the rank of the VIs [30].

While Breiman showed that in general, the Gini VI is consistent with the permutation VI, there are also reports that Gini VI is in favor of features with many categories and alternative implementation of the random forest to overcome this issue has been proposed [34]. The permutation VI is an intuitive concept, but it is time consuming to compute. Furthermore, its magnitude does not have a range and can be negative. These shortcomings lead to several recent measures of VI in bioinformatics and genetics studies. Chen et al. proposed to use a depth importance measure, VI(j,t) = 2^−L(t) S(j,t), where L(t) is the depth of the node in the tree and S(j,t) is the χ² test statistic for the split based on feature j at node t. The depth importance is similar to the Gini VI in the sense that both measures reflect the quality of the split. The major difference is that the depth importance takes into account the position of the node. This importance measure was shown to be effective in identifying risk alleles in complex diseases [31].

Although most VI measures reflect the average contribution among all trees in a forest, there are measures based on extreme statistic in a forest as well. A good example is maximal conditional chi-square (MCC) importance measure [35], which is defined as the maximal chi-square statistic among all nodes split on a specific feature as its importance score,

MCC_i = max(x, x∊{S(j,t)}, t is any node splitted by feature j).

MCC was shown to improve the performance of RF and have better power in identifying feature interactions in simulations [35].

The performance of RF and VIs with correlated predictors is also an intensively investigated topic without consensus. Strobl et al. suggested that the VIs of correlated variables could be overestimated and proposed a new conditional VIs [36] while Nicodemus and Malley showed permutation based VIs are unbiased in genetic study [37]. In addition, Meng et al. recommended a revised VIs with the original RF structure to handle the correlation among predictors [38].

The smallest forest

Although a forest often significantly improves the classification accuracy, it is usually more difficult to interpret many trees in the forest than a single tree. To address this problem, Zhang and Wang [39] introduced a method to find the smallest forest in order to balance the pros and cons between a random forest and a single tree. The recovery of the smallest forest makes it possible to interpret the remaining trees and at the same time, avoid the disadvantage of tree-based methods. The smallest forest is a subset of the trees in the forest that maintain a comparable or even better classification accuracy relative to the full forest. Zhang and Wang employed a backward deletion approach, which iteratively removes a tree with the least impact on the overall prediction. This is done by comparing the misclassification of the full forest with the misclassification of the forest without a particular tree. As the forest shrinks in size, we can track its misclassification trajectory and use sample-reuse methods or oob samples to determine the optimal size of the sub-forest, which is chosen as the one whose misclassification is within one standard error from the lowest misclassification. This one-standard-error is to improve the robustness of the final choice. Zhang and Wang demonstrated that a subforest with as few as 7 trees achieved similar prediction performance (Table 1) to the full forest of 2000 trees on a breast cancer prognosis data set [40].

Table 1.

Comparison of prediction performance of the initial random forest, the optimal sub-forest, and a previously established 70-gene classifier.

Method	Error rate	predicted True	Good	Poor
Random Forest	26.0%	Good	141	17
		Poor	53	58
Smallest forest	26.0%	Good	146	22
		Poor	48	53
70-gene Classifier	35.3%	Good	103	4
		Poor	91	71

Applications in bioinformatics and genetics studies

The classification tree and tree-based approaches have been applied to a variety of bioinformatic problems, including sequence annotation, biomarker discovery, protein-protein interaction prediction, regulatory network modeling, protein structure prediction and statistical genetics. In this section, we briefly survey some representative applications. Based on the aims of the tree-based applications, we roughly divide them into two major categories: classification/prediction and identification of important features.

Classification

Many applications of classification tree and forest approaches in bioinformatics focused on classification purposes.

Sequence annotation is a traditional area of applications for tree-based methods. Salzberg evaluated the use of classification trees in protein coding sequence prediction [1] and Davuluri et al. achieved good performance in predicting the promoter and first exon for genes by combining quadratic discriminant functions with decision trees [41]. Recently, Gupta et al. developed an RF-based algorithm to distinguish gene promoter sequences from other non-specific Pol-II binding sequences from Chip-seq data [2]. Tree-based approaches have also been applied in the classification of non-protein coding genes [42] as well as mitochondrial DNA [3].

Protein function prediction is another area where machine learning algorithms including tree-based approaches have been widely used. For example, using RF, Jung et al. achieved near optimal performance in predicting excellular matrix proteins [9]. Similar tree-based applications includes predicting membrane proteins [43,44] and classifying protein subcellular location [8].

Protein-protein interaction (PPI) is central to biological process and protein functions. However, experimental determination of pairwise PPIs is a labor-intensive and expensive process. Therefore, prediction of PPI from indirect information from individual protein is a rich field of applications of machine learning algorithms. Qi et al. [45] and Lin et al. [10] evaluated the performance of several classifiers in predicting PPIs. In both studies, RF achieved the best performance. Based on the RF classifier, Mohamed et al. proposed active learning schemes to further improve the classification accuracy with smaller training set [11]. Other tree-based approaches were also proposed on this topic [46,47].

An important task in biomedical research is to classify between disease group and non-disease group as well as to distinguish among different disease subtypes. After comparing several machine learning algorithms in cancer classification, Ben-Dol et al. concluded that the tree-based and SVM were the front-runners [4]. Using features generated from protein sequential and structural information, Satio et al. established a classification tree prediction model with 4 nodes, which achieves relatively high accuracy (86%) in distinguishing two forms of Fabry diseases [48]. Amaratunga et al. further improved the RF performance in biomedical sample classification by imposing weights on gene expression features [5].

Another topic in biomedical sample classification is to identify biomarker set. Tree based algorithms, especially ensemble approaches, are also widely used in this area since the VI measure could be used to rank the input biomarkers. The goal in biomarker identification is to select a small set of discriminating biomarkers that maintain high classification accuracy. Torri et al. used RF to derive a subset of 44 genes, whose expression profile could be used to identify inflammation in dendritic cells [49]. Chen et al. constructed a classification tree model with 5 genes to accurately predict the treatment outcome for non-small-cell lung cancer patients [50].

Tree based approaches have also been applied to other type of bioinformatics problems. Schierz employed a C4.5 implementation of classification tree algorithm and achieved good performance in virtual screening of bioassay data at PubChem database, where there is imbalance between active and inactive compounds [51]. Kirchner et al. demonstrated that using a RF-based approach, it is feasible to achieve real-time classification of fractional mass in mass spectrometry experiments [52]. Similarly, RF-based approaches also demonstrated its power in computer aided diagnosis of SPECT images [53] and in gene network [54]and pathway analysis [25].

Identification of important features

Using the VI measure estimated from classification trees or tree based ensembles, it is possible to identify important features that are associated with the outcome. Since tree approaches automatically take interactions among features into consideration, it is especially useful to identify those features that show small marginal effects, but a larger contribution when combined together. A typical application in this category is genomewide association studies (GWAs), where hundreds of thousands of SNPs are simultaneously assayed across the entire genome in relation to disease or other biological traits.

Both GWAs and biomarker discovery involve feature selection methodology and therefore they are related to each other. However, they have distinct goals for feature selection. While the goal in biomarker discovery is to find a small set of biomarkers to achieve good classification accuracy, which allows the development of economical and efficient diagnostic test, the goal in GWAs is to find important features that are associated with the traits and to estimate the significance level of the association.

Lunetta et al. compared the performance of random forest against Fisher’s exact test in screening of SNPs in GWAS using 16 simulated disease models [55]. They concluded that random forest achieved comparable power with Fisher’s exact test when there is no interaction among SNPs and outformed Fisher’s exact test when interaction existed. Several studies have proposed different VI measures in GWAs, where there are a large amount of potentially correlated predictors [36-38,56]. Using a depth related VI measure, Chen et al. proposed HapForest, a forest-based ensemble approach, to explicitly account for uncertainty in haplotype inference and to identify risky haplotypes [31]. Chen et al.[31] and Wang et al.[57] applied this approach to a GWAS dataset for age-related macular degeneration (AMD). Besides the well known risk haplotype in the complement factor H gene (CFH) on Chromosome 1 [58], a new potentially protective haplotype in BBS9 gene was also identified on Chromosome 7 in both studies at genomewide significance level of 0.05. The results were consistent with Wang et al. [35], which used the MCC VI measure.

A general concern regarding the tree-based approaches in GWAs is the difficulty in deriving the theoretical null distribution for the VI measures. Usually an empirical null distribution is generated through permutation, which can incur a high computational cost in ensemble methods. However, because most ensemble methods are easily parallelized, the efficiency problem could be potentially mitigated with the availability of high performance computer clusters.

Software availability

Classification tree and random forest are available in standard statistical and machine learning software, such as R, SPSS and Weka. The public can also download free software from many researchers’ websites, such as http://c2s2.yale.edu/software for many of the approaches described in this review, and http://www.randomjungle.org/ for a fast implementation of random forest for high dimensional data.

Concluding remarks

With the data explosion during the last two decades, machines learning algorithms are becoming increasingly popular in biological analyses where the data complexity is always rising. As non-parametric models, classification tree approaches and ensembles based on trees provide a unique combination of prediction accuracy and model interpretability. As a final note, although this survey focused on the tree based classification approaches, trees and forests are also commonly used in other statistical modeling such as survival analysis.