Multi-Atlas Multi-Shape Segmentation of Fetal Brain MRI for Volumetric and Morphometric Analysis of Ventriculomegaly

Abstract

The recent development of motion robust super-resolution fetal brain MRI holds out the potential for dramatic new advances in volumetric and morphometric analysis. Volumetric analysis based on volumetric and morphometric biomarkers of the developing fetal brain must include segmentation. Automatic segmentation of fetal brain MRI is challenging, however, due to the highly variable size and shape of the developing brain; possible structural abnormalities; and the relatively poor resolution of fetal MRI scans. To overcome these limitations, we present a novel, constrained, multi-atlas, multi-shape automatic segmentation method that specifically addresses the challenge of segmenting multiple structures with similar intensity values in subjects with strong anatomic variability. Accordingly, we have applied this method to shape segmentation of normal, dilated, or fused lateral ventricles for quantitative analysis of ventriculomegaly (VM), which is a pivotal finding in the earliest stages of fetal brain development, and warrants further investigation. Utilizing these innovative techniques, we introduce novel volumetric and morphometric biomarkers of VM comparing these values to those that are generated by standard methods of VM analysis, i.e., by measuring the ventricular atrial diameter (AD) on manually selected sections of 2D ultrasound or 2D MRI. To this end, we studied 25 normal and abnormal fetuses in the gestation age (GA) range of 19 to 39 weeks (mean=28.26, stdev=6.56). This heterogenous dataset was essentially used to 1) validate our segmentation method for normal and abnormal ventricles; and 2) show that the proposed biomarkers may provide improved detection of VM as compared to the AD measurement.

1. Introduction

This paper investigates a new multi-atlas multi-shape segmentation method to obtain novel quantitative analysis of fetal ventriculomegaly (VM). In this introduction we discuss the significance of the application, the background, and the purpose of this study, which includes a review of the related material and the specific contributions of this article.

1.1. Significance

Ventriculomegaly (VM) is the most frequently observed fetal brain abnormality, affecting 0.1-0.2 percent of all pregnancies (Garel et al., 2003), and is considered to be a pivotal finding for diagnosing anomalies of the central nervous system (CNS) (Guibaud, 2009). The sources and outcomes of VM have been investigated in numerous studies, e.g. by Kelly et al. (2001); Garel et al. (2003); Levine et al. (2002); Kazan-Tannus et al. (2007); Gaglioti et al. (2005); Guibaud (2009); Melchiorre et al. (2009a,b); Gaglioti et al. (2009); Kennelly et al. (2009); Beeghly et al. (2010); yet, much remains unknown due to its variable etiology, complicated pathophysiology, and poorly understood natural history (Gaglioti et al., 2009; Kennelly et al., 2009; Glenn, 2010). Improved imaging technology can dramatically improve the diagnosis, prognosis, and treatment of VM and the related CNS anomalies.

The analysis of fetal anomalies through medical imaging is currently limited to linear measurements by radiologists on two dimensional sections of prenatal sonography and magnetic resonance imaging (MRI). MRI has been shown to play a critical role in the resolution of ambiguous ultrasound findings (Garel, 2008; Guibaud, 2009). Fetal sonography, if successful, measures the far-field ventricle with precision; however, the proximal ventricle is almost always obscured by near-field artifact from the skull and cannot be properly analyzed with this modality (Garel et al., 2003; Guibaud, 2009). Fetal MRI, on the other hand, offers a superior tool for assessing the size and shape of both ventricles. MRI is more precise, permits higher reproducibility, and provides better contrast (Grossman et al., 2006; Rutherford et al., 2008; Garel, 2008; Limperopoulos and Clouchoux, 2009; Guibaud, 2009; Studholme, 2011).

The standard method for VM analysis, presented by Cardoza et al. (1988), suggests measuring the ventricular width at the level of the atrium on an axial slice including the septum pellucidum, just above the thalami. This measurement, known as atrial diameter (AD), has been accepted as a relatively reproducible measure among observers (Guibaud, 2009). Clinical diagnosis of VM is made if the AD measurement is greater than 10 mm.

A recent study by Levine et al. (2008) shows that even among highly experienced physicians, there can be a high rate of disagreement in diagnosing fetal VM through both sonography and MRI. Disagreements arise most often in the setting of (1) lack of appropriate image scans; and (2) observation errors caused by off-axis image planes of sections, angled measurements, or improper choice of ventricular boundaries. Current imaging practice, which relies primarily on 2D visualization and AD measurement based on 2D image sections, is neither sufficiently precise nor reproducible; and improved imaging techniques, specifically 3D volumetric MRI, may significantly reduce the frequency of disagreements in diagnosis.

1.2. Background

Fetal MRI is limited to 2D acquisitions by the low signal available from the small fetal organs, and by intermittent fetal and maternal motion that disrupts spatial encoding necessary for advanced 3D volumetric MRI. Ultra-fast imaging protocols, such as half-Fourier acquisition single-shot fast spin echo (SSFSE), are used to obtain high-quality high-resolution 2D slices. These slices are acquired as snapshots in a fraction of a second, thus freezing the motion of the fetus. The acquired scans represent anatomic details in the slice plane views, however, due to fetal motion between slices and the thick slice acquisitions necessary to maintain high signal-to-noise ratio (SNR), the out-of-plane views only poorly capture the 3D structure of the anatomy.

We have recently developed a technique for robust super-resolution volume reconstruction from slice acquisitions (Gholipour et al., 2010) which generates high-resolution 3D volumetric fetal brain MRI despite intermittent fetal and maternal motion. As compared to the previous methods based on scattered data interpolation (Rousseau et al., 2006; Jiang et al., 2007; Kim et al., 2010), our method is based on a model of MRI slice acquisition. Volume reconstruction is formulated as an inverse problem and is solved through minimizing the error between model-generated slices and the acquired slices. This method was first introduced in Gholipour and Warfield (2009).

Three-dimensional volumetric reconstruction has significantly improved the capacity of fetal MRI in the analysis of fetal brain development in-utero, for example in accurate brain volumetry (Gholipour et al., 2011), as well as in-vivo analysis of hippocampal development (Jacob et al., 2011) and cortical maturation (Clouchoux et al., 2011). Significant clinical applications such as quantitative analysis of the early brain development and the diagnosis and prognosis of brain anomalies are expected to be dramatically facilitated by using this technology.

Accurate segmentation of fetal brain MRI is a key component in many of such image analysis applications, but remains quite challenging due to the highly variable size, shape, and anatomy of the developing brain, possible structural abnormalities, the characteristics of the developing tissues, and the quality of the original images, which are adversely affected by (1) motion artifacts, (2) significant partial voluming caused by thick-slice acquisitions, and (3) severe intensity non-uniformity artifacts. Consequently, automatic segmentation of fetal brain MRI has been very rarely reported; a valuable segmentation approach has been recently developed by Habas et al. (2010b) for the evaluation of normal fetal brain anatomy based upon a spatiotemporal atlas of the developing brain. The atlas was created from 20 manually segmented high-resolution fetal brain MR images in the gestation age (GA) range of 20.57 to 24.71 weeks (Habas et al., 2010a).

1.3. Purpose

As compared to the previous work which is limited to segmentation of normal fetal brains at a narrow GA range, the purpose of this study is to develop automatic fetal brain MRI segmentation for normal and abnormal fetal ventricles at a wide GA range to achieve quantitative analysis of VM. The contributions of this work are twofold: first, the main technical contribution is a novel automatic multi-atlas multi-shape segmentation method that penalizes intersections among structures. This method is especially important in the segmentation of spatially adjacent structures with similar intensity values in subjects with high degrees of anatomic variability. The exemplary application of this method is the segmentation of normal and dilated fetal ventricles addressed here. Although ventricles present with high contrast on MRI, the highly variable size and shape of normal, dilated, and fused lateral ventricles poses important challenges in automatic segmentation, which require the design of a robust segmentation method. Second, the contribution from an application perspective is quantitative VM analysis based upon novel volumetric and morphometric biomarkers of VM. The methods presented here can be further developed to achieve other biomarkers of fetal development in-utero.

We propose to segment the fetal brain ventricles using a new multi-atlas multi-shape segmentation technique. This method utilizes inter-subject fetal brain MRI registration for label propagation and the simultaneous truth and performance level estimation (STAPLE) method (Warfield et al., 2004) for robust multi-atlas label fusion. Initialized with robust multi-atlas label fusion, automatic segmentation of the left and right lateral ventricles is obtained in our probabilistic approach through constrained optimization of multiple shapes incorporating intensity and local spatial information. By penalizing intersections among structures, this approach generates accurate shape segmentation of spatially adjacent structures in subjects with strong anatomic variability, e.g. lateral ventricles in normal fetuses as well as dilated ventricles and fused ventricles in fetuses with VM.

In this study we consider normal and abnormal brains over a wider GA range than the previous work, i.e. by Habas et al. (2010b). The 25 cases examined in this study are from a heterogenous dataset to validate the developed methods in the presence of significant anatomic variability. In this study we do not aim at making a conclusion on VM diagnosis, prognosis, or the prediction of its outcomes; rather the 25 cases examined here have been used to validate the developed segmentation method using statistical tests and the experiments indicate that quantitative volumetric VM analysis is feasible through volumetric reconstruction and automatic segmentation. The methods are presented in detail in Section 2 and the results are illustrated in Section 3. Section 4 contains the concluding remarks.

2. Methods

In this section we discuss the algorithms that constitute our novel approach to quantitative VM analysis based on fetal brain MRI. The first component of our analysis strategy is volumetric reconstruction of fetal brain MRI, which was described in our recent work (Gholipour et al., 2010). Volumetric fetal brain MRI plays a critical role in the analysis as it provides motion-corrected isotropic high-resolution volumetric images of the fetal brain despite intermittent fetal and maternal motion. These high-resolution volumetric images enable automatic 3D segmentation which is used for volumetry and shape analysis. Our automatic segmentation method is constructed over multi-atlas segmentation, therefore we briefly discuss multi-atlas segmentation in Section 2.1. In Section 2.2 we present our novel multi-atlas multi-shape segmentation method that contains the definition of a probabilistic framework for multi-shape segmentation as well as our novel energy functional and its analytical solution for non-intersecting multi-shape optimization. This analytical solution is derived in Appendix B.

2.1. Multi-Atlas Segmentation

Atlas-based segmentation has been known as a promising approach of incorporating prior knowledge to achieve automatic segmentation (Rohlfing et al., 2004; Klein et al., 2008; Heckemann et al., 2006; van der Lijn et al., 2008). Atlas-based segmentation relies on the registration of an atlas to the query image to achieve segmentation of the query image through label propagation. Registration errors translate to segmentation errors. Errors can be reduced by using multiple atlases and label fusion (Aljabar et al., 2009; Artaechevarria and Munoz-Barrutia, 2009; Isgum et al., 2009; Lotjonen et al., 2010; van Rikxoort et al., 2010; Sabuncu et al., 2010). Majority voting (MV), the simplest label fusion strategy, is a probabilistic averaging of the multi-atlas label propagations; however, as a mean filter, MV is not robust to outliers of label propagation which are typically caused by failure or inaccuracy of inter-subject registration. In this study we use a robust label fusion strategy based on STAPLE algorithm (Warfield et al., 2004).

The goal of segmentation is to find the label map L(x) corresponding to the query image I(x), assigning a label l ∈ {0, 1, …, m} to each voxel x; where label 0 is assigned to the background. Thus m structures are segmented in addition to the background. We assume there are n training data sets used as multiple atlases A_i(x); i = 1, …, n with their corresponding label maps $L_i^A(x)$. A dense deformation field T_i is computed to map each atlas to the query image. This is performed through a specific multi-stage inter-subject registration algorithm discussed in Appendix A. The computed transformation defines the label propagation from each atlas to the query image. The propagated label maps are denoted by L_i(x); i = 1, …, n, and the collection of these labels is denoted by L.

In STAPLE label fusion less reliable propagated labels from registered atlases are given less weight than those from more reliable ones. The probability of assigning label L(x) = l to voxel x in the STAPLE formulation is written as

$$p(L(x)=l\mid \mathbf{L},\mathrm{\Theta })=\frac{p(L(x)=l)\mathbf{\prod }_{i}p(L_i(x)\mid L(x)=l,{\theta }_i)}{\mathbf{\sum }_{l\prime }p(L(x)=l\prime )\mathbf{\prod }_{i}p(L_i(x)\mid L(x)=l\prime ,{\theta }_i)}$$ (1)

where Θ is a collection of matrices θ_i which contain probability estimates of the reliability of propagated labels L_i(x). The elements of θ_i are defined as θ_ill′ = p(L_i(x) = l∣L_true(x) = l′), where L_true(x) is the true (but unknown) label of voxel x. The STAPLE algorithm solves Equation (1) without prior knowledge about the true labels. This is done by simultaneously estimating the reliability of the propagated labels and the consensus label on the query image through iterations of expectation maximization. The output is a robust estimation of the label fusion as well as reliability estimates for each of the propagated labels. The consensus label at voxel x is defined to be the most probable label. As described by Rohlfing et al. (2003) consensus voxels are ignored in the STAPLE algorithm. This avoids the presence of excessive background in the computations which may cause over-segmentation of structures if not labeled properly.

The output of label fusion is a multi-atlas segmentation of the image structures. However, multi-atlas segmentation is still strongly dependent on the accuracy of inter-subject registration, and thus may not perform well in the presence of large anatomic variations due to abnormalities or different maturation levels. Note that more accurate multi-atlas segmentation may be achieved by using increased number of atlases, however such atlases for different GA groups are not currently available for in-vivo fetal MRI. The construction of a large number of these atlases for each GA range is costly and time consuming, requiring significant fetal MR imaging effort, 3D reconstructions, and manual segmentations. To achieve more accurate segmentations by improving multi-atlas segmentations, we propose a novel multi-atlas multi-shape segmentation method here.

2.2. Multi-Atlas Multi-Shape Segmentation

Our novel segmentation method incorporates shape models of structures (Chan and Vese, 2001; Pham et al., 2000; Xu et al., 2004; Tsai et al., 2004) as well as regional intensity values and prior information from multi-atlas segmentations to achieve robust and accurate segmentation of brain structures. Using prior shape models obtained from multi-atlas segmentation, we optimize an energy functional to fit shape models into the corresponding anatomic structures. We formulate the problem in a probabilistic framework and solve the optimization problem through a numerical approach, in which the initial solution is perturbed and deformed to minimize the energy functional. This approach is based on the recently developed probabilistic shape optimization framework presented in Akhondi-Asl and Soltanian-Zadeh (2010). For a literature review of the previous multi-shape segmentation methods we refer to the recent papers by Akhondi-Asl and Soltanian-Zadeh (2009, 2010).

The energy functional we have developed in this study is different from the previous studies, specifically involves constraints to avoid intersections among structures, and also accounts for intensity coupling of different structures of the same tissue type to increase computational robustness and accuracy. This novel formulation is based on more realistic assumptions and is specifically important for the segmentation of spatially adjacent structures with similar intensity values, for example segmentation of fused lateral ventricles in fetuses with VM. This work is an extension of our recent conference paper by Akhondi-Asl and Warfield (2011) where preliminary results were reported on the segmentation of cortical structures in IBSR dataset. In this article we present a comprehensive description of the developed methodology and its analytical derivation along with the application in fetal brain MRI ventricular segmentation. The method is described in this section.

Each reconstructed volumetric fetal brain image is denoted by I(x). Similar to multi-atlas segmentation discussed in Section 2.1, the goal is to find a label map L(x) corresponding to this image, segmenting it to m + 1 structures labeled with l ∈ {0, 1, …, m}. The region corresponding to each label is denoted by Ω_l; thus for each voxel x in the image, the probability of belonging to label l is defined by p(x ∈ Ω_l) = p_l(x). In a probabilistic approach, the goal is to find the regions to maximize the sum of all probabilities over all m + 1 regions, therefore the cost function to be minimized is defined as

$$J({\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2,\dots ,{\mathrm{\Omega }}_m)=\mathbf{\sum }_{l=0}^m{\mathit{\int }}_{{\mathrm{\Omega }}_l}F(p_l(x))\mathit{dx}$$ (2)

where F(.) is a decreasing function. The background Ω₀ is a function of the other regions and is not an independent region.

In order to solve this minimization problem smooth estimations of the probability density functions (PDF) are needed, which can be obtained through Parzen window estimation in the form of $p_l(x)=\frac{1}{|{\mathrm{\Omega }}_l|}{\mathit{\int }}_{{\mathrm{\Omega }}_l}\mathrm{K}(I(x)-I(\widehat{x}))d\widehat{x}$; where K(.) is a Gaussian kernel function. Probabilistic methods of computing Gaussian mixture models for tissue type segmentation are considered as special cases of this formulation. The multi-shape segmentation problem formulated in this article is more general and covers segmenting different structures of the same tissue type, such as left and right lateral ventricles.

To account for tissue type contrast information we consider intensity coupling between different structures, thus all the structures of the same type are used to calculate the PDFs:

$$\begin{array}{lll}{p}_l(x)& =& \frac{1}{{\sum }_{i\in S_l}|{\mathrm{\Omega }}_i|}{\mathit{\int }}_{{\sum }_{i\in S_l}{\mathrm{\Omega }}_i}\mathrm{K}(I(x)-I(\widehat{x}))d\widehat{x},\\ & & l=1,\dots ,m,\mathit{and}\\ p_0(x)& =& \frac{1}{|{\mathrm{\Omega }}_0|}{\mathit{\int }}_{{\mathrm{\Omega }}_0}\mathrm{K}(I(x)-I(\widehat{x}))d\widehat{x}\end{array}$$ (3)

where S_l = {Ω_i ∈ family(Ω_l)}, and family(Ω_l) = {∀Ω_i∣PDF(Ω_i) ≡ PDF(Ω_l)}, where ≡ shows equivalency. The family of Ω_l includes all the regions that have the same tissue type and intensity distribution of structure l. For example the left and right lateral ventricles are in the same family. Incorporating intensity coupling among regions improves the stability of computations.

Next, an appropriate shape representation is needed for evolution of the shapes and their surfaces with correct and connected topology in the optimization process. One of the most effective methods of shape representation is through signed distance functions (SDFs) (Malladi et al., 1995). For each one of the structures an SDF, ϕ_l(x), is defined which determines how close each voxel x is to the boundary of the shape region. The SDF is negative inside the region, zero on the boundary, and positive outside of the region. The relationship between regions and shapes is thus defined as:

$$\begin{array}{r}{\mathrm{\Omega }}_l\equiv \{x\mid H(-{\varphi }_l(x))>0\},\mathrm{for}l=1,\dots ,m,\mathrm{and}\\ {\mathrm{\Omega }}_0\equiv \{x\mid \mathbf{\prod }_{l=1}^{m}H({\varphi }_l(x))>0\},\end{array}$$ (4)

where H(.) is the Heaviside function. With these definitions the problem is defined as computing the SDFs ϕ_l, l = 1, …, m that minimize the cost function in Equation (2).

By reformulating the problem with SDFs, using a Gaussian kernel function for PDF estimation, and choosing F(.) = −ln(.), the derivatives of the cost function can be calculated analytically. This results in a set of partial differential equations that can be solved iteratively, but require reliable initial estimates of the PDFs and the SDFs. The PDF estimates and the initial shape models (SDFs) are obtained from the multi-atlas segmentation discussed in Section 2.1.

The cost function in Equation (2) assumes that there is no intersection among different regions. This assumption is not correct and may reduce the accuracy of segmentation, in particular the segmentation of spatially adjacent structures in the same family. Therefore we introduce a modified cost function here, which is based on adding a constraint to the optimization problem to prevent intersections among structures. The constrained optimization based on shape representation with SDFs is thus defined as

$$\begin{array}{r}({\varphi }_1,\dots ,{\varphi }_m)=\underset{{\varphi }_1,\dots ,{\varphi }_m}{\mathrm{argmin}}J({\varphi }_1,\dots ,{\varphi }_m)\\ \mathrm{subject\; to}C({\varphi }_1,\dots {\varphi }_m)=0\end{array}$$ (5)

where

$$J({\varphi }_1,\dots ,{\varphi }_m)=\mathbf{\sum }_{l=0}^m{\mathit{\int }}_{{\mathrm{\Omega }}_l}-\ln (p_l(x))\mathit{dx}$$ (6)

and

$$C({\varphi }_1,\dots {\varphi }_m)=\mathbf{\sum }_{l=1}^m\mathbf{\sum }_{j=1,j\ne l}^m{\mathit{\int }}_{{\mathrm{\Omega }}_l}H(-{\varphi }_j(x)H(-{\varphi }_l(x))\mathit{dx}$$ (7)

It is observed that C(.) ≥ 0, and is equal to zero when there is no intersection among regions.

The constrained optimization is translated to the minimization of the following cost function based on Lagrange multipliers (λ) with an additional third term for the smoothness of the regions:

$$\begin{array}{lll}E& =& \mathbf{\sum }_{l=0}^m{\mathit{\int }}_{{\mathrm{\Omega }}_l}-\ln (p_l(x))\mathit{dx}\\ & & +\lambda \mathbf{\sum }_{l=1}^m\mathbf{\sum }_{j=1,j\ne l}^m{\mathit{\int }}_{\mathrm{\Omega }}H(-{\varphi }_j(x))H(-{\varphi }_l(x))\mathit{dx}\\ & & +\mathbf{\sum }_{l=1}^m{\mu }_l{\mathit{\int }}_{\mathrm{\Omega }}\delta ({\varphi }_l(x))|\nabla {\varphi }_l(x)|\mathit{dx}\end{array}$$ (8)

where $\mathrm{\Omega }={\cup }_{l=1}^m{\mathrm{\Omega }}_l$, and μ_ls are weighting coefficients defined heuristically based on an estimate of the relative magnitude of the three terms. The first term maximizes the log likelihood of PDF estimates, the second term penalizes shape intersections, and the third term penalizes the surface area of the shapes.

The derivatives of this energy function can be calculated analytically as detailed in Appendix B, and generate the following partial differential equation (PDE) for the time (t) evolution of the SDFs:

$$\frac{\partial {\varphi }_l(\widehat{x})}{\partial t}=|\nabla ({\varphi }_l(\widehat{x}))|\left\{M(\widehat{x})+2\lambda \mathbf{\sum }_{j=1,j\ne l}^{m}H(-{\varphi }_j(\widehat{x}))\right\}$$ (9)

where

$$\begin{array}{l}M(\widehat{x})=F(p_l(\widehat{x}))-\mathbf{\prod }_{j=1,j\ne l}^{m}H({\varphi }_j(\widehat{x}))\times F(p_0(\widehat{x}))\\ -{\mathit{\int }}_{\{{\mathrm{\Omega }}_j|j\in S_l\}}\frac{F^{\prime }(p_l(x))}{{\sum }_{j\in S_l}|{\mathrm{\Omega }}_j|}[p_l(x)-\mathrm{K}(I(x)-I(\widehat{x}))]\mathit{dx}\\ +{\mathit{\int }}_{{\mathrm{\Omega }}_0}\frac{F^{\prime }(p_0(x))}{|{\mathrm{\Omega }}_0|}\mathbf{\prod }_{j=1,j\ne l}^{m}H({\varphi }_j(\widehat{x}))[p_0(x)-\mathrm{K}(I(x)-I(\widehat{x}))]\mathit{dx}\\ +{\mu }_l\mathrm{div}(\frac{{\varphi }_l(\widehat{x})}{|\nabla {\varphi }_l(\widehat{x})|})+2\lambda \mathbf{\sum }_{j=1,j\ne l}^{m}H(-{\varphi }_j(\widehat{x}))\}\end{array}$$ (10)

The Lagrange multipliers in Equation (9) are computed as

$$\lambda =-\frac{{\sum }_{l=1}^m{\mathit{\oint }}_{{\mathrm{\Gamma }}_l}\left[M(x)|\nabla {\varphi }_j(x)|({\sum }_{j=1,j\ne l}^{m}H(-{\varphi }_j(x)))\right]\mathit{dx}}{2{\sum }_{l=1}^m{\mathit{\oint }}_{{\mathrm{\Gamma }}_l}(|\nabla {\varphi }_l(x)|{({\sum }_{j=1,j\ne l}^{m}H(-{\varphi }_j(x)))}^2)\mathit{dx}}$$ (11)

where Γ_l is the closed boundary of the region Ω_l.

Equation (9) is a PDE in the Hamilton-Jacobi form and can be solved numerically (Sethian, 1999; Osher and Fedkiw, 2003). Equations (10) and (11) are used iteratively to solve Equation (9) which minimizes the energy function in Equation (8). With this formulation the shapes move in the normal direction until they converge to a solution. The solution is a set of SDFs defining the shape structures that do not intersect but maximize the log likelihood of the PDFs of voxels belonging to different regions.

3. Results

To validate the methods and to evaluate and examine the novel biomarkers of VM in this study, we carried out experiments with a heterogenous fetal imaging dataset in a wide gestation age (GA) range for fetuses with normal and abnormal brains. We describe the details of data acquisition in Section 3.1. Then in Section 3.2 we validate our multi atlas multi shape (MA-MS) segmentation method for fetal ventricular segmentation and compare the results to atlas-based and shape-based segmentation methods. The accurate ventricular segmentations achieved through our algorithm are used for automatic ventricular volumetry and shape analysis to obtain volumetric and morphometric biomarkers of VM, as discussed in Section 3.3.

3.1. Data Acquisition

Fetal imaging data included diagnostic sonography and clinical fetal MRI acquired in the same day. Fetal MRI data was obtained from clinical MRI of pregnant patients with diagnosed or suspected cases of fetal anomalies after diagnostic ultrasonography. Clinical fetal MRI was performed using a 1.5-T TwinSpeed Signa system (GE healthcare) and an 8-channel phased-array cardiac coil, without maternal sedation or breath-hold, with the mother supine or in left decubitus position to minimize caval compression. The protocol involved acquisitions in the fetal sagittal, axial and coronal planes using half-Fourier acquisition single-shot fast spin echo (SSFSE) MR imaging with TR varying between 1000 and 4500 ms; TE varying between 80 and 100 ms; variable field of view based on the maternal and fetal body size (between 24-40 cm); variable matrix size between 160 and 512 pixels; and slice thickness between 3 and 6 mm.

Twenty five fetuses in the GA range of 19 weeks and 2 days (19.28) to 38 weeks and 3 days (38.43) (mean 28.26, stdev 6.56) were studied. This included thirteen fetuses with normal brains and twelve fetuses with VM. Table 1 shows the case numbers, GA in weeks, and the GA group (Gr) for each of the fetuses. The fetuses were considered in four GA groups: Group 1 covering 19 to 23 weeks, Group 2 covering 24 to 30 weeks, Group 3 covering 31 to 34 weeks, and Group 4 covering 35 to 39 weeks. The fetuses were considered in these different GA groups because atlases of the same GA range were used in atlas-based segmentation. The atrial diameter (AD) measurements for the left lateral ventricles (LLV) and right lateral ventricles (RLV) and the volumetric measures, i.e. intracranial volume (ICV) and ventricular volume (VV), have also been shown in Table 1. The AD measurements were calculated by radiologists as part of clinical practice. These measurements will be discussed in Section 3.3. The last column shows the consensus radiological assessment of VM for each case based on all the ultrasound and MR imaging data and contains classification of VM to mild (M) and severe (S).

Table 1.

Twenty five fetal MRI cases: gestational age (GA) in weeks, the GA group (Gr), atrial diameter (AD) measured for left lateral ventricles (LLV) and right lateral ventricles (RLV) in millimeters, volumetric measures including intracranial volume (ICV) in milliliters, ventricular volume (VV) in milliliters, and finally the consensus assessment of VM for each case (M for mild VM and S for severe VM). Values highlighted in BOLD indicate VM diagnosis based on those measures. The AD values shown in parentheses could not be measured by ultrasound due to obscured view by the nearfield artifact or difficult positioning, and were measured on fetal MRI by the radiologists (this was part of clinical evaluation).

	GA	Gr	AD-LLV	AD-RLV	ICV	VV	VM
	weeks		mm	mm	ml	ml
C01	19.28	1	(7.2)	7.1	54.1	2.78	-
C02	19.28	1	(8.4)	10.5	52.5	3.9	-
C03	19.43	1	10.7	9.8	53.0	6.05	M
C04	19.43	1	(9.3)	8.8	58.1	3.90	-
C05	19.86	1	15.9	13.9	76.1	10.5	S
C06	20.86	1	(18.5)	(19.1)	102	32.0	S
C07	21.28	1	(7.2)	7.0	88.6	4.00	-
C08	21.86	1	10.8	(11.5)	99.6	9.52	M
C09	24.00	2	(6.0)	(5.5)	101	3.11	-
C10	27.14	2	(8.1)	(9.3)	184	7.14	M
C11	27.86	2	(6.4)	(5.0)	210	3.21	-
C12	28.14	2	(5.5)	(5.2)	205	4.78	-
C13	29.00	2	(6.5)	(5.2)	275	5.15	-
C14	29.43	2	(13.4)	(7.7)	198	12.6	M
C15	31.43	3	7.8	(7.1)	309	4.08	-
C16	31.71	3	(12.5)	8.3	329	13.9	M
C17	33.28	3	(10.0)	(6.1)	434	7.16	M
C18	33.28	3	5.8	(7.1)	366	6.57	-
C19	33.43	3	(13.9)	13.3	455	27.6	S
C20	33.71	3	16.6	(13.1)	383	18.8	S
C21	35.00	4	(9.2)	(8.0)	421	5.75	-
C22	35.86	4	(6.6)	(6.0)	393	4.00	-
C23	36.28	4	(9.6)	(9.5)	544	17.3	M
C24	37.14	4	17.9	16.5	440	99.6	S
C25	38.43	4	(8.6)	(8.3)	373	5.82	-

3.2. Validating Segmentation

High-resolution volumetric fetal brain MRI was reconstructed for each case with uniform spatial resolution of 1 mm in all planes. The reconstructed volumetric images were processed with intensity non-uniformity correction using the non-parametric entropy maximization method developed by Mangin (2002) with the parameters discussed in Gholipour et al. (2011). The multi-atlas multi-shape (MA-MS) segmentation method developed in section 2.2 was applied to the cases in each group with a leave-one-out strategy for multiple atlas selection (i.e. the query image in each case was left out and the rest of the images in that GA group were used as atlases).

High-resolution reference segmentations of lateral and third ventricles were generated manually. These segmentations were performed on all 2D slices of the reconstructed high-resolution volumetric MR images and took between 15 to 45 minutes depending on the age of the fetus and the complexity of the structures. High-resolution images with corresponding manual segmentations were used as multiple atlases with a leave-one-out strategy for the segmentation of each subject in each GA group. Note that to minimize anatomic and shape differences due to different maturation levels only atlases in the same GA group were used for multi-atlas segmentation of each subject.

The MA-MS segmentation method was compared to several other methods, including single atlas (SA) segmentation, multi-atlas (MA) segmentation with majority voting, MA segmentation with local weighted voting (LWV) (Sabuncu et al., 2010), MA segmentation with LWV with intensity normalization (LWVwIN), MA segmentation with STAPLE label fusion, MA edge-based Laplacian level set segmentation referred to as MA-LLS, and multi-atlas single shape segmentation referred to as MA-SS. MA-LLS is an edge based level set segmentation method with the image Laplacian defining the speed function. We used the Insight toolkit (ITK) implementation of Laplacian level set segmentation developed by Whitaker (1998). MA-SS is a shape-based method using the framework defined in Section 2.2 but without intensity coupling and constraints penalizing shape intersections. All shape based methods, i.e. MA-LLS, MA-SS, and MA-MS used shape priors from multi-atlas STAPLE label fusion. We also compared MA-MS with MA-MS(MV) which used MV label fusion rather than STAPLE label fusion.

Figure 1 presents illustrative results, typical of all the cases, for case C02. Two axial slice planes of the 3D images are shown in this figure with segmentations of the lateral and third ventricles overlayed. The segmentation in (a) shows one of the best segmentations obtained from single-atlas (SA) label propagation, (b) shows one of the worst segmentations obtained from SA label propagation, (c) shows segmentation using multi-atlas majority voting label fusion: MA(MV), (d) shows segmentation using multi-atlas STAPLE label fusion: MA(STAPLE), and (e) shows segmentation using our multi-atlas multi-shape segmentation method (MA-MS). Finally (f) shows the manual segmentation used as the reference for evaluation.

Figure 1.

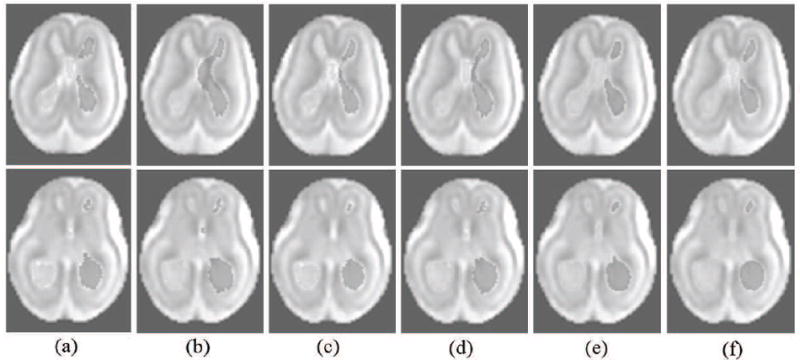
Segmentation results for case C02: two axial slices of the reconstructed volumetric MRI has been shown with segmentations obtained from different methods overlayed on this image; (a) is one of the best single-atlas segmentations, (b) is one of the worst single-atlas segmentations, (c) is segmentation using multi-atlas majority voting label fusion: MA(MV), (d) is segmentation using multi-atlas STAPLE label fusion: MA(STAPLE), and (e) is segmentation using our multi-atlas multi-shape segmentation method using STAPLE for robust label fusion (MA-MS). (f) is the manual segmentation used as reference for evaluation.

For quantitative evaluation, Dice similarity coefficient (DSC) was computed between automatic segmentations (S) and reference manual segmentations (R) for each case by voxel counts on the segmented regions $(\mathrm{DSC}=\frac{2|S\cap R|}{|S|+|R|})$. Table 2 shows the DSC metrics of ventricular segmentations using atlas-based segmentation methods. The first column shows the average (AVE) of DSC metrics obtained from single atlas segmentations, i.e. SA(AVE). The other columns show the DSC metrics for segmentations obtained from MA(MV), MA(LWV), MA(LWVwIN), and MA(STAPLE). The best value for each case is highlighted in bold text. Paired two-tailed t-tests were performed to test the null hypothesis of no difference in the DSC metrics of segmentations of the N = 25 cases in comparing MA(STAPLE) with the other label fusion methods. An α = 0.05 was selected to indicate a statistically significant difference and the null hypothesis was rejected in all t-tests with a significant level of p < 0.05.

Table 2.

The DSC metrics of ventricular segmentations using atlas-based segmentation methods: (1) SA(AVE) for average of DSC metrics of single-atlas segmentations, (2) MA(MV) for multi-atlas label fusion via majority voting, (3) MA(LWV) for multi-atlas label fusion via local weighted voting, (4) MA(LWVwIN) for MA label fusion via local weighted voting with intensity normalization, and (3) MA(STAPLE) for multi-atlas label fusion via STAPLE. The best value for each case is highlighted in bold text. The results indicate that MA(STAPLE) generated significantly better segmentations than all other label fusion methods.

	SA(AVE)	MA(MV)	MA(LWV)	MA(LWVwIN)	MA(STAPLE)
C01	0.805	0.882	0.872	0.849	0.838
C02	0.839	0.857	0.894	0.903	0.915
C03	0.859	0.911	0.906	0.908	0.868
C04	0.840	0.839	0.869	0.876	0.902
C05	0.825	0.812	0.863	0.873	0.901
C06	0.850	0.857	0.876	0.890	0.905
C07	0.851	0.892	0.857	0.892	0.900
C08	0.872	0.897	0.881	0.909	0.901
C09	0.670	0.762	0.688	0.780	0.723
C10	0.586	0.605	0.686	0.577	0.617
C11	0.560	0.684	0.547	0.720	0.570
C12	0.401	0.335	0.436	0.345	0.437
C13	0.567	0.640	0.760	0.641	0.758
C14	0.602	0.663	0.476	0.623	0.740
C15	0.510	0.588	0.582	0.658	0.644
C16	0.379	0.260	0.310	0.339	0.398
C17	0.593	0.711	0.567	0.667	0.706
C18	0.580	0.697	0.504	0.730	0.622
C19	0.637	0.592	0.563	0.693	0.798
C20	0.576	0.711	0.583	0.701	0.587
C21	0.363	0.541	0.333	0.569	0.580
C22	0.422	0.621	0.538	0.628	0.660
C23	0.137	0.073	0.082	0.142	0.232
C24	0.206	0.273	0.258	0.296	0.328
C25	0.323	0.436	0.517	0.544	0.547
ave	0.594	0.646	0.618	0.670	0.683
stdev	0.215	0.224	0.229	0.212	0.194

Note that by using uniform priors the STAPLE algorithm started as MV label fusion in our experiments and refined label fusion by estimating the reliability of propagated labels. With this setup STAPLE generates equal or more accurate results than MV in an expectation maximization sense. The results indicate that MA(STAPLE) generated significantly better segmentations than all other label fusion methods in our experiments. On the basis of this analysis MA(STAPLE) was used for prior shape model construction in all shape based segmentation methods developed and examined here. This includes the MA-MS, MA-LLS, and MA-SS methods.

In Table 3 we compared the DSC metrics obtained from shape based segmentation methods. In particular in this Table we have compared the MA(STAPLE) label fusion with MA-LLS, MA-SS, MA-MS(MV) for MA-MS with majority voting priors, and MA-MS. The best value for each case is highlighted in bold text. All shape based methods significantly improved the segmentations obtained from robust multi-atlas label fusion. The average and standard deviation of the DSC metrics over the 25 cases show that our MA-MS method outperformed the other methods. Paired two-tailed t-tests were performed to test the hypothesis of no difference in the DSC metrics of segmentations of the N = 25 cases in comparing MA-MS with MA(STAPLE), MA-LLS, MA-SS, and MA-MS(MV). An α = 0.05 was selected to indicate a statistically significant difference. The p values of these tests were p < 2 × 10⁻⁶, p < 0.005, p < 0.002, and p < 0.004, for MA-MS vs. MA(STAPLE), MA-LLS, MA-SS, and MA-MS(MV), respectively. These results indicate that MA-MS generated significantly better segmentations than the alternative methods.

Table 3.

The DSC metrics of ventricular segmentations for: (1) MA(STAPLE) for multiatlas segmentation by STAPLE label fusion, (2) MA-LLS for multi-atlas edge-based Laplacian level set segmentation, (3) MA-SS for multi-atlas single shape segmentation, (4) MA-MS(MV) for MA-MS segmentation with MV label fusion priors, and (5) MA-MS for MA-MS segmentation with STAPLE label fusion priors. The best value for each case is highlighted in bold text. An α = 0.05 was selected in paired two-tailed t-tests to indicate a statistically significant difference in DSC metrics of the methods for N = 25 cases, and the results indicated that MA-MS was significantly more accurate than the other methods.

	MA(STAPLE)	MA-LLS	MA-SS	MA-MS(MV)	MA-MS
C01	0.838	0.922	0.907	0.917	0.917
C02	0.915	0.960	0.941	0.928	0.947
C03	0.868	0.948	0.922	0.936	0.942
C04	0.902	0.931	0.913	0.934	0.937
C05	0.901	0.933	0.955	0.905	0.948
C06	0.905	0.923	0.949	0.926	0.956
C07	0.900	0.918	0.938	0.964	0.965
C08	0.901	0.944	0.929	0.933	0.941
C09	0.723	0.694	0.753	0.784	0.842
C10	0.617	0.930	0.879	0.946	0.894
C11	0.570	0.739	0.742	0.796	0.781
C12	0.437	0.741	0.609	0.723	0.763
C13	0.758	0.832	0.858	0.750	0.859
C14	0.740	0.905	0.853	0.828	0.883
C15	0.644	0.844	0.867	0.828	0.866
C16	0.398	0.749	0.876	0.857	0.861
C17	0.706	0.862	0.900	0.913	0.916
C18	0.622	0.715	0.824	0.786	0.858
C19	0.798	0.877	0.920	0.937	0.935
C20	0.587	0.737	0.948	0.942	0.953
C21	0.580	0.809	0.777	0.763	0.775
C22	0.660	0.801	0.772	0.805	0.795
C23	0.232	0.603	0.837	0.786	0.843
C24	0.328	0.809	0.823	0.876	0.877
C25	0.547	0.738	0.705	0.689	0.747
ave	0.683	0.835	0.856	0.858	0.880
stdev	0.194	0.098	0.088	0.082	0.067

Figure 2 shows the average of the DSC metrics for different GA groups and also for all cases. The results presented in this figure confirm the results of statistical tests performed on the data in Tables 2 and 3, and conclude that (1) multi-atlas methods are more accurate than single-atlas methods, (2) STAPLE label fusion outperforms MV label fusion, (3) shape-based segmentation methods improve the multi-atlas segmentations, (4) MA-MS outperforms all other atlas-based and shape-based methods, and (5) as the anatomy becomes more complex with higher GA, the accuracy of the segmentations decreases, however, the shape-based methods and in specific MA-MS appear to be more robust to the registration and label propagation errors caused by excessive anatomic variability in higher gestation ages. The DSC metrics obtained from MA-MS segmentation for all GA groups are still very high.

Figure 2.

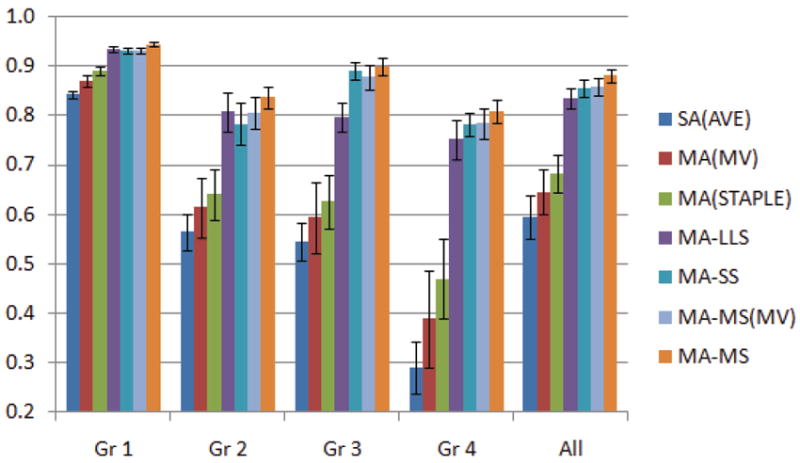
Average DSC metrics over GA groups and also over all cases for six segmentation methods. Error bars show standard errors. These results along with the statistical tests on the data reported in Table 3 indicate that the MA-MS method outperformed all other methods.

Figure 3 shows coronal slices of case C21, a case that the MA-MS method under-performed and generated a relatively low DSC metric (0.775). The segmentation results reported as overlay values in this Figure are generated by (a) MV label fusion, (b) STAPLE label fusion, (c) MA-LLS segmentation, and (d) MA-MS segmentation. The image in (e) shows the reference manual segmentation. In this case MA-LLS generated the best segmentations according to the DSC metric (0.809).

Figure 3.

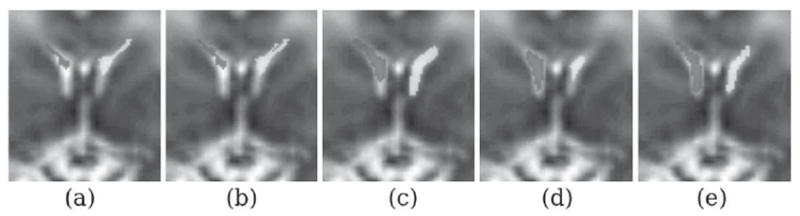
Segmentation results for case C21: coronal slices of the reconstructed volumetric MRI has been shown with segmentations obtained from different methods overlayed on this image; (a) is segmentation using multi-atlas majority voting label fusion: MA(MV), (b) is segmentation using multi-atlas STAPLE label fusion: MA(STAPLE), (c) is segmentation using multi-atlas Laplacian level set segmentation with STAPLE for robust label fusion (MA-LLS), (d) is segmentation using MA-MS with STAPLE for robust label fusion, and (e) is the manual segmentation used as reference for evaluation.

To the best of our knowledge, automatic segmentation of ventricles for fetal MRI of normal and abnormal brains at this wide GA range has not been reported before. Our proposed MA-MS segmentation method shows robust performance in this challenging application, where the atlas-based methods fail due to significant errors in registration and label propagation. Although we only applied our methods to ventricular segmentation, our developed MA-MS method is not theoretically limited to ventricular shapes and can be applied to the segmentation of other structures. Atlases with labeled structures are required to establish automatic segmentations. The accurate ventricular segmentations achieved through our volumetric reconstruction and automatic segmentation methods enable automatic ventricular volumetry, shape analysis, and the computation of volumetric and morphometric biomarkers of VM, which will be discussed in Section 3.3.

3.3. Volumetric and Morphometric Biomarkers of VM

The ventricular volume (VV) and intracranial volume (ICV) (Gholipour et al., 2011) were computed in milliliters (ml) based on automatic segmentation of volumetric fetal brain MRI. These values along with AD measurements of the left lateral ventricles (LLV) and right lateral ventricles (RLV) have been reported for all cases in Table 1. The AD values shown in parentheses could not be measured by ultrasound due to obscured view by the nearfield artifact from the skull or difficult position of the fetal head. These values were measured on 2D fetal MRI instead. All AD measurements were reported based on the clinical evaluation process. For each case the values indicating VM (i.e. AD > 10 mm) have been highlighted in bold text.

Figure 4 shows a visual comparison of the ventricular volumes obtained from volumetric fetal brain MRI and AD measurements on ultrasound images for five fetuses in the first GA group. For each fetus, a marching cubes surface rendering of the automatically segmented ventricles is shown on a transparent surface model rendering of the intracranial volume (ICV) in the top row. The VV and ICV measurements are shown below each volumetric image. The corresponding ultrasound image for each case is shown in the bottom row along with the AD measured using the pointers placed by a radiologist. Note that in four cases out of five the AD could only be measured for the far-field ventricle, and the proximal ventricle was obscured by nearfield artifact and could not be properly visualized and analyzed with ultrasound.

Figure 4.

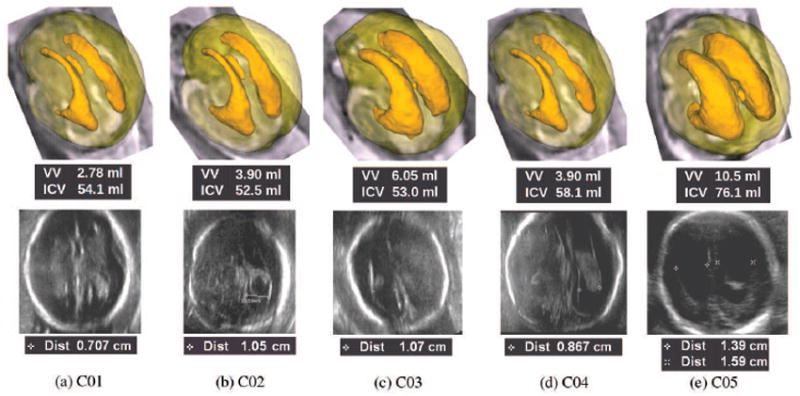
Volumetry based on volumetric fetal brain MRI as compared to 2D AD measurement based on fetal ultrasonography for five fetuses in group 1; the top image for each case shows a marching cubes surface model rendering of fetal ventricles over a transparent surface model rendering of the intracranial volume (ICV) based on volumetric fetal brain MRI. The ventricular volume (VV) and the ICV are computed in milliliters for each case and shown under each corresponding image. The bottom image in each case shows an ultrasound image captured by a radiologist for the measurement of AD. The AD is measured in millimeters via the pointers placed by radiologist at the boundary of the ventricles on the ultrasound image. Note that in most cases, AD could only be measured on the far-field ventricle. Except in one case, the proximal ventricles were almost always obscured by the nearfield artifact of the skull and could not be visualized by ultrasonography. The variation in VV is much higher than the 2D AD measurement, therefore VV appears to be more distinctive in the analysis of fetal VM. Volumetric fetal brain MRI reconstruction and automatic segmentation allows 3D visualization of the ventricles which is quite useful in the analysis of VM.

In this GA group cases C01, C02, and C04 were classified as normal, while cases C03 and C05 were diagnosed with mild and severe VM, respectively. Note that based on AD measurements cases C02 and C03 could be both considered as borderline VM; the normalized difference between the AD measurement on ultrasound for these cases was 2%, while the normalized difference between the VV measurements was 43.2%. VV appears to be more distinctive in the analysis of VM.

For quantitative ventricular shape analysis we used the spherical harmonics basis function model (SPHARM) description as developed by Gerig et al. (2001). SPHARM provides a hierarchical, parametric, multi-scale boundary description of structures with spherical topology, and has been successfully applied in morphological analysis of various brain structures including lateral ventricles, for example in schizophrenia patients (Styner et al., 2005). We used the SPHARM-PDM toolkit which is available through the Neuroimaging Informatics Tools and Resources Clearinghouse (NITRC). For mathematical details of SPHARM analysis and the toolkit the reader is referred to Gerig et al. (2001) and Styner et al. (2006).

The segmentation of the lateral ventricles obtained using our segmentation algorithm were pre-processed by morphological closing operation and Gaussian smoothing to achieve spherical topology required for SPHARM representation. In our parametric analysis we used spherical harmonics with a degree of 15. We did not scale the SPHARM surfaces and used icosahedron subdivision level of 10 for spherical parametrization of each ventricular shape model. Based on point-to-point SPHARM correspondences we computed shape distance maps and global shape difference metrics between normal and abnormal fetuses in each GA group. For each case, a mean global shape difference metric was computed by SPHARM-PDM analysis with respect to the normal cases in that GA group. For normal cases in each GA group we used a leave-one-out strategy (i.e. we computed the mean global shape difference between that case and the other normal cases in that group).

On the basis of the VM assessments for the fetuses listed in Table 1 we compared volumetric measurements, i.e. ICV and VV, as well as mean and maximum of global shape difference metrics of LLV and RLV with 2D biometric measurements, i.e. the average of AD measured for LLV and RLV (Mean AD) and the maximum of AD measured for LLV and RLV (Maximum AD), for each case. This comparison is shown in Figure 5, in which, each measurement is shown in one plot for all cases vs. their GA. In these plots, normal cases are represented by dots (·), cases with mild VM are represented by circles (○), and cases with severe VM are represented by stars (*). A linear fit was computed for each metric based on the normal cases only and has been shown with error bars of two standard deviations at the query points. The AD measurement plots are shown in (a) and (b), the volumetric metrics are shown in (c) and (d), and the global shape difference metrics are shown in (e) and (f). Note that a logarithmic scale was used for the VV plot.

Figure 5.

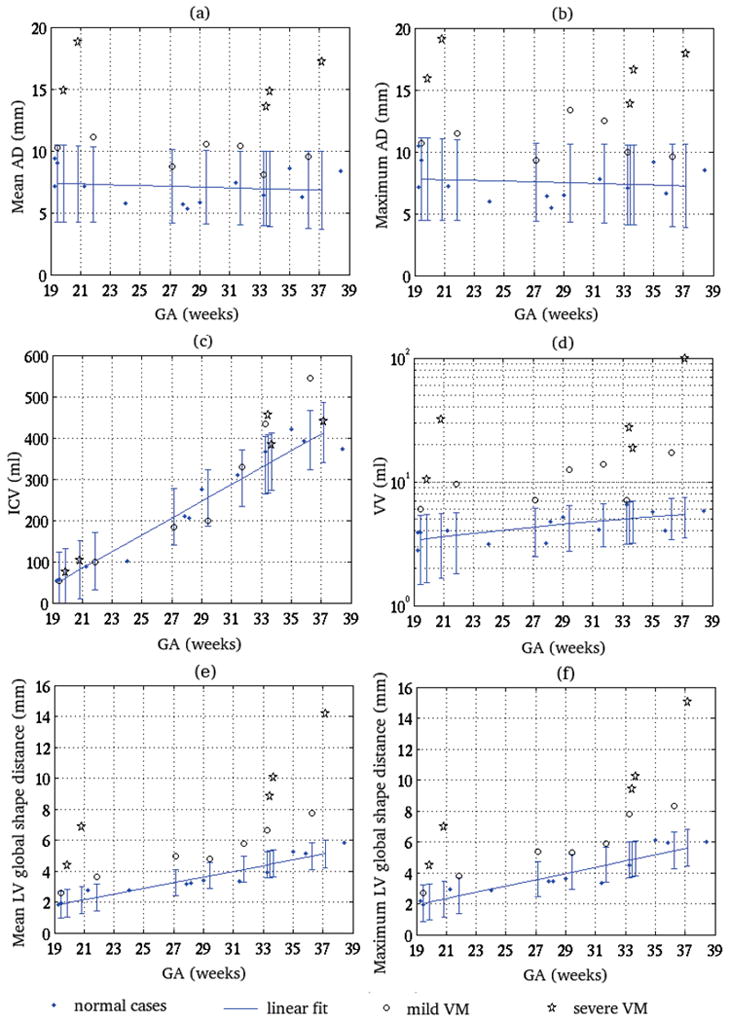
Comparing 2D AD measurement vs. GA and volumetric and morphometric biomarkers of VM vs. GA with respect to the presence and extent of fetal VM in 25 cases; (a) shows the average AD of LLV and RLV measured for each case (Mean AD), (b) shows the maximum AD of LLV and RLV measured for each case (Maximum AD), (c) shows the ICV in ml, (d) shows the VV in ml, (e) shows the mean of global shape distance between LLV and RLV, and (f) shows the maximum of global shape distance between LLV and RLV. Normal cases are represented by dots (·), cases with mild VM are represented by circles (○), and cases with severe VM are represented by stars (*). A linear fit was computed for each metric based on the normal cases and has been shown with error bars of two standard deviations at the query points. This analysis shows that the VV measurement and the shape distance metrics are quite distinctive between the normal and abnormal cases, while the Mean AD and Maximum AD are not. The plot shown in (c) for ICV vs. GA shows that there is no statistically significant difference between the ICV of normal cases and the cases with mild or severe VM. Note the logarithmic scale of the plot for VV in (d), which indicates that VV varies significantly between the normal and abnormal cases, while the variations in 2D biometric measurements are relatively small.

The first observation based on the linear fits on normal cases is that the values of ICV and VV for normal cases increased with GA, but the values of AD measurements for normal cases were almost constant with GA. Both mean and maximum AD values averaged between 7 and 7.5 mm for the normal cases. This complies with the literature on VM assessment based on AD, which effectively assumes that the AD is almost constant during brain maturation. According to the current VM analysis routine, any value of AD above or equal to 10 mm can lead to VM diagnosis regardless of the GA of the fetus. In order to see if the difference in various measurements was significant between the group of normal fetuses and fetuses with VM, we carried out two-sample two-tailed t-tests for each metric. We normalized the volumetric measurements with the GA of the fetuses. The results of the t-tests indicated that except for ICV, the difference between the two groups was statistically significant for all measurements (i.e. for normalized VV, mean AD, and maximum AD) at p values less than 0.02.

Two sample t-tests showed that the mean of the groups were significantly different for all metrics. A more detailed and informative analysis was drawn from the linear fits with respect to the GA and the two standard deviation (95%) prediction confidence intervals shown on the plots. Five major points were inferred from the plots shown in Figure 5: (1) From plot (c), no statistically significant difference was drawn between the ICV values of the normal cases and the cases with mild or severe VM. (2) From plot (d) the VV measurements for cases with VM were always outside of the 95% prediction confidence interval of the linear fit to normal cases. On the other hand the Mean and Maximum AD measurements for cases with VM, shown in plots (a) and (b), were not always outside of the 95% prediction confidence intervals (e.g. cases C03, C10, C17 and C23); (3) The variation in VV between the normal and abnormal cases (note the logarithmic scale) was much bigger than the variations in AD measurements. (4) For all measurements, i.e. VV, Mean AD and Maximum AD, the values for cases with severe VM were outside of four standard deviation margin of the normal linear fits. This indicated all measurements were good predictors of severe VM in our statistical analysis. (5) The mean and maximum LV shape distance metrics are also relatively distinctive indicators of fetal VM. Comparison of the mean and maximum metrics can be used in the classification of VM to symmetric/asymmetric or bilateral/unilateral for each case; a significant difference between the mean and maximum metrics indicates asymmetry between the shape of LLV and RLV. This was observed for case C17 (GA=33.28 weeks).

When comparing the volumetric (VV) and morphometric biomarkers in plots (d), (e), and (f), VV appears to be more accurate that shape measurements for the detection of VM as it quantifies the ventricular dilatation in units of volume (cubic millimeters); while the shape measurements quantify shape abnormalities in units of length (mm). The shape measurements, on the other hand, provide information on the shape variations from normal morphology. The use of both volume and shape measurements seems to be the best approach in detecting all abnormal cases (ventricular dilatation and/or abnormal morphology). For example abnormalities were better detected in cases C03, C08, and C14 by volume and in C18 by shape.

Finally we carried out a group comparison of normal cases vs. VM cases in Group 1. Figure 6 shows an average SPHARM shape representation of the left and right lateral ventricles for this group. The shape model is color-coded with mean shape distance map of the group in millimeters. An interesting finding in this analysis is that the mean shape distance between the normal fetuses and fetuses with VM is relatively low in the body of the lateral ventricles where AD is measured. This indicates that AD may not be a sufficiently sensitive measure for VM analysis. However, AD has been widely accepted and routinely used because of its straightforward definition and easy measurement process by radiologists. AD remains to be the best manually identifiable metric for VM assessment. The volumetric and morphometric biomarkers of VM introduced in this study are computed automatically, can be used in the resolution of borderline AD measurements, and may significantly improve the capacity of fetal MRI for enhanced quantitative analysis of VM and the related CNS anomalies.

Figure 6.

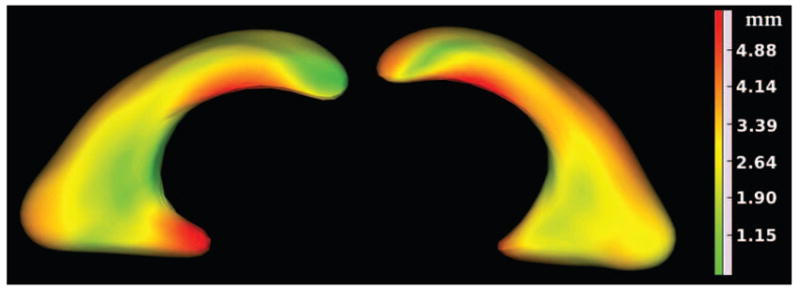
Group mean shape distance map of LLV and RLV obtained from statistical group comparison of SPHARM shape representations between four normal fetuses and four fetuses with VM in group 1. The mean shape distance map has been shown with color-coding on an average SPHARM shape representation of the group. This figure shows the local spatial extent of differences between normal and dilated ventricles of fetuses in group 1.

4. Discussion

The algorithms developed in this study allow, for the first time, accurate automatic in-vivo volumetric segmentation of normal and abnormal fetal ventricles which leads to a novel volumetric approach to ventriculomegaly analysis. The developed algorithm is based on a robust super-resolution volumetric fetal brain MRI reconstruction technique recently developed by the authors (Gholipour et al., 2010) and a novel multi-atlas multi-shape automatic segmentation method developed in this paper. The segmentation method designed in this article has been validated with a heterogeneous dataset of normal and abnormal brains over a wide gestation age range.

The novel VM analysis approach discussed in this article involves scalar volumetric measurements, i.e. ventricular volume (VV) and global shape difference metrics, as well as shape analysis based on global shape distance maps. The statistical analysis performed through linear model fitting of the atrial diameter (AD) and the volumetric and shape measurements vs. GA shows that VV and global shape difference measures are more reliable and distinctive biomarkers of VM as compared to AD measurement. Group comparison of eight fetuses in the first GA group (four normal fetuses and four fetuses with VM), depicted in Figure 6, shows average shape distance map between normal ventricles and dilated ventricles.

Atrial diameter (AD) is measured through manual detection of ventricular boundaries on prenatal ultrasound and is the first measurement used for the analysis of fetal ventricles. The volumetric measurements will be useful in the resolution of ambiguous or borderline AD measurements and also for improved classification and analysis of cases diagnosed with VM. The computation of volumetric and morphometric measurements is dependent upon the feasibility of the MRI processing pipeline discussed in this article. The feasibility of the pipeline is mainly dependent upon the success rate of the volumetric super-resolution fetal brain MRI reconstruction. The success rate of the volumetric reconstruction depends on the quality of the images which varies based on the scanner, the coil, and the imaging protocol; we achieved success rate of up to 75% on fetal MRI scans acquired with a 1.5 Tesla Philips scanner.

In the follow-up studies we will apply the developed image analysis pipeline to a larger cohort of fetuses. This will help us to determine the feasibility of the pipeline in a clinical context and to express the additional value of the proposed methods in the evaluation of VM. The analysis of a larger number of fetuses will lead to more accurate statistical tests on the diagnostic accuracy of volumetric measurements as compared to AD measurement. Long-term application of the proposed methods will also help us to quantify and compare the imaging protocols on different scanner platforms and to design and choose the protocols that generate the most accurate evaluation of fetal brain anomalies. Application of our novel volumetric and morphological analysis approach to larger cohorts of fetuses may help in better evaluation of early brain development in-utero and thus improved diagnosis, prognosis, and evaluation of complex neurodevelopment disorders.

The segmentation method developed and detailed in this study incorporates prior knowledge in the form of training data, shape models, and regional voxel intensity values within a probabilistic framework to achieve automatic segmentation of multiple shapes with similar intensity values. The PDF estimation in this approach is based on the query image and is updated in each iteration of shape optimization, and is hence robust to intensity and contrast differences between images and atlases. This is a major advantage over many of the previous methods, such as the approach developed by van der Lijn et al. (2008). Updating PDF estimation is particularly important in applications similar to the one reported in this study where the multi-atlas segmentation priors are not sufficiently accurate due to significant anatomic variability between subjects. In addition, constrained optimization has been formulated in this study which avoids intersections among multiple shape structures. This establishes a theoretically more advanced segmentation method. The importance of this contribution is clearly observed in the segmentation of spatially adjacent structures with similar intensity values in subjects with strong anatomic variability. Fetal brain ventricular segmentation, addressed in this article, is an exemplary application of this method, where the multi-atlas segmentations are prone to significant errors.

One important aspect of the work is the use of multi-atlas methods to achieve automatic segmentation. Due to the limitations of in-vivo fetal MRI the number of atlases used in this study was limited. The effect of the number and type of atlases (normal and abnormal fetal brain atlases) on the accuracy of segmentations should be addressed in detail in the future work. The use of much larger number of GA-matched atlases may result in more accurate results using both MV and STAPLE label fusions; however, due to strong anatomic variability between subjects, outliers are typically observed in label propagations. Outliers render non-Gaussian distribution of errors in label fusion. Under this condition, MV, as a mean filter, is no longer the maximum likelihood estimator for label fusion. Therefore in the presence of strong anatomic variability between subjects the robust solution using STAPLE is strongly suggested. Future work also involves the comparison of different label fusion and atlas selection strategies. In particular with a larger number of age-matched atlases the methods described by Artaechevarria and Munoz-Barrutia (2009); Sabuncu et al. (2010); Commowick and Warfield (2009, 2010) should be compared in a verified standard processing framework.

Future work also involves the application of the developed segmentation methodology to other structures in the fetal brain. Separation of different tissue types and structures requires training data that involves accurate manual segmentation of those structures on a number of fetuses in each GA range. Theoretically with more structures defined on the training data more accurate estimation of shape PDFs may be achieved due to better distinction between structures and their intensity values. This may lead to more accurate segmentations; however, many structures represent with much lower contrast than ventricles on fetal brain MRI. Therefore the segmentation of those structures will be more challenging. The preparation of atlas data and the development and evaluation of the segmentation method for other fetal brain structures is the subject of future work. When addressing the segmentation of a larger number of structures, the use of spatially varying label fusion strategies, such as those proposed by Asman and Landman (2011); Weisenfeld and Warfield (2011), should be considered for improved results. In addition to the specific application in fetal brain MRI, the developed robust multi-atlas multi-shape segmentation method is expected to have widespread applicability in medical imaging.

Research Highlights.

• We developed novel multi-atlas multi-shape fetal ventricular segmentation.

• The developed method accurately segmented normal and abnormal ventricles.

• Volumetric fetal brain MRI and automatic segmentation enabled volumetric analysis.

• We introduced novel volumetric and morphometric biomarkers of fetal ventriculomegaly.

• The new biomarkers show improvements to current analysis based on atrial diameter.

Appendix A. Inter-Subject Registration

The accuracy of multi-atlas segmentation is strongly dependent upon the accuracy of inter-subject registration between the atlas images and the query image. A dense deformation field transformation T_i is computed between each fetal MRI atlas image A_i(x) and the query image I(x) through a specific fetal MRI inter-subject registration algorithm. T_i is then applied to the atlas label maps $L_i^A(x)$ to obtain propagated label maps L_i(x), i = 1…n. The computation of T_i through inter-subject registration is discussed here.

Reconstructed volumetric images of the fetuses are obtained in the physical coordinate system of the scanner, and since the fetuses are in arbitrary positions with respect to the scanner coordinate system, the obtained volumetric images can be in any orientation in the 3D space. Registration of such images with different orientations can be very challenging. To overcome this issue, for each fetus we apply the transpose of one of the original scan orientation matrices to the reconstructed volumetric image to automatically bring it into an orthogonal orientation of the fetus. This brings the fetuses to one of the orthogonal orientations and thus simplifies inter-subject registration.

Our atlas-to-image registration algorithm involves four stages. In the first stage the atlas and the query (target) image are brought into the same spatial location and rough alignment using first order geometric moment (center of gravity). The major axes of the images are also computed for the alignment of the image orientations (see page 95 of (Goshtasby, 2005)). The next three stages of the algorithm consist of rigid, affine, and dense deformable registration, respectively. We use a multi-resolution mutual information (MI) based rigid registration algorithm with Powell optimization in the second stage. The Powell optimization method in this algorithm refines six parameters (three rotations and three translations) of a 3D rigid transformation applied to the atlas image to maximize its similarity to the target image. The similarity is measured by MI using a smooth non-parametric estimation of the joint and marginal entropies between the transformed atlas image and the target image (Thevenaz and Unser, 2002; Mattes et al., 2003). Information theoretic measures such as MI have shown great performance in medical image registration (see Gholipour et al. (2007) for a survey). MI performed better than other similarity measures for rigid registration in this application.

After the second stage the atlas and the target image will be in rough rigid realignment. For affine and dense deformable registration in stages 3 and 4 of our algorithm, we use the symmetric spatial normalization (SyN) tool (Avants et al., 2008) in ANTS software package. The metric for deformable registration is the mean square intensity differences of the images and is computed as ${\sum }_{x\in A_i(x)\cap I(x)}\Vert T_i\circ A_i(x)-I(x)\Vert$. After the fourth stage of the registration algorithm, the computed mapping T_i for each atlas is applied to the atlas label maps $L_i^A(x)$ to generate the propagated label maps L_i(x) used in Section 2.1.

Appendix B. Calculating the Derivatives of the Multi-Shape Optimization Energy Function

The energy function in Equation (8) has three terms. We show these terms with E₁, E₂, and E₃, respectively, and will calculate their derivatives with respect to the shape variation time t. These calculations will show how equations (9), (10), and (11) minimize the energy function in Equation (8).

$$\frac{\partial E_1}{\partial t}=\mathbf{\sum }_{j=0}^m\frac{\partial {\mathit{\int }}_{{\mathrm{\Omega }}_j}F({\widehat{p}}_j(x))\mathit{dx}}{\partial t}=\mathbf{\sum }_{j=1}^m\frac{\partial {\mathit{\int }}_{\mathrm{\Omega }}H(-{\varphi }_j(x))F({\widehat{p}}_j(x))\mathit{dx}}{\partial t}+\frac{\partial {\mathit{\int }}_{\mathrm{\Omega }}{\mathbf{\prod }}_{k=1}^{m}H({\varphi }_k(x))F({\widehat{p}}_0(x))\mathit{dx}}{\partial t}$$ (B.1)

Using $\frac{\partial {\prod }_{k=1}^{m}H({\varphi }_k(x))}{\partial t}={\sum }_{k=1}^m(\delta ({\varphi }_k(x))\frac{\partial {\varphi }_k(x)}{\partial t}{\mathbf{\prod }}_{l=1,l\ne k}^{m}H({\varphi }_l(x)))$, and after simplification we get

$$\begin{array}{l}\frac{\partial E_1}{\partial t}={\mathit{\int }}_{\mathrm{\Omega }}\mathbf{\sum }_{j=1}^m(\delta ({\varphi }_j(x))\frac{\partial {\varphi }_j(x)}{\partial t})\times (\mathbf{\prod }_{l=1,l\ne j}^{m}H({\varphi }_l(x))F({\widehat{p}}_0(x))-F({\widehat{p}}_j(x)))\mathit{dx}\\ +\mathbf{\sum }_{j=1}m{\mathit{\int }}_{\mathrm{\Omega }}H(-{\varphi }_j(x))F\prime ({\widehat{p}}_j(x))\frac{\partial p_j(x)}{\partial t}\mathit{dx}\\ +{\mathit{\int }}_{\mathrm{\Omega }}\mathbf{\prod }_{k=1}^{m}H({\varphi }_k(x))F\prime ({\widehat{p}}_0(x))\frac{\partial p_0(x)}{\partial t}\mathit{dx}\end{array}$$ (B.2)

To compute this derivative we need to compute $\frac{\partial p_j(x)}{\partial t}$ for j = 1, …, m and $\frac{\partial p_0(x)}{\partial t}$. Knowing that ${\sum }_{k\in S_i}{\mathit{\int }}_{\mathrm{\Omega }}H(-{\varphi }_k(\widehat{x}))d\widehat{x}={\sum }_{k\in S_i}|{\mathrm{\Omega }}_k|$ and ${\mathit{\int }}_{\mathrm{\Omega }}{\mathbf{\prod }}_{k=1}^{m}H({\varphi }_k(\widehat{x})d\widehat{x}=|{\mathrm{\Omega }}_0|$, and also by using Equation (3) the following equations are obtained:

$$\begin{array}{l}\frac{\partial p_i(x)}{\partial t}=\frac{\partial }{\partial t}(\frac{{\sum }_{k\in S_i}{\mathit{\int }}_{\mathrm{\Omega }}H(-{\varphi }_k(\widehat{x}))K(I(x)-I(\widehat{x}))d\widehat{x}}{{\sum }_{k\in S_i}{\mathit{\int }}_{\mathrm{\Omega }}H(-{\varphi }_k(\widehat{x}))d\widehat{x}})\\ =\frac{{\sum }_{k\in S_i}{\mathit{\int }}_{\mathrm{\Omega }}\delta ({\varphi }_k(\widehat{x}))\frac{\partial {\varphi }_k(\widehat{x})}{\partial t}(p_i(x)-K(I(x)-I(\widehat{x})))d\widehat{x}}{{\sum }_{k\in S_i}|{\mathrm{\Omega }}_k|}\end{array}$$ (B.3)

$$\begin{array}{r}\frac{\partial p_0(x)}{\partial t}=\frac{\partial }{\partial t}(\frac{{\mathit{\int }}_{\mathrm{\Omega }}{\mathbf{\prod }}_{k=1}^{m}H({\varphi }_k(\widehat{x}))K(I(x)-I(\widehat{x}))d\widehat{x})}{{\mathit{\int }}_{\mathrm{\Omega }}{\mathbf{\prod }}_{k=1}^{m}H({\varphi }_k(\widehat{x}))d\widehat{x}})\\ =\frac{1}{|{\mathrm{\Omega }}_0|}\mathbf{\sum }_{k=1}^m{\mathit{\int }}_{\mathrm{\Omega }}(\mathbf{\prod }_{l=1,l\ne k}^{m}H({\varphi }_l(\widehat{x})))\delta ({\varphi }_k(\widehat{x}))\frac{\partial {\varphi }_k(\widehat{x})}{\partial t}\times (K(I(x)-I(\widehat{x}))-p_0(x))d\widehat{x}\end{array}$$ (B.4)

Substituting Equations (B.3) and (B.4) in Equation (B.2) and further calculations result in

$$\begin{array}{l}\frac{\partial E_1}{\partial t}=\mathbf{\sum }_{j=1}^m{\mathit{\oint }}_{{\mathrm{\Gamma }}_j}\frac{\partial {\varphi }_j(x)}{\partial t}\\ \times (\mathbf{\prod }_{l=1,l\ne j}^{m}H({\varphi }_l(x))F({\widehat{p}}_0(x))-F({\widehat{p}}_j(x)))\mathit{dx}\\ +\mathbf{\sum }_{j=1}^m\mathbf{\sum }_{k\in S_j}{\mathit{\int }}_{{\mathrm{\Omega }}_j}{\mathit{\oint }}_{{\mathrm{\Gamma }}_k}\frac{\partial {\varphi }_k(\widehat{x})}{\partial t}\frac{F\prime ({\widehat{p}}_j(x))}{{\sum }_{k\in S_j}}\\ \underset{\mathrm{②}}{\underbrace{\times (p_j(x)-K(I(x)-I(\widehat{x})))d\widehat{x}\mathit{dx}}}\\ -\mathbf{\sum }_{j=1}^m\frac{1}{|{\mathrm{\Omega }}_0|}{\mathit{\int }}_{{\mathrm{\Omega }}_0}{\mathit{\oint }}_{{\mathrm{\Gamma }}_j}\frac{\partial {\varphi }_j(\widehat{x})}{\partial t}\mathbf{\prod }_{l=1,l\ne j}^{m}H({\varphi }_l(\widehat{x}))\\ \times F\prime ({\widehat{p}}_0(x))(p_0(x)-K(I(x)-I(\widehat{x})))d\widehat{x}\mathit{dx}\end{array}$$ (B.5)

In order to calculate the second term represented by ② in this equation, we define G(x, x̂) = F′(p̂_j(x)) × (p_j(x) − K(I(x) − I(x̂))). The following holds

$$\begin{array}{l}\mathbf{\sum }_{j=1}^m\mathbf{\sum }_{k\in S_j}\frac{1}{{\mathbf{\sum }}_{p\in S_j}|{\mathrm{\Omega }}_p|}{\mathit{\int }}_{{\mathrm{\Omega }}_j}{\mathit{\oint }}_{{\mathrm{\Gamma }}_k}\frac{\partial {\varphi }_k(\widehat{x})}{\partial t}\times G(x,\widehat{x})d\widehat{x}\mathit{dx}=\\ \mathbf{\sum }_{j=1}^m\mathbf{\sum }_{k\in S_j}{\mathit{\oint }}_{{\mathrm{\Gamma }}_k}\frac{\partial {\varphi }_k(\widehat{x})}{\partial t}\frac{1}{{\sum }_{p\in S_j}|{\mathrm{\Omega }}_p|}{\mathit{\int }}_{{\mathrm{\Omega }}_j}G(x,\widehat{x})\mathit{dxd}\widehat{x}\end{array}$$ (B.6)

By defining a function Q(j, k) where Q(j, k) = 1 if k ∈ S_j and Q(j, k) = 0 if k ∉ S_j, Equation (B.6) can be modified as follow

$$\begin{array}{l}\mathbf{\sum }_{k=1}^m{\mathit{\oint }}_{{\mathrm{\Gamma }}_k}\frac{\partial {\varphi }_k(\widehat{x})}{\partial t}\mathbf{\sum }_{j=1}^m\frac{Q(j,k)}{{\sum }_{p=1}^{m}Q(j,p)|{\mathrm{\Omega }}_p|}{\mathit{\int }}_{{\mathrm{\Omega }}_j}G(x,\widehat{x})\mathit{dxd}\widehat{x}\\ =\mathbf{\sum }_{k=1}^m{\mathit{\oint }}_{{\mathrm{\Gamma }}_k}\frac{\partial {\varphi }_k(\widehat{x})}{\partial t}\mathbf{\sum }_{j=1}^m\frac{1}{{\sum }_{p\in S_j}|{\mathrm{\Omega }}_p|}{\mathit{\int }}_{{\mathrm{\Omega }}_j}G(x,\widehat{x})\mathit{dxd}\widehat{x}\\ =\underset{\mathrm{③}}{\underbrace{\mathbf{\sum }_{k=1}^m{\mathit{\oint }}_{{\mathrm{\Gamma }}_k}\frac{\partial {\varphi }_k(\widehat{x})}{\partial t}\mathbf{\sum }_{j\in S_k}\frac{1}{{\sum }_{p\in S_k}|{\mathrm{\Omega }}_p|}{\mathit{\int }}_{{\mathrm{\Omega }}_j}G(x,\widehat{x})\mathit{dxd}\widehat{x}}}\\ =\mathbf{\sum }_{k=1}^m{\mathit{\oint }}_{{\mathrm{\Gamma }}_k}\frac{\partial {\varphi }_k(\widehat{x})}{\partial t}\frac{1}{{\sum }_{p\in S_k}|{\mathrm{\Omega }}_p|}{\mathit{\int }}_{\left\{{\mathrm{\Omega }}_j\mid j\in S_k\right\}}G(x,\widehat{x})\mathit{dxd}\widehat{x}\end{array}$$ (B.7)

where in writing the third equation represented by ③ we have used the fact that ${\forall }_j\in S_k:{\sum }_{p\in S_j}|{\mathrm{\Omega }}_p|={\sum }_{p\in S_k}|{\mathrm{\Omega }}_p|$. After changing the dummy variables k with j, and p with k in Equation (B.7), the following is obtained for the derivatives of the first term:

$$\begin{array}{l}\frac{\partial E_1}{\partial t}=\mathbf{\sum }_{j=1}^m\{{\mathit{\oint }}_{{\mathrm{\Gamma }}_j}\frac{\partial {\varphi }_j(\widehat{x})}{\partial t}\times \{\mathbf{\prod }_{l=1,l\ne j}^{m}H({\varphi }_l(\widehat{x}))(F({\widehat{p}}_0(\widehat{x}))\\ -F({\widehat{p}}_j(\widehat{x})))+\frac{1}{{\sum }_{k\in S_j}|{\mathrm{\Omega }}_k|}{\mathit{\int }}_{\{{\mathrm{\Omega }}_k|k\in S_j\}}F\prime ({\widehat{p}}_j(x))\\ \times (p_j(x)-K(I(x)-I(\widehat{x})))\mathit{dx}\\ -\frac{1}{|{\mathrm{\Omega }}_0|}\mathbf{\prod }_{l=1,l\ne j}^{m}H({\varphi }_l(\widehat{x})){\mathit{\int }}_{{\mathrm{\Omega }}_0}F\prime ({\widehat{p}}_0(x))\\ \times (p_0(x)-K(I(x)-I(\widehat{x})))\mathit{dx}\}d\widehat{x}\}.\end{array}$$ (B.8)

The derivative of the second term is calculated as

$$\begin{array}{l}\frac{\partial E_2}{\partial t}=\frac{\partial }{\partial t}\{\mathbf{\sum }_{j=1}^m\mathbf{\sum }_{i=1,i\ne j}^m{\mathit{\int }}_{\mathrm{\Omega }}H(-{\varphi }_j(\widehat{x}))H(-{\varphi }_i(\widehat{x}))d\widehat{x}\}\\ =\mathbf{\sum }_{j=1}^m{\mathit{\oint }}_{{\mathrm{\Gamma }}_j}\frac{\partial {\varphi }_j(\widehat{x})}{\partial t}\mathbf{\sum }_{i=1,i\ne j}^m-2H(-{\varphi }_i(\widehat{x}))d\widehat{x}\end{array}$$ (B.9)

Finally, the derivatives of the third term will be

$$\begin{array}{l}\frac{\partial E_3}{\partial t}=\frac{\partial }{\partial t}\{\mathbf{\sum }_{j=1}^m{\mu }_j{\mathit{\int }}_{\mathrm{\Omega }}\delta ({\varphi }_j(\widehat{x}))|\nabla {\varphi }_j(\widehat{x})|d\widehat{x}\}\\ =-\mathbf{\sum }_{j=1}^m{\mathit{\oint }}_{{\mathrm{\Gamma }}_j}\frac{\partial {\varphi }_j(\widehat{x})}{\partial t}{\mu }_j\mathrm{div}(\frac{{\varphi }_j(\widehat{x})}{|\nabla {\varphi }_j(\widehat{x})|})d\widehat{x}\end{array}$$ (B.10)

By adding these three terms and replacing $\frac{\partial {\varphi }_j(x)}{\partial t}$ by the formula defined in Equation (9), $\frac{\partial E}{\partial t}=-{\sum }_{j=1}^m{\mathit{\int }}_{\mathrm{\Omega }}{(\frac{\partial {\varphi }_j(x)}{\partial t})}^2$ is achieved, which minimizes the energy function E.