Using the R Package crlmm for Genotyping and Copy Number Estimation

Abstract

Genotyping platforms such as Affymetrix can be used to assess genotype-phenotype as well as copy number-phenotype associations at millions of markers. While genotyping algorithms are largely concordant when assessed on HapMap samples, tools to assess copy number changes are more variable and often discordant. One explanation for the discordance is that copy number estimates are susceptible to systematic differences between groups of samples that were processed at different times or by different labs. Analysis algorithms that do not adjust for batch effects are prone to spurious measures of association. The R package crlmm implements a multilevel model that adjusts for batch effects and provides allele-specific estimates of copy number. This paper illustrates a workflow for the estimation of allele-specific copy number and integration of the marker-level estimates with complimentary Bioconductor software for inferring regions of copy number gain or loss. All analyses are performed in the statistical environment R.

1. Introduction

Duplications and deletions spanning kilobases of the genome contribute to a substantial proportion of the genetic variation between individuals. Copy number variants (CNV) account for a greater proportion of differences in terms of sequence composition between two individuals than single nucleotide polymorphisms (SNPs, Zhang et al. 2009). CNV can arise through a number of mechanisms during meiosis and mitosis and are well known to be implicated in cancer through deletions that disrupt tumor suppressor genes or the amplification of oncogenes. Copy number alterations have also been implicated in several genomic disorders, including complex diseases such as schizophrenia and autism (Karayiorgou et al. 2010; Pinto et al. 2010).

Current estimates regarding the frequency and size of segmental duplications and deletions in the human genome are largely based on high-throughput arrays that quantitate copy number on a genomic scale. Two such technologies are array comparative genomic hybridization (aCGH) and genotyping platforms such as the Affymetrix oligonucleotide arrays and the Illumina BeadArrays. While each of these platforms rely on the hybridization of probes to sample preparations containing target DNA sequence, differences exist in the size of the probes, the number of probes per target sequence, and whether the hybridization is competitive. Unlike aCGH, genotyping arrays can be used to identify copy-neutral regions of homozygosity that, while common in apparently normal individuals, can suggest rare genetic events such as uniparental isodisomy (UPD). UPD has been implicated in heritable diseases such as Prader-Willi syndrome (Altug-Teber et al. 2005). While the resolution is potentially much greater in genotyping arrays due to the shorter probe length, shorter probe lengths tend to result in more probe-to-probe variability with respect to cross-hybridization to the alternative allele, nonspecific binding, and differences in basepair composition. Reliable inference of copy number gain or loss at a single 25 – 100 basepair locus is not currently possible, and statistical methods that smooth the locus-level estimates as a function of the physical position in the genome are needed.

Despite robust-to-outlier approaches for normalization, we have observed systematic differences in the copy number between groups of samples that can be perfectly predicted by the timestamp on the CEL files. We refer to such systematic difference in copy number between groups of samples as batch effects. That larger studies tend to have more substantial batch effects than smaller studies is consistent with our conjecture that the nonstatic nature of experimental reagents and laboratory conditions contribute over time to batch effects. Irrespective of etiology, we have found that the scan date of the array and chemistry plate are useful surrogates for batch (Scharpf et al. 2011b). With an appropriate experimental design that involves randomization of samples to chemistry plate, batch effects are a nuisance variable that can be successfully modeled and removed.

Existing analytic strategies for identifying alterations in copy number have largely adopted a one- or two-step approach. In the one-step approach, assessments of CNV are made from the raw intensities using the joint distribution across samples. For instance, Zhang et al. (2009) developed a Correlation Matrix Diagonal Segmentation (CMDS) that identifies recurrent alterations in a population. While we have not formally evaluated the impact of batch effects using this approach, it is important to note that the differences in raw intensities between groups of samples, whether driven by biological causes or by technological artifacts such as batch effects, are similar in terms of their effects on the data. A safe strategy when adopting such an approach would be to filter loci associated with experimental factors such as chemistry plate or scan date.

In contrast to the one-step approach, two-step approaches generally derive estimates of copy number and uncertainty at each marker, followed by smoothing of the marker-level estimates at the second stage. The motivation for the two-step approach is that the marker-level estimates are too imprecise to provide reliable copy number estimates. However, marker-specific estimates can be useful for at least two reasons. First, single-locus estimates are typically derived from the joint distribution of intensities across samples and, through inspection of the joint distribution, batch effects can be modeled and removed. Secondly, plots of the marker-level estimates can be useful for assessing copy number mosaicism. Mosaicism occurs when mixtures of cell populations with different mutations give rise to noninteger copy number estimates. For instance, many tumors are comprised of a mixture of cell populations representing different levels of tumor evolution. The choice of appropriate statistical methods for smoothing at the second stage can therefore be informed by visualizations of the marker-level estimates. In particular, hidden Markov models (HMMs, Fridlyand et al. 2004; Colella et al. 2007; Wang et al. 2007; Scharpf et al. 2008) are generally more appropriate for germline diseases in which latent, integer copy number states are reasonable. By contrast, segmentation algorithms such as circular binary segmentation (Olshen et al. 2004; Venkatraman and Olshen 2007) may be more appropriate for diseases such as cancer. While segmentation algorithms estimate segment means, HMMs provide direct inference about the latent copy number states of interest and can be used to identify copy-neutral regions of homozygosity.

This paper describes software for the first of a two-stage approach for identifying CNV in high-throughput genotyping arrays. All software was written using the statistical language R (R Development Core Team 2011) and available from Bioconductor (Gentleman et al. 2004) at http://www.Bioconductor.org/packages/release/bioc/html/crlmm.html We illustrate our approach on 1258 HapMap samples that were assayed on the Affymetrix 6.0 platform (International HapMap 3 Consortium et al. 2010). Section 2 gives a brief overview of the the statistical methods for preprocessing, genotyping, and copy number estimation. Section 3 describes current data structures used by the crlmm package for organizing and annotating large datasets, as well as the organization of the compendium package for reproducing the figures in this manuscript. Section 4 describes the 2-step approach for identifying copy number alterations, highlighting the type of exploratory data analysis made possible in the crlmm package. Closing remarks are provided in Section 5. A compendium for reproducing the analysis is available from the author’s website at http://www.biostat.jhsph.edu/~rscharpf/crlmmCompendium/.

2. Methods

This section describes the steps for processing the raw fluorescence intensities from scanned arrays, genotyping the polymorphic markers, and deriving bivariate normal prediction regions for allele-specific copy number. The bivariate normal prediction regions have several possible useful applications with respect to copy number estimation, including a simple translation to estimates of raw copy number at each marker.

2.1. Preprocessing

Preprocessing refers to normalization of the raw fluorescence intensities to remove array-toarray variability and the summarization of the normalized intensities of replicate probes. The crlmm package adapts the robust multichip average (RMA), originally described for gene expression microarrays (Irizarry et al. 2003), to genotyping platforms. We refer to this algorithm as SNP-RMA (Carvalho et al. 2007). Recent platforms for Affymetrix and Illumina include probes for polymorphic loci as well as probes for nonpolymorphic regions. At polymorphic loci, the raw intensities for each allele are quantile normalized (Bolstad et al. 2003) to a target reference distribution obtained from the HapMap phase 2 samples (Carvalho et al. 2007). The Affymetrix 6.0 platform contains 3 or 4 identical probes for each allele. The normalized intensities for a set of identical probes are summarized by the median. For nonpolymorphic loci, only one probe per loci is available and the intensities are quantile normalized without a subsequent summarization step. Additional details regarding the preprocessing of Affymetrix CEL files and Illumina IDAT files are described elsewhere (Carvalho et al. 2007; Ritchie et al. 2009).

2.2. Genotyping

Following the normalization and summarization of intensities at polymorphic loci, we apply the corrected robust linear mixture model (CRLMM) algorithm to genotype SNPs. This algorithm extends previous algorithms for genotyping, namely RLMM (Rabbee and Speed 2006) and BRLMM (Affymetrix 2006). A key difference of our approach and our predecessors is the use of HapMap samples to train our algorithm. The CRLMM algorithm originally described in Carvalho et al. (2007) has been adapted to accommodate changes in the technology of the more recent Affymetrix 5.0 and 6.0 platforms. Specifically, the probes for each locus are identical and lie on the same strand for the 5.0 and 6.0 platforms, simplifying the estimation procedure. In addition, the implementation of CRLMM in the crlmm package does not provide a correction for fragment-length as the improvement to model fit has, in our experience, not justified the additional computation. A recent comparison paper describes genotyping algorithms for Illumina’s Infinium arrays (Ritchie et al. 2009).

The CRLMM algorithm provides genotype calls and quality scores for all polymorphic markers through a hierarchical model described in detail elsewhere (Carvalho et al. 2010). One critical aspect of our the procedure is to formulate the genotype classification problem in the space of the log-ratio of the observed intensities I for the A and B alleles versus the overall strength of the A and B intensities. More precisely, the y and × axes in a M versus S scatter plot are defined by log₂(I_A/I_B) and ${\text{log}}_2(\sqrt{I_A\times I_B})$, respectively. Our previous work has demonstrated that the M are more robust to batch effects than the bivariate distribution of log A and log B. For example, see Supplementary Figure 1 in Scharpf et al. (2011b). We also note that the separation of the M values for the diallelic genotypes g, g ∈ {AA, AB, BB}, is smaller for SNPs with very low or very high values of S. For example, Figure 7B of Carvalho et al. (2007) depicts the relationship of M and S for one sample. Taken together, these observations motivated the development of a hierarchical model to account for systematic sources of variation from batch and intensity strength. Following the estimation procedure for model parameters outlined elsewhere (Carvalho et al. 2010), the inferred genotypes are based on the derivation of the posterior probability for the true genotype Z. Assuming that there are no batch effects, a simplification of the posterior probability for SNP i in sample k is given by

$$\mathtt{P}(Z_{\mathit{\text{ik}}}=g|M_{\mathit{\text{ik}}}=m)=\frac{\mathtt{P}(Z_{\mathit{\text{ik}}=g})h_{M_{\mathit{\text{ik}}}|Z_{\mathit{\text{ik}}}=g}(m)}{{\displaystyle {\sum }_{g\prime }}\mathtt{P}(Z_{\mathit{\text{ik}}=g\prime })h_{M_{\mathit{\text{ik}}}|Z_{\mathit{\text{ik}}}=g\prime }(m)}\text{ for }g\prime \in \{\mathit{\text{AA}},\mathit{\text{AB}},\mathit{\text{BB}}\},$$ (1)

where h_mik|Zik (m) represents a normal density. See equations (4) and (6) of Carvalho et al. (2010) for the derivation of the mean and variance for the normal density. The genotype call, Ẑ_ik, and confidence score, q_ik, for SNP i in sample k are given by

$${\widehat{Z}}_{\mathit{\text{ik}}}={\text{arg max}}_g\mathtt{P}(Z_{\mathit{\text{ik}}}=g|M_{\mathit{\text{ik}}}=m)\text{and}$$ (2)

$$q_{\mathit{\text{ik}}}=\underset{g}{\text{max}}\mathtt{P}(Z_{\mathit{\text{ik}}}=g|M_{\mathit{\text{ik}}}=m),$$ (3)

respectively. Our implementation maps the scores q_ik from the [0, 1] interval to integers using the relationship

$$M(q_{\mathit{\text{ik}}})=\text{round}(-1000*\text{log}2(q_{\mathit{\text{ik}}})),$$

as it allows efficient storage with minimum loss.

In summary, the CRLMM algorithm estimates genotypes through a hierarchical model for the log ratios of A:B intensities that accounts for the dependency on intensity strength, batch effects, and the uncertainty of parameters estimated from the training step. For each platform design supported by our software, we provide one annotation package that contains parameters estimated from the training data for every SNP-genotype combination.

2.3. Bivariate normal prediction regions for integer copy number

In large studies, batch effects become evident as the strength of the A and B intensities is sensitive to changes to laboratory conditions, reagents, or personnel that change over time. Estimation of absolute copy number is a more difficult enterprise than genotyping in part because batch effects and true differences in copy number are similar in terms of their effects on the data. While quantile normalization is an effective means for removing array to array variation and provides additional robustness to outliers in individual samples, such normalization procedures are insufficient for removing batch effects. However, algorithms that assign biallelic genotypes to samples based on the ratio of log intensities, as implemented in the crlmm algorithm, are robust to batch effects. We utilize CRLMM’s robustness to batch effects to guide the estimation of parameters in a multilevel model for copy number.

This section briefly describes the algorithm for estimating batch-specific bivariate normal prediction regions of integer copy number. Typically, the 96-well chemistry plate is a useful surrogate for batch as the samples from a given plate are often processed at similar times. As indicated above, the resulting prediction regions can be used to (i) compute a posterior mean copy number at each marker, (ii) incorporated directly into a hidden Markov model to infer regions of copy number gain and loss, or (iii) used to derive an estimate of raw copy number. The estimation procedure extends probe-level models for estimating gene expression (see Wu and Irizarry 2005) and an early version of an algorithm for estimating copy number described by Wang et al. (2008). As of this writing, the algorithm requires the genotypes of the experimental dataset and does not use any training data, such as HapMap, as priors. As a consequence, the current implementation requires a minimum of 10 samples per batch for estimating parameters for copy number, with larger batch sizes (e.g, 90 or more samples) preferred.

At each SNP, we (i) calculate robust estimates of the mean and variance for each of the diallelic genotypes, (ii) shrink the empirical estimates to the within-batch averages estimated from a large number of SNPs, (iii) impute the location and variance of unobserved genotypes, and (iv) fit a linear model to the within-genotype cluster medians. More formally, we propose the following theoretical model for the observed intensity I at SNP i, batch j, sample k, and allele l:

$$[I_{\mathit{\text{ijkl}}}]=[({\text{Optical}}_{\mathit{\text{ijl}}}+{\text{Nonspecific}}_{\mathit{\text{ijl}}})\times ({\delta }_{\mathit{\text{ijkl}}})]+[{\text{Specific}}_{\mathit{\text{ijl}}}\times {\epsilon }_{\mathit{\text{ijkl}}}]\equiv [{\nu }_{\mathit{\text{ijl}}}\times {\delta }_{\mathit{\text{ijkl}}}]+[{\varphi }_{\mathit{\text{ijl}}}{c}_{\mathit{\text{ijkl}}}\times {\epsilon }_{\mathit{\text{ijkl}}}]\text{ for }l\in \{A,B\},$$ (4)

where the errors δ and ε account for array to array variation within a batch and are assumed to be approximately log-normal. Fluorescence arising from nonspecific hybridization and optical background are collectively parameterized by ν. To estimate the ν and ϕ in model (4), we assume that the c_l are known from the diallelic genotype calls. For instance, c_A takes the value 0, 1, or 2 for genotypes BB, AB, and AA, respectively. Next, we fit a regression line to estimates of the median intensity for each genotype stratum using weighted least squares (Equation 7 of Scharpf et al. 2011b). The intercept and slope of the regression line correspond to our estimates of ν_A and ϕ_A in model (4), respectively. We repeat the procedure for allele B. As in Wang et al. (2008), we assume that the joint distribution of the log intensities conditional on the allelic copy number is approximately bivariate normal:

$$\left[\begin{array}{c}{\text{log}}_2(I_{\mathit{\text{ijkA}}})\hfill \\ {\text{log}}_2(I_{\mathit{\text{ijkB}}})\hfill \end{array}\right|\begin{array}{c}{C}_{\mathit{\text{ijkA}}}=c_A\hfill \\ C_{\mathit{\text{ijkB}}}=c_B\hfill \end{array}]~\mathrm{N}(\left[\begin{array}{c}{\text{log}}_2({\nu }_{\mathit{\text{ijA}}}+c_A{\varphi }_{\mathit{\text{ijA}}})\hfill \\ {\text{log}}_2({\nu }_{\mathit{\text{ijB}}}+c_B{\varphi }_{\mathit{\text{ijB}}})\hfill \end{array}\right],{\mathbf{\Sigma }}_{\mathit{\text{ij}}})$$ (5)

We obtain initial estimates of the covariance Σ empirically, and subsequently shrink the the covariance to improve estimates for genotypes with few observations (Scharpf et al. 2011b). The means of the bivariate normal in Equation 5 are obtained by plugging in estimates of ν and ϕ from the linear model. Section 4 provides code for plotting the predictions regions as well as the raw copy number. The raw copy number is the sum of the allele-specific estimates, ĉ_A + ĉ_B, obtained through the following relationship:

$${\widehat{c}}_{\mathit{\text{ijkl}}}=\text{max}\{\frac{1}{{\widehat{\varphi }}_{\mathit{\text{ijl}}}}(I_{\mathit{\text{ijkl}}}-{\widehat{\nu }}_{\mathit{\text{ijl}}}),0\}\text{ for }l\in \{A,B\}.$$ (6)

For nonpolymorphic markers and monomorphic SNPs, we follow a similar procedure using SNPs with complete data to predict the unobserved genotypes. For example, the unobserved ‘A’ and ‘null’ genotypes for monomorphic AA SNPs and nonpolymorphic loci are imputed from a regression model using SNPs with all three diallelic genotypes observed as explanatory variables. The linear model is fit to the imputed genotype-cluster medians and variances using weighted least squares as described previously (Scharpf et al. 2011b).

3. Implementation

This section provides a brief overview of this compendium and the data structure adopted by crlmm for binding information on the samples, markers, and experiment in a single object.

Compendium

This document is written using Sweave (Leisch 2002) and is included in the crlmmCompendium R package. The crlmmCompendium package can be downloaded from http://www.biostat.jhsph.edu/~;rscharpf/crlmmCompendium/. The raw CEL files used in this analysis are publicly available (http://hapmap.ncbi.nlm.nih.gov/downloads/raw_data/hapmap3_affy6.0/). Manageable subsets of the markers and samples from the processed data are included with the crlmmCompendium package for the purpose of reproducing the figures and illustrating key features of the software. The website for the compendium places code extracted from this Sweave document for each of the figures alongside thumbnail versions of the figures. Reproducing the complete analysis described in this Sweave file requires two additional steps. First, one would need to obtain the CEL files for the HapMap phase 3 data and verify that any additional R packages beyond those that are required for installing the compendium are available. See Section 6 for the complete R session information from our analysis. Secondly, the following code chunk specifying the path to the CEL files and the directory to store results should be edited as appropriate.

R>  outdir  <- "<PATH_TO_CEL_FILES>"

In addition to the above tasks, we suggest caching long computations such that repeated Sweave calls can be loaded from disk. We used the R package cacheSweave (Peng 2010) for this purpose and alert the user to blocks of code in Section 4 that may be useful for caching (Peng and Eckel 2009). Subsequent Sweave’s calls of this file are fast and can be performed in an interactive session as cached computations are lazy loaded into the global environment.

crlmm

The R package crlmm is available from Bioconductor (Gentleman et al. 2004). New releases of crlmm are available twice per year. The crlmm package utilizes the S4 class ‘CNSet’ container for encapsulating the normalized intensities and various other aspects of the experiment and samples. The ‘CNSet’ class extends the basic ‘eSet’ container defined in Biobase. As with other ‘eSet’ extensions, phenotypic data on the samples, annotation for the probes, and meta-data on the experiment are also included in the container. Through inheritance, all of the general methods defined for the ‘eSet’ class are available for the ‘CNSet’ class. The ‘CNSet’ is specialized for copy number estimation as follows. Elements of the assayData slot include the normalized intensities for the A and B alleles, the CRLMM genotype calls, and the CRLMM confidence scores. Data and meta-data for the samples and probes are stored in the phenoData and featureData slots, respectively. The class defines two additional slots important for copy number estimation: batch and batchStatistics. The batch slot contains a character vector that describes the batch in which the CEL files were processed. The character vector must be the same length as the number of samples. The batchStatistics slot is similar to the assayData slot, but as the name implies the elements in the environment are SNP- and batch-specific statistical summaries needed for copy number estimation, including robust estimates of the mean and variance for each genotype cluster and parameters from the linear model in equation (4). Each element in the batchStatistics environment has dimension I × J, where I is the total number of markers (SNPs and nonpolymorphic probes) and J is the total number of batches. Several examples for accessing the batch statistics are illustrated in Section 4. Objects of the ‘CNSet’ class are typically instantiated by the genotype. However, new objects can also be derived by the “[” method that subsets rows (markers) and columns (samples).

Parallelization and large data support

Several of the algorithms described in the previous section have been written to allow parallelization of computation across multiple processors or nodes. For instance, the SNP-RMA and CRLMM algorithms, as well as the algorithm for copy number estimation allow for parallel computing. The infrastructure for parallel computing is handled by the R package snow (Tierney et al. 2008; Rossini et al. 2007).

We have made several adaptations to reduce the memory footprint of key functions for processing large datasets. The reduction is primarily made possible by the use of data structures and protocols provided by the ff package (Adler et al. 2011) for storing objects on disk rather than in memory. Algorithms such as SNP-RMA and CRLMM require only subsets of the samples or markers, respectively. As a consequence, data can be read into memory, processed, and summaries written to file without excessive memory requirements. We manage the location of files on disk and the size of the data chunks (subsets of rows and/or columns) through three utility functions provided as part of the oligoClasses package (Carvalho and Scharpf 2011): ldPath, ocProbesets, and ocSamples. Documentation for these functions is available in the oligoClasses package and illustrated in Section 4. Currently, all of the elements in the assayData slot and batchStatistics slot are ff objects, as opposed to ordinary matrices. While the use of ff objects has many advantages, operations on these objects require more careful attention to avoid accidentally calling too much data from disk and swamping the available memory. In general, this can be achieved by specify both the i and j arguments to the “[”method. However, one should be careful in the order of operations for accessing data from a ‘CNSet’ object. For example, the normalized A allele intensities for the first 5 SNPs could be obtained by either of the following commands:

R> as.matrix(A(cnSet)[1:5,  ])
R> as.matrix(A(cnSet)[1:5, ]))

While the results from both commands would be identical, the first command is the preferred approach as the I/O for the second command can be substantially greater. In particular, the second command subsets every element in the assayData and batchStatistics slot prior to extracting the normalized A allele intensities. Note also that we have wrapped both calls by the function as.matrix. This is important when dealing with ff objects as the object returned by assessors for assayData and batchStatistics can be either of class ‘data.frame’ or ‘matrix’, depending on the size of the data set. Explicit coercion to class matrix avoids bugs that could arise, for instance, by a method that behaves differently for ‘data.frame’ and ‘matrix’ objects.

Known limitations

A limitation of the current design is that the assayData elements must all have the same dimension. However, the nonpolymorphic markers only interrogate one allele and we do not estimate a genotype at these markers. Implicitly, the assay data elements for allele B, the genotype calls, and the genotype confidence scores for nonpolymorphic markers are larger than required and store many NAs. For example, the matrix for genotype calls in the Affymetrix 6.0 platform are almost twice as large as needed. The advantage of equally-sized assay data elements is that (i) information on the features can be represented in a single location that is bound to the assay data and feature annotation, (ii) subsetting objects of the class does not require any special handling, and (iii) fewer bugs due to the simplicity of the design and the inheritance of well-tested methods that are defined for the ‘eSet’ class. We prefer the added reliability of the current structure to the potential improvements in efficiency, particularly since the implementation does not generally effect the memory requirements as the ff package stores the data on disk.

Currently, copy number estimation is not available for samples in which the batch size is fewer than 10. Unlike the log₂(A/B) ratio, the strength of A and B intensities is sensitive to batch making training with data such as HapMap more difficult. The practical consequence is that crlmm does not currently estimate the parameters in the linear model for batches with fewer than 10 samples, and may provide noisy estimates of copy number for batches with fewer than 50 samples. Future versions of crlmm may include solutions for small data scenarios. Finally, several files for storing the data will be created by utilities in the ff package. If these files are later moved to a different location or removed, the accessors for data in the ‘CNSet’ object will no longer work. Users should either use the clone utility in the ff package for relocating files on disk, or be prepared to rerun the genotyping and copy number estimation steps. As in any statistical analysis using R, saving the exact session information can be useful for reproducing a previous analysis.

4. Results

This section describes a 2-step approach for identifying regions of copy number alterations. In the first step, raw copy number estimates at each marker are obtained using the crlmm package. In the second step, the raw copy number estimates are smoothed using a hidden Markov model implemented in the VanillaICE package (Scharpf et al. 2011a) and by circular binary segmentation implemented in the DNAcopy package (Seshan and Olshen 2011). The visualizations provided in this section use lattice graphics for effective multi-panel displays (Sarkar 2008).

4.1. Fitting the multilevel model

We begin our analysis of the HapMap data by loading the compendium and various dependencies – including ff, VanillaICE, and crlmmCompendium as well as genefilter (Gentleman et al. 2011), IRanges (Pages et al. 2011), and MASS (Venables and Ripley 2002) – for our analysis of the HapMap data.

R> library("ff")
R> library("genefilter")
R> library("IRanges")
R> library("MASS")
R> library("VanillaICE")
R> library("crlmmCompendium")

As the result of the above commands, the ff package is in the search path and support for large datasets is automatically enabled. We set the path to store objects on disk and fine-tune the size of the data chunks used by the CRLMM algorithm using the three utility functions mentioned in the previous section.

R> ldPath(outdir)
R> ocProbesets(50000)
R> ocSamples(200)

Finally, the cacheSweave package is loaded for caching output from long code chunks and a directory for storing the cached computations is declared.

R> library("cacheSweave")
R> setCacheDir(outdir)

We complete the set-up for our analysis of the HapMap samples by specifying the names of the CEL files and defining a surrogate for batch. As indicated previously, a useful surrogate for batch is the scan date of the array or the chemistry plate. For the HapMap phase 3 data, the chemistry plate is the first 5 letters of the CEL filename. We extract the plate names from the filenames in the following code.

R> filenames <- list.celfiles(pathToCels, full.names = TRUE,
+    pattern = ".CEL")
R> plate <- substr(basename(filenames), 1, 5)

The steps for preprocessing and quantile-normalizing Affymetrix CEL files in crlmm are wrapped in the function genotype. (Users that only require the genotype calls and do not intend to estimate copy number should use the crlmm function instead.) The genotype function is a wrapper for several important steps. First, the function initializes an object of class ‘CNSet’, verifying the validity of the data passed to the batch argument of this function. Secondly, the function reads the raw intensities from the CEL files and normalizes the intensities in a memory efficient manner via the SNP-RMA algorithm (Bolstad et al. 2003; Carvalho et al. 2007). The nonpolymorphic markers are also quantile-normalized to a target reference distribution estimated from HapMap. Finally, we call the CRLMM algorithm to genotype and estimate genotype confidence scores at SNPs. As the preprocessing and genotyping is computationally intensive, we set cache = TRUE in the declaration of the following code chunk.

R> cnSet <- genotype(filenames = filenames, cdfName = "genomewidesnp6"),
+    batch = plate)

The object returned by the genotype function, assigned to the name cnSet in the above command, is an instance of the S4 class ‘CNSet’. In addition to specifying batch as an argument to genotype, one may optionally specify the gender. If gender is not specified as in the above example, the gender is imputed. Typically, the imputed gender should be accurate as a large number of markers are available to estimate gender. However, in cancer samples or diseases with chromosome X or Y aneuploidy, the gender calls may be incorrect or ambiguous. Otherwise, one reason to allow the imputation is as a check for possible inconsistencies in the supplied documentation. The show method for class ‘CNSet’ provides a concise summary of its contents.

R> show(cnSet)

CNSet (assayData/batchStatistics elements: ffdf)
CNSet (storageMode: lockedEnvironment)
assayData: 1852215 features, 1258 samples
  element names: alleleA, alleleB, call, callProbability
protocolData
  rowNames:
    CHEAP_p_HapMapP3Redo2_GenomeWideSNP_6_A04_235570.CEL
    CHEAP_p_HapMapP3Redo2_GenomeWideSNP_6_A07_235576.CEL ...
    TESLA_p_CEU_Trio_GenomeWideSNP_6_A03_223714.CEL (1258
    total)
  varLabels: ScanDate
  varMetadata: labelDescription
phenoData
  sampleNames:
    CHEAP_p_HapMapP3Redo2_GenomeWideSNP_6_A04_235570.CEL
    CHEAP_p_HapMapP3Redo2_GenomeWideSNP_6_A07_235576.CEL ...
    TESLA_p_CEU_Trio_GenomeWideSNP_6_A03_223714.CEL (1258
    total)
  varLabels: SKW SNR gender
  varMetadata: labelDescription
featureData
  featureNames: SNP_A-2131660 SNP_A-1967418 ... CN_954736
    (1852215 total)
  fvarLabels: chromosome position isSnp
  fvarMetadata: labelDescription
experimentData: use 'experimentData(object)'
Annotation: genomewidesnp6
batch:    CHEAP 8, CORER 8, CUPID 77, DINGO 73, EPODE 89, ...
batchStatistics: 29 elements, 1852215 features, 19 batches

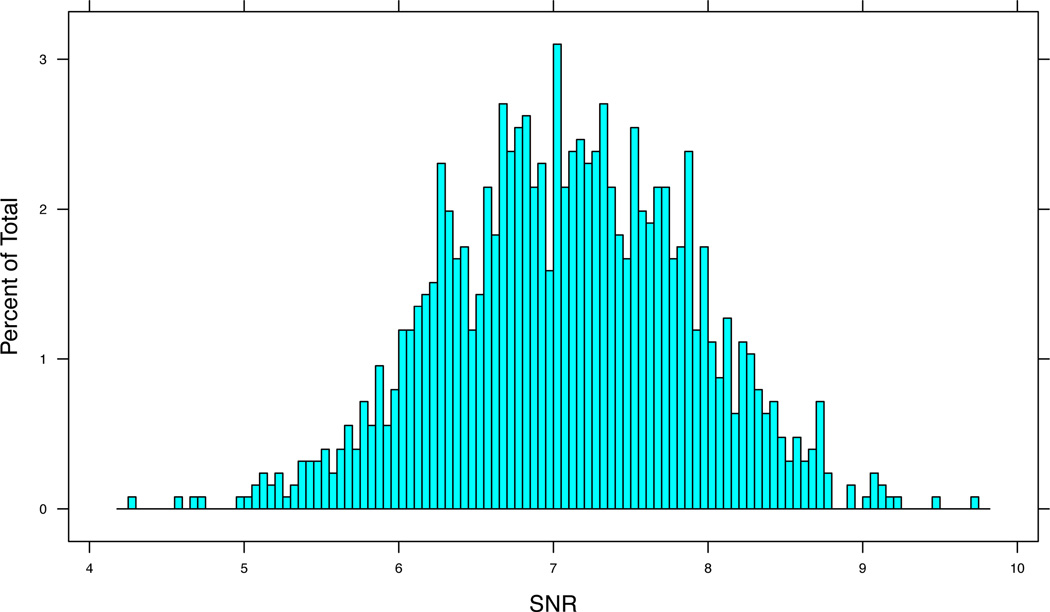
Following preprocessing and genotyping, the SNR (see Section 2) can be a useful statistic for quality control. In some instances, it may be preferable to remove samples with low SNR from downstream analyses. The SNR is stored in the phenoData slot of the cnSet object and can be accessed and plotted as follows. See Figure 1 for a histogram of the SNR values in the HapMap phase 3 study.

R> open(cnSet$SNR)

[1] FALSE

R> SNR <- cnSet$SNR[]
R> close(cnSet$SNR)

[1] TRUE

R> (snrfig <- histogram(~SNR, breaks = 100))

Figure 1.

Signal to noise ratio for the HapMap phase 3 data. Signal to noise ratios below 5 can indicate problems with data quality.

By default, the sample names for the cnSet, accessible by sampleNames(cnSet) are the CEL filenames. The crlmmCompendium contains a mapping from the CEL filenames to the more familiar HapMap identifiers. The following code changes the sample labels from the filename to the HapMap identifiers. Note that we generally suggest using the filenames for the sample names, but have adopted the more concise HapMap names in this analysis to improve readability of the resulting output.

R> cnSet$celFiles <- sampleNames(cnSet)
R> sampleNames(cnSet) <- getHapMapIds(cnSet)
R> sampleNames(cnSet)[1:5]

The metadata on the samples and features can be listed with the varLabels and fvarLabels, respectively.

R> varLabels(cnSet)

[1] "SKW"      "SNR"    "gender"    "celFiles"

R> fvarLabels(cnSet)

[1] "chromosome" "position"   "isSnp"

Recall that the assay data elements in the cnSet object contain pointers to large objects on disk. One can list all of the ff files created during the initialization of the container as in the following code chunk. Once created, these files should not be moved or deleted.

R> list.files(ldPath(), pattern = "\\.ff$")[1:2]

[1] "call-_134b9efb7.ff" "call-_24ad295a7.ff"

The underlying data structures are intended to be handled seamlessly through the provided interface in crlmm. For instance, in the following code chunk we open file connections to the ff objects and access the quantile normalized intensities for the first 5 markers and the first 6 samples for allele A.

R> invisible(open(cnSet))
R> as.matrix(A(cnSet)[1:5, 1:6])

              NA12045 NA20881 NA18873 NA19652 NA19679 NA18625
SNP_A-2131660    3263    5087    4655    3225    3368    4736
SNP_A-1967418     180     233     188     271     228     267
SNP_A-1969580     577     724     782     752     486     751
SNP_A-4263484    2100    1287    1658     462    2205     336
SNP_A-1978185    1571    1369    2116    1810    1861    1292

The above query is not instantaneous as these items pull data from the ff files on disk to active memory. The bracket operator without arguments, as in [,], would pull data from all markers and all samples from disk to active memory, defeating the purpose of using the ff package.

In the analysis of genomewide association data, it is often useful to visualize the genotype clusters for loci of interest. All that is required for such a visualization is the platform-specific identifier for the SNP of interest. In the example below, we plot the genotype clusters for SNP A-2131660. The object genotypeSet that contains the data for this SNP is available in the crlmmCompendium package and was generated from the following commands.

R> invisible(open(cnSet))
R> genotypeSet <- cnSet[match("SNP_A-2131660", featureNames(cnSet)), ]
R> invisible(close(cnSet))

The R function prePredictPanel in the crlmmCompendium package extracts the normalized intensities, the genotype calls, and the confidence scores for the genotypes and stores the results in an object of class ‘data.frame’. The resulting ‘data.frame’ object will be useful for creating trellis displays with the lattice package.

R> df <- prePredictPanel(genotypeSet)

We will construct 3 scatterplots of this SNP using colors to annotate different aspects of the data. The following code selects a color for the plotting symbols that indicates the CRLMM genotype call.

R> fill1 <- brewer.pal(3, "Set1")[df$gt]

CRLMM provides a genotype call for all SNPs (no missing values) and a confidence score for the called genotype (Equation 2). If one wishes to exclude SNPs with low confidence scores, visualizations of the confidence scores in the context of the scatterplot can be useful. In the following code, we select a grey scale for the confidence score with darker shades of grey indicating less confidence ranging to which (confidence = 1). As the confidence scores for this SNP were all high (≥ 0.89), we selected a scale such that scores near 0.89 are shaded dark.

R> gt.conf <- df$gt.conf
R> min.conf <- min(gt.conf)
R> max.conf <- max(gt.conf)
R> sc <- (gt.conf - min.conf)/(max.conf - min.conf)
R> fill2 <- sapply(sc, grey)

Finally, we choose a subset of samples to highlight the batch effects frequently observed in large studies in which the samples are processed over an extended period of calendar time. As mentioned previously, the scan date of the array or the chemistry plate are often useful surrogates for batch effects. The scan dates of the array are stored in the protocolData slot of the ‘CNSet’ object and can be extracted using the $ operator:

R> dt <- strftime(protocolData(genotypeSet)$ScanDate, "%Y-%m-%d",
+    usetz = FALSE)
R> range(dt)

[1] "2007-04-03" "2008-04-19"

We expect that the normalized intensities for samples processed near the beginning of the study may be systematically different from samples processed near the end of the study. As we are using plate as a surrogate for batch, we select two plates in which the samples were processed at very different times.

R> dt.batch <- split(dt, batch(genotypeSet))
R> sapply(dt.batch, range)

     CHEAP        CORER        CUPID        DINGO        EPODE
[1,] "2008-04-17" "2008-03-19" "2007-09-17" "2007-08-30" "2007-08-30"
[2,] "2008-04-19" "2008-04-02" "2007-09-18" "2007-09-14" "2007-09-13"
     GIGAS        HOMOS        HUFFS        HUSKS        IONIC
[1,] "2007-04-06" "2007-09-14" "2008-01-19" "2008-01-31" "2007-09-14"
[2,] "2007-05-25" "2007-09-17" "2008-01-22" "2008-02-01" "2007-09-17"
     LOVED        NIGHS        PICUL        POSIT        SAKES
[1,] "2007-09-14" "2007-10-27" "2007-08-30" "2007-08-30" "2007-08-30"
[2,] "2007-09-15" "2007-11-06" "2007-09-13" "2007-09-13" "2007-12-18"
     SCALE        SHELF        SLOTH        TESLA
[1,] "2007-04-03" "2007-04-06" "2008-01-19" "2008-02-06"
[2,] "2007-04-04" "2007-04-09" "2008-01-22" "2008-02-06"

Note that the samples on the SCALE plate were processed at the beginning of April of 2007, whereas samples on the SLOTH plate were processed in January of 2008. We select different colors for SCALE and SLOTH, and use white for the remaining samples.

R> batch.scale <- which(batch(genotypeSet) == "SCALE")
R> batch.sloth <- which(batch(genotypeSet) == "SLOTH")
R> plate.cols <- brewer.pal(8, "Accent")[c(3, 8)]
R> fill3 <- rep("white", nrow(df))
R> fill3[batch.scale] <- plate.cols[1]
R> fill3[batch.sloth] <- plate.cols[2]

Next we replicate the ‘data.frame’ object 3 times, attaching a different set of fill colors for each replicate. The factor colorby will be used as a conditioning variable in the lattice graphic such that a separate panel is created for each factor.

R> df2 <- rbind(df, df, df)
R> df2$fill <- c(fill1, fill2, fill3)
R> colorby <- c("genotype", "confidence score", "plate")
R> df2$colorby <- factor(rep(colorby, each = nrow(df)), levels = colorby,
+    ordered=TRUE)

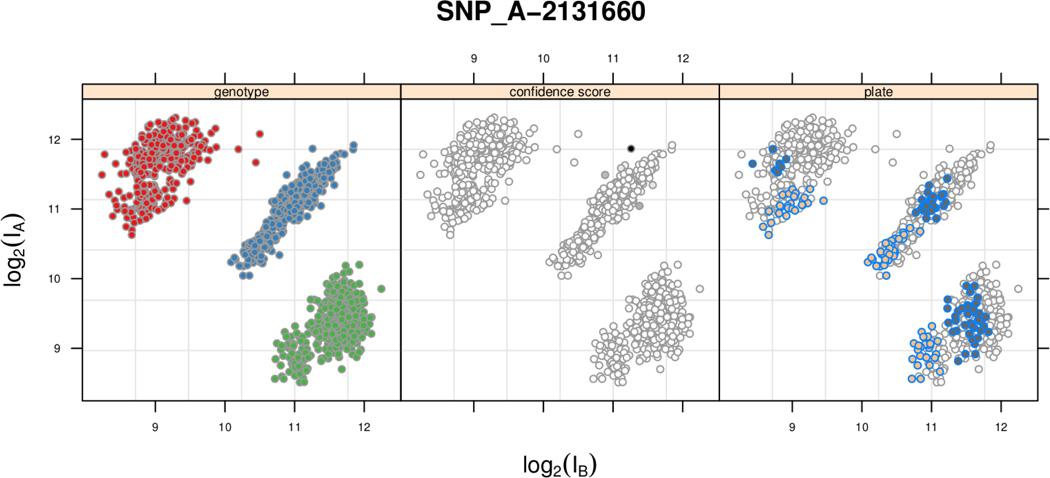
The following call to the xyplot creates the desired multi-panel display in Figure 2. Note that the plate- (batch-) effect is in the A+B direction and that the genotypes are robust to the batch-effect. As described in Section 2, our copy number analysis will use chemistry plate as a surrogate for batch and the robust-to-batch CRLMM genotypes to train the linear model.

R> (ABfig <- xyplot(A ~ B | colorby, df2, panel = function(x, y,
+    col, fill, plate.cols, ..., subscripts){
+    panel.grid(h = 5, v = 5)
+    panel.xyplot(x, y, col = "grey60", fill = fill[subscripts], ...)
+    if(panel.number() == 3){
+       lpoints(x[batch.scale], y[batch.scale], fill = plate.cols[1], ...)
+       lpoints(x[batch.sloth], y[batch.sloth], fill = plate.cols[2], ...)
+   }
+  }, aspect = "iso", fill = df2$fill, col = df2$col, cex = 0.6,
+    pch = 21,plate.cols = plate.cols, xlab = expression(log[2](I[B])),
+    ylab = expression(log[2](I[A])), main = featureNames(genotypeSet),
+    layout = c(3,1), par.strip.text = list(lines = 0.9, cex = 0.6)))

Figure 2.

Scatterplots of the normalized log A versus log B intensities for one SNP. The panel labels indicate whether the plotting symbols are colored by genotype (left), the CRLMM genotype confidence score (middle), or chemistry plate (right). The CRLMM confidence scores were all high, ranging from 0.89 (dark grey) to 1 (white). The HapMap phase 3 samples were processed over a time interval of approximately 1 year. The two highlighted in the right panel had scan dates that were processed approximately 8 months apart.

Alternatives

Alternatives to the the R package crlmm for genotyping Affymetrix arrays include BRLMM (Rabbee and Speed 2006; Affymetrix 2006), Birdseed (Korn et al. 2008; McCarroll et al. 2008), SNPiPer-HD (Hua et al. 2007), CHIAMO (Wellcome Trust Case Control Consortium 2007), and the Affymetrix Genotyping Console (GTC) software. (GTC uses Birdseed to genotype Affymetrix 6.0 arrays and BRLMM to genotype Affymetrix 5.0 arrays.) An alternative to quantile-normalization for preprocessing Affymetrix arrays is implemented in the R package aroma.affymetrix (Bengtsson et al. 2008).

4.2. Marker-level copy number estimation

Following preprocessing and genotyping by the genotype function, we call the R function crlmmCopynumber to estimate the parameters for copy number estimation outlined in Section 2. The crlmmCopynumber function requires an object of class CNSet and returns the value TRUE upon successful completion. Additional arguments to the crlmmCopynumber are available and are documented in the crlmm package. As with the genotype function, we set the cache = TRUE flag in the delimiter for the following code chunk.

R> invisible(open(cnSet))
R> cnSet.updated <- crlmmCopynumber(cnSet)

Note that the crlmmCopynumber returns TRUE upon successful completion and does not return an object of class ‘CNSet’. Rather, updates to elements of the batchStatistics slot in the cnSet object are written to disk using the ff interface and are not returned by the function. Batch-specific summary statistics are computed as part of the copy number estimation step. Accessors defined in the crlmm package return these summary statistics as arrays. The following code chunk illustrates a few of the available accessors for batch-specific summary statistics, including the genotype frequencies (Ns), the median absolute deviation (across samples) of the normalized intensities (mads), and the median intensity (medians). The argument j is used to indicate the batch. In the example below, we extract the above summary statistics for the 3rd and 4th batch.

R> table(batch(cnSet))

CHEAP CORER CUPID DINGO EPODE GIGAS HOMOS HUFFS HUSKS IONIC LOVED
    8     8    77    73    89    92    63    81    19    85    72
NIGHS PICUL POSIT SAKES SCALE SHELF SLOTH TESLA
   81    85    83    85    85    91    78     3

R> Ns(cnSet, i = 1:3, j = 3:4)

, ,  CUPID

     AA  AB BB
[1,]  2  15 60
[2,]  0  17 60
[3,]  0   0 77

, ,  DINGO
     AA AB BB
[1,] 15 46 12
[2,]  5 21 47
[3,]  0  0 73

R> mads(cnSet, i = 1:3, j = 3:4)[, "A", , ]

, ,  CUPID

           AA       AB        BB
[1,] 151.4578  91.9212 112.95644
[2,] 154.1904 145.2049  48.80338
[3,] 154.1904 114.1602 135.41080

, ,  DINGO

           AA       AB        BB
[1,] 214.3052 109.7514  99.51649
[2,] 100.5422 115.9605  48.98757
[3,] 135.6579 105.2646 127.34562

R> medians(cnSet, i = 1:3, j = 3:4)[, "A", , ]

, ,  CUPID

       AA   AB   BB
[1,] 2886 2380  644
[2,]  817  542  226
[3,] 3404 2398  902

, ,  DINGO

       AA   AB   BB
[1,] 3242 2247  761
[2,]  695  477  228
[3,] 3097 2212  859

The regression coefficients from model (4) for copy number are also stored in the batch-Statistics slot. A useful means to inspect model fit is to plot the normalized intensities and overlay the fitted regression line. In the following code chunk, we instantiate a new CNSet object containing 16 randomly selected SNPs and all of the samples on the GIGAS chemistry plate.

R> invisible(open(cnSet))
R> invisible(open(cnSet$gender))
R> set.seed(123)
R> snp.index <- sample(which(isSnp(cnSet) == 1), 16, replace = FALSE)
R> sample.index <- which(batch(cnSet) == "GIGAS")
R> exampleData1 <- cnSet[snp.index, sample.index]
R> invisible(close(cnSet))
R> invisible(close(cnSet$gender))

The exampleData1 object is provided in the crlmmCompendium package and can be loaded as follows.

R> if (!exists("exampleData1")) data(exampleData1)

Next we extract the normalized intensities for the A and B alleles, the genotype calls, and the estimated coefficients for the intercept (nuA) and slope (phA) for the A allele. Figure 3 illustrates the fit of the linear model to the A allele intensities for the SNPs in the exampleData1 object.

R> a <- t(as.matrix(A(exampleData1)))
R> gt <- t(as.matrix(calls(exampleData1)))
R> nuA <- as.numeric(nu(exampleData1, "A"))
R> phA <- as.numeric(phi(exampleData1, "A"))
R> col <- brewer.pal(7, "Accent")[c(1, 4, 7)]
R> NN <- Ns(exampleData1, i = 1:16, j = 1)[, , 1]
R> fns <- featureNames(exampleData1)
R> snpId <- matrix(fns, nrow(a), ncol(a), byrow = TRUE)
R> snpId <- factor(snpId, levels = fns, ordered = TRUE)
R> ldat <- data.frame(A = as.integer(a),
+    gt = as.factor(c("AA", "AB", "BB")[as.integer(gt)]), snp = snpId)
R> boxplotfig <- bwplot(A ~ gt | snp, ldat, cex = 0.6, panel = lmPanel,
+    nu = nuA,ph = phA,fill = "lightblue", Ns = NN,
+    par.strip.text = list(lines = 0.9,cex = 0.6),ylab = expression(I[A]),
+    xlab = expression(I[B]),ltext.y = 2500, label.cex = 0.6)

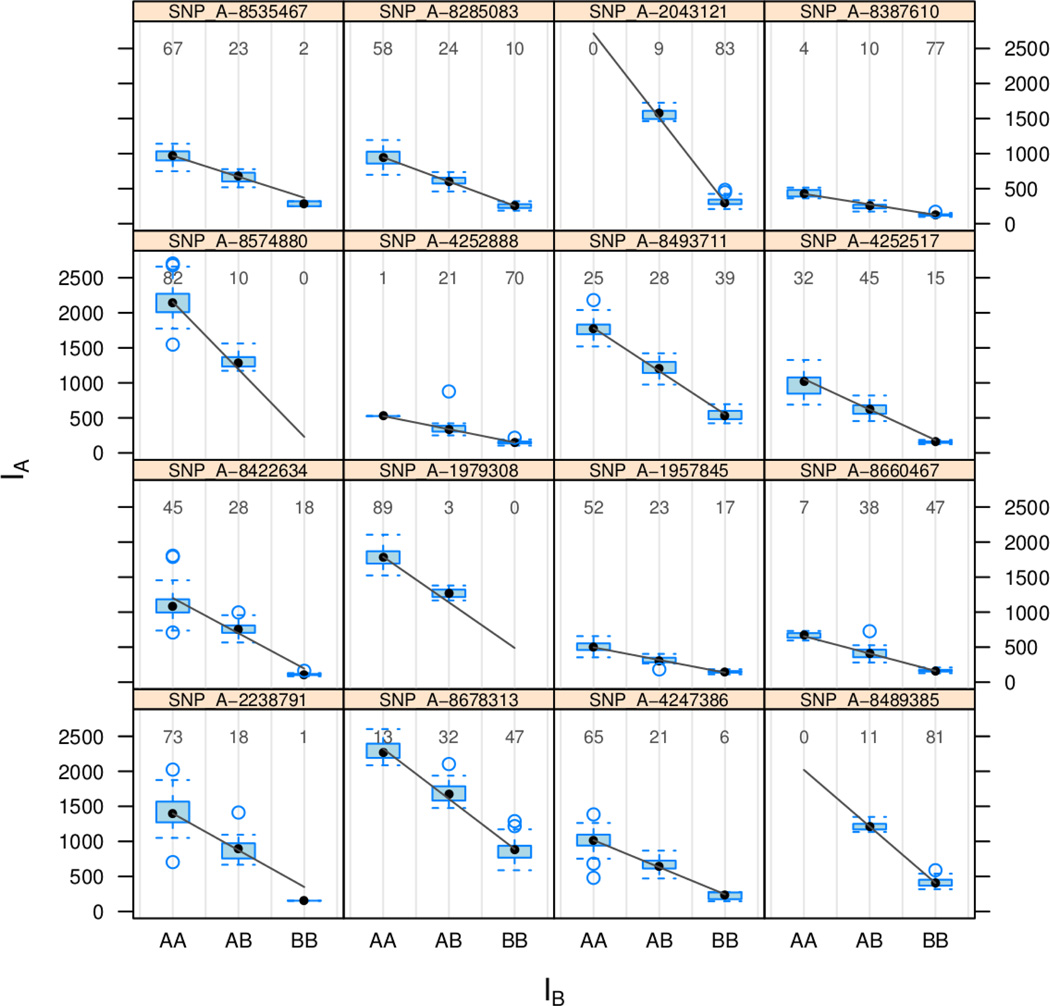
Figure 3.

Each panel displays the intensities for the A allele for all samples on the GIGAS plate stratified by the genotype call. The linear model is fitted on the intensity scale (as opposed to the log-scale) with parameters for the intercept and slope that are SNP- and batch-specific. The straight line over-plotted is the estimated background and slope for the GIGAS plate. The numbers in each panel indicate the genotype frequencies.

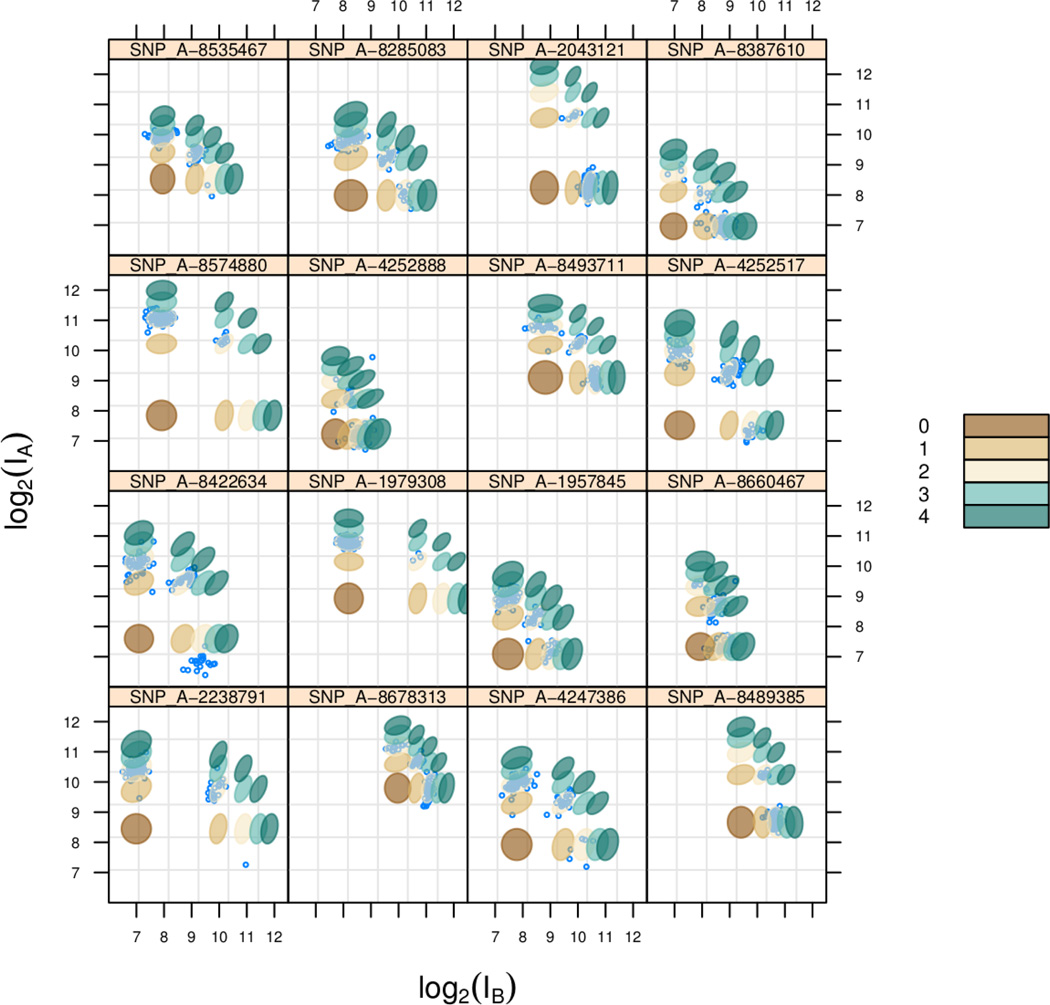
Scatterplots of the log-transformed normalized intensities for the A and B alleles can be useful for visualizing the bivariate normal prediction regions for integer copy number (see Equation 5). Using the same set of randomly selected SNPs in the previous code chunk, we plot the prediction regions for copy numbers 0, 1, 2, 3, and 4. To set up this graphic, we use two functions provided with the crlmmCompendium package: prePredictPanel and makeTransparent. The prePredictPanel and makeTransparent functions are used to organize the genomic data into a ‘data.frame’ object and to allow a partially transparent rendering of the prediction regions, respectively. Finally, we set up a legend for the figure using the lattice function simpleKey and create an object of class ‘trellis’ with the function xyplot. The resulting trellis object is displayed in Figure 4

R> ldat <- prePredictPanel(exampleData1)
R> shades <- makeTransparent(brewer.pal(6, "BrBG"),
+    alpha = 0.6)[c(1,2,3,5,6)]
R> mykey <- simpleKey(as.character(0:4), points = FALSE,
+    rectangles = TRUE, col = "black", space = "right", cex = 0.7)
R> mykey$rectangles[["col"]] <- shades
R> (bvnfig <- xyplot(A ~ B | snp, ldat, cex = 0.3, panel = cnPredictionPanel,
+    object = exampleData1, x.axis = "B", copynumber = 0:4,
+    line.col = shades, line.lwd = 1.5, shades = shades,
+    ylab = expression(log[2](I[A])), xlab = expression(log[2](I[B])),
+    par.strip.text = list(lines = 0.9, cex = 0.6),
+    xlim = c(6, 12.5), ylim = c(6, 12.5), key = mykey))

Figure 4.

A scatter plot of the log 2 normalized intensities for 16 randomly selected SNPs. The bivariate normal prediction regions derived from the linear model are plotted for copy numbers 0–4.

In most applications, the raw copy number estimates are intermediate values and passed directly to segmentation algorithms or hidden Markov models. Rather than estimate the raw copy number for all markers and samples and deal with I/O of data storage and access, our preference is to summarizes these estimates by the genomic intervals obtained by by a segmentation or hidden Markov model. In the following code, we create a ‘CNSet’ object containing only the markers on chromosome 8 and the samples in batch SHELF. (For reasons discussed in the following section, we are particularly interested in the NA19007 sample.)

R> marker.index <- which(chromosome(cnSet) == 8)
R> sample.index <- match("NA19007", sampleNames(cnSet))
R> batch.index <- which(batch(cnSet) == batch(cnSet)[sample.index])
R> invisible(open(cnSet))
R> shelfSet <- cnSet[marker.index, batch.index]
R> shelfSet <- shelfSet[order(position(shelfSet)), ]
R> invisible(close(cnSet))
R> dup.index <- which(duplicated(position(shelfSet)))
R> if (length(dup.index) > 0) shelfSet <- shelfSet[-dup.index, ]

Using the relationship defined in equation (6), we obtain estimates of the total copy number for the shelfSet object using the rawCopynumber function. Specifically, this function computes ĉ_A + ĉ_B. The robustSds function provided in the VanillaICE package can be used to provide estimates of uncertainty.

R> tcn <- rawCopynumber(shelfSet, i = seq(length = nrow(shelfSet)),
+    j = seq(length = ncol(shelfSet)))
R> sds <- robustSds(tcn)

Alternatives

An alternative to absolute allele-specific copy number estimation in crlmm is the R package aroma.affymetrix that provides estimates of copy number relative to a reference set (Bengtsson et al. 2008).

4.3. Downstream tools for inferring regions of copy number gain and loss

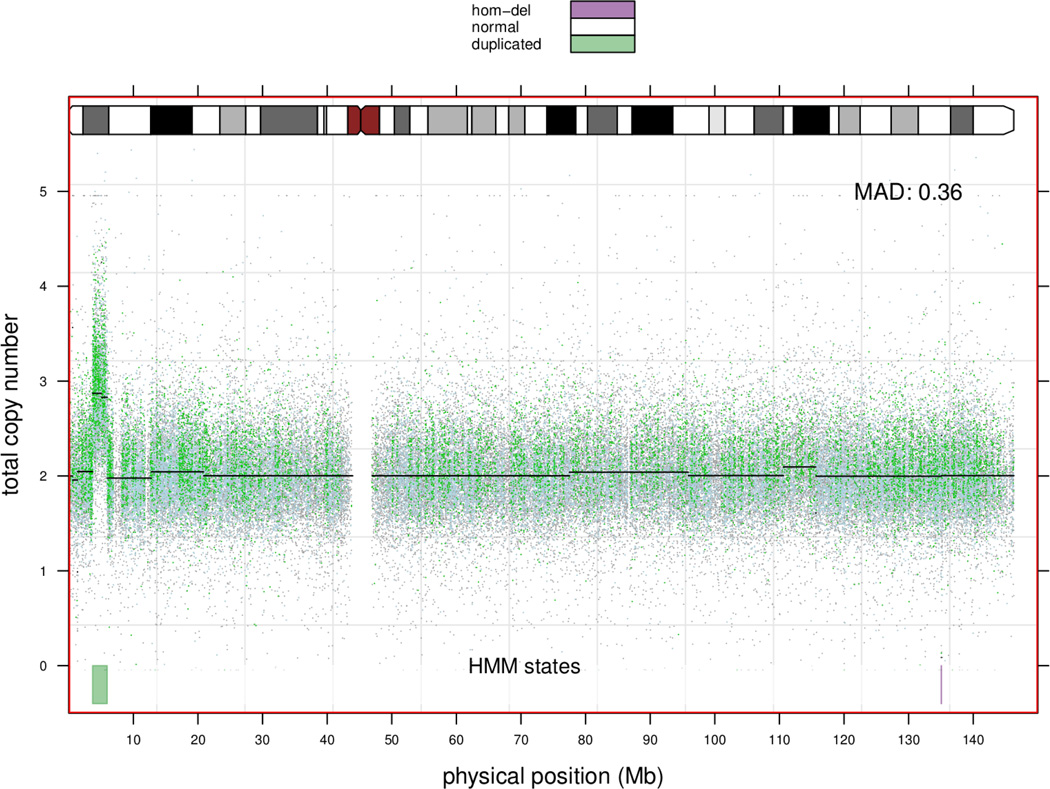
Marker-level estimates of copy number for Affymetrix and Illumina platforms are too noisy to reliably quantitate copy number at a single marker. Approaches that smooth the copy number estimates as a function of the physical position are useful for inferring regions of copy alterations and copy-neutral regions of homozygosity (ROH). This section illustrates how the marker-level estimates of copy number from crlmm can be passed to downstream segmentation and HMM algorithms. We illustrate our approach on chromosome 8 of HapMap sample NA19007 for which a large amplification on the p-arm has been previously identified (Redon et al. 2006).

For fitting a HMM or segmenting estimates of copy number, it is convenient to put estimates of copy number into a container for genotypes and copy number. The container oligoSnpSet defined in the oligoClasses package serves this purpose and can be instantiated directly from a ‘CNSet’ object. The redonSet object created in the following code chunk is provided with the compendium.

R> sample.index <- match("NA19007", sampleNames(shelfSet))
R> j <- match("NA19007", sampleNames(shelfSet))
R> redonSet <- new("oligoSnpSet", copyNumber = tcn[, j, drop = FALSE],
+    cnConfidence = 1/sds[, j, drop = FALSE],
+    call = as.matrix(calls(shelfSet)[, j, drop = FALSE]),
+    callProbability = as.matrix(snpCallProbability(shelfSet)[, j,
       drop = FALSE]), phenoData = phenoData(shelfSet)[j, ],
+    featureData = featureData(shelfSet))

Centering the copy number estimates by the median for the chromosome ensures that the baseline state is centered at 2. Note that for cancer samples, centering by the median copy number calculated across all autosomes would enable one to identify deletions or duplications that effect most of a chromosome.

R> copyNumber(redonSet) <- copyNumber(redonSet) -
+    median(copyNumber(redonSet),na.rm = TRUE) + 2

A hidden Markov model

The HMM implemented in the R package VanillaICE allows some flexibility for the data inputs and the definition of the hidden states. For example, the vignette included in the VanillaICE package documents how one can fit a HMM to copy number-only data (e.g, if genotypes were not available as in array comparative genomic hybridization), copy number and genotype data (SNP chips), and genotype-only data. Of course, the hidden states depend on the data type. For copy number and genotype data, one could have copy number alterations as well as copy-neutral regions of homozygosity as hidden states. For genotype-only data, the hidden states are region of homozygosity and normal. In the following code, we specify homozygous deletion, hemizygous deletion, normal, and amplification as the hidden states of interest. For each of the hidden states, the user must indicate the corresponding initial state probability (log-scale) and the probability of a homozygous genotype. The object returned by the hmm.setup function contains various parameters used for fitting the HMM as well as the estimated emission probabilities.

R> hmmOpts <- hmm.setup(redonSet, c("hom-del", "hem-del", "normal", "amp"),
+    copynumberStates = c(0:3), normalIndex = 3, log.initialP = 
+    rep(log(1/4), 4), prGenotypeHomozygous = c(0.8, 0.99, 0.7, 0.75))

Next, we apply the Viterbi algorithm to estimate the optimal sequence of states (Viterbi 1967). The transition probabilities used in the HMM are a function of the distance between markers and can be scaled by the TAUP object to control the smoothness of the state path. In particular, larger values of TAUP make it more difficult to transition between states and provide a smoother state path. Future versions of the VanillaICE package may estimate TAUP.

R> fit.cn <- hmm(redonSet, hmmOpts, verbose = FALSE, TAUP = 1e+10)
R> hmm.df <- as.data.frame(fit.cn)
R> print(hmm.df[, c(2:4, 7:9)])

      start       end     width state numMarkers        LLR
1     31242   3685554   3654313     3       3378    0.00000
2   3686944   5944996   2258053     4       3281 5083.21823
3   5950611  46954695  41004085     3      27354    0.00000
4  46993884 135058308  88064425     3      55559    0.00000
5 135061243 135066696      5454     1         16   70.85309
6 135075197 146298143  11222947     3       7281    0.00000

The evidence for the deletions and alternations is summarized by the log likelihood ratio (LLR) comparing the predicted amplification or deletion to the null model of no copy number alteration. The LLR can be a useful statistic for ranking copy number alterations.

R> hmm.df[hmm.df$state == 4, "LLR"]

[1] 5083.218

Circular binary segmentation

For somatic cell diseases such as cancer, DNA is collected from tissue that may contain a mixture of cell populations. For example, cells that represent different stages of cancer evolution. At any given locus, it is possible that a fraction of the cells have different integer copy numbers. As a result, the aggregate copy number measured by an array is not necessarily an integer and the concept of a genotype in a mixture of cell types is ambiguous. Unlike hidden Markov models that often assume an integer copy number state, segmentation algorithms identify genomic segments with constant copy number. Note that there is no implicit assumption that the copy number at any given locus is an integer. As a result, segmentation algorithms such as circular binary segmentation (Olshen et al. 2004; Venkatraman and Olshen 2007) are well-suited for the analysis of genomic data from cancers.

In this section, we fit the circular binary segmentation (CBS) algorithm to the copy number estimates from HapMap sample NA19007. The CBS algorithm is implemented in the R package DNAcopy. Following the vignette accompanying the DNAcopy package, we create an object of class ‘CNA’ and use the smooth.CNA to smooth single point outliers.

R> CNA.object <- CNA(genomdat = copyNumber(redonSet),
+    chrom = chromosome(redonSet), maploc = position(redonSet),
+    data.type = "logratio", sampleid = sampleNames(redonSet))
R> smu.object <- smooth.CNA(CNA.object)

Next, we apply the CBS algorithm to the smoothed data using the function segment in the package DNAcopy. As the segmentation can be slow, we use the cache = TRUE in the declaration of the following code chunk.

R> cbs.segments <- segment(smu.object)
R> print(cbs.segments, showSegRows = TRUE)

The output from the segment function is a collection of genomic intervals annotated by the mean copy number and the number of markers in the segment. While the above example contains genomic ranges from the segmentation of a single subject’s chromosome 8, a typical analysis may contain multiple subjects and chromosomes. The IRanges package (Pages et al. 2011) provides an extensive infrastructure for manipulating and organizing genomic ranges, as well as efficient functions for common queries such as findOverlaps that operate on objects of the class. We therefore illustrate how one can extract the segmentation results and create an object of class ‘RangedData’ defined in the IRanges package that may be useful in downstream applications. The functions RangedData and IRanges in the following code instantiate instances of the corresponding class. Additional details on these classes and functions are provided in the help files and vignettes accompanying the IRanges package available from Bioconductor.

R> cbs.out <- cbs.segments$output
R> cbs.segs1 <- RangedData(IRanges(cbs.out$loc.start, cbs.out$loc.end),
+    numMarkers = cbs.out$num.mark, seg.mean = cbs.out$seg.mean, chrom = 8L)

The helper function addCentromereBreaks included in the crlmmCompendium is used to add breaks for the centromere. The copy number estimates and genotype calls are then collected into a simple ‘data.frame’ that will be passed to the lattice function xyplot for visualizing the data.

R> cbs.segs1 <- addCentromereBreaks(cbs.segs1)
R> cn <- as.numeric(copyNumber(redonSet))
R> gt <- as.integer(as.matrix(calls(redonSet)))
R> df <- data.frame(cn = cn, gt = gt, position = position(redonSet)/1e+06)

Finally, we select colors for distinguishing homozygous from heterozygous genotypes, and a second set of colors to indicate the hidden states inferred from the hidden Markov model.

R> genotype.cols <- c("lightblue", "green3", "lightblue")
R> states <- unique(fit.cn$state)
R> shades <- brewer.pal(10, "PRGn")
R> shades <- shades[c(2, 4, 1, 8)]
R> shades[3] <- "white"
R> shades <- makeTransparent(shades, alpha = 0.6)
R> mykey <- simpleKey(c("hom-del", "hem-del", "normal",
+    "duplicated")[states[order(states)]], points = FALSE,
+    rectangles = TRUE, col = "black", space = "top", cex = 0.7)
R> mykey$rectangles[["col"]] <- shades[states[order(states)]]

The panel function cnPanel provided with the crlmmCompendium is used to plot the the copy number and genotype calls. Copy number alterations inferred from the hidden Markov model are indicated at the bottom of Figure 5. The segment means from the CBS are indicated by the black segments overlaying the copy number estimates. Approaches for calling deletions and amplifications from the segment means have been described elsewhere (Willenbrock and Fridlyand 2005).

R> stdev <- mad(df$cn, na.rm = TRUE)
R> redonfig <- xyplot(cn ~ position, df, pch = ".", panel = cnPanel,
+    ylim = c(−0.5,6), ylab = "total copy number", pch.cols = genotype.cols,
+    gt = df$gt, hmm.segs = fit.cn, cbs.segs = cbs.segs1,
+    scales = list(x = list(tick.number = 12)), lwd = 1,
+    shades = shades, key = mykey, xlim = c(0, 150), draw.key = TRUE,
+    xlab = "physical position (Mb)", add.ideogram = TRUE,
+    par.strip.text = list(lines = 0.9, cex = 0.6))
R> print(redonfig)
R> trellis.focus("panel", 1, 1)
R> ltext(median(df$position), 0, "HMM states", cex = 0.9)

Figure 5.

An amplification on the p-arm of chromosome 8 for HapMap sample NA19007. Estimates of raw copy number and the results of the HMM fit to the raw copy number. The segment means from circular binary segmentation overlay the copy number estimates. The colors of the plotting symbols indicate whether the CRLMM genotype is AA/BB (light blue) or AB (green). Nonpolymorphic markers are plotted in grey.

Alternatives

Alternative packages for smoothing copy number estimates include the HMMs in the packages Birdseye (Korn et al. 2008) and PennCNV (Wang et al. 2007), and the break-point detection algorithms implemented in the packages GLAD (Hupe et al. 2004), segclust (Picard et al. 2005, 2007), and GADA (Pique-Regi et al. 2008).

5. Discussion

We have applied the crlmm software to the HapMap phase 3 data, illustrating the steps of preprocessing, the genotyping of polymorphic markers, and the estimation of allele-specific copy number. We organize the normalized intensities, statistical summaries from the genotyping and copy number estimation steps, and meta-data on the features and samples in a single container. This organization facilitates visualizations that allow inspection of the genotypes and copy number estimates in the context of the lower-level data. In addition, several of the algorithms have been adapted to allow parallelization and the underlying data structures currently implement utilities in the ff package to minimize crlmm’s memory footprint. We have provided several useful visualizations related to low-level copy number analysis using the HapMap data as an exemplar. Note that it would be straightforward to proceed in the opposite direction – to target genomic regions in which copy number estimates are associated with a particular phenotype, followed by more detailed inspection of the loci in the region.

Batch effects are common in large studies due to the extended period of time required to process the samples. The crlmm package models the variation driven by batch as part of the estimation procedure for copy number, permitting inference of copy number gain and loss from batch-adjusted locus-level summaries. We expect that such an approach will reduce the occurrence of spurious associations induced by temporal artifacts such as batch effects. Users should carefully inspect that the resulting inferences from the copy number analysis are not driven by technological artifacts. Future versions of crlmm may provide an interface with software specifically designed for batch detection, such as surrogate variable analysis implemented in the sva package (Leek and Storey 2007). Approaches for detecting and adjusting for batch effects have been described in a recent review (Leek et al. 2010).

While smoothing the locus-level estimates of copy number to infer regions of gain and loss is beyond the scope of the crlmm package, the ability to easily integrate with packages that provide these utilities is essential. Our analysis of the HapMap data illustrates a general workflow that begins with the raw fluorescence intensities from the array scanners and concludes with inferences of amplified regions and deletions from a hidden Markov model. The flexibility to tailor complex genomic analyses to specific use-cases, such as copy number inference in family-based studies, is a strength of the modular framework illustrated here.

6. Session information

The R package crlmm is available from Bioconductor (http://www.bioconductor.org/). This document was prepared using Sweave. Computationally intensive steps, such as the genotype calling and copy number estimation were cached using the cacheSweave package (Peng and Eckel 2009).

• R version 2.13.0 Patched (2011-04-22 r55594), x86_64-unknown-linux-gnu

• Locale: LC_CTYPE=en_US.iso885915, LC_NUMERIC=C, LC_TIME=en_US.iso885915, LC_COLLATE=en_US.iso885915, LC_MONETARY=C, LC_MESSAGES=en_US.iso885915, LC_PAPER=en_US.iso885915, LC_NAME=C, LC_ADDRESS=C, LC_TELEPHONE=C, LC_MEASUREMENT=en_US.iso885915, LC_IDENTIFICATION=C

• Base packages: base, datasets, graphics, grDevices, methods, stats, tools, utils

• Other packages: Biobase 2.12.1, bit 1.1–6, cacheSweave 0.4–5, crlmm 1.10.0, crlmmCompendium 1.1.0, DNAcopy 1.26.0, ellipse 0.3–5, ff 2.2-1, filehash 2.1-1, genefilter 1.34.0, IRanges 1.10.0, lattice 0.19–23, MASS 7.3-13, oligoClasses 1.14.0, RColorBrewer 1.0–2, SNPchip 1.16.0, stashR 0.3–3, VanillaICE 1.14.0

• Loaded via a namespace (and not attached): affyio 1.20.0, annotate 1.30.0, AnnotationDbi 1.14.1, Biostrings 2.20.0, DBI 0.2–5, digest 0.4.2, grid 2.13.0, mvtnorm 0.9–96, preprocessCore 1.14.0, RSQLite 0.9–4, splines 2.13.0, survival 2.36-8, xtable 1.5–6