A model for leaf initiation

Abstract

A biophysical model is proposed for how leaf primordia are positioned on the shoot apical<br /> meristem in both spiral and whorl phyllotaxes. Primordia are initiated by signals that propagate<br /> in the epidermis in both azimuthal directions away from the cotyledons or the most recently<br /> specified primordia. The signals are linear waves as inferred from the spatial periodicity of the<br /> divergence angle and a temporal periodicity. The periods of the waves, which represent actively<br /> transported auxin, are much smaller than the plastochron interval. Where oppositely directed<br /> waves meet at one or more angular positions on the periphery of the generative circle, auxin<br /> concentration builds and as in most models this stimulates local movement of auxin to<br /> underlying cells, where it promotes polarized cell division and expansion. For higher order<br /> spirals the wave model requires asymmetric function of auxin transport; that is, opposite wave<br /> speeds differ. An algorithm for determination of the angular positions of leaves in common leaf<br /> phyllotaxic configurations is proposed. The number of turns in a pattern repeat, number of leaves<br /> per level and per pattern repeat, and divergence angle are related to speed of auxin transport and<br /> radius of the generative circle. The rule for composition of Fibonacci or Lucas numbers<br /> associated with some phyllotaxes is discussed. A subcellular model suggests how the shoot<br /> meristem might specify either symmetric or asymmetric transport of auxin away from the<br /> forming primordia that produce it. Biological tests that could make or break the mathematical<br /> and molecular hypotheses are proposed.

Introduction

The way in which plants initiate their leaves and organs such as flower parts at the stem apex has fascinated scientists from early times, but it has proved difficult to describe satisfactorily either the guiding mathematical rules predicting developmental patterning or the molecular mechanisms underlying it. It is our purpose to provide a fresh, integrated examination of these two subjects. Here, we focus on the post-embryonic initiation of leaf primordia per se; the vegetative phase of development is less intricate than the reproductive phase. Leaf primordia are initiated in relatively simple patterns within a so-called generative circle, and are moved out radially by growth of the continually dividing cells at their central edges. Secondary influences of stem outgrowth from the shoot apical meristem and of the resultant degree of packing provide interesting geometric and physiologically significant elaborations, but these can distract from our immediate concern.

The geometric phyllotaxic patterns of leaves, florets, bracts, etc. on plants have been reported and analyzed since at least the eighteenth century, and we shall provide only a brief introduction to the subject. Histories of phyllotaxis has been given by Richards¹ and by Adler et al.² More recent accounts and analyses include Sachs,³ Jean,⁴ Cummings and Strickland,⁵ Green,⁶ Kelly and Cooke,⁷ King et al.,⁸ and Newell et al.^9,10 The regular geometric order of these phyllotaxic patterns led to the major pattern classifications of a spiral, with distichous a special case, and a whorl, with decussate a special case. The generative spiral patterns of leaves wind along the stem with one leaf on each level. The distichous pattern has a single leaf at each level along the plant stem where the leaves rotate 180 degrees at the successive levels. The higher order spiral patterns have a fixed divergence (azimuthal) angle between successive leaves. When the spiral patterns are projected onto a plane perpendicular to the stem, a spiral pattern is seen on that plane also. In addition there are parastichy-associated spiral patterns on the projected plane with right and left twists. Many generative and parastichy spiral patterns can be identified with the Fibonacci series of numbers,¹¹ although not uncommon are other series such as the Lucas series which is actually a member of the general Fibonacci series. The fixed divergence (azimuthal) angle between successive emerging leaves gives a periodicity. There is in addition the repeat periodicity of the pattern along the stem. The whorl patterns have a number of leaves on each level evenly spaced with respect to angle. The decussate pattern of whorls has two leaves at each level with the leaves rotated 90 degrees at successive levels. The whorl patterns rotate at half the angle between the adjoining leaves at the next level.

Recent years have seen an explosion of phyllotaxic studies fusing molecular biology, dynamic imaging, and diverse approaches to mathematical modeling. In particular, computational modeling is being explored. Recent reviews such as that by Garnett et al.¹² and Krupinski and Jönsson¹³ make clear on the one hand that much has been gained by these integrated biophysical approaches but on the other hand that none has achieved a fully satisfactory and predictive model bringing together a full range of available morphological and molecular facts. We have sought to contribute to the ferment of ideas by providing a novel mathematical model matched with a novel, testable proposal for its cellular basis. For those wishing to consider how approaches to modeling have varied over the decades, the following summary may be useful.

Some attempts to explain the origin of leaf patterns have been based on constraint by imposition of a cost function such as an entropy-like cost function4,^4,14,15 or minimization of energy.⁵ Some models invoked contact pressure.¹⁶ A number of models employed diffusion of molecules termed morphogens. Diffusion equations have been proposed to describe the geometric patterns as steady-state diffusion by Young¹⁷ and Cummings and Strickland⁵ or time-dependent diffusion by Turing¹⁸ and Newell et al.^9,10 The influential school of thought led by Green^6,19-22 premised that foci of mechanical stresses and strains among the growing cells in the meristem and its primordia create patterns of initials by activating and orienting cell division, with consequent expansion to produce primordia.

The “plant growth hormone” auxin produced by developing leaf primordia has long been considered to play a patterning role,^23,24 and the discovery of a set of proteins responsible for its directed transport from cell to cell has enabled a sophisticated consideration of how formative auxin distributions might be achieved. References on auxin transport include Reinhardt et al.,^25,26 Reinhardt and Kuhlemeier,²⁷ Reinhardt,²⁸ Heisler et al.,²⁹ Jönsson et al.,³⁰ Fleming,³¹ Smith et al.,³² and Newell et al.;^9,10 more recent ones will be considered in the Discussion.

Also invaluable for background information is a comprehensive analysis of the past 20 y of the genetic and molecular research on the shoot apical meristem by Barton.³³ It includes review of the influential paper by Jackson and Hake³⁴ on control of phyllotaxis in maize by the abphl1 gene.

The connection between geometric patterns of plant leaves and the timing of the appearance of the leaves has not received as much study as the phyllotaxic geometry or the cell biology of plant apices. Since growth is a time dependent process, the role of time is important. The plastochron interval T, the time interval between successive appearances of leaves, has been reported to be nearly constant in many cases; this is one of the first of the hypotheses of Hofmeister.³⁵ The spiral phyllotaxic patterns have been modeled by analog physics experiments that vary in time.³⁶ Also numerical simulations were run for time-periodic iterations. Nonlinear reaction-diffusion equations have been suggested for chemical and biological systems that vary in time.¹⁸ These equations support traveling wave solutions. However, the two-component nonlinear reaction-diffusion equation has instabilities and bifurcations. Recent models by Jönsson et al.,³⁰ Smith et al.,³² and Sahlin et al.³⁷ on movement of auxin between cells invoke time-dependent, nonlinear ordinary differential equations for concentrations of auxin and one of its transporters PIN1 in cells on the periphery of the shoot apical meristem. Enhanced auxin concentrations at cells where the leaf primordia emerge are solutions of these equations but where divergence angles are computed for spiral patterns they are not reported in terms of Fibonacci numbers. The wave model we introduce here is also based on evidence that emerging leaf primordia produce auxin and that its transport creates the new maxima of auxin concentrations initiating new primordia, but the control of auxin transport differs.

Auxin-induced cell expansion and resulting mechanical strains, considered primary pattern determinants in some models, are not represented in our equations because as processes apparently participating in almost all plant tissue growth they are seen as coordinating the outgrowth of a primordium rather than guiding its placement.

The presentation of our auxin wave model will begin with its general features. Phyllotaxic geometry that must be explained will be considered. Waves will be specified as solutions of partial differential equations for linear waves that move out azimuthally from young primordia in both clockwise and counterclockwise directions, colliding to specify where new primordia will be initiated. Spiral and whorl geometries will then be computed, and for each case the periodicity of the divergence angle and the temporal periodicity will be connected by the partial differential equations. The wave theory will be discussed in terms of present knowledge about transport and cellular activities of auxin, and a molecular mechanism of controlling wave speed will be proposed.

Wave Model: Divergence Angle and auxin Basis

The specific aim of the wave model is to calculate the angular locations of the emerging leaf primordia as a function of time on the generative circle (periphery of the shoot apical meristem). The calculated azithmuthal angles will be compared with the observed divergence angles of some examples of leaf phyllotaxis, and the time for appearance of successive emerging leaf primordia will be related to the observed plastochron. As a first step in presenting the model, the features of the plant essential for the wave model are abstracted.

Plant Geometry

The pertinent geometry of the plant shoot with its apical meristem is illustrated in Figure 1 where the circular cylindrical coordinates are the radius r, the azimuthal angle ϕ and the axial coordinate z. The plant stem is modeled as a cylinder of radius a₁ along most of its length and an axis coincident with the z-axis. It tapers apically. Its tip is capped with the shoot apical meristem which has azimuthal symmetry. A generative circle of radius a₀ lies in a plane crossing the apical meristem. For mathematical purposes the circle lies on the meristem surface but the term is sometimes used more generally to refer to the cells immediately under the formally defined circle. It is at the generative circle that the leaf primordia are initiated or “generated.” (When, in a real plant they bulge out from the basal region of the expanding meristem, they break the modeled tip symmetry). The divergence (azimuthal) angle between successive leaf primordia is ϕ_d. Oval or elliptical meristems are not considered. The stem radius and generative circle radius are assumed constant. (The latter can of course shift importantly during developmental events such as the transition to the reproductive state, but we leave such shifts for future consideration). As the shoot apex grows vertically upward the position of the leaf primordia on the stem remains basipetal to the meristem. By symmetry each primordium moves radially outward; this has been experimentally observed since the time of Hofmeister.³⁵ The radial position of the leaf primordium increases until it reaches the radius of the mature stem. Meanwhile it undertakes the developmental path to make a leaf per se. The leaf thus formed from its leaf primordium then is located on the stem at radius a₁ and at an azimuthal angle ϕ₀.

Figure 1.

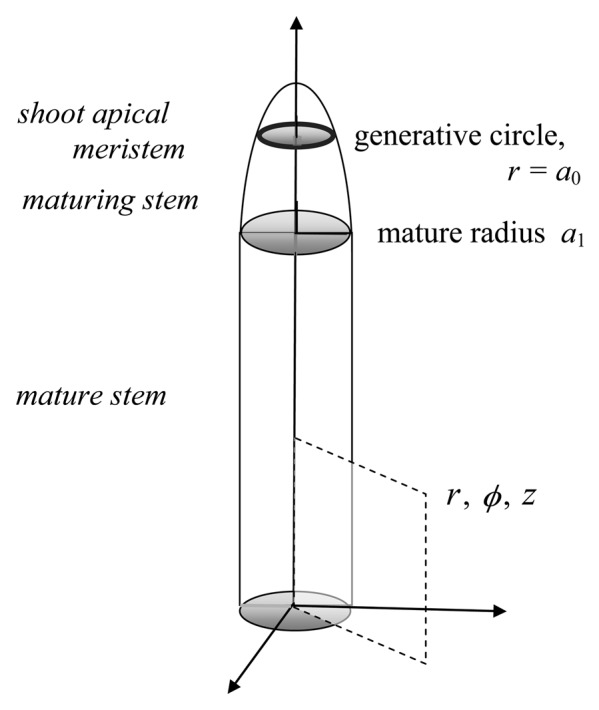
An abstraction of the plant stem. Key geometric features of the mathematical wave model are shown: in particular, the shoot apical meristem and the generative circle within it are indicated atop the stem. The circular cylindrical coordinates are defined.

To compare the meristematic surface featured in the abstraction of Figure 1 with images from a living plant, see Movie 2 by Reddy et al.³⁸ at URL http://dev.biologists.org/content/131/17/4225/suppl/DC1. This pioneering 65 h time-lapse record shows positions of epidermal cell walls during primordium formation at an Arabidopsis apex during an early reproductive stage, studied because it is larger than the challengingly small vegetative apex. For such studies, primordium initiation is considered geometrically comparable to that in the purely vegetative stage abstracted in Figure 1.

Leaf Positions, Divergence Angles and Propagating Waves

The wave model we propose is supported by macroscopic and molecular evidences of patterning. The macroscopic evidence of patterning is analyzed first because based on it the mathematical evaluation of macroscopic patterns can stand alone without specific molecular considerations. However, the proposed hormonal basis will be referred to even in the analytical analysis because recognition of the putative but well-recognized hormonal basis makes the model more intuitively attractive. The mathematical model has wider scope if it can integrate macroscopic and microscopic features.

The observed divergence angle is crucial in the mathematical analysis of the wave model for leaf phyllotaxis where the regularity of the divergence angle introduces angular (spatial) periodicity. The divergence angle for the spiral phyllotaxis is the acute angle between a leaf primordium (cotyledons may in some cases be treated as the first leaves) and the next emerging leaf primordium which before full emergence is sometimes described as a primordium initial. The divergence angle is one half the angle between two adjacent leaf primordia in one level for a whorl phyllotaxis. The divergence angle ϕ_d and the complement of the divergence angle ϕ_c for the spiral phyllotaxis in radians are

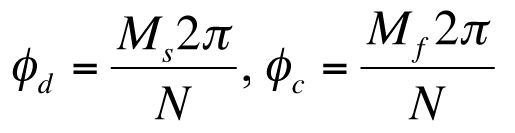, (1)

(2)

where M_s is the smaller number of turns, M_f is the larger number of turns and N is the number of leaves in the repeat. The number of turns in a repeat varies depending on a clockwise or counterclockwise rotation in the azimuthal angle. Then we find from (1A) and (1B) that

M_s + M_f = N (3)

The integers M_s, M_f and N are consistent with the composition rule for the Fibonacci series or the related Lucas series but are not restricted to those series by (2) that is found from the observed divergence angles.

The relations (1) and (2) for the divergence angle and its complement are based on observations of many plants. It is frequently said that the “golden angle” of ~137.5° is a fixed hallmark of the Fibonacci series of divergence angles; and in the limit as high Fibonacci numbers are attained the angles do approach this value. But if divergence angles in all Fibonaccci phyllotaxes were the same, all spirals would have the same N, which is clearly not the biological situation. Indeed, many plant spirals have diverse divergence angles. Examples given by Knott in a frequently updated but permanent site describing the dynamics of Fibonacci patterning at the apex (http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibnat.html#plants) include: 180° for elm, 120° for blackberry, 144° for oak, 135° for rose, and 138.5° for pussy willow.

The repeat units specified by Fibonacci and Lucas series are often seen in relatively primitive stems but are not always presented, especially in more advanced stems with determinate growth and a relatively small number of leaves. It has been debated why these series should occur phyllotaxically,³⁹ but certainly their evolution provided one way to prevent developmentally impractical or even disastrous irregularity of leaf spacing when N is large (Knott, above). Consistent leaf placement not only leads to smooth flow of developmental events but also often provides other advantages such as favorable collection of sunlight for photosynthesis and rainwater for conveying to the root system.

For the whorl phyllotaxis the divergence angle is

(4)

where the number of leaves in each level is L and N = 2L.

The temporal periodicity of leaf phyllotaxis is complex. The observed plastochron is the time between the emergence of two successive leaf primordia and is periodic under constant daily conditions, but many processes occur in that interval. The plastochron is a composite of intervals including signal wave generation and propagation, cellular recognition of a signal maximum, initiation of an outgrowth by oriented cell division, and outgrowth sufficient to begin the cycle again by producing new azimuthal signal waves. The time for signal propagation from a leaf primordium to the site of a new leaf primordium is much smaller than the plastochron.

A reasonable expectation from the precise angular periodicity and temporal periodicity is that the signal for initiation of the leaf primordium consists of waves that meet. If the waves were postulated as solutions of nonlinear reaction-diffusion equations, bifurcations and instabilities would be introduced. Accordingly, for simplicity we choose linear waves, and assume that they move azimuthally away from newly forming leaf primordia.

The basic assumption of this wave model, then, is that two waves propagate in opposite angular directions, counter-clockwise (increasing ϕ) and clockwise (decreasing ϕ) along the generative circle of radius a₀. Where the waves meet is the site of the new emerging leaf primordium. The waves are supported by the hormone auxin, which is considered in almost all models to underlie apical patterning. Also in common with other models, the auxin builds up at the meeting site until a sufficient level and gradient in auxin concentration initiates the new leaf primordium. It is not necessary to specify “up-the-gradient,” “with-the-gradient” transport or certain other styles of carrying out transportin commentary in Bayer et al.⁴⁰ or mathematical analysis in Krupinski and Jönsson.¹³

In a spiral phyllotaxis the waves propagate initially from a single cotyledon or primary leaf primordium. It is obvious that this should occur in monocots but for dicots the model specifies that auxin transport is suppressed from one of the cotyledons or primary leaves. Thereafter, the waves propagate from the most recent emerging leaf primordium. The speeds of the waves are the average values as details of auxin passage in and out of the cells are ignored. The timing of auxin wave signals is essential in our model where the travel distances of waves on the generative circle depend on auxin wave speeds and elapsed time for propagation of wave fronts. The travel distances in the clockwise and counter-clockwise directions around the generative circle must differ in the spiral phyllotaxis to produce a divergence angle other than 180°. Two possibilities for different travel distances of the two waves include different average auxin wave speeds if the waves start simultaneously or identical wave speeds but delayed initiation of one wave. The former possibility is chosen here. The relative wave speeds are calculated from the divergence angles. Divergence angles for spirals in this model converge toward the Fibonacci “golden angle” of slightly more than 137° as N increases, as is the case biologically.

In the decussate phyllotaxis the waves propagate at the same speed, initially from the two opposite cotyledons and thereafter from the opposite leaf primordia. In the higher order whorl phyllotaxis (L ≥ 3) the waves propagate at the same speed from each evenly spaced leaf primordium. The initial formation of a whorl with L ≥ 3 is not presently analyzed in this model.

Transport of Auxin as Basis for Waves

A hypothesis is proposed for regulation of the auxin transport in the generative circle early in the plastochron; this early regulation is envisioned as the molecular basis of the patterning. This hypothesis is based more specifically on the complex membrane-associated proteins and electrochemical potentials known to participate in directed auxin transport;^41-44 and a particularly thoughtful up-to-date account has been provided by Zazímalová et al.⁴⁵ Insofar as our own hypothesis differs substantially from current hypotheses that are based on imaging of the auxin transporter PIN1, it should be contemplated whether all auxin transporters performing critical roles at the apex have yet been discovered and characterized. In any case, discovery of realtime auxin concentrations and movements per se will be required to fully substantiate any theory. Like many other emerging ideas on how auxin regulates pattern, ours is indebted to the influential discovery by Sachs that was reviewed by him³ that in axial organs the auxin “concentration” can orient and enhance its own transport; for a discussion of expansions of Sach’s ideas, see Santos et al.,⁴⁶ Grunewald and Friml⁴⁷ and Bayer et al.⁴⁰

Auxin is produced by very young leaf primordia as they are formed on the generative circle, and as the hormone builds up it appears to orient its own transport within the meristem. In our molecular model, transport will initially be enhanced away from these newly forming primordia, especially in cells of the generative circle. Transport will be more or less excluded from the central stem cell region or minimally active there and hence, although there will always be some auxin in the center, at the time critical for placing the next primordia there will be more auxin moving in waves running azimuthally clockwise and counterclockwise. The hypothetical inactivity of the transport system within the central stem cells of the apex relies on the generally accepted idea that the function of these central cells as generators of new cells for the stem is separated from the functions of those in the generative circle by expression of the gene WUSCHEL, and is connected with action by the cytokinin hormone system.⁴⁸

According with general observations, the young auxin-producing primordia continue to develop, creating more cells by division and expansion; and those cells that are interposed between the expanding primordia and the central stem cell zone in effect push the primordia away from that zone. Symmetry of the apical dome is broken, pending restoration by development of creases separating the young primordia from cells newly positioned in the generative circle. Among possibilities for termination of the postulated azimuthal waves, it seems plausible that this might be an early consequence of the outgrowth: the gradient of auxin synthesized by a primordium has been changed with respect to the meristem center and reforming generative circle. Still presuming that the transcellar distribution of auxin transporters is continually controlled with respect to auxin gradients (or derivative gradients), the remainder of the plastochron will feature auxin gradients that originate outside the generative circle, as the expanding primordia that generate auxin move away from the central shoot meristem. It is possible that different sets of transporters come into play during this process, given that the cell types and cell stages in play are shifting and undergoing redefinition.

It may be specially reiterated that while the wave model predicts that each plastochron features very early transient auxin waves that have not been systematically sought, it also accords with the well-established observation that there is a long-lasting stage of the plastochron during which transgenically expressed PIN1-GFP distribution radiates away from enlarging primordia.

Symmetry and asymmetry of the proposed auxin waves (and profound accompanying electrochemical shifts and feedbacks) might well be determined by sensitivity of key positioning and enabling macromolecules of the auxin transport complex to the extent of chirality of mechanically important peripheral cell structures. Chiral features are common in plants, though underlying causes are not generally well understood and no general relevance of all chiral features to apical patterning is here suggested. Some such features, such as stem twining, can famously have a Mendelian basis.

One common, variably expressed chiral feature of the cell periphery is helical orientation of microtubules. Consistent with but not uniquely specified by models in which mechanical stress and strain play a critical or even the decisive patterning role,^{9,10,21,22,49,50} microtubules can be aligned by mechanical stress.^49,51-53 However, there is no reason to believe that auxin transporters are controlled by microtubules; for example, the evidence from years of experimentation on polarization during gravitropism indicates that effects of auxin distribution control microtubules and not vice versa.⁵⁴ Moreover, recent experiments on the shoot apex show that distribution of one auxin transporter, PIN1, can be correlated with while not controlled by microtubules.⁴⁹

On the other hand unpublished studies (B.G. Pickard and D.W. Ehrhardt) provide evidence that major chiral bias can also occur for certain membrane-anchored, apparently structurally important, arabinogalactan protein found in stems, roots and leaves. The structures may well be closely associated with related molecules containing fasciclin groups known to anchor at the same sites as elements of the transporter system such as PINs.²⁹ A situationally engendered preference for the extent of chiral orientation of some feature of the auxin transport system might influence the speed of the net auxin transport vector—it might better enable the transport wave in one direction than in the other. Organized orientation of membrane anchoring assemblies might have a much more elaborate range of geometries than is currently envisioned. Thus, it remains an open question whether the symmetries and asymmetries of auxin transport suggested by the wave model relate to cytoskeletal asymmetries. Coevolutionary elaboration of the auxin transport system and sometimes-asymmetric peripheral macromolecular structures during the adaptation of early plants to relatively dry environments, driven by enhancement of photosynthetic light collection, is a testable possibility for the origin environments, driven by enhancement of photosynthetic light collection, is a testable possibility for the origin of phyllotaxis in land plants.

Mechanoresponses Accompany but Do Not Impel the Auxin Waves

According to some above-mentioned recent computational modeling, primary morphogenetic guidance at the apex is provided by mechanical stress and strain that develop in consequence of cell growth responses to the auxin gradients generated by developing primordia; and the mechanical strain in turn directs asymmetric distribution of auxin transporters in cell membranes, asymmetric distribution of auxin transporters in cell membranes, which iteratively intensifies and elaborates the geometric specification of their localization and ultimately creates phyllotaxic patterns. Such modeling often employs force analysis within a homogeneous tissue viewed as a simple skeleton of walls, rather than as a heterogeneous structure of turgid cells with elaborate molecular connections between walls and membranes with cytoskeletal associations and clusters of mechanosensory channels and partner proteins. Doubtless, there is much to be learned from such modeling, which provides an interesting alternative to older approaches to modeling discussed e.g., by Green.⁶ But it is far from established that mechanical models, among all the models proposed, best explain the specification of phyllotaxic patterns.

Recognition that mechanical force can control auxin transport is of course as old as the discovery of auxin transport itself. Polarization of auxin transport is a key feature of most symmetry-breaking plant development; and in particular asymmetric application of force brings about the asymmetric auxin transport and subsequent growth that produces gravitropic curvature.^55,56 Indeed, the discovery of mechanosensitive ion channels in plants,⁵⁷ and particularly the detailed characterization of multimodally modulated calcium-selective mechanosensitive channels^58-60 was motivated in part by the concept that only a molecular sensing device that strongly amplifies distortion at the plasma membrane could account for kinetics of the auxin-mediated curvature of gravitropic roots and shoots.^55,56 Our unpublished evidence shows that even after enzymatic of walls the growth hormone auxin can sensitize mechanosensory Ca²⁺ permeable cation channels in an onion epidermal cell, by a path that is apparently indirect but reliable. It was early suggested⁶¹ that coordination between growing cells generally requires not only a stream of auxin but also moment-by-moment channel-mediated signaling about the precise micro-regions in which a cell must grow in order to maintain structural harmony with its neighbors. Such electromechanical feedbacks apparently involve the Ca²⁺ and H⁺ ions widely acknowledged to help regulate both auxin transport and action. We deem mechanical coordination as essential for polarization and expansion of primordial cells as it is for most other kinds of cells. On slightly different grounds, Kuhlemeier³⁹ reaches a similar conclusion about how auxin transport and action and mechanoresponses relate to each other. In sum, data invoked by Hamant et al.^21,22 and Heisler et al.⁴⁹ that mechanical perturbation can influence morphogenetic activity at the apex do not – in the absence of more specific evidence – press strongly for stress distribution as a primary determinant of phyllotaxic pattern. For this reason, the auxin wave model we espouse is not substantially more dependent on mechanical forces than is ordinary coordination of cell division and expansion.

We next quantitatively detail how the auxin wave model determines primordium placement.

Wave Equations

The waves obey linear wave equations that in general possess both slow and fast wave solutions. The concentrations of the waves are A for the slow wave and B for the fast wave. They obey the wave equations

(5)

(6)

where the wave speeds are V_s for a slow wave and V_f for a fast wave, the subscripts are s for slow and f for fast and again a₀ is the radius of the generative circle. There are cases where both waves have the same wave speed; in that case A and B obey the same partial differential equation. By convention the slow wave is a forward wave that propagates counterclockwise and the fast wave is a backward wave that propagates clockwise. The fast (slow) wave may be a forward (backward) wave in some plants. The solutions must be periodic in the azimuthal angle ϕ and in the time t. The divergence angles are also given by wave model equations. The divergence angle ϕ_d and its complement ϕ_c are related to the wave speeds and angular frequencies ω_s and ω_f by

(7)

(8)

where τ is the time for the wave front to travel from a leaf primordium to the meeting point of two waves on the generative circle. From (1A), (1B), (2), (5A and B) the turns ratios and number of leaves in a repeat can be connected to the wave speeds or angular frequencies.

Many solutions of the wave equations (5) and (6) are possible but without more experimental evidence we make a simple choice, a square wave of temporal length T₂. The wave is zero at the input after the time interval T₂ and both waves have the same time interval here. This choice approximates a pulse in the auxin transport. The auxin that supports the waves builds up in concentration as the oppositely directed waves stop their angular propagation when they meet. This concentration build up is modeled simply and conserves mass. Equations for the wave solutions are given in the Appendix.

The point of wave collision specifies position, but the new primordium is initiated only when the auxin concentration builds at the point of collision. Beyond that time, the wave model is no longer applicable. Instead, a further auxin-based process emerges: the high concentration and gradient established between the surface cells and cells of the two underlying layers causes polarized auxin movement into those deeper layers. There, at its focus, in a small number of the underlying cells the increased auxin and associated gradient promotes polarized division of local cells, with new crosswalls forming parallel to the surface. The daughter cells, still under the influence of high auxin, expand back toward the original shape and volume of the mother cells. During the process, neighbor cells are recruited and the forming cell mass bulges to become a new primordium. This process is the same regardless of the patterns of collision loci; therefore, the next section will be devoted to the modeled wave patterns specific for initiating primordia.

Wave patterns specific to the different phyllotaxes

Two Classes of Phyllotaxis

The auxin-supported waves that travel around the generative circle in the shoot apical meristem are solutions of equations (5) and (6); these solutions are reserved for the Appendix. There are two distinct wave processes for positioning leaf primordia, resulting in two different classes of phyllotaxis. In the first process, which produces spiral phyllotaxes, two waves propagate at different angular speeds except for the distichous phyllotaxis. The waves propagate in opposite directions from one cotyledon or from one leaf primordium in monocots or dicots. (There are dicot taxa that are distichous in mature form but in which the first pair or pairs of true leaves are apparently generated in the embryo by a decussate mechanism.) The two waves meet at some position on the generative circle to specify where a new leaf primordium will be initiated. The examples discussed below for the spiral phyllotaxes obey the Fibonacci numbers for the number of leaves in a repeat and the turns ratio in both rotation senses. In the second process, which produces whorl phyllotaxes, two waves of the same angular speed propagate from each of two cotyledons or each of the two first true leaf primordia for the decussate phyllotaxis, or from each primordium in an existing multi-primordium whorl. The two waves moving out from each primordium meet midway between adjacent leaf primordia on the generative circle to specify initiation loci. In the following text sections the wave propagation specified in the equations of the Appendix will be shown in two complimentary ways. The drawings of Figures 2 and 3 will depict the propagation of waves in the circular geometry of the generative circle, and are especially useful for compact presentation of the diverse ways in which the various phyllotaxies are established. These drawings do not convey the dynamic of wave travel, however, so they will be followed by Figure 4 containing a set of plots computed in the program Mathematica showing time frames in Cartesian format. These plots make clear how the auxin-supported square waves of the model propagate and, upon collision, create peaks of auxin concentration.

Figure 2.

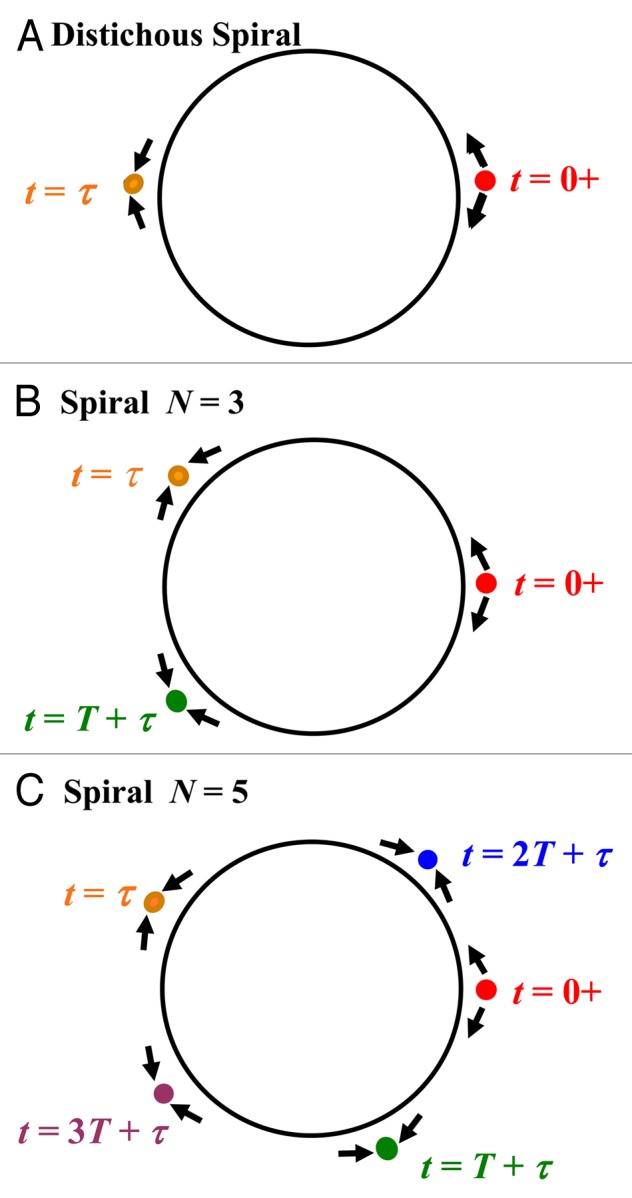
Modeled positions of auxin-supported wave collisions in the generative circle for three spiral phyllotaxes. For compact display of successive positioning of primordial initials, the radially outward movement of expanding primordia is not indicated, and all the plastochrons of one phyllotaxic repeat unit are shown in projection. That is, objects in planes at different z values are projected on an xy plane. (A–C) Waves propagate azimuthally from initially forming primordia (red bullets; colors guide the eye but the labels suffice to identify time points) in the clockwise and counterclockwise directions as indicated by “outward”-directed arrows at zero times. The wave fronts meet at sites that specify new primordium positions, as indicated by orange bullets with “inward”-directed arrows at t = τ. The meeting of the waves at time τ is not per se the immediate cause of primordium initiation; rather it is the buildup of auxin concentration that occurs at the sites in the interval between times τ and τ + T₂. A new primordium emerges later in the plastochron T >>τ + T₂. Waves generated anew at the orange bullets repeat the process. In B and C they collide at the green bullets; and in C successive rainbow colored bullets with sequential time labels indicate how the process repeats to complete a turn. The clockwise and counterclockwise waves A_F,i+1 and B_B,i+1 are given in equations (A.1) and (A.2) respectively.

Figure 3.

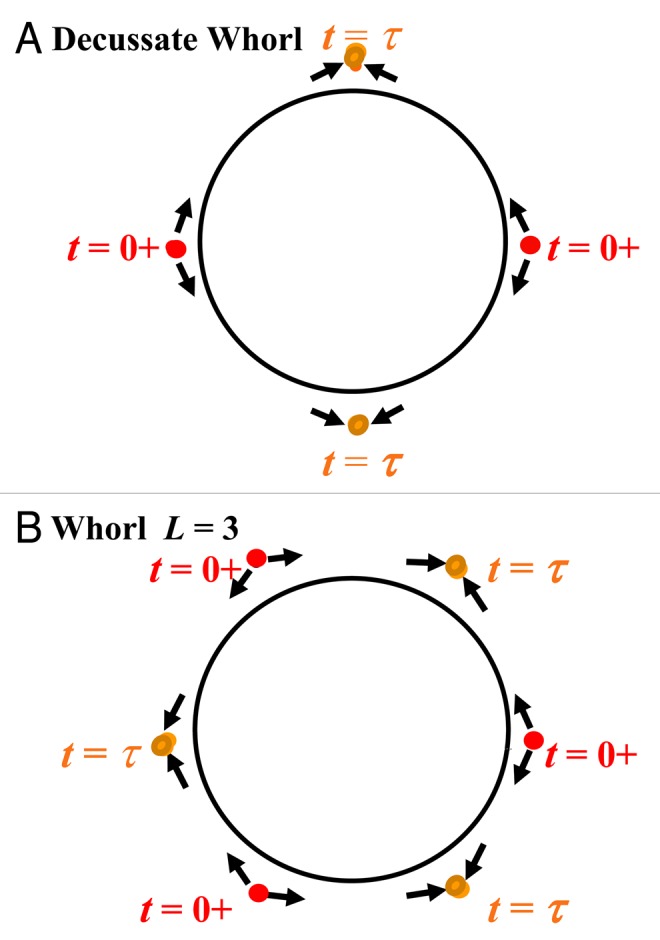
Positions of auxin wave collisions in the generative circle for two whorl phyllotaxes. Bullets, arrows, and graphic symbolism are as in Figure 2. The whorl phyllotaxic repeat units are defined in two plastochrons. (A) Decussate phyllotaxy, for which N = 4. Waves A_F,1,1 and B_B,1,1 propagate in forward and backward directions respectively from ϕ = 0 at t = 0 and A_F,1,2 and B_B,1,2 propagate from ϕ = π. At t = τ the wave fronts A_F,1,1 and B_B,1,2 collide at ϕ = π/2 and the wave fronts A_F,1,2 and B_B,1,1 collide at ϕ = 3π/2. At t = T + τ the wave fronts A_F,2,1 and B_B,2,2 collide at ϕ = π and the wave fronts A_F,2,2 and B_B,2,1collide at ϕ = 0. The repeat starts with the emergence of leaf primordia at t = 2T. (B) Alternating whorl of L = 3, for which N = 6. Waves A_F,1,1 and B_B,1,1 propagate from ϕ = 0, waves A_F,1,2 and B_B,1,2 propagate from ϕ = 2π/3 and waves A_F,1,3 and B_B,1,3 propagate from ϕ = 4π/3 at t = 0. At t = τ A_F,1,1 and B_B,1,2 collide at ϕ = π/3, A_F,1,2 and B_B,1,3 collide at ϕ = π and A_F,1,3 and B_B,1,1 collide at ϕ = 5π/3. The repeat starts at t = 2T.

Figure 4.

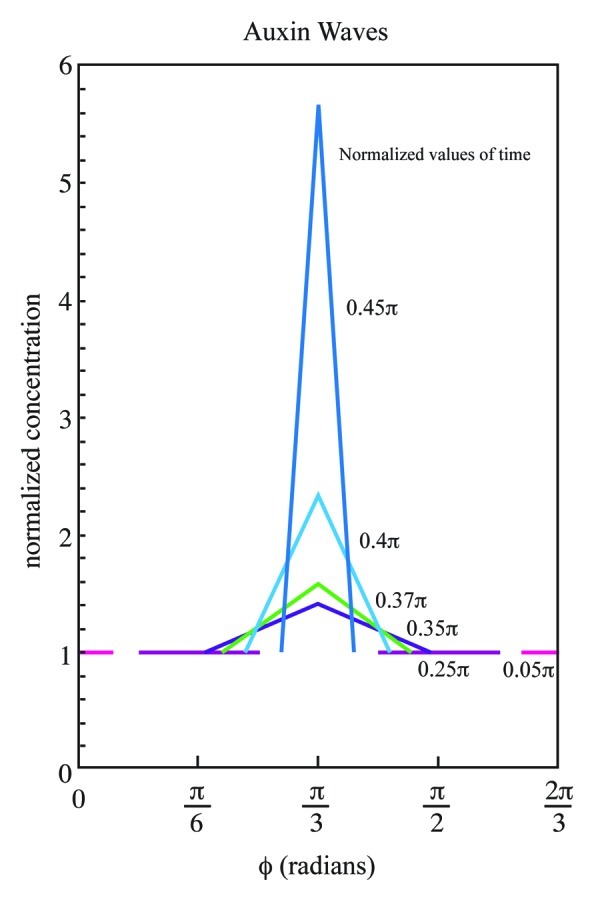
Illustration of propagation. Using equations A3 and A4 of the Appendix, square waves in the L = 3 whorl pattern are plotted in Cartesian format at six arbitrarily selected times as normalized auxin concentration vs. the angle ϕ = ωt, where t ranges from 0 through a few τ. Only one third of the generative circle is graphed, since each third is the same. Note that the equations provide auxin concentrations over a range of ϕ for each value of ωt. Here, the forward wave starts at ϕ = 0 and the backward wave starts at ϕ = 2π/3. The successive values of normalized time ωt represented by variously colored lines but also labeled with values for ωt, are indicated beside the plots. The waves meet at ϕ = π/3; afterward there is build up of auxin concentration which peaks at the end of the wave propagation interval of τ + T₂.

In the drawings of Figures 2 and 3 the arrows leaving a bullet that locates the cotyledon or leaf primordium denote the directions of the two waves traveling clockwise and counterclockwise along the generative circle. The time when departure starts is indicated beside the bullet. The meeting location of the two waves is indicated by arrows directed into another bullet and the meeting time is indicated beside the bullet. The bulleted angular locations are indicated in the captions. Again the travel time for propagation of the wave fronts is τ, the temporal length of the square wave is T2, and the period between the emergence of successive primordia is the plastochron T, where both τ and T2 are much smaller than the plastochron.

Spiral patterns.

Distichous pattern.

We start with the distichous pattern that is the simplest spiral. The pattern has one leaf per level and the subsequent leaves are rotated successively by π, the angle in radians. In Figure 2A two waves with the same wave speed start at the origin, ϕ = 0, t = 0, and move in opposite directions around the generative circle. A typical monocot would be compatible with this phyllotaxic pattern, as would a dicot if the signals were to start at only one cotyledon or early leaf primordium. A_F,1 is a forward wave in the counter clockwise direction and B_B,1 is a backard wave in the clockwise direction.

During distichous patterning, forward and backward auxin-supported waves in the mathematically defined generative circle are indicated by arrows adjacent to the drawn circle. They start at ϕ = 0, t = 0 and arrive simultaneously at ϕ = π. The waves do not propagate beyond their point of collision, which defines the locus for initiation of the next primordium. However, for the duration of the wave pulse T₂ the auxin concentration builds up. Once there is sufficient amount and gradient of auxin a new leaf primordium will be initiated at ϕ = π. The initiation per se, which as noted above is not included in our equations for specifying its locus, involves a further developmental step in which auxin transport is directed into the cells underlying the site of collision in the generative circle. As the auxin builds up in them, it promotes the growth of a morphologically visible primordium by the end of the plastochron T. Meanwhile, the shoot apical meristem grows forward leaving the penultimate leaf primordium basal to the newest leaf primordium on the stem. The divergence angle ϕ_d is computed from (1A) to be π where M_s = 1 and N = 2. This result can be verified for actual plants. The waves start propagating again from ϕ = π at t = T and arrive at ϕ = 0, t = T + τ where the process repeats at t = 2T. With two plastochrons, the phyllotaxic repeat unit is complete.

Higher order spiral patterns.

The higher order spiral patterns are more complex to realize than the distichous pattern because the opposing wave speeds differ. Consider the case of M_f = 2, M_s = 1 and N = 3, where the number of leaves in the repeat is also the Fibonnaci number. This is shown schematically in Figure 2B. The wave solutions comprise one forward slow wave A_F,1 and one backward fast wave B_B,1. The fast wave travels twice as fast as the slower wave. A_F,1 and B_B,1 start at ϕ = 0, t = 0 and propagate counterclockwise and clockwise respectively. The slow wave A_F,1 meets the fast wave B_B,1 at ϕ = 2π/3, t = τ. The auxin continues to build up until there is enough concentration and inward-directed gradient in concentration to initiate a leaf primordium. At time t = T the new leaf primordum starts the wave supported by auxin transport again. Next A_F,2 travels counterclockwise and B_B,2 travels clockwise such that both meet at ϕ = 4π/3, t = T + τ. A second leaf primordium then emerges at ϕ = 4π/3. At t = 2T + τ all waves are back at ϕ = 0. The next phylotaxic repeat unit starts at t = 3T. The wave positions at t = 0, t = τ and t = T + τ are shown in Figure 2B on the generative circle. As in Figure 2A arrows denote wave directions and the bullets label the leaf primordium sites on the generative circle. The divergence angle is ϕ_d = 2π/3.

Next consider another spiral pattern example with M_f = 3, M_s = 2 and N = 5, where the number of leaves in the repeat is also the Fibonacci number (Fig. 2C). Since the fast wave B_B,1 travels three halves as fast as the slow wave A_F,1, the divergence angle is ϕ_d = 4π/5. The waves A_F,1 and B_B,1 meet at ϕ = 4π/5, t = τ. At t = T waves supported by auxin start from the new leaf primordium at ϕ = 4π/5. The waves A_F,2 and B_B,2 meet at ϕ = 8π/5, t = T + τ. Later the waves A_F,3 and B_B,3 meet at ϕ = 2π/5, t = 2T + τ. Waves A_F,4 and B_B,4 meet at ϕ = 6π/5, t = 3T + τ. Waves A_F,5 and B_B,5 meet at ϕ = 0, t = 4T + τ. The repeat starts at t = 5T. The leaf primordium positions on the generative circle are shown in Figure 2C at t = 0, t = τ, t = T + τ, t = 2T + τ and t = 3T + τ. As before, wave directions are denoted by arrows and bullets label the leaf primordium sites. M_s = 2 for a counterclockwise rotation. The number of turns for a clockwise rotation is M_f = 3.

Alternating whorled patterns.

The alternating whorled patterns have evenly spaced multiple leaves of number L on each level. The leaf configuration shifts on successive levels by half the divergence angle. The number of leaves in a repeat is N = 2L.

Decussate pattern.

The decussate pattern is a special case of an alternating whorl pattern with L = 2 and N = 4.

The decussate pattern, shown schematically in Figure 3A, has two leaves an angle π apart on one level, and on the next level the two leaves are π apart but rotated π/2 with respect to the first set. As there are two leaves on one level, there are forward and backward waves at the origin and at ϕ = π. This pattern occurs for many dicots but never for grasses which are monocots.³⁴ The two cotyledons or an opposite pair of the first leaves can be the initial site for the start of the signals at t = 0. The waves arrive at their new sites simultaneously as the wave speeds are the same. The waves A_F,1,1 and B_B,1,2 arrive at ϕ = π/2 and the waves B_B,1,1 and A_F,1,2 arrive at ϕ = 3π/2 at t = τ as required for emergence of two leaf primordia on one level. The divergence angle is π/2. Next four waves depart from the two sites. Then A_F,2,1 and B_B,2,2 arrive at ϕ = π and A_F,2,2 and B_B,2,1 arrive at the origin at t = T + τ. The repeat starts at t = 2T. The number of turns in a repeat is M = 1. The leaf primordium positions at the generative sites are specified in Figure 3A at t = 0 and t = τ labeled with bullets; arrows denote wave directions.

Alternating whorl for three leaves.

A higher order alternating whorled pattern for L = 3 and N = 6 has three sets of waves. We start from the L = 3 whorl as established where the leaves are located at the origin, ϕ = 2π/3 and ϕ = 4π/3. At t = 0 forward and backward waves propagate with equal speeds from those three locations. At t = τ the forward and backward waves arrive at ϕ = π/3, ϕ = π and ϕ = 5π/3. Leaf primordia emerge after enough auxin builds up and gradients of auxin develop. Later waves propagate from the three new leaf primordium sites and arrive at ϕ = 2π/3, ϕ = 4π/3 and ϕ = 0, t = T + τ. The repeat starts at t = 2T. The number of turns in a pattern repeat is M = 1. The primordium positions on the generative circle are specified in Figure 3B at t = 0 and t = τ. As in Figure 3A, arrows denote wave directions and the bullets label the leaf primordium sites on the generative circle.

Visualization by plotted solutions.

A systematic way to visualize how the waves propagate is to calculate and plot solutions of the equations in a Cartesian format where the normalized concentration is plotted on the ordinate and the azimuthal angle is plotted on the abscissa. Wave amplitude is determined as a function of the angular distance at various increments of ⌉t where t has a value no more than a few |, ⌉| is the product of angular velocity and the time for the wave front to travel from a leaf primordium to the meeting point of two waves on the generative circle. We present such a composite of plots for selected values of ⌉t. These plotted solutions are shown in Figure 4. To express the model in biological context, the mathematical concept of concentration is represented as auxin concentration. An alternating whorl phyllotaxis with three leaves on a level, L = 3, also has three leaves on the next level resulting in N = 6. Two waves propagate clockwise and counter clockwise from each of the three leaf primordia. Consider events in one third of the generative circle, since it is redundant to plot the entire circle. We use (A3) and (A4) with ψ₁ = 0, ψ₂ = 2≠/3 and ψ₃ = ≠/3 for two adjacent leaf primordia. The new leaf primordium emerges at ϕ = ψ₃ = ≠/3. Figure 4 illustrates the forward and backward waves for the L = 3 whorl phyllotaxis with one wave starting at the origin and the other at ϕ = 2≠/3. The most striking feature of the sequence is how the auxin concentration builds sharply to a high value following wave collision. It is easy to imagine that such buildup would have profound consequences for the physiology of the small group of cells in which it occurs, and might lead to a repolarization of auxin movement to the underlying two layers of cells in which the first morphological signs of primordium initiation (polarized cell division and expansion) are seen. The other two leaf primordia emerge at ϕ = ≠ and ϕ = 5≠/3.

Discussion

The Wave Model Makes Molecular Predictions

The model that has been presented for determining the positions where leaf primordia will emerge on apical meristems of shoots of higher plants could be supported by further experiments. The long-known participation of auxin in initiation of primordia²³ could usefully be elaborated by two kinds of future experiments. One kind builds on the methods and evidences already seeming possibly to provide a molecular basis for the model, whereas the other kind is uniquely based on our speculation about how symmetric and asymmetric waves can be generated by molecular features of the cells in the generative circle.

Current Evidence on Auxin Transport at the Apex

In Arabidopsis an important auxin transport protein PIN1 has been visualized in the epidermis of the apical meristem of Arabidopsis at certain developmental stages,^29,42,49,62 and in particular it is found in the epidermis underlying the generative circle as mathematically defined here. It has been found spatially inhomogeneous and quasi-periodic in its distribution. The experimental system reviewed by Reddy et al.⁶² has been particularly important in acquiring data on auxin transport: with Arabidopsis expressing GFP-labeled proteins, the shoot meristem is exposed and imaged in multiple dimensions. The technique is, as the investigators would be the first to admit, a delicate one. And, even if some of the imaged plants can recover on restoration to a growth chamber, the abilities of damaged apices to regain function are remarkable.⁶³ Despite their usefulness, we deem the techniques and parameters of measurements to date insufficient to evaluate our model. Importantly, the wave model assumes that the waves propagate intermittently, lasting a brief time followed by a quiescent interval during which other biological processes occur at the meristem. Also, the model as currently set forth is specific for steady-states of gene expression during successive similar plastochrons, rather than addressing transitions between different vegetative states or between vegetative and reproductive states. Visualization of label in the tiny vegetative apex of Arabidopsis, and even in its larger transitional and reproductive apices,²⁹ may not always represent the normal distribution because of effects of handling and consequent ionic and electrical gradients. Certainly, these gradients are influential in polarized placement of membrane proteins, and wounding can demonstrably alter PIN1 distribution in Arabidopsis meristems.⁴⁹

We reiterate that the PIN1 protein has been treated in the recent literature as the major auxin transporter at the shoot apex. However, given that at this point it has not been demonstrated that it is the only PIN at the apex, it should be evaluated whether multiple PINs might be expressed in apical tissues. Such a situation would be comparable to that at the root apex, where multiple PINs work together to coordinate development.⁶⁴ Moreover, and very importantly, PINs are only one kind among the several proteins that must be assembled and activated to effect normal transport^13,65-68 and especially see Zazímalová et al.,⁴⁵ and activity during the dynamic process of beginning and finishing wave production may give incomplete insight into the dynamics of the transport system.

These two kinds of qualifications do not detract from the impact of current publications on auxin transport at the apex as seminal and inspiring, and together with our model they suggest how closer specification of experimental parameters during a plastochron could be sought.

New Options for Studying Auxin Transport at the Apex

Among the many models for determination of phyllotaxes, ours is unique in mathematically predicting azimuthal auxin-supported waves in the generative circle of the shoot apical meristem.

The model does not specify exactly when or where with-the-gradient or up-the-gradient auxin and transporter feedback dominates the transport vector,^13,40 nor does it uniquely specify the location of individual macromolecules (as contrasted with full sets of macromolecules) that participate in auxin transport. The best way to discriminate between this model and others is to examine the movement of auxin per se. A new, sensitive technique for high resolution noninvasive assessment of auxin transport has been developed⁶⁹ and it is compatible with optical imaging. The much-studied Arabidopsis apex is a possible subject for such studies, but it is inconveniently small and hence subject to manipulation-induced data distortions. The roles of auxin transport in phyllotaxis must be universal and it will be important to exploit the direct and dynamic in planta measuring technique of McLamore et al.⁶⁹ in plants with large apices as well as in Arabidopsis. Direct measurements of auxin during transport in large apices with diverse phyllotaxes could ultimately set a baseline for investigation of transport proteins and associated molecules.

Guidance of Auxin Transport — a Molecular Hypothesis

Our mathematical model motivates a molecular prediction that clockwise and counterclockwise wave speeds are controlled by the configuration of peripheral elements helping to anchor the auxin transport system – certain structures containing a set of arabinogalactan proteins (AGPs) that are, by our own definition, “cytoskeletal.” It is only at the cell periphery – the composite, intricately configured association of cell wall, membrane, cortical cytoskeleton molecules, and associated bound microscopic features - that such polarization of transport could be stably maintained. Comparing a variety of plants to check the extent of chirality of the organismic phyllotaxes and the cellular peripheral AGP-based “cytoskeletal elements” could likely test the validity of the model.

We focus interest on AGPs because at least some of these have already been visualized at the periphery as sometimes-asymmetric architectural components: unpublished images (B.G. Pickard and David W. Ehrhardt) of one kind of GFP-labeled tomato AGP in Arabidopsis show a variety of spiraling or helical “striae” or “strands” and other asymmetries as dramatic as those of microtubule bundles, and often with dramatically finer dimensions and closer spacing. (Verification will depend on obtaining comparable images from Arabidopsis of the labeled homologous Arabidopsis protein per se expressed in knockout mutants and restoring them to standard phenotype.) The carbohydrate portions of the AGPs bind extensively into the cell wall and the protein per se attaches to the cell membrane. There is evidence that some of these AGP-containing structures are load-bearing during steady-state conditions, but they can undergo dynamic shifts when cells shift to a new state. AGPs constitute a large and still mostly mysterious group of macromolecules with many suspected functions.^70,71 Probably several of them coexist in functional aggregates. Thus, the association of some cytosol-resident AGP “tails” with cytosolic portions of a group of other membrane-associated proteins that include the meristem-situated auxin transporter PIN1 in Titapiwatanakun et al.,⁶⁷ and numerous references therein deserves attention.

In contrast, control by one sort of often-asymmetric cytoskeleton can be ruled out: the microtubule bundle system. For some time this system has been studied in elongate easier-to-image cells of seedling shoot axes, where spiraling patterns of peripheral microtubules set the pattern for spiraling cellulose deposition in the wall where see especially Paredez et al.,^72,73 Gutierrez et al.;⁷⁴ note also demonstrations by Chan et al.,⁷⁵ of shifts in pattern during development and see Burian and Hejnowics,^52,53 for new biophysical studies of microtubule orientation in a simple system). More recently, disposition of microtubules has been studied at the shoot apex,⁴⁹ where interesting correlations with distributions of auxin transporters of phyllotactic patterning have been identified but causal correlations have been ruled out. Based on the extensive historical comparisons of auxin transport and microtubule arrangements during gravitropism referenced above, this is not surprising.

The organization of cellulose microfibrils at the apex should not be ignored simply because microtubules, though fundamental organizers of cellulose deposition, do not control phyllotaxis. Many of the complexities of cellulose microfiber deposition and function remain to be worked out. We speculate that the AGP-containing cytoskeleton elements might have some geometric relation to cellulose deposition in a variety of circumstances and this relation might be functionally meaningful. Thus, net peripheral cellulose microfiber orientation might be sought by high-resolution polarization microscopy,^76-78 by spinning disc confocal microscopy of walls with stained cellulose⁷⁹ and possibly by other emerging techniques.

As the databases and methods of molecular biology are improved, it becomes practical to expand the number of taxa in which apical meristem “cytoskeletal” biology is studied. It bears repeating that it would be useful not only to study apices of larger size but also to compare apices with diverse phyllotaxes. If, then, the geometry of peripheral “cytoskeleton” at the generative circle can be better evaluated, phyllotaxic and “cytoskeletal” arrangements can be compared. Initital studies might simply assess the degree of chiral correspondence for whorled and decussate phyllotaxes vs. for the higher order spiral patterns. Subtler evaluation might take advantage of the fact that, depending on taxon, Fibonacci and Lucas patterns manifest with generative spirals that are genetically defined as always clockwise, always counterclockwise, or both in specific proportions. It is particularly helpful that chirality can be determined by limited genetic differences within a particular taxon. In sum, If the model is correct it should be possible to find that asymmetries and symmetries in the chirality of phyllotaxic pattern and some components of the peripheral “cytoskeleton” show strict, stable correspondence under steady-state conditions.

Another Kind of Shoot Phyllotaxis

Finally, it should be repeated that this model applies only to stems without a dorsiventral bias perpendicular to the cotyledonary axis. In fact, it is our observation that many shoots have such a bias in some features early in development (witness the common hooks of hypocotyls and epicotyls) and a fair number have a pronounced bias throughout development (consider stems of many shrubs, or stems formed by budding from rhizomes). It may ultimately prove worthwhile to compare morphogenetic patterms of dorsiventrally biased stems with those of leaves,^80-82 which after all have a dorsiventral bias by their very placement on a main stem. A model for regulatory mechanisms in dorsiventrally biased shoots, presumed to be more evolutionarily advanced, will likely bear some fundamental similarities to that proposed here but may require imposition of one or more additional assumptions and may have some unique characteristics.

Conclusions

A model for determining the positions where leaf primordia emerge on shoot apical meristems of higher plants has been presented. It is developed for meristems without dorsiventral asymmetry, which appear to be more primitive than those which retain asymmetric bias after arising from a lateral position much in the way leaves do as they develop. The observational data for the nearly constant divergence angle and plastochron interval are consistent with a process periodic in space (angle) and time. Data are consistent with a wave frequency much greater than the inverse of the plastochron time; several processes must occur between initiation and emergence of a morphologically detectable primordium. The new contribution is the introduction of linear waves as the signals for the timing of the emergence of leaf primordia and determination of their angular positions. The linear wave equations for the azimuthal angle and time include forward and backward wave solutions. It is suggested that the waves propagate in a channel within the “epidermis” or outer layer of cells underlying the formally defined generative circle on the shoot apical meristem; but for mathematical simplicity the model considers the propagation on the circumference of the generative circle. We choose a square wave to model a pulse but wave shape could easily be modified. The effects of dispersion and damping of the waves have been ignored. A realistic signal would be a wave pulse that contains several frequencies and is subject to pulse spreading due to dispersion. A molecular basis for the control of auxin transport specified by the model has been presented and experiments are proposed that can refute or confirm the model.

The common phyllotaxic leaf patterns such as spiral including distichous and alternating whorls including decussate can be computed with this model. The forward and backward wave speeds differ for the higher order spiral phyllotaxes. They are the same in decussate phyllotaxis and in whorls. Our computation for a higher order whorl assumes starting from an initial whorl leaf arrangement. Examples of leaf phyllotaxis are presented where the turns ratio and the number of leaves in a repeat are related to Fibonacci series. The numbers of leaves and number of turns in a pattern repeat and the divergence angle between successive leaf primordium emergence are computed by the model algorithm. The wave speed can be related to the generative circle radius and the time for wave propagation of the wave front.

Appendix

The detailed wave solutions for our model are developed in this appendix. The solutions are for the general case of either the spiral phyllotaxis or the whorl phyllotaxis. We start with the simplest spiral phyllotaxis, the distichous phyllotaxis. Two waves start from a cotyledon located at the origin, ϕ = 0, on the generative circle of the apical meristem. The waves travel clockwise and counter clockwise at the same speed meeting at ϕ = π. The forward wave A_F1 and backward wave B_B1 are respectively

(A1)

and

(A2)

where the subscript F is for a forward wave and the subscript B is for a backward wave. The Heaviside function is defined for its argument x as H(x) = 1, x > 0 and H(x) = 0, x < 0. T is the plastochron interval, the integer i, i = 0, 1, 2…, denotes the plastochron interval, ω_s is the slow wave angular frequency, and ω_f is the fast wave angular frequency. For the distichous case the angular frequencies are the same, ω_s = ω_f = ω. One key aspect is designation of the starting position of the waves and the final position. We use the same subscripts for starting angular positions for the forward and backward waves and for the meeting positions for the different plastochron intervals but the values change. The starting angular position for the forward wave is ψ₁ and the starting angular position for the backward wave is ψ₂. Actually ψ₁ and ψ₂ are the same angle for our first example but for the two waves to meet we place the backward wave at ψ₂. The i = 0 case is for waves that start from the cotyledon ϕ = 0 (ϕ = 2π). The angle where the two waves meet is ψ₃ = π for i = 0. Again τ is the travel time to collision of the wave fronts. The Equations (A1) and (A2) are valid for all plastochron intervals. The cotyledon is replaced by leaf primordia for even values of i greater than zero. The initial angles change for odd values of i. Then ψ ₁ = π for the forward wave, ψ ₂ = π for the backward wave, ψ ₃ = 2π for the forward wave and ψ ₃ = 0 for the backward wave.

The spiral case for N = 3, M_s = 1 and M_f = 2 is similar to the distichous case. The waves are given by (A1) and (A2). Two waves start from a cotyledon located at the origin, ϕ = 0, on the generative circle of the shoot apical meristem. For i = 0, ψ₁ = 0 for the slow forward wave, ψ ₃ = 2π for the fast backward wave and ψ ₃ = 2π/3 at the angular location where the two waves meet. Next, for i = 1 ψ ₁ = 2π/3 for the slow forward wave, ω₂ = 8π/3 for the fast backward wave and ψ₃ = 4π/3 at the angular location where the two waves meet. The i = 2 case returns the emerging leaf primordium to the origin, ϕ = 0.

The wave solutions for the decussate phyllotaxis (a whorl phyllotaxis) have the general form below. There are two waves propagating clockwise and counter clockwise initially from both cotyledons at ϕ = 0 and ϕ = π.

(A3)

and

(A4)

where l = 1,…L. For the two waves that meet at ϕ = π/2 with i = 0 we have ψ₁ = 0, ψ₂ = π, ψ₃ = π/2. For the two waves that meet at ϕ = 3π/2 with at i = 0 we have ψ₁ = π, ψ₂ = 2π, ψ₃ = 3π/2. For i = 1 two waves start at ϕ = π/2 and at ϕ = 3π/2. Then for one leaf primordium ψ₁ = π/2, ϕ = 3π/2 and ψ₃ = π and for the other leaf primordium ψ₁ = -π/2, ψ₂ = π/2 and ψ₃ = 0. The even values of i follow the i = 0 case and the odd values of i follow the i = 1 case.

A whorl phyllotaxis with L = 3 leaves on one level has three leaves on the next level resulting in N = 6. Two waves propagate clockwise and counter clockwise from each of the three leaf primordia. Consider one example. We use (A3) and (A4) with ψ₁ = 0, ψ₂ = 2π/3 and ψ₃ = π/3 for two adjacent leaf primordia. The new leaf primordium emerges at ψ₃ = π/3.