ENCODING AND DECODING V1 FMRI RESPONSES TO NATURAL IMAGES WITH SPARSE NONPARAMETRIC MODELS

Abstract

Functional MRI (fMRI) has become the most common method for investigating the human brain. However, fMRI data present some complications for statistical analysis and modeling. One recently developed approach to these data focuses on estimation of computational encoding models that describe how stimuli are transformed into brain activity measured in individual voxels. Here we aim at building encoding models for fMRI signals recorded in the primary visual cortex of the human brain. We use residual analyses to reveal systematic nonlinearity across voxels not taken into account by previous models. We then show how a sparse nonparametric method [bJ. Roy. Statist. Soc. Ser. B 71 (2009b) 1009–1030] can be used together with correlation screening to estimate nonlinear encoding models effectively. Our approach produces encoding models that predict about 25% more accurately than models estimated using other methods [Nature 452 (2008a) 352–355]. The estimated nonlinearity impacts the inferred properties of individual voxels, and it has a plausible biological interpretation. One benefit of quantitative encoding models is that estimated models can be used to decode brain activity, in order to identify which specific image was seen by an observer. Encoding models estimated by our approach also improve such image identification by about 12% when the correct image is one of 11,500 possible images.

1. Introduction

One of the main differences between human brains and those of other animals is the size of the neocortex [Frahm, Stephan and Stephan (1982); Hofman (1989); Radic (1995); Van Essen (1997)]. Humans have one of the largest neocortical sheets, relative to their body weight, in the entire animal kingdom. The human neocortex is not a single undifferentiated functional unit, but consists of several hundred individual processing modules called areas. These areas are arranged in a highly interconnected, hierarchically organized network. The visual system alone consists of several dozen different visual areas, each of which plays a distinct functional role in vision. The largest visual area (indeed, the largest area in the entire neocortex) is the primary visual cortex, area V1. Because of its central importance in vision, area V1 has long been a primary target for computational modeling.

The most powerful tool available for measuring human brain activity is functional MRI (fMRI). However, fMRI data provide a rather complicated window on neural function. First, fMRI does not measure neuronal activity directly, but rather measures changes in blood oxygenation caused by metabolic processes in neurons. Thus, fMRI provides an indirect and nonlinear measure of neuronal activity. Second, fMRI has a fairly low temporal and spatial resolution. The temporal resolution is determined by physical changes in blood oxygenation, which are two orders of magnitude slower than changes in neural activity. The spatial resolution is determined by the physical constraints of the fMRI scanner (i.e, limits on the strength of the magnetic fields that can be produced, and limits on the power of the radio frequency energy that can be deposited safely in the tissue). In practice, fMRI signals usually have a temporal resolution of 1–2 seconds, and a spatial resolution of 2–4 millimeters. Thus, a typical fMRI experiment might produce data from 30,000–60,000 individual voxels (i.e., volumetric pixels) every 1–2 seconds. These data must first be filtered to remove nonstationary noise due to subject movement and random changes in blood pressure. Then they can be modeled and analyzed in order to address specific hypotheses of interest.

One recent approach for modeling fMRI data is to use a training data set to estimate a separate model for each recorded voxel, and to test predictions on a separate validation data set. In computational neuroscience these models are called encoding models, because they describe how information about the sensory stimulus is encoded in measured brain activity. Alternative hypotheses about visual function can be tested by comparing prediction accuracy of multiple encoding models that embody each hypothesis [Naselaris et al. (2011)]. Furthermore, estimated encoding models can be converted directly into decoding models, which can in turn be used to classify, identify or reconstruct the visual stimulus from brain activity measurements alone [Naselaris et al. (2011)]. These decoding models can be used to measure how much information about specific stimulus features can be extracted from brain activity measurements, and to relate these measurement directly to behavior [Raizada et al. (2010); Walther et al. (2009); Williams, Dang and Kanwisher (2007)].

Most encoding and decoding models rely on parametric regression methods that assume the response is linearly related with stimulus features after fixed parametric nonlinear transformation(s). These transformations may be necessitated by nonlinearities in neural processes [e.g., Carandini, Heeger and Movshon (1997)], and other potential sources inherent to fMRI such as dynamics of blood flow and oxygenation in the brain [Buxton, Wong and Frank (1998); Buxton et al. (2004)] and other biological factors [Lauritzen (2005)]. However, it can be difficult to guess the most appropriate form of the transformation(s), especially when there are thousands of voxels and thousands of features, and when there may be different transformations for different features and different voxels. Inappropriate transformations will most likely adversely affect prediction accuracy and might also result in incorrect inferences and interpretations of the fitted models.

In this paper we use a new, sparse and flexible nonparametric approach to more adequately model the nonlinearity in encoding models for fMRI voxels in human area V1. The data were collected in an earlier study [Kay et al. (2008a)]. The stimuli were grayscale natural images (see Figure 1). The original analysis focused on a class of models that included a fixed parametric nonlinear transformation of the stimuli, followed by linear weighting. Here we show by residual analysis that this model does not account for a substantial nonlinear response component (Section 4). We therefore model these data by a sparse nonparametric method [Ravikumar et al. (2009b)] after preselection of features by marginal correlation. The resulting model qualitatively affects inferred tuning properties of V1 voxels (Section 6), and it substantially improves response prediction (Section 4.2). The sparse nonparametric model also improves decoding accuracy (Section 5). We conclude that the nonlinearities found in the responses of voxels measured using fMRI impact both model performance and model interpretation. Although our paper focuses entirely on area V1, our approach can be extended easily to voxels recorded in other areas of the brain.

Fig. 1.

Examples of natural image stimuli. The natural images used in the experiment were sampled from a large database of images obtained from a commercial digital library (Corel Stock Photo Libraries from Corel Corporation). The images covered 20× 20 degrees of the field of view, and were cropped to a circular aperture and blended into the background to reduce edge effects.

2. Background on V1

Brain area V1 is located in the occipital cortex and is an early processing area of the visual pathway. It receives much of its input from the lateral geniculate nucleus—a small cluster of cells in the thalamus that is the brain’s primary relay center for visual information from the eye. Many of the properties of V1 neurons have been described by visual neuroscientists [see De Valois and De Valois (1990) for a summary]. In most cases these neurons are described as spatiotemporal filters that respond whenever the stimulus matches the tuning properties of the filter. The important spatial tuning properties for V1 neurons are related to spatial position, orientation and spatial frequency. Thus, each V1 neuron responds maximally to stimuli that appear at a particular spatial location within the visual field, with a particular orientation and spatial frequency. Stimuli at different spatial positions, orientations and frequencies will elicit lower responses from the neuron. Because V1 neurons are tuned for spatial position, orientation and spatial frequency they are often modeled as Gabor filters (whose impulse response is the product of a harmonic function and a Gaussian kernel) [De Valois and De Valois (1990)].

Although tuning for orientation and spatial frequency can be described using a linear filter model, it is well established that individual V1 neurons do not behave exactly like linear filters. Studies using white noise stimuli have reported a nonlinear relationship between linear filter outputs and measured neural responses [e.g., Sharpee, Miller and Stryker (2008); Touryan, Lau and Dan (2002)]. Furthermore, it is known that the responses of V1 neurons saturate (like $\sqrt{x}$ or log x) with increasing contrast [e.g., Albrecht and Hamilton (1982); Sclar, Maunsell and Lennie (1990)]. Finally, there is evidence that the responses of V1 neurons are normalized by the activity of other neurons in their spatial or functional neighborhood. This phenomenon—known as divisive normalization—can account for a variety of nonlinear behaviors exhibited by V1 neurons [Carandini, Heeger and Movshon (1997); Heeger (1992)]. It is reasonable to expect that the nonlinearities at the neural level will affect voxel responses evoked by natural images, so a statistical model should describe adequately these nonlinearities.

3. The fMRI data

The data consist of fMRI measurements of blood oxygen level-dependent activity (or BOLD response) at m = 1,331 voxels in area V1 of a single human subject [see Kay et al. (2008a)]. The voxels, measuring 2× 2 × 2.5 millimeters, were acquired in coronal slices using a 4T INOVA MR (Varian, Inc., Palo Alto, CA) scanner, at a rate of 1Hz, over multiple sessions. Two sets of data were collected during the experiment: training and validation. During the training stage the subject viewed n = 1,750 grayscale natural images randomly selected from an image database, each presented twice (but not consecutively) in a pseudorandom sequence; see Figure 1. Each image was presented in an ON-OFF-ON-OFF-ON pattern for 1 second with an additional 3 seconds OFF between presentations. For the validation data the subject viewed 120 novel natural images presented in the same way as in the training stage, but with a total of 13 presentations of each image. Data collection required approximately 10 hours in the scanner, distributed across 5 two hour sessions.

Data preprocessing is necessary to correct several sampling artifacts that are intrinsic to fMRI. First, volumes were manually co-registered (in-house software) to correct for differences in head positioning across sessions. Slice-timing and automated motion corrections (SPM99, http://www.fil.ion.ucl.ac.uk/spm) were applied to volumes acquired within the same session. These corrections are standard and their details are explained in the supplementary information of Kay et al. (2008a).

Our encoding and decoding analyses depend upon defining a single scalar fMRI voxel response to each image. The procedures used to extract this scalar response from the BOLD time series measurements acquired during the fMRI experiment are described in the Appendix. In short, we assume that each distinct image evokes a fixed timecourse response, and that the response timecourses evoked by different images differ by only a scale factor. We use a model in which the response timecourses and scale factors are treated as separable parameters, and then use these scale factors as the scalar voxel responses to each image. By extracting a single scalar response from the entire timecourse, we effectively separate the salient image-evoked attributes of the BOLD measurements from those attributes due to the BOLD effect itself [Kay et al. (2008b)].

4. Encoding the V1 voxel response

An encoding model that predicts brain activity in response to stimuli is important for neuroscientists who can use the model predictions to investigate and test hypotheses about the transformation from stimulus to response. In the context of fMRI, the voxel response is a proxy for brain activity, and so an fMRI encoding model predicts voxel responses. Let Y_v be the response of voxel v to an image stimulus S. We follow the approach of Kay et al. (2008a) and model the conditional mean response,

$${\mu }_v(s):=\mathbb{E}(Y_v\mid S=s),$$

as a function of local contrast energy features derived from projecting the image onto a 2D Gabor wavelet basis. These features are inspired by the known properties of neurons in V1, and are well established in visual neuroscience [see, e.g., Adelson and Bergen (1985); Jones and Palmer (1987); Olshausen and Field (1996)]. A 2D Gabor wavelet g is the pointwise product of a complex 2D Fourier basis function and a Gaussian kernel:

$$g(a,b)\propto exp(2\pi i\omega \stackrel{\sim }{a})\times exp\left(-\frac{{\stackrel{\sim }{a}}^2}{2{\sigma }_1^2}-\frac{{\stackrel{\sim }{b}}^2}{2{\sigma }_2^2}\right),$$

where

$$\begin{array}{l}\stackrel{\sim }{a}=(a-a_0)cos\theta +(a-a_0)sin\theta ,\\ \stackrel{\sim }{b}=(b-b_0)cos\theta -(b-b_0)sin\theta .\end{array}$$

The basis we use is organized into 6 spatial scales/frequencies (ω, σ₁, σ₂), where wavelets tile spatial locations (a₀, b₀) and 8 possible orientations θ, for a total of p = (1² + 2² + 4² + 8² + 16² + 32²) × 8 = 10,920 wavelets. Figure 2 shows all of the possible scale and orientation pairs.

Fig. 2.

Examples of Gabor wavelets. The basis used by the encoding model is organized into 6 spatial scales (rows) and 8 orientations (columns). The imaginary part of the wavelets is not shown.

Let g_j denote a wavelet in the basis. The local contrast energy feature is defined as

$$X_j(s):={\left[\sum _{a,b}Re{g}_j(a,b)s(a,b)\right]}^2+{\left[\sum _{a,b}Im{g}_j(a,b)s(a,b)\right]}^2$$

for j = 1, …, p = 10,920. The feature set is essentially a localized version of the (estimated) Fourier power spectrum of the image. Each feature measures the amount of contrast energy in the image at a particular frequency, orientation and location.

4.1. Sparse linear models

The model proposed in Kay et al. (2008a) assumes that μ_v (s) is a weighted sum of a fixed transformation of the local contrast energy features. They applied a square root transformation to X_j to make the relationship between μ_v (s) and the transformed features more linear. Thus, their model is

$${\mu }_v(s)={\beta }_{v0}+\sum _{j=1}^p{\beta }_{vj}\sqrt{X_j(s)}.$$ (4.1)

We refer to (4.1) as the sqrt(X) model. Kay et al. (2008a) fit this model separately for each of the 1,331 voxels, using gradient descent on the squared error loss with early stopping [see, e.g., Friedman and Popescu (2004)], and demonstrated that the fitted models could be used to identify, from a large set of novel images, which specific image had been viewed by the subject. They used a simple decoding method that selects, from a set of candidates, the image s whose predicted voxel response pattern (μ̂_v (s): v = 1, 2, …) is most correlated with the observed voxel response pattern (Y_v: v = 1, 2, …). Although Kay et al. (2008a) focused on decoding, the encoding model is clearly an integral part of their approach. We found a substantial nonlinear aspect of the voxel response that their encoding sqrt(X) model does not take into account.

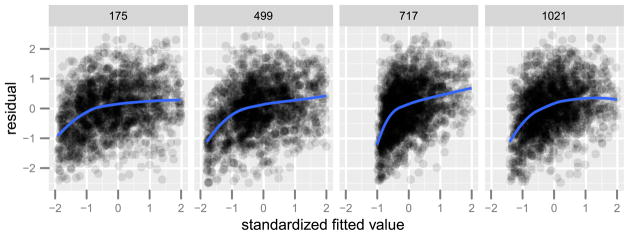
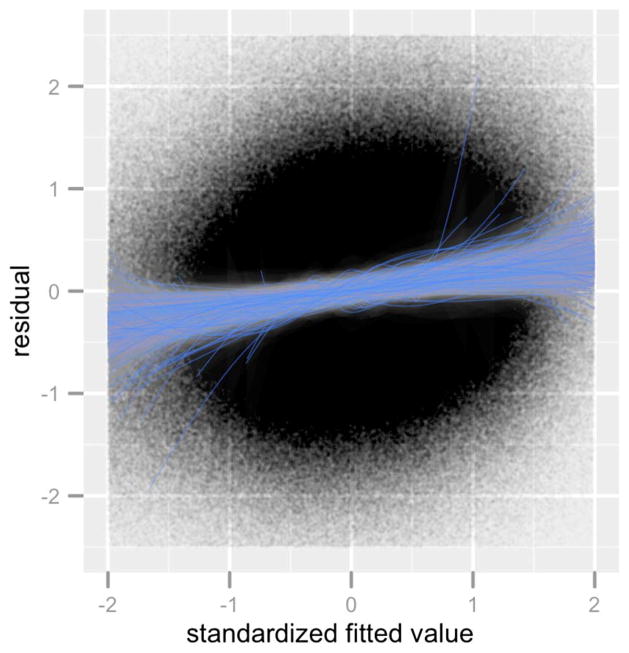
Since the gradient descent method with early stopping is closely related to the Lasso method [Friedman and Popescu (2004)], we fit the model (4.1) separately to each voxel [as in Kay et al. (2008a)] using Lasso [Tibshirani (1996)], and selected the regularization parameters with BIC (using the number of nonzero coefficients in a Lasso model as the degrees of freedom). Figure 3 shows plots of the residuals and fitted values for four different voxels. With the aid of a LOESS smoother [Cleveland and Devlin (1988)], we see a nonlinear relationship between the residual and the fitted values. This pattern is not unique to these four voxels. We extended this analysis to all 1,331 voxels. By standardizing the fitted values, we can overlay the smoothers for all 1,331 voxels and inspect for systematic deviations from the sqrt(X) model across all voxels. Figure 4 shows the result. Nonlinearity beyond the sqrt(X) model is present in almost all voxels, and, moreover, the residuals appear to be heteroskedastic.

Fig. 3.

Residual and fitted values of model (4.1) for four different voxels (labeled above). The solid curves show a LOESS fit of the residual on the fitted values.

Fig. 4.

Residual and standardized fitted values of model (4.1) blended across all 1,331 voxels. The solid curves show the LOESS fits of the residuals on the fitted values for each voxel.

Composing the square root transformation with an additional nonlinear transformation could absorb some of the residual nonlinearity in the sqrt(X) model. Instead of the square root, $log(1+\sqrt{x})$ was used by Naselaris et al. (2009) to analyze the same data set as we do in this paper and it has also been used in other applications [see Kafadar and Wegman (2006) for an example in the analysis of internet traffic data]. The resulting model is

$${\mu }_v(s)={\beta }_{v0}+\sum _{j=1}^p{\beta }_{vj}log(1+\sqrt{X_j(s)}),$$ (4.2)

and we refer to it as the log(1 + sqrt(X)) model.

We fit model (4.2) using Lasso with BIC, and compared its prediction performance with model (4.1) by evaluating the squared correlation (predictive R²) between the predicted and actual response across all 120 images in the validation set. Figure 5 shows the difference in predictive R² values of the two models for each voxel. There is an improvement in prediction performance (median 5.5% for voxels where both models have an R₂ > 0.1) with model (4.2). However, examination of residual plots (not shown) reveals that there is still residual nonlinearity.

Fig. 5.

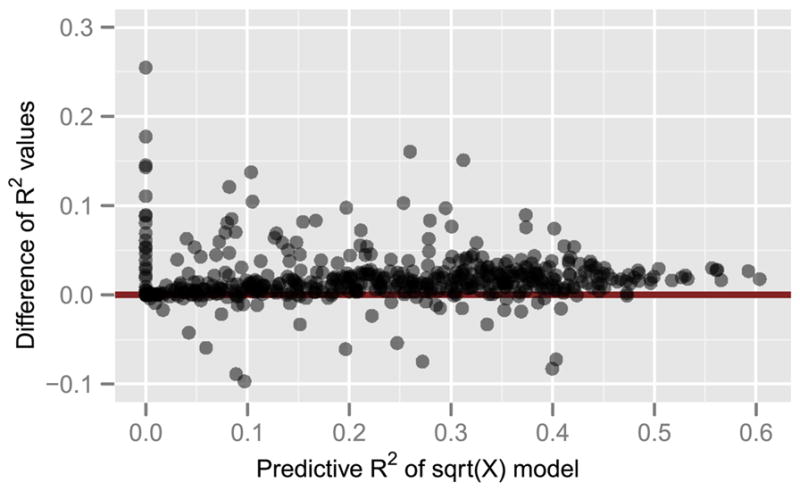
Comparison of voxel-wise predictive R² (based on the validation data) of the log(1 + sqrt(X)) model (4.2) and the sqrt(X) model (4.1). The vertical axis shows the difference R² of (4.2) −R² of (4.1). The median improvement of model (4.2) is 5.5% for voxels where both models have a predictive R₂ > 0.1.

4.2. Sparse additive (nonparametric) models

The $\sqrt{x}$ and $log(1+\sqrt{x})$ transformations were used in previous work to approximate the contrast saturation of the BOLD response. Rather than trying other fixed transformations to account for the nonlinearities in the voxel response, we employed a sparse nonparametric approach that is based on the additive model. The additive model [cf. Hastie and Tibshirani (1990)] is a useful generalization of the linear model that allows the feature transformations to be estimated from the data. Rather than assuming that the conditional mean μ is a linear function (of fixed transformations) of the features, the additive (nonparametric) model assumes that

$$\mu ={\beta }_0+\sum _{j=1}^p{f}_j(X_j),$$ (4.3)

where f_j ∈ 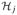are unknown, mean 0 predictor functions in some Hilbert spaces 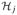. The linear model is a special case where the predictor functions are assumed to be of the form f_j (x) = β_j x. The monograph of Hastie and Tibshirani describes methods of estimation and algorithms for fitting (4.3), however, the setting there is more classical in that the methods are most appropriate for low-dimensional problems (small p, large n).

Ravikumar et al. (2009b) extended the additive model methodology to the high-dimensional setting by incorporating ideas from the Lasso. Their sparse additive model (SPAM) adds a sparsity assumption to (4.3) by assuming that the set of active predictors {j: f_j ≠ 0} is sparse. They propose fitting (4.3) under this sparsity assumption by minimization of the penalized squared error loss

$$\underset{f_j\in {\widehat{\mathcal{H}}}_j,{\beta }_0}{min}{\Vert \mathbf{Y}-{\beta }_0\mathbf{1}-\sum _{j=1}^p{f}_j({\mathbf{X}}_j)\Vert }^2+\lambda \sum _{j=1}^p\left|\right|f_j({\mathbf{X}}_j)\left|\right|,$$ (4.4)

where ||·|| is the Euclidean norm in ℝⁿ, Y is the n-vector of sample responses, 1 is the vector of 1’s, f_j (X_j) is the vector obtained by applying f_j to each sample of X_j, and λ ≥ 0. The penalty term, $\lambda {\sum }_{j=1}^p\left|\right|f_j({\mathbf{X}}_j)\left|\right|$, is the functional equivalent of the Lasso penalty. It simultaneously encourages sparsity (setting many f_j to zero) and shrinkage of the estimated predictor functions by acting as an L1 penalty on the empirical L2 function norms ||f_j (X_j)||, j = 1, …, p. The algorithm proposed by Ravikumar et al. (2009b) for solving the sample version of the SPAM optimization problem (4.4) is shown in Figure 6. It generalizes the well-known back-fitting algorithm [Friedman and Stuetzle (1981)] by incorporating an additional soft-thresholding step. The main bottleneck of the algorithm is the complexity of the smoothing step.

Fig. 6.

The SPAM backfitting algorithm.

We did not apply SPAM directly to the feature X_j (s), but instead applied it to the transformed feature, $log(1+\sqrt{X_j(s)})$. We refer to the model

$${\mu }_v(s)={\beta }_{v0}+\sum _{j=1}^p{f}_{vj}(log(1+\sqrt{X_j(s)}))$$ (4.5)

as V-SPAM—“V” for visual cortex and V1 neuron-inspired features. There is no loss in generality of this model when compared with (4.3), but there is a practical benefit because the $log(1+\sqrt{X_j(s)})$ feature tends to be better spread out than the X_j (s) feature. This has a direct effect on the smoothness of f_vj. Although we did not try other transformations, we found that applying the SPAM model directly to the X_j (s) features rather than $log(1+\sqrt{X_j(s)})$ resulted in poorer fitting models.

We fit the V-SPAM model separately to each voxel, using cubic spline smoothers for the f_vj. We placed knots at the deciles of the $log(1+\sqrt{X_j})$ feature distributions and fixed the effective degrees of freedom [trace of the corresponding smoothing matrix; cf. Hastie and Tibshirani (1990)] to 4 for each smoother. This choice was based on examination of a few partial residual plots from model (4.2) and comparison of smooths for different effective degrees of freedoms. We felt that optimizing the smoothing parameters across features and voxels (with generalized cross-validation or some other criterion) would add too much complexity and computational burden to the fitting procedure.

The amount of time required to fit the V-SPAM model for a single voxel with 10,920 features is considerably longer than for fitting a linear model, because of the complexity of the smoothing step. So for computational reasons we reduced the number of features to 500 by screening out those that have low marginal correlation with the response, which reduced the time to fit one voxel to about 10 seconds.⁸ We selected the regularization parameter λ using BIC with the degrees of freedom of a candidate model defined to be the sum of the effective degrees of freedom of the active smoothers (those corresponding to nonzero estimates of f_j).

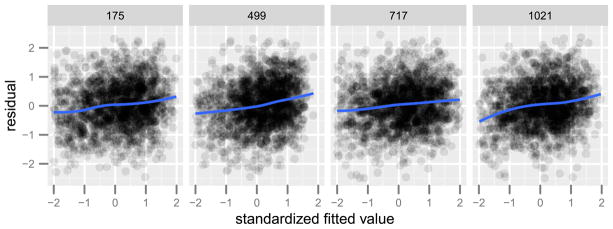
Figure 7 shows residual and fitted value plots for the four voxels that we examined in the previous section. Little residual nonlinearity remains in this aspect of the V-SPAM fit. The residual linear trend in the LOESS curve is due to the shrinkage effect of the SPAM penalty—the residuals of a penalized least squares fit are necessarily correlated with the fitted values. Figure 8 shows the residuals and fitted values of V-SPAM for all 1,331 voxels. In contrast to Figure 4, there is neither a visible pattern of nonlinearity, nor a visible pattern of heteroskedasticity.

Fig. 7.

Residual and fitted values of V-SPAM (4.5) for four different voxels (labeled above). The solid curves show a LOESS fit of the residual on the fitted values. Compare with Figure 3. The linear trend in the residuals is due to the shrinkage effect of the penalty in the SPAM criterion (4.4).

Fig. 8.

Residual and standardized fitted values of V-SPAM (4.5) for all 1,331 voxels. The solid curves show the LOESS fits of the residuals on the fitted values for each voxel. Compare with Figure 4.

The V-SPAM model better addresses nonlinearities in the voxel response. To determine if this model leads to improved prediction performance, we examined the squared correlation (predictive R²) between the predicted and actual response across all 120 images in the validation set. Figure 9 compares the predictive R² of the V-SPAM model for each voxel with those of the sqrt(X) model (4.1) and the log(1 + sqrt(X)) model (4.2). Across most voxels, there is a substantial improvement in prediction performance. The median (across voxels where both models have a predictive R₂ > 0.1) is 26.4% over the sqrt(X) model, and 19.9% over the log(1 + sqrt(X)) model. Thus, the additional nonlinear aspects of the response revealed in the residual plots (Figures 3 and 4) for the parametric sqrt(X) and log(1 + sqrt(X)) models are real and they account for a substantial part of the prediction of the voxel response.

Fig. 9.

Comparison of voxel-wise predictive R² (based on the validation data) of the sqrt(X) model (4.1), the log(1 + sqrt(X)) model (4.2) and V-SPAM (4.5). (a) Histograms of the predictive R₂ value across voxels. They are displayed sideways to ease comparison. (b) Difference of predictive R₂ values of V-SPAM (4.5): (left) sqrt(X) model (4.1); (right) log(1 + sqrt(X)) model (4.2).

5. Decoding the V1 voxel response

Decoding models have received a great deal of attention recently because of their role in potential “mind reading” devices. Decoding models are also useful from a statistical point of view because their results can be judged directly in the known and controlled stimulus space. Here we show that accurately characterizing nonlinearities with the V-SPAM encoding model (presented in the preceding section) leads to substantially improved decoding.

We used a Naive Bayes approach similar to that proposed by Naselaris et al. (2009) to derive a decoding model from the V-SPAM encoding model. Recall that Y_v (v = 1, …, m and m = 1,331) is the response of voxel v to image S. A simple model for Y_v that is compatible with the least squares fitting in Section 4 assumes that the conditional distribution of Y_v given S is Normal with mean μ_v (S) and variance ${\sigma }_v^2$, and that Y₁, …, Y_m are conditionally independent given S. To complete the specification of the joint distribution of the stimulus and response, we take an empirical approach [Naselaris et al. (2009)] by considering a large collection of images similar to those used to acquire training and validation data. The bag of images prior places equal probability on each image in :

$$\mathbb{P}(S=s)=\{\begin{array}{ll}\frac{1}{\mid \mathcal{B}\mid },\hfill & \text{if}s\in \mathcal{B},\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$

This distribution only implicitly specifies the statistical structure of natural images. With Bayes’ rule we arrive at the decoding model

$$p(s\mid y_1,\dots ,y_s)\propto exp\left\{-\sum _{v=1}^m\frac{{(y_v-{\mu }_v(s))}^2}{2{\sigma }_v^2}\right\}\times \mathbb{P}(S=s).$$

This model suggests that we can identify the image s that most closely matches a given voxel response pattern (Y₁, …, Y_m) by the rule

$$\underset{s}{argmax}p(s\mid y_1,\dots ,y_s)=\underset{s\in \mathcal{B}}{argmax}\sum _{v=1}^m\frac{1}{{\sigma }_v^2}{(y_v-{\mu }_v(s))}^2.$$ (5.1)

The fitted models from Section 4 provide estimates of μ_v. Given μ̂_v, the variance ${\sigma }_v^2$ can be estimated by

$${\widehat{\sigma }}_v^2=\frac{{\left|\right|{\mathbf{Y}}_v-{\widehat{\mu }}_v(\mathbf{S})\left|\right|}^2}{n-\text{df}({\widehat{\mu }}_v)},$$

where df(μ̂_v) is the degrees of freedom of the estimate μ̂_v (the number of nonzero coefficients in the case of linear models, or 4 times the number of nonzero functions in the case of V-SPAM; cf. Section 4.2). Substituting these estimates into (5.1) gives the decoding rule

$$\underset{s\in \mathcal{B}}{argmin}\sum _{v=1}^m\frac{1}{{\widehat{\sigma }}_v^2}{\left(y_v-{\widehat{\mu }}_v(s)\right)}^2.$$

Although we have estimates for every voxel, not every voxel may be useful for decoding—μ̂_v may be a poor estimate of μ_v or μ_v (s) may be close to constant for every s. In that case, we may want to select a subset of voxels 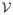⊆ {1, …, m} and restrict the summation in the above display to 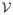. Thus, we propose the decoding rule

$${\widehat{S}}_{\mathcal{V}}(y_1,\dots ,y_m\mid \mathcal{B})=\underset{s\in \mathcal{B}}{argmin}\sum _{v\in \mathcal{V}}\frac{1}{{\widehat{\sigma }}_v^2}{\left(y_v-{\widehat{\mu }}_v(s)\right)}^2.$$ (5.2)

One strategy for voxel selection is to set a threshold α for entry to 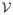based on the usual R² computed with the training data,

$$\text{training}{R}^2(v)=1-\frac{{\left|\right|{\mathbf{Y}}_v-{\widehat{\mu }}_v(\mathbf{S})\left|\right|}^2}{{\left|\right|{\mathbf{Y}}_v-{\overline{\mathbf{Y}}}_v\left|\right|}^2},$$ (5.3)

so that = {v: training R₂(v) > α}. We will examine this strategy later in the section.

To use (5.2) as a general purpose decoder, the collection of images 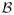should ideally be large enough so that every natural image S is “well-approximated” by some image in 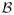. This requires a distance function over natural images in order to formalize “well-approximate,” but it is not clear what the distance function should be. We consider instead the following paradigm. Suppose that the image stimulus S that evoked the voxel response pattern is actually contained in 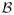. Then it may be possible for (5.2) to recover S exactly. This is the basic premise of the identification problem where we ask if the decoding rule can correctly identify S from a set of candidates 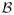∪ {S}. Within this paradigm, we assess (5.2) by its identification error rate,

$$\text{id}\text{error}\text{rate}:=\mathbb{P}({\widehat{S}}_{\mathcal{V}}(Y_1^{\prime },\dots ,Y_m^{\prime }\mid \mathcal{B}\cup \{S^{\prime }\})\ne S^{\prime }\mid {\widehat{S}}_{\mathcal{V}}(\cdots )),$$ (5.4)

on a future stimulus and voxel response pair { $S^{\prime },(Y_1^{\prime },\dots ,Y_m^{\prime })$} that is independent of the training data.

The identification error rate should increase as | 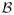| = b increases. However, the rate at which it increases will depend on the model used for estimating μ̂_v. We investigated this by starting with a database of 11,499 images (as in Figure 1) that are similar to, but do not include, the images in the training data or validation data, and then repeating the following experiment for different choices of b:

1. Form by drawing a sample of size b without replacement from .

2. Estimate the identification error rate (5.4) using the 120 stimulus and voxel response pairs { $S^{\prime },(Y_1^{\prime },\dots ,Y_m^{\prime })$} in the validation data.

3. Average the estimated identification error rate over all possible ⊆ of size b.

The average identification error rate can be computed without resorting to Monte Carlo. Given { $S^{\prime },(Y_1^{\prime },\dots ,Y_m^{\prime })$},

$${\widehat{S}}_{\mathcal{V}}(Y_1^{\prime },\dots ,Y_m^{\prime }\mid \mathcal{B}\cup \{S^{\prime }\})=S^{\prime }$$ (5.5)

if and only if

$$\sum _{v\in \mathcal{V}}\frac{1}{{\widehat{\sigma }}_v^2}{\left(Y_v^{\prime }-{\widehat{\mu }}_v(S)\right)}^2<\sum _{v\in \mathcal{V}}\frac{1}{{\widehat{\sigma }}_v^2}{\left(Y_v^{\prime }-{\widehat{\mu }}_v(s)\right)}^2$$ (5.6)

for every s ∈ . Since is drawn by a simple random sample, the number of times that event (5.6) occurs follows a hypergeometric distribution. So the conditional probability that (5.5) occurs is just the probability that a hypergeometric random variable is equal to b. The parameters of this hypergeometric distribution are given by the number of images in that satisfy (5.6), the number of images in that do not satisfy (5.6), and b. Counting the number of images in that satisfy/do not satisfy (5.6) is easy and only has to be done once for each S in the validation data, regardless of b. Thus, the computation involves evaluating (5.6) 120× 11,499 times (since there are 120 images in the validation data and 11,499 images in ), and then evaluating 120 hypergeometric probabilities for each b.

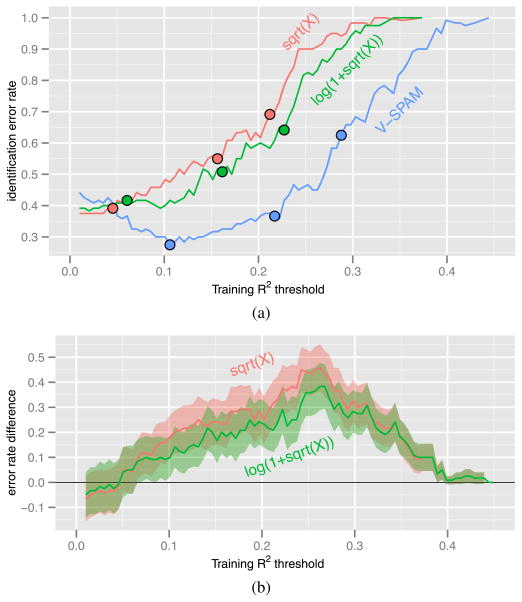
Figure 10 shows the results of applying the preceding analysis to the fixed transformation models (4.1) and (4.2) and the V-SPAM model (4.5). Each model has its own subset of voxels 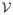used by the decoding rule. We set the training R² thresholds (5.3) so that the corresponding decoding rule used | 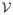| = 400 voxels for each model. When | 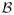| is small, identification is easy and all three models have very low error rates. As the number of possible images increases, the error rates of all three models increase but at different rates. At maximum, when 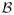= and there are 11,499 + 1 = 11,500 candidate images (11,499 images in plus 1 correct image not in ) for the decoding rule to choose from, the fixed transformation models have an error rate of about 40%, while the V-SPAM model has an error rate of about 28%.

Fig. 10.

Estimated average identification error rate (5.4) as a function of the number of possible images (| 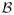| + 1). The error rates were estimated using the validation data and 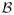randomly sampled from a database of 11,499 images.

The ordering of and large gap between the fixed transformation models and V-SPAM at maximum does not depend on our choice of | 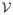| = 400 voxels. Fixing 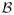= so that the number of possible images is maximal, we examined how the identification error rate varies as the training R² threshold is varied. Figure 11 shows our results. The threshold corresponding to 400 voxels is larger for V-SPAM than the fixed transformation models. It is about 0.1 for V-SPAM and 0.05 for the fixed transformation models. When the threshold is below 0.05, the error rates of the three models are indistinguishable. Above 0.05, V-SPAM generally has a much lower error rate than the fixed transformation models. In panel (a) of Figure 11 we also see that V-SPAM can achieve an error rate lower than the best of the fixed transformation models with half as many voxels (≤200 versus ≥400). These results show that the substantial improvements in voxel response prediction by V-SPAM can lead to substantial improvements in decoding accuracy.

Fig. 11.

Identification error rate (5.4) as a function of the training R² threshold (5.3) when the number of possible images is 11,499 + 1. (a) Estimated identification error rate. The solid circles on each curve mark the points where the number of voxels used by the decoding rule is (from left to right) 400, 200 or 100. (b) Pointwise 95% confidence bands for the difference between the identification error rates of (upper) sqrt(X) model (4.1) and V-SPAM; (lower) log(1 + sqrt(X)) model (4.2) and V-SPAM. The confidence bands reflect uncertainty due to sampling variation of the validation data.

6. Nonlinearity and inferred tuning properties

In computational neuroscience, the tuning function describes how the output of a neuron or voxel varies as a function of some specific stimulus feature [Zhang and Sejnowski (1999)]. As such, the tuning function is a special case of an encoding model, and once an encoding model has been estimated, a tuning function can be extracted from the model by integrating out all of the stimulus features except for those of interest. In practice, this extraction is achieved by using an encoding model to predict responses to parametrized, synthetic stimuli. One way to assess the quality of an encoding model is to inspect the tuning functions that are derived from it [Kay et al. (2008a)].

For vision, the most fundamental and important kind of tuning function is the spatial receptive field. Each neuron (or voxel) in each visual area is sensitive to stimulus energy presented in a limited region of visual space, and spatial receptive fields describe how the response of the neuron or voxel is modulated over this region. In the primary visual cortex, response modulation is typically strongest at the center of the receptive field. Response modulation is much weaker at the periphery, but has been shown to have functionally significant effects on the output of the neuron (or voxel) [Vinje and Gallant (2000)].

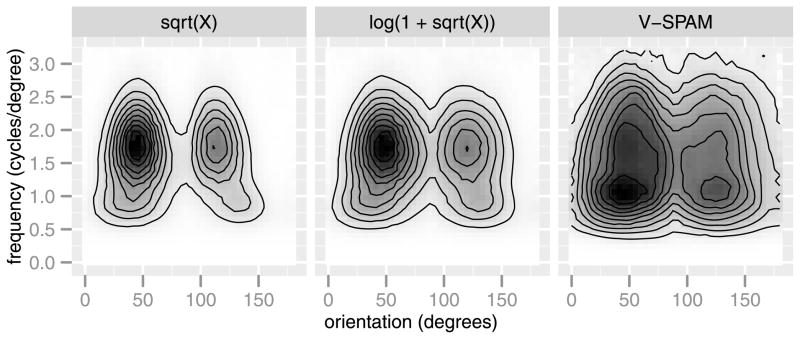
The panels in Figure 12 show estimated spatial receptive fields for voxel 717 using the three different models considered here [we chose this voxel because its predictive R² varied greatly among the three models: 0.26 for the sqrt(X) model (4.1), 0.42 for the log(1 + sqrt(X)) (4.2), and 0.57 for V-SPAM (4.5)]. These estimated receptive fields indicate the locations within the spatial field of view that are predicted to modulate the response of the voxel by each model. All three models agree that the voxel is tuned to a region in the lower-right quadrant of the field of view; however, for V-SPAM the receptive field is more expansive, and is thus able to capture the weak but potentially important responses at the far periphery of the visual field.

Fig. 12.

Estimated spatial receptive field for voxel 717. The contours show the predicted response to a point stimulus placed at various locations across the field of view. They indicate the sensitivity of the voxel to different spatial locations.

Like spatial tuning, orientation and frequency tuning are fundamental properties of V1, so it is essential to inspect the orientation and frequency tuning functions that are derived from encoding models for this area. As seen in the panels of Figure 13, the V-SPAM model is better able to capture the weaker responses to orientations and spatial frequencies away from the peaks of the tuning.

Fig. 13.

Estimated frequency and orientation tuning for voxel 717. The contours show the predicted response to a 2D cosine stimulus (a 2D Fourier basis function) parameterized by frequency and orientation. Darker regions correspond to greater predicted responses. The plot reveals sensitivity of the voxel to different spectral components.

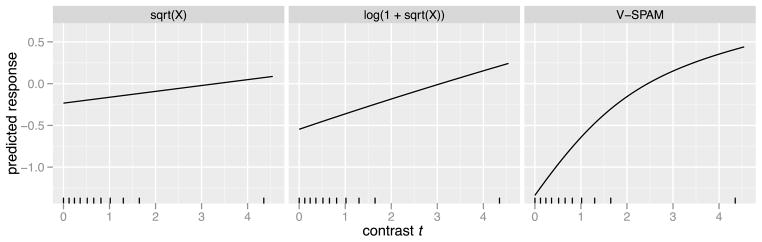
Finally, we examine tuning to image contrast, which is another critical property of V1. Image contrast strongly modulates responses in V1 and is also perceptually salient, so contrast tuning functions are frequently used to study the relationship between activity and perception [Olman et al. (2004)]. The contrast tuning function describes how a voxel is predicted to respond to different contrast levels. It is constructed by computing the predicted response to a stimulus of the form t · w, where w is standardized 2D pink noise (whose power spectral density is of the form 1/|ω|), and t ≥ 0 is the root-mean-square (RMS) contrast. At zero contrast the noise is invisible and only the background can be seen; as contrast increases the noise becomes more visible and distinguishable from the background. Figure 14 shows the contrast response function for the voxel as estimated by the three models. The first two, the sqrt(X) and log(1 + sqrt(X)), look nearly linear and relatively flat over the range of contrasts present in the training images. The V-SPAM prediction tapers off as contrast increases, and it is much more negative for low contrasts than predicted by sqrt(X) and log(1 + sqrt(X)). The V-SPAM prediction is closer to what is expected based on previous direct measurements [Olman et al. (2004)], and suggests that V-SPAM is more sensitive to responses evoked by lower contrast stimulus energy.

Fig. 14.

Estimated contrast tuning function for voxel 717. This is the predicted response to a pink noise stimulus at different levels of RMS contrast t. The tick marks indicate the deciles of RMS contrast in the training images (e.g., fewer than 10% of training images have contrast between 2 and 4).

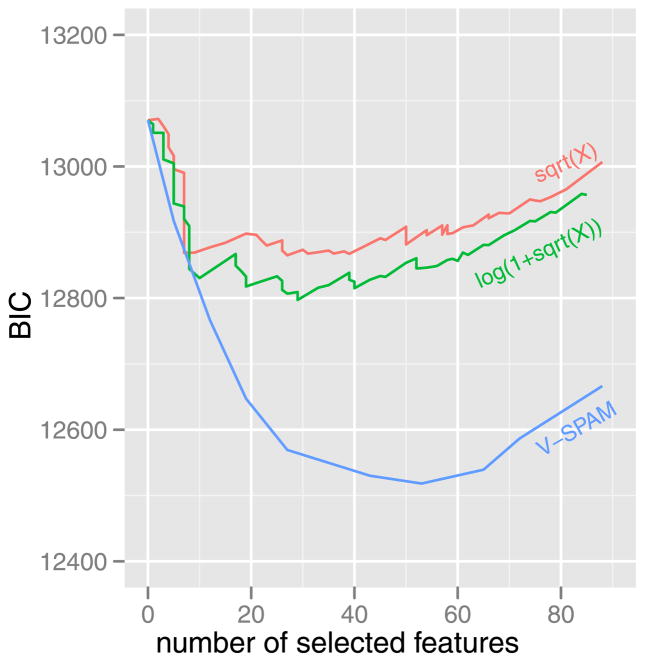
The relatively more sensitive tuning functions derived from the V-SPAM model of voxel 717 have a simple explanation. The models selected by BIC for this voxel included different numbers of features: 7 for sqrt(X), 29 for log(1 + sqrt(X)), and 53 for V-SPAM. Since the features are localized in space, frequency, and orientation, the number of features in the selected model is related to the sensitivity of the estimated tuning functions in the periphery. BIC forces a trade-off between the residual sum of squares (RSS) and number of features. The models with fixed transformations have much larger RSS values than V-SPAM, and the trade-off (see Figure 15) favors fewer features for them because the residual nonlinearity (as shown in Figure 3) does not go away with increased numbers of features. This suggests that the sensitivity of a voxel to weaker stimulus energy is not detected by the sqrt(X) and log(1 + sqrt(X)) models, because it is masked by residual nonlinearity. So the tuning function of a voxel can be much broader than inferred by the model when the model is incorrect.

Fig. 15.

Comparison of BIC paths for different models of voxel 717: the sqrt(X) model (4.1), the log(1 + sqrt(X)) model (4.2), and V-SPAM (4.5).

7. Conclusion

Using residual analysis and a start-of-the-art sparse additive nonparametric method (SPAM), we have derived V-SPAM encoding models for V1 fMRI BOLD responses to natural images and demonstrated the presence of an important nonlinearity in V1 fMRI response that has not been accounted for by previous models based on fixed parametric nonlinear transforms. This nonlinearity could be caused by several different mechanisms including the dynamics of blood flow and oxygenation in the brain and the underlying neural processes. By comparing V-SPAM models with the previous models, we showed that V-SPAM models can both improve substantially prediction accuracy for encoding and decrease substantially identification error when decoding from very large collections of images. We also showed that the deficiency of the previous encoding models with fixed parametric nonlinear transformations also affects tuning functions derived from the fitted models.

Since encoding and decoding models are becoming more prevalent in fMRI studies, it is important to have methods to adequately characterize the nonlinear aspects of the response-stimulus relationship. Failure to address nonlinearity effectively can lead to suboptimal predictions and incorrect inferences. The methods used here, combining residual analysis and sparse nonparametric modeling, can easily be adopted by neuroscientists studying any part of the brain with encoding and decoding models.

APPENDIX: EXTRACTING THE FMRI BOLD RESPONSE

The fMRI signal Z_v (t) measured at voxel v can be modeled as a sum of three components: the BOLD signal B_v (t), a nuisance signal N_v (t) (consisting of low frequency fluctuations due to scanner drift, physiological noise, and other nuisances), and noise ε_v (t):

$$Z_v(t)=B_v(t)+N_v(t)+{\epsilon }_v(t).$$

The BOLD signal is a mixture of evoked responses to image stimuli. This reflects the underlying hemodynamic response that results from neuronal and vascular changes triggered by an image presentation. The hemodynamic response function h_v (t) characterizes the shape of the BOLD response (see Figure 16), and is related to the BOLD signal by the linear time invariant system model [Friston, Jezzard and Turner (1994)],

Fig. 16.

A model hemodynamic response function.

$$B_v(t)=\sum _{k=1}^n\sum _{\tau \in T_k}{A}_v(k)h_v(t-\tau ),$$

where n is the number of images, T_k is the set of times at which image k is presented to the subject, and A_v (k) is the amplitude of the voxel’s response to image k.

To extract A_v (·) from the fMRI signal, it is necessary to estimate the hemodynamic response function and the nuisance signal. We used the method described in Kay et al. (2008b), modeling h_v (t) as a linear combination of Fourier basis functions covering a period of 16 seconds following stimulus onset, N_v (t) as a degree 3 polynomial, and ε_v (t) as a first-order autoregressive process. The resulting estimates Â_v (·) are the voxel responses for each image.