Training at High and Low Accuracy Levels Leads to Perceptual Learning Without Feedback

Abstract

In this study, we investigated whether mixing easy and difficult trials can lead to learning in the difficult conditions. We hypothesized that while feedback is necessary for significant learning in training regimes consisting solely of low training accuracy trials, training mixtures with sufficient proportions of high accuracy training trials would lead to significant learning without feedback. Thirty-six subjects were divided into one experimental group in which trials with high training accuracy were mixed with those with low training accuracy and no feedback, and five control groups in which high and low accuracy training were mixed in the presence of feedback; high and high training accuracy were mixed or low and low training accuracy were mixed with and without feedback trials. Contrast threshold improved significantly in the low accuracy condition in the presence of high training accuracy trials (the high-low mixture group) in the absence of feedback, although no significant learning was found in the low accuracy condition in the group with the low-low mixture without feedback. Moreover, the magnitude of improvement in low accuracy trials without feedback in the high-low training mixture is comparable to that in the high accuracy training without feedback condition and those obtained in the presence of trial-by-trial external feedback. The results are both qualitatively and quantitatively consistent with the predictions of an augmented Hebbian learning model. We conclude that mixed training at high and low accuracy levels can lead to perceptual learning at low training accuracy levels without feedback.

Introduction

Perceptual learning, the phenomenon that observers’ performance improves after repetitive practice, has been documented in many perceptual tasks (Fahle & Poggio, 2002). The study of perceptual learning has both theoretical and practical significance: theoretically it furthers our understanding of brain plasticity (see Sasaki, Nanez & Watanabe, 2010 for a review); practically it has the potential to provide possible remediation methods for clinically challenged populations such as adults with amblyopia (Huang, Lu & Zhou, 2008; Levi & Li, 2009; Polat, Sagi & Norcia, 1997). Examination of conditions that enable or disrupt learning may generate new insights into the functions and mechanisms of perceptual learning. In this study, we investigate whether mixing easy and difficult trials can lead to learning in the difficult trials that otherwise show little or no improvement with practice.

Most traditional perceptual learning studies have examined how performance accuracy in a single stimulus condition improves over the course of training (Fiorentini & Berardi, 1980, 1981; Poggio, Fahle & Edelman, 1992; Shiu & Pasher 1992; Fahle, Edelman & Poggio, 1995; Vania, Sundareswaran & Harris, 1995; Herzog & Fahle, 1997, 1999), or how threshold at a fixed accuracy level decreases as a result of training (Vogels & Orban, 1985; Karni & Sagi, 1991; Saarinen & Levi, 1995; Ahissar & Hochestein, 1997; Dosher & Lu, 1999, 2005). Some studies have used either mixtures of fixed stimuli that led to different performance accuracies (Petrov, et al, 2005, 2006), or mixtures of stimuli that track different performance accuracies (Dosher & Lu, 1998; 1999; Lu & Dosher, 2004). Whereas we (Liu, Lu & Dosher, 2010) found that thresholds in a Gabor orientation identification task in the low training accuracy condition did not improve in the absence of trial-by-trial feedback, Petrov, et al (2005, 2006) found that observers’ performance improved with virtually the same amounts with and without trial-by-trial external feedback in a training mixture consisting of three fixed contrast levels that resulted in high, intermediate, and low performance accuracies. Put together, these results suggest that mixing easy and difficult training trials – here higher and lower contrast trials – may facilitate perceptual learning in the low accuracy (difficult) condition in the absence of feedback. However, because three fixed contrasts were always mixed together in Petrov et al (2005, 2006), training accuracies changed throughout the experiment; the contributions of mixed training accuracy in perceptual learning were not explicitly manipulated.

The “Eureka” effect is another interesting phenomenon that involves training at multiple accuracy levels: Incorporating several very easy or “insightful” trials of the same type in the beginning of training has been reported to establish otherwise absent learning in subsequent training of a difficult task (Ahissar & Hochestein, 1997; Rubin, Nakayama & Shapley, 1997; Papathomas, Gorea, Feher & Conway, 1999). In addition, fast learning in an easy task has been shown to benefit a subsequent difficult task (Liu & Weinshall, 2000). In these studies, experience with the same task on the easy trials in the beginning of training may have led to some improvements of the perceptual system such that the originally difficult conditions become easier and therefore can be learned in subsequent training. In the current study, we took a different approach in order to better understand the role of training mixtures in perceptual learning. First, we mixed easy and difficult trials throughout the entire training course to “monitor” the state of the perceptual system throughout training. Second, we kept observers’ performance accuracy levels constant throughout training to investigate effects of fixed training accuracies in training mixtures.

Facilitation of learning in low accuracy trials through intermixing high-accuracy training trials in the absence of trial-by-trial external feedback is predicted by the Augmented Hebbian Reweighting Model (AHRM; Figure 1; Petrov, Dosher, and Lu, 2005, 2006). The augmented Hebbian learning algorithm of the AHRM incorporates external feedback, when present, simply as another input to the decision unit that shifts the postsynaptic activation in the correct direction and fosters appropriate weight changes. Without feedback, the model uses the internal response of the observer to update the weights: the weights still move in the correct direction on average because the activation of the decision unit correlates with the correct stimulus classification, and the optimization of weights can be achieved without feedback if the level of training accuracy is high enough. As the optimization resulting from practicing in high accuracy trials occurs, it should benefit a similar task with a lower level of training accuracy as well. Therefore, tasks of high training accuracy cause learning in the system that then show improved performance – and indeed potentiated learning -- in conditions in which learning is otherwise absent in unmixed training conditions, such as training at low training accuracy without feedback.

Figure 1.

The Augmented Hebbian Reweighting Model (AHRM). (Adopted from Petrov, Dosher, & Lu 2005, 2006).

In this study, we systematically examined the effects of mixing easy and difficult trials in perceptual learning. We hypothesized that while feedback is necessary for significant learning in training conditions that consist of only low training accuracy trials, training mixtures with sufficient proportions of high accuracy training trials would lead to significant learning without feedback. Low or high accuracy training trials are defined by the low or high accuracy controlled by staircases in contrast threshold measurements. Thirty-six adult observers practiced a Gabor orientation identification task in the fovea over six training days. They were divided into six equal-sized groups: one experimental group in which observers were trained with mixtures of high and low accuracy trials without feedback and five control groups. In one of the control groups, observers were trained with mixtures of high and low accuracy trials but with feedback. In the other four control groups, observers were trained with mixtures consisting of trials at high-high or low-low training trials, with and without feedback. The five control conditions provided estimates of possible magnitudes of perceptual learning in the task for us to compare the effects of training mixtures. The augmented Hebbian reweighting model (AHRM) of perceptual learning (Petrov et al., 2005; 2006) was used to account for the experimental results.

Methods

Observers

Thirty-six observers, all undergraduate or graduate students at the University of Southern California, participated in the study. They were randomly assigned into six groups: high-high training accuracy mixture with and without feedback, low-low training accuracy mixture with and without feedback, and high-low training accuracy mixture with and without feedback. High and low training accuracies were set at 85% and 65% correct. All observers had normal or corrected-to-normal vision and provided written consent following the protocol approved by the USC Institutional Review Board. All were naive to the purpose of the experiment and were paid for participation.

Apparatus

The experiment was run in a dark room using a Macintosh Power PC G4 computer running Matlab. All stimuli were generated in real time in Matlab with Pschotoolbox extensions (Brainard, 1997, Pelli, 1997). The stimuli were then displayed on a Nanao Technology Flexscan 6600 monitor with a P4 phosphor, a spatial resolution of 480 × 640, and a refresh rate of 120 Hz. A special circuit combined two eight-bit outputs of a video card to produce 6144 (12.6 bit) distinct gray levels (Pelli & Zhang, 1991). A psychophysical procedure was conducted to generate a lookup table for luminance calibration (Li, Lu, Xu, Jin & Zhou, 2003). The stimuli were viewed binocularly through natural pupil at a distance of 72cm, with a chinrest maintaining observers’ head position.

Stimuli

Each stimulus consisted of an oriented Gabor patch integrated with two Gaussian noise frames. The Gabor signal stimuli were Gaussian-windowed sinusoidal gratings, oriented ±10° from 45°. The luminance profile of the stimuli is described by:

$$L(x,y)=L_0\{1.0+c\text{sin}\left[2\pi f(x\text{cos}\theta +y\text{sin}\theta )\right]e^{-\frac{x^2+y^2}{2{\sigma }^2}}\},$$ (1)

where L₀ is the background luminance, set in the middle of the dynamic range of the display (L_min = 1 cd/m²; L_max = 53 cd/m²), c is the peak signal contrast, f = 1.29 c/d is the center spatial frequency of the Gabor, and = 0.77 deg is the standard deviation of the Gaussian window. The Gabors were rendered on a 64 ×64 pixel grid, extending 3.09°×3.09° of visual angle (Figure 2).

Figure 2.

Examples of a “Left” (top left) and a “Right”(top right) stimulus, and their corresponding power spectra (bottom, left and right). Gabor targets oriented +/-10° from 45° direction are embedded in extenal Gaussian noise. The Gabor spatial frequency is 1.29 cyc/deg. The spectra are plotted in polor coordinates, with log frequency along the radial axis and orientation along the angular axis.

External noise images with 64 ×64 pixels (3.09° ×3.09°) were constructed using 2 ×2 pixel elements (0.097° ×0.097°). 2 ×2 pixel elements were used to increase the overlap of the Fourier energy spectra of the signal and external noise stimuli and therefore the impact of external noise on observer performance. In every trial, the contrasts of all noise elements were drawn randomly and independently from the same Gaussian distribution with mean 0 and standard deviation 0.25. The external noise images were then filtered through a second-order Butterworth band-pass filter with cutoff frequencies of 0.70 c/d and 2.82 c/d. Because the display contrast ranged from -1.0 to 1.0, a sample with standard deviation of 0.25 conforms reasonably well to a Gaussian distribution. Both signal and noise images were centered at fixation and combined via temporal integration.

Design and Procedure

This study used a three by two between-subject design. Six groups of observers, each with one mixture of training accuracies (85% with 85%, 65% with 65%, or 65% with 85% correct) and one feedback condition (trial-by-trial or no feedback), participated in the study. There were six observers in each group, and each observer ran six days of the experiment in his or her designated group condition. In each day, observers ran two blocks of the experiment. In the first day, some additional trials were also given to the observers to familiarize them with the experiment and to estimate their pre-training thresholds.

In the beginning of the first day of the experiment, noise-free Gabor stimuli were used in several instruction trials to familiarize the observer with the task. A QUEST procedure (Watson & Pelli, 1983) with 60-80 trials was then used to estimate the starting contrast for each subject in the presence of external noise. After that, an accelerated stochastic staircase method (Kesten, 1958) was used to estimate subjects’ thresholds that track designated training accuracies in two interleaved but independent staircases with 80 trials each in a block of 160 trials. The initial contrast of each staircase in every block was set to be that of the last trials in the previous block.

Each trial started with a key press, a fixation display that lasted 150 ms, followed by an external noise, a signal, and an independent external noise image, each lasting 33 ms, and a blank window that lasted until the end of the trial. Observers responded by pressing different keys on the computer keyboard to indicate whether the Gabor was tilted clockwise (“Right”) or counter clockwise (“Left”) relative to the 45 reference angle. An auditory beep followed each correct response in three trial-by-trial feedback groups. No feedback was provided to the other three groups.

Training accuracy was controlled by the accelerated stochastic approximation method (Kesten, 1958), an adaptive procedure that converges to any specified accuracy level. In this method, the stimulus contrast in every trial was determined by the stochastic approximation procedure (Robbins & Monro, 1951). To converge to a target performance level , stimulus contrasts in the first two trials are given by:

$$c_{n+1}=c_n-\frac{s}{n}(Z_n-\varphi ),$$ (2)

where n is the trial number, c_n is the stimulus contrast in trial n, Z_n=0 (incorrect) or 1 (correct) is the response accuracy in trial n, c_n+1 is the stimulus contrast for the next trial, and s is the pre-chosen step size at the beginning of the trial sequence. From the third trial on, the sequence is “accelerated”:

$$c_{n+1}=c_n-\frac{s}{2+m_{shift}}(Z_n-\varphi ),$$ (3)

where m_shift is the number of shifts in response category (switches from consecutive correct responses to incorrect responses and vice versa). In an influential review of adaptive psychophysical procedures, Treutwein (1995) recommended the accelerated stochastic approximation procedure as one of the best available procedures for measuring thresholds. Simulation studies prior to the experiments suggest that the optimal s is equal to c₁ and the optimal c₁ is equal to the true threshold, which can be estimated from the QUEST procedure stated above.

Analysis

Contrast thresholds were collected for each group over the course of training. Learning curves under different mixture and feedback conditions were then analyzed using linear regression and conventional statistical testing.

The behavioral results were also fit by the augmented Hebbian reweighting model (AHRM, Petrov et al., 2005, 2006). The AHRM is a multi-channel neural network model implementation of the channel reweighting hypothesis outlined in (Dosher & Lu, 1998). It consists of four types of units (Figure 1): representation units that encode input images as activation patterns, a task-specific decision unit that receives weighted inputs from the representation units, an adaptive bias unit that accumulates a running average of the response frequencies and works to balance the frequency of the two responses, and a feedback unit that makes use of external feedback when (and if) it is presented. Learning in the model occurs exclusively through incremental Hebbian modification of the weights between representation units and the decision unit; while the early processing pathway that constructs representations from the retinal image remains fixed throughout training. Detailed descriptions of the augmented Hebbian reweighting model can be found in (Petrov et al., 2005; 2006) and Liu, Lu and Dosher (2010).

The AHRM was implemented in a MATLAB program. The program takes grayscale images as inputs, produces binary (Left/Right) responses as outputs, and learns on a trial-by-trial basis. Eight parameters, including six scaling factors (a), one for each group, internal multiplicative noise (σ₂), and decision noise (σ_d), were adjusted to fit the experimental data. All other parameters, including orientation tuning bandwidth (h_θ), frequency tuning bandwidth (h_f), and radial kernel width (h_r) were set a priori based on publications in the literature. The learning rate η was set at 0.00025, the value used in Liu et al (2010). The scaling factors and internal noises allow a match to the overall performance shown in the initial threshold measure. Critically, a single learning rate, constrained to be the same as the value used in Liu et al (2010), was used to model the learning curves in all six experimental conditions, and the predicted differences between conditions entirely reflect differential effectiveness of Hebbian learning and feedback in these conditions.

Each iterations of parameter adjustment to improve the match of the Hebbian learning model to the data took place in two steps. First, the initial weights were set in proportion to the preferred orientation of the units: w_i = (_i/30)w_init, reflecting general prior knowledge about orientation. These initial weights were fixed. The eight “free-to-vary” parameters, six a's, σ₂, and σ_d, were adjusted, with two of them (internal multiplicative noise and decision noise) restricted to be the same for all 6 groups. The six scaling factors, a, were free to vary among the groups such that the model performance approximately matched the initial contrast thresholds of the human observers in the beginning of the experiment, and so reflected small random differences in performance level for these randomly assigned groups.

The adjustment was based on Least Squared error:

$$L=\sum {[\text{log}\left(c_{\tau }^{theoretical}\right)-\text{log}\left(c_{\tau }^{measured}\right)]}^2,$$ (4)

where $c_{\tau }^{measured}$ and $c_{\tau }^{theoretical}$ represent measured and model-generated contrast thresholds, and ∑ represents summation over the first data point across all six experimental conditions.

In the second step, the weights were allowed to change, corresponding to learning on each trial with the Hebbian mechanism. The output of the decision unit and/or the external feedback was used to update the weights depending on the specific feedback condition. The accelerated stochastic approximation procedure was used to generate the training sequence. The model performance was then compared to that of the human observers using Least Squared error defined in Eq. 4 with summation over all the estimated contrasts for all the training sessions in the six experimental conditions. The two steps were repeated until the model predictions were reasonably matched to the data.

For every experimental condition, the model, just as the human observers, ran 12 blocks with 160 trials/block in each simulated experiment. This was repeated 1000 times. A bootstrap procedure was used to generate confidence intervals on model performance. In each bootstrap step, we sampled performance curves from six simulations to generate the average performance curve of six simulated observers. This was repeated 1000 times. Following standard bootstrap procedures, we computed the mean and standard deviations of the slope of the learning curves of the model from the 1000 learning curves. Analysis of variance on model performance was also performed based on the mean and standard deviations of the model curves.

Results

Learning Curves

To examine the training accuracy in the course of the experiment, we computed the average performance accuracy for every forty trials for the six groups of human observers. Most of the observed average accuracies were indeed within ±5% of the target accuracies specified for each accelerated stochastic approximation staircase (Figure 3).

Figure 3.

The proportion correct of every 40 trials for all 6 groups. Every point in a graph is the average of the proportion correct of 6 subjects in a group and the error bar shows the standard error of the mean. (a) 65% + 65% correct (low mixed with low accuracy) with feedback. (b) 65% + 65% correct (low mixed with low accuracy) without feedback. (c) 85% +85% correct (high mixed with high accuracy) with feedback. (d) 85% + 85% correct (high mixed with high accuracy) without feedback. (e) 65% + 85% correct (low mixed with high accuracy) with feedback. (f) 65% + 85% correct (low mixed with high accuracy) without feedback.

Learning curves, log (contrast threshold) versus log (training block), are shown in Figure 4. The magnitudes of threshold reduction are listed in Table 1. We found that mixing high and low training accuracy trials without feedback indeed enabled significant perceptual learning in the low accuracy trials: threshold reduced 32.2±7.6% at the 65% accuracy level and 30.7±3.8% at the 85% accuracy level in the high-low mixture without feedback group (p<0.01). In comparison, no significant threshold reduction was observed in the low-low mixture without feedback group (10.1±8.9%; p>0.10); and a 38.2±9.4% threshold reduction was observed in the high-high mixture without feedback condition (p<0.01). The magnitude of learning at the 65% accuracy level was significantly greater in the high-low mixture than that in the low-low mixture (p<0.01).

Figure 4.

Average learning curves for all six groups. Every point in a graph is the average of the contrast thresholds of 6 subjects in a group and the error bar shows the standard error of the mean. The red line is the linear regression of the log contrast threshold against the log of the training blocks. A negative slope indicates the existence of learning, showing the drop of contrast threshold over time. The gray area in each panel covers the 95% range of confidence of the regressed slope. (a) 65% + 65% correct (low mixed with low accuracy) with feedback. (b) 65% + 65% correct (low mixed with low accuracy) without feedback. (c) 85% + 85% correct (high mixed with high accuracy) with feedback. (d) 85% + 85% correct (high mixed with high accuracy) without feedback. (e) 65% + 85% correct (low mixed with high accuracy) with feedback. (f) 65% + 85% correct (low mixed with high accuracy) without feedback.

Table 1.

Learning rate and magnitude of contrast threshold changes in the experiment and model simulation

Group	Learning Rate		Learning Magnitude
	Experiment	AHRM	Experiment	AHRM
65%+65% w/	-0.18±0.05	-0.16±0.04	36.5±8.1%	32.9±7.0%
65%+65% w/o	-0.04±0.04	-0.02±0.05	10.1±8.9%	5.9±10.8%
85%+85% w/	-0.14±0.02	-0.17±0.02	28.8±3.6%	33.7±4.1%
85%+85% w/o	-0.19±0.06	-0.15±0.03	38.2±9.4%	30.3±4.4%
65%+85% w/ --65%	-0.18±0.03	-0.13±0.04	36.3±4.5%	27.7±10.5%
65%+85% w/ --85%	-0.14±0.03	-0.13±0.03	28.7±5.6%	28.0±6.0%
65%+85% w/o --65%	-0.16±0.04	-0.12±0.04	32.2±7.6%	25.1±11.0%
65%+85% w/o --85%	-0.15±0.02	-0.12±0.03	30.7±3.8%	26.4±6.7%

The presence of feedback enabled perceptual learning in all the mixture conditions: there were 36.3±4.5% and 28.7±5.6% threshold reduction at the 65% and 85% accuracy levels in the high-low mixture condition, 36.5±8.1% threshold reduction at the 65% accuracy level in the low-low mixture condition, and 28.8±3.6% at the 85% accuracy level in the high-high mixture condition.

Additional analyses were performed on the slopes of the learning curves (Table 1). The slopes were -0.18±0.05 (SE) and -0.04±0.04 for the low-low groups with and without feedback, respectively; and -0.14±0.02 and -0.19±0.06 for the high-high groups with and without feedback, respectively. The slopes were -0.18±0.03 and -0.16±0.04 for the 65% training accuracy condition in the high-low groups with and without feedback, and -0.14±0.03 and -0.15±0.02 for the 85% training accuracy condition in these groups. Analysis based on nested model tests showed that only two slopes were necessary to account for all these learning curves: one for the low-low group without feedback, and the other for all other conditions. This two-slope model was significantly better than a one-slope model (p<0.01), but not significantly worse than a model with eight slopes, one for each training accuracy level in each condition (p>0.10). These results demonstrated that the main difference in learning effect is between the low-low without feedback group and all other groups. There was no significant difference in those other groups.

To summarize, mixing training trials tracking high and low accuracy levels resulted in otherwise absent learning in the low accuracy without feedback condition. Moreover, the magnitude of learning in the low accuracy without feedback condition in a high-low training mixture is comparable to that in the high accuracy training without feedback condition and those obtained in the presence of trial-by-trial external feedback.

AHRM Fits

The AHRM simulations provided reasonably good fits to all the data (see Table 2 for model parameters). The best fitting learning curves of the AHRM are plotted in Figure 5 along with the behavioral data. Quantitatively, the model accounted for 90.7% of the variance. The performance pattern of the model was essentially the same as that of the human observers (Table 1). In the model, the average magnitudes of learning, calculated as the percentage of threshold reduction between the last and first training blocks, were 32.9±7.0%, 5.9±10.8%, 33.7±4.1%, and 30.3±4.4%, for the low-low mixture with feedback and without feedback conditions, and high-high mixture with and without feedback conditions, respectively. In the high-low mixture conditions, the magnitudes were 27.7±10.5% and 25.1±11.0% for the 65% training accuracy with and without feedback, and 28.0±6.0% and 26.4±6.7% for the 85% training accuracy with and without feedback. The slopes of the learning curve for the four same-accuracy mixture groups were: -0.16±0.04 (SD), -0.02±0.05, -0.17±0.02, -0.15±0.03. For the two high-low mixture groups, the slopes of the 65% training accuracy condition were -0.13±0.04 and -0.12±0.04 with and without feedback, and -0.13±0.03 and -0.12±0.03 for the 85% training accuracy with and without feedback. Statistical testing found no significant learning in the low-low mixture without feedback group but significant learning in all the other groups. Analysis of variance found significant differences among the six groups (p< 0.001). Scheffe post-hoc analysis (α= 0.05) identified a significant difference only between the group with a low-low training mixture without feedback and the other five groups; there was no significant difference among those five.

Table 2.

Model parameters

	Parameter	Value
Parameters set a priori	Orientation spacing Spatial frequency spacing Maximum activation level Weight bounds Running average rate Activation function gain Bias weight Normalization constant Internal additive noise Initial weight scaling factor Feedback weight	Δθ=15° Δf = 0.5 oct Amax = 1 wmin/max = ±1 ρ= 0.02 γ= 5 wb = 2.2 k = 0 σ1 = 0 wini = 0.090 wf = 1.0
Parameters constrained by published data	Orientation tuning bandwidth Frequency tuning bandwidth Radial Kernel width	hθ = 30° hf = 1.0 oct hr = 2.0 dva
Parameters optimized to fit the present data	Representation scaling factor	a = 0.22~1.2
	Internal multiplicative noise	σ2= 0.1
	Decision noise	σd= 0.15
	Learning rate	η= 0.00025

Figure 5.

Model fits to the behavioral results. The points and error bars represent the average contrast thresholds and the standard error of the mean in each training condition. The red lines represent performance of the simulated AHRM. Shaded areas represent ±1 SD of the model performance. (a) 65% +65% correct (low mixed with low accuracy) with feedback. (b) 65% + 65% correct (low mixed with low accuracy) without feedback. (c) 85% +85% correct (high mixed with high accuracy) with feedback. (d) 85% + 85% correct (high mixed with high accuracy) without feedback.

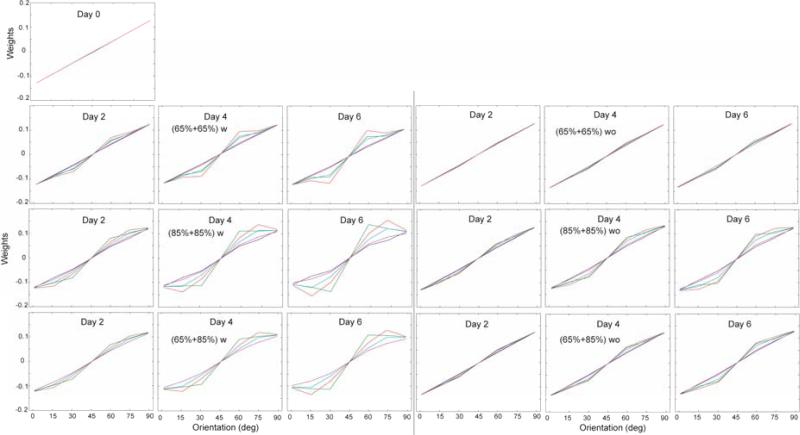
The weight dynamics for all six groups are shown in Figure 6. The initial weights embodied general directional information, yet carried very little information about which spatial frequency and orientation channels contained the target. With practice, the weights on the different channels were adjusted to match the statistical structure of the stimulus. At the end of learning, the most significant weight optimization occurred in the high-high mixture with feedback group. The weight changes in all groups with significant learning were similar. The weights in the low-low mixture without feedback group changed little, consistent with the observation of no learning in that condition.

Figure 6.

Weight dynamics of the AHRM. The first row is the initial weights before any training, which are the same for all the groups. The second to seventh rows show the weights after 2, 4 and 6 days of training for all the groups, with each group labelled on the right side of the figure. The different colors of the curves represent the channels with different spatial frequencies as shown in the inset.

Discussion

In this study, we found a facilitatory effect of high training accuracy trials to low training accuracy trials: while feedback is necessary for significant learning in training consisting of only low training accuracy trials, training mixtures with sufficient proportions of high accuracy training trials can lead to significant learning without feedback. Moreover, the magnitude of learning in the low accuracy without feedback condition in a high-low training mixture is comparable to that in the high accuracy training without feedback condition and those obtained in the presence of trial-by-trial external feedback. The pattern of results here are both qualitatively predicted and quantitatively accounted for by an augmented Hebbian re-weighting model (Petrov et al., 2005; 2006)

The facilitatory effect of high training accuracy trials is related to the results of Petrov et al (2006), who found that observers’ performance improved by virtually the same amounts with and without trial-by-trial external feedback in a training mixture consisting of three fixed contrast levels that resulted in high, intermediate, and low performance accuracies. Through tracking contrast thresholds at fixed accuracy levels, the current study allowed us to reveal the contributions of training accuracy in the mixture.

Our results are also related to the “Eureka effect” (Ahissar & Hochestein, 1997; Rubin, Nakayama & Shapley, 1997; Papathomas, Gorea, Feher & Conway, 1999), but provide an explicit mechanism and structure for understanding the quantitative requirements of the facilitatory process. In the Eureka effect, learning is often rapid: the experience with the same task on the easy trials in the beginning of training may have led to some improvements of the perceptual system such that the originally difficult conditions become easier and therefore can be learned in subsequent training. The abrupt nature of the Eureka effect makes it difficult to measure changes of the perceptual system. In our study, the learning is gradual because we mixed easy and difficult trials throughout the entire training course. This allowed us to “monitor” the state of the perceptual system throughout training. Keeping observers’ performance accuracy levels constant throughout training also allowed us to investigate effects of fixed training accuracies in training mixtures.

It has been shown previously that either high training accuracy or trial-by-trial feedback alone is enough to elicit learning in an orientation discrimination task (Liu, Lu & Dosher, 2010), but if neither condition is available, learning is very slow, if not impossible. Here we show that mixing high training accuracy trials to low ones can enable learning in these low training accuracy trials even when there is no feedback. In other words, high training accuracy trials can be used instead of trial-by-trial feedback to improve performance. This is consistent with the principles of the Augmented Hebbian Reweighting Model (AHRM), which applies Hebbian learning rules when there is no feedback, and uses feedback as another input to the system when feedback is available. AHRM has been able to accommodate all these experimental results.

Two training accuracy levels (65% and 85% correct) were mixed in three different proportions in this study: 100/0, 50/50, and 0/100% of 65% and 85%, respectively. We found that, with feedback, all three mixtures led to significant perceptual learning; without feedback, the 100/0 mixture led to no significant learning, yet the 50/50 and 0/100% mixtures led to nearly comparable magnitudes of perceptual learning. One interesting question is what the minimum proportion of training trials at the high accuracy level is necessary for the observers to learn the task without feedback. Figure 7 shows the predictions of the AHRM for 1920 total training trials consisting of mixtures with different fractions of 65% and 85% correct trials. Roughly speaking, a mixture with more than 25% high accuracy training trials is necessary for the observer to learn the task without feedback. Future empirical studies are necessary to test the prediction.

Figure 7.

AHRM predictions of threshold reduction after 1920 trials of training with many different mixtures of 65% and 85% correct trials. The magnitudes of threshold reductions are plotted as functions of percent of 85% correct trials in the random mixture. Even a small number of high-accuracy trials may enable some learning.

Many have investigated the role of external feedback in perceptual learning. Whereas most perceptual learning studies used trial-by-trial feedback, significant perceptual learning has also been found in training without external feedback (Ball & Sekuler, 1987; Crist, Kapadia, Westheimer & Gilbert, 1997; Fahle & Edelman, 1993; Herzog & Fahle, 1997; Karni & Sagi, 1991; McKee & Westheimer, 1978; Shiu & Pashler, 1992; Petrov, Dosher & Lu, 2006), with only block feedback (Herzog & Fahle, 1997; Shiu & Pashler, 1992), or with feedback to an irrelevant task (Seitz & Watanabe, 2003; Watanabe, Nanez & Sasaki, 2001; Watanabe, Nanez, Koyama, Mukai, Liederman & Sasaki, 2002; Seitz, Nanez, Holloway, Tsushima & Watanabe, 2006). Two studies found that providing external feedback had little effect after training without feedback (Herzog & Fahle, 1997; McKee & Westheimer, 1978). Others found external feedback improved the rate of learning (Ball & Sekuler, 1987; Fahle & Edelman, 1993), and was necessary for perceptual learning, especially for difficult stimuli (Herzog & Fahle, 1997; Shiu & Pashler, 1992; Seitz et al., 2006). Shibata et al (2009) showed that arbitrary block-feedback facilitated perceptual learning if it is more positive than the observer's actual performance. Liu, Lu & Dosher (2010) found that, at high training accuracies, feedback is not necessary, but no significant learning was found in low training accuracies without feedback.

The complex pattern of empirical results concerning the role of feedback in perceptual learning rules out both a pure supervised mode (Hertz, Krogh & Palmer, 1991) and a pure unsupervised mode of learning (Polat & Sagi, 1994; Vaina, Sundareswaran & Harris, 1995, Weiss; Edelman & Fahle, 1993). In the pure supervised mode, explicit trial-by-trial feedback serves as the teaching signal. No learning is possible without trial-by-trial feedback. In contrast, unsupervised learning rules do not depend on feedback. Herzog and Fahle (1998) suggested feedback changes the learning rate through (unspecified) top-down control but does not act as a teaching signal in perceptual learning. Dosher and Lu (2009) concluded that the ARHM can account for this complex pattern of results on feedback. Shibata et al. (2009) proposed a Bayesian model, which can adjust its learning rate based on block feedback: When the block feedback is positively exaggerated, the model increases its learning rate and learns faster. When the feedback is negatively exaggerated, the model does not significantly change its learning rate and learns at the “normal” pace. Recently, we (Liu, Lu & Dosher, 2010) conducted a computational analysis of Shibata et al (2009) with the AHRM, in which block feedback was used to modify the weight of the criterion control unit in the model. The simulation results are both qualitatively and quantitatively consistent with the data.

A number of models have been proposed in perceptual learning (Herzog & Fahle, 1998, Petrov et al., 2006, Petrov et al., 2005, Vaina, Sundareswaran & Harris, 1995, Vallabha & McClelland, 2007, Weiss, Edelman & Fahle, 1993, Zhaoping, Herzog & Dayan, 2003) (see Tsodyks & Gilbert, 2004, for a review). All these models assume an appropriate stimulus representation and postulate incremental learning; none proposes systematic changes in representation. The ARHM (Petrov et al, 2005, 2006) belongs to this class of incremental re-weighting models. In developing and applying the ARHM, we have focused on standard representations, biological plausibility, explicit top-down inputs, and quantitative testing against complex data sets. The AHRM has been used to successfully account for complex patterns of perceptual learning in an orientation discrimination experiment under destabilizing non-stationary manipulations both with and without trial-to-trial feedback (Petrov et al., 2005, 2006). The model has recently been used to account for a large number of data patterns in external noise studies of perceptual learning (Lu, Liu & Dosher, 2010). The observed facilitatory effect of high training accuracy trials on low training accuracy trials provides further support for the augmented Hebbian re-weighting model of perceptual learning.

Highlights.

> We hypothesized that mixing easy and difficult trials can lead to perceptual learning in the difficult conditions.

> Contrast threshold improved significantly in the low accuracy condition in high-low accuracy training mixture.

> The Augmented Hebbian Reweighting Model (AHRM) successfully explained our data.