Abstract
It has been hypothesized that the generalization patterns that accompany learning carry the signatures of the neural systems that are engaged in that learning. Reach adaptation in force fields has generalization patterns that suggest primary engagement of a neural system that encodes movements in the intrinsic coordinates of joints and muscles, and lesser engagement of a neural system that encodes movements in the extrinsic coordinates of the task. Among the cortical motor areas, the intrinsic coordinate system is most prominently represented in the primary sensorimotor cortices. Here, we used transcranial direct current stimulation (tDCS) to alter mechanisms of synaptic plasticity and found that when it was applied to the motor cortex, it increased generalization in intrinsic coordinates but not extrinsic coordinates. However, when tDCS was applied to the posterior parietal cortex, it had no effects on learning or generalization in the force field task. The results suggest that during force field adaptation, the component of learning that produces generalization in intrinsic coordinates depends on the plasticity in the sensorimotor cortex.
Introduction
A useful method with which one can infer the neural architecture of a learning process is by quantifying the generalization patterns (Shadmehr, 2004). If cells that participate in encoding a novel input–output map have consistent tuning properties, the shape of these tuning functions will leave its signature in the patterns of generalization. For example, practicing discrimination of a visual vernier stimulus results in increased acuity, but does not generalize to nearby locations on the retina, resulting in the inference that learning occurs at an early processing stage in the visual pathway (Poggio et al., 1992), In the motor domain, training of reaching movements in a force field produces broad generalization in position space (Shadmehr and Mussa-Ivaldi, 1994; Shadmehr and Moussavi, 2000; Malfait et al., 2002) and narrow generalization in direction space (Thoroughman and Shadmehr, 2000), suggesting involvement of cells that encode state of the limb in the intrinsic coordinates of joints and muscles (Hwang and Shadmehr, 2005). From this framework, a prediction has emerged that learning of reaching in force fields is primarily (but certainly not exclusively) due to plasticity in the motor areas that encode movements in the intrinsic coordinates of joints and muscles (Sing et al., 2009; Bock and Thomas, 2011).
In the cerebral cortex, an intrinsic coding of movements has been observed in the primary motor cortex (M1) and the adjacent somatosensory areas (Scott and Kalaska, 1997). Indeed, during reach adaptation in force fields, M1 neurons show changes in their activity that appear correlated with formation of a memory that predicts the forces (Gandolfo et al., 2000; Li et al., 2001; Arce et al., 2010), and the details of this encoding have provided some rationale for the shape of the generalization function (Arce et al., 2010). If the formation of the memory during force-field adaptation depends on the motor cortex, then altering how the motor cortex encodes the memory might alter the patterns of generalization in a predictable way. Here, our aim was to alter mechanisms of plasticity in the human motor cortex and quantify its impact on the encoding of the motor memory.
Although the mechanisms of plasticity in the cortex are still poorly understood, it appears that short-term learning involves weakening of existing inhibitory connections (Hess and Donoghue, 1994), resulting in unmasking of existing excitatory connections. The inhibitory connections rely on the neurotransmitter GABA, which can be manipulated via transcranial direct current stimulation (tDCS). For example, application of either cathodal or anodal tDCS to the human motor cortex for 10 min results in the reduction of GABA concentrations by ∼10% (Stagg et al., 2009b). In addition, application of anodal tDCS to M1 promotes synaptic plasticity in rat brain slices, producing synaptic long-term potentiation (LTP) (Fritsch et al., 2010), and enhances overnight retention of a sequential motor task (Reis et al., 2009). These results raise the possibility that tDCS can be used as an experimental tool to enhance synaptic plasticity in the human brain and alter the process of motor learning. Together, these ideas lead to an interesting prediction: tDCS of M1 might alter representation of the motor memory, increasing generalization in the intrinsic coordinates of joints and muscles during adaptation to force fields.
Materials and Methods
Forty-three neurologically intact, right-hand-dominant human subjects (18–40 years old, 19 males) were recruited and provided written consent. The subjects were naive to the purpose of the experiment and the procedures were approved by the Johns Hopkins University School of Medicine Institutional Review Board.
Behavioral task.
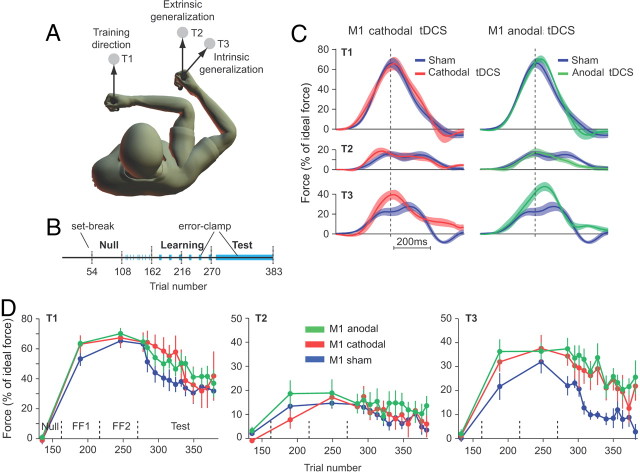
Volunteers held the handle of a robotic arm and made reaching movements in a standard force-field task (Shadmehr and Mussa-Ivaldi, 1994). The paradigm was adapted from Haswell et al. (2009). Briefly, participants were trained in reaching movements in one workspace and were tested for generalization patterns in another workspace (Fig. 1A). The start position for the movements in the training workspace was 90° elbow and shoulder angles. The start position in the testing workspace was a 90° elbow and a 45° shoulder angle. In the training workspace, target (T)1 was positioned 8 cm in front of the start position. In the testing workspace, targets 2 and 3 were placed so that they represented the same displacement as target 1 in extrinsic and intrinsic coordinates, respectively. At the start of the trial, the robot brought the hand to the start position, a target appeared (6 mm square, 8 cm distance) and the subjects were required to move their hand to land within the target [squared vectorial velocity smaller than 3 (cm/s)2] in <500 ms after movement start. If they succeeded, the target exploded. The target turned blue to indicate if movement duration was too long. Throughout the experiment, visual feedback of hand position was provided via a cursor. We recorded the force at the handle and the position and velocity of the hand at 100 Hz.
Figure 1.
Learning and generalization of reaching in a force-field task. A, Subjects were trained to reach under force-field perturbation to T1. Generalization in intrinsic and extrinsic coordinates was tested with reaching movements to test T2 and T3. T2 required identical hand and cursor motion (as compared with T1) whereas T3 required identical joint motion (as compared with T1). B, The experiment started with 162 trials in a null field followed by 108 trials under force-field perturbation. During the field trials, the learning and generalization were assessed every 15 trials with one error-clamp trial to each of the three targets (blue zones). In an error-clamp trial, the robot produces a stiff channel from start position to the target, minimizing movement errors and allowing us to measure the forces that subjects produce against channel walls. These forces are a proxy for the perturbation that the brain expects on that trial. The test block started with five reaching movements under force-field perturbation to T1 followed by 108 error-clamp trials to T1, T2, or T3 in random order (blue zone). Note that, after the baseline blocks, all movements to T2 and T3 are in error-clamp trials. C, Normalized force profiles recorded during the first three error-clamp trials to each of the three targets during the test block. Force profiles were aligned on peak tangential velocity and normalized with ideal force at peak tangential velocity. Data are across subject mean and SEM. D, Evolution of the normalized force at peak tangential velocity over the course of error-clamp trials. Force data were averaged over three error-clamp trials (bin size) and are presented for each target separately. Error bars are SEM.
The experiment began with three baseline blocks in which reaching movements were performed in a null field (N1–N3; 54 trials each, blocks separated by a brief set break) (Fig. 1B). The set continued with two learning blocks in a velocity-dependent curl force field (FF1 and FF2; viscosity matrix: [0 13; −13 0] N·s/m), and concluded with one test block (113 trials). In the baseline blocks, the subjects made reaches to a pseudorandomly chosen target among the three possible. We interspersed 18 error-clamp trials during the last baseline block. In an error-clamp trial, the hand path was constrained to a straight line by a channel (spring coefficient, 2500 N/m; damping coefficient, 25 N·s/m) (Scheidt et al., 2000). Error-clamp trials provide movements with almost zero error, hence minimally disrupting the learning process. This is in contrast to catch trials, in which the force field is removed, causing unlearning (Thoroughman and Shadmehr, 2000). The learning blocks (FF1 and FF2) consisted of three sets of 18 movements: 15 movements to T1 under force-field perturbation followed by three error-clamp trials (one to each of the three targets). The test block started with a series of five field trials to T1 followed by 108 error-clamp trials pseudorandomly distributed to the three targets.
Brain stimulation procedures.
Transcranial direct current stimulation was delivered through two 25cm2 sponge electrodes soaked in saline solution. One of the electrodes was positioned on the skin overlying the contralateral supraorbital region whereas the other covered the left M1 or the left posterior parietal cortex (PPC). For M1 stimulation, the electrode was centered on the hotspot of the first dorsal interosseus muscle, which corresponded to the optimal position for eliciting a consistent motor-evoked potential using transcranial magnetic stimulation (70 mm coil coupled with a Magstim 200). Given the size of the electrode, the arm area of M1 was also stimulated. The PPC was localized using the 10–20 EEG system (marker P3). Following Herwig et al. (2003), this electrode placement should overlay the posterior parietal cortex (especially the intraparietal sulcus) with sufficient accuracy. For instance, the same electrode placement has been shown to influence performance in a visuospatial task (Sparing et al., 2009). After the second null block (N2), the electrodes were placed on the subject's head and a 1 mA current was delivered through the electrodes using a Phoresor II Auto (Model PM850; IOMED) without any obvious changes in performance. The stimulation lasted until the end of the experiment for the active tDCS groups (20 min). For the sham group, the brain stimulation lasted for 30 s.
Experimental groups.
We recruited five groups of subjects. These groups were differentiated based on which brain area was stimulated. For the M1 cathodal tDCS group (n = 8), the cathodal electrode was placed on M1. For M1 anodal tDCS group (n = 8), the anodal electrode was placed on M1. For M1 sham group (n = 11), the anodal electrode was placed on M1 and turned on for 30 s and then turned off. For the PPC cathodal tDCS group (n = 8), the cathodal electrode was placed on the PPC. For the PPC anodal tDCS group (n = 8), the anodal electrode was placed on the PPC.
Data analysis.
Performance was measured via the force produced against channel walls during error-clamp trials and via the position and velocity of the hand during field trials. All trials were aligned with respect to peak tangential velocity. Baseline force profiles were subtracted from force profiles measured during the learning and test phases for each target and each subject separately. To quantify adaptation, during error-clamp trials, we measured the force subjects exerted at the time of peak velocity. For each subject, we normalized this force by the ideal force that the subjects should have had produced at that time. The ideal force is the velocity-dependent force that would counteract the force field perfectly. It is obtained by multiplying the velocity profile of the hand trajectory by the strength of the force field (13 N·m/s). The ratio between measured and ideal forces taken at the time of peak velocity was then multiplied by 100, which yields an adaptation index expressed as percentage of force. This index is equal to 100 for full adaptation and zero for no adaptation. To quantify generalization from T1 to T2 or T3, we divided the adaptation index computed for T2 or T3 by the adaptation index for T1 at the end of the learning (first three error-clamp trials to T1 at the start of the test period) and multiplied the result by 100. This normalization procedure yielded a generalization index in which 100 corresponds to full transfer of learning and zero to no transfer.
To investigate the influence of tDCS on the generalization patterns independently of the possible effect of tDCS on retention, we first focused on the start of the test period and averaged the generalization index over the first three error-clamp trials for each target and each subject separately. This measure was then submitted to an ANOVA with group and target (T2 and T3) as between- and within-subject factors, respectively. To analyze the effect of tDCS on the generalization index during the learning period, we averaged the generalization index over the three error-clamp trials (of each learning block) for each target separately. For each target, we ran a separate ANOVA with block (FF1 and FF2) and group as within- and between-subject factors, respectively. During the test period, we binned the error-clamp trials to a given target by groups of three. A multivariate ANOVA (Wilks' lambda statistic) with bin as within-subject factor (12 multivariate levels) and group as between-subject factor was then performed. To analyze the effect of tDCS on the kinematics during the learning period, we averaged the maximum perpendicular deviation and the initial perpendicular velocity (measured 100 ms after movement onset) over the second half of each set of 15 movements toward T1. We used these kinematic measures as the dependent variable in a multivariate ANOVA with group as a between-subject factor and set as a within-subject factor (six multivariate levels). Tukey's post hoc test was used to assess one-to-one differences. All statistical analyses were performed using Statistica (Statsoft).
We examined the rate of decay of the force output during the error-clamp trials (to T1) of the test period. This rate was estimated by fitting a single exponential of the form f(n) = a exp(−bn) to the dataset for each subject. In this equation, f(n)is the adaptation index on trial n. This continuous-domain equation can be well approximated in the discrete domain: f(0) = a and f(n + 1) = (1 − b)f(n), in which (1 − b) is an estimate of sensitivity of the memory to trial. Therefore, b is fraction of the force that is lost from one trial to the next. To assess between-group differences in rate of decay, we ran a bootstrap analysis on the parameter b with 10,000 resamplings (bootstrap function in Matlab).
Results
Volunteers adapted to a force field by reaching to a single target in one workspace (trained direction, T1) (Fig. 1A) and were tested for generalization in another workspace (T2 and T3). Figure 1C displays the raw forces that subjects produced immediately after completion of the training for T1 [i.e., when all movements were in error-clamp trials (Fig. 1B)]. The traces are presented as a percentage of the largest force exerted by manipulandum during the same trial (see Materials and Methods). During these error-clamp trials, subjects produced some force to oppose the expected perturbation. How much force was produced during an error-clamp trial to T1 is a proxy of how much subjects have learned. In contrast, for T2 and T3, the force produced during error-clamp trials is a measure of how much subjects transfered their learning from T1 to other targets as subjects had never experienced any perturbation during movements toward T2 or T3.
The similarity of the force profiles across various groups to T1 indicates that all the groups learned the task comparably and M1 stimulation did not affect performance toward T1 (Fig. 1C, top). Similarly, M1 stimulation (regardless of modality) did not alter the force patterns toward T2 (extrinsic generalization) (Fig. 1C, middle). However, both anodal and cathodal M1 stimulation appeared to increase the forces subjects produced to target T3 (Fig. 1C, bottom). In other words, M1 stimulation increased the transfer of learning from T1 to T3.
For each error-clamp trial, the force profile was quantified by the amount of force at peak velocity (Fig. 1C, dashed vertical line). The evolution of this force measure over the course of trials (Fig. 1D) illustrates that the increased force observed for T3 (Fig. 1D, right) lasted throughout the test period for both anodal and cathodal stimulation. In contrast, the force index did not exhibit any major differences between the three groups for T1 and T2 (Fig. 1D, left and middle).
Statistical analysis suggested that there were no significant effects of tDCS on forces that subjects produced for T1 during the learning period (Fig. 1D, left; Table 1). There were also no significant effects of tDCS for T1 during the test period that followed training (Table 1). Given the surprising absence of effect of tDCS on how fast subjects forgot [absence of interaction between bin number and group (Table 1)], we performed a second, more sensitive analysis to determine whether tDCS influenced the rate of decay during the test period. To do so, we fitted an exponential to the T1 adaptation index (Fig. 1D) during the test period (see Materials and Methods) and computed the corresponding confidence interval by bootstrapping. We obtained the following confidence intervals for the sensitivity to trials (parameter b): sham group, 0.0038–0.0123; cathodal M1 group, 0.0029– 0.0149; and anodal M1 group, 0.0023–0.0087. The large overlap between the different confidence intervals suggests that tDCS did not influence the decay rate. Note that this result also held true at the test location T3: sham group, 0.006–0.024; cathodal M1 group, 0.0042–0.0148; and anodal M1 group, 0.0028–0.0097. In summary, tDCS did not influence the learning or the retention of the behavior for target T1.
Table 1.
Results of the different ANOVAs used to compare the performance of the sham, anodal, and cathodal groups
| Factors | F statistics | p Value | |
|---|---|---|---|
| Force | |||
| T1 during learning | Group | F(2,24) = 0.34 | 0.71 |
| Block | F(1,24) = 6.34 | 0.02 | |
| Group × block | F(2,24) = 0.6 | 0.56 | |
| T1 during test | Group | F(2,24) = 0.78 | 0.47 |
| Bin | F(11,14) = 14.14 | 0.00001 | |
| Group × bin | F(22,28) = 1.27 | 0.27 | |
| Generalization index | |||
| First three movements | Group | F(2,24) = 3.15 | 0.06 |
| Target | F(1,24) = 25.31 | 0.00004 | |
| Group × target | F(2,24) = 4.3 | 0.025 | |
| T2 during learning | Group | F(2,24) = 0.16 | 0.86 |
| Block | F(1,24) = 1.13 | 0.3 | |
| Group × block | F(2,24) = 0.47 | 0.63 | |
| T2 during test | Group | F(2,24) = 0.14 | 0.87 |
| Bin | F(11,14) = 2.14 | 0.09 | |
| Group × bin | F(22,28) = 0.63 | 0.86 | |
| T3 during learning | Group | F(2,24) = 1.12 | 0.34 |
| Block | F(1,24) = 1.8 | 0.19 | |
| Group × block | F(2,24) = 2.97 | 0.07 | |
| T3 during test | Group | F(2,24) = 5.67 | 0.01 |
| Bin | F(11,14) = 4.21 | 0.007 | |
| Group × bin | F(22,28) = 0.77 | 0.73 | |
| Kinematic measures | |||
| Maximum perpendicular deviation | Group | F(2,24) = 1.17 | 0.33 |
| Set | F(5,20) = 17.41 | <0.00001 | |
| Group × set | F(10,40) = 0.97 | 0.48 | |
| Initial perpendicular velocity | Group | F(2,24) = 0.49 | 0.61 |
| Set | F(5,20) = 1.91 | 0.14 | |
| Group × set | F(10,40) = 0.57 | 0.83 |
Boldface highlights important comparisons.
To quantify how much people generalized their learning and whether M1 stimulation altered this generalization pattern, we measured the force produced for T2 or T3 as a fraction of force produced in T1 at the end of adaptation (first three error-clamp trials to T1 at the start of the test period) for each subject separately. This index (expressed as a percentage) is shown in Figure 2A for the first three movements of the test period to T2 and T3, and for the entire experiment in Figure 2, B and C. Focusing on the first three error-clamp trials to each target allowed us to measure differences in generalization independently of possible differences in retention.
Figure 2.
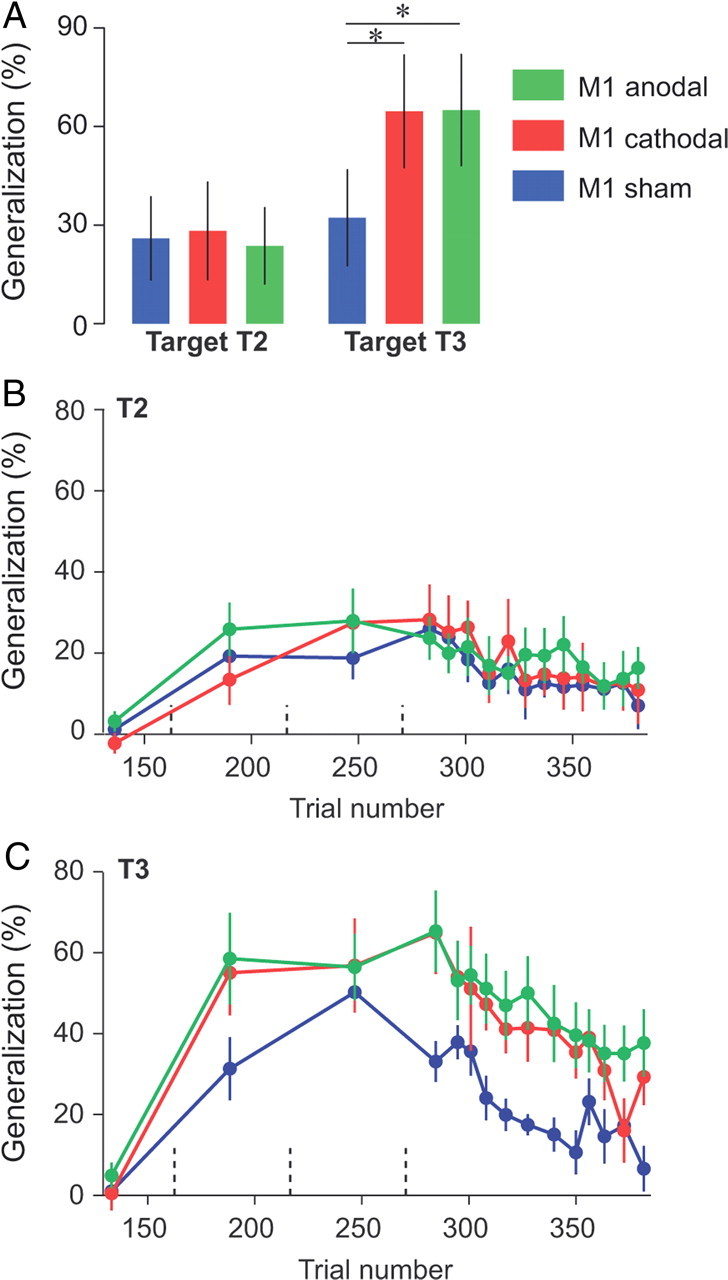
Effect of tDCS on the generalization index. A, Generalization index immediately following learning. The average force at tangential peak velocity for T2 and T3 across the first three channel trials was divided by the same force for T1 for each individual subject. Error bars are confidence intervals. B, C, Evolution of the generalization index over the course of error-clamp trials. Data were averaged over three error-clamp trials (bin size) and are presented for each target separately. Dashed vertical lines represent set breaks. Asterisks indicate significant differences. Error bars are SEM.
For the first three movements to T2 and T3 in the test period (Fig. 2A), we found that M1 stimulation enhanced generalization to T3, but not to T2. Indeed, for these trials, a repeated-measure ANOVA with the generalization index as dependent measure and group (sham, anodal, and cathodal) and target (T2 and T3) as between- and within-subject factors, respectively, revealed an interaction between group and targets (p = 0.025). This interaction was driven by a higher generalization for T3 in both the anodal and cathodal groups than in the sham group (p = 0.027 and p = 0.03, respectively). We did not find any significant effect of tDCS for T2 (both p > 0.95). Rather, tDCS of M1 appeared to increase the generalization to T3, i.e., M1 tDCS increased generalization in intrinsic coordinates. Importantly, this effect was independent of the polarity of tDCS.
This increased generalization to T3 but not T2 was evident throughout the entire learning and test periods (Fig. 2B,C). For example, for T2 (Fig. 2B), which quantifies generalization in extrinsic coordinates, we found no significant effect of tDCS during the learning or test periods (Table 1). However, for T3 (Fig. 2C, Table 1), we found a marginal interaction between groups and blocks during the learning period (p = 0.07) and a clear main effect of group during the test period (p = 0.01). In summary, the generalization index for T3 tended to increase faster during the learning period and stayed higher during the test period for both M1 tDCS groups than for the sham group, with no apparent effect of tDCS on the decay rate during the test period.
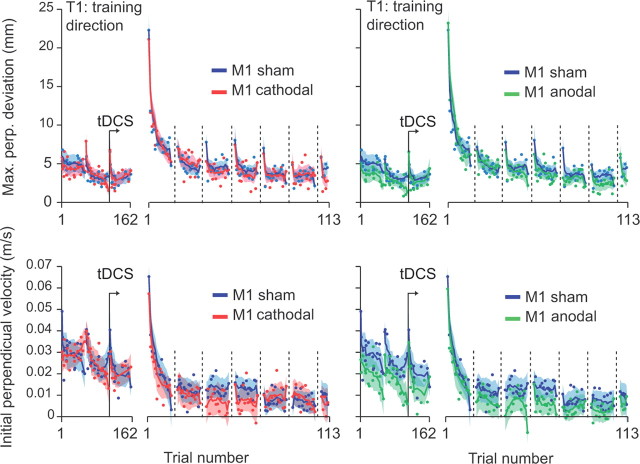
Figure 3 displays measures of kinematics (top, maximum perpendicular error; bottom, initial perpendicular velocity) that the subjects produced during baseline and learning periods. During the learning period, the force field was present for T1, whereas all trials for T2 and T3 were in error clamps. During the subsequent test period, movements to all targets were error-clamp trials. We found no significant effect of tDCS on maximum perpendicular error to T1 during the learning period (Fig. 3); the performance was nearly identical in the anodal, cathodal, and sham conditions. For example, note the slight forgetting that took place for T1 during the learning period (Fig. 3A, top, dashed vertical lines). This forgetting followed the movements to targets T2 and T3. The patterns of acquisition and forgetting were essentially identical in the three groups. To quantify the evolution of the kinematics over the course of learning, we measured the average maximum perpendicular deviation of the last seven field trials to T1 of each set of 18 movements during the learning block (see Materials and Methods, above). An ANOVA on this parameter with group (sham, anodal, and cathodal) as between-subject factor and set as within-subject factor did not reveal any influence of tDCS on the kinematics during learning (Table 1). The subjects from the three groups improved similarly throughout the different sets. During movements, both feedforward (planned) and feedback pathways influence the trajectory of the hand. Only the first 100–150 ms of the movements are likely devoid of any influence of the feedback pathway because of sensory delays. Therefore, the maximum perpendicular deviation measure (∼350 ms after movement onset) reflects the contribution of both feedforward and feedback pathways. To isolate the possible effect of tDCS on the feedforward pathway, we also analyzed the initial perpendicular velocity (Fig. 3B). Again, we did not find any evidence of tDCS on movement kinematics (Table 1). Therefore, although M1 tDCS increased generalization patterns in intrinsic coordinates (T3) (Figs. 1D, 2C), acquisition and decay rates for movement kinematics (Fig. 3) and forces (Fig. 1D) in the training T1 were unaffected.
Figure 3.
Measures of kinematics during baseline (1–162) and learning periods (1–113). Evolution of the maximum perpendicular (Max. perp.) deviation (top) and the perpendicular velocity 100 ms after movement onset across trials for cathodal versus sham groups (left) and anodal versus sham (right). Each point represents the average of all subjects for one trial and the solid lines represent a running average over 10 trials and interrupted every 15 trials during the field blocks.
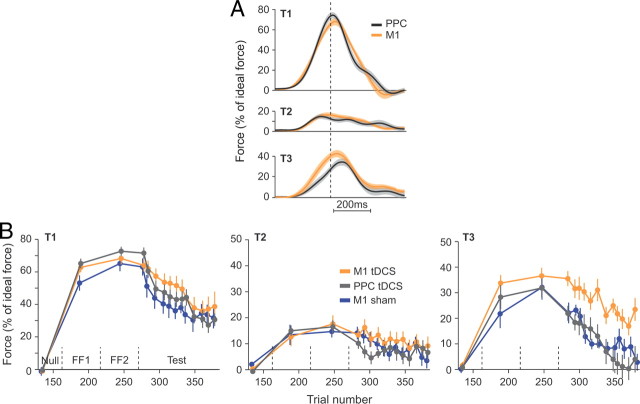
To test for specificity of our generalization results to M1, we recruited two additional groups in which tDCS were delivered over the PPC (anodal and cathodal) (Figs. 4, 5). As we found no main effect of tDCS polarity on performance (see below), we combined the anodal and cathodal groups together and represented the combined PPC tDCS group and the combined M1 tDCS group (Fig. 4B), although the polarity of the stimulation was taken into account in the statistical analyses (Table 2). The raw force profiles that subjects produced in the first three trials of the test period are shown in Figure 4A. As compared with M1 tDCS, PPC tDCS appeared to have no effect on extrinsic generalization (T2). In contrast, M1 tDCS produced a greater intrinsic generalization (T3) than PPC tDCS. The evolution of the force index over the course of trials (Fig. 4B) highlights the fact that the increased force observed for T3 immediately at the end of the learning (Fig. 4A) lasted throughout the test period. The data in Figure 4, A and B, also highlight the fact that the PPC and sham groups behaved very similarly.
Figure 4.
Site specificity of the tDCS effect: M1 versus PPC. A, Normalized force profiles recorded during the first three error-clamp trials to each of the three targets during the test block. Force profiles were aligned on peak tangential velocity and normalized with ideal force at peak tangential velocity. B, Evolution of the normalized force at peak tangential velocity over the course of error-clamp trials. Force data were averaged over three error-clamp trials (bin size) and are presented for each target separately. Data from the sham group (Fig. 1) were added for the sake of comparison between the sham and the PPC groups. Dashed vertical lines represent set breaks.
Figure 5.
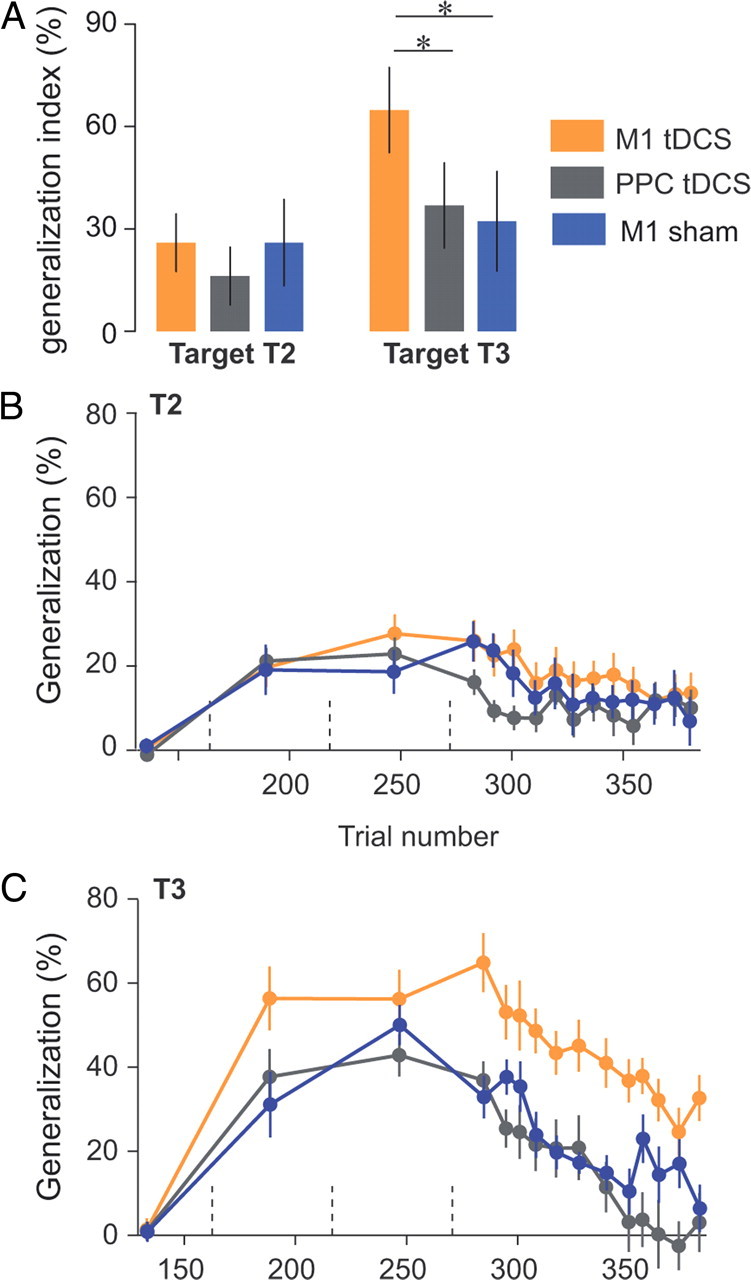
Site specificity of the tDCS effect: M1 versus PPC. A, Generalization patterns at the beginning of test period (same as Fig. 2A). Error bars are confidence intervals. B, C, Evolution of the generalization index over the course of error-clamp trials. Generalization index was averaged over three error-clamp trials (bin size) and are presented for each target separately. Data from the sham group (Fig. 2) were added for the sake of comparison between the sham and the PPC groups. Dashed vertical lines represent set breaks. Asterisks indicate significant differences.
Table 2.
Results of the different ANOVAs used to compare the performance of the anodal M1, cathodal M1, anodal PPC, and cathodal PPC groups
| Generalization index | Factors | F statistic | p Value |
|---|---|---|---|
| First three movements | Area | F(1,28) = 9.51 | 0.005 |
| Polarity | F(1,28) = 0.66 | 0.42 | |
| Target | F(1,28) = 53.75 | <0.00001 | |
| Area × polarity | F(1,28) = 0.22 | 0.64 | |
| Area × target | F(1,28) = 5.01 | 0.033 | |
| Polarity × target | F(1,28) = 0.37 | 0.55 | |
| Area × polarity × target | F(1,28) < 0.0001 | 0.998 | |
| T2 during learning | Area | F(1,28) = 1.01 | 0.32 |
| Polarity | F(1,28) = 0.12 | 0.74 | |
| Block | F(1,28) = 0.73 | 0.4 | |
| Area × polarity | F(1,28) = 0.26 | 0.62 | |
| Area × block | F(1,28) = 0.61 | 0.44 | |
| Polarity × block | F(1,28) = 0.65 | 0.43 | |
| Area × polarity × block | F(1,28) = 0.21 | 0.65 | |
| T2 during test | Area | F(1,28) = 2.27 | 0.14 |
| Polarity | F(1,28) = 0.6 | 0.45 | |
| Bin | F(11,18) = 2.45 | 0.044 | |
| Area × polarity | F(1,28) = 0.8 | 0.38 | |
| Area × bin | F(11,18) = 1.06 | 0.44 | |
| Polarity × bin | F(11,18) = 0.87 | 0.58 | |
| Area × polarity × bin | F(11,18) = 1.56 | 0.2 | |
| T3 during learning | Area | F(1,28) = 3.2 | 0.084 |
| Polarity | F(1,28) = 0.53 | 0.47 | |
| Block | F(1,28) = 0.74 | 0.4 | |
| Area × polarity | F(1,28) = 0.02 | 0.88 | |
| Area × block | F(1,28) = 1.6 | 0.22 | |
| Polarity × block | F(1,28) = 0.64 | 0.43 | |
| Area × polarity × block | F(1,28) = 0.02 | 0.89 | |
| T3 during test | Area | F(1,28) = 13.9 | 0.0009 |
| Polarity | F(1,28) = 0.2 | 0.65 | |
| Bin | F(11,18) = 12.37 | <0.00001 | |
| Area × polarity | F(1,28) = 0.12 | 0.28 | |
| Area × bin | F(11,18) = 0.97 | 0.5 | |
| Polarity × bin | F(11,18) = 1.03 | 0.46 | |
| Area × polarity × bin | F(11,18) = 0.97 | 0.56 |
Boldfance indicates •.
As in the comparison between sham and M1 tDCS groups, we quantified the patterns of generalization via a generalization index (Fig. 5). We initially focused on the first three error-clamp trials of the test period directed to T2 and T3. For these trials, we performed an ANOVA on the generalization index with polarity (anodal and cathodal) and area (M1 and PPC) as between-subject factors and target (T2 and T3) as a within-subject factor (Fig. 5A, Table 2). The ANOVA revealed an interaction between area and targets (p = 0.03). At the start of the test period, post hoc testing indicates that generalization index for T3 was higher during M1 stimulation than during PPC stimulation (p = 0.002). Again, we did not find any differences in generalization for T2 (p = 0.55). Finally, the polarity factor did not produce any significant main effects or interactions (Table 2). A more detailed view of the generalization index during learning and test periods is provided in Figure 5, B and C. M1 tDCS produced clearly increased forces in direction T3 during the whole test period (p = 0.0008). In contrast, for T2, we found no significant effect of area during the test period (Table 2).
The patterns of M1 versus PPC stimulation (Figs. 4, 5) resembled what we had previously observed in the comparison of M1 versus sham stimulation (Figs. 1, 2). Indeed, when we compared the PPC group to the sham group, we found that the two groups were indistinguishable; ANOVA on the generalization index at the start of the test period (similar to Figs. 2A, 5A) with groups (sham, PPC anodal, and PPC cathodal) as between-subject factor and target as within-subject factor did not reveal any significant effect of groups (main effect: F(2,24) = 1.01, p = 0.38; interaction: F(2,24) = 1.77, p = 0.2; PPC cathodal vs sham: T2, p = 0.99; T3, p = 0.91; PPC anodal vs sham: T2, p = 0.33; T3, p = 0.99; Tukey's post hoc). Similarly, kinematic measures from the PPC and sham groups during baseline and learning periods did not differ (data not shown). In summary, M1 tDCS stimulation but not PPC stimulation produced increased generalization in intrinsic coordinates, and this increase was independent of stimulation polarity.
Discussion
The driving hypothesis of our study was that enhancing plasticity of M1 by means of tDCS would leave a specific signature: alter the patterns of motor learning to increase generalization in the intrinsic coordinates of joints and muscles. Subjects made reaching movements in a force field in a training workspace and were tested in error-clamp trials in a test workspace (i.e., a new shoulder posture). In the error-clamp trials, a channel guided the reaching movements to the target, removing errors while allowing us to measure the forces that subjects produced against channel walls. Previous work has shown that in this task, in the test workspace, the forces are larger for movements that have the same joint rotations as the movement in the trained workspace (termed intrinsic generalization), and smaller for movements that have the same hand motion as the movement in the trained workspace (termed extrinsic generalization). The use of a single target for force-field adaptation yields a behaviorally narrow generalization function (Mattar and Ostry, 2007), allowing us to minimize the spillover of generalization between the extrinsic and intrinsic directions. A previous study confirms that, in this paradigm, those two directions are separable (Haswell et al., 2009). We found that when tDCS was applied to M1 (regardless of its polarity), it did not alter the adaptation patterns in the training workspace. However, it increased generalization in intrinsic coordinates, while leaving no effects on the extrinsic generalization patterns.
To test for the spatial specificity of the observed effects, we applied tDCS to the PPC. This area is involved in the voluntary control of movements (Andersen and Cui, 2009) and is anatomically connected to M1 (Strick and Kim, 1978; Zarzecki et al., 1978; Koch et al., 2007), but unlike M1, does not represent movements in the intrinsic coordinates of joints and muscles (Scott et al., 1997). We found that unlike M1, tDCS over PPC had no effect on generalization patterns. This does not mean that PPC does not play a role in extrinsic generalization. Indeed, there is no direct relationship between the absence of effect of tDCS on a given area during a particular task and the involvement of the same area in the same task. For instance, modulation of the supplementary motor area or the dorsolateral prefrontal cortex by tDCS does not influence learning in a serial reaction time task (Nitsche et al., 2003), although both areas are involved in this task (Willingham, 1998).
The patterns of generalization during force-field adaptation have been widely investigated behaviorally and theoretically (Shadmehr and Mussa-Ivaldi, 1994; Shadmehr and Moussavi, 2000; Malfait et al., 2002; Criscimagna-Hemminger et al., 2003; Donchin et al., 2003; Hwang et al., 2003, 2006; Malfait and Ostry, 2004; Shadmehr, 2004; Krakauer et al., 2006; Berniker and Kording, 2008; Kluzik et al., 2008; Haswell et al., 2009), but the neural substrates underlying this generalization remains poorly understood. The consistent finding has been that adaptation generalizes strongly in intrinsic coordinates, and a long-standing hypothesis has been that this generalization reflects learning in a network in which the neurons primarily encode movements in the coordinates of joints and muscles. Here, we uncovered evidence that agents that modulate motor cortex plasticity and facilitate motor learning (Reis et al., 2009) elicit greater generalization in intrinsic coordinates. This change in generalization could result either from a larger recruitment of cells during the learning (increase in population number) or from a larger modification of the activity of the cells involved in the learning (increase in modulation). Therefore, our results are a useful test of the hypothesis that the behaviorally quantified generalization patterns are due to the tuning properties of cells in a specific cortical network.
Our task involved learning of a new relationship between motor commands and their proprioceptive and visual-sensory consequences. In this way, the learning was fundamentally different from studies that consider repetition-dependent plasticity (Classen et al., 1998; Galea and Celnik, 2009), in which the focus is on repetition of simple movements like thumb flexion. The effects of M1 tDCS that we observed are consistent with enhancing repetition-dependent plasticity in the coordinates of muscles but not in the extrinsic coordinates of the task. However, in our study, this enhancement was exhibited at a new arm posture, and not merely in the same position in which the task was practiced. This is crucial because a change in arm posture produces fundamental changes in the tuning of cells in the motor cortex (Caminiti et al., 1990, 1991). Note that the arm posture is very carefully controlled in all the repetition-dependent plasticity experiments (Classen et al., 1998), as posture affects the results of brain stimulation (Wassermann et al., 1998).
One implication of our work is that in patient populations in which reach adaptation is abnormal, the specific abnormality may be a signature of the locus of the neural disorder. For example, in children with autistic spectrum disorders, reach adaptation in force fields is comparable to typically developing children (Gidley Larson et al., 2008), but produces a greater than normal generalization in intrinsic coordinates (Haswell et al., 2009). Our inference has been that movements of these children rely more heavily on networks that represent movements in the intrinsic coordinates of joints and muscles, e.g., the motor cortex. This conjecture is consistent with recent neuroimaging results that show increased motor cortex white matter volume in autistic children (Mostofsky et al., 2007).
Our work produced two novel and somewhat surprising results: first, the effect of tDCS on M1 was not associated with the polarity of the stimulation; and second, despite the dense connections between some subregions of PPC and M1, the effect of tDCS was specific to M1. These results provide insights in the use of tDCS to study brain function, as elaborated below.
Our study produced the surprising observation that there were no behavioral differences in the modality of tDCS stimulation: both anodal and cathodal tDCS of M1 increased generalization in intrinsic coordinates. Previous work had found positive effects of tDCS during motor learning for only anodal tDCS (Galea and Celnik, 2009; Hunter et al., 2009; Reis et al., 2009). What might explain our modality-independent result? A single session of motor learning strengthens horizontal excitatory connections in M1 (Rioult-Pedotti et al., 1998), weakens inhibitory connections (Floyer-Lea et al., 2006), and induces formation of postsynaptic dendritic spines (Xu et al., 2009; Yang et al., 2009). This rewiring of M1 results in the formation of new cortical ensembles (Komiyama et al., 2010) through micro-rewiring (DeBello, 2008). A significant component of this micro-rewiring is an unmasking of existing excitatory connections because of weakening of existing inhibitory connections. For example, during motor learning, there is a decrease in GABA concentration in M1 (Floyer-Lea et al., 2006), and this decrease is a necessary component of the micro-rewiring (Jacobs and Donoghue, 1991; Rioult-Pedotti et al., 1998). Indeed, drugs that act as GABA agonists tend to inhibit formation of cortical LTP (Hess and Donoghue, 1994), resulting in reduced plasticity in the motor cortex (Bütefisch et al., 2000; McDonnell et al., 2007). In humans, drugs that act as GABA agonists produce impairments in reach adaptation in force fields (Donchin et al., 2002). Therefore, GABA is a key neurotransmitter involved in M1 short-term plasticity.
Long periods of both anodal and cathodal tDCS of human M1 reduce GABA concentrations (Stagg et al., 2009b; Stagg and Nitsche, 2011). This reduction can promote unmasking of excitatory connections in M1. Indeed, a decrease in GABA concentration promotes short-term modulation of potentiation but does not elicit long-term potentiation (Fritsch et al., 2010), which can only be elicited via NMDA-dependent processes. Anodal tDCS but not cathodal tDCS acts on NMDA-dependent processes (Fritsch et al., 2010). Therefore, both anodal and cathodal tDCS can increase potentiation of synapses, but this potentiation is maintained longer for anodal stimulation. Accordingly, motor learning experiments in which there have been positive effects of both anodal and cathodal stimulation have revealed these effects during the period of stimulation (Nitsche et al., 2003; this study), whereas motor learning tasks that have found a positive effect of anodal stimulation have found their effects during a period after the stimulation (Cogiamanian et al., 2008; Galea et al., 2009). This explanation is in accordance with the tDCS literature: anodal tDCS influences offline changes in skill level but not cathodal tDCS (Reis et al., 2009) and cathodal tDCS aftereffect is short lasting compared with anodal tDCS (Nitsche and Paulus, 2000). We speculate that the similarity of behavioral effects produced by anodal and cathodal stimulation might arise from short-term potentiation elicited by tDCS on GABA.
A second surprisingly component of our result was the regional specificity of the effects of tDCS. Whereas M1 tDCS increased generalization in intrinsic coordinates, PPC tDCS had no effect. Modeling studies indicate that peak current is located immediately below the tDCS electrode and spreads widely throughout the brain (Miranda et al., 2006; Wagner et al., 2007a,b; Sadleir et al., 2010). Imaging studies draw similar conclusions with respect to the spatial influence of tDCS (Baudewig et al., 2001; Lang et al., 2005; Kwon et al., 2008; Stagg et al., 2009a). Therefore, spatial selectivity of tDCS needs to be addressed directly to confirm the origin of the effect. In the present study, we found that the patterns of generalization after M1 and PPC tDCS stimulation differed (Fig. 5), although some subregions of PPC are densely connected to M1 (Strick and Kim, 1978; Zarzecki et al., 1978).
We found that M1 stimulation affected generalization patterns but had no effect on adaptation rates. A recent study that also examined effects of tDCS on reach adaptation suggested that tDCS of M1 increased adaptation rates (Hunter et al., 2009). That result, however, appears to be mainly due to effects of tDCS on movement speed, which were not controlled in that study but were controlled in our task. Transcranial direct-current stimulation of the motor cortex has been associated with increased retention of a newly learned behavior.
In conclusion, we demonstrated that a process that likely modulates M1 plasticity influences the association between proprioceptive errors and motor commands, increasing generalization patterns in the intrinsic coordinates of joints and muscles. This finding is relevant for rehabilitation procedures, which aim at maximizing the learning about the limb (i.e., in intrinsic coordinates) and not the learning about the training environment (i.e., in extrinsic coordinates). Therefore, in addition to increasing plasticity and allowing further improvement in motor function after stroke (Schlaug and Renga, 2008; Schlaug et al., 2008), we have shown that tDCS can enhance the generalization of motor learning in the intrinsic coordinates of the limb.
Footnotes
This work was supported by National Institutes of Health Grant NS057814. J.J.O.d.X. is a fellow of the Belgian American Educational Foundation and is also supported by the Fondation pour la Vocation (Belgium) and an internal research grant (Fonds Spéciaux de Recherche) of the Université catholique de Louvain (Belgium).
The authors report no competing financial interests.
References
- Andersen RA, Cui H. Intention, action planning, and decision making in parietal-frontal circuits. Neuron. 2009;63:568–583. doi: 10.1016/j.neuron.2009.08.028. [DOI] [PubMed] [Google Scholar]
- Arce F, Novick I, Mandelblat-Cerf Y, Israel Z, Ghez C, Vaadia E. Combined adaptiveness of specific motor cortical ensembles underlies learning. J Neurosci. 2010;30:5415–5425. doi: 10.1523/JNEUROSCI.0076-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baudewig J, Nitsche MA, Paulus W, Frahm J. Regional modulation of BOLD MRI responses to human sensorimotor activation by transcranial direct current stimulation. Magn Reson Med. 2001;45:196–201. doi: 10.1002/1522-2594(200102)45:2<196::aid-mrm1026>3.0.co;2-1. [DOI] [PubMed] [Google Scholar]
- Berniker M, Kording K. Estimating the sources of motor errors for adaptation and generalization. Nat Neurosci. 2008;11:1454–1461. doi: 10.1038/nn.2229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bock O, Thomas M. Proprioception plays a different role for sensorimotor adaptation to different distortions. Hum Mov Sci. 2011 doi: 10.1016/j.humov.2010.10.007. [DOI] [PubMed] [Google Scholar]
- Bütefisch CM, Davis BC, Wise SP, Sawaki L, Kopylev L, Classen J, Cohen LG. Mechanisms of use-dependent plasticity in the human motor cortex. Proc Natl Acad Sci U S A. 2000;97:3661–3665. doi: 10.1073/pnas.050350297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caminiti R, Johnson PB, Urbano A. Making arm movements within different parts of space: dynamic aspects in the primate motor cortex. J Neurosci. 1990;10:2039–2058. doi: 10.1523/JNEUROSCI.10-07-02039.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caminiti R, Johnson PB, Galli C, Ferraina S, Burnod Y. Making arm movements within different parts of space: the premotor and motor cortical representation of a coordinate system for reaching to visual targets. J Neurosci. 1991;11:1182–1197. doi: 10.1523/JNEUROSCI.11-05-01182.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Classen J, Liepert J, Wise SP, Hallett M, Cohen LG. Rapid plasticity of human cortical movement representation induced by practice. J Neurophysiol. 1998;79:1117–1123. doi: 10.1152/jn.1998.79.2.1117. [DOI] [PubMed] [Google Scholar]
- Criscimagna-Hemminger SE, Donchin O, Gazzaniga MS, Shadmehr R. Learned dynamics of reaching movements generalize from dominant to nondominant arm. J Neurophysiol. 2003;89:168–176. doi: 10.1152/jn.00622.2002. [DOI] [PubMed] [Google Scholar]
- Cogiamanian F, Marceglia S, Ardolino G, Barbieri S, Priori A. Improved isometric force endurance afrer transcranial direct current stimulation over the human motor cortical areas. Eur J Neurosci. 2007;26:242–249. doi: 10.1111/j.1460-9568.2007.05633.x. [DOI] [PubMed] [Google Scholar]
- DeBello WM. Micro-rewiring as a substrate for learning. Trends Neurosci. 2008;31:577–584. doi: 10.1016/j.tins.2008.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donchin O, Sawaki L, Madupu G, Cohen LG, Shadmehr R. Mechanisms influencing acquisition and recall of motor memories. J Neurophysiol. 2002;88:2114–2123. doi: 10.1152/jn.2002.88.4.2114. [DOI] [PubMed] [Google Scholar]
- Donchin O, Francis JT, Shadmehr R. Quantifying generalization from trial-by-trial behavior of adaptive systems that learn with basis functions: theory and experiments in human motor control. J Neurosci. 2003;23:9032–9045. doi: 10.1523/JNEUROSCI.23-27-09032.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Floyer-Lea A, Wylezinska M, Kincses T, Matthews PM. Rapid modulation of GABA concentration in human sensorimotor cortex during motor learning. J Neurophysiol. 2006;95:1639–1644. doi: 10.1152/jn.00346.2005. [DOI] [PubMed] [Google Scholar]
- Fritsch B, Reis J, Martinowich K, Schambra HM, Ji Y, Cohen LG, Lu B. Direct current stimulation promotes BDNF-dependent synaptic plasticity: potential implications for motor learning. Neuron. 2010;66:198–204. doi: 10.1016/j.neuron.2010.03.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galea JM, Celnik P. Brain polarization enhances the formation and retention of motor memories. J Neurophysiol. 2009;102:294–301. doi: 10.1152/jn.00184.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gandolfo F, Li C, Benda BJ, Schioppa CP, Bizzi E. Cortical correlates of learning in monkeys adapting to a new dynamical environment. Proc Natl Acad Sci U S A. 2000;97:2259–2263. doi: 10.1073/pnas.040567097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gidley Larson JC, Bastian AJ, Donchin O, Shadmehr R, Mostofsky SH. Acquisition of internal models of motor tasks in children with autism. Brain. 2008;131:2894–2903. doi: 10.1093/brain/awn226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haswell CC, Izawa J, R Dowell LR, H Mostofsky SH, Shadmehr R. Representation of internal models of action in the autistic brain. Nat Neurosci. 2009;12:970–972. doi: 10.1038/nn.2356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herwig U, Satrapi P, Schönfeldt-Lecuona C. Using the international 10–20 EEG system for positioning of transcranial magnetic stimulation. Brain Topogr. 2003;16:95–99. doi: 10.1023/b:brat.0000006333.93597.9d. [DOI] [PubMed] [Google Scholar]
- Hess G, Donoghue JP. Long-term potentiation of horizontal connections provides a mechanism to reorganize cortical motor maps. J Neurophysiol. 1994;71:2543–2547. doi: 10.1152/jn.1994.71.6.2543. [DOI] [PubMed] [Google Scholar]
- Hunter T, Sacco P, Nitsche MA, Turner DL. Modulation of internal model formation during force field-induced motor learning by anodal transcranial direct current stimulation of primary motor cortex. J Physiol. 2009;587:2949–2961. doi: 10.1113/jphysiol.2009.169284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang EJ, Shadmehr R. Internal models of limb dynamics and the encoding of limb state. J Neural Eng. 2005;2:S266–278. doi: 10.1088/1741-2560/2/3/S09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang EJ, Donchin O, Smith MA, Shadmehr R. A gain-field encoding of limb position and velocity in the internal model of arm dynamics. PLoS Biol. 2003;1:E25. doi: 10.1371/journal.pbio.0000025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang EJ, Smith MA, Shadmehr R. Adaptation and generalization in acceleration-dependent force fields. Exp Brain Res. 2006;169:496–506. doi: 10.1007/s00221-005-0163-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobs KM, Donoghue JP. Reshaping the cortical motor map by unmasking latent intracortical connections. Science. 1991;251:944–947. doi: 10.1126/science.2000496. [DOI] [PubMed] [Google Scholar]
- Kluzik J, Diedrichsen J, Shadmehr R, Bastian AJ. Reach adaptation: what determines whether we learn an internal model of the tool or adapt the model of our arm? J Neurophysiol. 2008;100:1455–1464. doi: 10.1152/jn.90334.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koch G, Fernandez Del Olmo M, Cheeran B, Ruge D, Schippling S, Caltagirone C, Rothwell JC. Focal stimulation of the posterior parietal cortex increases the excitability of the ipsilateral motor cortex. J Neurosci. 2007;27:6815–6822. doi: 10.1523/JNEUROSCI.0598-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komiyama T, Sato TR, O'Connor DH, Zhang YX, Huber D, Hooks BM, Gabitto M, Svoboda K. Learning-related fine-scale specificity imaged in motor cortex circuits of behaving mice. Nature. 2010;464:1182–1186. doi: 10.1038/nature08897. [DOI] [PubMed] [Google Scholar]
- Krakauer JW, Mazzoni P, Ghazizadeh A, Ravindran R, Shadmehr R. Generalization of motor learning depends on the history of prior action. PLoS Biol. 2006;4:e316. doi: 10.1371/journal.pbio.0040316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwon YH, Ko MH, Ahn SS, Kim YH, Song JC, Lee CH, Chang MC, Jang SH. Primary motor cortex activation by transcranial direct current stimulation in the human brain. Neurosci Lett. 2008;435:56–59. doi: 10.1016/j.neulet.2008.02.012. [DOI] [PubMed] [Google Scholar]
- Lang N, Siebner HR, Ward NS, Lee L, Nitsche MA, Paulus W, Rothwell JC, Lemon RN, Frackowiak RS. How does transcranial DC stimulation of the primary motor cortex alter regional neuronal activity in the human brain? Eur J Neurosci. 2005;22:495–504. doi: 10.1111/j.1460-9568.2005.04233.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li CS, Padoa-Schioppa C, Bizzi E. Neuronal correlates of motor performance and motor learning in the primary motor cortex of monkeys adapting to an external force field. Neuron. 2001;30:593–607. doi: 10.1016/s0896-6273(01)00301-4. [DOI] [PubMed] [Google Scholar]
- Malfait N, Ostry DJ. Is interlimb transfer of force-field adaptation a cognitive response to the sudden introduction of load? J Neurosci. 2004;24:8084–8089. doi: 10.1523/JNEUROSCI.1742-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malfait N, Shiller DM, Ostry DJ. Transfer of motor learning across arm configurations. J Neurosci. 2002;22:9656–9660. doi: 10.1523/JNEUROSCI.22-22-09656.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattar AA, Ostry DJ. Modifiability of generalization in dynamics learning. J Neurophysiol. 2007;98:3321–3329. doi: 10.1152/jn.00576.2007. [DOI] [PubMed] [Google Scholar]
- McDonnell MN, Orekhov Y, Ziemann U. Suppression of LTP-like plasticity in human motor cortex by the GABAB receptor agonist baclofen. Exp Brain Res. 2007;180:181–186. doi: 10.1007/s00221-006-0849-0. [DOI] [PubMed] [Google Scholar]
- Miranda PC, Lomarev M, Hallett M. Modeling the current distribution during transcranial direct current stimulation. Clin Neurophysiol. 2006;117:1623–1629. doi: 10.1016/j.clinph.2006.04.009. [DOI] [PubMed] [Google Scholar]
- Mostofsky SH, Burgess MP, Gidley Larson JC. Increased motor cortex white matter volume predicts motor impairment in autism. Brain. 2007;130:2117–2122. doi: 10.1093/brain/awm129. [DOI] [PubMed] [Google Scholar]
- Nitsche MA, Paulus W. Excitability changes induced in the human motor cortex by weak transcranial direct current stimulation. J Physiol. 2000;527:633–639. doi: 10.1111/j.1469-7793.2000.t01-1-00633.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nitsche MA, Schauenburg A, Lang N, Liebetanz D, Exner C, Paulus W, Tergau F. Facilitation of implicit motor learning by weak transcranial direct current stimulation of the primary motor cortex in the human. J Cogn Neurosci. 2003;15:619–626. doi: 10.1162/089892903321662994. [DOI] [PubMed] [Google Scholar]
- Poggio T, Fahle M, Edelman S. Fast perceptual learning in visual hyperacuity. Science. 1992;256:1018–1021. doi: 10.1126/science.1589770. [DOI] [PubMed] [Google Scholar]
- Reis J, Schambra HM, Cohen LG, Buch ER, Fritsch B, Zarahn E, Celnik PA, Krakauer JW. Noninvasive cortical stimulation enhances motor skill acquisition over multiple days through an effect on consolidation. Proc Natl Acad Sci U S A. 2009;106:1590–1595. doi: 10.1073/pnas.0805413106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rioult-Pedotti MS, Friedman D, Hess G, Donoghue JP. Strengthening of horizontal cortical connections following skill learning. Nat Neurosci. 1998;1:230–234. doi: 10.1038/678. [DOI] [PubMed] [Google Scholar]
- Sadleir RJ, Vannorsdall TD, Schretlen DJ, Gordon B. Transcranial direct current stimulation (tDCS) in a realistic head model. Neuroimage. 2010;51:1310–1318. doi: 10.1016/j.neuroimage.2010.03.052. [DOI] [PubMed] [Google Scholar]
- Scheidt RA, Reinkensmeyer DJ, Conditt MA, Rymer WZ, Mussa-Ivaldi FA. Persistence of motor adaptation during constrained, multi-joint, arm movements. J Neurophysiol. 2000;84:853–862. doi: 10.1152/jn.2000.84.2.853. [DOI] [PubMed] [Google Scholar]
- Schlaug G, Renga V. Transcranial direct current stimulation: a noninvasive tool to facilitate stroke recovery. Expert Rev Med Devices. 2008;5:759–768. doi: 10.1586/17434440.5.6.759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlaug G, Renga V, Nair D. Transcranial direct current stimulation in stroke recovery. Arch Neurol. 2008;65:1571–1576. doi: 10.1001/archneur.65.12.1571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott SH, Kalaska JF. Reaching movements with similar hand paths but different arm orientations. I. Activity of individual cells in motor cortex. J Neurophysiol. 1997;77:826–852. doi: 10.1152/jn.1997.77.2.826. [DOI] [PubMed] [Google Scholar]
- Scott SH, Sergio LE, Kalaska JF. Reaching movements with similar hand paths but different arm orientations. II. Activity of individual cells in dorsal premotor cortex and parietal area 5. J Neurophysiol. 1997;78:2413–2426. doi: 10.1152/jn.1997.78.5.2413. [DOI] [PubMed] [Google Scholar]
- Shadmehr R. Generalization as a behavioral window to the neural mechanisms of learning internal models. Hum Mov Sci. 2004;23:543–568. doi: 10.1016/j.humov.2004.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadmehr R, Moussavi ZM. Spatial generalization from learning dynamics of reaching movements. J Neurosci. 2000;20:7807–7815. doi: 10.1523/JNEUROSCI.20-20-07807.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadmehr R, Mussa-Ivaldi FA. Adaptive representation of dynamics during learning of a motor task. J Neurosci. 1994;14:3208–3224. doi: 10.1523/JNEUROSCI.14-05-03208.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sing GC, Joiner WM, Nanayakkara T, Brayanov JB, Smith MA. Primitives for motor adaptation reflect correlated neural tuning to position and velocity. Neuron. 2009;64:575–589. doi: 10.1016/j.neuron.2009.10.001. [DOI] [PubMed] [Google Scholar]
- Sparing R, Thimm M, Hesse MD, Küst J, Karbe H, Fink GR. Bidirectional alterations of interhemispheric parietal balance by non-invasive cortical stimulation. Brain. 2009;132:3011–3020. doi: 10.1093/brain/awp154. [DOI] [PubMed] [Google Scholar]
- Stagg CJ, Nitsche MA. Physiological basis of transcranial direct current stimulation. Neuroscientist. 2011;17:37–53. doi: 10.1177/1073858410386614. [DOI] [PubMed] [Google Scholar]
- Stagg CJ, O'Shea J, Kincses ZT, Woolrich M, Matthews PM, Johansen-Berg H. Modulation of movement-associated cortical activation by transcranial direct current stimulation. Eur J Neurosci. 2009a;30:1412–1423. doi: 10.1111/j.1460-9568.2009.06937.x. [DOI] [PubMed] [Google Scholar]
- Stagg CJ, Best JG, Stephenson MC, O'Shea J, Wylezinska M, Kincses ZT, Morris PG, Matthews PM, Johansen-Berg H. Polarity-sensitive modulation of cortical neurotransmitters by transcranial stimulation. J Neurosci. 2009b;29:5202–5206. doi: 10.1523/JNEUROSCI.4432-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strick PL, Kim CC. Input to primate motor cortex from posterior parietal cortex (area 5). I. Demonstration by retrograde transport. Brain Res. 1978;157:325–330. doi: 10.1016/0006-8993(78)90035-5. [DOI] [PubMed] [Google Scholar]
- Thoroughman KA, Shadmehr R. Learning of action through adaptive combination of motor primitives. Nature. 2000;407:742–747. doi: 10.1038/35037588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner T, Valero-Cabre A, Pascual-Leone A. Noninvasive human brain stimulation. Annu Rev Biomed Eng. 2007a;9:527–565. doi: 10.1146/annurev.bioeng.9.061206.133100. [DOI] [PubMed] [Google Scholar]
- Wagner T, Fregni F, Fecteau S, Grodzinsky A, Zahn M, Pascual-Leone A. Transcranial direct current stimulation: a computer-based human model study. Neuroimage. 2007b;35:1113–1124. doi: 10.1016/j.neuroimage.2007.01.027. [DOI] [PubMed] [Google Scholar]
- Wassermann EM, Tormos JM, Pascual-Leone A. Finger movements induced by transcranial magnetic stimulation change with hand posture, but not with coil position. Hum Brain Mapp. 1998;6:390–393. doi: 10.1002/(SICI)1097-0193(1998)6:5/6<390::AID-HBM11>3.0.CO;2-W. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willingham DB. A neuropsychological theory of motor skill learning. Psychol Rev. 1998;105:558–584. doi: 10.1037/0033-295x.105.3.558. [DOI] [PubMed] [Google Scholar]
- Xu T, Yu X, Perlik AJ, Tobin WF, Zweig JA, Tennant K, Jones T, Zuo Y. Rapid formation and selective stabilization of synapses for enduring motor memories. Nature. 2009;462:915–919. doi: 10.1038/nature08389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang G, Pan F, Gan WB. Stably maintained dendritic spines are associated with lifelong memories. Nature. 2009;462:920–924. doi: 10.1038/nature08577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zarzecki P, Strick PL, Asanuma H. Input to primate motor cortex from posterior parietal cortex (area 5). II. Identification by antidromic activation. Brain Res. 1978;157:331–335. doi: 10.1016/0006-8993(78)90036-7. [DOI] [PubMed] [Google Scholar]