Skip to main content
PMC home page
Heredity logoLink to Heredity
. 2011 Nov 30;108(5):515–520. doi: 10.1038/hdy.2011.115

Genotype-dependent responses to levels of sibling competition over maternal resources in mice

R Hager 1,*, J M Cheverud 2, J B Wolf 3
PMCID: PMC3330683  PMID: 22126849

Abstract

Research on phenotypic plasticity has often focused on how a given genotype responds to the changing physical environments such as temperature or diet. However, for many species the social environment has an equally important role because of competition for resources. During early development, the level of competition for limited (maternally provided) resources will often depend critically on the number of siblings. Therefore, competition among siblings should drive the evolution of genes that allow flexible responses to realized levels of competition and maternal resource availability. However, it is unknown whether genetically based differences between individuals exist in their response to the social environment that affect their future development. Using a quantitative trait locus approach in an experimental population of mice we demonstrate that effects of sibling number on body weight depend on individual genotype at seven loci, over and above the general negative litter size effect. Overall, these litter size-by-genotype interactions considerably modified the degree to which increasing litter size caused reduced weight. For example at one locus this effect leads to a 7% difference in body weight at week 7 between individuals experiencing the extremes of the normal range of litter sizes in our population (five to nine litter mates). The observed interaction between genotype and the competitive environment can produce differences in body weight that are similar in magnitude to the main effect of litter size on weight. Our results show that different genotypes respond to the social environment differentially and that interaction effects of genotype with litter size can be as important as genotype-independent effects of litter size.

Keywords: sibling competition, mice, QTL, litter size, complex trait, plasticity

Introduction

Phenotypic plasticity describes the ability of organisms to respond to changes in the environment (West-Eberhard, 2003) and is generally referred to as flexibility when phenotypic change is reversible and as developmental plasticity when it is not (Stearns, 1989; Piersma and Drent, 2003). Plasticity may be adaptive if the range of phenotypes shown by a given genotype across environments, or the reaction norm, increases fitness when compared with a single phenotype in these environments (Via & Lande, 1985; DeWitt et al., 1998). Given the obvious fitness advantages of plasticity, studies sought to elucidate associated costs and constraints as plasticity has not been as universally observed as one might have expected (Snell-Rood et al., 2010). A large part of this research focused on how a given genotype responds to changes in the physical environment such as diet or temperature. Yet, for many species the social environment is certainly of equal importance in determining individual fitness and explaining trait variation. How do given genotypes respond to changing social environments? Further, research into costs and constraints of plasticity requires an understanding of the underlying genetics as pleiotropy is an important source of evolutionary constraint, and because genetic variation is the prerequisite for evolution (for example, Scheiner, 1993; DeWitt et al., 1998; Auld et al., 2010). In this study, we tackle these issues and investigate whether genetic variants can respond differentially to a changing social environment in an experimental population of mice by focusing on effects of the competitive environment on body weight.

An adaptive response to changing levels of competition may be favored by natural selection as the associated cost/benefit trade-off will change as well (for example, Stockley and Parker, 2002; Wright and Leonard, 2002). This seems particularly relevant to early development because levels of competition may be indicative of available resources during this crucial developmental period (Gyekis et al., 2011). Sibling competition over access to resources is common in species that provide significant parental care and have multiple offspring in a litter or brood (Mock and Parker, 1997). In mammals with multiple offspring per litter, sibling competition is manifested largely in scramble competition, rather than contest competition, and is thus crucially dependent on the number of competitors (MacNair and Parker, 1979; Mock and Parker, 1997; Hager and Johnstone, 2005). In mice the number of litter mates is rarely greater than the number of nipples (10), but access is often limited to one side of the female and offspring remain staunchly attached until all milk supply is depleted (Gilbert, 1995). Moreover, teats differ in their productivity (Barnard et al., 1998), exacerbating sibling competition over the most productive nipples (usually the anterior ones). Females have been shown to increase milk supply as litter size increases (Knight et al., 1986), which may mitigate competition on average but, at the same time, per capita milk supply may decrease and thus competition will increase.

The number of siblings at birth may serve as an indicator of expected postnatal sibling competition for maternal resources, and the number of litter mates at weaning may be indicative of postweaning competition for resources. In rodents, the number of competitors may decrease or increase before weaning because pups may die or fall victim to prey, or another female may produce a litter in the same nest (several females often litter together in mice, König, 1997) and pups are nursed by either female (König, 1994). Consequently, levels of competition and associated costs (Trivers, 1974; Clutton-Brock, 1991; Godfray, 1991) can increase or decrease postnatally. The key question we address here is whether any response to this change in the competitive environment has a genetic basis that differs between individuals or populations.

Our aim for this study was to investigate whether bodyweight and growth during the first 10 weeks of life is affected by the number of litter mates at birth or at weaning and whether these effects depend on individual genotype. Body weight is a key indicator of resource utilization during development and often a good predictor of fitness under natural conditions where weight is associated with higher reproductive potential, advantages in intra-sexual competition and female mate choice. Using a quantitative trait locus (QTL) design, we first investigate main effects of litter size, independent of genotype, and then establish whether individual genotype interacts with the number of litter mates at birth or at weaning. This enables us to investigate genetic variation in the response to the competitive environment, manifested in differential responses to the number of competitors for different genotypes. We predict that genotypes show different responses to the postnatal competitive environment.

Methods

Our study population is an intercross of two inbred mouse strains that were selected for (their)divergent bodyweight at day 60, the Large (LG/J) and Small (SM/J) strains (Goodale, 1938; MacArthur, 1944). The two strains differ in litter size: although LG/J has an average litter size of 6.1, SM/J has an average litter size of 5.0, a difference of 18% Ehrich et al., 2003). For our analysis we used the F2 and F3 generation that originated from the matings of ten LG/J males to ten SM/J females resulting in 52 F1 individuals. These F1 individuals were randomly mated to generate 510 F2 mice, which, after random mating, produced 1632 individuals of the F3 generation in 200 full-sib families. At birth half litters were cross-fostered in 158 families (Kramer et al., 1998). Thus, the size of cross-fostered litters may be larger or smaller compared with litter size at birth. It is important to bear in mind that such differences in litter size can cause effects from as early as week 1 body weight and not just after weaning. In this analysis we focus on body weights taken once weekly from week 1 to week 10, as well as pre-weaning (week 1–3) and postweaning growth (week 3–10) as phenotypes. We have previously analyzed these traits for main effects considering the autocorrelation between the weights, splitting the growth period in two, early and late (Hager et al., 2009b). A genome scan using such a multivariate approach will pick up QTL that affect growth in this particular period. However, a disadvantage of this approach is that loci that affect only few traits will be missed and given the pleiotropic nature of most QTL does not yield a picture of when during development QTL begin to show their effect, when they decrease and stop. We have thus analyzed the above traits separately, following Wolf et al. (2008).

All F2 and F3 mice were genotyped at 353 polymorphic single-nucleotide polymorphic markers that were evenly spaced (4–5 cM apart) across the genome, except where the two strains are monomorphic, using the Illumina Golden Gate assay (Wolf et al., 2008). Haplotypes were reconstructed in Pedphase using the Integer Linear Programming (ILP) algorithm (Li and Jiang, 2005) to produce a set of unordered haplotypes for the F2 generation and a set of ordered (by allelic parent-of-origin) haploytpes for the F3. We distinguish four ordered genotypes denoted LL, LS, SL, SS (paternal/maternal allele) with the L allele originating from the LG/J strain and the S allele from the SM/J strain.

We first analyzed the effects of two litter size parameters on growth and development: litter size at birth (LSB; that is, size of the litter born by the dam) and litter size at weaning (LSW). Using the Mixed Procedure in SAS (SAS version 9.1.3; SAS Institute, Cary, NC, USA) we fitted a mixed model using maximum likelihood to model the trait as a function of two litter size parameters with biological and foster family (dam, nurse) as random effect class variables to control for shared environmental effects. Our aim was to establish which litter size parameter, if any, affected weekly weights and growth.

We then used the marker loci to scan the genome for QTL that interacted with either litter size at birth or with litter size at weaning to affect weekly weights and growth. In a first step we assigned the four ordered genotypes at the marker loci additive (a), dominance (d), and parent-of-origin (i) genotypic index scores following Wolf et al. (2008). These index scores are arrayed in a genetic design matrix to relate variation in the mean phenotypes (that is, genotypic values) of each of the ordered genotypes (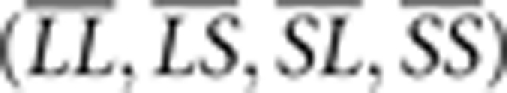Inline graphic) to a vector of genetic effects:

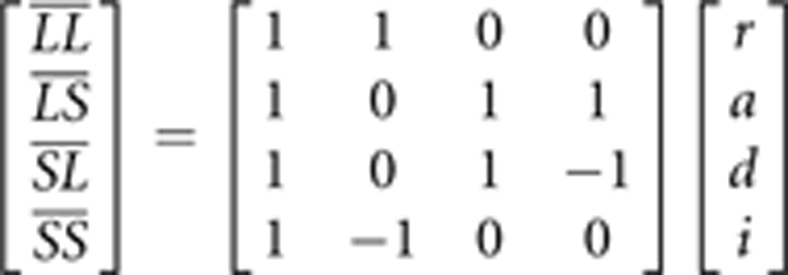graphic file with name hdy2011115e1.jpg

This linear equation can be used to solve for the genetic effects by inverting the design matrix and multiplying it by the vector of genotypic values to yield a definition of the genetic effects (in terms of genotypic values):

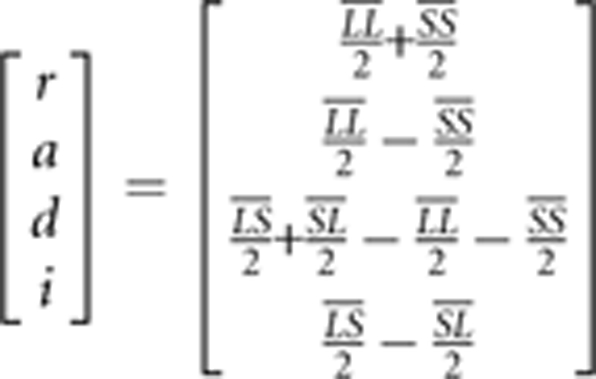graphic file with name hdy2011115e2.jpg

where r is the reference point for the model (the mid-point between homozygotes), the additive effect is defined as half the difference in the mean phenotype of the two homozygotes, the dominance effect is the difference of the mean heterozygote phenotype from the mean of the homozygotes, and the genomic imprinting effect is half the difference in mean phenotype between the two reciprocal heterozygotes (Wolf et al., 2008).

The genotypic index scores for a locus were used in a linear mixed model fitted by maximum likelihood using the Mixed Procedure in SAS. In the first of these models (Model 1) we included the three genetic effects (a, d, i) and the two litter size parameters (LSB and LSW) as main effects, and the six pair-wise interactions between the genetic and litter size parameters. The biological and foster family (dam, nurse) were included as random effect class variables to control for the background influences of other loci and shared environmental effects that can inflate significance values. Cross-fostering was not included in this model as we have previously shown that there is no main effect of cross-fostering in this data set (Hager et al., 2009a). The fixed effects in Model (1) can be expressed as a linear model where Yj is the trait value (ten weekly weights or growth) of individual j and Xa(j), Xd(j), Xi(j) are the genotypic index scores for the direct genetic effects (additive, dominance and imprinting) of individual j:

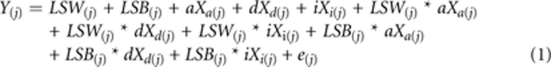graphic file with name hdy2011115e3.jpg

To generate a test for the overall effect of a locus we generated a likelihood ratio test by subtracting the −2 log likelihood from Model 1 generated by the Mixed Procedure from the −2 log likelihood from a reduced model that included only LSB, LSW, and the same random effects as in Model (1). This difference in the −2 log likelihoods of the two models (reduced model minus full model, which always gives a positive value) is approximately χ2 distributed with nine degrees of freedom (that is, the two models differ by a total of nine model terms). The probability values calculated from the χ2 distribution (with 9 d.f.) were then transformed into a log probability ratio (LPR) in order to make them comparable to LOD scores (LPR=–log10[probability]).

To distinguish between interactions of genotype with litter size at birth or at weaning we fitted two further models with the same random effects as in Model (1), the three main genetic effects, the two litter size parameters and either the interactions of genotype and litter size at birth (2) or genotype and litter size at weaning (3):

graphic file with name hdy2011115e4.jpg
graphic file with name hdy2011115e5.jpg

Models (2) and (3) were then individually compared (using the –2 log likelihood values as described above) to a further reduced model (Model 4) that contained only the three genetic effects and the two litter size parameters but not the interactions:

graphic file with name hdy2011115e6.jpg

Thus, the only difference between Models (2) and (3) is the type of interaction effect included. Using Models (2), (3) and (4) we generated two tests of interaction effects. The comparison of Model (2) to Model (4) (−2 log likelihood of Model 4 minus that of Model 2) provides a chi-square test (with 3 d.f.) of the interaction of the three genetic effects with litter size at birth. The comparison of Model (3) to Model (4) (−2 log likelihood of Model 4 minus that of Model 3) provides a chi-square test (with 3 d.f.) of the interaction of the three genetic effects with litter size at weaning. Depending on which of the interaction effects (with litter size at weaning or at birth) was significant, we identified whether litter size at birth or at weaning is causal to the interaction effect.

To generate significance thresholds we used the effective number of markers method, which is based on the eigenvalues of the marker correlation matrix (Li and Ji, 2005). This approach calculates the number of independent tests in a genome scan and adjusts significance using a Bonferroni correction. Briefly, one first calculates the correlation matrix for the marker loci and then estimates the eigenvalues of the correlation matrix. The integer parts of the eigenvalues are replaced by 1 when the value is ⩾1 and 0 when the value is <1. This integer part is then added to the original decimal part to yield the effective number of markers contained in that eigenvalue. For example, an eigenvalue of 3.75 yields 1.75 effective markers, whereas an eigenvalue of 0.75 yields 0.75 effective markers. The sum of these converted values represents the effective number of markers, which we used in the Sidak equation to generate the threshold for genome-wide tests (that is, we used the effective number of markers on the whole genome to generate thresholds). We have previously demonstrated that the thresholds obtained are very similar to those obtained through computationally intensive simulation (Hager et al., 2008a). We thus determined the thresholds for all traits and identified significant loci when the overall locus LPR value or the interaction effect LPR value exceeded the genome-wide threshold. To investigate pleiotropic effects we included QTL effects whenever the effect of a given locus is significant at the pointwise threshold (P<0.05; LPR>1.3) assuming the QTL has exceeded the genome-wide significance threshold for a different trait (Wolf et al., 2008).

We have previously established that parent-of-origin dependent effects on offspring phenotypes may be caused by either maternal genetic effects or genomic imprinting (Hager et al., 2008b). In essence, differences in maternal genotype can cause differences between phenotypes of heterozygous offspring and thus cause the same parent-of-origin effect patterns as those caused by genomic imprinting effects. This also applies to the appearance of additive effects due to the genetic correlation of offspring with their parents at a locus (where, at a particular locus, the correlation is 1/2). Thus, a locus expressed in the mother may affect her offspring's phenotype, but as offspring inherit one allele from their mother it appears as if that locus directly affects offspring phenotype. This scenario applies to non-cross-fostered animals only as the autocorrelation between maternal and offspring genotype is broken in cross-fostered animals. We therefore tested all loci with a significant interaction to determine whether the interaction effect could be explained by a maternal genetic effect or was associated with a change in the direct effect of a locus. This was achieved by using a mixed model to test whether the parent-of-origin-dependent effect or additive effect differed significantly between individuals reared by homozygous versus heterozygous mothers (Hager et al., 2009a).

Results

We first analyzed main effects of litter size, independent of any genotype effects. The average litter size at birth in our experimental population was 8.54 with a range from 4 to 13 pups per litter. All traits were highly significantly affected by litter size at weaning (that is, postnatal litter size), including week 1 body weight, whereas litter size at birth only affected weeks 1 to 3. Invariably, litter size effects were negative such that average individual weight decreased as litter size increased. Litter size at birth had a standardized effect of –0.15 for week 1 weight, decreasing to –0.07 for week 3. To illustrate the magnitude of these effects we compare litter sizes of five and nine individuals at week 1. Pups born into the larger litter would then be 14.38% or 0.61 g smaller compared with those born with five litter mates (average weight at week 1 is 4.23 g). Unsurprisingly, the effects of litter size at weaning are greatest for week 2 and week 3 (NB: cross-fostering took place at birth) with standardized estimates of −0.55 and −0.43. However, these effects extend all the way to week 10 (standardized estimate −0.19), at which time pups born into litters of nine are still 2.6% smaller on average compared with those born into litters of five.

After having established the main effects of litter size, we performed a genome scan across all 19 autosomes for loci that showed a significant interaction between genetic (additive or dominance) or epigenetic (genomic imprinting) effects and litter size at birth or weaning on weight and growth. We denote loci that show interaction effects with litter size at birth LSBy.z and loci interacting with litter size at weaning LSWy.z. LSB refers to litter size at birth, LSW to litter size at weaning, y identifies the chromosome and z the individual QTL on that chromosome in case several QTL are found on one chromosome. For all loci we confirmed that any imprinting or additive interaction effect is not caused by a maternal genetic effect.

Five loci on separate chromosomes (chromosomes 1, 4, 6, 11 and 16) showed an interaction with litter size at birth (Table 1). Two loci showed interactions with additive effects, two loci interacted with dominance and one with imprinting effects. One might have expected that the interaction of genotype with litter size at birth predominantly affects early weights; however, late weights are equally affected and LSB16.1 only affected body weight from week 5 onward. Turning to loci that interacted with litter size at weaning, we identified two QTL located on chromosomes 10 and 15 (Table 1). With the exception of LSB11.1 all loci affected several traits showing clearly when during development their effects become manifested, when they are greatest and when they cease to show detectable effects (see LPR values in Table 1). A locus on chromosome 10 showed an unusual pattern in that additive interactions with litter size at birth influenced pre-weaning growth, whereas dominance interactions affected weeks 4–10 (at the same locus).

Table 1. Interaction of QTL with LSB and LSW.

QTL Location
 Confidence interval Trait Full LPR Interaction effect (estimate) Test
  cM Mb          
LSB1.1 42.66 93.21 87.02–99.36 Week 1 4.18 a (0.036) 1.58
      87.02–99.36 Week 2 6.85 a (0.063) 2.98
      87.02–99.36 Week 3 3.30 a (0.078) 1.98
LSB4.1 37.28 84.31 78.87–87.93 Week 4 5.11 −a (−0.161) 2.43
        Week 5 5.02 −a (−0.172) 1.85
        Week 6 6.06 −a (−0.195) 1.72
LSB6.1 29.25 65.37 105.62–117.19 Week 4 7.79 −i (−0.131) 1.69
      94.76–134.72 Week 5 7.44 −i (−0.181) 1.99
      94.76–134.72 Week 6 7.21 −i (−0.242) 2.43
      94.76–134.72 Week 7 6.76 −i (−0.302) 2.82
      94.76–134.72 Week 8 6.50 −i (−0.320) 2.64
      94.76–134.72 Week 9 6.97 −i (−0.406) 3.50
      94.76–134.72 Week 10 5.68 −i (−0.384) 2.86
      94.76–134.72 Growth 3–10 4.99 −i (−0.003.) 2.44
LSW10.1 49.16 111.3 99.22–117.08 Week 4 2.66 −d (−0.223) 2.62
      99.22–128.85 Week 5 4.59 −d (−0.265) 2.41
      99.22–117.08 Week 6 3.86 −d (−0.263) 1.79
      99.22–128.85 Week 7 3.97 −d (−0.295) 1.73
      99.22–117.08 Week 8 4.88 −d (−0.370) 2.12
      99.22–117.08 Week 9 4.68 −d (−0.383) 1.99
      99.22–117.08 Week 10 4.72 −d (−0.443) 2.30
LSB11.1 11.90 24.47 60.48–72.28 Week 4 2.37 d (0.243) 3.14
LSW15.1 30.19 69.47 62.91–76.75 Week 2 3.49 d (0.074) 2.71
      56.81–83.18 Week 3 4.63 d (0.127) 3.15
      62.91–76.75 Week 4 2.16 d (0.162) 1.66
LSB16.1 44.61 46.92 36.99–50.54 Week 5 2.16 d (−0.336) 3.73
      36.99–50.54 Week 6 2.84 d (−0.454) 4.64
      36.99–50.54 Week 7 3.32 d (−0.559) 5.27
      36.99–50.54 Week 8 2.90 d (−0.613) 5.14
      36.99–50.54 Week 9 2.72 d (−0.624) 4.70
      36.99–50.54 Week 10 2.95 d (−0.713) 5.36
      36.99–50.54 Growth 310 3.81 d (−0.714) 6.10
Open in a new tab

Abbreviations: cM, centiMorgans; LPR, log probability ratio; LSB, litter size at birth; LSW, litter size at weaning; Mb, megabases; QTL, quantitative trait locus. [2]The first column identifies the QTL followed by the genomic location in F2 equivalent cM and the coordinates in Mb based on mouse genome build 36. This is followed by the traits affected. The column ‘Full LPR' lists the overall model LPR for the test of main effects and interaction effects. Under ‘Interaction effect' we specify which of the three effects showed an interaction with the sign of effect, where ‘a' refers to additive, ‘d' to dominance and ‘i' to imprinting effects. In parentheses we give the interaction estimates. The column headed ‘Test' gives the LPR for the interaction effect. ‘Growth 13' and ‘Growth 310' refer to preweaning and postweaning growth, respectively. Confidence intervals (Mb) for the interaction QTL positions were determined using a one LOD drop (using LPR values) following Lander & Botstein (1989). As a locus may affect several traits, the LPR for the interaction effects may be different and hence the confidence intervals.

Effects of litter size interactions

The nature of the interaction can be examined by looking at the litter-size effect in individuals with specific alleles at a locus, which can be inferred from the sign of the interaction given in Table 1. Overall, average body weight decreases with increasing litter size regardless of genotype at all loci. However, the degree to which increasing litter size leads to a reduction in weight across genotype varies and is manifested in the interaction. A positive interaction of additive effects and litter size (+a × LS) means that LL homozygotes show a smaller reduction in weight compared with SS homozygotes with increasing values of the litter size parameter (either litter size at birth, LSB, or litter size at weaning, LSW, respectively). The reverse applies to a negative interaction effect (−a × LS). Positive dominance interactions indicate that heterozygotes showed a smaller reduction in weight compared with homozygotes with increasing litter size values. Again, the reverse applies to negative dominance interaction effects. Finally, for positive imprinting interactions, SL heterozygotes showed a stronger decrease in their weight compared with LS heterozygotes with increasing litter size.

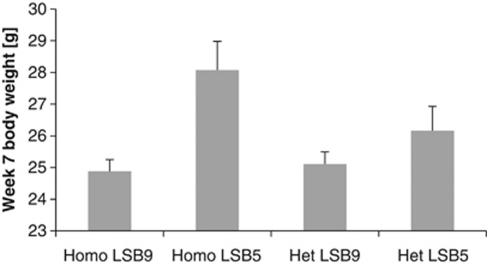
Overall, the loci show both positive and negative interactions with litter size for additive and dominance effects. Thus, no general pattern can be established across all traits for the direction of effect for a given genotype such that, for example, LL homozygotes always increased in weight with increasing litter size. However, we can illustrate the effects of the interactions for body weight, for example comparing homozygotes and heterozygotes at LSB16.1 where we assume a difference in litter size of four, for example, comparing homozygous and heterozygous pups born into litters of five versus those born in litters of nine litter mates (about the average litter size in our population). Figure 1 shows the average phenotype of both homo- and heterozygotes for week 7 bodyweight when litter size at birth was nine next to their average weights when litter size was five. We see that while homozygotes showed a reduction in weight of 11.3%, from their average weight with litter size of nine to their average weight with litter size of five, the corresponding value for heterozygotes was only 4%. The differences between genotypes in their weight increase when comparing litters of greater size difference. For example, focusing on differences between the two heterozygotes (at LSB6.1) and comparing litters of five and 11 pups, we find that SL heterozygotes would be over 11% smaller, whereas LS heterozygotes would be only ∼5% smaller in litters of 11 compared with litters of five litter mates.

Figure 1.

Figure 1

Open in a new tab

Difference in average week-7 bodyweight for the homozygotes and heterozygotes at LSB16.1 shown for two different litter sizes at birth. The graph illustrates that homozygotes suffer a greater reduction in weight than heterozygotes for the same litter size difference. Error bars indicate the s.e.m.

Discussion

Although the effects of litter size on growth and levels of competition have been demonstrated in different systems (Mock and Parker, 1997; Stockley and Parker, 2002), we show that such effects can depend on the genotype of individuals at specific loci. This advances on previous studies that generally demonstrated a genetic basis for such interactions (for example, Merilä and Fry, 1998). In addition, our study confirms the existence of a substantial main effect of litter size on weight such that average weight was inversely proportional to litter size (for example, Reading, 1966; Epstein, 1978). The effects of litter size on weight decrease over time but even at week 10 are still significant: body weight at week 10 is affected by litter size at weaning with a standardized effect of −0.19, which would cause a reduction of 2.6% of weight comparing pups with nine litter mates at weaning to those that had five litter mates. This suggests that, although compensation for lower body weight caused by being born in larger litters is possible, such compensatory growth is only partial and, consequently, a negative effect in terms of smaller body size remains even weeks later. Our previous work analyzed main genetic and genomic imprinting effects on weight and growth in this population (Hager et al., 2009b) and we can thus compare these loci with those found in the present study. We had discovered 18 main-effect loci on 13 chromosomes that show additive, dominance or imprinting effects (Hager et al., 2009b, Table 1 therein). Although none are identical to the interaction loci we found in this present study, three of the interaction loci (LSB4.1, LSW10.1 and LSW15.1) are located directly adjacent to main effect loci (adi4.1, adi10.1 and adi15.1). The locus on chromosome 4 shows an additive main effect on weights and growth and an interaction of the additive effect with litter size at birth. Loci on the other chromosomes, however, do not show the same main and interaction effects and it seems thus less likely that they could be the same. In conclusion, with one exception on chromosome 4 (LSB4.1), the main effect QTL are different from those showing the interaction with litter size suggesting that the litter size interaction QTL described here are more specifically responding to the social environment, unlike the main effect QTL.

Overall, we detected five loci with effects on weight and growth that were dependent on (that is, showed an interaction with) the number of siblings at birth, and two that were dependent on litter size at weaning. Such genotype by (social) environment interactions may enable genotypes to respond differentially to changes in environmental conditions in relation to sibling competition and resource availability. The differential effects of the prenatal (uterine) competitive environment (that is, pre-natal litter size) on postnatal growth could arise from differential genetic priming of offspring to expectations of future resource availability and sibling competition. For example, an individual born into a small litter might expect lower competition levels because of adequate milk supply for all litter mates, whereas individuals born into large litters may expect high levels of competition. Only a direct investigation of competitive behavior of pups cross-fostered into litters that differ in their size at birth and at weaning would allow a confirmation of this hypothesis.

We were able to clearly demonstrate that genetic variants modulate individual responses to changes in the competitive environment, in essence phenotypic plasticity in social environments. However, whether or not the observed effects are adaptive is more difficult to ascertain. If the effects were adaptive and selection favored larger body size, then we might expect genotypes adapted to larger litter size to show better performance (that is, larger body weight) as litter size increases compared with genotypes adapted to smaller litter size. However, we do not find a consistent allele effect in that, for example, individuals being homozygous for the L allele show a smaller reduction in weight (or increased fitness) compared with SS homozygotes. Instead, as indicated by the sign of the interaction for additive effects in Table 1, being homozygous for the L allele results in a negative effect at one locus (LSB1.1), but a positive effect at another (LSB4.1). For example, one might have expected that in the strain that produces larger litters (LG/J has an average litter size of 6.1 compared with an average litter size of SM/J of 5.0, a difference of 18% Ehrich et al., 2003), levels of competition are higher than in strains with smaller litters and thus LG/J pups were to some degree selected to develop in a more competitive environment. The L alleles might thus confer a competitive advantage compared with S, reflected in increased fitness of LL homozygotes when litters increase in size. This is not the case. Similarly inconsistent is the pattern of interaction for dominance interactions, which overall suggests non-adaptive reasons for the observed plasticity.

One explanation for the absence of clear adaptive benefits of plasticity is that the loci may have pleiotropic effects on other traits that are not plastic (DeWitt et al., 1998). Although this remains an untested possibility, it seems more likely that the condition of litter size change experienced in our experimental population is outside the range of conditions in the original populations. Given that the average litter size and range in our population exceeds that in both pure strains by about three individuals, levels of competition may be different as may be the costs (Chappel and Bachman, 2002).

The key result emerging from our study is that a given genotype results in different phenotypes depending on the number of siblings. This genotype by social environment interaction can be similar in magnitude as the strong main effects of litter size (which results in considerable reduction in weight with increasing litter size) and thus should be ascribed biological importance equivalent to the main effect. In contrast to litter size main effects, the genotype by litter size interactions do not show a consistent effect across genotypes. Therefore, although genetic variation to respond to changes in the competitive environment exists, the observed phenotypic plasticity in our study may be regarded as non-adaptive at present.

Data archiving

Data have been deposited at Dryad: doi:10. 5061/dryad.8qq3p0d8.

Acknowledgments

This research was supported by grants from the Biotechnology and Biological Sciences Research Council, UK (BBSRC), an Underwood Fellowship from the BBSRC and NIH grant DK055736. RH is supported by a NERC Research Fellowship.

The authors declare no conflict of interest.

References

  1. Auld JR, Agrawal AA, Releya RA. Re-evaluating the costs and limits of adaptive phenotypic plasticity. Proc R Soc Lond B. 2010;277:503–511. doi: 10.1098/rspb.2009.1355. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Barnard CJ, Behnke JM, Gage AR, Brown H, Smithurst PR. Maternal effects on the development of social rank and immunity trade-offs in male mice (Mus musculus) Proc R Soc Lond B. 1998;265:2087–2093. doi: 10.1098/rspb.1998.0544. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Chappel MA, Bachman GC.2002Energetic costs of beggingIn: Wright J, Leonard ML (eds).The Evolution of Begging Kluwer Academic Press: Doordrecht; 143–162. [Google Scholar]
  4. Clutton-Brock TH. The Evolution of Parental Care. Princeton University Press: Princeton; 1991. [Google Scholar]
  5. DeWitt TJ, Sih A, Wilson DS. Costs and limits of phenotypic plasticity. Trends Evol Ecol. 1998;13:77–81. doi: 10.1016/s0169-5347(97)01274-3. [DOI] [PubMed] [Google Scholar]
  6. Ehrich TH, Kenney JP, Vaughn TT, Pletscher S, Cheverud JM. Diet, obesity and hyperglycemia in LG/J and SM/J mice. Obesity. 2003;11:1400–1410. doi: 10.1038/oby.2003.189. [DOI] [PubMed] [Google Scholar]
  7. Epstein HT. The effect of litter size on weight gain in mice. J Nutr. 1978;108:120–123. doi: 10.1093/jn/108.1.120. [DOI] [PubMed] [Google Scholar]
  8. Gilbert AN. Tenacious nipple attachment in rodents: the sibling competition hypothesis. Anim Behav. 1995;50:881–891. [Google Scholar]
  9. Godfray HCJ. Signalling of need by offspring to their parents. Nature. 1991;352:328–330. [Google Scholar]
  10. Goodale HD. A study of the inheritance of body weight in the albino mouse by selection. J Heredity. 1938;29:101–112. [Google Scholar]
  11. Gyekis J, Blizard DA, Stout JT, Vandenbergh DJ, McClearn GE, Hager R. Genetic and maternal effects on offspring mortality in mice. Evol Biol. 2011;38:434–440. [Google Scholar]
  12. Hager R, Cheverud JM, Leamy LJ, Wolf JB. Sex dependent imprinting effects on complex traits in mice. BMC Evol Biol. 2008a;8:e303. doi: 10.1186/1471-2148-8-303. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hager R, Cheverud JM, Wolf JB. Maternal effects as the cause of parent-of-origin-dependent effects that mimic genomic imprinting. Genetics. 2008b;178:1755–1762. doi: 10.1534/genetics.107.080697. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Hager R, Cheverud JM, Wolf JB. Change in maternal environment induced by cross-fostering alters genetic and epigenetic effects on complex traits in mice. Proc R Soc Lond B. 2009a;276:2949–2954. doi: 10.1098/rspb.2009.0515. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hager R, Cheverud JM, Wolf JB. Relative contribution of additive, dominance and imprinting effects to phenotypic variation in body size and growth between divergent selection lines of mice. Evolution. 2009b;65:1118–1128. doi: 10.1111/j.1558-5646.2009.00638.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hager R, Johnstone RA. Differential growth of own and alien young in mixed litters of mice: a role for genomic imprinting. Ethology. 2005;111:705–711. [Google Scholar]
  17. Knight CH, Maltz E, Docherty AH. Milk yield and composition in mice: effects of litter size and lactation number. Comp Biochem Physiol. 1986;84A:127–133. doi: 10.1016/0300-9629(86)90054-x. [DOI] [PubMed] [Google Scholar]
  18. König B. Components of lifetime reproductive success in communally and solitarily nursing house mice – a laboratory study. Behav Ecol Sociobiol. 1994;34:275–283. [Google Scholar]
  19. König B. Cooperative care of young in mammals. Naturwissenschaften. 1997;84:95–104. doi: 10.1007/s001140050356. [DOI] [PubMed] [Google Scholar]
  20. Kramer MG, Vaughn TT, Pletscher LS, King-Ellison K, Adams E, Erikson C, et al. Genetic variation in body weight gain and composition in the intercross of Large (LG/J) and Small (SM/J) inbred strains of mice. Genet Mol Biol. 1998;21:211–218. [Google Scholar]
  21. Lander ES, Botstein D. Mapping Mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics. 1989;121:185–199. doi: 10.1093/genetics/121.1.185. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Li J, Ji L. Adjusting multiple testing in multilocus analyses using the eigenvalues of a correlation matrix. Heredity. 2005;95:221–227. doi: 10.1038/sj.hdy.6800717. [DOI] [PubMed] [Google Scholar]
  23. Li J, Jiang T. Computing the minimum recombinant haplotype configuration from incomplete genotype data on a pedigree by integer linear programming. J Comp Biol. 2005;12:719–739. doi: 10.1089/cmb.2005.12.719. [DOI] [PubMed] [Google Scholar]
  24. Macarthur J. Genetics of body size and related characters. I. Selection of small and large races of the laboratory mouse. Am Nat. 1944;78:142–157. [Google Scholar]
  25. MacNair MR, Parker GA. Models of parent-offspring conflict. III. Intra-brood conflict. Anim Behav. 1979;27:1202–1209. [Google Scholar]
  26. Merilä J, Fry JD. Genetic variation and causes of genotype-environment interaction in the body size of blue tit (Parus caeruleus) Genetics. 1998;148:1233–1244. doi: 10.1093/genetics/148.3.1233. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Mock DW, Parker GA. The Evolution of Sibling Rivalry. Oxford University Press: Oxford; 1997. [Google Scholar]
  28. Piersma T, Drent J. Phenotypic plasticity and the evolution of organismal design. Trends Ecol Evol. 2003;18:228–233. [Google Scholar]
  29. Reading AJ. Effects of parity and litter size on the birth weight of inbred mice. J Mamm. 1966;47:111–114. [PubMed] [Google Scholar]
  30. Scheiner SM. Genetics and evolution of phenotypic plasticity. Annu Rev Ecol Syst. 1993;24:35–68. [Google Scholar]
  31. Snell-Rood EC, van Dyken JD, Cruickshank T, Wade MJ, Moczek AP. Toward a population genetic framework of developmental evolution: the costs, limits and consequences of phenotypic plasticity. Bioessays. 2010;32:71–82. doi: 10.1002/bies.200900132. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Stearns SC. The evolutionary significance of phenotypic plasticity. Bioscience. 1989;39:436–445. [Google Scholar]
  33. Stockley P, Parker GA. Life history consequences of mammal sibling rivalry. Proc Natl Acad Sci USA. 2002;99:12932–12937. doi: 10.1073/pnas.192125999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Trivers R. Parent-offspring conflict. Am Zool. 1974;14:249–264. [Google Scholar]
  35. Via S, Lande R. Genotype–environment interaction and the evolution of phenotypic plasticity. Evolution. 1985;39:505–522. doi: 10.1111/j.1558-5646.1985.tb00391.x. [DOI] [PubMed] [Google Scholar]
  36. West-Eberhard MJ. Developmental Plasticity and Evolution. Oxford University Press: Oxford; 2003. [Google Scholar]
  37. Wright J, Leonard ML. Begging. Kluwer: Amsterdam; 2002. [Google Scholar]
  38. Wolf JB, Cheverud JM, Roseman C, Hager R. Genome-wide analysis reveals a complex pattern of genomic imprinting in mice. PLoS Genet. 2008;4:e1000091. doi: 10.1371/journal.pgen.1000091. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES