Skip to main content
PMC home page
Heredity logoLink to Heredity
. 2011 Oct 26;108(5):490–499. doi: 10.1038/hdy.2011.103

The relationship between parental genetic or phenotypic divergence and progeny variation in the maize nested association mapping population

H-Y Hung 1, C Browne 2, K Guill 2, N Coles 1, M Eller 1, A Garcia 2, N Lepak 2, S Melia-Hancock 2, M Oropeza-Rosas 1, S Salvo 1, N Upadyayula 3, E S Buckler 2,4,5, S Flint-Garcia 2,6, M D McMullen 2,6, T R Rocheford 3,7, J B Holland 1,2,*
PMCID: PMC3330692  PMID: 22027895

Abstract

Appropriate selection of parents for the development of mapping populations is pivotal to maximizing the power of quantitative trait loci detection. Trait genotypic variation within a family is indicative of the family's informativeness for genetic studies. Accurate prediction of the most useful parental combinations within a species would help guide quantitative genetics studies. We tested the reliability of genotypic and phenotypic distance estimators between pairs of maize inbred lines to predict genotypic variation for quantitative traits within families derived from biparental crosses. We developed 25 families composed of ∼200 random recombinant inbred lines each from crosses between a common reference parent inbred, B73, and 25 diverse maize inbreds. Parents and families were evaluated for 19 quantitative traits across up to 11 environments. Genetic distances (GDs) among parents were estimated with 44 simple sequence repeat and 2303 single-nucleotide polymorphism markers. GDs among parents had no predictive value for progeny variation, which is most likely due to the choice of neutral markers. In contrast, we observed for about half of the traits measured a positive correlation between phenotypic parental distances and within-family genetic variance estimates. Consequently, the choice of promising segregating populations can be based on selecting phenotypically diverse parents. These results are congruent with models of genetic architecture that posit numerous genes affecting quantitative traits, each segregating for allelic series, with dispersal of allelic effects across diverse genetic material. This architecture, common to many quantitative traits in maize, limits the predictive value of parental genotypic or phenotypic values on progeny variance.

Keywords: genetic variance, heritability, QTL mapping

Introduction

Geneticists have abundant choices of parents to use for mapping population development, and may have numerous extant mapping populations from which to choose for mapping quantitative trait loci (QTL) (Young, 1996). For example, the publicly available maize nested association mapping (NAM) population consists of 25 recombinant inbred line (RIL) families derived from crosses between the reference parent B73 and 25 diverse inbred lines (McMullen et al., 2009). Each mapping family is composed of 200 RILs; hence, evaluation of the entire population requires testing 5000 inbred lines, beyond the capability of many researchers to assay, particularly for phenotypes that are difficult to measure. Thus, methods that could effectively predict which families are maximally segregating for genetic variation for a trait would aid geneticists by permitting efficient use of resources. Maximizing genetic variance results in higher power of QTL detection. Theoretically, progeny variance is increased in crosses between genetically more distant parents because the number of segregating loci is maximized (Cox et al., 1984). Studies in wheat (Triticum aestivum), oat (Avena sativa) and soybean (Glycine max) suggest that pedigree divergence between parents, estimated on the basis of the coefficient of parentage (Kempthorne, 1969), could be used to predict genetic variance in F2 or later segregating generations (Bhatt, 1970, 1973; Cowen and Frey, 1987; Manjarrez-Sandoval et al., 1997). However, other studies in the same species (Moser and Lee, 1994; Helms et al., 1997; Kisha et al., 1997; Burkhamer et al., 1998; Bohn et al., 1999) indicated that the relationship between parental pedigree distance and progeny genetic variance was neither consistent nor strong enough to permit reliable prediction of genetic variance. One possible explanation for the limited relationship between pedigree divergence and progeny variance observed in these studies is that coefficients of parentage may be inaccurate because the parents of some specific crosses might differ for many genes affecting a trait.

An alternative to estimating parental genetic divergence on the basis of pedigree information is the use of molecular marker-based genetic distance (GD). GD between two individuals or populations was defined by Goodman and Lasker (1974) and Nei (1974) as the proportion of non-matching nucleotide bases at homologous nucleotide sites between the genomes of two individuals or two populations. Although GD estimates based on molecular marker estimates have been effective at grouping related germplasm (Melchinger et al., 1998), the relationship between GD in parents and genotypic variance components (GVCs) in their progenies has been reported as weak or non-significant across many studies (Helms et al., 1997; Manjarrez-Sandoval et al., 1997; Burkhamer et al., 1998; Melchinger et al., 1998; Bohn et al., 1999; Gumber et al., 1999; Brachi et al., 2010).

Another alternative is to use parental phenotypic differences (PDs) to predict progeny GVC, because greater parental PD should be due to allelic differences at more loci for polygenic traits. However, parental PD was weakly related to or unrelated to progeny genetic variances in studies in maize, oat and wheat (Souza and Sorrells, 1991; Melchinger et al., 1998; Utz et al., 2001). Kuczyñska et al. (2007) found that, among five traits, only the differences between parents for spike length were significantly associated with the GVC of their progeny in barley. Melchinger et al. (1998) suggested that one cause of the weak relationship between PD and GVC in their maize study was that although larger values of PD were associated with larger values of GVC, smaller values of PD were not necessarily indicative of smaller values of GVC.

In summary, results from a range of plant species suggest that the relationship between genetic or PDs of parents and genetic variances of progenies is not strong enough to recommend the use of this relationship as a practical approach to select parental combinations to maximize within-family variation either for breeding or for trait analysis studies. Limitations in these studies include a lack of sufficient range of parental genotypic or phenotypic diversity, evaluation of small progeny sample sizes and use of limited samples of molecular markers. For example, the study by Melchinger et al. (1998) was based on crosses among elite inbred lines within two early-maturing European heterotic groups, and most of the other studies also involved elite germplasm representing limited diversity within those species. Therefore, it remains untested whether a stronger relationship between PD and genetic variance may exist in crosses between more diverse maize germplasm.

The maize NAM population represents an ideal resource to test this question. It represents the largest progeny sample evaluated for QTL mapping of any species to date (Buckler et al., 2009). The 25 diverse founder inbred lines selected to create mapping families in crosses with the reference parent B73 were chosen to maximally sample the genetic diversity available in global public maize inbreds (Liu et al., 2003; Buckler et al., 2009). The maize NAM families were genotyped with a common set of 1106 single-nucleotide polymorphism (SNP) markers (McMullen et al., 2009) and evaluated jointly for numerous quantitative traits across multiple environments. Furthermore, the gene-rich regions of all NAM parental lines have been sequenced with next-generation sequencing methods to produce a maize HapMap composed of 1.6 million SNPs (Gore et al., 2009). The combination of large genetic diversity, dense genetic maps, founder sequence information and robust phenotypic data associated with the maize NAM has permitted high-resolution genetic mapping of QTL and genes affecting important quantitative traits (Buckler et al., 2009; Kump et al., 2011; Tian et al., 2011).

The objective of this study was to use genotypic and phenotypic data of the 25 NAM families to evaluate the potential to select families for QTL mapping with high genetic variance based on phenotypic distance or GDs between the parental lines.

Materials and methods

Population development

B73 was crossed as a female parent to 25 genetically diverse inbred lines (Table 1) to form 25 F1 combinations. A sample of 200 randomly selected RILs from the intermated B73 × Mo17 (IBM) population (Lee et al., 2002) was also added to the evaluation. B73 was chosen as the common reference parent because it is well adapted to the evaluation environments, is the most important public inbred in commercial maize pedigrees in the United States (Mikel and Dudley, 2005) and is the source of the reference maize genome sequence (Schnable et al., 2009).

Table 1. The 26 RIL families and the most probable subpopulation assignment of the diverse (non-reference) parent based on SSR-based population structure analysis (Non-Stiff Stalk, NSS; Stiff Stalk, SS; Tropical/Subtropical, TS; Popcorn, Pop and Sweet corn, Sweet; Liu et al. (2003)).

Pop. no. Pedigree Diverse parent Origin Subpopulation
1 B73 × B97 B97 Iowa, USA NSS
2 B73 × CML103 CML103 México (CIMMYT) TS
3 B73 × CML228 CML228 Zimbabwe (CIMMYT) TS
4 B73 × CML247 CML247 México (CIMMYT) TS
5 B73 × CML277 CML277 México (CIMMYT) TS
6 B73 × CML322 CML322 México (CIMMYT) TS
7 B73 × CML333 CML333 México (CIMMYT) TS
8 B73 × CML52 CML52 Mexico (CIMMYT) TS
9 B73 × CML69 CML69 México (CIMMYT) TS
10 B73 × Hp301 Hp301 Indiana, USA Popcorn
11 B73 × Il14H Il14H Illinois, USA Sweet
12 B73 × Ki11 Ki11 Thailand TS
13 B73 × Ki3 Ki3 Thailand TS
14 B73 × Ky21 Ky21 Kentucky, USA NSS
15 B73 × M162W M162W South Africa NSS
16 B73 × M37W M37W South Africa Mixed
17a B73 × Mo17 (IBMa) Mo17 Missouri, USA NSS
18 B73 × Mo18W Mo18W Missouri, USA Mixed
19 B73 × MS71 MS71 Michigan, USA NSS
20 B73 × NC350 NC350 North Carolina, USA TS
21 B73 × NC358 NC358 North Carolina, USA TS
22 B73 × Oh43 Oh43 Ohio, USA NSS
23 B73 × Oh7B Oh7B Ohio, USA NSS
24 B73 × P39 P39 Indiana, USA Sweet
25 B73 × Tx303 Tx303 Texas, USA Mixed
26 B73 × Tzi8 Tzi8 Nigeria TS
Open in a new tab

Abbreviations: NAM, nested association mapping; RIL, recombinant inbred line; SSR, simple sequence repeat.

*Reference parent B73 is from Iowa, USA, and is derived from the SS subpopulation.

a

Developed independently of NAM (Lee et al., 2002), but evaluated with NAM.

Several F1 plants of each cross were selfed to form F2 generation families. Self-fertilization for 3 additional generations with minimal conscious selection was practiced to form 200 F5 progenies per family. Each F5 descended from a unique F2 plant. The self-fertilized progeny from each F5 plant were harvested in bulk to form an F5:6 RIL. To produce seed for field evaluations, at least 15 plants within each F5:6 line were sib-mated. Approximately one-third of RILs were developed by each of the USDA-ARS (US Department of Agriculture–Agricultural Research Service) maize genetics programs at North Carolina State University (Raleigh, NC, USA), University of Missouri (Columbia, MO, USA) and Cornell University (Ithaca, NY, USA). Each program used a summer pollination season at their location and a winter pollination season in Homestead, Florida, or Ponce, Puerto Rico, each year to create the NAM RILs.

Field evaluation

The NAM population was evaluated across a total of 11 environments, although not all traits were measured in all environments. In 2006, the evaluation of the populations was carried out in four summer locations: Clayton, North Carolina, Columbia, Missouri, Ithaca, New York, and Urbana, Illinois and two winter locations: Homestead, Florida and Ponce, Puerto Rico. In 2007, the experiment was grown in the same four summer locations and one winter location in Homestead, Florida. The genetic entries consisted of 5000 NAM RILS representing 25 families, 200 randomly selected RILs from the intermated B73 × Mo17 (IBM) population (Lee et al., 2002) and 281 inbred lines representing the global diversity of public maize inbreds (including all NAM founders) and useful as an association analysis panel (Flint-Garcia et al., 2005). Thus, the experiment contained 5481 unique inbred maize lines.

Within a location, the experimental design was a sets design (Federer, 1955), in which each set contained all lines of a family or population (Supplementary Figure 1). The positions of the 27 sets (25 NAM families, the IBM family and the association panel) were randomized across environments. Each set was randomized across environments as a 10 × 20 incomplete block α-lattice design (Patterson and Williams, 1976). The α-design was augmented by including the two parental lines of the family within each incomplete block (Federer, 1961). Thus, each incomplete block included 20 random RILs plus B73 and the other parental line of the family were included as a repeated check in all family sets. The order of the 22 entries within each incomplete block was randomized. The association panel (with 280 entries after excluding Mo17) was arranged as a 14 × 20 α-lattice design, and the incomplete blocks were augmented by adding B73 and Mo17 to random positions within each incomplete block (Supplementary Figure 1). In 8 of 11 environments, 1 complete replication of the experiment was grown. In North Carolina in 2006, a second replication of families derived from crosses between B73 and lines CML247, CML277, Ki3, M162W, Mo17, Tzi8, and the association mapping population was grown adjacent to the first complete replication of the experiment. In Missouri, 2006, families corresponding to CML247, CML322, IL14H, M162W, Mo18W, MS71, NC350, NC358 and P39 were not scored because of the germination rate and drought condition. In Missouri 2007, the Mo17 family (IBM) was not grown.

Experimental units were single row plots of variable size at each location. In Clayton, North Carolina, plots were ∼1.07 m in length with a 0.61-m alley at the end of each plot. Inter-row spacing was 0.97 m. Plots were thinned to approximately eight plants per row. In Columbia, Missouri, the experiment was planted in plots that were 2.14 m in length with a 0.92-m alley at the end of each plot. Inter-row spacing was 0.90 m. Nine kernels were planted in each plot and they were not thinned. In Aurora, New York, the plots were ∼2.60 m in length with a 1.22-m alley at the end of each plot. Inter-row spacing was 0.76 m. In all, 12 kernels were planted in each plot and they were not thinned. In Urbana, Illinois, plots were ∼4.57 m in length with a 1.0-m alley at the end of each plot. Inter-row spacing was 0.76 m. In all, 25 kernels were planted in each plot and they were thinned to ∼15 plants per row. In Homestead, Florida, plots were ∼1.07 m in length with a 0.76-m alley at the end of each plot. Inter-row spacing was 1.1 m. Plots were thinned to approximately eight plants per row. In Ponce, Puerto Rico, plots were ∼1.83 m in length with a 0.91-m alley at the end of each plot.

Traits evaluated in this study

The traits evaluated were days to anthesis (DTA, days after planting until 50% of plants in the row shedding pollen), days to silk (DTS, days after planting until 50% of plants in the row silking), anthesis-silk interval (ASI, difference between DTA and DTS), plant height (distance from soil surface to the base of flag leaf), ear height (distance from soil surface to the highest ear-bearing node), tassel length (length from the bottom branch to the tip of the tassel), tassel primary branches (a count of the number of tassel primary braches), upper leaf angle (angle between the leaf immediately below the flag leaf and the stalk at or near flowering time), leaf length (distance from base to tip of the leaf below the primary ear, at or near flowering time,), leaf width (distance of the widest section of the leaf below the primary ear at or near flowering time), ear row number (number of rows of kernels around the diameter of the ear), cob diameter, cob length (length of a cob from base to tip), number of kernels per row (EKPR, number of potential kernels per row from base to tip of the ear), ear mass, cob mass (weight of a cob after shelling seeds), total seed weight (KW, difference of ear mass and cob mass), 20-kernel weight (TWKW, weight of 20 randomly chosen kernels) and total kernel number (KNUM, KW multiplied by 20 and divided by TWKW). DTA, DTS and ASI were measured on a plot basis. Plant height, ear height, tassel length, tassel primary branch, upper leaf angle, leaf length and leaf width were measured on one random representative plant per row. Ear traits (ear row number, cob diameter, cob length, EKPR, ear mass, cob mass, KW, TWKW and KNUM were measured on two open-pollinated ears harvested from each plot. Not all traits were measured in all locations; the locations where each trait was measured are listed in Supplementary Table 1.

Genotyping to calculate GDs

Genotyping of simple sequence repeats and SNPs on the parental inbred lines was described by Liu et al. (2003), Flint-Garcia et al. (2005), Wright et al. (2005) and McMullen et al. (2009). Genotype data were extracted from the publicly available Panzea database (http://www.panzea.org). Among the SNPs available, 1144 were used to create the NAM map because B73 had a relatively rare allele at them (McMullen et al., 2009). We excluded these 1144 SNPs from our estimates of parental GD because they have very strong ascertainment bias, which is expected to influence relationship estimates. After removing loci with any missing data, GDs based on SNPs were calculated from the remaining 2303 SNP markers by computing the percentage of matched alleles between inbred line B73 and the other 26 parental lines and dividing by total number of alleles (Goodman and Lasker, 1974). Similarly, a separate GD estimate was computed based on 44 simple sequence repeat loci with complete data.

Statistical analyses

Outliers were detected from initial analysis fitting only environment, set and genotype effects and their interactions using the DFFITS criterion, which measures the influence of each observation on predicted values (Belsley et al., 2004). We used 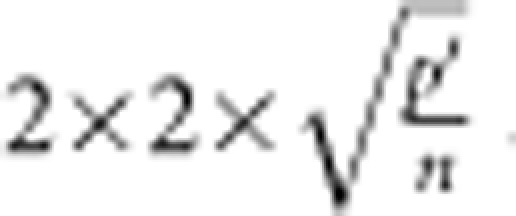Inline graphic as the DFFITS threshold value, where p′ is model df+1 and n the sample size, and we deleted observations exceeding this threshold. This is twice the DFFITS threshold suggested by Rawlings et al. (1998), resulting in a conservative approach to dropping outliers from the analysis. Genotypic analysis of the 5000 NAM lines (McMullen et al., 2009) performed after field experiments were completed revealed that some lines were contaminated (contained non-parental alleles) or had high levels of heterozygosity. We considered contaminated lines or lines with >8% heterozygosity as genetic outliers, and these 301 genetic outliers were excluded from the set of NAM seed stocks deposited at the USDA Maize Genetics Cooperation Stock Center for public release (http://maizecoop.cropsci.uiuc.edu/nam-rils.php). However, we maintained the genetic outliers in the statistical analysis, as they provide information on genotype-by-environment variation and within-environment spatial variation, but we did not want their phenotypic values to influence the estimates of genetic variation within or among the NAM families. Therefore, we coded the 301 genetic outliers as belonging to family P=28. The mean value of family 28 was excluded from computation of the among-family variation and the variation within family 28 was excluded from the computation of average within-family variation.

The next step of analysis was to analyze each combination of trait and environment separately to account for as much extraneous variation due to spatial variation as possible (Gilmour et al., 1997). Mixed model analyses implemented with ASReml version 2 (Gilmour et al., 2006) were used to account for the unbalanced design and data structure. Within each environment, the initial model included random effects due to sets, incomplete blocks, families and lines within families. Families, sets and incomplete blocks were not confounded because the parental lines were considered to be from the association population, B73 was repeated across all incomplete blocks and sets and the other parental line of each population was repeated across incomplete blocks within a set. Therefore, the experimental design enables estimation of genetic effects of lines separately from field design effects. In environments in which the experiment was grown in adjacent but separate fields, we also fit a field effect and nested sets and blocks within fields. For Clayton, 2006, where a partial second replication was grown, we also fit a main effect because of the complete replication and nested sets and blocks within complete replications.

The basic model was then enhanced by including random effects due to the rows and columns of the physical layout of the grid of plots in the field and by fitting separate spatially autoregressive correlations in the row and column directions among plot residuals (AR1 × AR1 error structure) (Cullis and Gleeson, 1991; Gilmour et al., 1997; Smith et al., 2001). Model terms were tested with likelihood ratio tests (Littell et al., 1996), and terms not significant at P<0.05 were dropped from the final model for an environment. If the residual autocorrelation in one direction but not the other was significant, we fit AR1 × AR1 error structures.

Next, a combined model was fitted including all environments. We included within-environment non-genetic sources of variation only in those environments in which they were significant in the individual location analyses. The full model across environments was:

graphic file with name hdy2011103e2.jpg

where, Yijklmnopq=individual observation; μ=overall mean; envi=the effect of the ith environment (location-by-year combination), i∈ {1, …, 11}.; field(env)ij=the effect of the jth field within the ith environment (multiple fields within a location were used only at Missouri, 2007, and Illinois, 2007); rep(field*env)ik=the effect of the kth replication within the jth field within the ith environment (modeled only for North Carolina in 2006); set(rep*field*env)ijkl=the effect of the lth set within the kth replication within the jth field within the ith environment; block(set*rep*field*env)ijklm=the effect of the mth incomplete block within the lth set within the kth replication within the jth field within the ith environment; row(field*env)ijn=the effect of the nth plot grid row direction within the jth field within the ith environment; column(field*env)ijo=the effect of the oth plot grid column within the jth field within the ith environment; familyp=the effect of the pth family; RIL(family)pq=effect of the qth RIL within the pth family which are two levels of genotypes; env*familyip=the effect of the interaction between the pth family and the ith environment; env*RIL(family)ipq=the effect of the interaction between the qth RIL within the pth family and the ith environment; and ɛijklmnopq=the experimental error on plot containing all the experimental factors above.

Unique error variances (σ̂ɛi2) and spatial autoregressive error correlations were modeled for each environment. Unique genetic (line within family) variance components, σ̂RIL(family)p2, were modeled for each family. We also attempted to fit unique environment-by-RIL(family) variance components for each family for flowering traits, but obtained variance estimates equal to zero for numerous families, which we regarded as unlikely for this trait. This result likely occurred because of the high level of confounding between environment-by-RIL(family) and residual effects for most genotypes. Therefore, we chose to fit a homogeneous variance component for environment-by-RIL(family) for all traits to avoid overfitting the mixed models.

For ear traits, which were measured on one or two open-pollinated ears per plot, depending on productivity of the lines, we averaged individual ear measurements for each plot. Plot mean values were then analyzed with a weighted mixed model, with the number of observations per plot used for weighting. We attempted to include correlated error terms with these weighted analysis models, but convergence consistently failed. Therefore, residual effects within an environment for ear traits were modeled as independent and identically distributed. Otherwise, these traits were analyzed with similar mixed models as the other traits, including row, column and block effects to account for spatial effects, and unique residual variances for each environment.

Likelihood ratio tests were used to test the significance of factors with variance components near zero in the combined analysis (Littell et al., 1996). Non-significant terms were dropped from the combined model. The final model containing only significant terms was used to estimate the parameters reported in this study, which included unique genetic components of variance for each family. Best linear unbiased predictors for RILs were also obtained from these models for use in QTL mapping and genome-wide association studies (Buckler et al., 2009; Kump et al., 2011; Tian et al., 2011). Heritabilities on an individual plot basis (hp2) (Holland et al., 2003) were estimated for the entire NAM population as:

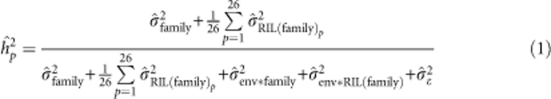graphic file with name hdy2011103e3.jpg

In this and other heritability equations, the residual error variance is the mean residual error variance across all environments. Heritabilities on a line mean basis (hl2; Holland et al., 2003) were estimated for the entire NAM population as:

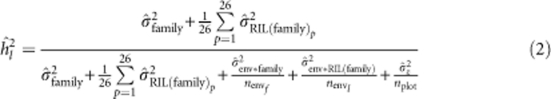graphic file with name hdy2011103e4.jpg

To account for unbalanced data, we used the harmonic means of the number of environments in which each family was observed for (nenvf), the harmonic mean of the number of environments in which each RIL was observed for (nenvl) and the harmonic mean of the total number of plots in which each RIL was observed for (nplot) in equation (2) (Holland et al., 2003; Piepho and Möhring, 2007).

Heritabilities on a line mean basis within only the pth NAM family (hlwp2) were estimated as:

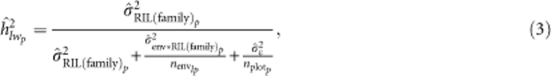graphic file with name hdy2011103e5.jpg

where envlp is the harmonic mean of the number of environments in which each RIL was observed for each family and nplotp the harmonic mean of the total number of plots in which each RIL was observed for each family. Mean within-family heritabilities were estimated by averaging the heritabilities obtained for each family, except the association panel.

An alternate estimator of heritability (hc2) that pertains to an entire experiment (in this case the entire NAM population, IBM population and the association panel) was given by Cullis et al. (2006):

graphic file with name hdy2011103e6.jpg

Where, VPPE is the average prediction error variance for all possible pairwise comparisons (including repeated check lines), obtained directly from the ASReml prediction output.

The s.e. of the estimators of heritabilities from equations (1), (2) and (3) were estimated using the delta method (Holland et al., 2003) in ASReml. The among-family variance components (σ̂family2) in equations (1) and (2) were computed based only on NAM and IBM family means to exclude the effect of the association panel, but this estimator is not directly available from the ASReml output. Therefore, we used the s.e. of the heritability estimate including the association panel as an approximation to the s.e. for equations (1) and (2). Approximate s.e. for each heritability estimated were computed. However, the s.e. for heritability estimators from equation (4) was not described in Cullis et al. (2006).

To test the hypothesis that family genetic variance increases with increasing phenotypic parental differences and genetic differences for a given trait, the estimates of within-family genetic variance (σ̂RIL(family)2) and heritability (ĥlwp2) were regressed separately on the parental PD (estimated as the absolute value of difference between B73 and other parental line means; PD) or on the parental GD estimate from simple sequence repeat markers (GDssr) and SNP markers (GDsnp) using PROC REG in SAS version 9.1 (SAS Inc., Cary, NC, USA) (SAS Institute, 2004).

Results

Among the 135 spatial autocorrelation coefficients fit for residual effects across all traits and environments, only 2 were negative, suggesting that spatial variability in the trials was primarily due to physical variation due to soil and management, rather than inter-plot competition (Stringer and Cullis, 2002). The experimental design used involved replication of NAM lines across environments but not within environments, as a means to most efficiently estimate their genotypic main effects across environments. The additional use of repeated checks within environments permits modeling non-genetic field effects within environments and estimation of within-environment error variance separately from genotype-by-environment interaction variance. Thus, the design provided efficient estimation and testing of genotype main effects, as well as genotype-by-environment interactions, although it sacrifices somewhat the precision of environment-specific genotypic values compared with designs with more replication within fewer environments.

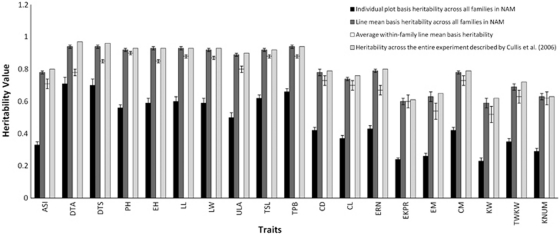
Within-family genotypic variation varied significantly among families for all measured traits (Supplementary Table 2). The maize association panel had larger genetic variation than all biparental families for 13 of 19 traits (Supplementary Table 2). Estimated heritabilities on a plot-basis (ĥp2.) ranged from 23 to 71%, whereas estimates of heritabilities on a RIL mean basis (ĥl2) ranged from 59 to 94%. Average within-family heritability estimates on a RIL mean basis (hlwp2) ranged from 52 to 90%, and were always lower than the heritability for the entire NAM population (ĥc2) (Figure 1; Supplementary Table 3). The difference between the average within-family heritabilities and corresponding heritability estimates for the entire NAM population ranged from close to 0 (EKPR) to 19 (DTA) percentage points (Figure 1; Supplementary Table 3) among traits. This difference reflects the relative amount of genetic variation among and within families, and was not consistent among the different types of trait measurements.

Figure 1.

Figure 1

Open in a new tab

Heritability estimates and their s.e. for 19 traits based on evaluation of the maize NAM population across up to 11 environments. Black bars represent individual plot basis heritability across all families in NAM (ĥp2), dark gray bars represent heritability on a line mean basis heritability across all families in NAM (ĥl2), white bars represent average within-family line mean basis heritability (ĥlwp2), and light gray bars represent heritability across the entire experiment (ĥc2) described by Cullis et al. (2006).

Most estimates of line mean-basis heritability based on Cullis et al. (2006) were within 2% point of, and were never >2.7% points different from the heritabilities estimated with equation (2) (Figure 1; Supplementary Table 3). Heritabilities based on the Cullis et al. (2006) equation (ĥc2) were in all cases greater than ĥl2, because they include the genetic variation within the association panel (inflating the numerator) and reflect the greater precision for measurements on the repeated check founder lines (reducing the denominator).

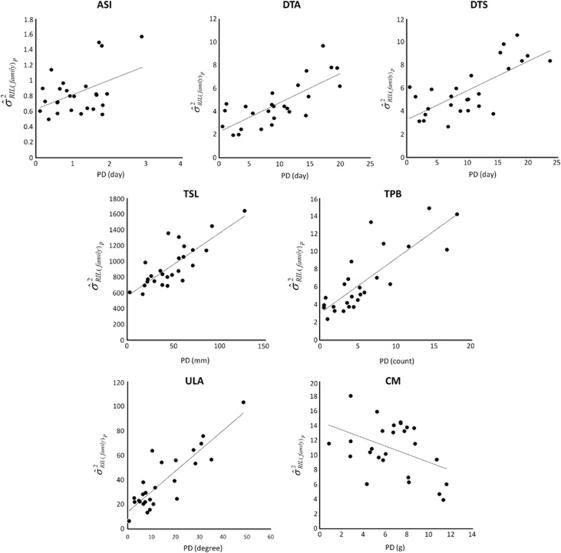
Phenotypic differences (Supplementary Table 4) between founder best linear unbiased predictors (BLUPs) (Supplementary Table 5) were used to predict within-family genetic variation. The regression of within-family GVC (σ̂RIL(family)2) on between-parent PD was significant (P<0.05) for 7 of 19 traits, with r2 values for these significant regressions ranging from 18 to 75% (Table 2). Increasing parental phenotypic diversity was positively correlated with GVC for the three flowering traits (ASI, DTA and DTS), for upper leaf angle and for both tassel architecture traits (tassel length and tassel primary branch). Increasing parental phenotypic diversity was negatively correlated with GVC for cob mass (Figure 2). Only cob length showed significance for regressions of GVC on GDssr (r2 ranged among traits from ∼0 to 28% Supplementary Figure 2). GDsnp was not significantly related to GCV for any trait. The pattern of significant regressions of within-family heritability (ĥlwp2) on parental PD and GD closely followed the pattern observed for GVC (Supplementary Table 6; Supplementary Figures 3 and 4), as expected because GVC is the numerator of the heritability estimates.

Table 2. r2, β̂ and P-value of regressions of GVC (σ̂RIL(family)p2) on the absolute value of parental phenotypic difference (PD), genetic distance estimate from SSR markers (GDssr) and genetic distance estimate from SNP markers (GDsnp).

Trait GVC on PD
 GVC on GDssr
 GVC on GDsnp
  r2 β̂ P-value r2 β̂ P-value r2 β̂ P-value
ASI 0.1969 0.1871 0.0232* 0.0026 0.4103 0.8039 0.0005 0.2837 0.4687
DTA 0.5669 0.2524 <0.0001* 0.0156 6.8031 0.5430 0.0220 12.2071 0.1319
DTS 0.5164 0.2524 <0.0001* 0.0303 10.8410 0.3952 0.0116 10.1635 0.2662
PH 0.0166 −0.4424 0.5302 0.0088 113.0194 0.6478 0.0034 106.5538 0.7765
EH 0.0515 0.4496 0.2651 0.0198 84.6488 0.4929 0.0300 157.5134 0.8846
LL 0.0032 −0.5417 0.7843 0.0898 −4902.8916 0.1370 0.0540 −5753.6697 0.2401
LW 0.0023 −0.0774 0.8151 0.0032 19.5327 0.7847 0.0406 105.7939 0.4690
ULA 0.7461 1.6619 <0.0001* 0.0151 80.0869 0.5504 0.2319 475.5614 0.8156
TSL 0.6392 7.9810 <0.0001* 0.0108 791.8914 0.6130 0.0377 2234.8499 0.6775
TPB 0.6727 0.6206 <0.0001* 0.0036 −6.0435 0.7710 0.0108 −15.8606 0.6576
CD 0.0067 −0.0363 0.6902 0.0414 4.5614 0.3186 0.2789 17.9060 0.1389
CL 0.0699 1.6666 0.1919 0.2795 737.3411 0.0055* 0.0743 575.2599 0.2944
ERN 0.0648 −0.1085 0.2095 0.0207 1.8651 0.4830 0.0893 5.8581 0.5025
EKPR 0.0086 0.0814 0.6514 0.1071 18.0459 0.1027 0.0639 21.0821 0.1149
EM 0.0216 −0.8489 0.4732 0.0961 578.0206 0.1232 0.0025 142.3639 0.3757
CM 0.1830 −0.5528 0.0293* 0.0254 16.0619 0.4364 <0.0001 −0.8173 0.6819
KW 0.0621 −1.2319 0.2196 0.0809 383.0612 0.1591 <0.0001 −11.0908 0.2980
TWKW 0.0025 −0.0113 0.8100 0.0161 0.4312 0.5368 0.0033 −0.2975 0.2817
KNUM 0.0031 −1.6361 0.7868 0.0049 1693.5033 0.7341 0.0072 −3099.2993 0.5905
Open in a new tab

Abbreviations: GVC, genotypic variance component; SNP, single-nucleotide polymorphism; SSR, simple sequence repeat.

*Significant at P=0.05.

Figure 2.

Figure 2

Open in a new tab

Significant regressions of progeny genetic variance component (GVC) on parental phenotypic difference (PD). The X axis is PD and the Y axis is GVC. ASI, anthesis-silking interval; CM, cob mass; DTA, days to anthesis; DTS, days to silk; TPB, tassel prime branches; TSL, tassel length; ULA, upper leaf angle.

Discussion

Heritability estimates ĥl2 and ĥp2 are functions of genotypic and phenotypic variations across the entire NAM population. Importantly for genetic mapping applications, the line mean-basis heritability across the entire NAM population corresponds to the maximum amount of phenotypic variation among NAM lines that can be attributed to genetic effects and thus to the cumulative effects of QTL (Buckler et al., 2009; Kump et al., 2011). Correspondingly, heritability on a line-mean basis within a family indicates that the proportion of variation among line means that can be attributed to QTL within that family. On average, within-family variation heritability for the whole NAM population was always less than the average heritability of the whole NAM population, demonstrating the greater potential for QTL identification by incorporating the genetic variation among and within families. Flowering time (except ASI) and whole plant, leaf and tassel architecture traits had line mean-basis heritabilities of ⩾89%, indicating that we have good power to detect and resolve QTL for these traits. In contrast, traits measured on ears consistently had lower line mean-basis heritabilities (from 61 to 79% Figure 1; Supplementary Table 3). These traits tend to be more highly related to fecundity, and thus are more strongly affected by environmental variation in inbreds (Falconer and Mackay, 1996). Indeed, KW, which represents fecundity directly, had the lowest heritability among all traits (Figure 1). Nevertheless, the line mean-basis heritabilities for all traits measured were sufficiently high to permit reasonable power for QTL detection.

The relationship between the genetic variance component (GVC) of the traits and PDs between the parental lines was examined by linear regression, with 6 of 19 traits exhibiting significant positive regression coefficients. We inspected the scatter plots of GVC vs PD for consistent non-linear trends, but did not observe any (Figure 2, Supplementary Figure 5). Therefore, predicting progeny genetic variance based on the absolute PDs of parents may be moderately effective when a large number of genetically diverse populations and traits are evaluated in multiple environments. In contrast to Melchinger et al. (1998), we did not observe a trend whereby PD and GVC seemed to be related for higher but not lower values of PD. Instead, we observed that larger values of PD were associated with lower GVC values as often as not for those traits that did not exhibit a significant association between PD and GVC (Supplementary Figure 5).

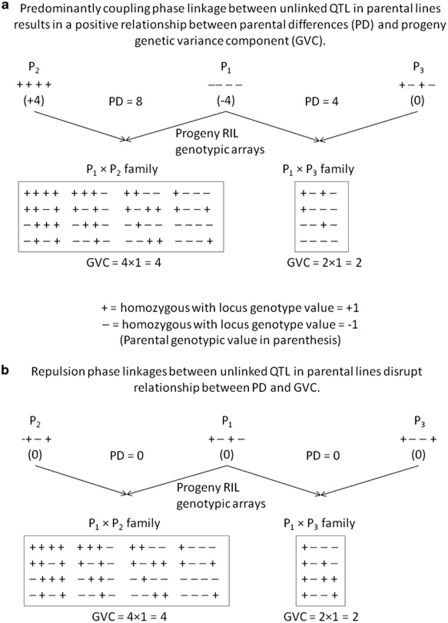
Under relatively simple models of genetic architecture, the relationship between PD and GVC is expected to be strongest when alleles conferring positive effects are concentrated in one set of parents and those conferring negative effects are concentrated in other parents, such that the magnitude of parental PDs is associated with the number of polymorphic loci that affect the trait, and as a consequence, the magnitude of the progeny genetic variation (Figure 3a). In this situation, most pairs of loci affecting the trait tend to be in coupling-phase gametic disequilibrium in F1 parents of the mapping families.

Figure 3.

Figure 3

Open in a new tab

Gametic phase of positive trait alleles among founders affects the relationship between parental phenotypic differences (PDs) and progeny genetic variance components (GVCs). Idealized simple genetic architecture affected by four unlinked QTL with equal effects (+1 or −1 for each homozygous class) is shown. Each segregating locus contributes a variance of +1 in progeny RIL generation. In a, negative alleles are concentrated in reference parent (P1), resulting in a positive linear relationship between PD, the number of segregating loci and GVC. In b, both negative and positive alleles are more equitably distributed among founders, resulting in no relationship between PD and GVC.

For highly polygenic traits, most pairs of QTL will be unlinked because the component loci will be located on different chromosomes. Thus, most gametic disequilibrium that occurs in the F1 generation will be eliminated by independent assortment in the F2 and later inbreeding generations. Therefore, gametic disequilibrium between unlinked QTL may have a significant impact on parental PDs but will have little or no effect on progeny variance. Thus, when unlinked QTL are predominantly in repulsion-phase gametic disequilibrium in the F1 generations, large progeny variances can be generated by crosses between parents with similar phenotypes (Figure 3b). In summary, polygenic traits with largely additive (non-epistatic) genetic control will tend to exhibit a positive relationship between PD and GVC when allelic effects at QTL are consistent within a parent and distinct between parents (unlinked coupling-phase gametic disequilibrium). In contrast, when positive and negative allelic effects are distributed among parents (resulting in more unlinked repulsion-phase gametic disequilibrium in F1 generations), the relationship between PD and GVC will break down. Furthermore, more complex genetic architectures, such as those involving epistasis, are expected to reduce the relationship between PD and GVC.

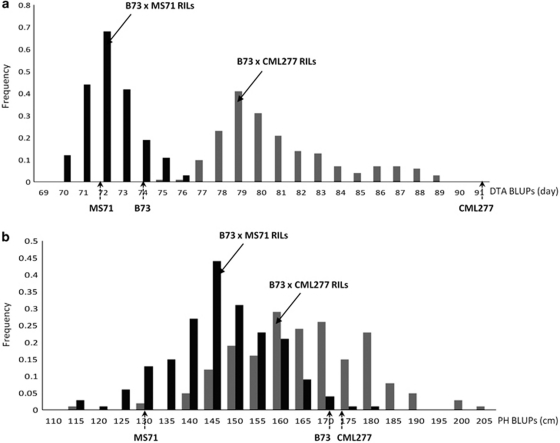
The predictive ability of parental PD was strongly dependent on the traits evaluated. For example, there is a moderately strong relationship between PD and GVC for flowering time but not for plant height (Table 2). For DTA, the larger difference between CML277 and B73 values is reflected in the larger within-family variation for the B73 × CML277 RIL family compared with the smaller parental differences and progeny variation for the B73 × MS71 family. In contrast, the parental difference for plant height was much larger for B73 × MS71 than for B73 × CML277, and the progeny means were quite different for the two families, but the progeny variation was quite similar (Figure 4).

Figure 4.

Figure 4

Open in a new tab

Distributions of parental and progeny RIL BLUPs for (a) DTA and (b) PH. Arrows indicate BLUPs for founder line MS71, reference line B73 and founder line CML277. Black bars represent the histogram of B73 × MS71 RILs. Gray bars represent the histogram of B73 × CML277 RILs.

All three flowering time traits measured, DTA, DTS and ASI, had significant linear relationships between PD and GVC. Buckler et al. (2009) demonstrated that the genetic architecture of flowering time in the maize NAM population is characterized by series of additive small-effect allelic variants at a moderately large number of loci. Alleles conferring positive and negative flowering time effects relative to B73 are dispersed among other parental lines, but there is a general trend of later flowering alleles being concentrated in later flowering parents and earlier flowering alleles being concentrated in earlier flowering parents. This is congruent with the finding that flowering time traits are more strongly related to maize adaptation and population structure compared with other traits measured in this study (Flint-Garcia et al., 2005). Thus, the flowering time allele effects tended to be in the coupling phase among the NAM founder F1s, enhancing the relationship between PD and GVC.

However, for most traits, we observed no significant relationship between GVC and PD. We suggest that the lack of a relationship is likely due to larger proportions of repulsion-phase gametic disequilibrium between unlinked QTL pairs among the parental F1s for those traits. It is also possible that non-additive gene action due to epistasis could have a strong effect of reducing the relationship between parental PDs and progeny variation. However, limited epistasis has been detected for these traits in QTL analysis with NAM. We also observed one trait (cob mass) for which parental difference was strongly negatively related to within-family genetic variation (Table 2; Figure 2), suggesting that the genetic architecture of this trait is distinct from others, and perhaps is more strongly controlled by epistasis.

Genetic distance estimated by the percentage of matched markers between the parental lines was not a better predictor than the parental PD of genetic variances. The poor association between marker-based estimates of GDs and genetic variance is likely due to the inclusion of markers not linked to QTL affecting the trait in distance estimation. Such markers are not uninformative, but rather are mis-informative, as they disrupt the relationship between genetic differences and phenotype differences, as demonstrated by Charcosset et al. (1991), Bernardo (1992) and Flint-Garcia et al. (2009) for prediction of heterosis from random marker data. The distribution of QTL effects seems quite different from that of sequence variation among the NAM founders (Buckler et al., 2009), and this will tend to make random marker information less predictive of genetic segregation. In addition, epistasis will reduce the relationship between genetic differences and trait variation (Moser and Lee, 1994). By design, the maize NAM population involves crosses between a single reference parent, B73, and unrelated, genetically diverse inbreds to maximize the genetic diversity sampled. Therefore, the NAM does not include crosses between closely related inbred lines that would be typical of applied maize breeding programs; it is possible that inclusion of such crosses would result in a more obvious relationship between GD and GVC.

For researchers unable to evaluate the entire NAM population due to resource limitations, we offer the following suggestions regarding sampling subsets of the NAM for phenotypic evaluations. Sampling strategies should reflect the goal of the research. Sampling fewer families with more progeny per family seems to provide higher power for QTL detection, but sampling more families with fewer progeny seems to provide more reliable estimates of the overall genetic architecture (for example, general and specific combining ability variances), allele number and QTL variance (Wu and Jannink, 2004; Verhoeven et al., 2006). Different analysis approaches have different optimal sampling strategies as well. For example, QTL mapping based on joint linkage analysis with lower marker density strives to explain within-family variation within marker effects nested within families (Buckler et al., 2009). In contrast, high-density marker information provided by the maize HapMap (Gore et al., 2009) provides new opportunities to account for both among- and within-family variation based on identity-in-state models (Kump et al., 2011; Tian et al., 2011). In the latter case, the association between SNPs and variation among families can be modeled, such that sampling of more families becomes more advantageous.

Sampling should include as many NAM families as possible if high-density marker analysis is an option, as we observed that for most traits, parental phenotype differences were poor indicators of within-family variation, and variation among families was a significant component of genetic variation for all traits. However, if marker effects are to be tested as nested within families, a minimum sample of at least 40 progeny per family seems necessary to maintain good power of QTL detection (Wu and Jannink, 2004; Verhoeven et al., 2006; Yu et al., 2008). Larger sample sizes could be drawn from mapping families with greater parental PD, as some traits do exhibit a moderate relationship between PD and GVC. Thus, sampling among as many NAM families as possible with a weighted sampling scheme based on PD seems to be a reasonable compromise approach. Alternatively, for a given total sample size, a sample of RILs with maximum GDs based on available marker data could drawn from the entire NAM. Although we found that parental genotypic differences based on random markers were not predictive of progeny genotypic variance, it is possible that progeny marker variation would have a better relationship with progeny genotypic variance simply by ensuring adequate sampling of the available progeny genotypic combinations. As more traits are dissected with NAM, we expect to have a robust empirical data set with which to address these questions.

If the major objective is to identify the most important QTL for a trait (rather than attempt a more complete evaluation of genetic architecture), reasonable power of QTL detection is possible with ⩽20% sample of NAM RILs if trait heritability is ⩾70% and 20 or fewer QTL affect the trait (Yu et al., 2008). At the other extreme, at which a single gene affects a trait, for example, su1 and seed type or Ga1 and cross-incompatibility (McMullen et al., 2009), only the NAM families segregating for the causative locus are informative and they should be sampled in full. Li et al. (2011) demonstrated that the power of detection of rare QTL in NAM (those that are limited to one or a few families) is higher for individual family analysis if the QTL effect is moderate or greater. Of course, one must sample the correct family to be able to detect the QTL in this situation.

Data archiving

Raw data for all traits analyzed are available at http://www.panzea.org/db/gateway?file_id=Hung_etal_2011_Heredity_data.

Acknowledgments

This research was supported by the National Science Foundation (DBI-0321467, IOS-0820619 and IOS-0604923) and funds provided by USDA-ARS (to ESB, JBH and MDM) and NC State University (to HH). We thank all staffs of the maize breeding programs at the NC State University and Central Crops Research Station. We also thank the editor and anonymous reviewers, particularly for drawing our attention to sampling to maximize total genetic variation.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies the paper on Heredity website (http://www.nature.com/hdy)

Supplementary Material

Supplementary Information
Click here for additional data file. (157.8KB, pdf)

References

  1. Belsley DA, Kuh E, Welsch RE. Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. Wiley-Interscience: Hoboken, NJ, USA; 2004. [Google Scholar]
  2. Bernardo R. Relationship between single-cross performance and molecular marker heterozygosity. Theor Appl Genet. 1992;83:628–634. doi: 10.1007/BF00226908. [DOI] [PubMed] [Google Scholar]
  3. Bhatt G. Multivariate analysis approach to selection of parents for hybridization aiming at yield improvement in self-pollinated crops. Aust J Agric Res. 1970;21:1–7. [Google Scholar]
  4. Bhatt G. Comparison of various methods of selecting parents for hybridization in common bread wheat (Triticum aestivum L.) Aust J Agric Res. 1973;24:457–464. [Google Scholar]
  5. Bohn M, Utz HF, Melchinger AE. Genetic similarities among winter wheat cultivars determined on the basis of RFLPs, AFLPs, and SSRs and their use for predicting progeny variance. Crop Sci. 1999;39:228–237. [Google Scholar]
  6. Brachi B, Faure N, Horton M, Flahauw E, Vazquez A, Nordborg M, et al. Linkage and association mapping of Arabidopsis thaliana flowering time in nature. PLoS Genet. 2010;6:e1000940. doi: 10.1371/journal.pgen.1000940. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Buckler ES, Holland JB, Bradbury PJ, Acharya CB, Brown PJ, Browne C, et al. The genetic architecture of maize flowering time. Science. 2009;325:714–718. doi: 10.1126/science.1174276. [DOI] [PubMed] [Google Scholar]
  8. Burkhamer RL, Lanning SP, Martens RJ, Martin JM, Talbert LE. Predicting progeny variance from parental divergence in hard red spring wheat. Crop Sci. 1998;38:243–248. [Google Scholar]
  9. Charcosset A, Lefortbuson M, Gallais A. Relationship between heterosis and heterozygosity at marker loci- A theoretical computation. Theor Appl Genet. 1991;81:571–575. doi: 10.1007/BF00226720. [DOI] [PubMed] [Google Scholar]
  10. Cowen NM, Frey KJ. Relationship between genealogical distance and breeding behaviour in oats (Avena sativa L.) Euphytica. 1987;36:413–424. [Google Scholar]
  11. Cox T, Kiang Y, Gorman M, Rodgers D. Relationship between coefficient of parentage and genetic similarity indices in the soybean. Crop Sci. 1984;25:529–532. [Google Scholar]
  12. Cullis BR, Gleeson AC. Spatial analysis of field experiments –an extension to two dimensions. Biometrics. 1991;47:1449–1460. [Google Scholar]
  13. Cullis BR, Smith AB, Coombes NE. On the design of early generation variety trials with correlated data. J Agric Biol Environ Stat. 2006;11:381–393. [Google Scholar]
  14. Falconer D, Mackay T.1996Introduction to Quantitative Genetics4th ednAddison-Wesley Longman: Harlow, UK [Google Scholar]
  15. Federer W. Experimental Design, Theory and Application. Macmillan: New York; 1955. [Google Scholar]
  16. Federer W. Augmented designs with one-way elimination of heterogeneity. Biometrics. 1961;17:447–473. [Google Scholar]
  17. Flint-Garcia SA, Buckler ES, Tiffin P, Ersoz E, Springer NM. Heterosis is prevalent for multiple traits in diverse maize germplasm. PLoS One. 2009;4:e7433. doi: 10.1371/journal.pone.0007433. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Flint-Garcia SA, Thuillet AC, Yu JM, Pressoir G, Romero SM, Mitchell SE, et al. Maize association population: a high-resolution platform for quantitative trait locus dissection. Plant J. 2005;44:1054–1064. doi: 10.1111/j.1365-313X.2005.02591.x. [DOI] [PubMed] [Google Scholar]
  19. Gilmour AR, Cullis BR, Verbyla AP. Accounting for natural and extraneous variation in the analysis of field experiments. J Agric Biol Environ Stat. 1997;2:269–293. [Google Scholar]
  20. Gilmour AR, Gogel BJ, Cullis BR, Thompson R. ASReml User Guide Release 2.0. VSN International Ltd: Hemel Hempstead, HP1 1ES, UK; 2006. [Google Scholar]
  21. Goodman M, Lasker G.1974Measurement of distance and propinquity in anthropological studiesIn Crow J, Denniston C (eds).Genetic Distance Plenum Press: New York; 5–21. [Google Scholar]
  22. Gore MA, Chia J, Elshire RJ, Sun Q, Ersoz ES, Hurwitz BL, et al. A first-generation haplotype map of maize. Science. 2009;326:1115–1117. doi: 10.1126/science.1177837. [DOI] [PubMed] [Google Scholar]
  23. Gumber RK, Schill B, Link W, von Kittlitz E, Melchinger AE. Mean, genetic variance, and usefulness of selfing progenies from intra- and inter-pool crosses in faba beans (Vicia faba L.) and their prediction from parental parameters. Theor Appl Genet. 1999;98:569–580. [Google Scholar]
  24. Helms T, Orf J, Vallad G, McClean P. Genetic variance, coefficient of parentage, and genetic distance of six soybean populations. Theor Appl Genet. 1997;94:20–26. doi: 10.1007/s001220050376. [DOI] [PubMed] [Google Scholar]
  25. Holland JB, Nyguist WE, Cervantes-Martínez CT.2003Estimating and interpreting heritability for plant breeding: an updateIn Janick J (ed)Plant Breeding Reviews John Wiley and Sons: Hoboken, New Jersey [Google Scholar]
  26. Kempthorne O. An Introduction to Genetic Statistics. Iowa State University Press: Ames, Iowa; 1969. [Google Scholar]
  27. Kisha TJ, Sneller CH, Diers BW. Relationship between genetic distance among parents and genetic variance in populations of soybean. Crop Sci. 1997;37:1317–1325. [Google Scholar]
  28. Kuczynska A, Surma M, Kaczmarek Z, Adamski T. Relationship between phenotypic and genetic diversity of parental genotypes and the frequency of transgression effects in barley (Hordeum vulgare L.) Plant Breed. 2007;126:361–368. [Google Scholar]
  29. Kump KL, Bradbury PJ, Wisser RJ, Buckler ES, Belcher AR, Oropeza-Rosas MA, et al. Genome-wide association study of quantitative resistance to southern leaf blight in the maize nested association mapping population. Nat Genet. 2011;43:163–168. doi: 10.1038/ng.747. [DOI] [PubMed] [Google Scholar]
  30. Lee M, Sharopova N, Beavis WD, Grant D, Katt M, Blair D, et al. Expanding the genetic map of maize with the intermated B73 x Mo17 (IBM) population. Plant Mol Biol. 2002;48:453–461. doi: 10.1023/a:1014893521186. [DOI] [PubMed] [Google Scholar]
  31. Li H, Bradbury P, Ersoz E, Buckler ES, Wang J. Joint QTL linkage mapping for multiple-cross mating design sharing one parent. PLoS One. 2011;6:e17573. doi: 10.1371/journal.pone.0017573. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Littell RC, Milliken GA, Stroup WW, Wolfinger R. SAS System for Mixed Models. SAS Publishing: Cary, NC; 1996. [Google Scholar]
  33. Liu KJ, Goodman M, Muse S, Smith JS, Buckler E, Doebley J. Genetic structure and diversity among maize inbred lines as inferred from DNA microsatellites. Genetics. 2003;165:2117–2128. doi: 10.1093/genetics/165.4.2117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Manjarrez-Sandoval P, Carter TE, Webb DM, Burton JW. RFLP genetic similarity estimates and coefficient of parentage as genetic variance predictors for soybean yield. Crop Sci. 1997;37:698–703. [Google Scholar]
  35. McMullen MD, Kresovich S, Villeda HS, Bradbury P, Li H, Sun Q, et al. Genetic properties of the maize nested association mapping population. Science. 2009;325:737–740. doi: 10.1126/science.1174320. [DOI] [PubMed] [Google Scholar]
  36. Melchinger AE, Gumber RK, Leipert RB, Vuylsteke M, Kuiper M. Prediction of testcross means and variances among F3 progenies of F1 crosses from testcross means and genetic distances of their parents in maize. Theor Appl Genet. 1998;96:503–512. doi: 10.1007/s001220050767. [DOI] [PubMed] [Google Scholar]
  37. Mikel M, Dudley J. Evolution of North American dent corn from public to proprietary germplasm. Crop Sci. 2005;46:1193–1205. [Google Scholar]
  38. Moser H, Lee M. RFLP variation and genealogical distance, multivariate distance, heterosis, and genetic variance in oats. Theor Appl Genet. 1994;87:947–956. doi: 10.1007/BF00225789. [DOI] [PubMed] [Google Scholar]
  39. Nei M.1974A new measure of genetic distanceIn Crow J, Denniston C (eds)Genetic Distance Plenum Press: New York; 63–76. [Google Scholar]
  40. Patterson HD, Williams ER. A new class of resolvable incomplete block designs. Biometrika. 1976;63:83–92. [Google Scholar]
  41. Piepho H, Möhring J. Computing heritability and selection response from unbalanced plant breeding trials. Genetics. 2007;177:1881–1888. doi: 10.1534/genetics.107.074229. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Rawlings JO, Pantula SG, Dickey DA.1998Applied Regression Analysis: A Research Tool2nd edn.Springer: New York, NY, USA [Google Scholar]
  43. SAS Institute . SAS/STAT 9.1 User's Guide. SAS Institute: Cary, NC; 2004. [Google Scholar]
  44. Schnable PS, Ware D, Fulton RS, Stein JC, Wei F, Pasternak S, et al. The B73 maize genome: complexity, diversity, and dynamics. Science. 2009;326:1112–1115. doi: 10.1126/science.1178534. [DOI] [PubMed] [Google Scholar]
  45. Smith A, Cullis B, Gilmour A. Applications: the analysis of crop variety evaluation data in Australia. Aust N Z J Stat. 2001;43:129–145. [Google Scholar]
  46. Souza E, Sorrells M. Prediction of progeny variation in oat from parental genetic-relationships. Theor Appl Genet. 1991;82:233–241. doi: 10.1007/BF00226219. [DOI] [PubMed] [Google Scholar]
  47. Stringer JK, Cullis BR. Application of spatial analysis techniques to adjust for fertility trends and identify interplot competition in early stage sugarcane trials. Aust J Agric Res. 2002;53:911–918. [Google Scholar]
  48. Tian F, Bradbury PJ, Brown PJ, Hung H, Sun Q, Flint-Garcia S, et al. Genome-wide association study of leaf architecture in the maize nested association mapping population. Nat Genet. 2011;43:159–162. doi: 10.1038/ng.746. [DOI] [PubMed] [Google Scholar]
  49. Utz HF, Bohn M, Melchinger AE. Predicting progeny means and variances of winter wheat crosses from phenotypic values of their parents. Crop Sci. 2001;41:1470–1478. [Google Scholar]
  50. Verhoeven KJF, Jannink J-L, McIntyre LM. Using mating designs to uncover QTL and the genetic architecture of complex traits. Heredity. 2006;96:139–149. doi: 10.1038/sj.hdy.6800763. [DOI] [PubMed] [Google Scholar]
  51. Wright SI, Bi IV, Schroeder SG, Yamasaki M, Doebley JF, McMullen MD, et al. The effects of artificial selection on the maize genome. Science. 2005;308:1310–1314. doi: 10.1126/science.1107891. [DOI] [PubMed] [Google Scholar]
  52. Wu X-L, Jannink J-L. Optimal sampling of a population to determine QTL location, variance, and allelic number. Theor Appl Genet. 2004;108:1434–1442. doi: 10.1007/s00122-003-1569-5. [DOI] [PubMed] [Google Scholar]
  53. Young ND. QTL mapping and quantitative disease resistance in plants. Annu Rev Phytopathol. 1996;34:479–501. doi: 10.1146/annurev.phyto.34.1.479. [DOI] [PubMed] [Google Scholar]
  54. Yu J, Holland JB, McMullen MD, Buckler ES. Genetic design and statistical power of nested association mapping in maize. Genetics. 2008;178:539–551. doi: 10.1534/genetics.107.074245. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (157.8KB, pdf)

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES