Epidemiological models of Mycobacterium tuberculosis complex infections

Abstract

The resurgence of tuberculosis in the 1990s and the emergence of drug-resistant tuberculosis in the first decade of the 21st century increased the importance of epidemiological models for the disease. Due to slow progression of tuberculosis, the transmission dynamics and its long-term effects can often be better observed and predicted using simulations of epidemiological models. This study provides a review of earlier study on modeling different aspects of tuberculosis dynamics. The models simulate tuberculosis transmission dynamics, treatment, drug resistance, control strategies for increasing compliance to treatment, HIV/TB co-infection, and patient groups. The models are based on various mathematical systems, such as systems of ordinary differential equations, simulation models, and Markov Chain Monte Carlo methods. The inferences from the models are justified by case studies and statistical analysis of TB patient datasets.

1. Introduction

Tuberculosis (TB) is a bacterial disease acquired through airborne infection. Mycobacterium tuberculosis complex (MTBC) is the causative agent of tuberculosis. According to the World Health Organization, one-third of the world’s population is infected, either latently or actively, with tuberculosis [1].

Epidemiology is the science of public health. It studies the distribution and determinants of disease status or events in populations, with the aim of controlling public health problems. The study of epidemiology ranges from cluster investigation at the individual level to building mathematical models to simulate disease dynamics at the population level.

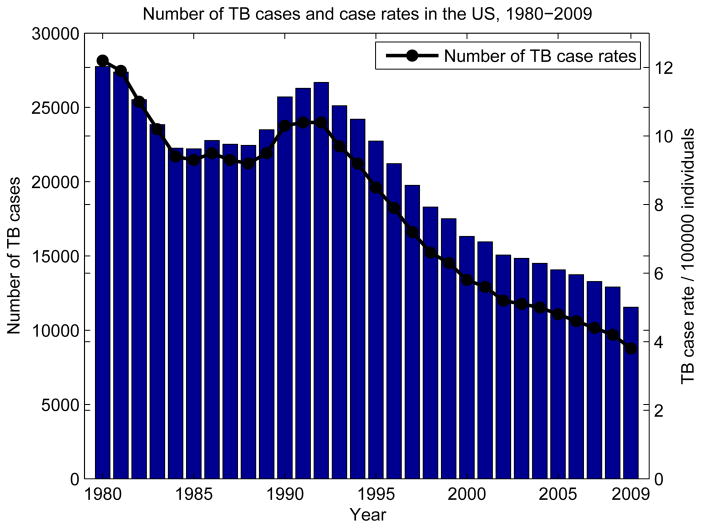
Tuberculosis case counts and case rates have changed in the US and worldwide over the years. Figure 1 shows the number of TB cases and case rates in the US from 1980 to 2009. The number of cases and case rates both follow a decreasing trend, with the exception of increasing TB cases and case rates in the early 1990s. The increase of TB in this period was attributed to several factors: the increasing HIV epidemic in the early 1990s leading to HIV/TB co-infection, the emergence of drug resistant TB, immigration to the US from developing countries, and increased mass transportation [2, 3, 4]. In order to understand these trends, we need to focus on the long-term consequences of tuberculosis epidemics, which can be observed with the analysis of epidemiological models.

Figure 1.

Number of cases and case rates per 100000 individuals in the US between 1980–2009 shows a general downward trend with the exception of a sudden rise in 1990s. The plot is generated using data from [5].

Tuberculosis has slow intrinsic dynamics. The incubation period, latent period, and infectious period span long time intervals, in the order of years on average. The slow progression of tuberculosis at the individual level leads to slow temporal dynamics and long-term outcomes of tuberculosis at the population level. Therefore, mathematical models are needed to estimate prolonged results and future trends of tuberculosis [6, 7, 8]. In this study, we present a literature review of mathematical models that characterize various components of tuberculosis epidemics: transmission, treatment, drug resistance, co-infection, and patient population characteristics.

The organization of this survey is as follows: In section 2, we give a brief background on the epidemiology of tuberculosis and the framework for describing epidemiological models. In section 3, we explain the transmission dynamics of tuberculosis at the population and individual levels, in different demographics, and in heterogeneous populations using a variety of models. In section 4, we describe models for treatment and give a brief summary of treatment strategies for different types of tuberculosis infections and the effects of combinations of control strategies for compliance to treatment. Section 5 covers drug-resistant strains of TB: we explain the dynamics of drug resistance and give an overview of models built for different levels of drug resistance as well as models for control strategies for compliance to drug resistant tuberculosis treatment. In section 6, we explain the co-epidemics of tuberculosis with HIV and AIDS using epidemiological models. In section 7, we present an overview of models based on patient groups to identify risk factors of tuberculosis.

2. Background

In this section, we give a brief introduction to the epidemiology of tuberculosis, as well as some of the commonly used terms. We also provide an introduction to epidemiological models of tuberculosis, their typical units, and central parameters for predicting the future of an epidemic.

2.1. Epidemiology of tuberculosis

Tuberculosis is an infectious disease. Progression of tuberculosis within the body of a susceptible individual with no history of TB starts with infection with MTBC. The disease can remain latent, become active, or it can progress from latent TB to active TB either by endogenous reactivation or exogenous reinfection. Another way of acquiring TB is through co-infection of TB with other diseases. TB can be treated. However, noncompliance to treatment causes drug resistant TB to develop in the individual. In this section, we review the components of the epidemiology of tuberculosis.

• Latent TB infection and active TB infection: After infection with MTBC, the symptoms of TB are not immediately observed. An individual is said to have latent TB if s/he is infected with MTBC, but not infectious. The latent period is the period from the point of infection to the beginning of the state of infectiousness. When latent TB progresses to active TB, the infectious period starts and the symptoms of TB show up with a delay. An individual with active TB is both infected and infectious, therefore the individual can spread the disease. Data from various sources suggest that after TB infection, the likelihood of lifetime risk of developing active TB is approximately 10%.

• Endogenous reactivation and exogenous reinfection: The progression from latent TB to active TB occurs in two ways: endogenous reactivation or exogenous reinfection. Endogenous reactivation is the activation of latent TB with MTBC which reside inside the body and had infected the individual earlier. Exogenous reinfection is caused by a secondary external infection in which the new MTBC makes the individual infectious, thereby causing the active TB infection. Such infections by more than one type of MTBC pathogen are called mixed infections.

• Treatment: Control of tuberculosis is managed by two types of treatment. The treatment of latent TB is called chemoprophylaxis and treatment of active TB is called therapeutics. Treatment of TB lasts long, therefore control strategies have been developed for compliance to TB treatment. DOTS (Directly Observed Treatment, Short-Course) is a treatment program used for compliance with treatment of drug-sensitive TB. Another control program is DOTS-plus, which is developed for compliance with treatment of drug-resistant TB. A good public health treatment strategy combines different control strategies to control all types of TB infections.

• Drug resistance: If TB treatment is ineffective or if the patient does not comply to treatment, MTBC may become resistant to first-line anti-TB drugs. Drug resistance can either be acquired during treatment or transmitted from individuals infected with drug-resistant strains. An individual develops acquired drug resistant TB (ADR-TB) due to treatment failure. Spread of TB via individuals infected with drug resistant TB causes the newly-infected individuals to develop transmitted drug resistant TB. Acquired drug resistance always initiates an epidemic of drug-resistant TB, but if the drug-resistant pathogen is transmissible, the risk of primary drug resistance increases over time.

• Co-infection: Co-infection is the infection of a host by at least two different types of pathogens. TB and HIV dynamics have a correlation, as HIV weakens the immune system of the host, which creates a proper medium for MTBC to infect the host. Therefore, in areas with high HIV prevalence, TB is one of the main causes of death.

2.2. Epidemiological models of tuberculosis

Long-term effects of tuberculosis can be examined using epidemiological models. Epidemiological models consist of compartments which represent sets of individuals grouped by disease status. The links between compartments represent transitions from one state of disease to another state. The future of an epidemic can be estimated by finding the basic reproductive number of the model. Epidemiological models of tuberculosis by Waaler et al., Ferebee et al., and Revelle et al. are the pioneering models of tuberculosis [9, 10, 11, 12, 13]. In this section, we give an introduction to epidemiological models of tuberculosis and their determinants.

2.2.1. Epidemic unit: Individual

The basic unit of an epidemiological TB model is an individual. Epidemiological models divide the host population into compartments of individuals by disease status. Common abbreviations for compartments used in population biology literature are:

• S: Susceptible. Individuals not yet infected.

• E: Exposed, latent. Infected, but not infectious.

• I: Infected and infectious.

• R: Recovered by treatment, self cure, or quarantine.

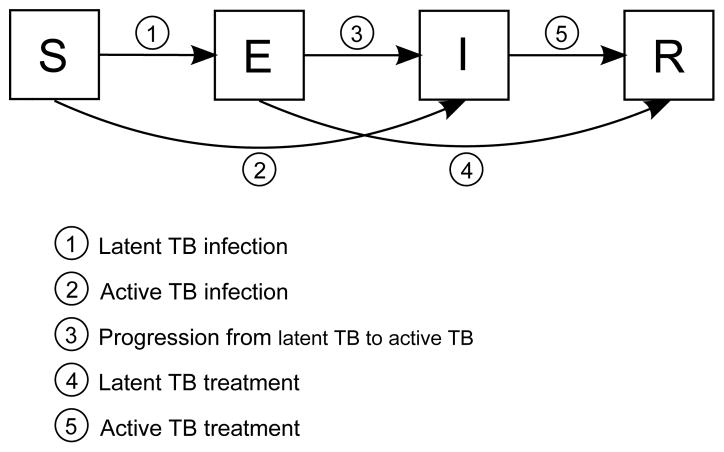
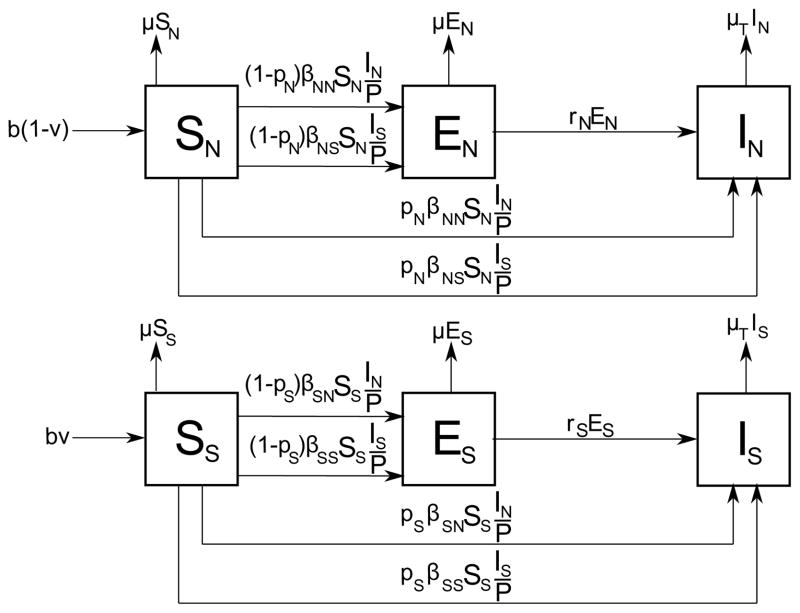
Various epidemiological models can be built using these compartments: SIR is a model that includes susceptibles, infected individuals and recovered individuals, but does not account for latent TB infection. SEI is a model that includes latently infected individuals, but does not account for TB treatment/recovery. An SEIR model accounts for both latent TB infection and TB treatment/recovery. Different compartments can be included or excluded according to the assumptions of the epidemiological models. A generic SEIR model is shown in Figure 2, along with transitions between compartments. Commonly used parameters of the SEIR model are shown in Table 1, and the same symbols will be used throughout this study, unless otherwise stated.

Figure 2.

SEIR model. Each compartment refers to the set of individuals by disease status: Susceptible, Exposed, Infected, Recovered. Newborn individuals are assumed susceptible. A TB infection can remain latent, or can directly develop into active TB. The latent TB infection can become active through endogenous reactivation or exogenous reinfection. Patients with latent or active TB can recover from TB by treatment, self cure, or quarantine.

Table 1.

Common parameters of epidemiological models of tuberculosis. SEIR model can be extended by incorporating additional parameters to the model.

Parameter	Description	Unit
β	Transmission rate	1/year
π	Recruitment rate	1/year
c	Natural cure rate	1/year
v	Progression rate from latent TB to active TB	none
r1	Latent TB treatment rate	1/year
r2	Active TB treatment rate	1/year
μ	Natural mortality rate	1/year
μT	Mortality rate due to TB	1/year
p	Proportion of new infections that produce active TB case	1/year

2.2.2. Basic reproductive number

The basic reproductive number (R₀) is an important parameter that determines the future of an epidemic. It is the average number of secondary infections produced when one infected individual is introduced into a host population where everyone is susceptible [14]. In other words, it is the average number of successful offspring that a parasite is intrinsically capable of producing. Basic reproductive number, R₀, can be derived from the model parameters in Table 1. The derivation of an analytical expression for R₀ depends on the epidemiological model.

The rate at which new susceptibles are introduced to a host population is called the recruitment rate, and is equivalent to birth rate for closed populations. When an infection becomes established in a host population, the fraction of susceptible individuals starts to decrease. Eventually, the rate at which new susceptibles are introduced to the population equals the rate at which susceptibles are being infected, and an endemic equilibrium is obtained [14]. At equilibrium, each infected individual produces one secondary infection on average. Given S susceptibles in a homogeneous population of size N, the equilibrium condition is:

$$R_0\frac{S}{N}=1$$

Epidemic infections show rapid changes in the prevalence of infection and can disappear from host population for time periods of varying length. Endemic infections, on the other hand, persist for short or long periods with little fluctuation in prevalence [15]. A pathogen must have R₀ > 1 if it is capable of establishing an endemic infection in a host population to ensure that the number of cases is nondecreasing.

One of the primary goals of building an epidemiological model of tuberculosis is to determine under what conditions the disease will reach an endemic state. Epidemiologically, this question is answered by determining the basic reproductive number of an infection for a population. R₀ > 1 implies that the endemic steady state is stable and the infection will spread in the population. R₀ ≤ 1 implies that the uninfected steady state is stable, and the infection will die out in the population. An exception to this rule occurs in the presence of exogenous reinfection, where endemic state can be supported even when R₀ ≤ 1 [16]. This result is based on the threshold theory introduced by the Kermack-McKendrick model, an SIR model with homogeneous population [17]. Variations of the Kermack-McKendrick model for different types of epidemiological models are introduced by Brauer et al. [18].

2.2.3. Incidence and prevalence

TB incidence and prevalence are central to the rate of tuberculosis transmission. TB incidence is defined as the rate of appearance of new TB cases per unit time. TB prevalence is the proportion of infected individuals at one point in time, or over a short time period. The measurement of incidence and prevalence is often based on stratification of the population by a variety of factors, such as age, ethnicity, etc.

Styblo found a relationship between the incidence of TB, the prevalence of TB and the annual risk of TB infection in the population, using the surveys from the pre-drug era [19]. He assumed that death per year, the incidence per year and the prevalence per year holds the ratio 1:2:4, meaning an average infectious period of 2 years, and 50% mortality rate. Using the data from 16 countries, the ratio of the number of new infections per 100000 per year to the number of prevalent TB cases per 100000, as derived from annual risk of TB infection, ranged from 8 to 12, known as the Styblo rule. With the new TB control programs and interventions, the Styblo rule is no longer valid. A recent study by van Leth et al. shows that the number of TB infections per prevalent TB case ranged from 2.6 to 5.8 in recent surveys [20, 21]. Therefore, with improved TB control programs, the Styblo rule can no longer estimate the incidence of TB. Surveys from countries with high and intermediate TB burden are currently the most reliable sources for estimating the incidence and prevalence of TB.

Other parameters that characterize an epidemic include epidemic doubling time, epidemic length, and threshold population size. Epidemic doubling time is the time period required for the number of cases in the epidemic to double. It is a measure of the rate of spread of the disease and it changes over the course of an epidemic. Epidemic length is the time it takes for an epidemic to rise, fall, and reach an endemic equilibrium, or die out. The age of an epidemic is determined by its epidemic length: an epidemic is called a young epidemic if it did not yet reach its endemic equilibrium, and it is a mature epidemic if it reached its endemic equilibrium. Critical community size is the minimum number of susceptibles above which disease fadeout over a given period is less probable than persistence of the disease [22]. A related parameter specific to models that conform to pseudo mass-action law is the threshold population size, which is the minimum number of susceptibles that have to be present before a tuberculosis epidemic can occur. We will frequently refer to these terms to either characterize the common structures of epidemics or distinguish between different epidemics.

3. Transmission dynamics

Tuberculosis case rates declined in the last decades due to reduction in transmission and progression of the disease as a consequence of improvements in living and working conditions and drug treatment or quarantine of more patients due to increased and early detection of tuberculosis [8, 23]. However, the brief increase in incidence rate around 1990 suggests a change in the epidemiology of tuberculosis. This increase is attributed to increased pathogen resistance to antituberculosis drugs and to the HIV epidemic that arose at the beginning of the 1990s. Hence, tuberculosis is still one of the leading diseases responsible for many human deaths despite all efforts. In this section, we explain the dynamics of tuberculosis epidemics. We expand tuberculosis transmission models for heterogeneous populations and transmission in small social clusters. We finally present genotype-based epidemiological models.

3.1. Intrinsic dynamics of tuberculosis epidemics

A patient infected with tuberculosis has a higher risk of developing an active TB case in the earlier stages of infection. The likelihood of developing active disease after infection decreases with the age of the infection, unless the individual is exogenously reinfected by another MTBC strain. This likelihood is higher within the first 2 years of infection, and latency periods vary [24, 25]. This suggests that tuberculosis is a slow disease. In this section, we provide time-dependent analysis of epidemiological models to show the slow progression of TB and further details of its spread.

3.1.1. Tuberculosis epidemic as a series of linked subepidemics

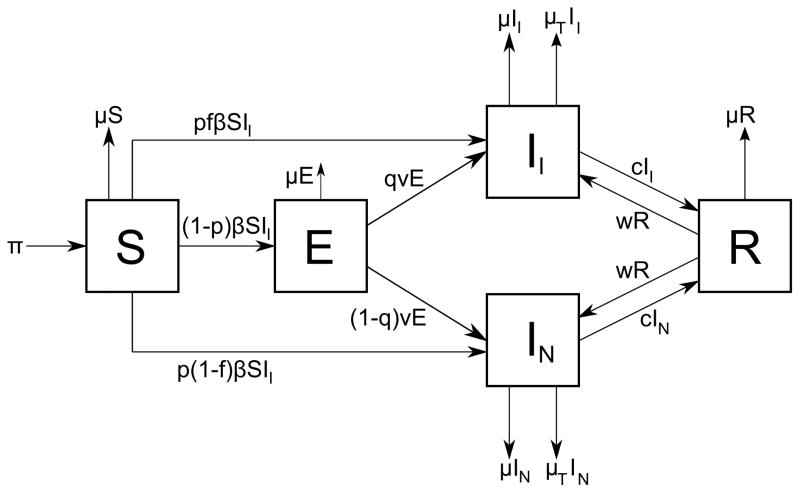
Blower et al. demonstrated that it takes several hundred years for a tuberculosis epidemic to rise, fall, and reach an endemic state [26]. The authors built an SEIR model in which the infectious class I is subdivided into two classes: (a) infected and infectious individuals I_I and (b) infected and noninfectious individuals I_N. There are two ways of infection according to the model, primary infection (fast tuberculosis) and secondary infection by endogenous reactivation (slow tuberculosis). It is assumed that exogenous reinfection does not occur. The model is a system of five nonlinear ordinary differential equations, one for each compartment, which can be traced by the help of Figure 3:

$$\begin{gathered} \frac{dS}{dt}=\pi -\beta S{I}_I-\mu S \\ \frac{dE}{dt}=(1-p)\beta S{I}_I-(v+\mu )E \\ \frac{d{I}_I}{dt}=pf\beta S{I}_I+\mathit{qvE}+wR-(\mu +{\mu }_T+c)I_I \\ \frac{{dI}_N}{dt}=p(1-f)\beta S{I}_I+(1-q)vE+wR-(\mu +{\mu }_T+c)I_N \\ \frac{dR}{dt}=c(I_I+I_N)-(2w+\mu )R \end{gathered}$$ (1)

where f and q are probability of developing infectious TB if one develops fast and slow TB respectively, 2w is the relapse rate to active TB, and the remaining parameters are defined in Table 1. Most of the parameters are taken from the medical literature with their minimum, maximum, and peak values by Blower et al., and other parameters are derived from estimates of these parameters. The model is based on pseudo mass-action law and the transmission term of the model is βSI_I. Therefore, as in all pseudo mass-action models, the basic reproductive number of the epidemic depends on the total population size, N. As a result, there exists a threshold population size above which the disease persists when the recruitment rate reaches a critical value [27].

Figure 3.

SEIR model of Blower et al. in [26] with infectious and noninfectious infected individuals. Class S represents susceptible individuals, E represents latently infected individuals, I_I and I_N represent infectious and non-infectious infected individuals respectively, and R represents recovered individuals.

Simulation results of model (1) showed that a tuberculosis epidemic can be viewed as a series of linked subepidemics: a fast tuberculosis subepidemic driven by direct progression, a slow tuberculosis subepidemic driven by endogenous reactivation, and a relapse tuberculosis subepidemic driven by relapse cases. This proves that young and mature tuberculosis epidemics behave differently and it suggests that different control strategies may be necessary for controlling each subepidemic. The basic reproductive number of tuberculosis epidemics modeled by system (1) is:

$$R_0={R_0}^{\mathit{fast}}+{R_0}^{\mathit{slow}}+{R_0}^{\mathit{relapse}}$$ (2)

where R₀^fast, R₀^slow, R₀^relapse are the basic reproductive numbers of the fast, slow, and relapse tuberculosis subepidemics respectively, formulated as:

$$\begin{gathered} {R_0}^{\mathit{fast}}=\left(\frac{\beta \pi }{\mu }\right)\left(\frac{1}{\mu +{\mu }_T+c}\right)pf \\ {R_0}^{\mathit{slow}}=\left(\frac{\beta \pi }{\mu }\right)\left(\frac{1}{\mu +{\mu }_T+c}\right)\left(\frac{q(1-p)v}{v+\mu }\right) \\ {R_0}^{\mathit{relapse}}=\left(\frac{\beta \pi }{\mu }\right)\frac{1}{(\mu +{\mu }_T+c)\left((\mu +{\mu }_T+c)-\frac{2wc}{2w+\mu }\right)}\left(\frac{p+(1-p)v}{v+\mu }\right)\left(\frac{wc}{2w+\mu }\right) \end{gathered}$$ (3)

According to the model defined in system (1), epidemic doubling time decreases as the average number of secondary infections produced by one infectious case per year increases. Also, the threshold population size increases as the transmission rate decreases. Tuberculosis epidemic length rises first, then falls and reaches an endemic equilibrium. Based on the simulations by Blower et al. on system 1, the length of an epidemic ranges from 31 years to 7524 years, with a median of 100 years, which proves the slow progression of tuberculosis epidemics.

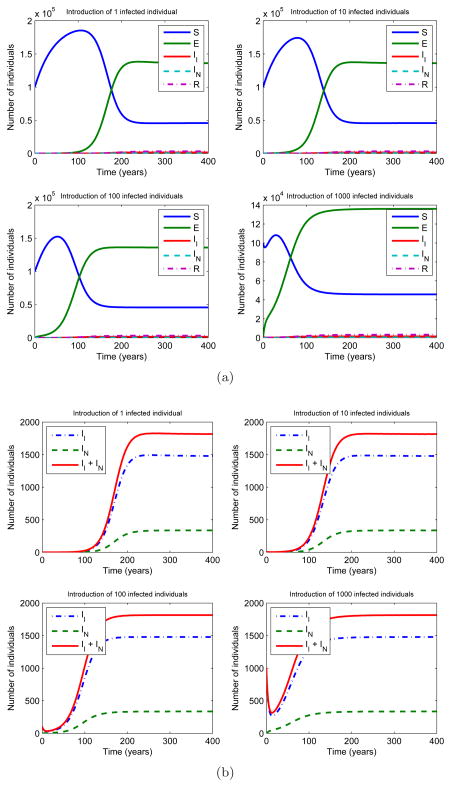
We ran simulations of model (1) with different population settings. We initiated four epidemics by introducing 1, 10, 100, and 1000 infected and infectious individuals respectively at time zero to a fully susceptible population of 100000 individuals. The epidemics were observed for 400 years to ensure that they reach an endemic equilibrium. Figure 4a shows the results of simulations of tuberculosis epidemics based on the model. The plots show that all four epidemics reach endemic equilibrium in the first 200 years. Moreover, as the number of infectious individuals introduced to the fully susceptible population decreases, the time it takes to reach endemic equilibrium increases. Figure 4b shows the number of infected individuals, either infectious or non-infectious, for the same set of simulations. Notice that all four epidemics have around 1800 infected individuals at equilibrium, independent of the number of infectious individuals introduced to fully susceptible population at t=0.

Figure 4.

(a) A numerical simulation of four tuberculosis epidemics using the model in Figure 3. The epidemics were initiated by introducing 1, 10, 100, 1000 infected and infectious individuals respectively at time zero to a fully susceptible population of 100000 (S = 100000, I_I = 1, 10, 100, 1000). The following parameter values were used: π = 4400, μ = 0.0222, μ_T = 0.139, v = 0.00256, p = 0.05, f = 0.70, q = 0.85, w = 0.005, c = 0.058, β = 0.00005. The epidemics were observed for 400 years to ensure they reach an endemic equilibrium. The plots show that all four epidemics reach endemic equilibrium in the first 200 years. As the number of infectious individuals introduced to the fully susceptible population decreases, the equilibrium time increases. (b) Number of infected individuals in four epidemics throughout the years. All epidemics have around 1800 infected individuals at equilibrium, independent of the number of infectious individuals introduced to fully susceptible population at t=0.

The SEIR model built by Blower et al. demonstrates the temporal dynamics of susceptibles, latently infected individuals, infectious and noninfectious infected individuals, and recovered individuals. Only a fraction of infected individuals are assumed infectious. Patients in hospitals or quarantined patients are classified as noninfectious infected individuals. This detailed model accounts for transitions among compartments and gives an estimate of population dynamics classified by all possible disease states.

3.1.2. Time-dependent analysis of tuberculosis epidemics

Progression of tuberculosis in an individual is slow and therefore progression of a tuberculosis epidemic in a population spans a long time period. A time-dependent analysis of tuberculosis epidemics is necessary to understand tuberculosis transmission dynamics in a population over time. Porco et al. analyzed model (1) using time-dependent uncertainty and sensitivity analysis in order to understand tuberculosis transmission dynamics [28]. The exact values of the input parameters to the model are uncertain, therefore Latin Hypercube Sampling (LHS) was used for uncertainty analysis. LHS generates multivariate samples of statistical distributions [29]. It is used to understand how an output Y of a model, which is a function of X₁, X₂, …, X_k, varies when the X_i’s, where i ∈ {1, .., k}, vary according to a joint probability distribution. For parameters with minimum, peak, and maximum values, a triangular distribution function is used for LHS. For parameters with minimum and maximum values, a uniform distribution function is used for LHS. Uncertainty analysis of the model suggested that initial doubling time ranges from 0.35 years to 539 years, with a median of 2.3 years, for 99.5% of all simulations for epidemics with R₀ > 1. The median of equilibration time is 100.1 years with a minimum value of 35.9 years, proving the slow progression of tuberculosis epidemics.

Young and mature tuberculosis epidemics follow different patterns. The median, first quartile, and third quartile of incidence of infection and incidence of disease are further apart at the beginning of an epidemic, and in later stages of the epidemic these values converge. This suggests that the variances of incidence of infection and incidence of disease are higher in a young epidemic. Prevalence of infection follows a similar pattern over time. The median prevalence of infection is lower than 20% in the first 26 years, while prevalence of infection for first quartile and third quartile are 1% and 83% respectively. In the later stages of the epidemic, the epidemic reaches equilibrium, and the median prevalence of infection is 74%, while the first quartile is 64% and third quartile is 81%. This also suggests that variance of prevalence of infection is high in a young epidemic, whereas it is lower in a mature epidemic when the epidemic reaches equilibrium.

Time-dependent sensitivity analysis using partial rank correlation coeffcients (PRCC) determines which input parameters of the model generate the most variability in the outputs of the model over time [30]. The input parameters found to contribute most to the variability of model outputs are:

• Effective Contact Rate (Contagiousness parameter): $\mathit{ECR}=\frac{\beta \pi }{\mu }$

• Fraction of newly infected individuals who develop fast tuberculosis: p

• Mortality rate due to tuberculosis: μ_T

PRCC of p suggests that the uncertainty of p contributes to the variability of incidence of infection at the beginning of the epidemic, but its importance drops as the epidemic progresses. Therefore, the effect of the fraction of newly infected individuals who develop fast tuberculosis (direct progression from susceptible class to infected class) is high in a young epidemic, and its effect decreases as the epidemic reaches equilibrium in later stages. PRCC of prevalence of disease with respect to ECR, p, and μ_T are always high during the course of an epidemic.

3.2. Tuberculosis transmission in heterogeneous populations

The dynamics of tuberculosis transmission vary in heterogeneous populations. Transmission dynamics in high-risk countries and low-risk countries are different. In microcosm, individuals in the same disease state can also differ by their infectiousness. For such heterogeneous populations, the epidemiological models have to be modified to account for differences within the population.

3.2.1. High-risk countries and low-risk countries

Tuberculosis transmission rates vary in different parts of the world. Prevalence and incidence in high-risk countries are greater than in low-risk countries. For instance, prevalence of tuberculosis in India is around 50%, whereas it is 5% in the US.

Murphy et al. developed an epidemiological model to examine the effects of demographics on tuberculosis transmission [31]. They based their model on the fact that the frequency of the HLA-DR2 allele in the human genome, which is strongly associated with pulmonary TB, is high in India [32, 33]. A modified SEI model is used to reflect this observation by subdividing compartments of the model into two: S_N, E_N, I_N and S_S, E_S, I_S, where subscript N stands for neutral and denotes individuals without a susceptible genotype, and subscript S stands for susceptible and denotes individuals with a susceptible genotype. The model, shown in Figure 5, differentiates individuals by their genetic susceptibility, which is the highlighted difference between populations in India and in the US.

Figure 5.

TB model by Murphy et al. which captures TB dynamics in high-risk and low-risk countries. The compartments of SEI model are subdivided into two: S_N, E_N, I_N and S_S, E_S, I_S, where subscript N stands for neutral and denotes individuals without a susceptible genotype, and subscript S stands for susceptible and denotes individuals with a susceptible genotype. β_ij represents progression rate of a susceptible individual with genetic susceptibility i to active TB case with genetic susceptibility j, where i, j ∈ {S, N}. The probability p_i represents direct progression rate to active TB, and r_i represents reactivation rate of latent TB. The population is represented by P = S_N + E_N + I_N + S_S + E_S + I_S.

Murphy et al. tested the hypothesis that enhanced susceptibility observed with HLA-DR2 allele explains why the prevalence of tuberculosis in India is higher than it is in the US. They studied the direct progression rate to active TB (p_s), reactivation rate from latent TB to active TB (r_s), and transmission and receptive rates of infection, β_ij, where i, j ∈ {S, N}. β_ij represents progression rate of a susceptible individual with genetic susceptibility i to active TB case with genetic susceptibility j. A PRCC of these input parameters of the model indicates that p_s, r_s, β_NN and β_NS = β_SN are the main contributors to the variation from baseline prevalence, while p_s and r_s are the main contributors to the variation from baseline incidence.

In the model shown in Figure 5, birth rate (b), natural death rate (μ), fraction of population genetically susceptible to infection (v), and transmission parameters β_ij, where i, j ∈ {S, N} are the paremeters influenced by demographics:

• As μ increases, the number of individuals at risk decreases, thereby decreasing the prevalence of TB.

• As v increases, leading to a large genetically susceptible population, prevalence is not strongly dependent on β_ij. As v decreases, leading to a small genetically susceptible population, such as the US, prevalence is more sensitive to β_ij, especially to β_NN. This is because the classes S_N and I_N constitute the majority of such populations.

• The higher the population density, the higher the likelihood of encountering an infectious individual, which increases transmission paremeters β_ij. Population density in India is 15 times larger than that of the US, which leads to higher β_ij values.

This analysis shows that the model parameters may differ according to demographics and change the tuberculosis transmission dynamics.

3.2.2. Reasonable and unreasonable infectives

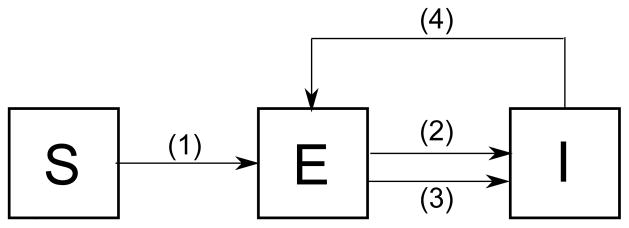
Heterogeneity of a population can be observed within a compartment, depending on the behavior of individuals. Nyabadzaa et al. subdivided infectives into two classes: reasonable infectives, the infectives who are careful not to spread the infection, and unreasonable infectives who spread the infection without caring about it [34]. TB interactions in this community are investigated using a graph theoretic approach, based on an SEI model. Among all |I| infectives, |R| of them are assumed reasonable infectives and the proportion $\alpha =\frac{\mid R\mid }{\mid I\mid }$ is defined as the fraction of reasonable infectives. Only four transitions between states shown in Figure 6 are considered: primary infection, endogenous reactivation, exogenous reinfection, and recovery from active TB, which is the transition from I to E, since there is no compartment for recovered individuals. The network of individuals in the community can be defined as a graph G = (V, E) where the vertices of the graph represent individuals and edges of the graph represent contacts between individuals. At time t, a vertex belongs to one of S, E or I in the network.

Figure 6.

Transitions showing the interaction of the individuals in the network model of Nyabadzaa et al. Transition (1) represents infection of susceptibles through contact with a suffcient number of infectives, called the primary infection. Transitions (2) and (3) represents TB reinfection through exogenous reinfection and endogenous reactivation. Transition (4) represents recovery from active TB.

The simulations based on transition rules for primary infection, endogenous reactivation, exogenous reinfection, and recovery show that an increase in the number of contacts results in a high number of active TB cases. Another simulation was run with the introduction of an infective into a population with a mean of three contacts. If this infected individual is reasonable, the number of infections that occur in the population is small. If the infective is unreasonable, this unreasonable infective results in many new infections in the population. In this network model of n individuals, if $\alpha \ge 1-\frac{1}{n}$, the epidemic dies out. This loose upper bound on α suggests that even one unreasonable infective in the network can result in the persistence of the disease.

3.3. Tuberculosis transmission in microcosm

Tuberculosis transmission can be observed at the social cluster level as well as at the population level. In microcosm, the risk factors are social clusters, public transportation, and overcrowding in confined spaces. Jia et al. reviews the effect of two risk factors: casual/random contact and public transportation [35].

3.3.1. Social clusters

The types of relationships between individuals in a social cluster can be used to define types of contacts. The quality of the contact is related to its frequency and its duration [36]. Close contacts are individuals who are daily and prolonged contacts in the local network. They are intimate contacts in families, schools or at the workplace. On the other hand, casual contacts are individuals who are close but infrequent contacts in the global network. They are random contacts such as people sharing the same bus route every day. The basic cluster model distinguishes between a close contact and a casual contact [3, 37]. A generalized household or cluster is defined as a group of close contacts. An epidemiologically active cluster is a generalized household with infectious individuals. When there is no infected individual, the cluster is inactive. If an infected individual is introduced into the fully susceptible cluster, then the status of the cluster changes and it becomes an active cluster.

Generalized households are defined as reasonable epidemiological units. Aparicio et al. built an SEI-like model, and subdivided the compartments S and E into two: individuals who belong to an epidemiologically active cluster (S₁ and E₁), and those who do not (S₂ and E₂), such that N₁ = S₁ + E₁ and N₂ = S₂ + E₂ [3]. The basic reproductive number of this model is:

$$R_0=\frac{\beta n}{\beta +\gamma }\frac{v}{\mu +v}$$

where γ is the removal rate from the population, n is the average generalized household size, and β, μ, v are defined as in Table 1. When an infectious individual has contacts in another epidemiologically active cluster which results in a secondary infection, then this infection is the result of a casual contact, instead of a close contact. Assuming that such infections occur in population N₂, we get a slightly modified model with 5 compartments. This model suggests that the emergence of new social dynamics due to urbanization has increased transmission rate for casual infection. Therefore, casual infections such as the ones occurring in mass transportation may be one of the reasons for re-emergence of TB in the last decades.

One can consider a community as a square lattice on ℤ^d, and each site of the lattice as a cluster. Schinazi et al. presented this spatial stochastic model for the spread of tuberculosis among clusters and within a cluster [38]. The model considers three parameters: cluster size N, inter-cluster transmission rate λ, and within cluster transmission rate φ. Neighbours of a cluster are the sites which have a common border to the site of the cluster. Figure 7 shows a community represented as a 2-D square lattice. The stochastic process, denoted as η_t, is as follows: For a site x, η_t(x) = i means that there are i infected individuals among N individuals at site x. Hence, each site can take one of N+1 possible states. Let the initial configuration of the community be composed of susceptible individuals and one infected individual in the cluster at the origin of ℤ^d. Let |η_t| denote the total number of infected individuals at time t. The probability that the infection will persist in the population can be formulated as:

$$P(\mid {\eta }_t\mid \ge 1;\text{for}\text{all}\text{t}\ge 0)$$

which increases with λ, φ, N. Given N, φ, we define the critical value for transmission rate as:

$${\lambda }_c(N,\phi )=\mathit{inf}\{\lambda >0:P(\mid {\eta }_t\mid \ge 1;\text{for}\text{all}\text{t}\ge 0)>0\}$$

Figure 7.

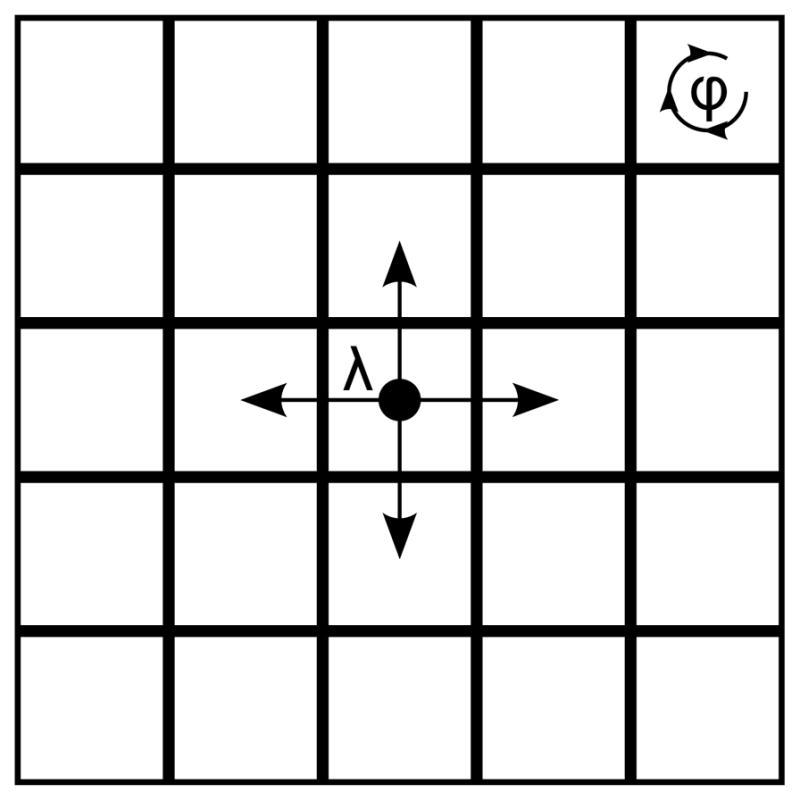
Representation of a community as a square lattice on ℤ². Each site represents a cluster and neighbours of a cluster are the sites which have a common border to the site of the cluster. Inter-cluster transmission rate is λ, and within cluster transmission rate is φ.

If λ < λ_c(N, φ), the infection dies out. If λ > λ_c(N, φ), the infection persists in the population. This model with N = 1 is called the basic contact process, in which each cluster has one individual, and two possible states: susceptible or infected. The critical value λ_c(N = 1, φ) does not depend on φ, because there is only one individual in each cluster. Therefore, λ_c(1, φ) = λ_c(1) is the critical value for transmission rate. The analysis of the model for general cluster size leads to three cases:

1. If λ > λ_c(1), then the epidemic will persist in the population independent of the cluster size N.

2. If λ < λ_c(1), there are two cases:

   1. If $N<\frac{{\lambda }_c(1)}{\lambda }$, the epidemic dies out.

   2. If $N>\frac{{\lambda }_c(1)}{\lambda }$, the epidemic can only persist if the within cluster transmission rate φ is above critical value φ_c of within cluster transmission rate, that is, φ > φ_c.

This square lattice model simulation shows that the future of an epidemic in a community depends on social cluster size, within cluster transmission rate and inter-cluster transmission rate.

The static network model of transmission with varying clustering coefficient built by Cohen et al. compares the contribution of different infection routes: primary progression, endogenous reactivation of latent TB infection, and exogenous re-infection [39]. Higher clustering coefficient causes MTBC to be transmitted locally and results in higher density of infection in the neighborhood of the infected individual. In such a setting where local mixing predominates, Cohen et al. found that exogenous reinfection makes a larger contribution to disease dynamics than previously recognized. This suggests that in large communities with low TB incidence, the network structure of the population allows exogenous reinfection to play an important role in disease burden.

3.3.2. Public transportation

Tuberculosis infection is possible not only within a social cluster, but also among social clusters, as people move freely using public transportation, which enables contact with people from different clusters. Castillo-Chavez et al. used a model to simulate this clustered community for public transportation [40]. According to the model, a city is divided into n neighborhoods. The individuals in a neighborhood are subdivided into two categories according to whether they frequently take a bus or not. Call the infrequent bus-takers type I individuals and frequent bus-takers type II individuals. The resulting model is a variant of an SEIR model: The population of type j individuals in the i-th neighborhood is described as N_i^j = S_i^j + E_i^j + I_i^j + R_i^j. Using this model, it is found that the larger the difference of prevalence between neighborhoods, the larger the basic reproductive number. After estimating relevant parameters, it is found that 100 people enter and leave a bus in an hour on average, and one TB infection per 1000 bus-takers occurs. This suggests that one TB infection in 10 hours will occur in a bus on average.

A case study on public transportation held in Peru by Horna-Campos et al. supports the effect of public transportation on new TB cases [41]. The study focuses on the significance of public transportation in Latin America, as more passengers than permitted by law are carried by public transportation. The analysis of results points out that a large proportion of susceptible individuals, a disseminator of MTBC such as public transportation, overcrowding, and lack of ventilation are main factors resulting in TB outbreaks in public transportation. In areas with endemic pulmonary TB, daily use of public transportation is a risk factor for acquiring TB. It is also observed from patient statistics that long travel time is another important risk factor. These results suggest that duration of exposure to TB infection and density of the cluster are the main factors for acquiring TB in public transportation.

3.3.3. Models of overcrowding in confined spaces

Overcrowding in confined spaces increases the likelihood of TB transmission. Beggs et al. compared three models which estimate the transmission of airborne diseases in confined spaces: the Mass Action Model (MA), Riley-Murphy-Riley’s Model (RMR), and Gammaitoni and Nucci’s model (GN) [42, 43, 44]. These models focus on TB transmission in spaces with overcrowding or poor ventilation, which enables close contact with infected individuals.

The Mass Action model states that the number of infectious transmissions per infected case is a function of the number of susceptible individuals in the population. It has been used to model the dynamics of measles outbreaks, in which an increase in the number of infected individuals causes the number of susceptible individuals to decrease. The number of new cases is

$$C=\mathit{rIS}$$

according to the MA model, where C is the number of new infections, S is the number of susceptibles, I is the number of infected individuals, and r is the effective contact rate. As the outbreak progresses, S decreases and I initially increases. If C/I > 1, the infection spreads in the population with the outbreak. If C/I < 1, then the outbreak fades out. If C/I = 1, the outbreak is in steady state and each infected individual infects exactly one susceptible individual.

The Riley-Murphy-Riley model (RMR), or Wells-Riley model, focuses on the probability of a susceptible individual becoming infected by inhaling a quanta of infection. Their model suggests the following equation for the number of new cases:

$$C=S(1-e^{-\phi pt/Q})$$

where φ is the average number of infectious doses generated per infector (quanta/min), p is the pulmonary ventilation rate (m³/min), t is the duration of exposure to infection (min) and Q is the room ventilation rate.

Gammaitoni and Nucci’s model (GN) accounts for the change of quanta level over time. The number of new cases according to this model is:

$$C=S_0(1-e^{f(p,I,\phi ,V,N,n_0,t)})$$

where S₀ is the number of susceptibles at time t = 0, V is the room volume (m³), N is the ventilation rate (air changes/min) and n₀ is the initial quanta amount at time t = 0.

Comparison of these three models suggests that the GN model is the most comprehensive model, and it is the most suitable model for estimating the risk of disease in confined spaces. RMR model is a more comprehensive model than the simple MA model.

In this section, we presented the transmission dynamics of tuberculosis epidemics using epidemiological models. Parameters used in these epidemiological models are either obtained from the medical literature or estimated from patient datasets. One parameter that is commonly estimated is the transmission rate. Markov Chain Monte Carlo methods and Approximate Bayesian Computation are commonly used methods to estimate transmission rate [45, 46, 47, 48, 49, 50]. The transmission rate can also be estimated from numbers of patients and distinct genotypes from patient datasets [51, 52]. In the next section, we present epidemiological models which explain the effect of treatment on tuberculosis transmission dynamics.

4. Treatment

Control strategies for TB treatment have to be modeled mathematically to observe their long-term effects. Although treatment is expected to decrease the number of cases intuitively, an incorrect choice of treatment strategy can lead to severe epidemics through various levels of drug resistance or to an insufficient decrease in the number of cases to eradicate the disease [53]. Therefore, proper care has to be given to the choice of combinations of treatment strategies.

4.1. Effects of treatment on tuberculosis transmission dynamics

Different types of tuberculosis treatment are available. Chemoprophylaxis is the treatment of latent TB infections and therapeutics is the treatment of active TB infections. Strains may gain resistance to anti-tuberculosis drugs and may thus require advanced treatment rather than chemoprophylaxis or therapeutics. In this section, we will focus on the effects of chemoprophylaxis and therapeutics on one-strain models and two-strain models.

4.1.1. One-strain models

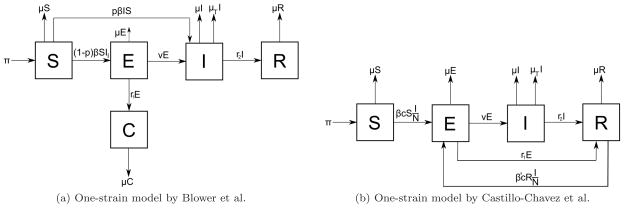
One-strain models account only for drug-sensitive cases only. Blower et al. developed a model for designing effective control strategies to determine levels of eradication of tuberculosis [54]. The model is a single-strain model, similar to the SEIR model, and the set of recovered individuals is subdivided into two classes to distinguish between treatment of individuals with latent TB and active TB, as in Figure 8a: the class of individuals effectively treated by chemoprophylaxis (C) and the class of individuals effectively treated by therapeutics (T). The effective reproductive number R of this model, defined as the average number of secondary infections produced by an infected individual during the entire period of infectiousness [55], is:

$$R=\left(\frac{\beta \pi }{\mu }\right)\left(\frac{1}{\mu +{\mu }_T+r_2}\right)\left(p+(1-p)\frac{v}{v+\mu +r_1}\right)$$

where all parameters are defined in Table 1. Therefore, the basic reproductive number of the model is the product of the effective contact rate, the average duration of infectiousness of a case, and the probability that an infected individual will become an infectious case. Blower et al. conducted an experiment with mild (R = 4), moderate (R = 9) and severe (R = 17) epidemics with different combinations of therapeutics and chemoprophylaxis success rates. The results indicate that it is possible to eradicate tuberculosis either by therapeutics alone or by a combination of therapeutics and chemoprophylaxis, but not by chemoprophylaxis alone. Even when a small fraction of infected but non-infectious individuals are treated by chemoprophylaxis, TB incidence decrease significantly, but the disease does not eradicate [56].

Figure 8.

a) One-strain model of Blower et al. b) One-strain model of Castillo-Chavez et al. c denotes per-capita contact rate. β and β′ denote the probabilities that susceptible and recovered individuals become infected by one infectious individual per contact per unit time.

A similar one-strain model was proposed by Castillo-Chavez et al. with the assumption of homogeneous mixing of the population and ignoring long latency periods [57]. They propose the simple SEIR model shown in Figure 8b. Compared to the one-strain model of Blower et al., this model lacks the compartment for individuals treated by chemoprophylaxis, and it uses the transition from E to R to simulate the effect of chemoprophylaxis. The basic reproductive number of this model is given by the product of average number of susceptibles infected by one infectious individual during the infectious period and the fraction of population which survives the latent period:

$$R_0=\left(\frac{\beta c}{\mu +{\mu }_T+r_2}\right)\left(\frac{v}{\mu +v+r_1}\right)$$

where c is the per-capita contact rate and the other parameters are defined in Table 1. There are two possible equilibria for this model:

1. If R₀ ≤ 1, the population is in disease-free equilibrium. If R₀ < 1, then disease-free equilibrium is globally asymptotically stable.

2. If R₀ > 1, the population is in endemic equilibrium. The infection will spread in the population.

4.1.2. Two-strain models

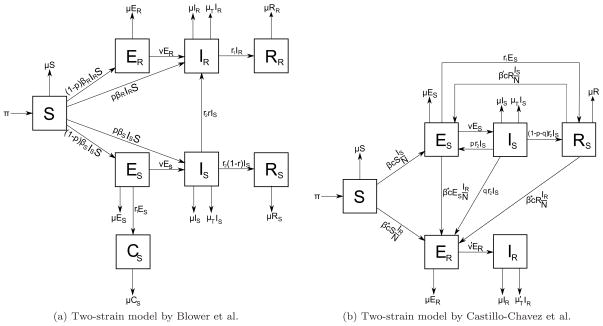
Treatment failure can lead to drug resistance, which is a challenge to control programs, as these drug-resistant strains are more difficult to treat. To account for drug resistance, Blower et al. built a two-strain model, a linked control model, by integrating drug resistance [54]. This model consists of eight compartments: susceptible (S), latently infected individuals with drug-sensitive TB and drug-resistant TB (E_S and E_R), infected individuals with drug-sensitive TB and drug-resistant TB (I_S and I_R), individuals with drug-sensitive TB who are treated by chemoprophylaxis (C_S), and effectively treated individuals with drug-sensitive and drug-resistant TB (R_S and R_R). It is assumed that chemoprophylaxis can not treat drug-resistant TB. The linked control model is shown in Figure 9a. To evaluate drug resistance in the context of control strategies, maximum acceptable probability of treatment failure, r_max, defined as the probability of treatment failure at which X cases of drug resistance are generated for each treated drug-sensitive case, is used. It is formulated as:

$$r_{\mathit{max}}=\frac{X}{1+R_{DR}}$$

where X is the percentage of drug-resistant cases generated during treatment of a drug-sensitive case and R_DR is the number of primary drug-resistant cases that are produced by one drug-resistant case. r_max is proportional to the effectiveness of treatment of a drug-resistant case relative to the effectiveness of treatment of a drug-sensitive case. The criterion r_max can be used to evaluate a control strategy as follows: if the treatment strategy results in a probability of treatment failure < r_max, then the strategy is beneficial, and ineffective otherwise.

Figure 9.

a) Two-strain model by Blower et al. b) Two-strain model by Castillo-Chavez et al. β^* is the probability that treated individuals become infected by one DR-TB individual per contact per unit time. v′ is the progression rate from latent TB to active TB for DR-TB cases. ${\mu }_T^{\prime }$ is the mortality rate due to DR-TB. p and q are the proportions of infected individuals who did not complete treatment and became latent DS-TB and DR-TB case respectively.

A two-strain model is also proposed by Castillo-Chavez et al. by subdividing classes E and I of the SEIR model into two: E_S, E_R and I_S, I_R, where subscript S represents drug-sensitive TB cases and R represents drug-resistant TB cases [57]. According to this model, shown in Figure 9b, the basic reproductive numbers of drug-sensitive and drug-resistant TB, R_0s and R_0r, are given by:

$$\begin{gathered} R_{0s}=\left(\frac{\beta c+{pr}_2}{\mu +{\mu }_T+r_2}\right)\left(\frac{v}{\mu +v+r_1}\right) \\ {R}_{0r}=\left(\frac{{\beta }^{\ast }c}{\mu +{{\mu }_T}^{\prime }}\right)\left(\frac{v^{\prime }}{\mu +v^{\prime }}\right) \end{gathered}$$

where c is the per-capita contact rate, defined as the average number of susceptible individuals that one infectious individual infects per unit time. β^* is the probability that treated individuals become infected by one drug-resistant TB infectious individual per contact per unit time. Therefore, the basic reproductive number of this model is the maximum of the two: R₀ = max (R_0s, R_0r). Assuming β^* = β and given q as the rate of progression from the infectious state with drug-sensitive TB to the latent state with drug-resistant TB, this system has four possible equilibria:

• E₁, disease-free equilibrium. (q ≠ 0)

• E₂, the equilibrium in which only the drug-resistant strain is present. (q ≠ 0)

• E₃, the equilibrium in which both strains are present. (q ≠ 0)

• E₄, boundary equilibrium, in which only the drug-sensitive strain is present. (q = 0)

Numerical simulations of this model show that coexistence of naturally resistant strains, which become resistant through acquisition rather than transmission, is possible, but rare. This suggests that competitive exclusion of strains is preferred rather than coevolution. Moreover, the incorporation of age of infection as a parameter to two-strain models by Feng et al. shows that distributed delays in the latency period do not change the transmission dynamics of DS-TB and DR-TB [58].

4.2. Treatment strategies in different demographics

Treatment in demographically distinct, heterogeneous populations requires combinations of treatment strategies to cover and focus on genetically susceptible individuals and individuals in high-risk countries. An epidemiological model was created by Murphy et al. to examine the effects of different treatment strategies in different demographics [59]. The model is based on the same model they used in [31], the SEI model shown in Figure 5, in which each compartment is subdivided into two depending on the genetic susceptibility of the host: genetically neutral or genetically susceptible. The model was tested for high growth (HG) populations and low growth (LG) populations. The simulations for the following cases are performed : 1) Therapeutics, treatment of active TB only and 2) Chemoprophylaxis, treatment of latent TB only. These two simulations suggest that a treatment strategy consisting of chemoprophylaxis only is not as effective as a treatment strategy consisting of therapeutics only, which produces a more rapid reduction in TB prevalence. Therefore, the model suggests that an effective treatment strategy should consider therapeutics alone or together with chemoprophylaxis, which is concordant with the results of the one-strain model built by Blower et al [54]. A treatment strategy consisting of both chemoprophylaxis and therapeutics is ideal for targeting individuals infected with latent TB and active TB. This treatment strategy is more successful than either approach alone in reducing the prevalence.

These three treatment strategies were tested on both HG (e.g. India) and LG (e.g. the US) populations. The results proved that TB in high growth populations can not be reduced to zero with treatment, independent of genetic susceptibility rate of the population. In addition, a treatment strategy that only targets genetically susceptible individuals can be successful. This suggests that TB treatment focusing on genetically susceptible individuals is a good treatment strategy to reduce the prevalence of TB.

4.3. Class of loss of sight

TB treatment is hard to comply with due to the long duration of treatment which requires 6–9 months of taking pills every day. Therefore, infectious individuals who begin effective therapy in hospitals may not be tracked if they never return back to the hospital for examinations after being discharged. For such individuals, we lack information about whether the individual died, recovered, or is still infectious. Therefore, Bowong et al. introduced a new epidemiological class, class of loss of sight [60]. This epidemiological model consists of four compartments: susceptible (S), latent (E), infectious (I), and loss of sight (L). The infectivity of classes I and L are different, since all individuals in class I are infectious, but the percentage of infectious individuals in class L is unknown. An analysis of the model based on basic reproductive number suggests that the system has two possible equilibria:

1. If R₀ ≤ 1, the disease-free equilibrium is globally asymptotically stable, which means that the disease naturally dies out. The system is in state (S,E,I,L) = (S^*,0,0,0).

2. If R₀ > 1, there exists a unique endemic equilibrium (S^*, E^*, I^*, L^*) and this equilibrium is globally asymptotically stable, which means that the disease will persist in the population.

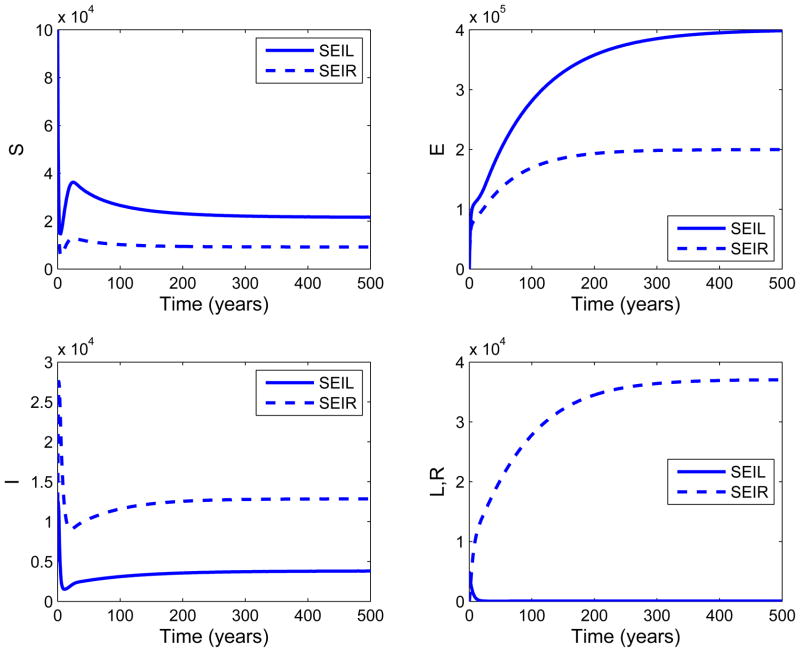
The SEIL model of Bowong et al. built for class of loss of sight is similar to the SEIR model of Blower et al. in [26]. However, they are different due to the incomplete information in the SEIL model. If R₀ ≤ 1, then both models have the same behavior for classes S, E, I, L (R for SEIR model). For R₀ > 1, we ran simulations of this case to compare the epidemiological outcomes of SEIL and SEIR model. Figure 10 shows the time trajectories of S, E, I, and L(R) classes over 500 years. If R₀ > 1, time trajectories of classes S, E, and I have the same behaviour through time for both models. However, the time trajectory of class L decreases over time, whereas the time trajectory of class R increases over time. This is because an infected individual returns to the latent class E in the SEIL model after recovery, whereas it goes to class R in the SEIR model. Due to this same reason, the number of latently infected individuals at endemic equilibrium in the SEIL model is higher than that of the SEIR model.

Figure 10.

Comparison of SEIL and SEIR models when R₀ > 1. For common parameters of the SEIL and SEIR models, the following values are used: π = 4400, μ = 0.0101, v = 0.005, p = 0.3, β = 0.00005. For other parameters of SEIL and SEIR models, the values in [26] and [60] are used respectively. For the SEIL model, the epidemics were initiated by introducing 5000 infected individuals and 5000 individuals in the class of loss of sight at time zero to a fully susceptible population of 100000 (S=100000, I = 5000, L = 5000). For the SEIR model, the epidemics were initiated by introducing 10000 infected and infectious individuals at time zero to a fully susceptible population of 100000 (S=100000, I_I = 10000). The infected class I in the SEIR model is referred to as the sum of infected infectious and infected noninfectious classes. The plots show that the time trajectories of S, E, I classes of both models have the same behaviour. On the other hand, the number of individuals in class L decreases over time, while the number of individuals in class R increases. This is due to the fact that, in the SEIL model, an infected individual returns to class E after treatment, whereas it moves to class R in the SEIR model. Therefore, the number of latently infected individuals in class E of the SEIL model is higher than that of the SEIR model.

Bowong et al. extends this model by including n latent classes to account for long latency periods [61]. The model has the compartments S, E₁,..,E_n, I, L, R. The results show that, independent of the number of latent classes, the model is globally asymptotically stable, as in the previously developed SEIL model. This implies that the disease will fade out from the population when R₀ ≤ 1 holds.

4.4. Compliance to tuberculosis treatment: DOTS

Tuberculosis treatment is long and hard to complete. Therefore, there is a need for a program to force tuberculosis patients to complete their treatment. For this purpose, DOTS (Directly Observed Treatment, Short-Course) is used as an effective strategy for controlling TB epidemics. This program ensures compliance to treatment by making sure the steps of TB treatment are followed and the right amount of pills are taken on time.

Tuberculosis dynamics with DOTS can be simulated by varying the treatment success rate due to DOTS. Okuonghae et al. presented a mathematical model of tuberculosis dynamics with DOTS in Nigeria [62, 63]. The model subdivides the infectious class of the SEIR model into two: undetected infected individuals (I) and detected infected individuals (J) and uses an SEIJR model with two infectious classes. The individuals in class J are treated under the DOTS program, as these infected individuals are detected. The results of the model show that if the critical case detection rate is not reached, then R₀ > 1 and the disease will persist in the population endemically. In practice, DOTS has not succeeded in reducing the incidence of TB in Nigeria, despite all efforts. Only a small fraction of infected individuals are actually treated under DOTS, and the rest of the infected individuals are undetected and they cause an increase in the number of new cases. Therefore, the DOTS program in Nigeria should be expanded to ensure that more cases are detected [63]. The model by Murray et al shows that extending the DOTS strategy with various other control strategies such as mass preventive therapy, active case-finding using mass miniature radiography, breakdown vaccines, single-dose treatment regimen alone or combined with active screening can decrease TB incidence to a lower level [64, 65].

DOTS is a treatment program that handles drug-sensitive TB cases. Drug-resistant TB cases, although rare compared to drug-sensitive cases, require different stages of treatment. Therefore, a variant of DOTS, called DOTS-plus, is used to ensure compliance to the treatment of drug-resistant cases. In the next section, we present the effects of drug resistance on tuberculosis transmission dynamics using epidemiological models.

5. Drug resistance

If the treatment is not accurate or if it is incomplete due to non-compliance, MTBC can become immune to first-line drugs. This new type of TB, called drug-resistant TB (DR-TB), is harder to treat, and second-line drugs are needed for treatment. After acquisition of drug-resistant TB, resistant strains can also be transmitted, leading to new drug-resistant cases.

The emergence of resistance to anti-TB drugs was noted very soon after anti-TB drugs were introduced, in the 1950s. However, there were no systematic attempts to measure resistance prior to the World Health Organization (WHO) effort in the mid 1990s. Therefore, information about the drug resistance burden before the 1990s is scant (Ted Cohen, personal communication). Due to this insufficient data, the role of drug resistance in tuberculosis infections and epidemics has only been considered in the last two decades.

5.1. Intrinsic dynamics of drug resistance

Epidemiological models can be modified in order to design and improve control programs to minimize the evolution of drug resistance. The coexistence of DS-TB and DR-TB, relative fitness of DS and DR strains, and the treatment efficacies of DS-TB and DR-TB are the main foci of these models. Other models are built to account for mixed infections in the latent phase, which become active with either sensitive or resistant strains. In this subsection, we will explain the dynamics of DS-TB and DR-TB via epidemiological models.

5.1.1. Epidemiological outcomes of coexistence of DS-TB and DR-TB

Drug resistance is initiated by treatment failure during the course of a tuberculosis epidemic. This type of drug resistance is called acquired drug resistance (ADR-TB). In the later stages of the epidemic, drug resistance is also spread to other individuals through airborne transmission. This type of drug resistance is called transmitted drug resistance.

To understand the dynamics of drug resistance in a tuberculosis epidemic, Blower et al. analyzed the linked control model mentioned earlier in Figure 9a [54, 66]. The model is a system of eight nonlinear ordinary differential equations, one for each compartment:

$$\begin{gathered} \frac{dS}{dt}=\pi -S({\beta }_S{I}_S+{\beta }_R{I}_R+\mu ) \\ \frac{{dE}_S}{dt}=(1-p){\beta }_S{I}_{S}S-(v+\mu +r_1)E_S \\ \frac{{dE}_R}{dt}=(1-p){\beta }_R{I}_{R}S-(v+\mu )E_R \\ \frac{{dC}_S}{dt}=r_1{E}_S-\mu C_S \\ \frac{{dI}_S}{dt}=p{\beta }_S{I}_{S}S+{vE}_S-(\mu +{\mu }_T+r_2)I_S \\ \frac{{dI}_R}{dt}=p{\beta }_R{I}_{R}S+{vE}_R+r_2{rI}_S-(\mu +{\mu }_T+\delta r_2)I_R \\ \frac{{dR}_S}{dt}=r_2(1-r)I_S-\mu R_S \\ \frac{{dR}_R}{dt}=\delta r_2{I}_R-\mu R_R \end{gathered}$$ (4)

where r is the probability of DR-TB emerging during treatment, β_S and β_R are the transmission rates of DS-TB and DR-TB, δ is the treatment efficacy of DR-TB relative to DS-TB, and the other parameters are as in Table 1. The possible outcomes of treatment of an infected individual with DS-TB are:

1. Treatment cures the patient.

2. Treatment fails, and the patient remains infected with DS-TB.

3. Treatment fails, the patient acquires DR-TB (ADR-TB).

The importance and strength of DR-TB relative to DS-TB is modeled by assuming that (1) chemopro-phylaxis is ineffective for latently infected individuals with DR-TB and (2) the effective treatment rate of DR-TB is lower than that of DS-TB, as observed in system (4). The effective reproductive rates for DS-TB and DR-TB for this model are:

$$\begin{gathered} R_{0s}=\left(\frac{{\beta }_S\pi }{\mu }\right)\left(\frac{1}{r_2+\mu +{\mu }_T}\right)\left(p+(1-p)\frac{v}{\sigma +v+\mu }\right) \\ {R}_{0r}=\left(\frac{{\beta }_R\pi }{\mu }\right)\left(\frac{1}{\delta r_2+\mu +{\mu }_T}\right)\left(p+(1-p)\frac{v}{v+\mu }\right) \end{gathered}$$

If acquired resistance can emerge, that is, if r > 0, then three outcomes are possible. These three epidemiological outcomes are summarized in Table 2. Note that eradication of DR-TB and persistence of DS-TB is impossible to achieve together when r > 0.

Table 2.

Three possible outcomes of tuberculosis epidemics in the presence of acquired drug resistance.

Case	Epidemiological outcome	Fitness condition
DS-TB −, DR-TB −	Eradication of DS-TB and DR-TB, disease eradication	RS < 1, RR< 1
DS-TB −, DR-TB +	Persistence of DR-TB and eradication of DS-TB	RR > 1, RR > RS
DS-TB +, DR-TB +	Persistence of both DS-TB and DR-TB	RS > 1, RS > RR

An untreated epidemic with R₀ = 5 was simulated to analyze the dynamics of DS-TB and DR-TB with treatment. After the epidemic reached its equilibrium incidence rate, the treatment was introduced to the population starting with 70% effective treatment rate, 0.10 probability of DR-TB emerging during treatment, and with 0.70 relative treatment efficacy for DR-TB. The observations are interesting:

• Treatment decreases the incidence of DS-TB and increases the incidence of DR-TB. The incidence of DS-TB declines steeply at first, and then more gradually. This two-phase decline is due to the reduction in the pool of prevalent cases in the first half, when the treatment is introduced to the population.

• The incidence rate of DR-TB first rises, peaks, and then falls. This is because, after starting the treatment, the DS-TB cases are converted into DR-TB, and as the incidence rate of DS-TB decreases in the second half, the incidence of DR-TB first peaks and then falls.

• Three phases occur in sequence in the relative contribution of DR-TB to the total number of cases: it sharply increases, then decreases, and gradually increases again. The first two phases are straightforward from the two observations mentioned above. The third phase occurs because the treatment strategy is still effective in decreasing the incidence of DS-TB, but is less effective in decreasing the incidence of DR-TB. Therefore, the contribution of DR-TB cases to all cases that require treatment increases.

• DR-TB can arise from three sources: acquired drug resistance (ADR-TB), fast primary drug resistance (due to primary progression) and slow primary drug resistance (due to endogenous reactivation). Therefore, DR-TB epidemics can be considered as a series of three linked subepidemics. Initially, DR-TB emerges mainly due to ADR-TB, which arises from the treatment of DS-TB cases. After a period, fast and slow primary drug resistance contributes more than ADR-TB. After a period again, the contribution of slow primary drug resistance contributes more than fast primary drug resistance.

This analysis shows that treatment strategies have long-term effects and both DS-TB and DR-TB have slow dynamics. Treatment strategies must take DR-TB into account, as well as DS-TB, in order to prevent DR-TB epidemics.

5.1.2. Relative fitness of drug resistant and drug sensitive strains

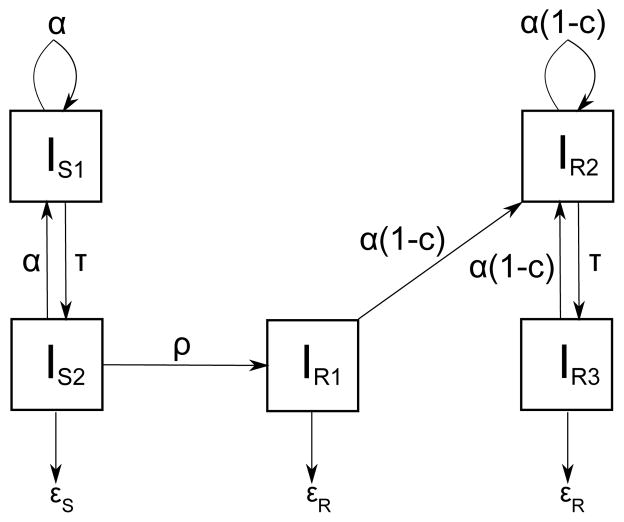
Fitness is a measure of the pathogen’s ability to survive, reproduce and be transmitted between hosts [67]. The fitness of drug-resistant strains is lower than that of drug-sensitive strains. To test this, Luciani et al. built a model which consists of infected individuals only: I_S1, I_S2 are classes for untreated and treated individuals infected with DS-TB and I_R1, I_R2, I_R3 are classes for treated individuals with ADR-TB, untreated individuals with transmitted DR-TB, and treated individuals with transmitted DR-TB respectively[68]. This model distinguishes between classes I_R1 and I_R3 to compare the proportion of DR-TB cases due to acquisition versus transmission. The model is shown in Figure 11.

Figure 11.

Relative fitness model of Luciani et al. in [68]. I_S1, I_S2 are classes for untreated and treated individuals infected with DS-TB and I_R1, I_R2, I_R3 are classes for treated individuals with ADR-TB, untreated individuals with transmitted DR-TB, and treated individuals with transmitted DR-TB respectively. α is the transmission rate, c is the transmission cost due to resistance, ρ is the evolution rate of resistance per individual per unit time, τ is the detection rate per individual per unit time, and ε_S and ε_R are the treatment success rates for DS and DR cases.

The transmission rate of resistant strains is defined as α (1 − c), where α is the transmission rate of drug-sensitive strains and c is the transmission cost of drug resistance, which is the cost of decreased transmission rate for resistant strains. Results from datasets of different countries show that the transmission cost of resistance is c = 0.1 for Cuba and Estonia, whereas c = 0.7 for Venezuela. This suggests that the fitness of resistant strains in Cuba and Estonia is relatively high. Indeed, Estonia has one of the highest rates of drug resistance in the world [1, 69]. In contrast, the low fitness of resistant strains in Venezuela is consistent with early introduction of a tuberculosis control program in the 1930s. Results of this model suggest that the contribution of transmission to DR-TB cases is above 90%, which is higher compared to acquired drug resistance. Moreover, Gagneux et al. showed that drug-resistant strains spread with no or low fitness defect, with a relative fitness cost c < 0.3 [70].

5.1.3. Treatment efficacy of DS-TB and DR-TB cases

Treatment efficacy decreases due to the emergence of drug-resistant strains. For instance, multi-drug resistant strains are immune to the first line drugs, isoniazid and rifampicin. A two-strain model for drug resistance is proposed by Rodrigues et al [71]. The model is based on SEI model with five compartments : S for susceptibles, E_s and E_r for latently infected individuals, and I_s and I_r for infected individuals, where subscripts s and r represent sensitive and resistant cases respectively. The model is shown in Figure 12. A differential selection pressure is imposed by treatment for mixed infections. An individual infected with both sensitive and resistant strains is assumed to either develop DR-TB if treated with drugs to which one of the strains is resistant, or develop DS-TB if untreated or if treated with a regimen set that overcomes the specific resistance pattern. It is initially assumed that when an individual is infected with both resistant and sensitive strains, there will be a preferential activation of resistant strains. The basic reproductive number for the sensitive and resistant strains are computed from the model as:

$$\begin{gathered} R_{0s}=\frac{{\beta }_s(w+p\mu )}{(\mu +w)(\mu +{\mu }_T+{\tau }_s)-(1-\gamma )w{\tau }_s} \\ {R}_{0r}=\frac{{\beta }_r(w+p\mu )}{(\mu +w)(\mu +{\mu }_T+{\tau }_r)-w{\tau }_r} \end{gathered}$$

and the basic reproductive number of the model is the maximum of the two:

$$R_0=\mathit{max}(R_{0s},R_{0r})$$

where β_s, β_r are the transmission rates of the sensitive and resistant strains, τ_s and τ_r are the treatment success rates of active DS-TB and DR-TB, w is the endogenous reactivation rate of latent TB, γ is the proportion of sensitive TB treatment failure that develops acquired resistance, and the other parameters are summarized in Table 1. As always, the disease dies out if R₀ < 1, which implies R_0s < 1 and R_0r < 1, and becomes endemic if R₀ > 1.

Figure 12.

Drug resistance model by Rodrigues et al. w is the endogenous reactivation rate of latent TB, σ is the immunity factor, τ_S and τ_R are treatment rates of active DS-TB and DR-TB cases.

There are four possible equilibria of this system. Let E = (S, E_s, E_r, I_s, I_r) represent the proportions of individuals in the five compartments. Then, four possible equilibria are:

• Disease-free equilibrium: E₀ = (1, 0, 0, 0, 0).

• Endemic equilibrium when only resistant strains are present: $E_r=(S^r,0,E_r^r,0,I_r^r)$.

• Endemic equilibrium when both types of strains are present: $E_{rs}=(S^{\ast },E_s^{\ast },E_r^{\ast },I_s^{\ast },I_r^{\ast })$.

• Endemic equilibrium when only sensitive strains are present: $E_s=(S^s,0,E_s^s,0,I_s^s)$. This is possible only if γ = 0, that is, there is no acquisition of drug resistance due to treatment failure.

5.1.4. Mixed infections with sensitive and resistant strains

Rodrigues et al. extends the drug resistance model mentioned in Figure 12 by allowing individuals with mixed infection to develop DS-TB. The proposed model with mixed infections has the following compartments: S for susceptibles; E_s, E_m, and E_r for latently infected individuals; and I_s, I_r, I_ms, and I_mr for infected individuals, where subscript m represents mixed infection [71]. If an individual in E_m develops DS-TB, the individual moves to I_ms. If the individual develops DR-TB, the individual moves to I_mr. Letting θ be the percentage of mixed infections that progress to active DR-TB, this model shows that the long-term behavior of mixed infections depends highly on θ. The worst case scenario occurs when θ = 1, when all latent mixed infections develop into active DR-TB.

5.2. Models for drug resistance types

Drug resistance is classified according to the resistance pattern of strains. According to this classification, there are two main types of drug resistance: Multi-drug-resistant tuberculosis (MDR-TB) and extensively drug-resistant tuberculosis (XDR-TB). Epidemiological models can be modified to capture these drug resistance patterns.

5.2.1. Multi-drug resistant tuberculosis (MDR-TB)

MDR-TB is defined as tuberculosis infection with a strain that is resistant to the two most important anti-TB drugs, isoniazid and rifampicin. MDR strains are resistant to these first-line drugs, therefore other combinations of tuberculosis drugs are required to treat MDR-TB. Moreover, if MDR-TB treatment fails, the strain can become resistant to other anti-TB drugs and can become a post-MDR strain.

Amplifier model

Inadequate treatment of DR-TB can result in progressive acquisition of resistance of DR strain to more drugs, which causes amplification of drug resistance of the strain during repeated episodes of treatment. Therefore, amplification of resistance is an important process in generating MDR-TB epidemics. For this reason, Blower et al. built an amplifier model that tracks the emergence and evolution of different resistant MTBC strain types in “hot zones” [72]. Hot zones are areas that have > 5% prevalence of MDR-TB, as defined by WHO. Epidemics of DR-TB cases are affected by three mechanisms: 1) transmitted resistance, transmission of DR strains to uninfected individuals 2) acquired resistance, conversion of DS-TB cases to DR-TB cases during treatment, and 3) amplified resistance, resistance acquisition to more drugs during repeated treatment episodes. Monte Carlo methods were used to estimate the basic reproductive numbers of four strain types:

• R₀(1): DS strains

• R₀(2): pre-MDR strains

• R₀(3): MDR strains

• R₀(4): post-MDR strains

where pre-MDR strains are strains resistant to either isoniazid, rifampicin, ethambutol, streptomycin, or to any combination of these drugs except isoniazid and rifampicin. Four thousand strains were generated and classified into these four categories. The amplifier model is a modified version of SEIR model, with E, I, R compartments for each strain type mentioned above. The amplifier model is used to estimate the basic reproductive numbers R₀(i), i = 1, 2, 3, 4. Potential evolutionary trajectories are reconstructed using the amplifier model and Monte Carlo methods. Hot zones are compared to non-hot zones and it is found that hot zones have lower R₀ for DS strains, pre-MDR strains, and MDR strains, whereas non-hot zones have higher R₀ for post-MDR strains. Within a hot zone, however, the order of basic reproductive numbers is: R₀(4) > R₀(3) > R₀(2) > R₀(1). The results demonstrated that many of the treatment programs that have been successful in reducing DS strains had paradoxically been most likely to create hot zones.

Estimates of the basic reproductive numbers for each strain type result in three epidemiological outcomes at equilibrium:

• TB eradication

• Persistence of only post-MDR strains

• Coexistence of MDR strains

Time-dependent multivariate sensitivity analysis is used to find the key factors in generating a hot zone: case detection rate, treatment rate, probability of pre-MDR amplifying to MDR, relative transmissibility of MDR strains, and cure rate of DS-TB. Quantification of sensitivity by calculating the partial rank correlation coefficient shows that case detection and treatment rates are the most influential parameters of the amplifier model contributing to generation of a hot zone.

Fitness of MDR strains

Mathematical models suggest that the threat of multi-drug resistance to TB control will depend on the relative fitness of MDR strains [73, 74]. Assuming that the relative fitness of MDR strains is heterogeneous, Cohen et al. modeled the impact of initial fitness estimates on the emergence of MDR-TB [75]. The model discriminates between DS strains, unfit MDR strains and fit MDR strains. This model consists of following compartments: S for susceptibles; L, L_U, L_F for latent infection, slow progression; E, E_U, E_F for latent infection, fast progression; T, T_U, T_F for infectious undetected TB; D, D_U, D_F for infectious detected TB; Y, Y_U, Y_F for infectious TB with failed therapy; and R, R_U, R_F for people cured by drugs; where subscripts U and F denote unfit MDR strains and fit MDR strains respectively. The compartments without subscript represent DS-TB cases. The strain-specific transmission parameter is defined as β(1 − c), where c is the fitness cost of resistance of the strain, which is defined as the cost of resistance mutations on protein stability and thereby the fitness of the resistant strain [76].

A DS-TB epidemic is initiated, followed by a 30-year period of unstructured treatment, followed by implementation of a DOTS program. DS-TB cases are taken under control after the introduction of the DOTS program. On the other hand, in contrast to the short-term results of MDR-TB, the long-term course of a TB epidemic depends highly on the relative fitness of the MDR strains. This happens because when the prevalence of DS-TB is reduced by DOTS, the impact of acquired drug resistance becomes less important and a majority of MDR infections are caused by transmission, which is dependent on the fitness of the strain. The model also demonstrates that even when the most fit MDR strain has a fitness smaller than that of the DS strain, the MDR strain will eventually outcompete the DS strain. The simulations suggest that DOTS policies should be supported with other strategies for the prevention of MDR-TB, e.g. DOTS-plus. It is also possible to prevent MDR-TB in a population in which drug-sensitive TB is prevalent using standard short-course chemotherapy (SCC) based on a combination of cheap and safe first-line drugs [77].

5.2.2. Extensively drug resistant tuberculosis (XDR-TB)

XDR-TB is defined as tuberculosis infection with a strain that is resistant to at least isoniazid and rifampicin among the first line drugs, to fluoroquinolone, and to at least one of capreomycin, kanamycin, and amikacin among second-line drugs used in TB treatment [78]. The term XDR-TB was first used in March 2006 in a report jointly published by the CDC and the WHO [79]. Soon after, XDR-TB cases were noted in 2006 in KwaZulu-Natal, South Africa, where HIV prevalence is high [80]. The factors that fueled this epidemic were low treatment success rate in the context of a high HIV prevalence and a low case detection rate. Recent studies indicate that XDR-TB strains are spread among all continents [81, 82].

The epidemiology of XDR-TB in the US summarized by Shah et al. reported a total of 83 XDR-TB cases in the US from 1993 to 2007 [83]. The number of XDR-TB cases worldwide is significantly larger. XDR-TB cases are hard to treat and therefore have limited therapeutic options, which results in poor treatment outcomes and high mortality. The survival rate after treatment is lower in XDR-TB cases than in MDR-TB cases, and the survival rate of MDR-TB cases is lower than the survival rate of DS-TB cases. Among patients in the survival analysis study, there were 26 deaths among XDR-TB cases, which constitutes 35% of XDR-TB cases, 707 deaths among MDR-TB cases, which constitutes 24% of MDR-TB cases, and 16398 deaths, which constitutes 11% of DS-TB cases.

Nosocomial transmission of tuberculosis has been suspected to be the main cause of XDR-TB cases in South Africa. Basu et al. showed that nosocomial transmission of XDR-TB emerges into community-based epidemics under the public health conditions of South African communities [84]. Infection control and rapid drug susceptibility testing in hospitals can prevent infected individuals from spending part of their infectious periods in the community. However, these hospital-based interventions are insufficient to control XDR-TB in South Africa. For instance, the effective reproductive number of XDR-TB in KwaZulu-Natal is around 2. Hospital-based interventions reduced this number, but it was still greater than 1, suggesting persistence of XDR-TB. To change future epidemics, community-based interventions must be included in addition to hospital-based interventions. Community-based screening and treatment of XDR-TB and early detection of XDR-TB patients before they arrive at hospitals can slow down the XDR-TB epidemic, and can even eradicate it.

Individualized treatment is required for controlling XDR-TB cases, as standardized treatment strategies do not accurately address both first-line and second-line treatment resistance [85]. WHO suggests that proper tuberculosis control programs must prevent the emergence of drug resistance in the first place. Proper treatment of MDR-TB cases prevents the emergence of XDR-TB cases. Incomplete treatment of MDR-TB cases, on the other hand, can lead to new XDR-TB cases [86].

Building a mathematical model that specifically captures XDR-TB cases is hard because of the patient-specific characteristics of each XDR-TB case. However, the amplifier model by Blower et al. accounts for post-MDR strains, which is the set of strains that are resistant to at least one more drug other than isoniazid and rifampicin, which can be further modified to include XDR strains [72].

Three-strain model

Different levels of drug resistance requires different treatment strategies. To account for all drug resistance types of tuberculosis, Bhunu et al. built a three-strain model, similar to SEIQR model, with 9 compartments: S for susceptible individuals, E_S, E_M, E_X for latently infected individuals, I_S, I_M, I_X for infected individuals, Q for quarantined individuals and R for treated individuals. The subscripts S, M, X represent individuals infected with DS-TB, MDR-TB, and XDR-TB respectively. Currently, there is no treatment regimen for XDR-TB in developing nations, therefore it is assumed in the model that individuals infected with XDR-TB can only be quarantined, but not treated. Analytical and numerical results of the three-strain model gives more insight into interaction of TB cases with different types of resistance:

• In the absence of TB treatment, only DS-TB cases exist.

• Treatment of DS-TB cases with first-line drugs reduces the spread of DS-TB, and increases the number of MDR-TB cases. In the later stages, the prevalence of DS-TB decreases, which leads to less prevalent MDR-TB.

• Treatment of MDR-TB cases with both first and second-line drugs reduces the spread of MDR-TB, and increases the number of XDR-TB cases. In the later stages, the prevalence of MDR-TB decreases, which leads to less prevalent XDR-TB.

• The quarantine of XDR-TB cases in addition to treatment of DS-TB and MDR-TB cases reduces the spread of TB.

5.3. Underestimation of the drug resistance burden

Emergence of drug resistance starts with the introduction of anti-TB drugs in the 1950s, but no records were kept until the mid 1990s. We used a dataset from New York State Department of Health (NYS-DOH) and noted the number of DS-TB, MDR-TB, and XDR-TB cases in New York State between 2004–2007 as in Figure 13. Consider a patient who was diagnosed with DS-TB in 2004 and recorded in this patient dataset. This patient might have acquired drug resistance during treatment and become an MDR-TB case in 2006. However, the records will keep this patient as infected with DS-TB in 2004, and not as infected with MDR-TB in 2006. Therefore, surveys may underestimate the number of DR-TB cases.

Figure 13.

Number of drug-sensitive TB, MDR TB, and XDR TB cases between 2004–2007 based on the NYS-DOH dataset.

Cohen et al. built an SEIR model to test their hypothesis that incidence-based samples may underestimate the total burden of drug-resistant tuberculosis in a community [87]. Individuals who present with DS-TB and acquire resistance during treatment are not identified as resistant cases in incidence-based surveys, because they would not have been identified as such at the time of diagnosis of DR-TB. Therefore, cases of acquired drug resistance are underestimated. Cohen et al. also showed that underestimation of DR-TB cases in incidence-based surveys is affected by the maturity of the epidemic. Incidence-based surveys will underestimate the actual proportion of DR-TB cases during the early stages of the epidemic when acquired resistance is important. As the epidemic matures and the transmission of DR-TB becomes an important mechanism for the emergence of resistance, as suggested by Blower et al. in [66], incidence-based surveys produce less biased results.

There are other reasons for underestimation of the DR-TB burden [88]. Individuals with HIV/TB co-infection are less likely to have smear-positive TB, therefore HIV infected cases may be underrepresented in these samples. Thus, in areas of high HIV/TB co-infection, it is possible that the drug resistance burden is underestimated. Another reason for underestimation is the treatment of TB cases in the private sector. A portion of TB treatment occurs in the private sector where TB treatment does not conform to recommended care. These settings enable the emergence of drug resistance. Therefore, the burden of DR-TB may be greater within this portion of the population who are treated in the private sector, which is the portion that is usually excluded from surveys. Geographic heterogeneity is another reason for underestimation of the drug resistance burden. In high-risk/low-resource settings, not all TB cases receive drug susceptibility testing (DST). Therefore, the use of sampling can lead to incorrect estimation of the DR-TB burden if the distribution of drug resistant cases is not homogeneous.

5.4. Compliance to treatment of drug-resistant cases: DOTS-plus

Drug-resistant tuberculosis requires different treatment steps than does drug-sensitive tuberculosis. One control program, mentioned earlier, is DOTS, which ensures compliance to treatment of DS-TB cases. DOTS is proven to decrease acquired drug resistance and transmission of drug-resistant strains [89]. However, rates of treatment failure among DR-TB patients are high [90]. Further interventions, such as drug-susceptibility testing and individualized treatment regimens, are needed for DR-TB cases [91]. Another control program, DOTS-plus, is an extension of DOTS and is specifically designed for controlling multi-drug-resistant TB. DOTS-plus uses more effective, but also more expensive and toxic drugs. It reduces the transmission rate of resistant strains by adapting the treatment regimen to better suit resistant cases.

To reflect the difference between DOTS and DOTS-plus, Rodrigues et al. extended the two-strain model in Figure 12 for mixed infections by adding three compartments: L_m for latent class with mixed infections, I_ms and I_mr for individuals who are latently infected with mixed infections and who become infected by a sensitive strain and resistant strain respectively [71]. They modeled DOTS by reducing the proportion of failed treatments that lead to acquired resistance. DOTS-plus is modeled by increasing the recovery rate from active DR-TB, thereby reducing the time during which individuals infected with resistant strains are infectious. DOTS-plus decreased not only the percentage of DR-TB in the coexistence region, but also the overall prevalence of resistant strains. Therefore, the impact on the coexistence region is highest for the DOTS-plus strategy. DOTS-plus forces a decrease in DR-TB prevalence for all endemic scenarios. DOTS, on the other hand, causes a decrease in DR-TB prevalence only below the superinfection threshold of resistant strains, where superinfection is defined as an infection following a previous infection.

6. Co-infection of TB and Other Diseases

Tuberculosis infection correlates with the infection of several other diseases. Most common of all is HIV (Human Immunodeficiency Virus), which causes the immune system to fail and leads to an infection-prone body. Given the deficient immune system of the host, MTBC can easily infect the individual with tuberculosis. It is estimated that one third of the HIV+ population is also infected with tuberculosis. Other diseases, including AIDS (HIV infection with symptoms), leprosy (Hansen’s Disease), and influenza, can also co-infect with TB.

The first mathematical model to describe the interaction of HIV and TB in the immune system was built by Kirschner et al. [92]. Four populations were represented in the model: T-cells, macrophages, HIV population and MTBC population. The results of the model show that TB infection in addition to HIV infection decreases the number of T-cells in the immune system. Moreover, the viral load and MTBC population are higher in the co-infected patient, compared to singly infected patient. This suggests that the presence of MTBC in the HIV-infected individuals weakens the immune system. Another model by Bauer et al. shows that the decline in the number of T-cells in HIV/TB co-infected patient leads to latent TB reactivation and more rapid progression to active TB [93].

6.1. Joint epidemics of TB and HIV

Co-epidemics of HIV and TB are modeled as the cartesian product of two models, one for each disease. Joint epidemics of TB and HIV are modeled by Bacaer et al. in a township near Cape Town, South Africa, where HIV prevalence is high [94]. The model is an SEI × SEI model, with six compartments: S₁, E₁, I₁, S₂, E₂, I₂; where subscripts 1 and 2 represent HIV- and HIV+ individuals respectively. Basic reproductive numbers are defined for four different settings: $R_0^{TB}$ for the model with TB but not HIV, $R_0^{\mathit{HIV}}$ for the model with HIV but not TB, $r_0^{TB}$ for the model of TB when introduced into a population at HIV endemic steady state, $r_0^{\mathit{HIV}}$ for the model of HIV when introduced into a population at TB endemic steady state. The stability analysis of the model suggests that:

• If $R_0^{\mathit{HIV}}<1$ and $R_0^{TB}<1$, the disease-free steady state is a global attractor of the system.

• If $R_0^{\mathit{HIV}}>1$ and $r_0^{TB}<1$, the HIV endemic steady state is a global attractor of the system.

• If $R_0^{TB}>1$ and $r_0^{\mathit{HIV}}<1$, the TB endemic steady state is a global attractor of the system.

• If $R_0^{\mathit{HIV}}>1,r_0^{TB}>1,R_0^{TB}>1$ and $r_0^{\mathit{HIV}}>1$, both the HIV endemic steady state and the TB endemic steady state exist.

• If $R_0^{\mathit{HIV}}>1,r_0^{TB}>1$ and $R_0^{TB}<1$, the HIV endemic steady state exists, but the TB endemic steady state does not exist.

Notice that $r_0^{TB}>R_0^{TB}$. This is because an individual infected with TB will produce more secondary cases if introduced into a TB-free population where HIV is endemic, than in a disease-free population. On the other hand, $r_0^{\mathit{HIV}}<R_0^{\mathit{HIV}}$, and therefore TB slows down the HIV epidemic.

The effects of control measures were tested in this system: when the TB detection rate increases, the TB incidence rate increases, whereas it has no impact on HIV prevalence. An increase in condom use decreases HIV prevalence, and therefore decreases the TB notification rate, as fewer TB cases are observed due to fewer HIV/TB coinfection cases. When isoniazid preventive therapy for TB cases is implemented, the TB notification rate decreases, and it has no impact on HIV prevalence. The implementation of highly interactive antiretroviral treatment (HAART) for HIV cases reduces the viral load, thereby decreasing the maximum transmission rate of HIV. On the other hand, it increases the life expectancy of HIV+ people by decreasing the death rate of individuals with or without TB. Therefore, the effect of HAART on HIV prevalence is not clear. For the same reason, the effect of HAART on TB is not clear, because HIV+ people under HAART live longer, which enables individuals with deficient immune system and prone to TB infection to survive longer, thus giving them more opportunity to develop TB. The effects of control measures on the TB notification rate and HIV prevalence are summarized in Table 3.

Table 3.

Effects of control measures on the TB notification rate and HIV prevalence.

Control measure	TB notification rate	HIV prevalence
TB detection rate ↑	↓	→
Condom use ↑	↓	↓
Isoniazid preventive therapy ↑	↓	→
HAART ↑	Not clear	Not clear

6.2. HIV-AIDS/TB co-infection

Initial HIV infection does not cause AIDS immediately, but most individuals infected with HIV eventually develop AIDS. Symptoms of HIV infection can be observed after the transition from HIV to AIDS. Therefore, we can name the state for HIV as infection with no symptoms (seropositive) and the state for AIDS as infection with symptoms. To distinguish between HIV and AIDS, Long et al. used an SII × SEI model to simulate HIV-AIDS/TB co-epidemics [95]. SII are the states of the HIV infection (susceptible, infected with no symptoms, infected with symptoms) and SEI are the states of the TB infection (susceptible, exposed, infected). Therefore there are 9 states X_HT in the model, where first subscript denotes HIV status (H ∈{S, I, A}), where S is for susceptible, I is for HIV, and A is for AIDS. The second subscript denotes TB status T ∈ {S, E, I}, where E is for latently infected individuals, and I is for infected individuals. The model captures disease progression for both diseases: transition from HIV to AIDS and transition from latent TB to active TB. The basic reproductive numbers of HIV and TB based on the system are:

$$\begin{gathered} R_0^H=\frac{{\beta }_I}{v_{IS}+\mu }+\frac{{\beta }_A{v}_{IS}}{(v_{IS}+\mu )(\mu +{\mu }_A)} \\ {R}_0^T=\frac{\tau {\lambda }_{SE}}{({\lambda }_{SE}+\mu )(\mu +{\mu }_T)} \end{gathered}$$

and the basic reproductive number of the model is maximum of the two:

$$R_0=\mathit{max}(R_0^H,R_0^T)$$

Notice that the basic reproductive numbers for HIV/AIDS and TB are not symmetric, because HIV/AIDS is modeled using the SII framework and TB is modeled with the SEI framework. Four equilibrium states are possible in this model:

• Disease-free equilibrium: $R_0^H<1$ and $R_0^T<1$.

• HIV-only quasi-disease-free equilibrium: $R_0^H>1,R_0^T<1$.

• TB-only quasi-disease-free equilibrium: $R_0^T>1,R_0^H<1$.

• Co-infection equilibrium: $R_0^T>1,R_0^H>1$.

A modification of the HIV-AIDS/TB model that adds treatment suggests that exclusive treatment of only one disease may reduce the epidemic by decreasing disease prevalence and preventing new infections and deaths, but may worsen the other epidemic. This paradox is due to the fact that individuals treated for the first disease but coinfected with the second disease may live longer due to treatment. Therefore, these individuals may infect more people with the second disease. The same result is found in a study focusing on the HIV/TB correlation in India, by Williams et al., and it is observed that HAART for HIV significantly reduces mortality in coinfected individuals, but doesn’t decrease TB incidence in India [96]. The immediate goal of TB control programs in high HIV prevalence settings should be to increase TB case detection rates and improve TB treatment rates [97].

6.3. Correlation between HIV/TB co-infection and ADR-TB

The recent increase in TB prevalence is claimed to be the result of HIV epidemics in certain locations of the world. Williamson et al. observed the correlation of ADR-TB and HIV in a case study in San Francisco between 1985 and 1994 [98]. Their analysis of the data showed that during the 10-year period encompassing most of the HIV epidemic in San Francisco, the frequency of resistance to anti-TB drugs has been low. However, there is a striking increase in the incidence of ADR-TB in the second half of this period, especially in patients who did not comply with the prescribed therapy. Several case reports also suggested that malabsorption of anti-TB drugs due to gastrointestinal problems encourages the development of ADR-TB, especially in HIV-infected patients.

The chain of reasoning which proves that HIV infection is an important risk factor for ADR-TB is as follows: first, the analysis suggests a possible ecological association between the increasing incidence of AIDS-associated TB and the increasing incidence of ADR-TB. Second, in the case control study, AIDS is a strong independent risk factor for ADR-TB. Third, resistance to rifampicin alone, which is an unusual drug resistance pattern, is found frequently and exclusively among patients with AIDS. As a result, it is concluded from the data that the substantial increase in ADR-TB in San Francisco is a product of the increasing prevalence of HIV/TB co-infections.

6.4. Co-infection of tuberculosis with other diseases

Tuberculosis infection can be correlated with other diseases, besides HIV and AIDS. Epidemics of tuberculosis and leprosy progress slowly, even lasting centuries. Experimental studies and the combined TB/leprosy transmission model based on SEI × SEI framework by Lietman et al. indicate that acquired immunity to tuberculosis can effectively eradicate leprosy [99]. On the other hand, immunity to leprosy can not eradicate tuberculosis, because cross-immunity is not symmetrical, that is, immunity to M. leprae is not effective in protecting the host against MTBC.

Since a tuberculosis epidemic is slow, co-infection of TB with another disease is possible only if the other disease also has slow dynamics. Therefore, influenza, which has a 5–10 day incubation period, can not cause a co-infection with TB, which has 2–5 years of incubation period. One exception to this is the Influenza Pandemic in 1918 [100]. It was found that the number of TB cases increased in 1918 and returned back to the previous level at the end of 1919. This is because latent TB cases exposed to the 1918 strain of influenza virus were likely to reactivate. Therefore, a fraction of TB cases exposed to this influenza strain, due to compromised immunity, were endogenously reactivated as a result of the influenza pandemic.

7. Modeling various patient groups

Mathematical models have been built to find patterns in the epidemiology of TB within specific groups of patients. Patients can be classified based on their age, homeless status, race, ethnicity, disease status, or other attributes. It is important to understand how TB morbidity differs among specific population groups by examining it in the context of various socio-demographic factors.

7.1. Ethnicity and country of birth (US vs. non-US)

Debanne et al. built a Markov model for the epidemiology of TB in the US by separating the patients into disaggregated groups defined by age, race, ethnicity, geography, and TB infection/disease status [101]. Possible TB infection/disease status states are: never infected, new infection, mature infection, infection with treatment, TB (symptomatic), TB with treatment, TB cured, new MDR-TB infection, mature MDR-TB infection, MDR-TB infection with treatment, MDR-TB, TB with incomplete treatment, MDR-TB with treatment, and MDR-TB cured. Projections of the model predict that the rate of decline in the number of cases in the first half of the 1990s among Hispanics will be slower than that of white non-Hispanics and blacks. A case study by Liu et al. based on TB surveillance data from New Jersey supports this result and shows that TB morbidity among foreign-born people in New Jersey continued to increase from 1992, despite the decline in overall TB morbidity [102]. Moreover, among foreign-born individuals with known dates of arrival, patients who lived in the US for less than 5 years are about 6 times more likely to have TB than patients who lived in the US for over 5 years.

7.2. Age of patient and age of infection

An earlier study by Frost et al. shows that age of patient and age of infection detetmine the tuberculosis mortality rate [103]. An age-structured model was built by Vynnycky et al. to estimate the age-specific risks of infection with primary progression, endogenous reactivation, and exogenous reinfection [104]. The model is based on the SEI model and it is dependent on the age of the patient at the time of infection. The estimates of the model based on patient data from England and Wales since 1900 show that the annual risk of infection by primary progression is 4%, 9%, and 14% for the age groups of 0–10 year olds, 10–20 year olds, and 20 year olds and above, respectively. This shows that the primary tuberculosis infection rate is higher for adults.

The estimated age-specific incidence also shows a relationship between age and the type of infection. For 0–10 year olds, the only cause of infection is primary progression. Therefore, the main cause of infections of 0–10 year olds is recent transmission. For 10–20 year olds, only primary progression and exogenous reinfection are observed as the reason for infection. For 20 year olds and above, endogenous reactivation is another cause but remains low compared to the other two types of infections. Starting from age 20, as the age of infection increases, the percentage of exogenous reinfection increases and converges to the rate of primary infection. On the other hand, the contribution of endogenous reactivation to the total number of infections remains low and constant. As a result, the ratio of primary infections to reinfections decreases as the age of the patient population increases [105]. As health care facilities developed from 1900 to 1960, average life expectancy increased, and this led to a similar distribution in the ratio of primary infections to reinfections, but spread over a wider age interval.

7.3. Treatment strategies targeting patient groups

Tuberculosis control strategies can be updated according to incidence rate and tuberculosis status in patient groups. Brewer et al. built a multilevel semi-Markov model that divided the US population into 3 age groups (0–15, 16–44, 45+), and each age group is subdivided into 18 clinical states based on the cartesian product of disease status for TB and HIV infection [106]. The six possible TB infection states are: no known infection, low/intermediate/high risk for active TB, active DS-TB, and active DR-TB. The three possible HIV infection states are: no known infection, HIV infected (seropositive), and AIDS. The effects of various treatment strategies were measured and it was found that a BCG vaccination program that reached 10% of children and 1% of adults each year would produce a 17% reduction in cases and an 11% decline in deaths due to TB over 10 years. A treatment strategy targeting HIV-infected patients would reduce HIV/TB co-infection cases and deaths 20%. A 10% improvement in the efficacy of both chemoprophylaxis and therapeutics, combined with a BCG vaccination program, would lead to a 47% decline in TB cases.

8. Conclusion

Tuberculosis has slow intrinsic dynamics, therefore the long-term effects of tuberculosis can not be observed by investigation of infected individuals. It can only be explained by population-level studies. Epidemiological models of tuberculosis help us understand the dynamics of tuberculosis transmission at the population level. In this study, we presented a number of models from the literature which are modified to capture different types of tuberculosis infection, different treatment strategies, drug resistance, and co-infection of TB with other diseases. We also presented models which focus on certain patient groups that are expected to follow different TB dynamics.

Epidemiological models focus on certain patient groups and infection types, and make assumptions about other compartments. Exclusion of immigration and emigration are common assumptions: models of tuberculosis in this study assume that the population is closed, and no immigrants are introduced into the population. However, in countries such as the US, immigration is common, and many new tuberculosis cases are introduced by foreign-born individuals. Therefore, models with no immigration assumption can not capture the real dynamics of tuberculosis in open populations with high diversity caused by immigrants. A model by Jia et al. accounted for the impact of immigration by SEIR models for both immigrant and local subpopulation, and found that immigrants have an important influence on the internal dynamics of tuberculosis in a population [107]. The model with Canadian born and foreign born subpopulations by Zhou et al. shows that increasing the mixing of two subpopulations increases the TB infection rate of Canadian born individuals [108]. More models have to include immigration in the population-level studies to capture the real dynamics of tuberculosis.

Quarantine is another assumption excluded from epidemiological models of tuberculosis. Quarantined individuals are infected, but not infectious. Therefore, their isolation from the population changes the dynamics of tuberculosis. Introduction of noninfectious infected individuals in the SEIR model of Blower et al. is one step in this direction, but further changes are needed to estimate the proportion of quarantined individuals [26]. In countries with proper health care facilities, early detection makes it easier to find infected individuals and quarantine them. An SEIQR model, with additional class Q for quarantined individuals, was studied for childhood diseases and can be applied to tuberculosis [109, 110].

Vaccination is the administration of weakened antigens to produce immunity to a disease. Bacillus Calmette-Guérin (BCG) is the vaccine against tuberculosis. Susceptible and latently infected individuals can be vaccinated for precaution prior to disease, because vaccination does not help after infection. Vaccination is excluded from most epidemiological models of tuberculosis. However, a vaccinated susceptible becomes isolated from the disease network and can not infect or be infected with tuberculosis. Therefore, vaccination influences the dynamics of tuberculosis. Few models include vaccination in their models and it is found that vaccination can have a significant effect on eliminating tuberculosis [111, 112].

The age structure of a population also has to be integrated into epidemiological models. The unrealistic assumption of a constant natural mortality rate in models causes divergence of estimations from tuberculosis dynamics in populations. More realistic age-dependent mortality rates are used in the epidemiological models by Aparicio et al. to reflect accurate survival of infected individuals [8]. Brooks-Pollock et al. integrates constant, exponential, and Gompertz-like life expectancy into epidemiological models of tuberculosis by age and time dependent analysis [113].

Although some assumptions are made in epidemiological models, mathematical models still capture the dynamics of tuberculosis to an extent. They anticipate the course of a tuberculosis epidemic, which is usually longer than the average lifetime of an individual. These estimates direct control efforts for tuberculosis and improve success for eradication of the disease. Models identify certain patient groups at risk, and treatment strategies start to focus on these groups in populations. Therefore, epidemiological models give an overall view of tuberculosis dynamics and direct efforts for surveillance and elimination of tuberculosis.

Highlights.

• This study provides a literature review of epidemiological models of tuberculosis.

• We present transmission dynamics of tuberculosis via epidemiological models.

• We explain the long-term outcomes of treatment based on model simulations.

• We use epidemiological models to simulate different levels of drug resistance.

• Simulations of co-infection of tuberculosis with other diseases are presented.