Radial and longitudinal diffusion of myoglobin in single living heart and skeletal muscle cells

Abstract

We have used a fluorescence recovery after photobleaching (FRAP) technique to measure radial diffusion of myoglobin and other proteins in single skeletal and cardiac muscle cells. We compare the radial diffusivities, D_r (i.e., diffusion perpendicular to the long fiber axis), with longitudinal ones, D_l (i.e., parallel to the long fiber axis), both measured by the same technique, for myoglobin (17 kDa), lactalbumin (14 kDa), and ovalbumin (45 kDa). At 22°C, D_l for myoglobin is 1.2 × 10⁻⁷ cm²/s in soleus fibers and 1.1 × 10⁻⁷ cm²/s in cardiomyocytes. D_l for lactalbumin is similar in both cell types. D_r for myoglobin is 1.2 × 10⁻⁷ cm²/s in soleus fibers and 1.1 × 10⁻⁷ cm²/s in cardiomyocytes and, again, similar for lactalbumin. D_l and D_r for ovalbumin are 0.5 × 10⁻⁷ cm²/s. In the case of myoglobin, both D_l and D_r at 37°C are about 80% higher than at 22°C. We conclude that intracellular diffusivity of myoglobin and other proteins (i) is very low in striated muscle cells, ≈1/10 of the value in dilute protein solution, (ii) is not markedly different in longitudinal and radial direction, and (iii) is identical in heart and skeletal muscle. A Krogh cylinder model calculation holding for steady-state tissue oxygenation predicts that, based on these myoglobin diffusivities, myoglobin-facilitated oxygen diffusion contributes 4% to the overall intracellular oxygen transport of maximally exercising skeletal muscle and less than 2% to that of heart under conditions of high work load.

Since Wittenberg (1, 2) demonstrated that myoglobin (Mb) diffusion facilitates O₂ transport in aqueous solutions, it has been postulated that facilitated O₂ diffusion may play an important role in respiring muscle. The extent of Mb-facilitated sarcoplasmic O₂ transport will depend mainly on the intracellular concentration of Mb, which is fairly well known for various muscle fiber types, and on the magnitude of its sarcoplasmic diffusion coefficient (D), which still is a matter of discussion. The direct measurement of translational Mb diffusivity in living skeletal muscle fibers (3–5) revealed an unexpectedly small value for D. However, in these studies, Mb diffusivity—for technical reasons—has been measured only along the longitudinal axis of muscle fibers and over long distances (tens or hundreds of sarcomere lengths). In contrast, facilitated O₂ transport in vivo mainly requires radial diffusion of Mb, from the sarcolemma to the mitochondria, i.e., in the direction perpendicular to the longitudinal fiber axis. It is conceivable that the highly ordered sarcoplasmic structures, e.g., the myofilaments, might give rise to significant differences between longitudinal (D_l) and radial (D_r) diffusion coefficients. Such an anisotropy has been reported for small molecules such as H₂O (6), Ca²⁺ (7), and O₂ (8), but it was not clear whether this also would be true for protein diffusion. Thus, the magnitude of D_r in living heart and skeletal muscle remained a matter of speculation. For example, Baylor and Pape (3) argued that the higher tortuosity in radial direction could lead to D_r being smaller than D_l by a factor of 2 or more. In contrast, Groebe (9) discussed that D_r could be considerably higher than D_l, because the hindrance imposed to longitudinal diffusion by the meshes of the M lines and the Z bands does not exist in radial diffusion direction. Measurements of rotational Mb diffusion in muscle (10, 11) added more confusion to the problem, because the high values found for rotational D in these studies were taken to be indicative of a generally high diffusional mobility of Mb in sarcoplasm.

Because no measurements of the radial diffusion coefficient of myoglobin existed so far for skeletal muscle and neither an axial nor a radial value of D was known for heart muscle, it was the aim of this study to determine these entities. The method used here is the fluorescence recovery after photobleaching (FRAP) technique (12, 13), which allows us to measure both D_l and D_r of proteins within living cells. The experiments were performed on single fibers of rat soleus muscle and on isolated rat cardiomyocytes. Besides Mb (17 kDa), lactalbumin (14.2 kDa), with a size comparable to Mb, and the larger ovalbumin (45 kDa) also were used to test whether the results obtained for myoglobin hold for other proteins as well.

The D_r values found for Mb in rat cardiac and skeletal muscle are used in a model calculation to estimate the importance of facilitated O₂ diffusion in working muscle. The results are compared with recent findings by other authors including the observations on Mb knockout mice (14, 15).

Materials and Methods

Soleus Fiber Bundles.

The preparation of fiber bundles from excised rat soleus muscles has been described in detail elsewhere (5). After preparation, the bundles were put into a measuring chamber perfused with Ringer's solution equilibrated with carbogen (95% O₂/5% CO₂), and the chamber was mounted onto an electronically driven scanning stage (Fig. 1). The sarcomere length of the fibers in the chamber was 2.52 ± 0.13 μm. Measurements on skeletal muscle fibers were done at 22°C.

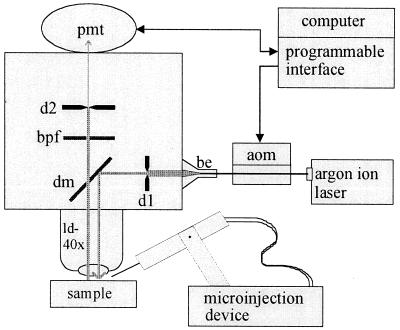
Figure 1.

Scheme of experimental setup. aom, acoustooptic modulator; be, beam expander; d, field diaphragm for laser beam (d1) and fluorescence (d2); dm, dichroic mirror (510 nm); bpf, band pass filter (500–530 nm); pmt, photo multiplier tube; ld-40x, water immersion long-distance objective with ×40 magnification (see text for details).

Cardiomyocytes.

Wistar strain rats weighing 200–330 g were anaesthetized with pentobarbitone (Nembutal; 1 ml/kg, i.p.) before they received 500 units of heparin i.p. The hearts were excised rapidly and subjected to retrograde Langendorff perfusion at 37°C. An initial perfusion (5 min) with carbogen-equilibrated, Ca²⁺-free solution (137 mM NaCl/5 mM KCl/22 mM NaHCO₃/1 mM MgCl₂/0.4 mM NaHPO₃/5 mM glucose/1 mM sodium pyruvate/0.1 mM EGTA) was followed by a second perfusion (10 min) with the same solution containing no EGTA but 20 μM CaCl₂ and 1 mg/ml collagenase (Worthington Type II). The hearts were removed from the Langendorff setup, and the ventricular tissue was minced with scissors and repeatedly taken up and discharged from a pipette to disaggregate the myocytes. Cells then were pelleted three times in a tabletop centrifuge (80 × g for 4 min), and the pellet was resuspended each time in Ca²⁺-free, Hepes-buffered solution (135 mM NaCl/4 mM KCl/10 mM Hepes/1 mM MgCl₂/0.3 mM NaHPO₃/10 mM glucose/0.1 mM EGTA). The resuspended myocytes were stored in 2- to 3-ml aliquots in 35-mm culture dishes (37°C) until used within 8 h. Sarcomere length was 1.82 ± 0.02 μm. Measurements on cardiomyocytes were done at either 22°C or 37°C.

Fluorescence Labeling of Proteins.

Fluorescein conjugates of lactalbumin (2.6 mol dye/protein molecule) and ovalbumin (3.0 mol dye/protein molecule) were purchased as lyophilized powder from Molecular Probes. Protein solutions (40 mg/ml) were prepared by dissolving 20 mg of the respective powder in 485 μl of phosphate buffer (24.7 mM KH₂PO₄/57.6 mM K₂HPO₄/10 mM NaCl; NaCl served to increase the osmolarity to 300 mosmol/liter; pH 7.17). The absence of notable amounts of free dye was indicated by the clear filtrate obtained when the solution was subjected to ultrafiltration by using membranes with a 1-kDa cut-off (Amicon). Solutions were frozen in liquid nitrogen in 30-μl aliquots and stored at −80°C until used.

The preparation of fluorescent Mb was similar to the procedure described by Molecular Probes (product information sheet MP 00143): FITC Isomer I (Sigma) was coupled to horse skeletal muscle metmyoglobin (Serva) by adding 1 ml of 10 mg/ml FITC solution in DMSO to 12 ml of 0.1 M NaHCO₃ (pH 9.0) containing 22 mg/ml myoglobin. After incubation for one hour at room temperature, 1 ml of freshly prepared 1.5 M hydroxylamine (pH 8.5) was added. The solution was then centrifuged (3500 g for 20 min at 4°C) to remove particulate matter and the supernatant was loaded on a 2.5 × 30 cm column of Sepharose 6B equilibrated with the phosphate buffer (4°C) described above. Gel filtration was then performed with the same buffer (containing 0.02% NaN₃) at a flow rate of 2 ml/min. Two bands, representing coupled and free fluorescent dye, respectively, appeared on the column. The peak fraction belonging to the fast moving band was collected (about 20 ml) and was transferred to an ultrafiltration chamber (Amicon) equipped with a 10-kDa cut-off membrane. The filtered volume was substituted several times by addition of phosphate buffer into the chamber until the filtrate was clear. Ultrafiltration then was continued without substitution until the volume of the FITC-myoglobin solution was reduced to ≈1.5 ml. To calculate the degree of labeling, the absorbance of free metmyoglobin at 494 nm (where FITC has its maximum absorbance) was subtracted from that of the labeled myoglobin. The value then was multiplied by 1.1, because the extinction of FITC decreases about 10% on protein conjugation (product information sheets; Molecular Probes). The concentration of the fluorophore in the final solution amounted to 6.9 mM and that of myoglobin was 3.7 mM, giving a degree of labeling of 1.9 mol of fluorophore per mole of myoglobin.

Experimental Setup.

Fig. 1 schematically depicts the essential components of the setup used for the measurements. Blue laser light (488 nm) was emitted by an argon ion laser (Innova 70C-2; Coherent Radiation, Palo Alto, CA) operating at 300–500 mW. Intensity of the laser beam was modulated by an acoustooptic modulator (AOMμ80; APE, Berlin) before the light passed a beam expander (be) and entered the microscope (UEM; Zeiss). A field diaphragm (dl) in the light path blocked all laser light except for a central portion of the expanded beam. This portion was reflected by a dichroic mirror (dm) and passed a water immersion objective with 2 mm of working distance (Nikon) before it reached the sample. The green fluorescence emitted by the sample passed through the dichroic mirror and a band pass filter (bpf). Only the fluorescence within the measuring field, as defined by adjustment of height and width of a second field diaphragm in the light path (d2), reached the photomultiplier tube (pmt). Beam modulator, pmt, and data acquisition were computer-controlled by using a programmable interface.

Microinjection of Proteins.

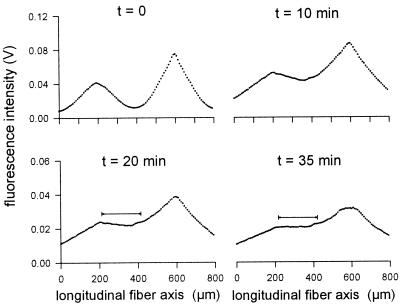
Microinjection pipettes were made from filamented borosilicate capillaries (1B100F-4; WPI Instruments, Waltham, MA) with inner and outer diameters of 0.8 and 1.0 mm, respectively. Micropipettes with tip diameters ≈1 μm were pulled on a programmable horizontal puller (BB-CH; Mecanex, Switzerland) and were backfilled immediately before microinjection with a small amount of thawed, centrifuged (14,000 × g for 10 min), and filtered (0.2-μm mesh) fluorescent protein solution. To perform a FRAP experiment, 1–20 pl of protein solution was injected into a muscle cell by means of pressure (Pneumatic PicoPump; WP Instruments). In cardiomyocytes, measurements began after the injected solution had been distributed homogeneously within the cell (usually 10 min after microinjection). The far greater length of skeletal muscle fibers required a different strategy: Here, the condition of homogeneous distribution of the microinjected protein was established only locally (Fig. 2). After microinjection at two neighboring sites along the fiber, the protein solution was allowed to distribute evenly in the segment between the injection sites (t = 20 min and t = 35 min in Fig. 2). The central parts of those segments were used for FRAP. The much smaller longitudinal extension of the measuring field (8.2 and 16.4 μm) compared with the length of the fiber segment with even fluorescence (usually ≥200 μm) made undisturbed diffusion measurements in skeletal muscle fibers possible.

Figure 2.

Microinjection procedure for FRAP measurements in skeletal muscle fibers. To achieve locally a state of evenly distributed fluorophores, microinjections were performed at two sites along the longitudinal fiber axis (abscissa, peaks of curves refer to injection sites). In most of the experiments, the distance between the injection sites was around 400 μm. Measurements of the fluorescence intensity (ordinate) distribution were performed at different times after microinjection (after 3, 10, 15, 20, and 35 min in this example). The scans at 20 min and 35 min reveal a fiber segment 200 μm in length (horizontal bar) with almost constant fluorescence intensity.

Muscle Cell Alignment to Measure D_l and D_r.

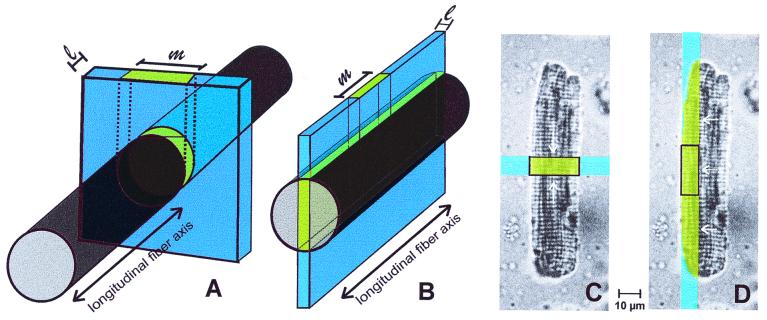
Fig. 3 shows how skeletal muscle fibers and cardiomyocytes were aligned to measure protein diffusion either in a longitudinal or radial direction. To measure D_l in soleus fibers, the long fiber axis was oriented perpendicular to the beam segment (Fig. 3A). The width (l) of the illuminated fiber segment was adjusted to 8.2 μm, and its length was large enough to exceed the muscle fiber diameter. The width of the measuring field was set identical to l, whereas the length of the measuring field (m) was equal to the fiber diameter. To measure D_r in skeletal muscle fibers, a thin, ≈120-μm-long segment of the beam was oriented parallel to the long fiber axis, illuminating the central part of the fiber (Fig. 3B). The width of the beam and of the measuring field again were l = 8.2 μm, and the length, m, of the measuring field amounted to 16.4 μm.

Figure 3.

Arrangement of bleached areas and measuring fields in muscle cells. Diffusion was recorded in skeletal muscle fibers in longitudinal (A) and in radial (B) direction and in cardiomyocytes in longitudinal (C) and in radial (D) direction.

Flat, wide cells with rectangular shape were chosen for microinjection to measure D_l and D_r in cardiomyocytes. As in skeletal muscle fibers, D_l in these cells was measured when the beam segment and the measuring field were oriented perpendicular to the long cell axis and covered the entire width of the cardiomyocyte (Fig. 3C). To determine D_r, the laser illuminated a lateral part of the cell over its entire length (Fig. 3D). Dimensions of the measuring field were as described for soleus fibers (Fig. 3B).

Photobleaching.

After alignment of the muscle cell, the prebleach fluorescence intensity within the measuring field was recorded for 1–2 s while exciting with low laser intensity. A short-duration (3–10 ms) exposure to laser light of 10,000-fold-higher intensity followed, during which the fluorescence in the fiber segment exposed to the beam was partly photobleached (bleach efficiency between 15% and 55%). The recovery of fluorescence during the postbleach period then was observed for 1–10 s. The fluorescence intensity sensed by the photomultiplier during a FRAP measurement was digitized (12-bit), and the data were transferred to the computer for analysis. Sampling frequency during the measurements was between 100 and 1,000 Hz.

Data Analysis.

The longitudinal diffusion of bleached molecules out of and that of unbleached molecules into the measuring field (Fig. 3A) can be regarded as one-dimensional diffusion, with a rectangular initial distribution of the bleached protein molecules. The solution of the corresponding diffusion equation is given by Crank (16). After integrating the solution over the measuring field, the calculated recovery curve was fitted to the experimental curve by varying D_l, using a least-squares method.

Fig. 3B schematically shows the configuration for measuring radial diffusion as it is seen in a muscle fiber immediately after bleaching. The subsequent radial diffusion is a two-dimensional process. For reasons of symmetry, the differential equation has to be solved only for one-quarter of the fiber cross-section. The corresponding area was divided into 120 × 120 elements, and the diffusion equation was solved numerically by using a Crank–Nicolson algorithm (16). The calculated course of fluorescence recovery was fitted to the observed curve by varying D_r, using a least-squares method.

The width of the muscle fiber was always determined directly from its microscopic image, but it was not possible to measure the height of the fiber. Therefore, deviations from a circular cross-section cannot be excluded. To estimate how much the calculated diffusion coefficients are influenced by the choice of the fiber geometry, the width was held constant at the measured value, and the assumed fiber height was varied between the value of the width (= circular cross-section) and either 50% greater or 50% smaller than the width (= elliptical cross-sections). It turned out that even these marked deviations from a circular cross-section do not lead to variations in the fitted value of D by more than ±5% of the value found for circular geometry.

The cardiomyocytes selected for the FRAP experiments were regarded as plane rectangular sheets. As indicated by the arrows in Fig. 3 C and D, diffusion in both longitudinal and radial (or transversal) direction then can be treated as one-dimensional. Therefore, the same analysis used to calculate D_l in skeletal muscle fibers can be applied to the FRAP data obtained in heart muscle cells; the only difference to consider is the finite extension of the diffusion path in cardiomyocytes for both radial and longitudinal diffusion (16). Calculations were performed by using matlab software (Mathworks, Natick, MA).

Measurements in Glass Capillaries.

To determine D of the proteins in aqueous solution, FRAP experiments were performed in small borosilicate glass capillaries with an inner diameter of 50 ± 2 μm (Hilgenberg, Malsfeld, Germany). Measurements and data analysis were done as described for skeletal muscle fibers. D in dilute aqueous solution was determined after the capillaries were filled with a solution of fluorescent protein (either 5 mg/ml lactalbumin, 13 mg/ml Mb, or 5 mg/ml ovalbumin). D in concentrated protein solution was measured after filling the capillaries with the labeled protein diluted 1:10 in 24 g/dl BSA (Fraction V; Sigma); 24 g/dl is representative for the total protein content of striated muscle cells.

Both values, longitudinal and radial D, were determined with the methods described above. Because no difference between the two values is to be expected in the aqueous solutions in glass capillaries, the results have been used to check the reliability of the calculation procedures.

Results

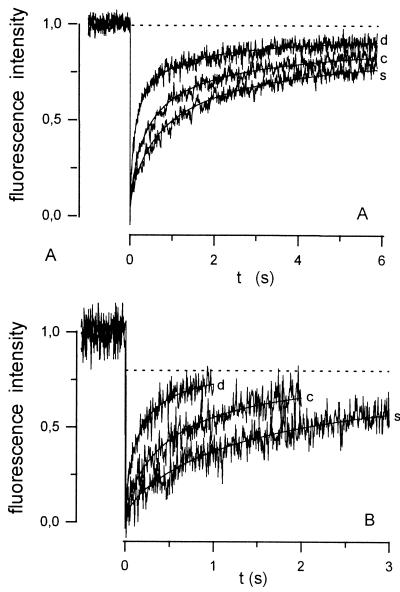
Fig. 4 shows an example of FRAP curves measured in glass capillaries in dilute (d) and concentrated (c) aqueous solution, as well as in skeletal muscle fibers (s). Obviously, recovery of fluorescence was fastest in d and slowest in s in both longitudinal and radial diffusion.

Figure 4.

Experimental FRAP curves recorded for fluorescently labeled Mb and their respective best-fit curves: longitudinal diffusion (A) and radial diffusion (B). Curves were measured in dilute (d) and concentrated (c) aqueous solution within glass capillaries and in soleus muscle fibers (s).

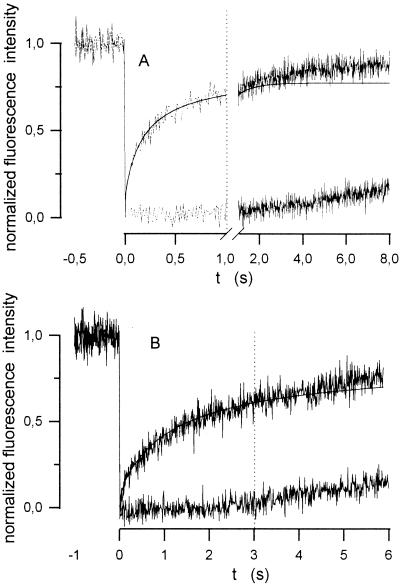
Nearly complete recovery of fluorescence occurred (dashed line in Fig. 4A) in the configuration of longitudinal diffusion, which is in accordance with what is expected from an infinite extension of the diffusion path outside of the measuring field. In contrast, the finite-extent model used for calculation of D_r predicts that recovery will be incomplete (dashed line in Fig. 4B) and that its degree will be determined by the width (l) of the bleached field in relation to the fiber diameter. In practice, however, the FRAP curves obtained during measurements of radial diffusion exhibited 100% recovery after an expanded time period (Fig. 5). This deviation reflects the influence of longitudinally oriented concentration gradients, created at both ends of the bleached stripe. The length of the laser beam stripe used for bleaching (around 110 μm, Fig. 3B) was considerably smaller than the length of both glass capillaries and skeletal muscle fibers (≥1 cm). Thus, a relatively short, centrally located stripe was bleached and it was only a matter of time until longitudinally diffusing molecules from unbleached regions entered the measuring field. The two flat curves in Fig. 5 with delayed recovery were measured after maximally opening the diaphragm d1 (Fig. 1)—i.e., with the beam width l exceeding the diameter of the glass capillary or muscle fiber, respectively. Consequently, no recovery resulting from diffusion in radial direction was possible in this situation, and, therefore, these curves represent the kinetics of the interfering longitudinal diffusion. As shown by the vertical, dotted lines in Fig. 5, this effect can be neglected only if relatively early parts of the recovery phase (≈1 s in glass capillaries, ≈3 s in muscle fibers) are used to calculate D_r. The best fits obtained for these portions of the curves also are shown in the figure. It can be seen that the measured curves deviate from the calculated ones only at later stages of the measurement.

Figure 5.

FRAP curves obtained for radial diffusion of Mb in a glass capillary filled with dilute aqueous solution (A) and in a soleus muscle fiber (B). The steep curves were recorded after bleaching for measurements of radial diffusion. The flat curves represent the superimposed effect of longitudinal diffusion. Best-fits for the radial diffusion process are shown as solid lines.

Table 1 summarizes the results obtained for D of fluorescently labeled lactalbumin, myoglobin, and ovalbumin in longitudinal (D_l) and radial (D_r) direction.

Table 1.

Protein diffusion coefficients^* in aqueous solutions and in muscle cells

Protein	t, °C	Glass capillary				Muscle cell
		Dilute		Concentrated		Soleus fiber		Cardiomyocyte
		Dl	Dr	Dl	Dr	Dl	Dr	Dl	Dr
Lactalbumin	22	11.3  ± 1.0 (13)	11.3  ± 1.6 (22)	3.1  ± 0.4 (19)	2.9  ± 0.6 (18)	1.3  ± 0.2  (31)	1.1  ± 0.3 (42)	1.2  ± 0.4 (24)	1.2  ± 0.5 (55)
Myoglobin	22	9.9  ± 0.8 (22)	9.7  ± 1.1 (15)	2.8  ± 0.4 (21)	2.9  ± 0.4 (27)	1.2  ± 0.4† (17)	1.2  ± 0.3 (46)	1.1  ± 0.4 (31)	1.1  ± 0.4 (38)
Myoglobin	37	14.8  ± 1.7 (24)				2.2  ± 0.1  (24)			2.0  ± 0.1 (4)
Ovalbumin	22	7.2  ± 0.9 (10)				0.52  ± 0.16 (4)			0.53  ± 0.25 (12)

Number of experiments for each is shown in parentheses. 

^*All values in 10⁻⁷ cm²/s, mean ± SE. 

^† Values measured previously with different techniques were (1.2 ± 0.1) × 10⁻⁷ cm²/s (4) and (1.3 ± 0.1) × 10⁻⁷ cm²/s (5). 

Diffusion in Solutions.

The D values obtained at 22°C in glass capillaries filled with dilute protein solution are in excellent agreement with the diffusion coefficients measured by others using unlabeled molecules and different techniques: for lactalbumin, 10.6 × 10⁻⁷ cm²/s (17); for Mb, 9.4 × 10⁻⁷ cm²/s (18) and 10.2 × 10⁻⁷ cm²/s (19); and for ovalbumin, 7.2 × 10⁻⁷ cm²/s (20) and 7.7 × 10⁻⁷ cm²/s (21). This indicates that translational D in aqueous solution was not affected by fluorescence labeling and shows the present FRAP technique to be appropriate for protein diffusion measurements.

The diffusion coefficients measured for lactalbumin and Mb in 24 g/dl concentrated albumin solution are all around 3 × 10⁻⁷ cm²/s. This is somewhat lower than the D of 3.3 × 10⁻⁷ cm²/s obtained for myoglobin at a myoglobin concentration of 24 g/dl (18), which may be due to the different environment experienced by the diffusing Mb in an albumin (69 kDa) compared with a Mb (17 kDa) solution of equal protein concentration.

D_l and D_r for both lactalbumin and Mb in glass capillaries were not significantly different, neither in dilute nor in concentrated solution. That the procedures described here to determine D_l and D_r led to identical values in isotropic media, as theoretically expected, provides support for their validity.

Protein Diffusion in Muscle Cells.

The diffusion coefficients measured longitudinally (at t = 22°C) for lactalbumin and Mb in muscle cells ranged between 1.1 × 10⁻⁷ cm²/s and 1.3 × 10⁻⁷ cm²/s, and they were not significantly different for skeletal and cardiac muscle. These values are almost three times lower than those measured in concentrated protein solution (24 g/dl) and are about one-ninth of the respective D in dilute protein solution. Ovalbumin, which has a larger molecular mass, exhibits a diffusivity in sarcoplasm that is decreased even to 1/14 of its value in dilute solution.

Radial D values of lactalbumin and Mb in skeletal and cardiac muscle cells were very similar to the respective D_l values. No significant differences between D_r and D_l were found for both proteins, with the exception of lactalbumin in soleus fibers, whose D_l was slightly higher than D_r (Table 1). In the case of ovalbumin, D_l in skeletal muscle fibers was not significantly different from D_r in cardiomyocytes.

Myoglobin Diffusion at 37°C.

When the temperature was raised from 22°C to 37°C in glass capillaries, D of Mb increased by 50%, corresponding to a Q₁₀ of 1.31. We observed a similar temperature dependence of D in aqueous solution for other proteins: lactalbumin (Q₁₀ = 1.36), ovalbumin (Q₁₀ = 1.29), and ferritin (Q₁₀ = 1.30; data not shown). In cardiomyocytes, D_r of myoglobin at 37°C was 80% higher than the value measured at 22°C (Q₁₀ = 1.49). We already have reported that the intracellular myoglobin diffusion coefficient (D_l) in skeletal muscle cells also exhibits a somewhat higher Q₁₀ (1.46) than is found in aqueous solutions (5).

Discussion

Translational Diffusion of Mb and of Other Proteins Is Very Slow Within Muscle Cells.

The data reported here for intracellular D of lactalbumin (diameter, 3.8 nm), Mb (diameter, 3.5 nm), and ovalbumin (diameter, 6.1 nm) when using the FRAP technique agree very well with our recent observations (22) on longitudinal sarcoplasmic diffusion of various proteins in skeletal muscle cells employing a different method. There, diffusion of proteins of sizes of 3–10 nm in diameter also was found to be about 10 times slower in skeletal muscle fibers than in dilute solution. For larger proteins such as catalase (diameter, 10.5 nm) and ferritin (diameter, 12.2 nm), even a decrease of D to ≈1/20 and 1/50 of the value in water was observed, whereas no diffusive flux of earthworm hemoglobin (diameter, 30 nm) could be detected at all along the fiber axis. However, D_r could not be measured with that method, and, thus, no conclusion on the size dependence of radial protein diffusion in muscle fibers was possible. The D values measured here for Mb and lactalbumin in glass capillaries filled with 24 g/dl protein solution are considerably higher than those found within muscle cells (Table 1). Mere effects of protein concentration thus cannot fully account for the slow translational diffusion in the sarcoplasm.

Interestingly, in measurements of rotational diffusion in living muscle, the Mb rotational correlation time was found to be only ≈1.4 times longer than in dilute solution (11). The observation of a relatively high rotational D versus that of a very low translational D of Mb in muscle is not contradictory. It is consistent with the notion of a sarcoplasmic diffusion space of moderate microviscosity but a high tortuosity imposed by the spatial properties of the myofilamental lattice (22). The moderate microviscosity allows a relatively high rotational diffusivity whereas the high tortuosity is responsible for a low translational diffusivity. Thus, there exists no real discrepancy in Mb diffusivities, as assumed recently (23), that needs to be resolved. An important point here is that the relatively high rotational mobility of Mb in muscle per se cannot contribute to facilitated O₂ diffusion in the sarcoplasm because the speed of the reaction of O₂ and Mb is far too slow to allow a facilitation by rotational diffusion of Mb to occur, as has been shown theoretically by Wyman (24). Only when substrate and carrier molecules react at the speed of the protonation reaction, which is orders of magnitudes faster, can a facilitated transport by rotation be demonstrated (25). No such limitation of the reaction velocity is present in the case of facilitated O₂ transport by translational diffusion of myoglobin (2, 24). As shown here and previously, this transport mechanism is limited by the slow translational diffusivity of Mb in muscle cells.

Myoglobin Diffusion in Muscle Cells Is Isotropic.

Anisotropy of sarcoplasmic diffusion has been reported for small molecules; for Ca²⁺ (7), O₂ (8), and H₂O (6), diffusion in radial direction is believed to be slower than along the longitudinal fiber axis. An anisotropy of sarcoplasmic D also appeared very likely for ATP and phosphocreatine (26). This phenomenon was attributed to a greater tortuosity effect exerted by the myofilamental lattice in radial direction. The structural anisotropy of the myofilamental lattice also has led Baylor and Pape (3) to assume that sarcoplasmic D_r of myoglobin might be significantly smaller (1.3 × 10⁻⁷ cm²/s when extrapolated to 37°C) than the D_l they measured. In contrast, Groebe (9) claimed that sarcoplasmic D_r of Mb should be considerably higher (5.5 × 10⁻⁷ cm²/s, 37°C) than D_l. Groebe argued that D of Mb, when measured in longitudinal direction, has to pass through many sarcomere lengths and Z discs, the latter probably representing strong obstacles to longitudinal Mb diffusion (5). The present work clearly shows that diffusion of myoglobin is not anisotropic, neither in skeletal muscle fibers nor in cardiomyocytes. It is not obvious which sarcoplasmic structures are responsible for this finding, but it is conceivable that the high tortuosity of the diffusion path in radial direction slows down diffusion to the same extent as does the hindrance imposed by the meshes of Z discs and M lines in longitudinal direction [see discussion in Papadopoulos et al. (22)].

Does Mb Contribute Significantly to Intracellular O₂ Transport in Muscle?

The values measured for the diffusion coefficient of Mb at body temperature (37°C) in mammalian skeletal [D = 2.2 × 10⁻⁷ cm²/s (5)] and cardiac (D = 2.0 × 10⁻⁷ cm²/s; this work) muscle are about seven times smaller than D of Mb in dilute aqueous solution (D = 14.8 × 10⁻⁷ cm²/s, 37°C). Jürgens et al. (27) have shown recently, employing a modified Krogh cylinder model to describe steady-state tissue oxygenation, that in maximally exercising human quadriceps femoris muscle Mb-facilitated O₂ diffusion with D_r = 2.2 × 10⁻⁷ cm²/s can enhance intracellular O₂ transport on average by 4%. A somewhat larger effect was seen in the blood perfusion rate required to avoid anoxia in the muscle cells. Because of the higher oxygen conductance of the tissue, blood perfusion can be ≈15% lower in the presence of mobile Mb than with immobile Mb. In heart muscle, where the mobility of Mb is almost identical to that of skeletal muscle, these figures are smaller. For the maximally working mouse heart (oxygen consumption = 270 ml O₂ per kg⋅min, radius of Krogh cylinder = 10 μm), an average contribution of Mb-facilitated O₂ diffusion of 1.6% to total intracellular O₂ transport is calculated by using the same Krogh model, and the necessary blood perfusion rate is found to be 0.2% lower with than without facilitated O₂ diffusion.

The absence of a substantial contribution of MbO₂ diffusion to intracellular O₂ transport is supported by recent observations of a high cardiac Mb oxygenation under both basal and increased-work conditions. Arai et al. (28) used scanning reflectance spectroscopy to monitor Mb oxygenation of the pig heart in vivo and found SO₂ to be >0.92 under basal conditions. An increase in heart work induced by phenylephrine infusion failed to reduce Mb oxygenation in this study, whereas coronary artery occlusion revealed massive deoxygenation of Mb. Zhang et al. (29) used ¹H magnetic resonance spectroscopy to evaluate the state of myocardial Mb oxygenation in dogs. Neither under basal state conditions nor during high cardiac work states could a desaturation of Mb be observed, whereas under coronary stenosis, Mb was desaturated to a marked degree. NMR techniques also were applied by Chung and Jue (30) and Jelicks and Wittenberg (31) to follow myoglobin oxygenation in perfused rat hearts at different work states. At a very high work rate (hearts paced at 600 beats/min, infusion of 80 ng/ml dobutamine), Chung and Jue found that oxygen saturation of Mb did not fall below 85%, and Jelicks and Wittenberg observed a mean myoglobin oxygen saturation of 76% irrespective of heart rate in the range of 50–500 min⁻¹.

These high mean oxygen saturations indicate that there are only small or moderate oxymyoglobin gradients within large areas of the heart tissue. Hence, in addition to low Mb diffusivity, the MbO₂ gradients in heart muscle may be relatively small and, thus, do not predict a major role of MbO₂ diffusion in intracellular O₂ transport in the heart.

Recently, results obtained with Mb knockout mice have been reported. Garry et al. (14) and Gödecke et al. (15) independently established a transgenic mouse model to investigate the implications of a complete lack of myoglobin in muscle. A main finding was that mice lacking Mb were not discernibly different from normal animals with respect to physical performance and O₂ consumption during treadmill testing, which was taken to argue strongly against a vital role of Mb in O₂ supply to muscle.

However, Gödecke et al. (15) investigated the hearts of these animals more closely and observed significant structural and functional differences between transgenic and normal mice. Among these differences was a higher capillary density and blood perfusion rate of the hearts of Mb knockout mice. The obvious existence of compensatory mechanisms in these hearts suggests that there are circumstances under which the presence of Mb is essential. Our Krogh cylinder model does not take into account the fluctuation in O₂ supply during the heart cycle. O₂ delivery to the heart tissue is diminished during systolic heart contraction when coronary perfusion transiently is greatly reduced. In this non-steady-state situation, two roles of Mb may become important: (i) its O₂ storage function, which is used to temporarily provide oxygen to the mitochondria when capillary oxygen supply is insufficient, and (ii) an enhanced O₂ conductance because of increased facilitated O₂ diffusion, which results from increasing oxymyoglobin gradients when tissue PO₂ falls and O₂ desaturation of myoglobin around the mitochondria progresses.

In Mb knockout mice, both of these roles are abolished, and the question arises of which of them requires the compensatory changes observed by Gödecke et al. (15). The authors suggest that the higher capillarity, i.e., lower diffusion distances and, hence, steeper PO₂ gradients between capillaries and mitochondria, serves to compensate for the loss of facilitated O₂ diffusion. Because higher capillarity and steeper PO₂ gradients also result in an increased amount of O₂ stored by hemoglobin per unit volume of tissue and, because of a higher mean tissue PO₂, in an increased mean tissue concentration of dissolved oxygen, these adaptations equally well could compensate for the loss of the O₂ storage function of Mb. The relative importance of these two possible roles of Mb has to be assessed by other experimental or theoretical approaches.

Abbreviations

Mb

myoglobin

D

diffusion coefficient

FRAP

fluorescence recovery after photobleaching