Hierarchy of direction-tuned motion adaptation in human visual cortex

Abstract

Prolonged exposure to a single direction of motion alters perception of subsequent static or dynamic stimuli and induces substantial changes in behaviors of motion-sensitive neurons, but the origin of neural adaptation and neural correlates of perceptual consequences of motion adaptation in human brain remain unclear. Using functional magnetic resonance imaging, we measured motion adaptation tuning curves in a fine scale by probing changes in cortical activity after adaptation for a range of directions relative to the adapted direction. We found a clear dichotomy in tuning curve shape: cortical responses in early-tier visual areas reduced at around both the adapted and opposite direction, resulting in a bidirectional tuning curve, whereas response reduction in high-tier areas occurred only at around the adapted direction, resulting in a unidirectional tuning curve. We also found that the psychophysically measured adaptation tuning curves were unidirectional and best matched the cortical adaptation tuning curves in the middle temporal area (MT) and the medial superior temporal area (MST). Our findings are compatible with, but not limited to, an interpretation in which direct impacts of motion adaptation occur in both unidirectional and bidirectional units in early visual areas, but the perceptual consequences of motion adaptation are manifested in the population activity in MT and MST, which may inherit those direct impacts of adaptation from the directionally selective units.

prolonged exposure to a visual pattern drifting in one direction alters perception of subsequently presented stimuli. Adaptation reduces the visibility of objects moving in the adapted direction (Raymond 1993; Tolhurst 1973), makes static or dynamic patterns appear to drift in the opposite direction (Mather et al. 1998), distorts the apparent speed of a moving stimulus (Stocker and Simoncelli 2009; Thompson 1981), or even shifts the perceived direction of motion away from the adapted direction (Levinson and Sekuler 1976).

These profound alterations in perception suggest that adaptation has substantial impacts on the neural systems for processing motion stimuli. Indeed, there have been many attempts at uncovering neural consequences of motion adaptation. Although these studies have demonstrated that adaptation substantially modifies neural activities in retina (Barlow and Hill 1963) or visual areas in the cortex (Hammond et al. 1985; Huk et al. 2001; Petersen et al. 1985; Tolias et al. 2001), it has been quite challenging to single out a neural locus or mechanism for motion adaptation. Given the hierarchical and distributed nature of cortical motion processing, which has been supported by a body of anatomical (Felleman and van Essen 1991; Maunsell and van Essen 1983), functional (Gegenfurtner et al. 1997; Movshon and Newsome 1996; Movshon et al. 1986; Zeki 1974), and computational studies (Rust et al. 2006), adaptation may have impacts on neurons at multiple stages along the hierarchy. Alternatively, adaptation may have a direct impact only at the very early stage of cortical motion processing, and apparent changes in neural activity at the following stages may be just consequences of changes in their feedforward inputs from the early stage (Bartels et al. 2008; Kohn and Movshon 2003; Krekelberg et al. 2006a).

To gain understanding of how adaptation generates different impacts across cortical areas in human brain, we conducted functional magnetic resonance imaging (fMRI) experiments, in which cortical responses to motion stimuli were probed before and after adaptation for a range of directions relative to the adapted direction, and obtained fine-scale directional tuning curves of cortical adaptation from multiple areas. In the middle temporal area (MT) and the medial superior temporal area (MST), response reduction was maximal at the adapted direction and decreased gradually with an increasing difference from the adapted direction, resulting in a “unidirectional” curve of adaptation. In early-tier visual areas (V1/2, V3) and V3A, on the other hand, response reduction occurred not only at the adapted direction but also at the opposite direction, resulting in a “bidirectional” curve. The shape of fMRI adaptation tuning curves in MT and MST best matched the shape of perceptual adaptation tuning curves that were measured in psychophysical experiments.

MATERIALS AND METHODS

Subjects

Three human subjects (26–27 yr old, 1 female) participated in both psychophysical and fMRI experiments. One of the subjects was an author, and the others were volunteers who were naive as to the purpose of the current study. All subjects had normal neural anatomy and had normal or corrected-to-normal vision. Experiments were carried out with the written consent of each subject and in compliance with the safety guidelines for magnetic resonance research as approved by the Human Subjects Review Boards at Seoul National University and New York University.

Stimuli and Procedures for Psychophysical Experiments

Stimuli consisted of randomly distributed dots that were drifting for a limited lifetime within an annular region around the fixation. Each dot started in a random position within the circular aperture (4.67° radius), moved in a single direction for three video frames (50 ms), and then disappeared and reappeared at a new, randomly selected position within the aperture. The temporal phases of life cycle for individual dots were randomly predetermined such that exactly one-third of the dots renewed their positions in each frame. We opted to use random-dot cinematograms rather than drifting gratings to avoid any unwanted adaptation to an orientation pattern orthogonal to direction of motion. For the main psychophysical experiments, stimuli were presented at 640 × 480-pixel resolution at a refresh rate of 60 Hz on a cathode ray tube (CRT) monitor (LG 291U). Gaussian, anti-aliased white (90 cd/m² at maximum contrast) dots (0.14° width at half-height) were presented on a black (5 cd/m²) background, resulting in the density of 2 dots/deg², and moved at the speed of 13°/s.

Subjects performed a two-interval forced-choice task, where they indicated which of two sequentially presented motion stimuli contained coherently moving dots (Fig. 1A). On each trial, a field of drifting dots whose directions were randomly distributed over 360° was presented during the “noise” interval, whereas a small number of coherently moving dots were embedded in the field of randomly moving dots during the “signal” interval. To promote and maintain adaptation, high-contrast (90%) random dots drifting in a single direction were shown for 60 s before each block of postadaptation trials and repeatedly presented for 4.4 s before each trial as a top-up adapter. The spatial and temporal parameters, including dot density, dot size, and speed, of the test and adapter stimuli were optimized for maximum adaptation effects via pilot experiments. Each subject participated in eight daily sessions (4 “contrast sensitivity” sessions and 4 “coherence sensitivity” sessions, described below) of experiments, each of which consisted of preadaptation blocks followed by postadaptation blocks. The direction of adapting stimuli was held constant to maximize adaptation effects in a given daily session and was varied across sessions (for example, 0°, 90°, 180°, and 270° were used for 4 different daily sessions, respectively) to avoid any potential direction-specific effects. Although we chose to use cardinal directions as adapting stimuli for practical reasons, this would not threaten the internal validity of our experiments because we measured adaptation effects by comparing performance not across different directions but between preadaptation and postadaptation conditions at a given direction of motion.

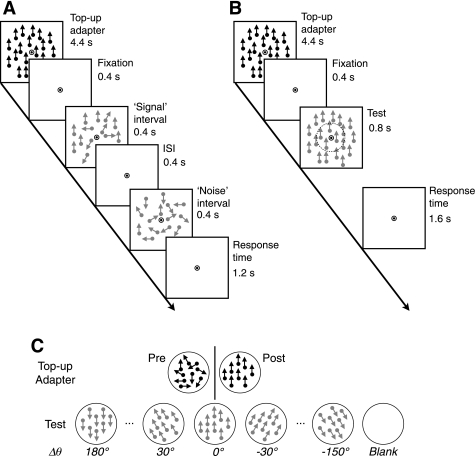
Fig. 1.

Stimuli and procedures for psychophysical and functional magnetic resonance imaging (fMRI) experiments. A: schematic diagrams of visual stimuli presented during psychophysical experiments. Each 7.2-s trial started with a high-contrast top-up adapter, which was followed by the “signal” and “noise” intervals in a random order. Subjects indicated which interval contained signal dots within 1.2 s after the offset of the second interval. ISI, interstimulus interval. B: schematic diagrams of visual stimuli during fMRI experiments. The adapter was identical to that in the psychophysical experiments. Subjects indicated whether or not motion directions were the same between the central and peripheral annulus. The imaginary circle with a broken line indicates the boundary between the 2 annuli. C: top-up adapter and test stimuli during fMRI experiments. High-contrast dots in a top-up adapter were moving in random directions before adaptation and in a single direction after adaptation. Low-contrast dots in the test period were moving always in a single direction. The relative direction difference between the adapter and test stimulus (Δθ) was varied at the 7 levels ranging from 0° to 180°. In fMRI experiments, “blank” trials were inserted randomly in between regular trials.

Estimation of Psychophysical Adaptation Effects

In the preadaptation blocks, dots moving in random directions (0% coherence) were presented during the top-up adaptation epoch. To probe adaptation-induced changes in motion perception, we obtained psychometric curves of coherent motion detection as functions of contrast and coherence separately before and after adaptation for a range of directions relative to the adapted direction [Δθ = (0°, 30°, 60°,…, 180°); Fig. 1C]. We acquired psychometric curves by varying the motion coherence of test stimuli with contrast held constant at 10% in half the blocks of trials or by varying the contrast of test stimuli with coherence held constant at 22% in the other half. To estimate thresholds at a fixed performance level of 75%, we fitted the curves with cumulative Gaussian functions using the maximum likelihood method. As results, we obtained dot contrast and motion coherence thresholds for each of the 7 adapter-test direction difference conditions before and after adaptation, resulting in 28 threshold estimates in total for each subject (Fig. 2, A and B). Trials containing test stimuli in two directions that were mirroring each other around the adapting direction (e.g., test stimuli with 30° and 150° directions when the adapting direction was 90°) were merged into a single absolute direction difference condition (e.g., Δθ = 60°) for threshold estimation. In addition, it should be reminded that the direction of adapting stimulus was varied across different daily sessions. Thus each of the threshold estimates was obtained from a set of test stimuli that differed in absolute direction of motion from session to session but had the same absolute amount of direction difference from a given adapter. Individual thresholds were estimated from 280 (adapted or opposite directions) to 560 trials, and their standard errors [84% confidence interval (CI), which corresponds to ±1 SD of a normal distribution, indicated by error bars in Fig. 2, A and B] were computed by applying a parametric bootstrap method (Efron 1985) to 1,000 resampled psychometric curves.

Fig. 2.

Perceptual effects of adaptation. A and B: coherence and contrast sensitivity measured before and after adaptation. Log sensitivity is plotted as a function of direction difference between adapter and test stimuli. Symbols and lines in light and dark colors indicate data from pre- and postadaptation trials, respectively. Thin lines with triangles, squares, and diamonds represent data from individual subjects; thick lines with circles are data averaged across subjects. The error bars represent 68% confidence intervals (CI) from bootstrap sample estimates. C: directional tuning curves of perceptual adaptation. Adaptation indexes (see methods and materials for definition) based on adaptation-induced changes in coherence (red symbols and lines) and contrast sensitivity (blue symbols and lines) are plotted as a function of direction difference between adapter and test directions. Broken lines indicate 68% CI from bootstrap sample estimates.

To quantitate an amount of adaptation for each test direction, we computed a psychophysical adaptation index (AIp) by contrasting a preadaptation threshold and a postadaptation threshold:

$$\text{AIp}\left(\Delta \theta \right)=\frac{{\text{LS}}_{\text{pre}}\left(\Delta \theta \right)-{\text{LS}}_{\text{post}}\left(\Delta \theta \right)}{\left|{\text{LS}}_{\text{pre}}\left(\Delta \theta \right)+{\text{LS}}_{\text{post}}\left(\Delta \theta \right)\right|},$$

where LS_pre(Δθ) and LS_post(Δθ) indicate log sensitivities [log₁₀(1/thresholds)] before and after adaptation, respectively, at a test direction difference, Δθ. An AIp could range from −1 to +1, positive for reduction in sensitivity after adaptation and negative for increase in sensitivity after adaptation. On the basis of this equation, we estimated the two separate types of AIp, one for coherence sensitivity (red symbols and lines in Fig. 2C) and the other for contrast sensitivity (blue symbols and lines in Fig. 2C). We tested the statistical significance of monotonic decreases in AIp as a function of direction difference between an adapter and a test as follows. First, for each psychometric curve, we generated 1,000 parametric bootstrap samples with an assumption of binary distribution of correct responses with a given number of observations (Wichmann and Hill 2001). Second, from those bootstrap sample curves, we obtained 1,000 75% threshold estimates. Third, we computed 1,000 bootstrap adaption indexes from the 1,000 pairs of threshold estimates from preadaptation and postadaptation psychometric curves at each relative direction difference condition. Fourth, for each of the 1,000 bootstrap adaptation curves made of the bootstrap adaptation indexes across the 7 direction difference conditions, we computed a Spearman's rank correlation coefficient (ρ). Finally, we determined a 95% CI by sorting out the bootstrap samples of ρ values separately for the coherence and contrast sensitivity adaptation curves.

Stimuli and Procedures for fMRI Experiments

Visual stimuli were displayed in 640 × 480-pixel resolution at a refresh rate of 60 Hz on a liquid crystal display (LCD), which was part of a custom-made display system (ISOL Technology, Taejon, Korea) mounted on a birdcage coil and viewed by subjects through a mirror attached to the coil. The response time (time taken to turn on and off pixels) of the LCD monitor varied depending on initial and target luminance values, ranging from 4 to 16 ms (5 and 12 ms on average for gray-to-gray response time and for rise-and-fall response time, respectively).

Each subject was scanned in nine sessions: four sessions for the main adaptation experiments, two for orientation adaptation control experiments, one to obtain high-resolution T1-weighted anatomic images, one to define retinotopic visual areas (Engel et al. 1994), and one to define areas MT and MST. In the main adaptation sessions, we measured fMRI responses from the same subjects using the procedure and stimuli identical to those used in the psychophysical experiment, with a few exceptions. These exceptions were introduced to increase the efficiency of fMRI experiments. During the test epoch, only a “signal” test stimulus with 100% coherence appeared for 800 ms (Fig. 1B) to specifically evoke a subpopulation of cortical neurons that are tuned around a single direction of motion by removing motion signal in any other directions (noise dots). The contrast of test stimuli was also fixed at an intermediate level (10%) to prevent fMRI signal from being constrained by any ceiling (due to saturation) or floor effects. Unlike in the psychophysical experiments, we asked subjects to indicate whether dots in the central and peripheral parts of the annulus (which were divided by an imaginary circle indicated by the dotted line in Fig. 1B) moved in the same direction or in slightly different directions (±2° around the target direction). This direction discrimination task was chosen not only to maintain the general level of attention but also to force subjects to pay attention evenly to the central and peripheral parts of the large test annulus. The other aspects of experimental design, including trial structure (Fig. 1C), relative differences between an adapter and test stimuli, and basic parameters for motion stimuli, were the same as those for the psychophysical experiments. Thus we conducted four daily sessions of fMRI scans on each of the same subjects who participated in the psychophysical experiment. In each session, we collected fMRI signal out of 12 4.08-min scan runs, 6 scan runs each before and after adaptation. As in the psychophysical experiments, we varied the direction of the adapter out of the four cardinal directions.

As results, we collected data from a total of 48 trials through 4 daily sessions for each of the 24 viewing conditions [12 direction differences × 2 (pre and post) adaptation conditions] for each subject. Functional MRI responses to each relative direction in each visual area were pooled across subjects to increase the signal-to-noise ratio of data given small numbers of observations for many test conditions [14 = 7 (direction differences from the adapter) × 2 (before or after adaptation)]. After trials were merged across subjects and sorted into the seven direction difference conditions on the basis of relative direction difference between an adapter and a test stimulus, a total of 144 (for the 0° and 180° conditions) or 288 trials (for the ±30°, ±60°,…, ±150° conditions) were obtained for each of the 14 viewing conditions (7 direction differences × 2 adaptation conditions).

To separate fMRI responses to a test stimulus from those to a top-up adapter, we inserted “blank” trials, in which the adapter was presented alone without a test stimulus (Fig. 1C), randomly among regular trials and then subtracted the mean response in the blank trials (top-up adapter only, red lines in Fig. 3) from those in the test trials (top-up adapter + test, blue lines in Fig. 3). To maintain attention and match the blank trials to the regular trials in terms of motor responses, subjects were asked to press a button after waiting for about 1.2 s (matched to the mean response time in the stimulus trials) since the offset of a top-up adaptation stimulus.

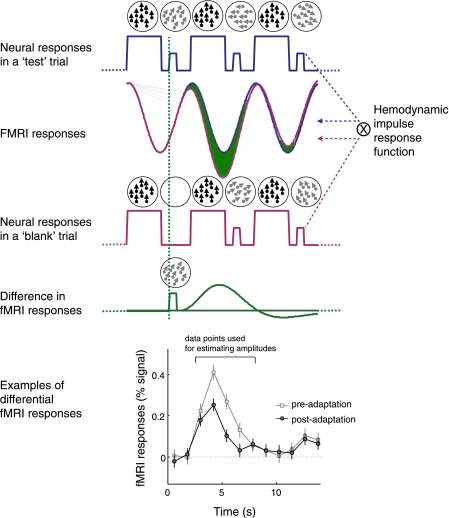
Fig. 3.

Rationale for extracting fMRI responses evoked by a test stimulus. Neural responses to a series of consecutive adapter and test stimuli are expected to fluctuate as a function of stimulus contrast, which is modeled by a boxcar function (blue and red solid lines in first and third rows, respectively). Neural responses are then convoluted by a hemodynamic impulse response function, resulting in time series of fMRI responses. With the assumption of linearity of fMRI signal, the subtraction of the “blank-onset-locked” fMRI responses (solid red curve in second row) from the “test-onset-locked” fMRI responses (solid blue curve in second row) can isolate fMRI responses evoked by a test stimuli (indicated by the green area between the blue and red curves in the second row and by the solid green curve in the fourth row). Graph at bottom shows 2 example time series of differential fMRI response from the middle temporal area (MT) when the test direction was identical to that of the adapter, one before adaptation and the other after adaptation.

Definition of Visual Areas and Regions of Interest

In the retinotopy session, we obtained a map of the polar angle representation of the visual field and defined boundaries between areas by identifying regions in which the polar angle phase reverses. The polar angle map was acquired by measuring the phase of the periodic fMRI response to a rotating wedge of black-white checkerboard stimulus (width, 45°; radius, 0.5–9° eccentricity; speed, 28.8 s/cycle). Similarly, a map of the eccentricity representation of the visual field was also obtained by measuring the phase of the response to a contracting or expanding annulus of checkerboard stimulus (width, 2.25°; speed, 28.8 s/cycle). Through this retinotopy session, which was conducted in a separate scan for each subject, we reliably identified the seven visual areas (V1, V2, V3, hV4, V3A, VO1, and LO1) for all of the six hemispheres from the three subjects. We defined LO1 (lateral occipital area 1) according to the retinotopic organization that was proposed by Larsson and Heeger (2006a).

We carried out MT/MST localizer functional scans in a separate session for each subject. The areas MT and MST were identified and distinguished in two steps (MT+ localizer scans and MT-MST separation scans) based on the criterion that MST(d) has a large ipsilateral representation of visual field (Huk et al. 2002; Raiguel et al. 1997; Smith et al. 2006; but see Kolster et al. 2010 for other detailed criteria). In the MT+ localizer scans, visual stimuli were presented in two circular apertures (4.67° radius) on the left and right sides of the fixation point. Low-contrast (10%) dots in both of the apertures moved in 1 of 12 directions (0°, 30°, 60°, …, 330°) in a randomized order, alternating directions every 1.2 s for 14.4 s, and then stopped and stayed stationary for another 14.4 s. This cycle repeated eight times. We defined MT+ by identifying a spatially extended cortical region in the middle temporal area in both hemispheres by finding a group of voxels whose activity were positively correlated (r > 0.5, uncorrected for multiple comparisons) with the periods of moving dots. In the MT-MST separation scans, we presented moving and stationary dots separately in the two apertures and swapped the two types of dots periodically. MT was defined by identifying a spatially extended subregion in which voxels showed significant modulation in fMRI activity with peaks matched to the contralateral presentation of moving dots.

In addition, we ran two reference scans in each main adaptation session, one before and the other after the main experimental scans, to define a subregion within each visual area that responded to motion stimuli appearing in the circular aperture. Only fMRI responses from these subregions were used for further data analysis.

fMRI Data Analysis

Data preprocessing.

We discarded images for the first 14.4 s (adaptation scans) or 28.8 s (reference scans) from each functional run to avoid transient effects of magnetic saturation. Head motion within and across scans was corrected using custom software (Nestares and Heeger 2000). The original time series from each voxel was high-pass filtered to compensate for slow drifts typical of fMRI signals and divided by its mean image value to compensate for variations in intensity with distance from the coil and to convert the data from arbitrary image intensity units to percent signal change. We discarded from further analysis trials whose fMRI responses were likely to be contaminated with eye blinks, abrupt head motion, or “k-space” spike noises, which can be introduced by potential imperfections in gradient coil, radiofrequency hardware, or other hardware components of an MRI scanner (Zhang et al. 2001), by detecting high-frequency fluctuations in time series occurring simultaneously in the majority of voxels.

Estimation of magnitudes of differential responses.

The magnitude of the differential (stimulus trial minus blank trial) responses was estimated as follows. First, 14.4-s-long fMRI time series in percent signal time-locked to the start of each trial were extracted and adjusted to a zero baseline by subtracting the mean of four time points before test stimuli (Fig. 4). Second, we then pooled all those zero-baseline-adapted differential time series from all of the regions of interest across all of the viewing conditions to identify a set of successive frames in which average responses were higher than baseline, as indicated by the line in the graph at bottom of Fig. 3. The frames of interest turned out five consecutive data points after the stimulus onset. Third, for each condition, we estimated the magnitude by taking an average of percent signals over those frames of interest. This procedure allowed us to estimate the magnitude of responses from all relevant image frames whose relative contributions to the magnitude computation were determined by an empirical hemodynamic response function. Alternative procedures for data fitting (hemodynamic response function) or amplitude estimation [measuring the amplitude of a peak of differential responses or computing a scalar response amplitude by projecting the differential response from a given viewing condition onto the across-condition mean of differential responses (Larsson and Heeger 2006b)] yielded similar patterns of results.

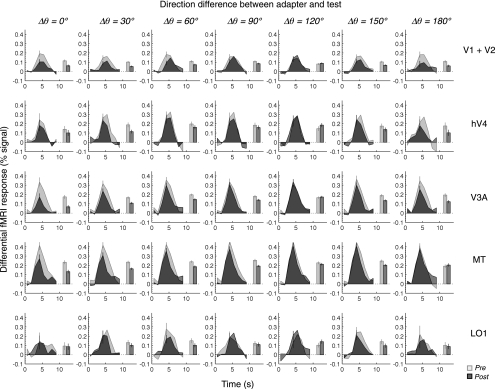
Fig. 4.

Pre- and postadaptation time series of differential fMRI response from representative areas. Time series of differential fMRI responses are sorted in columns by direction difference between the adapter and the test and in rows by different visual areas. The time series in the first row were obtained by averaging the data from V1 and V2. The light and dark gray lines indicate the time series from the pre- and postadaptation conditions, respectively. We averaged fMRI responses around the peak (the 3rd–7th data points) to compute response amplitudes, which are shown by the light (preadaptation) and dark (postadaptation) gray bars. The error bars on the time series are the means of ±1 SE across all the data points in a given time series; the error bars on the bars are 68% CI estimated by the bootstrap method. The time series were obtained by averaging the data from the 3 subjects.

Estimation of fMRI adaptation indexes.

For each of the seven test directions, an fMRI adaptation index (AIf) was obtained using an equation similar to that used for the psychophysical adaptation index:

$$\text{AIf}\left(\theta \right)=\frac{{\text{FR}}_{\text{pre}}\left(\theta \right)-{\text{FR}}_{\text{post}}\left(\theta \right)}{\left|{\text{FR}}_{\text{pre}}\left(\theta \right)+{\text{FR}}_{\text{post}}\left(\theta \right)\right|}$$

where FR_pre(θ) and FR_post(θ) are magnitudes of fMRI responses before and after adaptation, respectively, at a test direction, θ.

Statistical significance tests.

To determine whether an adaptation curve has a single mode or two modes at opposite directions, we performed a modified version of the Rayleigh test (Batschelet 1981). The Rayleigh test is typically applied to confirm the significance of orientation or direction selectivity of a neuron by testing whether a summed vector magnitude from an orientation or direction tuning curve of a neuron deviates from the one from a uniform distribution around the circle. Because we had adaptation indexes (AIf values), not observation numbers, for individual test directions, a bootstrap method was used to evaluate the statistical significance of summed vector magnitude (Bonhoeffer et al. 1995; Wörgötter and Eysel 1987). To compute vector magnitude (L) of an adaptation tuning curve, we first calculated two components, c and s, defined by

$$\begin{array}{cc}c={\displaystyle {\sum }_{i=1}^n\text{AIf}\left({\theta }_i\right)\cos \left(d·{\theta }_i\right)}& s={\displaystyle {\sum }_{i=1}^n\text{AIf}\left({\theta }_i\right)\sin \left(d·{\theta }_i\right),}\end{array}$$

where d = 1 for unidirectional tuning and d = 2 for bidirectional tuning. The vector magnitude was defined by

$$L=\frac{\sqrt{\left(c^2+s^2\right)}}{{\displaystyle {\sum }_{i=1}^n\text{AIf}\left({\theta }_i\right)}},$$

where c and s are as defined above. For each visual area, we generated a bootstrap sample (N = 10,000) of summed vector magnitudes by assigning randomly selected input vector magnitudes chosen from a Gaussian distribution whose mean and deviation were the mean fMRI response and standard deviation pooled across different test directions. Summed vector magnitudes greater than the top 5% of bootstrap sample L values were considered significant.

For only those visual areas that showed a significant L value, the significance of adaptation effects minus differences between FR_pre(θ) and FR_post(θ) was evaluated at individual test directions by using the bootstrap test (Cohen 1995; Wilcox 2005). The detailed steps were as follows. First, the original pre- and postadaptation data with a sample size of 144∼288 trials were resampled, respectively, with replacement to generate 1,000 bootstrap samples of the matched sample size. Second, the difference between those two sample means was computed for each pair of the random samples. Third, the location of the actual difference between the pre- and postadaptation magnitudes was defined in the distribution of the 1,000 bootstrap differences to estimate P values. The significant differences and P values are shown in Fig. 5. We used those same bootstrap samples to generate the bootstrap samples of AIf values and applied the same procedure used for the psychophysical data (AIp) to evaluate the statistical significance of monotonic decrease in AIf as a function of direction difference between an adapter and a test (Fig. 6).

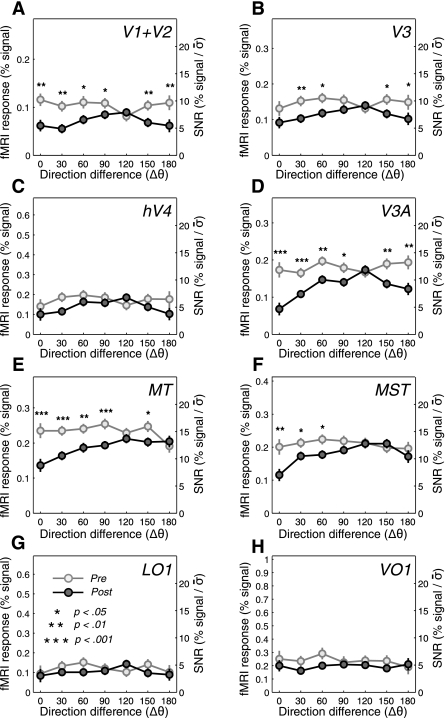
Fig. 5.

Pre- and postadaptation differential fMRI response amplitudes. A–H: the amplitudes of differential fMRI responses (bars in Fig. 4) are plotted against the direction difference between the adapter and the test. The light and dark gray circles indicate the data from the pre- and postadaptation conditions, respectively. The significant reductions in amplitude after adaptation are indicated by asterisks (*P < 0.05; **P < 0.01; ***P < 0.001; from pairwise 1-tailed t-tests). For comparisons across different visual areas in terms of signal-to-noise ratio (SNR), the y-axes were rescaled by dividing the %signal values with the pooled SEs (σ̄) of all the data in a given area.

Fig. 6.

Directional tuning curves of fMRI adaptation. A–H: the adaptation indexes of fMRI activity (AIf values) are plotted against the direction difference between the adapter and the test (black lines with symbols). To check whether the AIf decreases as a function of direction difference, the Spearman rank correlation test was run for each of the adaptation tuning curves. The mean and 95% CI of rank correlations (ρ values) out of 1,000 bootstrap samples are indicated above each plot. To check the presence and magnitude of bidirectional adaptation, the model for summation of the Gaussian curve of adaptation around the adapted direction (solid gray lines) and that around the direction opposite to the adapter (dashed gray lines) is fitted to the adaptation tuning curves. The goodness of fit is indicated by the percentage of variance explained (V.E.), indicated below each plot. The shaded gray areas are SEs. The y-axes were rescaled by dividing the adaptation indexes with the pooled SEs. MST, medial superior temporal area.

To assess whether a given adaptation tuning curve was unidirectional or bidirectional, we fitted two simple descriptive models to the curve: 1) the unidirectional adaptation with a single Gaussian curve,

$$\text{AIu}\left({\theta }_{\text{test}}\right)=a_{\text{A}}{e}^{-{\left({\theta }_{\text{test}}-{\theta }_{\text{adapt}}\right)}^2/2{\sigma }_{\text{A}}^2}+b,$$

where a_A and σ_A are the amplitude and width of the Gaussian curve centered at the adapted direction, respectively, and b is a term for baseline (direction nonspecific) adaptation; and 2) the bidirectional adaptation model based on a sum of two Gaussian curves, one centered at the adapted direction and the other at the opposite direction,

$$\text{AIb}\left({\theta }_{\text{test}}\right)=a_{\text{A}}{e}^{-{\left({\theta }_{\text{test}}-{\theta }_{\text{adapt}}\right)}^2/2{\sigma }_{\text{A}}^2}+a_{\text{N}}{e}^{-{\left({\theta }_{\text{test}}-{\theta }_{\text{adapt}}+\pi \right)}^2/2{\sigma }_{\text{N}}^2}+b,$$

where a_N and σ_N are the amplitude and width of the Gaussian curve centered at the null direction (direction opposite to the adapter), respectively. Because the unidirectional adaptation model, the parameters of which are a_A, σ_A, and b, is nested within the bimodal adaptation model, the parameters of which are a_A, σ_A, b, a_N, and σ_N, we judged whether the bidirectional model provides a significantly better fit to the data than does the unidirectional model by evaluating the amount of reduction in model prediction errors using F statistics. To evaluate the bimodality of adaptation curves, we compared the amplitudes of the two Gaussian functions (a_A and a_N) in the bimodal adaptation model fitted to the adaptation curve (Fig. 7A).

Fig. 7.

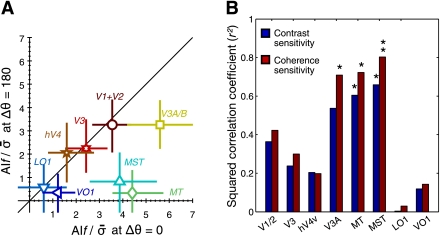
Comparisons of cortical adaptation curves across visual areas. A: the magnitudes of fMRI adaptation at the adapted direction on the x-axis is plotted against those at the direction opposite to the adapted direction across visual areas on the y-axis. For comparisons across visual areas, the normalized adaptation indexes (y-axes on right in Fig. 6) were used here. The error bars are the 68% CI of the mean adaptation indexes, which were estimated with the bootstrap procedure. B: squared correlation coefficients (r²) between fMRI and psychophysical adaptation tuning curves are shown separately for coherence (red bars) and contrast (blue bars) adaptation tuning curves across different visual areas. *P < 0.05; **P < 0.01, statistically significant correlations.

Comparison of psychophysical and fMRI adaptation curves.

For each of the visual areas under observation, we assessed the similarity of its adaptation tuning to the psychophysical adaptation tuning by computing two different types of correlation coefficients, a correlation coefficient of the fMRI adaptation curve in that area with the psychophysical adaptation curve based on contrast sensitivity (blue bars in Fig. 7B) and with the one based on coherence sensitivity (red bars in Fig. 7B).

Imaging Hardware and Scan Protocols

The main adaptation scans and MT and MST localization scans were acquired using a surface coil (Quadrature surface coil; ISOL Technology, transmitter/receiver) on a Varian 3T scanner in the Brain Research Center at Korea Advanced Institute of Science and Technology (KAIST). The anatomic scans for high-resolution (1-mm isovoxel) T1 volume images and the functional scans for definition of retinotopic visual areas were acquired using a transmit head coil (NM-011; NOVA Medical, Wakefield, MA) and a four-channel phased array receive coil (NMSC-021; NOVA Medical), respectively, on a Siemens 3T Allegra scanner in the Center for Brain Imaging at New York University (NYU). The parameters for the functional epi-polar imaging–blood oxygen level-dependent (EPI-BOLD) scans at KAIST were 1,200-ms repetition time (TR), 21.2-ms echo time (TE), 65° flip angle (FA), 64 × 64 matrix size, 2.5 × 2.5 × 3-mm voxel size, 160 × 160-mm field of view (FOV), and 14 slices. Those at NYU were 1,200-ms TR, 30-ms TE, 72° FA, 64 × 64 matrix size, 3 × 3 × 3-mm voxel size, 192 × 192-mm FOV, and 16 slices.

Motion Energy Analysis

To compute motion energy in stimuli, image sequences were three-dimensional (3-D) Fourier-transformed into frequency amplitude spectra and filtered by a bank of spatiotemporal frequency filters that were jointly defined by motion speed and direction. The speed and direction for a given filter were defined by constructing a slanted plane of amplitude spectrum defined by R(ω_r, ω_θ, ω_ϕ) in spherical frequency coordinates ω_r, ω_θ, and ω_ϕ, where ω_r is radial frequency that is defined by ω_r = $\sqrt{{\omega }_x^2+{\omega }_y^2+{\omega }_t^2}$, and ω_θ and ω_ϕ jointly define the 3-D orientation of the filter plane that is associated with the velocity of translational motion (Schrater et al. 2000). We generated 252 filter planes that were orthogonally defined by 21 speed levels (speed bins covering 1∼51°/s with an equal space in a linear scale, corresponding to gradually elevating the zenith angle of a filter plane) and 12 directions (direction bins covering 360° with a 30° interval, corresponding to gradually rotating the azimuth angle of a filter plane), and then took the mean of spectral amplitude passed by each of these filter planes (Fig. 8A). To make our motion energy analyzer sensitive enough to detect any potential artifactual motion energy that might arise “spatially” around the edge of the stimulus aperture or “temporally” from the particular time course of video refreshes of the LCD panel used in the fMRI experiments, we 1) included the peripheral background outside the aperture in the input arrays to the analyzer and 2) projected the known profile of LCD rise-and-fall time functions onto the magnified time scale (t = 2.08 ms). As shown in Fig. 8A, our analyzer revealed the presence of motion energy outside the target speed of motion (13°/s) but confirmed that the motion energy peaked around the adapted direction and decreased with an increasing difference from the adapted direction.

Fig. 8.

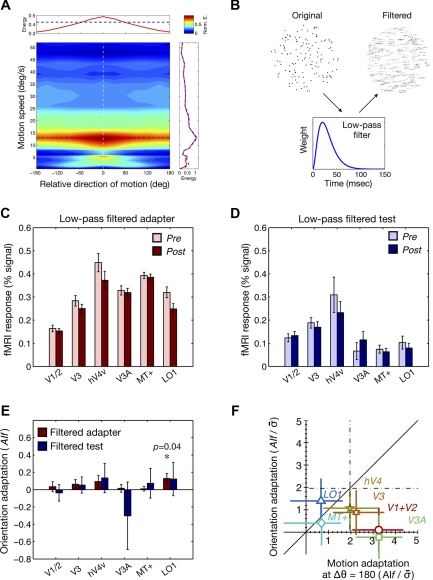
Translational motion energy in random-dot stimuli and results of control experiments. A: the average motion energy is represented by color on a map that is jointly defined by motion speed (y-axis) and direction relative to the signal direction (x-axis). The motion energy was normalized by the maximum energy, which occurs at the coordinate defined by the signal direction (white dashed line) and the signal speed (black dashed line). Top inset shows the average motion energy pooled across different motion speeds for coherent motion stimuli (red line) and for random (0% coherence) motion stimuli (blue dashed line). Right inset shows the average motion energy pooled across different directions for coherent motion stimuli (red line) and for random motion stimuli (blue dashed line). B: in the control experiments, in which potential orientation adaptation due to motion streaks was measured, either adapters or test stimuli were modified by applying the temporal low-pass filter (see materials and methods). C: in the first control experiment, where the adapters in the original experiments were low-pass filtered whereas the test stimuli were the same as in the original experiments, we measured fMRI responses to test stimuli whose directions were either the same as or opposite to the adapter. The light and dark red bars indicate pre- and postadaptation responses, respectively. The error bars indicate SEs of the means across trials. D: in the second control experiment, where the adapter stimuli were same as the original experiments whereas the test stimuli were low-pass filtered, we measured fMRI responses to the test stimuli whose directions were either the same as or opposite to the adapter. The light and dark blue bars indicate pre- and postadaptation responses, respectively. E: using the same formula as that for motion adaptation indexes, orientation adaptation indexes were computed for the 2 different control experiments across visual areas. Orientation adaptation was not significant except for the area LO1 in the first control experiment. F: the amounts of potential orientation adaptation in the 2 control experiments were compared with those of motion adaptation in the direction opposite to the adapter in the original experiments. The y-axis is the normalized mean of the orientation adaptation indexes from the 2 control experiments, whereas the x-axis is the normalized motion adaptation indexes from the original experiments, which are the same as the x-axis in Fig. 7A. Values to the left of the vertical dashed line on the x-axis and values above the horizontal dashed line on the y-axis are statistically significant based on pairwise t-tests.

Stimuli and Procedures for the Orientation Adaptation Control fMRI Experiments

To generate displays of stationary dots mimicking motion streaks, we first divided an original motion sequence into sequences with a 30-frame (0.5 s) length and then convoluted those selected sequences with a 1-D (temporal) low-pass filter (Fig. 8B), which was defined by h(t) = (t/τ)²e^t/τ, with τ = 10 ms, roughly associated with 40-ms integration time. Each of the filtered static images replaced the corresponding 30 frames of the original motion sequences, resulting in a consecutive set of images that were updated every 0.5 s. During the “filtered adaptor” session, both of the preadaptation (random motion) and postadaptation (100% coherent motion) adaptors in the original experiment were convoluted by the low-pass filter. The tested directions were two directions whose potential motion streaks matched that of the postadaptation adaptor (0 or 180° relative to the adaptor). During a filtered adaptor session, both of the preadaptation and postadaptation test stimuli at 0 and 180° different from the postadaptation adaptor were convoluted by the low-pass filter while the adaptors remained identical to those in the main motion adaptation experiment. The presence of motion streak-induced orientation adaptation was evaluated by using the same index used for motion adaptation index (AIf): dividing the subtraction of postadaptation BOLD amplitudes (light-colored bars in Fig. 8, C and D) from preadaptation BOLD amplitudes (dark-colored bars in Fig. 8, C and D) by the sum of those two amplitudes. The statistical significance was evaluated in the same manner as in the main experiment using the bootstrap method.

Stimuli and Procedures for the Orientation Adaptation Control Psychophysical Experiments

Stimuli were identical to those in the main experiments but presented on an LCD monitor (HP LP2065), the pixel response time of which matched that used in the fMRI experiments (response time was 8 ms for gray to gray and 16 ms for rise and fall). The pixel resolution, refresh rate, and luminance level were all determined to match those used in the fMRI experiments. Compared with the original psychophysical experiments, the only difference was the number of relative directions of test stimuli: test only for the adapted and opposite directions. Six subjects (26–44 yr old, 2 female) participated. The data analysis was identical to that used in the main psychophysical experiments. None of the subjects was an author, and all of them were volunteers who were naive as to the purpose of the control experiment. All subjects had normal neural anatomy and had normal or corrected-to-normal vision. Experiments were carried out with the written consent of each subject and approved by the Human Subjects Review Boards at Seoul National University.

Fitting the Two-Stage Model to fMRI Data

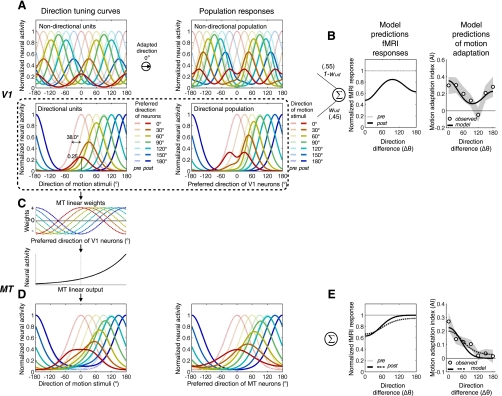
Inheritance hypothesis of motion adaptation.

To demonstrate that the two-stage model is consistent with the observed cortical adaptation curves in V1/2 and MT, we first fitted the model to the adaptation tuning curve from V1/2. The model describes how a population of V1 neurons is affected by adaptation and how their outputs are translated into fMRI responses before and after adaptation (see Fig. 10, A and B). The population of model V1 neurons consists of 36 bidirectional units and 36 unidirectional units. For simplicity, the model neurons are assumed to be same in the bandwidth of unidirectional tuning curve and differ only in terms of preferred direction. Tuning curves of unidirectional units before adaptation are modeled by a cyclic cosine function (also known as von Mises function),

$$\text{pre}{R}_{i\_\text{ud}}\left(\theta \right)=e^{b·\cos \left(\theta -{\theta }_i\right)},$$

where preR_{i_ud}(θ) is a response of the ith unidirectional neuron, whose preferred direction is θ_i, as a function of stimulus direction θ, and b determines tuning bandwidth. Tuning curves of bidirectional units are modeled by the summation of two cyclic cosine functions whose tuning centers are opposite to each other,

$$\text{pre}{R}_{i\_\text{bd}}\left(\theta \right)=e^{b·\cos \left(\theta -{\theta }_i\right)}+e^{b·\cos \left(\theta -{\theta }_i+\pi \right)}.$$

The maximum output of both unidirectional and bidirectional tuning curves is normalized to 1. The model assumes that adaptation reduces responses of V1 neurons by scaling down their tuning curves by a divisive ratio, dr, which is determined by postadaptation peak response, A_max, and preadaptation response of the neuron to an adapting direction:

$$\begin{array}{c}d{r}_i=A_{\max }\text{pre}{R}_i\left({\theta }_{\text{adapt}}\right)\\ \text{post}{R}_i\left(\theta \right)=d{r}_i\text{pre}{R}_i\left(\theta \right).\end{array}$$

Figure 10A illustrates an example of the model behavior when V1 neurons are adapted to dots drifting rightward. The balance between unidirectional and bidirectional populations is adjusted by determining relative contributions of the two populations to the sum of neural responses (Fig. 10B),

$$\begin{array}{c}\text{preSR}\left(\theta \right)=w_{\text{ud}}{\displaystyle \sum _{i=1}^n\text{pre}{R}_{i\_\text{ud}}\left(\theta \right)}+\left(1-w_{\text{ud}}\right){\displaystyle \sum _{i=1}^n\text{pre}{R}_{i\_\text{bd}}\left(\theta \right)\hspace{1em}\text{and}}\\ \text{postSR}\left(\theta \right)=w_{\text{ud}}{\displaystyle \sum _{i=1}^n\text{post}{R}_{i\_\text{ud}}\left(\theta \right)+\left(1-w_{\text{ud}}\right){\displaystyle \sum _{i=1}^n\text{post}{R}_{i\_\text{bd}}\left(\theta \right),}}\end{array}$$

where w_ud indicates the proportion of unidirectional units, ranging from 1 to 0. Based on pre- and postadaptation summed population responses across test directions, the model predicted an fMRI adaptation tuning curve,

$$A\mathrm{Im}\left(\theta \right)=\frac{\text{preSR}\left(\theta \right)-\text{postSR}\left(\theta \right)}{\left|\text{preSR}\left(\theta \right)+\text{postSR}\left(\theta \right)\right|}.$$

This model prediction of adaptation tuning curve, AIm(θ), was fit to the observed fMRI adaptation tuning curve, AIf(θ), by adjusting three free parameters: tuning bandwidth b (which is common to all model V1 neurons), postadaptation peak response A_max, and proportion of unidirectional units w_ud. We should emphasize that the model parameter for the proportion of directional units should not be taken as a value that can be directly compared with the proportion of unidirectional neurons in V1. We are aware of the fact that the degree of unidirectional selectivity is distributed widely among V1 cells as indexed typically by the ratio of responses to a preferred direction to those to the opposite direction. Rather than directly implementing the spectrum of direction selectivity degree, our model captures that spectrum approximately by varying the relative ratio of unidirectional neurons to bidirectional neurons.

Fig. 10.

Two-stage model of motion adaptation and its predictions of fMRI responses. A: the model assumes that V1 consists of directionally nonselective neurons (top panels) and direction-selective neurons (bottom panels). The curves in light and dark colors describe neural responses before and after adaptation, respectively. In left panels, the curves show direction tuning curves of 7 representative V1 neurons with direction preferences spaced in 30° steps (0∼180°). Here, different colors represent different preferred directions of those neurons. The curves in right panels show population responses to 7 different directions of motion. Here, different colors represent different directions of motion stimuli. B: the model predicts fMRI responses (left) of V1 to a certain direction of motion by summing population responses to that stimulus from both the directional and the nondirectional neurons with certain weights (w_ud and 1 − w_ud). The model predictions of motion adaptation indexes (right) are fit to the observed ones from V1/2 (○, means; shaded area, SE). C: only the outputs of direction-selective V1 neurons are linearly integrated in MT neurons according to the cosine weight function. The signal is then translated into a firing rate by a static nonlinearity function. D: the direction tuning curves of representative single neurons with different direction preferences (left) and the population responses to different motion directions (right), respectively. E: the model predictions of pre- and postadaptation fMRI responses (left) and adaptation indexes (right) of MT. Conventions are the same as in B.

In the second stage, the model describes linear and nonlinear processes of how outputs of unidirectional V1 neurons are transformed to responses of MT neurons to test stimuli. First, a model MT neuron computes a weighted sum of the outputs of unidirectional V1 neurons (Fig. 10C, top),

$${\text{LR}}_{i\_\text{MT}}\left(\theta \right)={\displaystyle \sum _{i\_\text{V}1\text{ud}}^n\cos \left({\theta }_{i\_\text{V}1\text{ud}}-{\theta }_{i\_\text{MT}}\right)R_{i\_\text{V}1\text{ud}}\left(\theta \right)},$$

where θ_{i_V1ud} and θ_{i_MT} are preferred directions of input V1 neurons and the MT neuron, respectively. This linear response is then converted into a final MT output by a static nonlinear function (Fig. 10C, bottom),

$${\text{NLR}}_{i\_\text{MT}}\left(\theta \right)=\left(1/s\right)e^{s·{\text{LR}}_{i\_\text{MT}}\left(\theta \right)}.$$

The model then does the same operations as it did to predict fMRI adaptation tuning curve for V1 and is fit to the fMRI adaptation tuning curve of MT+ with only a single parameter (s) set free (Fig. 10, D and E).

Accrual Hypothesis of Motion Adaptation

As a variant of the model described above, we made an alternative model in which additional response reduction also occurs on top of the imbalanced input from V1. This model is identical to the inheritance model, except that two additional parameters, dr and A_max, are also assigned to predict postadaptation response gains of MT neurons.

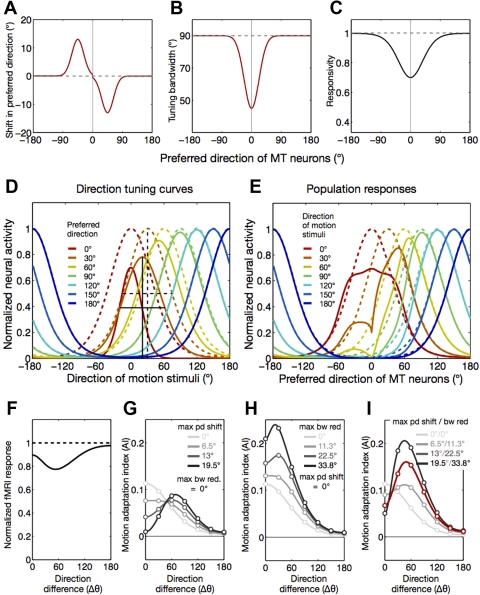
Simulation of Impacts of Preferred Direction Shift and Bandwidth Reduction

We also generated predictions of fMRI adaptation based on a recent finding that adaptation induces changes not only in response reduction but also in preferred direction and bandwidth tuning curves of MT neurons of macaque monkeys (Kohn and Movshon 2004). In this model, fMRI responses of MT to test directions are determined directly by the population responses of MT neurons with unidirectional tuning curves whose shapes are dynamically changed by adaptation: 1) preferred direction tends to be attracted toward an adapted direction, 2) tuning bandwidth tends to be narrower, and 3) responsivity tends to decrease. We approximated those three adaptation-induced changes in tuning curves from the text (p. 765) and figures (Fig. 7) of Kohn and Movshon (2004). The attractive shift of preferred direction was modeled by two Gaussian functions with opposite signs, which mirrored around the adapted direction. Both of those Gaussian functions peaked at directions 45° away from the adapted direction and had an equal size of σ, 18° (Fig. 11A). The size of shift at peak was varied across several levels to see the impact of preferred direction shift on adaptation tuning curves (Fig. 11H). The reduction of tuning bandwidth was also modeled by a Gaussian function with a peak at the adapted direction and σ of 22.5° (Fig. 11B). The size of maximum bandwidth reduction was also varied across several levels to evaluate how it affects the shape of adaptation tuning curves (in degrees; Fig. 11I). Adaptation-induced changes in responsivity were modeled in the same manner as in the other models. Unlike the other model variant described above, this model was not fitted to the fMRI adaptation curve because it always predicts nonmonotonic adaptation tuning curves with a peak at directions flanking the adapted direction (Fig. 11, F–I), which was obviously different from what was observed in our fMRI data (Fig. 8E).

Fig. 11.

Prediction of fMRI adaptation curves by the model of adaptation-induced changes in shape of direction tuning in MT neurons. A: the model assumes that MT neurons whose preferred directions are within 90° around the adapted direction before adaptation shift their preferred direction toward the adapted direction (red line). The direction and size for maximum shift were roughly estimated from Kohn and Movshon (2004). B: the model assumes that the tuning bandwidth decreased as a function of the similarity of a test direction to an adapted direction. Again, the data available in Kohn and Movshon (2004) were approximated by a Gaussian function (red line), whose amplitude and spread determines the maximum reduction in bandwidth and the range of neurons with bandwidth reduction due to adaptation. C: the model also assumes that the reduction in responsivity of MT neurons is determined as a function of their responsivity to an adapting stimulus before adaptation (solid black line). D: solid and dashed curves describe the pre- and postadaptation tuning curves, respectively, of 7 representative MT neurons with direction preferences spaced in 30° steps (0∼180°), indicated by different colors. These adaptation-induced changes in tuning shape are predicted by the model in which the parameters for tuning changes were the same as those described in A–C. Examples of adaptation-induced shift in preferred direction and reduction in tuning bandwidth are illustrated by the black dashed (preadaptation) and solid lines (postadaptation) for a model neuron whose preferred direction is 30° away from the adapted direction. E: the curves show population responses to test motion stimuli in 7 different directions, indicated by different colors. Again, the dashed and solid curves describe the pre- and postadaptation population responses, respectively. F: the lines depict the normalized fMRI responses predicted by the model, either before (dashed line) or after adaptation (solid line). These responses were obtained by taking the integral of the population responses across all of the MT model neurons. G–I: the lines in different colors and brightness show the tuning curves of fMRI adaptation indexes, each of which is predicted by a particular set of the model parameters for the maximum preferred direction shift (varied in G and I, set to zero in H) and for the maximum bandwidth reduction (varied in H and I, set to zero in G). The red line shows the adaptation curve that is predicted by the particular set of parameters illustrated in A–C.

RESULTS

Perceptual Adaptation Tuning Curves

Before collecting fMRI measurements, we conducted psychophysical experiments to confirm whether our stimuli and procedure that would be used in the fMRI experiments were effective enough to generate a substantial degree of adaptation. In addition, the resulting psychophysical tuning curves of adaptation were later compared with those from the fMRI experiments when we assessed how well the cortical activity of a given area matched perceptual effects of adaptation. Because responses of direction-selective neurons to stochastic dot motion are known to be strongly modulated by luminance contrast (Gegenfurtner et al. 1997; Thiele et al. 2000) and coherence among local motion signals (Britten et al. 1993; Rees et al. 2000), we probed perceptual sensitivity to motion signal while varying either the contrast or the coherence of random-dot motion stimuli.

In each trial, subjects first viewed a top-up adapter stimulus for several seconds and then two consecutive, brief random-dot motion stimuli (Fig. 1A) with coherence or contrast being varied across trials and indicated which interval contained coherent motion. Based on two types of psychometric curves, one as a function of motion coherence and the other as a function of dot luminance contrast, we estimated coherence (Fig. 2A) and contrast (Fig. 2B) thresholds for a range of test directions relative to the adapter (Fig. 1C, bottom). We manipulated adaptation by showing 0% and 100% coherence motion stimuli with high contrast in the top-up adapter epoch during the pre- and postadaptation blocks of trials, respectively (Fig. 1C, top). In addition, the 100% coherence adapter was shown for a minute each before a postadaptation block of trials. Although direct comparisons in performance between paired pre- and postadaptation trials at a given test direction provide adaptation effects that are invariant to particular choices of adapting direction, we used four different cardinal directions in four different daily psychophysical sessions to minimize the contribution of any direction-specific effects to adaptation measurements. We adopted the same adapter selection procedure in the fMRI experiments.

After adaptation, both the coherence sensitivity and the contrast sensitivity significantly decreased at the adapted direction in all of the subjects tested (Fig. 2, A and B), indicating that the current adaptation procedure and stimuli readily promote substantial perceptual adaptation effects. To quantify and normalize amounts of adaptation between the two different types of thresholds and across the different test directions, we generated two directional tuning curves of perceptual adaptation from coherence (red line in Fig. 2C) and contrast (blue line in Fig. 2C) sensitivity measurements, respectively, by computing psychophysical adaptation indexes (AIp values; see materials and methods for definition), which contrast paired pre- and postadaptation sensitivities at individual test directions. In both the coherence and the contrast sensitivity, the adaptation index was greatest at around the adapted direction and diminished gradually as the direction difference between the adapter and test increased [bootstrap test of Spearman's rank correlation: ρ = −0.78, 95% CI = (−0.68, −0.89) for coherence AIp; ρ = −0.76, 95% CI = (−0.50, −0.96) for contrast AIp], resulting in monotonic and unidirectional tuning curves of adaptation (Fig. 2C).

Cortical Adaptation Tuning Curves

Because the psychophysical experiments successfully demonstrated strong and reliable adaptation effects, we measured fMRI responses from the same subjects using the procedure and stimuli identical to those in the psychophysical experiments with a few exceptions, which were made to increase the efficiency of fMRI experiments. During a test epoch, only a signal test stimulus with 100% coherence appeared (Fig. 1B) to specifically evoke a subpopulation of cortical neurons that are tuned around a single direction of motion by removing motion signal in any other directions (noise dots). The contrast of test stimuli was also fixed at an intermediate level (10%) to prevent fMRI signal from being constrained by any ceiling (due to saturation) or floor effects. Unlike in the psychophysical experiments, we asked subjects to indicate whether dots in the central and peripheral parts of the annulus (which were divided by an imaginary circle indicated by the dotted line in Fig. 1B) moved in the same direction or in slightly different directions (±2° around the target direction). This direction discrimination task was chosen not only to maintain the general level of attention but also to force subjects to pay attention evenly to the central and peripheral parts of the large test annulus.

We identified fMRI responses to test stimuli with differential responses, which were obtained by subtracting the average time series of fMRI responses in the blank trials (third row in Fig. 3) from those in test stimulus trials (first row in Fig. 3). We then estimated the magnitudes of differential responses by averaging the positive data points (horizontal bracket in graph at bottom of Fig. 3) around the peak (see materials and methods for details and alternative methods of magnitude estimation). Functional MRI responses to each relative direction in each visual area were pooled across the three subjects to increase the signal-to-noise ratio of the data given small numbers of observations for many test conditions [14 = 7 (direction differences from the adapter) × 2 (before or after adaptation)].

Before adaptation, V1/2, V3, V3A, hV4, MT, MST, LO1, and VO1 showed robust fMRI responses to test stimuli, with magnitude being relatively small in early areas and becoming larger in higher areas along the dorsal pathway (light gray shading, lines, and symbols in Figs. 4 and 5). When summed across all the test directions, adaptation reduced overall fMRI amplitudes in all the visual areas inspected (11.0–33.3%; dark gray shading, lines, and symbols in Figs. 4 and 5), and the amounts of response reduction were statistically significant except in LO1 (11.0%, P = 0.23 in bootstrap test).

Adaptation-induced response reductions did not appear direction selective in several higher tier areas in the lateral (LO1), ventral (hV4 and VO1), or dorsal (V3A) pathways. V1/2, V3, and V3A actually showed a strong sign of bidirectional adaptation: an amount of response reduction tantamount to that in the adapted direction was also observed in the direction opposite to the adapted direction. By contrast, the amount of response reduction in MT and MST monotonically decreased as the direction of test stimuli was increasingly away from the adapted direction, producing adaptation tuning curves with a single mode. To quantitate the degree of direction-tuned adaptation and to normalize magnitudes of fMRI adaptation across areas in units comparable to those of psychophysical adaptation, we computed fMRI adaptation indexes (AIf values; see materials and methods for definition), as we did when computing the psychophysical adaptation indexes.

The extent and pattern of direction-selective adaptation were statistically evaluated in several ways. First, we tested whether the amount of adaptation, indexed by AIf, monotonically decreases as the test direction increasingly differs from the adapted direction by performing Spearman's rank correlation test, as we did for the psychophysical adaptation curves. The rank correlation was negative and significantly different from zero only in area MT [ρ = −0.86, 95% CI = (−1.00, −0.57); Fig. 6E] and MST [ρ = −0.66, 95% CI = (−0.96, −0.14); Fig. 6F]. Although the rank correlation analysis demonstrated the negative monotonic relationship between the degree of adaptation in MT/MST and the adapter-test direction difference, it failed to capture the nonmonotonic, bidirectional shape of tuning curves of adaptation, which was quite noticeable in several visual areas other than MT and MST (Fig. 6, A–D).

Second, to capture the presence of both bidirectional adaptation and unidirectional adaptation, we calculated a vector magnitude (L) of AIf values to measure directional tuning strength (Bonhoeffer et al. 1995; Wörgötter and Eysel 1987). This method allows us to estimate a bidirectional tuning strength simply by multiplying directional angles by two (Batschelet 1981). The vector magnitude analysis showed significant bidirectional tuning only for V1/2, V3, and V3A and significant unidirectional tuning only for MT and MST (bootstrap test with 95% CI; see materials and methods for detail). For only these areas with significant bidirectional or unidirectional adaptation tuning, we tested whether or not fMRI responses decreased after adaptation at each test direction. In MT and MST, significant response reductions (indicated by asterisks in Fig. 5, correction for multiple comparisons not applied) were observed mainly around the adapted direction. In V1/2, V3, and V3A, on the other hand, response reduction was significant in test directions both near and opposite to the adapted direction.

Third, we also built two simple models to capture the shape of an adaptation tuning curve and to compare the adaptation magnitude at the adapted direction and that at the opposite direction. Unidirectional tuning was modeled by a single Gaussian function with a center fixed at the adapted direction. Bidirectional tuning was modeled by two Gaussian functions with centers at the adapted and the opposite directions, respectively (see materials and methods for definitions). The bimodal adaptation model significantly enhanced the goodness of data fit in V1/2 [F(2,7) = 25.6; P = 0.0006], V3 [F(2,7) = 14.7; P = 0.0031], hV4 [F(2,7) = 11.5; P = 0.0062], and V3A/B [F(2,7) = 11.9; P = 0.0055], but not in the other areas, including MT and MST. In addition, we evaluated the bimodality of adaptation curves also by comparing the amplitudes of the two Gaussian functions (a_A and a_N) in the bimodal adaptation model fitted to the adaptation curve. In V1/2, V3, hV4, and V3A, the adaptation magnitudes were almost equal between the adapted and opposite directions (Fig. 7A). In contrast, the estimated magnitude of adaptation in MT and MST was quite substantial in the adapted direction but was close to zero in the opposite direction. In the high-tier areas in the lateral or ventral pathways (LO1 and VO1), the adaptation magnitudes in both directions were too small to reliably judge the shape of adaptation tuning.

We also compared the fMRI adaptation tuning curves from different areas (Fig. 6) in terms of how they matched the psychophysical adaptation tuning curves (Fig. 2C). The correlation coefficients between the perceptual and fMRI adaptation curves were significant in V3A (r² = 0.71, P < 0.05 for coherence adaptation), MT (r² = 0.72, P < 0.05 for coherence adaptation; r² = 0.60, P < 0.05 for contrast adaptation), and MST (r² = 0.79, P < 0.01 for coherence adaptation; r² = 0.64, P < 0.05 for contrast adaptation) (Fig. 7B). MT and MST were the only two areas where the fMRI adaptation curve was significantly correlated with both types (coherence and contrast sensitivity) of perceptual adaptation.

Spatiotemporal Energy Analysis of Motion Stimuli

In the experiments described in the current and the following two sections, we examined whether any potential artifacts in our stimuli might have caused adaptation in a direction opposite to the adapter. We first considered the possibility that limited-lifetime random-dot stimuli might contain motion energy not only for the signal direction but also for the opposite direction. This possibility is unlikely in many aspects. Because a fraction (25%) of dots that completed their limited-lifetime cycles (50 ms) in any given frame of a motion sequence reappeared in completely random positions, we have no obvious reason to believe that there was strong motion bias particularly toward the direction opposite to the signal direction. In addition, even if random motion in the adapter had happened to be biased toward the direction opposite to the signal direction, perceptual adaptation (decrease in motion sensitivity) also should have occurred at the opposite direction. This was not the case for either the coherence sensitivity or the contrast sensitivity measurements (Fig. 2). However, two factors may give a rise to artifactual energy at unwanted directions of motion. First, when a peripheral dot in our motion stimuli moved outside the boundary of the aperture, it abruptly disappeared and reappeared in a position near the boundary region diagonally mirrored around the fixation, with the same direction of motion as before disappearance. This abrupt disappearance and reappearance of dots around the boundary may cause unpredictable motion energy. Second, stimuli were presented on an LCD monitor whose luminance rises and falls slowly compared with that of CRT monitors. This sluggish sampling rate can potentially create unpredictable motion energy when combined with the limited lifetime of dots adopted in the current study. Thus we decided to inspect motion energy in our 100% coherence stimuli by conducting the 3-D spatiotemporal frequency analysis (Watson and Ahumada 1983). In this analysis, we computed translation motion energy for a range of motion speeds and directions by measuring the spatiotemporal energy within a given 3-D spectral plane associated with a specific pair of speed and direction (see materials and methods for details). The results indicate that motion energy occurred outside the target motion speed (13°/s) and spread broadly around the “signal” motion direction (Fig. 8A). However, compared with the motion energy spectrum for random-dot stimuli (dotted line in Fig. 8A, top), which were shown in the top-up adaptation epoch during the preadaptation runs, the motion energy for 100% coherence stimuli was relatively higher only in the narrow range of direction around the signal direction (solid line in Fig. 8A, top). Thus the analysis confirmed that maximal motion energy occurred at the speed and direction of signal dots, as expected. We conclude that random reappearances of dots contributed only to the overall spatiotemporal energy that is spread equally at across different directions and speed levels.

Control fMRI Experiments for Orientation-Selective Adaptation

The second possibility is that the bidirectional adaptation might have arisen by a potential presence of pattern information biased to a specific orientation in our random-dot motion stimuli. A dot moving in a single direction at high speed can appear smeared, generating a sensation of a straight line oriented along the direction of the motion (motion streak), due to temporal integration (or response persistence) of retinal or cortical visual neurons (Geisler 1999). Therefore, the opposite directions of motion might have adapted the same population of neurons whose preferred orientation is the same as the axis of the direction of motion, resulting in bidirectional adaptation. Although our careful selection of spatial and temporal parameters for stimuli [small-size (Gaussian dot with 0.07° visual angle half-width at half-maximum), low-contrast (10%), spatially nonoverlapping dots with a very short limited lifetime (50 ms)] makes unlikely the existence of strong motion streaks, we decided to conduct a pair of auxiliary control fMRI experiments in which either an adapting or test motion stimulus was replaced by a field of stationary dots mimicking motion streaks that would have been created by the original adapting or the test motion if motion smear occurred.

Displays of stationary dots mimicking motion streaks were created by applying a low-pass temporal filter to the original motion sequences (Fig. 8B; see materials and methods). The procedure, stimuli, and task of the control fMRI experiments were exactly identical to those of the main experiments except that 1) the motion streak displays with different orientations were used as test stimuli in the first control experiment and as the adapting stimuli in the second control experiment, and 2) fMRI responses were measured only for the directions the same as and opposite to the adapter. If our motion stimuli contained orientation information due to motion streaks and induced orientation-specific adaptation in neurons in the early visual areas, we would expect orientation-specific adaptation for both of the test directions. However, there was no significant reduction in response after adaptation in any of the two control experiments (Fig. 8, C–E). The lack of orientation adaptation was true for the majority of the visual areas tested in both of the two control experiments. Only the area LO1, where a bidirectional adaptation curve was not observed in the main experiments, showed a significant adaptation effect when the adapters were low-pass filtered (Fig. 8E). Compared with the motion adaptation indexes for the direction opposite to the adapter in the main experiments, the orientation adaptation indexes from V1/2, V3, and V3A, where significant bidirectional adaptation was observed in the main experiments, were a lot smaller in amplitude (Fig. 8F). On the basis of these results, we conclude that the orientation information, which might have existed due to potential motion streaks in our stimuli, was too little to induce orientation-specific adaptation that was comparable to the amount of adaptation in the direction opposite to the adapted direction in the main experiment.

Control Psychological Experiments for Orientation-Selective Adaptation

The possibility of orientation-selective adaptation due to motion streaks also was examined with a psychophysical control experiment. It should be noted that the type of stimulus display differed between the psychophysical and fMRI experiments: a CRT monitor and an LCD monitor were used (see materials and methods for detailed specifications), respectively. Because motion streaks are more likely to occur in the LCD display, where it takes a longer time to update luminance values in pixels, than in the CRT display, one may reason that the difference in stimulus displays could have caused the difference between the fMRI adaptation curves in the early visual cortex (bidirectional adaptation) and the psychophysical adaptation curves (unidirectional adaptation). To check this possibility, we repeated the main psychophysical experiments, but this time adaptation effects were measured only for test directions either the same as or opposite to an adapted direction. At the time when we were planning to conduct this control experiment, none of the three subjects who participated in the main experiments were available. Thus we conducted the control experiment on a new set of five naive subjects. In all subjects, both types of adaptation indexes were substantially large (AIp = 0.18∼0.40 for coherence sensitivity; AIp = 0.11∼0.24 for contrast sensitivity) and significant at the adapted direction (bootstrap test, P = 0.0007∼10⁻¹⁰; filled symbols and solid lines in Fig. 9). By contrast, the adaptation indexes at the opposite direction were close to zero (AIp = −0.002∼0.03 for coherence sensitivity; AIp = −0.03∼.03 for contrast sensitivity), not significant at all in any subjects or in either type of adaptation index (P = 0.37∼0.60, open symbols and dashed lines in Fig. 9). These results confirm that perceptual adaptation does not occur in the direction opposite to the adapted direction when motion stimuli are presented in the LCD display, whose pixel response times match the display used in the fMRI experiment.

Fig. 9.

Perceptual motion adaptation effects from motion stimuli presented on the liquid crystal display (LCD) monitor. Perceptual adaptation indexes (see materials and methods for definition) based on adaptation-induced changes in coherence and contrast sensitivity are plotted for the adapted direction (filled symbols and solid lines) and for the direction opposite to the adapted direction (open symbols and dashed lines). The vertical lines indicate 68% CI from bootstrap sample estimates. The different symbols represent the indexes obtained from 5 different subjects.

DISCUSSION

In designing our experiments and analyzing results, we exercised a couple of cautions based on the review of previous studies on motion adaptation. First, an observation of response reduction in a certain area does not necessarily mean that neural adaptation originates in that particular area because response reduction may be inherited from earlier stages (Kohn and Movshon 2003; Krekelberg et al. 2006a; Sawamura et al. 2006) or may be caused by modulatory inputs from other direction-sensitive areas (Tolias et al. 2005). Second, most previous fMRI studies compared responses to the adapted direction and those to the opposite direction only after adaptation without measuring responses for those directions before adaptation. Under this situation, a relatively weak response to the adapted direction cannot necessarily be interpreted as the reduction of neural responses to the adapted direction because it may also be caused by an increase in response to the opposite direction. Third, a lack of measurements for intermediate directions between the adapted and opposite directions limits the quality of comparisons between different cortical areas because perceptual or neural consequences of motion adaptation are not limited only to the adapting or opposite directions but also may be manifested in intermediate directions (Crowder et al. 2006; Hoffmann et al. 2001; Kohn and Movshon 2004).

By implementing these considerations in the design of our experiments, we were able to compare impacts of adaptation on different visual areas by inspecting how adaptation affects the shape of adaptation tuning curves in a fine scale. Our analyses revealed a dichotomy in direction adaptation tuning curve between early- and high-tier visual areas along the dorsal stream: the bidirectional tuning curves in V1/2, V3, and V3A versus the unidirectional curves in MT and MST. The behavioral adaptation curves, which were measured in separate psychophysical experiments, were unidirectional, suggesting MT/MST as neural loci substantiating adaptation-induced reduction in perceptual motion sensitivity. The motion energy analysis and the control fMRI and psychophysical experiments ruled out the possibility that cortical adaptation in the null direction in the early visual areas might have been caused by trivial artifacts in our motion stimuli, such as biased motion energy in the opposite direction and orientation adaptation by motion streaks.

Difference in Adaptation Between Early- and High-Tier Areas

There could be several explanations for the lack of unidirectional adaptation in early visual areas. Because optimal spatial and temporal parameters of stimuli may differ for direction-selective neurons across visual areas, enhanced direction selectivity in high-tier areas might have occurred simply because our motion stimuli are more optimal for high-tier areas than for early-tier areas. However, this is unlikely, because the spatial separation (Δx = 0.22°), the temporal separation (Δt = 16.7 ms), and accordingly, the speed (13°/s) of dots in our stimuli are all safely within the optimal range for both V1 and MT neurons in monkeys (Churchland et al. 2005; Mikami et al. 1986). Alternatively, the bidirectional adaptation in early visual areas may reflect a relatively small proportion of direction-selective neurons in early areas (Gegenfurtner et al. 1997; Hawken et al. 1988; Snowden et al. 1991). Because fMRI responses from a cortical region reflect population activity from a number of heterogeneous neurons, the proportion of direction-selective neurons can be translated into the degree of direction-selective adaptation. Another possibility is that if neurons in an early area receive balanced feedbacks from direction-tuned neurons in a high-tier area, neurons in early visual area can exhibit a moderate level of direction selectivity after adaptation (Tolias et al. 2005). However, this account cannot explain the difference in the shape of adaptation tuning curve between early (bidirectional) and higher tier (unidirectional) visual areas.

The dichotomy between early and high visual areas led us to favor an alternative explanation based on the two-stage model of motion processing, which posits that heterogeneous populations of neurons with varying degrees of direction selectivity comprise early visual areas, but only the directional units project their outputs to high-tier areas, such as MT. Findings by previous single-cell and anatomical studies are consistent with this view. A substantial fraction of neurons are not directionally selective in early visual areas (Albright 1984; Gur and Snodderly 2007; Hawken et al. 1988). In addition, in direction-selective neurons in early visual cortex, the significant amount of adaptation can be induced by their nonpreferred directions as well as by their preferred direction [(Crowder et al. 2006; Sengpiel and Bonhoeffer 2002; Vautin and Berkeley 1977); however, recent studies on monkeys showed that this is also true in MT neurons (Kohn and Movshon 2004; Krekelberg et al. 2006b; Petersen et al. 1985)]. Last, the population of spiny stellate neurons in layer 4B of V1 that receive inputs from layer 4Cα and project directly to MT (Yabuta et al. 2001) is highly selective for direction (Movshon and Newsome 1996). We propose an “inheritance” hypothesis as one way of interpreting the dichotomy of bidirectional versus unidirectional adaptation tuning curves between V1 and MT in the context of a two-stage model of motion processing. The inheritance hypothesis postulates that the bidirectional adaptation tuning curves are likely to arise from the amalgam of uni- and bidirectional adaptation in uni- and bidirection-selective cells in V1, respectively, and that only the unidirectional neurons transfer their outputs to MT, predicting the unidirectional adaptation tuning curves in MT. In the following section, we describe the building of a two-stage model that links population responses of V1 and MT neurons to motion stimuli with fMRI responses in those areas and show that the inheritance model can capture the dichotomy in fMRI adaptation tuning between V1 and MT.

Predicting fMRI Adaptation Curves by the Two-Stage Model

It is well known that a substantial fraction of neurons in early visual cortex respond to opposite directions of motion orthogonal to their preferred orientation (typically referred to as “direction nonselective” neurons in the literature, but we refer to these neurons as bidirectional neurons), whereas the majority of neurons in the high-tier motion-sensitive areas in the dorsal stream, such as MT and MST, show strong directional selectivity (Albright 1984; Gegenfurtner et al. 1997; Gur and Snodderly 2007; Hawken et al. 1988; Maunsell and Van Essen 1983; Schiller et al. 1976; Snowden et al. 1991). If we assume that an adapter that evokes stronger responses induces stronger adaptation effects, as supported by single-cell studies (Giaschi et al. 1993; Hammond et al. 1988; Marlin et al. 1988; Schiller et al. 1976; Vautin and Berkley 1977), response reduction of unidirectional units in early visual cortex will be confined to those whose preferred direction is similar to the adapted direction. By contrast, the responsivity of bidirectional units will be reduced not only to the adapted direction but also to the opposite direction after adaptation. Thus the early visual cortex would show a bidirectional adaptation tuning curve because adaptation to a single direction of motion reduces the pooled fMRI responses not only to the adapted direction (due to response reduction in both unidirectional and bidirectional units) but also to the opposite direction (due to response reduction in bidirectional units). On the other hand, although MT receives inputs from many cortical (V1, V2, V3, V4, MST, and ventral intraparietal area) and subcortical (lateral geniculate nucleus) regions (Maunsell and van Essen 1983; Sincich et al. 2004), responses of MT neurons are highly dependent on inputs originating in early visual cortex (Collins et al. 2003; Rodman et al. 1989). In particular, the selective projection of directionally tuned neurons in V1 to MT, as reported by Movshon and Newsome (1996), appears to be consistent with the observed dichotomy in our data. That is, the adaptation tuning curves in the early visual cortex are bidirectional because of the heterogeneity of neurons in directional selectivity but become unidirectional in MT if V1 neurons that project to MT comprise a homogeneous and special subpopulation with a high degree of unidirectional selectivity. We will refer to this hypothesis as the inheritance hypothesis of motion adaptation (“inheritance hypothesis,” in short) from now on.

To see whether the inheritance hypothesis is compatible with the observed fMRI adaptation curves, we implemented the key assumptions of this hypothesis into a two-stage model of motion processing (e.g., Rust et al. 2006) and examined whether the behavior of the two-stage model conforms to the fMRI data by linking model neural responses to fMRI responses. In the model, an fMRI response from a cortical region is modeled as a sum of population responses of neurons with different preferred directions within that region to a given test stimulus (Fig. 10).

In the first step, we fitted a set of parameters, tuning bandwidth b, postadaptation peak response A_max, and proportion of unidirectional units w_ud, for model V1 neurons (Fig. 10A) to the fMRI adaptation tuning curve obtained from V1/2 (Fig. 10B). Here, the model V1 neurons have a single peak in direction tuning curve (Fig. 10A, bottom), whereas the other model V1 neurons have bidirectional tuning curves (Fig. 10A, top). We simply assumed that adaptation just scales down the amplitude of a tuning curve of a given neuron linearly in proportion to its preadaptation response to the adapter but does not affect the bandwidth or shape of the tuning curve. This assumption may be too naive or untrue given previous reports of repulsive shifts in preferred orientation of V1 neurons (Dragoi et al. 2000, 2002; Felsen et al. 2002; Muller et al. 1999). However, there are several reasons to believe that the assumption of our model is likely to be appropriate for the stimuli and adaptation paradigm adopted in the current study. First, all of these studies measured orientation shifts, not direction shifts, and two of them (Felsen et al. 2002; Muller et al. 1999) used static gratings as adapting and test stimuli. Second, Dragoi et al. (2001) reported that the shifts in preferred orientation did not occur in the majority of V1 neurons, except for those located close to the pinwheel center. Third, no significant changes in preferred direction occurred in V1 cells when directional tuning curves were directly measured using drifting grating stimuli (Kohn and Movshon 2004). It also should be noted that our model assumes that V1 cells respond similarly to grating and random-dot stimuli, especially when positing the presence of unidirectional and bidirectional neurons in V1. Because, unlike grating stimuli, random-dot motion stimuli do not have any orientation information, it is possible that V1 cells that show bidirectional tuning for grating stimuli may not show bimodal direction tuning for dot stimuli. However, previous studies on complex cells in cat areas 17/18 showed that bidirectional cells indeed maintained the overall bidirectional shape of tuning curves for both grating stimuli and dots or pattern stimuli without any global orientation information (Figs. 3 and 4 in Crook 1990; Fig. 5 in Hammond and Smith 1983), although directional tuning curves become broad and bi-lobed around peaks at high-velocity dot or pattern stimuli (Crook 1990; Hammond and Reck 1980; Hammond and Smith 1983; Skottun et al. 1988).

For each test direction, an fMRI response is predicted by a weighted sum of responses of the unidirectional and bidirectional subpopulations of neurons to that test direction (Fig. 10B, left). The model curve of adaptation indexes was then fit to the observed one with the maximum likelihood method (Fig. 10B, right). The fits were good; the model curve captured the bimodal shape of the observed adaptation tuning curve while passing through nearly all of the error bars and explaining the 62.5% of the total variance of the fMRI data. At all of the relative direction difference conditions, the model prediction did not differ statistically (confirmed by bootstrap tests) from the observed fMRI data. The best-fit model parameters were 38.0° for the HWHM of the directional tuning curve, 0.25 for the postadaptation peak response, and 0.45 for the ratio of unidirectional units to the total of uni- and bidirectional units in V1 (Fig. 10, A and B). We emphasize that the model parameter for the proportion of unidirectional units should not be taken as a value that can be directly compared with the proportion of unidirectional neurons in V1. We are aware of the fact that the degree of directional selectivity is distributed widely among V1 cells as indexed typically by the ratio of responses to a preferred direction to those to the opposite direction. Rather than directly implementing the spectrum of direction selectivity degree, our model captured that spectrum approximately by varying the relative ratio of unidirectional neurons to bidirectional neurons.

In the second step, the pre- and postadaptation responses from only the unidirectional units (indicated by the box with dashed lines in Fig. 10A) are fed forward to model MT neurons, where the V1 outputs are linearly integrated according to the cosine weight function (Fig. 10C, top) and are then converted into firing rates via a static nonlinearity function (Fig. 10C, bottom). The model then predicted an fMRI adaptation tuning curve averaged for MT and MST (solid lines in Fig. 10, D and E) with the same procedure used in the first stage. However, unlike the first stage, we did not fit the model MT neurons directly to the observed fMRI tuning curve, except for a single parameter (s) for the static nonlinearity function (see materials and methods). Note that the behavior of model MT neurons was completely determined by the unidirectional V1 model outputs, the prefixed MT linear weight function, and the MT static nonlinearity function. The model curve succeeded in capturing the unidirectional shape of the fMRI data. The fits were reasonably good; the model predictions did not differ statistically (bootstrap tests) from the observed fMRI data except for only one data point (P = 0.03 at direction difference 90°) and explained the 77.3% of the total variance of the fMRI data (Fig. 10E, right).

Next, we tested a variant of the inheritance hypothesis, which posits that additional adaptation occurs in MT neurons on top of adaptation inherited from the V1 unidirectional units. Note that unlike the inheritance hypothesis, which assumes no further adaptation in MT itself, this hypothesis assumes that some proportion of the response reduction observed in MT is not inherited from the early stage but arises from adaptation of MT neurons themselves. This hypothesis will be referred to as the accrual hypothesis of motion adaptation (“accrual hypothesis,” in short). The plausibility of the accrual hypothesis was tested by examining whether or not additional adaptation in MT neurons themselves improve fits based on an amount of reduction in model prediction errors using F statistics, as we did previously when assessing the bidirectionality of fMRI adaptation tuning curves. Additional adaptation in MT was implemented simply by adding to the original model a parameter that governs additional response reduction of MT neurons due to adaptation at the second stage (see materials and methods for details). The model based on the accrual hypothesis gave a better fit to the fMRI data (83.3% of variance explained; dotted line in Fig. 10E, right) than the original inheritance model (77.3% of variance explained), possibly due to an increase of the number of model parameters. When the effect of an additional parameter of a nesting model was controlled, the improvement in fit (6.0%) was not significant [F(1,5) = 1.79, P = 0.24]. This result should not necessarily rule out the possibility that additional adaptation occurs in MT. Instead, what our model simulation demonstrated is that the majority of adaptation effects in MT can be explained by feedforward inputs from unidirectional units in V1 and that the amount of additional adaptation originating in MT neurons, if any, is probably small. It should be emphasized that this interpretation is valid only in the context of the two-stage model of motion processing.

So far, we have been interpreting our results in the framework of the two-stage model of motion processing. We also searched for possible implications of our results by predicting the fMRI adaptation tuning curve in MT directly from population responses from model MT neurons. This is important particularly because recent studies on MT neurons in monkeys provided strong evidence for adaptation effects that cannot be attributed to feedforward inputs from direction-selective neurons in V1 (Kohn and Movshon 2004; Krekelberg et al. 2006b). Of particular relevance to the current study, prolonged adaptation to a grating stimulus under translational motion not only reduces neurons' responsivity but also changes the shape of tuning curves both by attracting the preferred direction toward the adapted direction and by narrowing the bandwidth (Kohn and Movshon 2004). To know the consequences of implementation of these adaptation-induced changes in directional tuning curves of MT units in our model, we simulated MT population responses to test directions before and after adaptation, from which an adaptation tuning curve can be drawn and compared with the observed one (see materials and methods and Fig. 11 for details). In this simulation, MT neurons' tuning curves changed in all of the three major aspects, preferred direction (Fig. 11A), tuning bandwidth (Fig. 11B), and responsivity (Fig. 11C), in ways that best match the findings by Kohn and Movshon (2004). Intriguingly, the simulated adaptation tuning curve (Fig. 11F and red line in Fig. 11I) was quite different from that predicted when both the preferred direction and the bandwidth were assumed not to change at all after adaptation (lightest gray lines in Fig. 11, G and H). The maximum adaptation occurred not at the adapted direction but at around 60° away from the adapted direction. This shift in direction of maximum adaptation was not confined to a particular set of parameters that we chose in simulation. Rather, both the size of preferred direction shift and the size of bandwidth reduction independently (Fig. 11, G and H) and jointly (Fig. 11I) contributed to the shift of a maximum locus of adaption. Thus we can conclude that the implementation of adaptation-induced preferred direction shift and bandwidth reduction in MT model neurons always predicts a maximum adaptation effect at direction shifted away from the adapted direction, which is clearly inconsistent with the shape of fMRI adaptation curve in MT that we found (Fig. 6E). What could be the source for this discrepancy between single-cell results from monkey MT neurons and our results? Although we cannot exclude species differences as a potential source for the discrepancy, we suspect that the primary source is likely to be the difference in motion stimuli adopted by the two studies [gratings in Kohn and Movshon (2004) vs. random dots in the current study]. As shown in the motion energy analysis, the motion energy in random-dot stimuli is distributed broadly around the target direction (Fig. 8A). Kohn and Movshon (2004; p. 769–770) also talked about this possibility based on their preliminary results using random-dot stimuli and model simulations. It would be interesting to empirically confirm this possibility of differential consequences of adaptation to grating (strong and focal motion energy) and random-dot (weak and diffusive motion energy) stimuli by repeating our experiment using grating stimuli in a future study.

Origin of Neural Adaptation

We identified a constellation of visual areas, encompassing early- and high-tier areas in the dorsal pathway (V1/2, V3, V3A, MT, and MST), through which tuning curves of cortical adaptation become direction selective by transforming from a bidirectional shape to a unidirectional shape. This is consistent with the notion that motion information is processed in a distributed network of visual areas. Here arises a question about which areas in this distributed network are a locus or loci of motion adaptation. Previous fMRI studies (Huk et al. 2001; Huk and Heeger 2002), where cortical motion adaption was measured by comparing cortical responses to mixed directions of motion with those to a single direction of motion, reported that the magnitude of direction-selective adaptation was small in early visual areas (V1, V2, V3) and increased along the hierarchy, becoming maximal in MT+. Although one may interpret this to be consistent with the view that motion adaption occurs at multiple stages (Wenderoth et al. 1988), it is equally possible that MT+ is not a cortical region in which adaptation occurs but a region where consequences of adaptation in early visual area are carried over and manifested (Kohn and Movshon 2003). Our model simulations described in the previous section showed that this latter view (the inheritance hypothesis) is fairly compatible with our fMRI results. We demonstrated that early visual areas (V1/2, V3) showed a substantial amount of adaptation at around the adapted direction by directly comparing fMRI responses before and after adaptation. The degree of adaptation at the adapted direction was comparable between early visual areas and MT/MST. The relatively small adaptation of early visual cortex in the previous studies may be due to the fact that adaptation magnitude was estimated by comparing average fMRI responses to mixed directions and those to a single direction without direct comparisons between pre- and postadaptation activity. The model simulation results indicate that the selective inheritance of adaptation from the unidirectionally tuned neural population in early visual areas to MT can explain the pattern and magnitude of the fMRI adaptation tuning curve in MT.

Comparisons With Previous Imaging Studies on Motion and Orientation Adaptation

Previous fMRI studies have demonstrated that V3A is highly responsive to motion stimuli (Smith et al. 1998; Tootell et al. 1997) and is similar to MT/MST in many aspects. V3A has strong direction selectivity (Huk et al. 2001; Tootell et al. 1995), prefers coherent motion to incoherent, random motion (Braddick et al. 2001; Rees et al. 2000), and shows stronger adaptation to pattern motion than to component motion (Huk and Heeger 2002). More recently, it has been demonstrated that disruption of V3A activity via repetitive transcranial magnetic stimulation impaired speed discrimination performance in human subjects (McKeefry et al. 2008, 2010). Consistent with these findings, we found that V3A exhibited the greatest amount of response reduction at the adapted direction, besides MT/MST. However, our data revealed an important difference between V3A and MT/MST that could not be observed in the previous studies due to the lack of measurements of fMRI responses to intermediate directions between the adapted direction and the opposite direction. The directional tuning curve of adaptation was clearly bidirectional in V3A but unidirectional in MT/MST (Figs. 6 and 7A), implying that MT/MST is more closely linked to perceptual consequences of motion adaptation, reflected in adaptation-induced changes in contrast and coherence sensitivity observed in our psychophysical experiments. The presence of bidirectional adaptation in V3A also implies that a considerable fraction of neurons in V3A are not directionally selective.

Several previous fMRI studies on motion aftereffect (MAE) reported substantial increases in area MT+ while subjects were experiencing MAE after motion adaptation (Culham et al. 1999; He et al. 1998; Taylor et al. 2000; Tootell et al. 1995). However, Huk et al. (2001) showed that this elevation of MT+ activation during MAE is likely due to attentional modulation of MT+ fMRI signal and further demonstrated that MT+ activation was smaller when a single direction of motion was repeatedly presented than when mixed directions of motion were successively presented. Huk et al. concluded that adaptation to a single direction of motion reduces the activity of a population of neurons tuned to that direction and that the MAE reflects a temporary imbalance in activation of direction-sensitive neurons preferring different directions (Mather 1980; Sutherland 1961). Our results provide a further support to this imbalance theory of MAE by directly measuring responses of MT/MST to a range of directions relative to the adapted direction separately before and after adaptation and by showing that the amount of activation reduction after adaptation was modulated in a highly direction-selective manner.

On the basis of the results of the fMRI control experiment (Fig. 8), we concluded that potential orientation adaptation in our stimuli due to motion streaks was too small to account for the adaptation in the direction opposite to the adapted direction in early visual areas. We are not arguing that there was no orientation adaptation at all in our stimuli. Actually, most of the areas (except for V3A) indeed showed hints of orientation adaptation, albeit quite small and insignificant (Fig. 8, E and F). The critical observation was that the effect size of orientation adaptation is substantially smaller than that of motion adaptation that was observed in the direction opposite to the adapted direction (Fig. 8F). Krekelberg et al. (2005) showed that pairs of neighboring dots could give a rise to a significant level of adaptation when component dots were spatially arranged to carry biased orientation information, as in Glass patterns (Glass 1969). There could be several reasons for the discrepancy between their results and ours. First, pairs of coaligned dots existed “physically” in their stimuli but not in ours. It should be stressed that our filtered stimuli that mimicked motion streaks were only “hypothetical” and were likely to be “exaggerated” than experienced by subjects. Second, the duration of adapting stimuli was quite different between the two studies, 300 ms in their study and 4.4 s in ours. It is known that the magnitude of orientation adaptation is dependent on the timescale of adaptation: orientation adaptation was not induced by a second-scale adaptor (Boynton and Finney 2003) but successfully induced by a hundred-millisecond-scale adaptor (Kourtzi and Huberle 2005). Third, the contrast of test stimuli was quite lower than the adapting stimulus in our study. The relative difference in contrast gain function between orientation/sustained-channel (low-contrast gain) and motion/transient-channel (high-contrast gain) neural mechanisms (Gegenfurtner et al. 1997) may explain why motion information is more dominant than orientation information in generating adaptation effects in our study. It is worth noting that it was area LO that showed the biggest orientation adaptation effect in our study, which is consistent with the observation of Krekelberg et al. (2005). Interestingly, LO did not show any motion adaptation in the opposite direction at all. This supports our interpretation that even if there was some degree of orientation adaptation due to motion streaks, it is not associated with motion adaptation at the opposite direction of motion that was observed in our main experiment.

Implications for Perceptual Motion Adaptation

Although the fMRI data and model analysis suggests a possibility that early visual areas can be an origin of motion adaptation, the comparison between perceptual and cortical adaptation tuning curves indicates that the population activity of MT and MST is likely to be a neural correlate of perceptual consequences of motion adaptation. When correlations were computed between the perceptual and fMRI adaptation indexes across test directions relative to an adapting direction, the adaptation tuning curves in MT and MST most closely matched the perceptual adaptation tuning curves (Figs. 2C and 7B) in both contrast and coherence sensitivity reduction. In contrast, the correlations in directional adaptation tuning between V1/2 and psychophysics were relatively small and statistically not significant.

Although it is beyond the scope of questions in the current study, we note that our data exhibited a slight difference between adaptation effects probed by coherence sensitivity and those probed by contrast sensitivity. The individual differences were greater in the postadaptation coherence sensitivity curves (dark red symbols and lines in Fig. 2A) than in the postadaptation contrast sensitivity curves (dark blue symbols and lines in Fig. 2B). In particular, two subjects showed a reduction in coherence sensitivity after adaptation when the relative direction was 150° and 180°, respectively. Given the small number of subjects (n = 3) in the current study, it is hard to conclude whether impacts of adaptation on coherence and contrast sensitivity differ or not. This issue should be resolved by designing and conducting psychophysical experiments for this purpose [see Fine et al. (2004) for a good example] from a substantial number of subjects. Nevertheless, it should be noted that the averaged adaptation curves are clearly unidirectional in both the coherence and contrast sensitivity measurements (Fig. 2C). In addition, we confirmed that perceptual adaptation effects at the direction opposite to the adapted direction are not significant from five additional subjects in the control psychophysical experiment (Fig. 10).

Conclusions

Unlike previous fMRI studies on motion adaptation, our findings clearly distinguished early- and high-tier visual areas not in terms of overall magnitude of adaptation but in terms of the shape of adaptation tuning. We also showed motion detection sensitivity of human observers most closely matched the adaptation tuning curves from MT and MST. We also explored potential cortical mechanisms for our findings by implementing the key features of those mechanisms into the models that link fMRI responses and population responses of V1 and MT neurons. As one plausible interpretation of our results, we propose that initial impacts of motion adaptation occur in both unidirectional and bidirectional units in early visual areas, but its perceptual consequences are manifested in the population activity in MT and MST, which may inherit those direct impacts of adaptation from the directionally selective units without further adaptation in itself. Our favored interpretation is in line with single-unit studies demonstrating that adaptation fails to affect the contrast sensitivity of MT neurons by presenting adapter and test stimuli in two separate subregions inside the receptive fields of those neurons (Kohn and Movshon 2003) whereas adaptation modifies directional tuning curves of MT cells, not V1 cells, in a way consistent with motion repulsion experienced by human subjects (Kohn and Movshon 2004). However, our data do not exclude alternative explanations, in which additional adaptation in MT can be implemented via interactions among neurons in MT or independent adaptation mechanisms located separately in V1 and MT. Also, the explanation based on inheritance may be limited to the type of adaptation paradigm (long-term adaptation) and the type of motion stimuli (translational motion of random dots) that were adopted by the current study (Priebe et al. 2002). Additional adaptation in high-tier motion-sensitive areas may be necessary for full-blown adaptation to pattern motion or complex type of motion (Huk and Heeger 2002). Further studies using different types of motion stimuli and adaptation paradigm are required to fully resolve the issue of neural origin of motion adaptation.

GRANTS

This work was supported by the World Class University program through the National Research Foundation of Korea funded by Ministry of Education, Science and Technology Grant R31–10089 (S.-H. Lee) and in part by National Eye Institute Grant R01 EY16752 (S.-H. Lee). Some of these data were acquired while S.-H. Lee was a visiting scholar at New York University.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: H.A.L. and S.-H.L. performed experiments; H.A.L. and S.-H.L. analyzed data; H.A.L. and S.-H.L. interpreted results of experiments; H.A.L. and S.-H.L. prepared figures; H.A.L. and S.-H.L. drafted manuscript; S.-H.L. conception and design of research; S.-H.L. edited and revised manuscript; S.-H.L. approved final version of manuscript.