Robustness of muscle synergies underlying three-dimensional force generation at the hand in healthy humans

Abstract

Previous studies using advanced matrix factorization techniques have shown that the coordination of human voluntary limb movements may be accomplished using combinations of a small number of intermuscular coordination patterns, or muscle synergies. However, the potential use of muscle synergies for isometric force generation has been evaluated mostly using correlational methods. The results of such studies suggest that fixed relationships between the activations of pairs of muscles are relatively rare. There is also emerging evidence that the nervous system uses independent strategies to control movement and force generation, which suggests that one cannot conclude a priori that isometric force generation is accomplished by combining muscle synergies, as shown in movement control. In this study, we used non-negative matrix factorization to evaluate the ability of a few muscle synergies to reconstruct the activation patterns of human arm muscles underlying the generation of three-dimensional (3-D) isometric forces at the hand. Surface electromyographic (EMG) data were recorded from eight key elbow and shoulder muscles during 3-D force target-matching protocols performed across a range of load levels and hand positions. Four synergies were sufficient to explain, on average, 95% of the variance in EMG datasets. Furthermore, we found that muscle synergy composition was conserved across biomechanical task conditions, experimental protocols, and subjects. Our findings are consistent with the view that the nervous system can generate isometric forces by assembling a combination of a small number of muscle synergies, differentially weighted according to task constraints.

one of the fundamental questions in motor control is how the central nervous system (CNS) coordinates motor acts (Bernstein 1967). An extensive set of experimental evidence has shown that a relatively small number of movement modules, or muscle synergies (assemblies of muscles with fixed relative levels of activation), may underlie posture and movement (Bizzi et al. 2008; d'Avella et al. 2003; Hart and Giszter 2004; Lee 1984; Macpherson et al. 1986; Torres-Oviedo et al. 2006; Tresch and Jarc 2009). Animal behaviors studied within the framework of muscle synergies include terrestrial and aquatic movements in the frog (d'Avella and Bizzi 2005; d'Avella et al. 2003); postural responses, locomotion, and whole arm reaching in the cat (Krouchev et al. 2006; Lockhart and Ting 2007; McKay and Ting 2008; Ting and Macpherson 2005; Torres-Oviedo et al. 2006; Yakovenko et al. 2011); and grasping and reaching in the monkey (Overduin et al. 2008). Results of some of the animal studies suggest that neural circuits within the brain stem and/or spinal cord are involved in expressing muscle synergies (Giszter and Kargo 2000; Hart and Giszter 2010; Kargo and Giszter 2000a, 2000b; Roh et al. 2011a; Saltiel et al. 1998, 2001, 2005; Stein et al. 1995; Tresch et al. 1999). In addition to potentially simplifying the control of a redundant musculoskeletal system, there is evidence that muscle synergies provide explicit control of task-related variables. For example, muscle synergies underlying balance control in the cat may specify endpoint forces in a limb-centered coordinate system (McKay and Ting 2008; Ting and Macpherson 2005; Torres-Oviedo et al. 2006).

In humans, the task-dependent activation of just a few muscle synergies can be used to reconstruct global muscle activation patterns underlying postural responses (Krishnamoorthy et al. 2003; Torres-Oviedo and Ting 2007, 2010; Weiss and Flanders 2004) and locomotion (Clark et al. 2010; Monaco et al. 2010). With respect to the human upper extremity, several studies have presented evidence that combinations of a small number of muscle synergies, appropriately scaled in amplitude and shifted in time, can reconstruct complex spatiotemporal characteristics of muscle activation patterns recorded during point-to-point reaching movements (Cheung et al. 2009; d'Avella et al. 2006, 2008; Muceli et al. 2010; Sabatini 2002). The fact that the same set of synergies could reconstruct muscle activation patterns under different biomechanical conditions, including variations of load, posture, speed, or movement direction, supports the idea that synergies reflect the output of a general scheme for movement coordination, rather than arising solely from task constraints. Similarly, synergies underlying reflexes involved in postural stabilization of the human arm are conserved in both stiff and compliant environments, even though the long latency components of reflexes are systematically modulated by the direction of perturbation (Perreault et al. 2008). In terms of hand control, a set of muscle synergies could reconstruct a variety of electromyographic (EMG) patterns associated with static hand postures, coupled with fine adjustments for hand shaping or fingerspelling (Ajiboye and Weir 2009; Santello et al. 1998; Weiss and Flanders 2004).

It remains unclear whether isometric force generation at a predetermined posture in the human arm is also based on recruitment of a relatively limited set of muscle synergies. Previous studies have examined the spatial patterns of elbow and shoulder muscle activation underlying two- and three-dimensional (2-D and 3-D) isometric force or torque production tasks in the human arm (Buchanan et al. 1986, 1989; Flanders and Soechting 1990). Similar studies have also been conducted in the monkey (Kurtzer et al. 2006). Relationships between the activations of muscles were evaluated mainly using correlational methods, with an implicit assumption that muscles contributed to only one muscle synergy. These studies concluded that robust (fixed) synergies between pairs of muscles were relatively uncommon, with relationships between muscles dependent on force direction.

Correlational analyses may obscure synergic relationships when individual muscles are components of multiple synergies, which are recruited together in a task-dependent manner (Bizzi et al. 2008). In contrast, more advanced statistical algorithms, including non-negative matrix factorization (NMF) and independent-component analysis, can be used to decompose the activities of multiple muscles into underlying synergistic muscle coordination patterns (or muscle synergies) (Tresch et al. 2006) and to examine the robustness of the identified synergies across biomechanical conditions and subjects (Torres-Oviedo et al. 2006; Torres-Oviedo and Ting 2010). To our knowledge, the activation of human elbow and shoulder muscles during isometric force generation has not been studied using these advanced techniques.

There is also emerging evidence that the CNS uses independent, but different, strategies for force and movement control (Chib et al. 2009; Kurtzer et al. 2005; Valero-Cuevas et al. 2009; Venkadesan and Valero-Cuevas 2008). Approximately one-half of the neurons with load-related activity in the monkey primary motor cortex represents mechanical loads exclusively, either during posture or movement (Kurtzer et al. 2005). The same study also showed that neurons with load representation during both tasks randomly changed their activities, suggesting distinct neural control of posture and movement. Similarly, behavioral studies in humans indicate that different neural control strategies underlie the motion and static force phases of finger tapping (Venkadesan and Valero-Cuevas 2008). Of note, a related study (Valero-Cuevas et al. 2009) concluded that the variability of muscle activations associated with isometric force generation at the fingertip was not consistent with a synergy-based control mechanism (although muscle synergies were not explicitly identified). Accordingly, one cannot conclude a priori that the CNS uses a modular control strategy for isometric force generation, analogous to that used for reaching (Cheung et al. 2009; d'Avella et al. 2006, 2008; Muceli et al. 2010).

The goal of this study was to examine the ability of a limited set of muscle synergies (identified using NMF) to reconstruct the activation patterns of elbow and shoulder muscles underlying generation of 3-D isometric forces at the hand. Since the use of muscle synergies is directly related to their robustness, we recorded EMGs during three protocols that encompassed a wide range of biomechanical conditions. First, in the spatial protocol, we identified muscle synergies using a dense set of targeted force directions, and we evaluated the tuning of synergy activation. Second, the load protocol examined whether muscle synergies were conserved across a broad range of load levels. Finally, in the position protocol, we assessed the robustness of muscle synergy composition across hand positions that encompassed a substantial fraction of the arm's workspace. We hypothesized that a small number of muscle synergies could account for the vast majority of variance in each EMG dataset and that muscle synergy composition was conserved across task conditions. Accordingly, we evaluated the robustness of muscle synergies across the three experimental protocols, as well as across subjects recruited for the study.

MATERIALS AND METHODS

Subjects

Eight individuals (age 28.5 ± 3.1 years, three females, S1–S8) participated in the three experimental protocols of the study. All subjects were right-hand dominant, neurologically healthy, and had no muscular or orthopedic impairments of the upper limb. The study was performed in accordance with the Declaration of Helsinki, with the approval of the Northwestern University Institutional Review Board. Informed consent was obtained from each subject prior to testing.

Equipment

Multi-Axis Cartesian-based Arm Rehabilitation Machine.

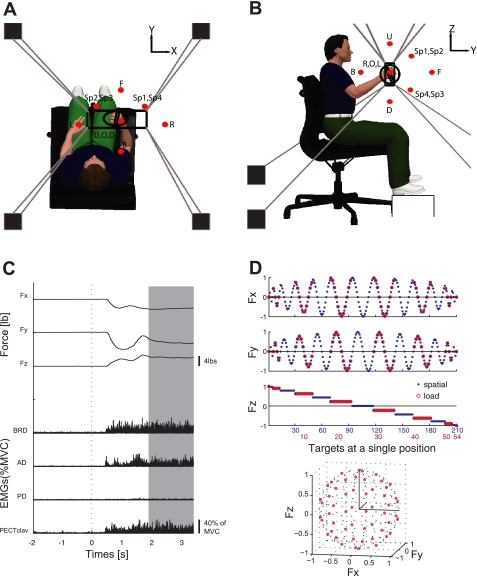
Hand position and 3-D forces generated at the hand were recorded using the Multi-Axis Cartesian-based Arm Rehabilitation Machine (MACARM; see Fig. 1, A and B), which is a cable-based robot comprised of a spatial array of eight active modules (i.e., motors; four active modules are indicated in Fig. 1A), connected via cables (Fig. 1A) to a centrally located end-effector (position O). The end-effector for this robot incorporates a gimbaled handle (a bar in the middle of an oval around the subject's right hand; see Fig. 1A), mounted on a six-degree-of-freedom (DOF) load cell (Model #45E15A, JR3, Woodland, CA). The mean positional accuracy of the robot is 2 mm over a >1-m³ workspace (Beer et al. 2008). We exploited the large workspace of MACARM in our experimental design to vary the hand position across the 3-D workspace of the upper limb, thereby maximizing the variance of EMGs in the position protocol (see below). Forces and handle position were sampled at 64 Hz and stored on a computer for subsequent analysis.

Fig. 1.

Experimental setup, exemplary target matching trial, and target force directions for the spatial and load protocols. A and B: top and lateral views of the experimental setup. Hand position and 3-dimensional (3-D) forces generated at the hand were recorded using the Multi-Axis Cartesian-based Arm Rehabilitation Machine (MACARM) cable robot. The MACARM is comprised of a spatial array of motors (indicated by black squares), which are connected to a central end-effector via cables (depicted by gray lines). The end-effector incorporates a gimbaled handle, the bar in the middle of an oval around the subject's right hand (A), mounted on a 6-degree-of-freedom load cell. The coordinate system for position and force measurements is indicated in the right upper corner. Hand positions used for the protocols are indicated by red-filled circles. The spatial and load protocols were performed in a central hand position (O), while all 11 hand positions were evaluated during the position protocol. Descriptions of the 11 hand positions are: backward (B), forward (F), left (L), right (R), down (D), and up (U). The remaining 4 targets were located in 4 quadrants with specific coordinates (Sp1–Sp4). C: for each trial, 3-D forces (Fx, Fy, Fz) and electromyographic (EMG) data from 8 arm and shoulder muscles were collected. [Representative EMGs for brachioradialis (BRD), anterior and posterior fibers of deltoid (AD and PD, respectively), and the clavicular fibers of pectoralis major (PECT_clav) muscles are shown.] Data recorded during 1.5 s of stable force generation (shaded area) were used for further analyses. MVC, maximum voluntary contractions. D: the 210 (blue dots) and 54 (red-unfilled circles) target force directions in the 3-D force space for the spatial and load protocols, respectively. The trial numbers along the x-axis are color matched with the force target of the 2 protocols in the Cartesian coordinate. Force directions for the load protocol were a subset of those used for the spatial protocol. The force directions were homogeneously distributed in 3-D force space to avoid bias.

Electromyography

Surface EMGs were recorded (Bagnoli 8, Delsys, Boston, MA) from eight elbow and shoulder muscles: brachioradialis (BRD); biceps brachii (BI); triceps brachii, long and lateral heads (TRI_long and TRI_lat, respectively); deltoid anterior (AD), medial (MD), and posterior fibers (PD); and pectoralis major (clavicular fibers; PECT_clav). Electrodes were placed in accordance with the guidelines of the Surface Electromyography for the Non-Invasive Assessment of Muscles–European Community Project (Delagi and Perotto 1980; Hermens et al. 1999). Maximum voluntary contractions (MVCs) were performed prior to data collection to verify correct electrode placement. One-minute rest periods followed each MVC to limit the possibility of fatigue. EMG signals were amplified (×1000), band-pass filtered (20–450 Hz), and sampled at 1,800 Hz. Data acquisition was synchronized between the MACARM and EMG data acquisition computers through the use of a common clock and trigger.

Protocols

During each protocol (see below), subjects grasped the gimbaled handle of the MACARM with their dominant (right) hand, while seated comfortably in an adjustable salon chair (Fig. 1, A and B). Wrist and trunk movements were restrained using a commercially available brace and strapping, respectively. Changes in shoulder position were monitored using a laser pointer directed on the acromion and verbally corrected if necessary. Although the limb was free to rotate about an axis defined by the shoulder and gimbal centers of rotation, all subjects maintained their limb approximately in a vertical plane during target matching, as verified using a three-DOF orientation sensor (Xsens Technologies B.V., The Netherlands) strapped to the upper arm. Rotations were minor (2.49 ± 3.32 degrees; mean ± SD) at a single posture across three protocols and across subjects. Prior to data collection at different hand positions, the load cell was re-zeroed to eliminate force signals associated with the weight of the limb.

For each trial, the target force was indicated by a sphere on a computer monitor, and real-time feedback of the force generated at the hand was provided by a spherical cursor. Subjects were given 9 s to achieve a target match in a self-paced manner, including a 2-s baseline period at the initial phase of each trial (Fig. 1C). A successful target match required the subject to maintain the center of the cursor in the target zone (a sphere around the target force with a radius equal to 20% of the targeted force magnitude) for 1.5 s. Three attempts at a match were allowed before proceeding to the next target in the random sequence (all subjects successfully matched targets within the trial limit). An intertrial interval of 10 s and a 1-min rest after each 10 trial block were provided to minimize the potential for fatigue.

Subjects completed each of three isometric force matching protocols (see below). For all protocols, force magnitude was set as a percentage of the maximum lateral force (MLF) that the subject could generate with the hand positioned directly in front of the shoulder at a distance of 60% of arm length (Fig. 1, A and B). The sequence of protocols, as well as the force direction within each protocol, was presented in a random order. A short training session was provided prior to data collection to ensure that the subject understood the task completely.

Spatial protocol.

Subjects generated voluntary forces in 210 different directions (Fig. 1D), approximately, uniformly distributed in 3-D force space, with their limb positioned in the middle of the workspace (Fig. 1, A and B). Load magnitude was set at 40% of MLF.

Load protocol.

Subjects generated voluntary forces in 54 different directions, roughly, uniformly spanning the 3-D force space (Fig. 1D), at a single hand position (Fig. 1, A and B) for each of four force magnitudes representing 10%, 25%, 40%, and 60% of MLF. The 54 target force directions were a subset of the 210 directions used in the spatial protocol. Due to technical issues, subjects S2 and S7 did not complete the trials at the 60% and 10% of MLF magnitudes, respectively.

Position protocol.

Subjects performed 3-D force matches for a series of 11 hand positions (Fig. 1, A and B) spanning a large fraction of the workspace. Eight force directions (Table 1) were used/position, for a total of 88 target matches. Load level was set at 40% of MLF. Hand position was specified in a spherical coordinate system (R, φ, θ), where R was the length of a vector from the shoulder center of rotation to the center of the gimbal, normalized by limb length, and φ and θ represented the elevation and azimuth angles of the vector, respectively. Hence, (1, 0°, 0°) and (1, 90°, 90°) corresponded to a fully extended arm, positioned at the side and directed along the y-axis (see Fig. 1, A and B), respectively. As shown in Fig. 1B, five of the 11 hand positions were in a horizontal plane at shoulder level (φ = 90°): position O, (0.6, 90°, 90°); backward (B), (0.4, 90°, 90°); forward (F), (0.8, 90°, 90°); left (L), (0.8, 90°, 135°); and right (R), (0.8, 90°, 45°). The two positions, down (D), (0.8, 45°, 90°), and up (U), (0.8, 135°, 90°), were located in a parasagittal plane below and above the shoulder, respectively. These target positions allowed us to examine potential changes in synergy structure with rotation of the limb about the global z (positions L and R)- and x (positions D and U)-axes and extension of the arm in a parasagittal plane (Fig. 1, A and B). The remaining four targets were located in four quadrants with specific coordinates as follows: Sp1, (0.8, 115°, 65°); Sp2, (0.8, 115°, 115°); Sp3, (0.8, 65°, 115°); and Sp4, (0.8, 65°, 65°), respectively. As described in Table 1, the eight force directions (d1–d8) for each hand position were uniformly distributed to span the 3-D force space without directional bias.

Table 1.

Force directions for the position protocol

Direction name	Unit force vector [Fx, Fy, Fz]
d1	[+0.577, +0.577, +0.577]
d2	[−0.577, +0.577, +0.577]
d3	[+0.577, −0.577, +0.577]
d4	[+0.577, +0.577, −0.577]
d5	[−0.577, −0.577, +0.577]
d6	[+0.577, −0.577, −0.577]
d7	[−0.577, +0.577, −0.577]
d8	[−0.577, −0.577, −0.577]

Note the global x-, y-, and z-axes paralleled the medio-lateral, backward-forward, and downward-upward directions, respectively (see Fig. 1).

Data analysis

EMG preprocessing.

EMGs were preprocessed by subtracting signal mean values to remove direct current offsets, then rectified, and averaged over the 1.5-s target matching interval. Mean baseline EMGs (recorded while subjects grasped the handle without force generation) were subtracted from the averaged data. As a result, EMG data for each trial included a vector whose dimension was eight (the number of muscles recorded) and reflected the muscle activity corresponding to active force production. Prior to synergy extraction, EMG data recorded from each muscle were concatenated across trials relevant to the purpose of the synergy extraction and normalized to have unit variance. This normalization procedure ensured that subsequent synergy extraction from preprocessed EMGs was not biased toward high-variance muscles.

Identification of muscle synergies.

We modeled EMG patterns collected under isometric conditions (EMG_isometric) as linear combinations of a set of N muscle synergies (W_isometric), each of which specified the balance of activation across eight muscles (Cheung et al. 2005, 2009; Hart and Giszter 2004; Perreault et al. 2008; Roh et al. 2011a; Torres-Oviedo et al. 2006; Tresch et al. 1999, 2006)

$$EM{G}_{isometric}=W_{isometric}·C_{isometric}$$ (1)

where W_isometric was an 8 × N matrix containing the N synergies (of unit magnitude) in each column, and C_isometric was an N × T (number of trials) matrix, with each column containing the synergy activation coefficients for a specific trial.

We applied a NMF protocol (Lee and Seung 1999, 2001) to pooled EMG datasets for each subject to identify the minimum number of muscle synergies that captured most of the total data variance (see below). For the spatial and position protocols, EMG_isometric was an 8 × 210 and 8 × 88 matrix, respectively. For the load protocol, EMG_isometric was either an 8 × 54 (data for each load level) or 8 × 216 (data pooled across four load levels) matrix. The number of target forces was limited to eight at a single posture in the position protocol to maximize the number of postures we could examine. To evaluate whether muscle synergy representation was conserved across different subregions of the arm's 3-D workspace, we pooled EMG data for subsets of hand positions (see Table 2).

Table 2.

Subregion definitions for the position protocol

Subregion	Included hand positions
Medio-Lateral Subregions
Medial	Sp2, L, Sp3
Parasagittal	U, O, D, F, B
Lateral	Sp1, Sp4, R
Superior-Inferior Subregions
Superior	Sp1, Sp2, U
Shoulder-level	L, R, F, O, B
Inferior	Sp3, Sp4, D

Hand positions include: L, left; U, up; O, central; D, down; F, forward; B, backward; R, right; Sp1–Sp4, targets located in 4 quadrants with specific coordinates.

As performed in an earlier study (Roh et al. 2011a), two stages of synergy extraction were performed. In stage I, we extracted muscle synergies separately from each dataset, which provided an estimate of the number of synergies required for reconstruction of the data. When comparing two datasets, in stage II, we pooled the data and used the estimated number of synergies as inputs to simultaneously extract shared and dataset-specific synergies. This stage II analysis was used for pairwise comparisons between different load levels (e.g., 25% of MLF vs. 40% of MLF), different subregions of the workspace (e.g., superior vs. inferior subregion), and the three experimental protocols (e.g., spatial vs. position protocol). In the case of simultaneous synergy extraction, we applied a modified NMF algorithm (Roh et al. 2011a) to the pooled EMG data. The purpose of the simultaneous synergy extraction was to maximize the chance to find the similarity between synergy sets underlying two EMG datasets without a sacrifice of variance-accounted-for (VAF) measures. Readers are referred to previous work (Cheung et al. 2005; Roh et al. 2011a) for details of the procedure.

Estimating the number of muscle synergies.

Various methods have been used to determine the appropriate number of muscle synergies underlying a given dataset (Cheung et al. 2005; Clark et al. 2010; Torres-Oviedo and Ting 2010). To identify the minimum number of muscle synergies that adequately reconstructed the spatial characteristic of a given EMG dataset, we first calculated VAF based on the entire dataset (global VAF). Here, the total data variation, defined as the trace of the covariance of the EMG-data matrix, was used to define a multivariate VAF measure

$$\text{VAF}=100\times \left(1-\text{SSE}/\text{SST}\right)$$ (2)

where SSE was the sum of the squared residuals, and SST was the sum of the squared EMG data [i.e., we used uncentered data; see Zar (1999)]. In addition, for cross-validation, we extracted synergies using 60% of the trials (randomly sampled) and used them to reconstruct the remaining trials (cross-validation VAF). VAF, as defined in Eq. 2, is sensitive to both the shape and magnitude of the measured and reconstructed datasets. Thus VAF is a more stringent measure than the centered Pearson correlation coefficient, which considers only the shape of data reconstruction.

The procedure described above was repeated 100 times to characterize the distribution of the global VAF and cross-validation VAF values. The number of synergies underlying each dataset was defined as the minimum number of synergies required to achieve a mean (n = 100) global VAF >90%, while satisfying local criteria of fit (see below), subject to the requirement that adding another synergy increased the mean global VAF <3%. As local criteria, we required the mean VAF for each muscle (muscle VAF) and subtask (load level or position VAF) to exceed 85%. This procedure ensured that the estimated number of synergies could reconstruct the nuances of each dataset, as well as the overall data.

Our stage I synergy analysis (synergies extracted from each dataset separately) indicated that four to five synergies were typically required to reconstruct both global and segmental features of a given dataset of each subject (see Figs. 3 and 4). Subsequently, for each subject, we extracted four synergies from the EMG datasets for the spatial and load protocols and five for the position protocol to facilitate comparison of synergy sets and their weights across subjects and performance conditions. This procedure characterized the structure of typical synergies and directional tuning of their associated weights (or activations). In the stage II synergy analysis (both shared and dataset-specific synergies simultaneously extracted from two datasets in consideration), we examined the robustness of synergy representation across different loads, positions, and protocols using the number of synergies identified in the stage I synergy analysis for each subject.

Fig. 3.

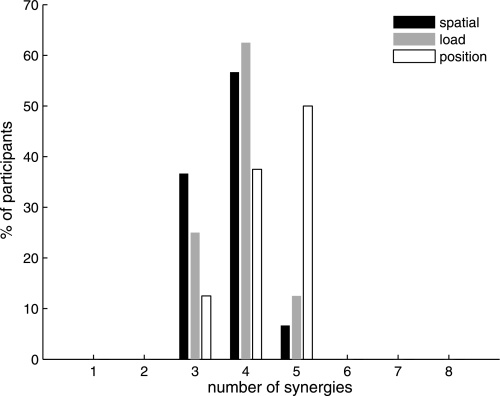
Number of muscle synergies required to reconstruct muscle activation patterns underlying 3-D isometric force generation. Typically, 4 or 5 synergies were required for each of the 3 protocols.

Fig. 4.

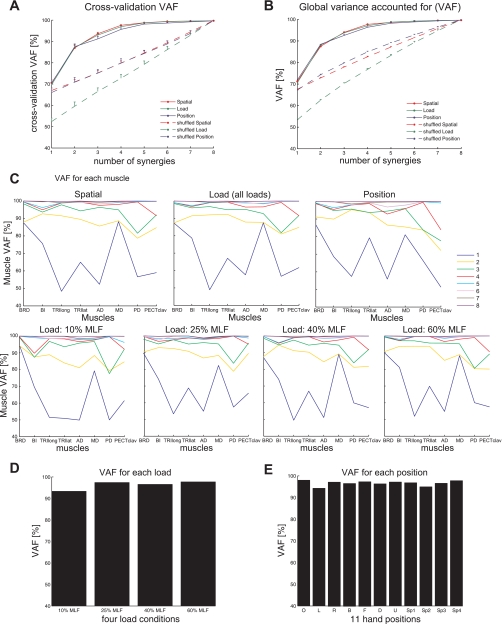
Variance-accounted-for (VAF) as a function of the number of muscle synergies used for reconstruction, based on EMG data for a representative subject (S5). A and B: the cross-validation VAF and global VAF curves for the spatial, load, and position protocols (red, green, and blue lines, respectively), for original (solid lines) and shuffled (dotted lines) EMG datasets. A: each cross-validation VAF curve (mean ± SD; n = 100) indicates the goodness of reconstructing 40% of an EMG dataset using 1–8 muscle synergies extracted from the remaining EMG data (see materials and methods for the detailed cross-validation procedure). B: each VAF curve (mean ± SD; n = 100) indicates how a set of 1–8 synergies extracted from an EMG dataset could reconstruct the full data. Note that with 4 synergies, both cross-validation VAF and global VAF values in 3 experimental protocols were >90% and significantly higher than the chance level (dotted lines; P < 0.05). C–E: 4 synergies (represented by the red line) extracted from each EMG dataset also provided a good reconstruction of the activation of each muscle (C) and datasets for each load level (load VAF in D) and hand position (position VAF in E). All values were significantly higher than the chance level (P < 0.05). Overall, these results support the ability of 4 synergies to reconstruct muscle activation patterns across widely varying biomechanical conditions.

We also extracted synergies from structureless EMG datasets to confirm that the synergies extracted from recorded EMGs were not biased by the algorithm used for extraction. Specifically, structureless EMG datasets were generated by shuffling the recorded EMG data independently for each muscle. This preserved the statistical characteristics of the original EMG samples for each muscle but removed intermuscular relationships at each data point. We computed the global VAF repeatedly (100 times) to define the VAF distribution associated with reconstruction of the structureless data by synergies extracted from such datasets. In all cases, the VAF values for the reconstruction of the original data using the identified synergies exceeded the 95th percentile of the VAF distribution for shuffled datasets.

Quantifying similarity of synergies.

We quantified the similarity between the sets of synergies underlying two datasets using the following metrics: the similarity index, global VAF, and muscle VAF (Cheung et al. 2005; Roh et al. 2011a; Torres-Oviedo and Ting 2010). These metrics were calculated for each subject and on a group basis. Whereas the similarity index is based on direct comparisons of individual synergies, the other metrics are more holistic measures of similarity, because they consider the synergy set as a whole. We reasoned that each metric reflected a different aspect of similarity between synergy sets. The use of multiple metrics enabled us to estimate the degree of similarity, a critical aspect of the study, in a rigorous way.

The similarity index in a simultaneous synergy extraction procedure was defined as the number of shared synergies divided by the smaller of the number of synergies underlying each dataset. The maximum number of synergies whose structures were similar was constrained by the smaller of the number of synergies independently extracted from two datasets under consideration.

In addition, we quantified the similarity between the sets of synergies underlying two datasets by calculating the VAF obtained by fitting the muscle synergies from one dataset A to another dataset B. VAF reflects the quality of the global reconstruction of a given dataset. We also calculated muscle VAFs to determine the goodness of reconstruction of EMG data for each muscle. A muscle VAF value was computed as in Eq. 2, based on the data for individual muscles.

To evaluate the statistical significance of the global and muscle VAF measure, we first simulated random synergies by randomly sampling the EMG amplitude, independently in each muscle, from the empirical distribution of the EMG dataset (d'Avella et al. 2006). Each random synergy was normalized to have unit variance. We then fit the random synergies to the original EMG data to estimate to what extent the original EMG data could be reconstructed by chance (random VAF value). The numbers of random and original synergies were matched. This procedure was repeated 200 times for each EMG dataset to define the distribution of random VAF values. Sets of identified synergies for which the reconstruction VAF exceeded the 95th percentile of the distribution were deemed significantly similar (P < 0.05).

Additional statistical tests.

Linear regression analysis was performed to test whether the activations (or weights; C_isometric in Eq. 1) of synergies (extracted from EMG data pooled across load levels) scaled with target force amplitude.

To evaluate the chance level of similarity of synergy structure in stage I analysis of synergy extraction, we first generated 1,000 random synergies for each of the two EMG datasets to be compared. Each random synergy consisted of random muscle weights sampled from the original EMG data for each muscle. We then calculated the scalar product of all possible pairs of random synergies from the two datasets (1,000 × 1,000 = 10⁶ pairs in total). The 95th percentile of the distribution of scalar products was then set to be our threshold scalar product magnitude (>0.863). With this criterion, we determined whether the scalar product of synergies was statistically significant (P < 0.05).

To evaluate the similarity of synergy recruitment across load levels or subjects, we first determined the tuning vector of synergy activation, calculated as the vector sum of unit vectors in the direction of each generated force scaled by the corresponding synergy activation (see Fig. 7B or Fig. 11). Across load levels or subjects, we then calculated the angular deviation of the preferred direction (direction of the tuning vector) of each synergy relative to the mean of the preferred directions. To characterize the distribution of angular deviations expected by chance, we generated 3-D random unit vectors (n = 1,000) and calculated the angular deviation of each vector from the mean of the random vectors. The fifth percentile of this distribution was used as the threshold for similarity. All statistical tests were performed using MatLab 7.8 (MathWorks, Natick, MA) with a significance level of P < 0.05.

Fig. 7.

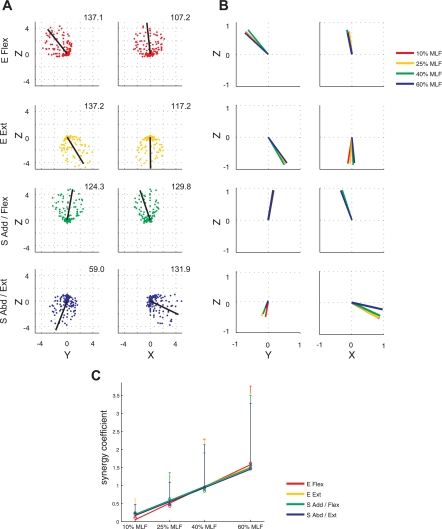
Synergy recruitment associated with performance of the spatial and load protocols by a representative subject (S4). A: each circle represents the endpoint of a vector in the generated force direction, whose amplitude corresponds to the activation coefficient for the associated, color-matched synergy (displayed in the 1st column of Fig. 5). The 3-D resultant of the activation vectors for each synergy, characterizing the “preferred” direction of synergy activation, is indicated by a black line. The number in the upper right corner of each 2-D subplot indicates the amplitude of the resultant of the activation vectors for each synergy. B: unit vectors representing the preferred direction of each synergy's activation for 4 force levels. The display sequence of the 4 synergies is matched to A. The spatial tuning of synergy activation was similar across force levels (P < 0.05). C: activation of synergies extracted from pooled (across load levels) datasets, scaled linearly with load level, suggesting that 4 synergies with appropriately scaled activation can reconstruct EMG patterns across different target force amplitudes.

Fig. 11.

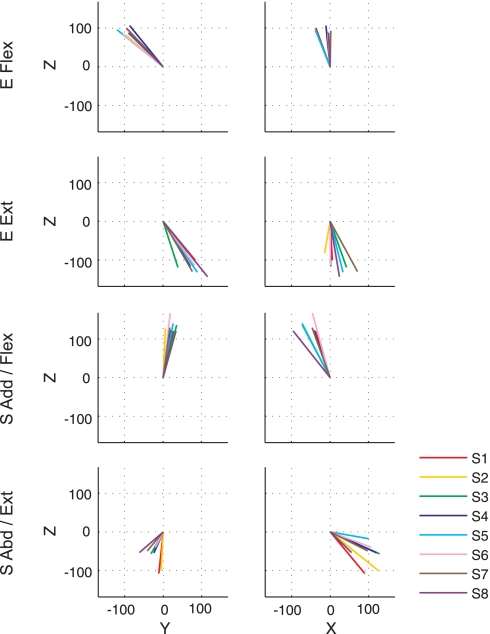
Tuning vectors of synergy activations for all subjects (S1–S8) in the 3-D force space for the spatial protocol. The length of each tuning vector provides an indication of the magnitude of the synergy activation. The angular deviation of the synergy preferred directions across subjects was less than the chance level (P < 0.05), supporting the idea that the preferred direction of synergy activation was similar across subjects.

RESULTS

The primary aims of the present study were to identify muscle synergies underlying isometric force generation in the human upper limb and to examine the robustness of synergy representation across different biomechanical constraints, including load levels and hand positions in the 3-D workspace. In the spatial protocol, data were collected with a dense set of targeted force directions (see Fig. 1D) to identify synergies and characterize the spatial tuning of synergy activation. During the load protocol, targeted force magnitude ranged between 10% and 60% MLF (10% = 1.8 ± 0.4 lb; 60% = 11.0 ± 2.3 lb across subjects) to examine whether muscle synergy structure was conserved across load levels. In the position protocol, data were collected at 11 hand positions using a limited number of force directions (see Table 1), and we evaluated the similarity of synergies across spatial subregions, each of which involved three or five out of the 11 hand positions defined in the 3-D workspace. Furthermore, we assessed the robustness of muscle synergies across experimental protocols and subjects (n = 8).

Variability of Muscle Activation Patterns Recorded During Isometric Force Generation Across Different Biomechanical Constraints

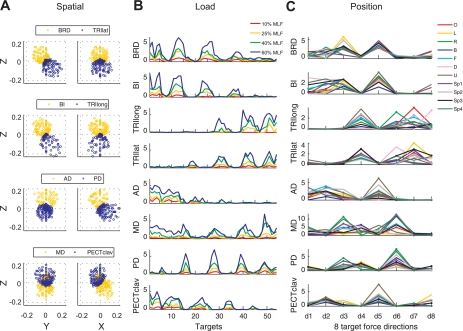
As illustrated in Fig. 2A, the activation of elbow and shoulder muscles recorded during the spatial protocol was broadly tuned with 3-D force direction, in a manner similar to earlier planar studies (Buchanan et al. 1986; Flanders and Soechting 1990). Each muscle exhibited a distinct pattern of activation. BRD and BI were predominately activated for backward (−Fy) and upward (+Fz) force directions, which required elbow flexion torque, whereas TRI_long and TRI_lat were mainly activated for forward (+Fy) and downward (−Fz) directions. Note that generation of a force in the ±x direction did not require flexion/extension torque at the elbow. At the shoulder, abduction/external rotation and adduction/internal rotation torques were required to generate forces in the +x and −x directions, respectively, whereas flexion and extension torques were required to generate +z and −z forces, respectively. The three heads of deltoids were activated accordingly: AD, left (−Fx) and upward (+Fz); MD, right (+Fx) and downward (−Fz); and PD, right (+Fx) and downward (−Fz). Similarly, PECT_clav was activated for force directions with leftward (−Fx) and upward (+Fz) components.

Fig. 2.

Variation of elbow and shoulder muscle activation across target force directions evaluated in the spatial, load, and position protocols (A–C, respectively) for subject S4. A: spatial tuning of EMGs underlying generation of force in 210 target directions (each circle represents data from a single trial). B: EMGs recorded during the load protocol scaled with load level, whereas spatial tuning was relatively unaffected. MLF, maximum lateral force. C: relative levels of muscle activation varied depending on the force direction (shown along the x-axis) and the position of the hand (indicated in the legend). Force directions and hand positions for C are identified in Table 1 and Fig. 1, A and B, respectively. Muscle names are indicated in an abbreviated form: BRD, brachioradialis; BI, biceps brachii; TRI_long and TRI_lat, long and lateral heads of triceps brachii, respectively; AD, MD, and PD, anterior, medial, and posterior fibers of deltoid, respectively; and PECT_clav, clavicular fibers of pectoralis major.

As illustrated by Fig. 2B, the spatial tuning of each muscle was qualitatively independent of load level for magnitudes ranging from 10% to 60% MLF. Whereas the spatial activation patterns for AD and PECT_clav appear similar in Fig. 2A, clear, target-dependent differences in the relative activation of these muscles are apparent in Fig. 2B. Similarly, whereas MD and PD were active for the same region of the force space (see Fig. 2A), the relative activation of these muscles was task dependent (Fig. 2B).

The variation of muscle activation with hand position was muscle specific (Fig. 2C). As such, the relative activation of muscles exhibited substantial variability across trials. As an example, consider force direction d6 (see Table 1). For hand position D, TRI_lat was substantially activated with little activation of TRI_long, whereas the reverse was apparent for hand position R. Similarly, the relative activation of the elbow flexors (E Flex; BRD and BI) varied with hand position (e.g., force direction d5; see Fig. 2C).

In summary, we observed task-dependent modulation of muscle activation across different force directions, load levels, and arm positions. The characteristic grouping of muscle activations, however, appeared as target-dependent modulation in the relationship of EMG amplitudes, which made it difficult to identify the synergistic patterns of muscle activation solely based on visual observation. Thus we proceeded to identify putative muscle synergies using NMF.

Four to Five Synergies Reliably Reconstruct Muscle Activation Patterns Across Protocols

Across the three experimental protocols, typically four or five synergies were required to reconstruct both global and individual muscle activation (Fig. 3; 3.88 ± 0.64, 3.70 ± 0.60, and 4.38 ± 0.74 synergies for the spatial, load, and position protocols, respectively). Of the datasets for individual load levels across subjects, 35.7% required three, 56.7% required four, and 6.7% required five synergies for reconstruction. The position protocol generally required one more synergy to meet our goodness-of-fit criteria, a finding that was not sensitive to a small change in our criteria (e.g., by changing the increment of global VAF from <3% to <5%). Thus the dimensionality of each dataset was low compared with the number of muscles examined (eight), with similar dimensionality observed across protocols.

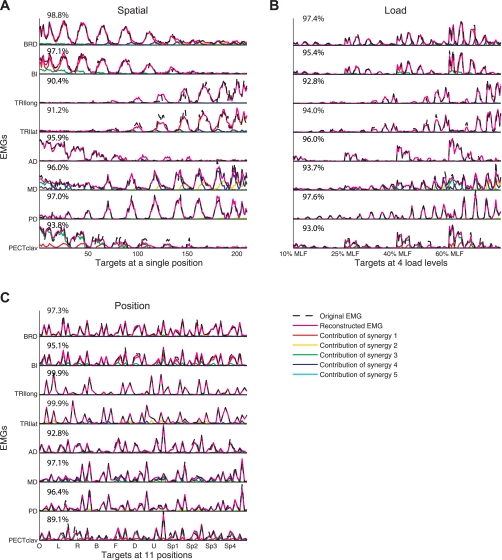
Figure 4, A and B, shows, for each protocol, representative plots of global VAF values as a function of the number of synergies extracted for a subject (S5). As the number of synergies extracted increased from one to eight, the cross-validation VAF increased, as expected. For the spatial, load, and position protocols, the cross-validation VAFs with four synergies were 96.6 ± 1.2%, 95.9 ± 1.5%, and 93.3 ± 2.6% (mean ± SD; n = 8), respectively, suggesting that the synergies extracted from a partial set of data could reliably reconstruct the remaining EMG data. All values were significantly greater than the chance level (typically, 65–75%; P < 0.05). When four synergies were extracted from full EMG datasets on a group basis, the synergy set explained 96.6 ± 1.3%, 96.2 ± 1.2%, and 94.5 ± 2.0% (mean ± SD; n = 8) of the total EMG variability (global VAF values; all values significant, P < 0.05) across the spatial, load, and position protocols, respectively. Increasing the number of synergies to five for the position protocol increased the cross-validation and global VAF values to 96.3 ± 1.8% and 96.9 ± 1.3% (mean ± SD; n = 8), respectively. These increments were significant (paired t-test, P < 0.05). However, the increases were small, indicating that the contribution of the fifth synergy to reconstruction of the global EMG pattern was not large in the position protocol.

To verify whether the NMF algorithm that we used biased our analyses to produce certain synergy vectors, the VAF levels for the synergies extracted from the original data (Fig. 4, A and B) were compared with the VAF values for synergies extracted from shuffled datasets (Fig. 4, A and B; see materials and methods for details). This comparison indicated that the VAF values with three to five synergies extracted from the original data were significantly higher than those for the same numbers of synergies extracted from the shuffled data (P < 0.05). This was consistently observed in all three experimental protocols for all eight subjects. The relatively higher VAF values for the original data imply that the structures of the synergies extracted from the original data reflect the actual spatial organization of elbow and shoulder muscle activation.

Synergies extracted from each EMG dataset explained not only the overall variability of each dataset but also provided a good reconstruction of the activation of each muscle (see Fig. 4C for representative data). Across subjects, the muscle VAF values (i.e., the fraction of total variance of the data for individual muscles; calculated as in Eq. 2) for the three protocols (i.e., spatial, load, and position protocols) were 96.5 ± 3.0%, 96.4 ± 2.7%, and 94.4 ± 4.1% (mean ± SD; n = 64; eight muscles/subject × eight subjects). Results for the load protocol are for pooled data (across load levels). For the individual load levels (i.e., 10%, 25%, 40%, and 60% of MLF), the muscle VAF values were 95.6 ± 4.1, 96.5 ± 2.9, 96.5 ± 3.0, 97.2 ± 2.3%, respectively. All values were significantly higher than the chance level (P < 0.05). When five synergies were used to reconstruct EMG data for the position protocol, minimum muscle VAF increased from 82.8% to 89.2%, suggesting that the fifth synergy contributed to goodness of reconstructing the activation of a single muscle for certain subjects (PECT_clav for two subjects and TRI_long for one subject).

We also examined to what extent four synergies could explain the data variance associated with each load level (load VAF) and each hand position (position VAF). Figure 4D shows that synergies underlying EMGs, pooled across four load levels, could account for >93% of variance of EMGs at each load. The VAF value for the 10% MLF condition was relatively lower than that for larger load levels, possibly because the low EMG amplitude at 10% MLF condition (Fig. 2B) resulted in a lower signal-to-noise ratio. Furthermore, Fig. 4E shows, for a single subject, that >94% of the variance of EMGs collected at 11 different hand positions in the 3-D workspace could be explained by four synergies. Overall, the results of synergy extraction from each dataset separately (stage I synergy analysis) demonstrate that typically four synergies accurately reconstruct muscle activation patterns in the spatial and load protocols, whereas a maximum of five synergies is required for the position protocol. In the stage II synergy analysis (extraction of shared and dataset-specific synergies from two datasets), we examined the robustness of synergy representation across different loads, positions, and protocols using the number of synergies identified in the stage I synergy analysis.

Muscle Synergies are Conserved Across Biomechanical Conditions

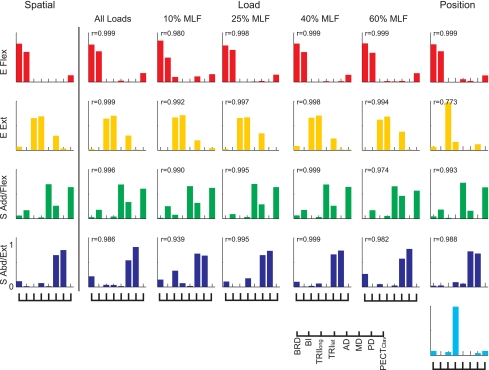
Figure 5 summarizes muscle synergies identified for each protocol (stage I synergy analysis) for a representative subject. For the load protocol, synergies are shown for both the total dataset (Fig. 5) as well as individual load levels. As shown in Fig. 5, each of four muscle synergies involved a characteristic pattern of muscle activation. The first and second synergies, which we refer to as the “elbow flexor” (E Flex) and “elbow extensor” (E Ext) synergies, consisted of relatively isolated activation of flexors (BRD and BI) and extensors (TRI_lat and TRI_long), respectively. The third “shoulder adductor/flexor” (S Add/Flex) synergy was dominated by activation of BI (a shoulder flexor), AD, MD, and PECT_clav. The fourth “shoulder abductor/extensor” (S Abd/Ext) synergy typically involved activation of MD and PD with one or more elbow muscles. This subject was one of four subjects who required five synergies to reconstruct the original EMG data in the position protocol. The E Ext synergy was simply split into two patterns (the second and fifth ones in Fig. 5), whereas others retained their structure.

Fig. 5.

Muscle synergies underlying isometric force generation were conserved across experimental protocols (spatial, load, and position protocols) and target force amplitudes (10–60% MLF). Data for subject S4 are shown. The 4 synergies are identified according to the mechanical action of the muscles activated within each synergy: elbow flexor (E Flex), elbow extensor (E Ext), shoulder adductor/flexor (S Add/Flex), and shoulder abductor/extensor (S Abd/Ext). Synergies extracted from spatial datasets (in the 1st column) were considered as control synergies, and their similarities with synergies extracted from the remaining datasets were assessed by calculating the scalar product (indicated by r values in each subpanel). When 4 synergies (not shown in this figure) were extracted for the position protocol, the synergies were similar to those in the spatial protocol (r values 0.999, 0.953, 0.995, and 0.988, respectively). When 5 synergies were extracted, the E Ext synergy appeared to split into 2 synergies dominated by TRI_long or TRI_lat. In all cases, except for the 2nd synergy out of the 5 synergies in the position protocol, the scalar products between matched synergy pairs were higher than the level expected by chance (P < 0.05).

Figure 5 also summarizes the results of an initial analysis of synergy similarity across protocols in a subject. Synergies extracted from spatial datasets were considered as control synergies, and their similarities with synergies extracted from the remaining datasets were assessed by calculating the scalar product (indicated by r values in each subpanel). In all cases, except for the second synergy out of the five synergies in the position protocol, the scalar products between matched synergy pairs were higher than the level expected by chance (P < 0.05). When four synergies were extracted for the position protocol, all synergies were similar to those in the spatial protocol (r values: 0.999, 0.953, 0.995, and 0.988, respectively).

After extracting synergies separately at each load level or for each protocol, we examined the similarity of synergies across load levels, spatial subregions, and protocols by simultaneously extracting shared and dataset-specific synergies (stage II synergy analysis). The advantage of this approach, simultaneous synergy extraction, is to maximize the number of shared muscle synergies discoverable, without sacrificing the quality of data description for both datasets under consideration. The metrics of synergy similarity that we used were the similarity index (the ratio of the number of shared synergies to the smaller of the number of synergies underlying two datasets), global VAF, and each muscle's variance explained (muscle VAF).

Comparisons across load levels.

In the load protocol, a majority of synergies was identified as common, shared ones across a sixfold load range equivalent to 10%, 25%, 40%, and 60% of MLF (absolute load levels were 1.8 ± 0.4, 4.6 ± 1.0, 7.3 ± 1.5, and 11.0 ± 2.3 lb, respectively; n = 6; data for two subjects were excluded in this analysis because of missing data for one load level). Table 3 summarizes the similarity measures obtained for all possible pair-wise comparisons of the four load levels. On a group basis, the similarity index was at or near unity for all comparisons, indicating that most synergies simultaneously extracted from the two datasets were identified as shared synergies (n = 6). Similarly, group mean global and muscle VAF exceeded 90% for all comparisons. For example, in the case of 25% of MLF vs. 40% of MLF, approximately four synergies (3.8 ± 0.4 and 3.7 ± 0.5 synergies at the two load levels, respectively) accounted for, on average, 98.0 ± 0.8% and 97.3 ± 1.0% of the total variance of the EMG datasets. For the same comparison, 96.9 ± 2.0% and 96.7 ± 2.4% of the total variance for individual muscle activation were explained by the shared and dataset-specific synergies. Over 83% of variance for global and muscle EMG data was accounted for by shared synergies (VAF_sh and muscle VAF_sh, respectively) in all comparisons as well. These results indicate that muscle synergies underlying isometric force generation with the upper limb were conserved across a broad range of submaximal force magnitudes.

Table 3.

Similarity of synergies across load levels in the load protocol (n = 6)

Comparison conditions (load A vs. load B)	Nsyn	Similarity index	VAF (%)	Muscle VAF (%)	VAFsh (%)	Muscle VAFsh (%)
10% MLF vs. 25% MLF
load A	3.7 ± 0.5	0.861 ± 0.155	98.4 ± 0.6	94.8 ± 5.1	94.3 ± 4.9	86.2 ± 25.1
load B	3.8 ± 0.4		97.5 ± 0.9	94.3 ± 10.9	88.2 ± 8.1	85.6 ± 22.0
10% MLF vs. 40% MLF
load A	3.7 ± 0.5	0.903 ± 0.153	98.4 ± 0.7	95.2 ± 4.8	95.1 ± 5.1	90.3 ± 19.1
load B	3.7 ± 0.5		96.5 ± 1.1	93.2 ± 13.4	93.1 ± 5.9	92.4 ± 8.8
10% MLF vs. 60% MLF
load A	3.7 ± 0.5	0.847 ± 0.170	98.3 ± 0.7	95.0 ± 5.7	91.7 ± 7.7	83.9 ± 36.7
load B	3.5 ± 0.5		96.3 ± 0.9	91.0 ± 17.5	89.3 ± 8.6	88.9 ± 15.9
25% MLF vs. 40% MLF
load A	3.8 ± 0.4	1.00 ± 0.00	98.0 ± 0.8	96.9 ± 2.0	97.5 ± 0.8	96.9 ± 2.4
load B	3.7 ± 0.5		97.3 ± 1.0	96.7 ± 2.4	97.0 ± 1.0	96.4 ± 2.6
25% MLF vs. 60% MLF
load A	3.8 ± 0.4	1.00 ± 0.00	97.9 ± 0.7	96.8 ± 2.1	97.0 ± 1.4	96.0 ± 4.3
load B	3.5 ± 0.5		96.8 ± 1.1	96.0 ± 3.5	96.4 ± 1.1	95.7 ± 3.1
40% MLF vs. 60% MLF
load A	3.7 ± 0.5	1.00 ± 0.00	97.3 ± 0.9	96.5 ± 2.3	96.8 ± 1.2	95.9 ± 3.1
load B	3.5 ± 0.5		96.9 ± 1.0	96.0 ± 2.9	96.7 ± 1.1	96.1 ± 2.9

All numbers are represented as mean ± SD. Two out of 8 subjects' data were omitted in the analysis, because data at 1 load level were not collected [for subject S2, 40% of maximum lateral force (MLF) and for subject S7, 10% of MLF]. N_syn, number of synergies extracted from each load condition; VAF, variance-accounted-for, obtained by fitting both shared and dataset-specific synergies; muscle VAF, the VAF for each muscle; VAF_sh, VAF acquired by fitting shared synergies only; and muscle VAF_sh, the VAF_sh for each muscle.

Comparisons across hand positions.

Similarity of synergy representation at various hand positions in the 3-D workspace of the arm was estimated by comparing synergies extracted from EMGs pooled for each of three subregions of the 3-D workspace (see Table 2 for a summary of how subregions were defined). We pooled the EMG data for each subregion because of the limited number (eight) of force target directions/hand position.

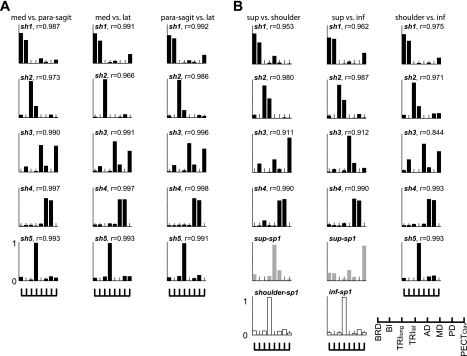
Figure 6, A and B, shows the shared and dataset-specific synergies underlying two subregional EMG datasets for subject S4. The “sh” indicates a synergy shared between two subregions, whereas “sp” refers to subregion-specific synergies. For example, five out of five synergies (sh1-5 in Fig. 6A) were shared between the “medial” and “parasagittal” subregions of the 3-D workspace. The r value indicated next to each sh was the mean of the scalar products of the given synergy paired with the corresponding synergy for the other pairwise comparisons. For example, the mean r value of the first shared synergy (sh1) in the medial vs. parasagittal region with the sh1 in the other two cases in Fig. 6A is 0.987. Intriguingly, all five synergies were identified as sh when three subregions identified along the medio-lateral axis were compared in subject S4 (Fig. 6A). In the case of the “superior” vs. “shoulder-level” regions, four out of five synergies were shared. The “shoulder-level-specific” synergy (Fig. 6B) appeared as a sh in the shoulder-level vs. “inferior” region, as expected. Regardless of how subregions were defined, the vast majority of synergies was identified as sh in the 3-D workspace, which resulted in >0.9 mean similarity indices across eight subjects (mean ± SD; Table 4). The similarity indices across the three comparisons in Table 4 were not statistically different (t-test, P = 0.931 and 0.6291 for medio-lateral and superior-inferior subregions, respectively). The small difference (<5%) between VAF (obtained by fitting both sh and sp synergies) and VAF_sh (acquired by fitting sh) suggests that most of data variance was explained by sh. Overall, our results consistently indicate that synergies underlying isometric force generation are conserved across different subregions in the 3-D workspace of the human arm.

Fig. 6.

Most of synergies were identified as shared, common synergies in the 3-D workspace of the human arm. A and B: sets of synergies that underlay 2 subregional EMG datasets in comparison in subject S4. Subregion names are abbreviated (med, medial; para-sagit, parasagittal; lat, lateral; sup, superior; shoulder, shoulder-level; inf, inferior; see Table 2 for the corresponding hand positions). The “sh” indicates a synergy (in black) shared between 2 subregions in comparison, whereas “sp” refers to the synergy (dataset 1 specific in gray; dataset 2 specific in white) specifically found in a subregion but not the other region. For example, 5 out of 5 synergies (sh1-5 in the 1st column in A) were commonly observed in both medial and parasagittal subregions of the 3-D workspace. The r value indicated next to each sh was the mean of the scalar products of the given synergy paired with any other comparison's corresponding synergy. For example, the mean r value of sh1 in the medial vs. parasagittal region with the sh1 in the other 2 cases in A is 0.987. Note that all 5 synergies were identified as sh when 3 subregions identified along the medio-lateral axis were compared in subject S4. In the case of the superior vs. shoulder-level region, 4 out of 5 synergies were shared. The shoulder-level-specific synergy (white synergy in the 1st column of B) appeared as a sh in the shoulder-level vs. inferior region, as expected. Taken as a whole, our results suggest that muscle synergies underlying isometric force generation are conserved across different hand positions in the 3-D workspace of the human arm.

Table 4.

Similarity of synergies across subregions in the 3-dimensional workspace in the position protocol (n = 8)

Comparison conditions (subregion 1 vs. subregion 2)	Nsyn	Similarity index	VAF (%)	Muscle VAF (%)	VAFsh (%)	Muscle VAFsh (%)
Medial vs. Parasagittal
subregion 1	4.4 ± 0.7	0.944 ± 0.105	96.4 ± 1.5	95.4 ± 3.7	94.6 ± 2.8	94.4 ± 5.2
subregion 2	4.4 ± 0.7		96.2 ± 2.0	95.2 ± 4.2	95.3 ± 2.1	94.7 ± 4.7
Medial vs. Lateral
subregion 1	4.4 ± 0.7	0.938 ± 0.116	96.5 ± 1.6	95.7 ± 3.9	92.6 ± 8.4	92.9 ± 13.4
subregion 2	4.4 ± 0.7		96.9 ± 1.4	95.6 ± 4.2	94.4 ± 4.8	93.3 ± 13.4
Parasagittal vs. Lateral
subregion 1	4.4 ± 0.7	0.958 ± 0.118	95.9 ± 1.9	95.5 ± 4.6	94.8 ± 3.8	93.7 ± 9.5
subregion 2	4.4 ± 0.7		97.4 ± 0.8	95.7 ± 4.5	95.1 ± 5.9	94.4 ± 9.9
Superior vs. Shoulder-Level
subregion 1	4.4 ± 0.7	0.944 ± 0.105	96.7 ± 1.6	94.7 ± 5.9	94.6 ± 4.7	94.2 ± 6.3
subregion 2	4.4 ± 0.7		96.2 ± 1.6	95.0 ± 5.2	93.7 ± 5.0	93.4 ± 7.6
Superior vs. Inferior
subregion 1	4.4 ± 0.7	0.919 ± 0.113	96.8 ± 1.5	94.6 ± 6.3	92.0 ± 6.9	92.1 ± 10.4
subregion 2	4.4 ± 0.7		96.9 ± 1.3	94.6 ± 7.5	92.8 ± 5.7	92.4 ± 10.7
Shoulder-Level vs. Inferior
subregion 1	4.4 ± 0.7	0.969 ± 0.088	95.4 ± 1.9	95.4 ± 5.0	93.7 ± 6.8	93.2 ± 12.6
subregion 2	4.4 ± 0.7		97.1 ± 1.2	95.6 ± 4.1	94.0 ± 8.2	93.3 ± 14.4

All numbers are represented as mean ± SD. Subregions defined along the medio-lateral axis: medial, parasagittal, and lateral regions; and subregions defined along the inferior-superior axis: superior, shoulder-level, and inferior regions.

Comparisons across protocols.

Table 5 summarizes the similarity measures obtained for all possible pair-wise comparisons of the three experimental protocols. For all comparisons, the similarity index was unity, indicating that the number of shared synergies equaled the smaller of the number of synergies extracted from the paired protocols. For instance, four out of four synergies were identified as shared synergies between the spatial and position protocols for subject S1 (spatial vs. position condition). The set of shared and dataset-specific synergies accounted for, on average, 97.5 ± 0.7% and 96.4 ± 1.5% of the global variance of EMGs for the two protocols, respectively (n = 8). In all comparisons, the VAF values were significantly greater than the chance level (the 95th percentile = 86.7%).

Table 5.

Similarity of synergies across 3 protocols (n = 8)

Comparison conditions (protocol 1 vs. protocol 2)	Nsyn	Similarity index	VAF (%)	Muscle VAF (%)	VAFsh (%)	Muscle VAFsh (%)
Spatial vs. Load
protocol 1	3.9 ± 0.6	1.00 ± 0.00	97.5 ± 1.0	96.7 ± 2.3	97.1 ± 0.9	96.6 ± 2.5
protocol 2	3.8 ± 0.7		97.0 ± 0.8	96.5 ± 2.4	96.7 ± 0.8	96.3 ± 2.4
Spatial vs. Position
protocol 1	3.9 ± 0.6	1.00 ± 0.00	97.5 ± 0.7	95.7 ± 3.5	97.1 ± 1.0	96.4 ± 2.9
protocol 2	4.4 ± 0.7		96.4 ± 1.5	96.6 ± 2.7	93.8 ± 2.6	93.1 ± 5.7
Load vs. Position
protocol 1	3.8 ± 0.7	1.00 ± 0.00	97.3 ± 0.8	95.2 ± 3.8	96.4 ± 1.1	95.9 ± 3.3
protocol 2	4.4 ± 0.7		96.7 ± 1.4	96.7 ± 2.7	93.9 ± 2.9	93.3 ± 5.9

All numbers are represented as mean ± SD.

The scalar products between the synergies extracted using simultaneous synergy extraction and the synergies extracted separately for each protocol for individual subjects (e.g., synergies summarized in Fig. 5) were typically >0.9. For example, the r values among four synergies identified in the stage I synergy analysis by separate synergy extraction (e.g., synergies in Fig. 5) and in the stage II analysis by simultaneous synergy extraction in the spatial vs. position protocol for subject S4 were 0.999, 0.998, 0.997, and 0.993, respectively. These high values indicate that the structure of synergies was conserved in the case of simultaneous synergy extraction compared with the separate synergy extraction. The results of the simultaneous synergy extraction analysis support the idea that muscle synergy structure was conserved across protocols involving different biomechanical constraints.

Muscle Synergy Recruitment Varies with Force Direction, Load Level, and Hand Position

We found that the activation of each muscle synergy was tuned to a specific region of the 3-D force space. Figure 7A shows the endpoint of a vector in the generated force direction, whose amplitude corresponds to the activation coefficient for the associated synergy (data are from subject S4). Typically, two or more synergies were substantially activated (C > 10% of the maximum C across targets; see Eq. 1) for a given force direction. Also shown is the direction of the 3-D resultant of the activation vectors for each synergy, the “preferred” direction of synergy activation in the spatial protocol (a black line in Fig. 7A), and the amplitudes of the preferred directions (the numbers displayed next to the lines). For example, activation of the E Flex (Fig. 7A) was broadly tuned to the force directions backward (−Fy) and upward (+Fz), whereas the E Ext (Fig. 7A) tended to be more activated during the generation of static force in forward (+Fy) and downward (−Fz) directions. The spatial tuning of the S Add/Flex and S Abd/Ext synergies (in Fig. 7A, respectively) contrasted as expected: the activation of S Add/Flex synergy was tuned toward left (−Fx) and upward (+Fz) force directions, whereas that of the S Abd/Ext synergy was tuned toward right (+Fx) and downward (−Fz) directions.

The tuning direction of synergy activation in isometric force generation, as characterized using the preferred direction of synergy recruitment, was similar across the four load levels examined in the load protocol. As an example, Fig. 7B shows the preferred direction of each synergy for each load level for a representative subject (S4). On a group basis, the angular deviation of the preferred directions for each load relative to the mean (across load levels) direction was 8.9 ± 7.3, 6.0 ± 4.7, 3.7 ± 2.8, and 8.0 ± 6.3 degrees (n = 24; four load levels/subject × six subjects) for the E Flex, E Ext, S Add/Flex, and S Abd/Ext synergies, respectively, which were significantly smaller than the chance level (P < 0.05). Interestingly, the recruitment of synergies, extracted from pooled (across load levels) datasets, increased relatively linearly with load magnitude; r values were 0.994, 0.996, 0.990, and 0.976 for the four synergies, respectively (Fig. 7C). This observation indicates that a set of four synergies with appropriately scaled activation can reconstruct EMG patterns across different target force amplitudes. Overall, these results suggest that synergy composition and tuning of synergy activation were conserved across a wide range of submaximal load levels.

Variation of recruitment of muscle synergies mediated the variability of the EMG patterns recorded for various target force directions and hand positions. Figure 8 shows how the five synergies (Fig. 5), which underlay the EMGs pooled across positions in a subject (S4), were activated to reconstruct EMGs recorded during isometric force generation in each of eight homogeneously distributed target force directions (Table 1) at 11 arm postures. As the synergy recruitment was broadly tuned to certain target force directions in the spatial and load protocols (Fig. 7, A and B), certain synergies were preferentially recruited to generate target forces in certain directions in the position protocol (Fig. 8). For instance, activation of the fourth synergy (W4), similar to the S Abd/Ext synergy in the spatial protocol, was higher when the target force directions were d3 (+Fx, −Fy, +Fz), d4 (+Fx, +Fy, −Fz), and d6 (+Fx, −Fy, −Fz). Interestingly, depending on hand position, the level of activation of certain synergies varied to generate the same 3-D force [e.g., the activation of the third synergy (W3), similar to the S Add/Flex synergy at the d5 (−Fx, −Fy, +Fz) force direction at 11 hand positions]. The combination of the synergies (Fig. 5) and their associated coefficients could reconstruct the original EMG data in each protocol (Fig. 9, A and C; original EMG data, reconstructed EMGs, and contribution of each synergy for the reconstruction). These results suggest that the activations of the synergies were modulated in a task-dependent manner to meet task-level requirements.

Fig. 8.

Synergy activation across the 8 target force directions at each of 11 hand positions evaluated in the position protocol (subject S4). The activation of each synergy was modulated to meet task-level requirements. The associated synergies (W1–W5) are displayed in the 7th column of Fig. 5. The 8 target force directions (d1–d8) are summarized in Table 1. Hand positions are identified in Fig. 1, A and B.

Fig. 9.

Reconstruction of EMGs for the spatial, load, and position protocols (A, B, and C, respectively) by linear combinations of 4 or 5 synergies based on data for subject S4. The original EMGs (dashed black lines), reconstructed data (solid magenta lines), and contribution of each muscle synergy (common color scheme used for associated synergies) to the reconstruction are shown. The associated synergies are displayed in the 1st, 2nd, and 7th columns of Fig. 5. The muscle VAF value is indicated for each associated muscle. B and C: the 54 and 8 trials at each load level and hand position are shown, respectively. All trials are ordered along the x-axis in the trial sequence shown in Figs. 1D and 2, B and C.

Muscle Synergies and Tuning Directions of Their Activation are Similar Across Subjects

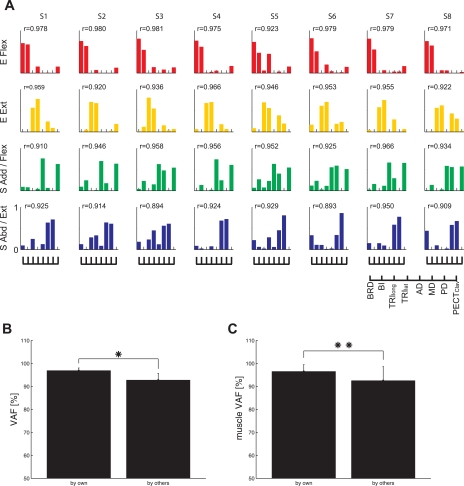
The similarity of synergy representation was examined across subjects. To facilitate this analysis, for each subject, we extracted four synergies for the spatial and load protocols and five synergies for the position protocol. Figure 10A shows four synergies for each subject, extracted from EMG data in the spatial protocol. The numbers (r values) at each synergy represent the mean of scalar products of the given synergy with any of the other seven subjects' corresponding synergy. For instance, the mean r values of four synergies for subject S1 with the other seven sets of synergies identified in the data of subjects S2–S8 were 0.978, 0.959, 0.910, and 0.925, respectively. All of these numbers were significantly higher than the chance level (P < 0.05). This result indicates that the synergy composition was consistent across subjects. The set of four synergies extracted from one subject could explain a large portion of total variance of other subjects' EMG data (Fig. 10, B and C) as well. For example, 92.7 ± 2.9% of total variance of one EMG dataset could be explained by using other subjects' synergies (mean ± SD; n = 7). However, the VAFs calculated using a subject's own synergies were significantly greater than the values obtained using another subject's synergies [Fig. 10B, VAF = 96.9 ± 1.1% vs. 92.7 ± 2.9% (mean ± SD), t-test, P < 10⁻³; Fig. 10C, muscle VAF = 96.5 ± 2.9% vs. 92.5 ± 6.1% (mean ± SD), t-test, P < 10⁻⁴]. Both VAF and muscle VAF values, calculated by fitting one's own or others' synergies to each EMG dataset, were above the chance level (the 95th percentile of VAF by random synergy sets = 79.5%, P < 0.05; see materials and methods). Overall, these results suggest that synergies were relatively similar across subjects; however, EMGs were best reconstructed by using one's own synergies.

Fig. 10.

Comparison of muscle synergies for the spatial protocol across subjects. A: muscle synergies were similar across 8 subjects (S1–S8). The 4 synergies are identified according to the mechanical action of the muscles activated within each synergy: E Flex, E Ext, S Add/Flex, and S Abd/Ext. The mean similarity of a synergy with other subjects' corresponding synergies (r value) exceeded the chance level (P < 0.05) and is indicated next to each synergy. B and C: goodness of reconstruction (VAF values) of EMG data recorded from a single subject using one's own synergies was relatively similar to that obtained using muscle synergies from other subjects (mean ± SD; n = 8). However, the global one's VAF and muscle VAF values associated with use of a subject's own synergies were significantly higher than those obtained using others' synergies (*P < 10⁻³; **P < 10⁻⁴).

The tuning direction of synergy activation in the spatial protocol was relatively similar across subjects. Figure 11 summarizes the 3-D tuning vector for each synergy across subjects. The angular deviation among the mean of eight subjects' 3-D tuning directions and each of the eight directions, per each of four synergies, was 7.2 ± 1.5, 10.7 ± 5.9, 7.2 ± 3.5, and 14.3 ± 8.6 degrees (n = 8), respectively. The angles were statistically smaller than the chance level (P < 0.5). In addition to the similarity of synergy composition (Fig. 10A), this small, angular deviation of tuning directions supports the idea that synergy representation is relatively similar across subjects.

DISCUSSION

The primary aim of our study was to identify muscle synergies underlying isometric force generation at the hand and to examine the robustness of the synergy representation across different biomechanical constraints. The four or five muscle synergies were identified in the three experimental protocols, and four synergies accounted for, on average, 95% of total variance of the EMG patterns during generation of isometric force. Synergy structure was conserved across three experimental protocols that involved a variety of load levels and hand positions in the 3-D workspace of the arm. The amplitude of synergy activations scaled with force magnitude, whereas spatial tuning remained invariant. Furthermore, muscle synergy representation, in terms of synergy composition and tuning direction, was consistent across subjects. Overall, these results suggest that the CNS coordinates patterns of muscle activation during isometric force generation in a modular fashion.

Coordination of Muscles in Isometric Force Generation

The relatively fixed covariations of elbow and shoulder muscle EMG amplitudes across various load levels during isometric force generation are congruent with previous studies of finger force generation. In single-digit and three-digit force generation, the amplitude of EMGs recorded from muscles that contributed to generate fingertip force scaled linearly across all hand muscles as a function of grasp force, suggesting that voluntary digit forces were produced by appropriately scaling the magnitude of underlying muscular coordination patterns (Poston et al. 2010; Valero-Cuevas 2000). Furthermore, a study of three-digit force generation reported that the EMG–EMG coherence was not significantly affected by force, suggesting that the distribution of neural drive to multiple hand muscles is force independent (Poston et al. 2010). Our study extended these findings to muscles of the elbow and shoulder. Furthermore, we explicitly demonstrated that different force magnitudes were generated by linear scaling of the activations of four underlying synergies. Accordingly, the spatial tuning of synergy activation was load independent.

Comparisons with Muscle Synergies Underlying Reaching and Maintenance of Arm Posture

Recent studies suggest that the CNS uses independent but different strategies for movement and force control (Chib et al. 2009; Kurtzer et al. 2005; Venkadesan and Valero-Cuevas 2008). There is strong evidence supporting a modular organization of muscle coordination during human voluntary arm movements; four or five synergies are capable of reconstructing the activation patterns of up to 19 muscles recorded during point-to-point reaching movements with different loads or forearm postures (d'Avella et al. 2006), whereas three synergies are sufficient to reconstruct multijoint movements performed in the horizontal plane (Muceli et al. 2010). Muscle activation patterns recorded during reaching performed at different speeds, as well as the maintenance of static arm postures, are also well captured by combinations of a few synergies (d'Avella et al. 2008). The current study suggests that isometric force generation is also based on a modular organization, with a similar number of underlying muscle synergies. However, due to methodological differences, we are unable to directly compare synergy structure across static and dynamic tasks.

Intriguingly, the muscle synergies identified in our study using the NMF algorithm are qualitatively similar to those underlying stretch reflex responses to multijoint positional perturbations, identified using independent component analysis/principal component analysis (Trumbower et al. 2010). Based on the same set of muscles examined in our study, Trumbower and colleagues (2010) found that four synergies were typically required to account for 90% of the variance of EMGs underlying stretch reflex responses in neurologically intact subjects. Their flexion pattern, comprised of dominant activation of BRD and BI with smaller MD and PD activity, is similar to the E Flex synergy identified in our study. The shoulder flexion pattern, consisting primarily of BI, AD, and PECT_clav activity, parallels our S Add/Flex synergy. Likewise, the remaining synergies that consisted of TRI_long and TRI_lat and MD and PD activation, respectively, are similar to our E Ext and S Abd/Ext synergies. Synergy structure has been shown to be insensitive to the methods used for synergy extraction (Tresch et al. 2006). Thus the similarities in synergy structure across these two studies suggest that the regulation of volitional isometric force control and multijoint stretch reflexes may be based on the same set of synergies. In animals, muscle synergies common to both voluntary movements, which include jumping, swimming, kicking, and stepping, and spinal reflexes have been reported (Roh et al. 2011a). Additional studies are necessary to address to what extent the synergy representation underlying volitional and reflexive motor behaviors in humans is shared.

Neural Circuitries Involved in Expressing Muscle Synergies

Potential neural substrates for encoding muscle synergies include neural circuits within the brain stem (Roh et al. 2011a) and divergent projections of spinal interneuronal systems to different motoneuronal pools in the spinal cord (Jankowska 1992, 2001; Tantisira et al. 1996). Neurons in the intermediate zone of the spinal cord, but neither proprioceptive-related neurons nor ventral horn neurons, correlate more strongly with motor primitives (conceptually equivalent to muscle synergies formulated in our study) than with the activities of individual muscles (Hart and Giszter 2010). In addition, monosynaptic connections between reticulospinal or vestibulospinal fibers and lumbar motoneurons (Cruce 1974; Magherini et al. 1974; Shapovalov 1975) may support the emergence of synergistic modules in motor coordination. Precise comparison between muscle synergies found pre- and post-transection at different levels of the neuraxis suggested that a majority of muscle synergies underlying natural movement in frogs is expressed by the neural circuits within the brain stem and spinal cord (Roh et al. 2011a). In addition, some electrophysiological and anatomical studies have suggested that neurons in the primary motor cortex (M1) are involved in expressing muscle synergies in mammals (Drew et al. 2008; Futami et al. 1979; Gentner and Classen 2006; Li and Martin 2002; Shinoda et al. 1976, 1981, 1986). We reason that the two views, derived from experiments with a lower vertebrate and mammals, respectively, could be reconciled in the sense that the “old” M1 (Rathelot and Strick 2009), sending descending fibers primarily to the spinal interneurons, generates movements by flexibly activating synergies expressed downstream, whereas the “new” M1 is involved in encoding the more diverse movements peculiar to higher primates and humans (Roh et al. 2011a; Yakovenko et al. 2011). Further studies may be needed to clarify how the synergy representation is organized in the cortex and downstream brain regions in the human.

Methodological Considerations

Muscle synergies are viewed as a means of simplifying the control of a highly redundant mechanical system. However, there have been cogent arguments advanced supporting the view that synergies are an emergent feature of a mechanical solution that may potentially be unique to the task chosen for testing (Bunderson et al. 2008; Kurtzer et al. 2006; Kutch et al. 2008; Valero-Cuevas et al. 2009). Accordingly, the robustness of muscle synergies across different tasks is strong evidence supporting their use by the CNS. However, many mechanical parameters (muscle moment arms, length-tension properties, or required joint torques) vary smoothly with spatial parameters (force direction or hand position), so it remains possible that an optimization-based solution could still be reasonably represented with just a few synergies (An et al. 1984; Crowninshield and Brand 1981; Davy and Audu 1987; Dul et al. 1984a, b; Van Zuylen et al. 1988). We think that additional musculoskeletal modeling and relevant experiments may be necessary to address this issue.

Cross talk among EMG channels can also be a potential factor that influences muscle synergy structure, because it may be (wrongly) regarded as synergistic activity. Although EMG cross talk is difficult to accurately identify or to eliminate (Farina et al. 2004), previous studies of reaching movements showed that the extracted synergies do not substantially change even after eliminating from the analysis the muscles mostly affected by potential cross talk (d'Avella et al. 2006, 2008). In addition, in the current study, each muscle exhibited a unique pattern of activation (Fig. 2), suggesting that the impact of cross talk was minimal. We estimated the level of muscle activity from the amplitude of the surface EMG. The relationship between the level of muscle activity and amplitude of the surface EMG recording is not exact (Clancy et al. 2002; Farina et al. 2004), and some intersubject variability existed regarding electrode placement, muscle size, and subcutaneous layer thickness across subjects. Thus we used unit-variance normalization in our synergy extraction to prevent bias in favor of large variance muscles.

The current protocol did not explicitly consider supination/pronation torques on the forearm. Reciprocal activation of BRD and BI has been reported (Jamison and Caldwell 1993). Additionally, studies in humans have revealed inhibitory projections from BRD and pronator teres to BI motoneurons (Naito et al. 1996, 1998). Thus whether inclusion of supination/pronation torques in the task would have resulted in the identification of additional synergies, or perhaps altered the structure of the synergies that we identified, is an issue requiring further study.

Future Studies

In summary, our results indicate that the activation patterns of elbow and shoulder muscles during isometric force generation are consistent with the task-dependent recruitment of a limited set of muscle synergies. The present study examined the putative existence of muscle synergies, based on an analysis of the intertrial variability of the original EMG data. In so doing, we confined our analysis to the region of stable force generation. To further establish the robustness of the identified synergies, we plan to examine whether the within-trial variability of muscle activation (see Fig. 1C) can also be explained by the same set of synergies.

We also plan to use the identified muscle synergies as a template to evaluate abnormal muscular coordination following stroke, particularly in individuals with severe impairment. A recent study of upper-limb movements reported alterations in muscle synergy recruitment, but not synergy composition, in chronic stroke survivors (Cheung et al. 2009). However, the majority (five out of eight) of participants was mildly impaired [i.e., Fugl-Meyer (FM) scores >57 out of 66], and there was some evidence of altered synergy structure in the case of a more-severely impaired stroke survivor (i.e., FM score 18 out of 66). Furthermore, a recent study found a reduction in the number of synergies underlying locomotion in stroke survivors, reflecting a merging of synergies identified in healthy subjects (Clark et al. 2010). Additional studies with severely impaired stroke survivors (Roh et al. 2011b) are required to fully understand whether functional deficits in motor coordination following stroke are associated with alterations in muscle synergy composition and/or activation.

GRANTS

This work was supported in part by the American Heart Association (Postdoctoral Fellowship 10POST3200026) and the National Institute on Disability and Rehabilitation Research (H133G060169).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: J.R., W.Z.R., and R.F.B. conception and design of research; J.R. performed experiments; J.R. analyzed data; J.R., W.Z.R., and R.F.B. interpreted results of experiments; J.R. prepared figures; J.R. drafted manuscript; J.R., W.Z.R., and R.F.B. edited and revised manuscript; J.R., W.Z.R., and R.F.B. approved final version of manuscript.