GEOSTATISTICAL ANALYSIS OF HEALTH DATA WITH DIFFERENT LEVELS OF SPATIAL AGGREGATION

Abstract

This paper presents a geostatistical approach to combine two geographical sets of area-based data into the mapping of disease risk, with an application to the rate of prostate cancer late-stage diagnosis in North Florida. This methodology is used to combine individual-level data assigned to census tracts for confidentiality reasons with individual-level data that were allocated to ZIP codes because of incomplete geocoding. This form of binomial kriging, which accounts for the population size and shape of each geographical unit, can generate choropleth or isopleth risk maps that are all coherent through spatial aggregation. Incorporation of both types of areal data reduces the loss of information associated with incomplete geocoding, leading to maps of risk estimates that are globally less smooth and with smaller prediction error variance.

1. Introduction

For cancer control activities and resource allocation, it is important to be able to compare incidence and survival rates, risk behaviors, screening patterns, diagnosis stage, and treatment methods across geographical and political boundaries and at as fine a spatial scale as possible. With the proliferation of geographic information systems (GIS) and related databases, it is becoming easier to gather information at the individual-level. The assignment of a set of spatial coordinates (geocode) to subjects’ residences is the cornerstone of any analysis of individual-level health data. Direct measurement of these coordinates is rare and researchers rely on cheaper geocoding methods, such as identification on orthophoto maps, address matching to a digital street map (automatic geocoding) or the local 911 listing (Rushton et al., 2006).

According to several studies (Cayo and Talbot, 2003; Ward et al., 2005; Strickland et al., 2007; Zimmerman and Li, 2010) the magnitude of geocoding errors can be substantial, up to several hundred meters and even more in rural areas where longer street segments and uneven spacing between houses increase interpolation errors when placing an address based on the street numbers assigned to the ends of each street segment. E911 geocodes are more accurate but still not available everywhere. Uncertainty about the exact location of a residence can also result from the aggregation or randomization performed on the resulting point to protect the identity of the geocoded object, which is often the case in the geocoding of health data (Goldberg et al., 2007; Wieland et al., 2008). These geocoding errors frequently hamper the statistical analysis of cancer data by reducing the power to detect cancer clusters (Zimmerman, 2008a; Jacquez and Rommel, 2009), the ability to identify relationships with geographically varying risk factors (Mazumdar et al., 2008), and the accuracy of fine-level cancer maps (Zimmerman, 2008b).

In addition to the uncertainty attached to the residence coordinates, addresses can fail to geocode. Indeed, the geocoding process is extraordinarily complex and many problems can affect either the residential address (e.g. spelling errors, post office box addresses, street suffix, prefix and abbreviation inconsistencies) or the reference files that can contain errors such as missing, incomplete, and incorrect street segments and address ranges. The end results are missing or incomplete data where coarser surrogates, such as ZIP code, replace precise coordinates. The percentage of incomplete encoding tends to increase for cases diagnosed several decades ago (Han et al., 2005), which hampers the quantification of temporal trends in health outcomes and the assessment of the benefits of prevention and control strategies to reduce cancer burden.

Since rural addresses are less likely to be successfully geocoded, a straight forward exclusion of incomplete data could lead to geographic selection bias and misleading results (Rushton et al., 2006). Simply assigning the data to the geographical or population-weighted centroid of the ZIP code is also unsatisfactory because this point could fall into inhabited areas and it is a crude estimate for large ZIP codes (Hibbert et al., 2009). One common way to handle incomplete data is through geographic imputation whereby latitude and longitude coordinates or some other appropriate geographic identifier are assigned to nongeocoded addresses (e.g. Klassen et al., 2005; Henry and Boscoe, 2008; Curriero et al., 2010). For example, Hibbert et al. (2009) compared the accuracy of eight deterministic and stochastic geo-imputation methods to allocate cases of diabetes from zip codes to census tracts. The allocation was based on either the land area or the population demographics (total population, population under 19, and race/ethnicity). They found that the imputation approach should be selected according to the study aims since deterministic approaches yield greater accuracy at the individual level (i.e. greater percentage of cases allocated correctly to a tract), whereas stochastic methods better reproduce the true spatial distribution of cases (greater group level accuracy).

Although geo-imputation methods are easily implemented within GIS and a measure of uncertainty can be computed for the imputed counts (Curriero et al., 2010), such an approach does not address the issue of rates instability in sparsely sampled areas and the limitations associated with the interpretation of choropleth maps when the user tends to assign more importance to larger polygons although they typically correspond to rural areas with smaller populations at risk. These effects are particularly important for census tracts since they typically display a wide range of sizes and shapes. The geostatistical approach adopted in this paper falls within the areas of change of support (Gotway and Young, 2002) and disease mapping (Waller and Got way, 2004). Areal data defined over different spatial supports are interpolated to a fine grid in order to map the underlying risk of developing the disease as a continuous surface.

Zimmerman and Fang (2011) recently demonstrated through simulation studies that using coarsened data improves substantially the accuracy of the maps of risk estimates relative to prediction based only on observations that were successfully geocoded. Their nonparametric coarsened-data methodology was very straight forward, both conceptually and computationally, yet no measure of prediction accuracy was provided and the approach assumes that geocoding errors were negligible. This latter assumption was also inherent to the geostatistical approach proposed by Goovaerts (2009) to incorporate both point and areal data in the mapping of health outcomes. This kriging technique however provides a measure of the variance of prediction errors and its recent generalization as “Area-and-Point kriging”(Goovaerts, 2010) allows the mapping of attribute values within each sampled geographical unit under the constraint that the average of point estimates returns the areal data (coherency constraint).

The kriging approach accounts for the shape and size of geographical units, hence it can accommodate different spatial supports for the data and the prediction, and it is not restricted to a single type of areal data at a time (e.g. ZIP code or census tracts). For example, Gotway and Young (2007) used kriging for mapping the number of low birth weight (LBW) babies at the census tract-level, accounting for county-level LBW data and covariates measured over different spatial supports, such as a fine grid of ground-level particulate matter concentrations or tract population. Such flexibility is needed when geocoded data are either unreliable or were randomized for confidentiality reasons (Hampton et al., 2010), making their spatial aggregation desirable before proceeding with any analysis.

This paper presents a geostatistical approach to combine two geographical sets of area-based data into the mapping of health outcomes. This form of binomial kriging (Goovaerts, 2009), which accounts for the population size and shape of each geographical unit, can generate choropleth or isopleth risk maps that are coherent with the noise-filtered real data (i.e. return the areal data through spatial aggregation). This methodology is here used to combine two types of areal data in the isopleth mapping of the percentage of prostate cancer that were diagnosed late across 25 counties of Florida: 1) census tract-level rates computed from geocoded data that were randomized within each tract for confidentiality reasons, and 2) ZIP code-level rates calculated using all records, including the ones that failed to geocode.The impact of incorporating the two types of data is illustrated by comparison to the results obtained using area-to-area and area-to-point kriging (Kyriakidis, 2004; Goovaerts, 2006) based only on ZIP code data.

2. Data and Methods

2.1 Prostate cancer data

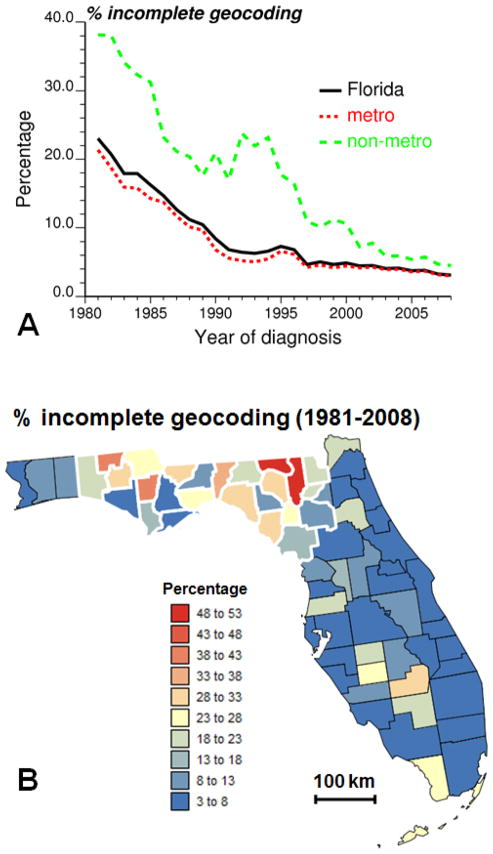
The geostatistical mapping approach will be illustrated using prostate cancer cases who were diagnosed during the calendar years 1981 through 2008 in Florida. The analysis will be restricted to non-Hispanic white males aged 40 years or older. Approximately 7.3% of the 293,651 records, which were compiled by the Florida Cancer Data System (FCDS) and processed by an independent geocoding firm, were not successfully geocoded at residence at time of diagnosis. This percentage however greatly varies with time and space. Figure 1A shows that incomplete geocoding is more likely for earlier years of diagnosis: on average over Florida the percentage decreases from 23% in 1981 to 3.12% in 2008. This percentage is also greater for counties classified as non-metropolitan (non-metro) on the basis of the US Department of Agriculture Rural-Urban Continuum Codes (USDA, 2004). This nine-part county codification distinguishes metro counties by the population size of their metro area, and non-metro counties by degree of urbanization and adjacency to a metro area or areas. This information was available for 1983, 1993 and 2003. For 1983 and 1993 codes 0 and 1 were combined to make these classifications comparable to the 2003’s codification. These codes were linearly interpolated over the periods 1983–1993 and 1993–2003.

Fig. 1.

Temporal change in the percentage of prostate cancer cases that failed to geocode on average over Florida and for metropolitan versus non-metropolitan counties (A). The bottom map shows the county-level percentage of incomplete geocoding averaged over the period 1981–2008 (B). Thick white borders highlight the subset of 25 counties used for the geostatistical analysis.

Discrepancies between both metro and non-metro counties were particularly large in the early nineties when the introduction of PSA screening caused a surge in the number of diagnosed cases. The frequency of incomplete geocoding was then more than four times larger for cases diagnosed in non-metro counties (Fig. 1A).This greater likelihood for rural addresses to be unsuccessfully geocoded has been well documented and is caused by various factors, such as disproportionate number of rural route addresses, post office box addresses, unofficial street names and streets missing from geocoding reference files (Whitsel et al., 2006; Kravets and Hadden, 2007). The county-level map of time averaged percentage of incomplete geocoding (Fig. 1B) reveals substantial geographical disparities that go beyond the dichotomy between metropolitan and non-metropolitan counties. Except for two Southern counties that include the Florida key Islands (Monroe County) and part of the Everglades (Glades County), most geocoding problems occurred in Northern Florida, in particular in the Panhandle.

The 21,365 incomplete records were assigned to their ZIP code centroids, whereas the geographical coordinates of the geocoded records were randomized within each census tract for confidentiality reasons. Data thus exist over two overlapping and non-nested sets of geographical units: ZIP codes and census tracts.

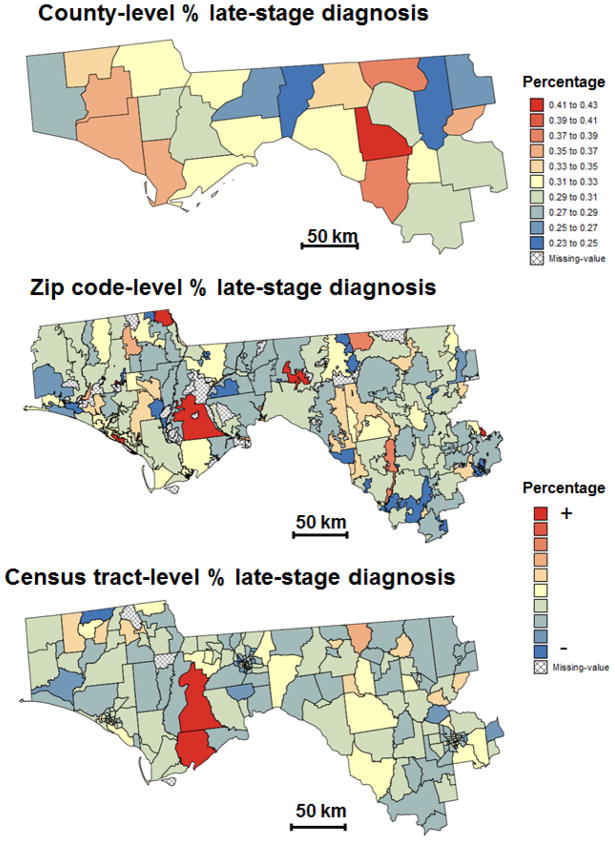
The present study will focus on 25 counties of Northern Florida where the largest percentage of incomplete geocoding was recorded and that are highlighted using thick white borders in Fig. 1B. This region (Fig. 2A) includes the centroids of 273 ZIP codes (Fig. 2B) and 222 census tracts (Fig. 2C) that form the two geographies available for mapping the percentage of late-stage diagnosis. Within these 25 counties 7,958 patients had their residence geocoded whereas 1,666 records were incomplete. The spatio-temporal analysis of health data aggregated at the ZIP code-level is challenging since the definition of these geographical units changes with time (Krieger et al., 2002) and shape files with ZIP code boundaries are not readily available prior to 2000. In addition, USPS ZIP codes represent postal delivery routes without true geographic boundaries. Since this paper is primarily concerned with the development of a new methodology instead of a detailed analysis of prostate cancer late-stage diagnosis in Florida, the ZIP code geography was simply based on the shape file of ZIP Code tabulation area (ZCTA) from the 2000 Census. US Census Bureau’s ZCTAs are aggregates of 2010 Census blocks, whose addresses use a given ZIP Code. Each resulting ZCTA is then assigned the most frequently occurring ZIP Code as its ZCTA code. In the remaining part of this paper, the terms ZIP codes and ZCTA will be used interchangeably. Out of the 1,666 incomplete records, 82 could not be assigned to one of these ZIP codes and were discarded.

Fig. 2.

Information available for mapping the percentage of prostate cancer late-stage diagnosis across 25 counties of Florida’s Panhandle and Northern Florida (A): Zip code-level rates (B) and census tract-level rates (C). The former were computed from all cases diagnosed between 1981 and 2008, whereas the census tract-level rates are based only on cases that were successfully geocoded. Shaded polygons denote geographical units where no case was diagnosed over the 28-year time period. Maps (B) and (C) share the same legend that is not documented for confidentiality reasons.

2.2 Area-to-point (ATP) binomial kriging

The key idea of this paper is to map health outcomes using two sets of rate data resulting from the aggregation of individual records over different geographical units because of confidentiality and incomplete geocoding. Let z(v_α), α = 1,…,K and y(v_β), β = 1,…,L denote the two sets of rates which are computed as the ratio of the number of late-stage cases over the total number of cases within each unit. Without loss of generality, assume that the total number of cases over units v_α exceeds the number of cases recorded in the second set of units v_β:

$$\sum _{\alpha =1}^{K}n(v_{\alpha })>\sum _{\beta =1}^{L}n(v_{\beta })$$ (1)

The geographical units v_α and v_β are denoted primary and secondary units, hereafter In the present application, they correspond to ZIP codes and census tracts.

The creation of an isopleth map requires the estimation of the noise-filtered rate, called risk, at every node u of an interpolation grid. This estimate, denoted r̂(u), is computed as a linear combination of rates z(v_α) and y(v_β):

$$\widehat{r}(\mathbf{u})={\lambda }_{{\alpha }^{\prime }}z(v_{{\alpha }^{\prime }})+\sum _{\alpha =1}^{K^{\prime }}{\lambda }_{\alpha }z(v_{\alpha })+{\lambda }_{{\beta }^{\prime }}y(v_{{\beta }^{\prime }})$$ (2)

where v_α′ and v_β′ are the primary and secondary units that include u, and the other K′ primary units are neighbors of v_α′. Thus, the estimation is based mainly on rates recorded in the primary units which are on average the most densely populated (i.e. more stable rates) according to assumption (1). Only the secondary unit in which u lies is used in the estimation to reduce the number of neighbors and the associated smoothing effect. The prediction error variance associated with the ATP estimate (equation 2), commonly known as kriging variance, is computed as:

$${\sigma }_K^2(\mathbf{u})=C(0)-\sum _{i=1}^{K^{\prime }+2}{\lambda }_i\overline{C}(v_i,\mathbf{u})-\mu (\mathbf{u})$$ (3)

The weights λ_i in Equations (2) and (3) are computed by solving the following system of linear equations; known as area-to-point “binomial kriging” system (Webster et al., 1994; Goovaerts, 2009):

$$\begin{array}{l}\sum _{j=1}^{K^{\prime }+2}{\lambda }_j\left[\overline{C}(v_i,v_j)+{\delta }_{ij}\frac{a}{n(v_i)}\right]+\mu (\mathbf{u})=\overline{C}(v_i,\mathbf{u})\text{i}=1,\dots ,(K^{\prime }+2)\\ \sum _{j=1}^{K^{\prime }+2}{\lambda }_j=1.\end{array}$$ (4)

where μ(u) is a Lagrange multiplier accounting for the unit sum constraint on the weights. The Kronecker delta δ_ij is 1 if i=j and 0 otherwise. The term a is defined as a = m * (1–m*) −C̄ (v_i, v_i), where m* is the population-weighted average of the K rates recorded in primary units. The quantity a/n(v_i) is an error variance term that increases the variance C̄ (v_i, v_i) of the units with small population size n(v_i) the most. Thus, smaller weights are assigned to less reliable late-stage rates based on fewer cases (small number problem).

Under the assumption of second-order stationarity, the area-to-area covariance C̄ (v_i, v_j) is numerically approximated by averaging the point-support covariance C(h) computed between any two locations discretizing the areas v_i and v_j. Likewise, the area-to-point covariance C̄ (v_i, u) is estimated as the average of the point-support covariance C(h) computed between u and a series of locations discretizing the area v_i. The point-support covariance C(h), or equivalently the point-support semivariogram γ(h) = C(0) - C(h), cannot be estimated directly from the observed rates, since only areal data are available. Only the regularized semivariogram can be estimated using the following population-weighted estimator (Goovaerts, 2005):

$$\widehat{\gamma }(\mathbf{h})=\frac{1}{2{\displaystyle \sum _{\alpha ,\beta }^{N(\mathbf{h})}}n(v_{\alpha })n(v_{\beta })}\sum _{\alpha ,\beta }^{N(\mathbf{h})}\left\{n(v_{\alpha })n(v_{\beta }){\left[z(v_{\alpha })-z(v_{\beta })\right]}^2\right\}$$ (5)

where N(h) is the number of pairs of primary units (v_α, v_β) whose centroids are separated by the vector h. The different spatial increments [z(v_α)-z(v_β)]² are weighted by the product of their respective population sizes to assign more importance to the more reliable rates. Derivation of a point-support semivariogram from the experimental semivariogram γ̂ (h) computed from areal data is called “deconvolution”, an operation that is conducted using an iterative procedure (Goovaerts, 2008).

2.3 Binomial kriging using only primary units

The impact of incorporating a second set of geographical units in the prediction will be assessed by comparison to the following estimate that is based only on primary units:

$$\widehat{r}(\mathbf{u})={\lambda }_{{\alpha }^{\prime }}z(v_{{\alpha }^{\prime }})+\sum _{\alpha =1}^{K^{\prime }}{\lambda }_{\alpha }z(v_{\alpha })$$ (6)

An important property of the ATP kriging estimator is its coherency: the average of all n(v_α′) point estimates within an area v_α′ is equal to the following area-to-area (ATA) estimate:

$$\frac{1}{n(v_{{\alpha }^{\prime }})}\sum _{k=1}^{n(v_{{\alpha }^{\prime }})}\widehat{r}({\mathbf{u}}_k)=\widehat{r}(v_{{\alpha }^{\prime }})={\omega }_{{\alpha }^{\prime }}z(v_{{\alpha }^{\prime }})+\sum _{\alpha =1}^{K^{\prime }}{\omega }_{\alpha }z(v_{\alpha })$$ (7)

The weights ω are computed using a set of linear equations similar to the binomial kriging system (equation 4), except that the area-to-point covariance C̄ (v_i, u) is replaced by the area-to-area covariance C̄ (v_i, v_α′):

$$\begin{array}{l}\sum _{j=1}^{K^{\prime }+1}{\omega }_j\left[\overline{C}(v_i,v_j)+{\delta }_{ij}\frac{a}{n(v_i)}\right]+\mu (v_{{\alpha }^{\prime }})=\overline{C}(v_i,v_{{\alpha }^{\prime }})\text{i}=1,\dots ,(K^{\prime }+1)\\ \sum _{j=1}^{K^{\prime }+1}{\omega }_j=1.\end{array}$$ (8)

The coherency constraint is met only if the same (K′+1) rates are used to estimate all the point estimates within the unit v_α′. The ATA kriging variance is computed as:

$${\sigma }_K^2(v_{{\alpha }^{\prime }})={\overline{C}}_{(v_{{\alpha }^{\prime }},v_{{\alpha }^{\prime }})}-\sum _{i=1}^{K^{\prime }+1}{\lambda }_i\overline{C}(v_i,v_{{\alpha }^{\prime }})-\mu (v_{{\alpha }^{\prime }})$$ (9)

where the within-area covariance C̄ (v_α′, v_α′) is computed as the average of the point-support covariance C(h) calculated between any two locations discretizing the area v_α′.

3. Results

Percentage of prostate cancer late-stage diagnosis was mapped over a region of Northern Florida that in cludes 25 counties, 273 ZIP codes and 222 census tracts (Fig. 2). All three choropleth maps in Fig. 2 display different spatial patterns, which illustrates the modifiable areal unit problem (MAUP) whereby the interpretation of a geographical phenomenon within a map depends on the scale and partitioning of the areal units that are imposed on the map (Waller and Got way, 2004; Gregorio et al., 2005; Meliker et al., 2009). In particular, zones with higher rate of late-stage diagnosis seem to shift east as the size of geographical units decreases. Such influence of the aggregation level (i.e. county, ZIP code or census tract) on the results highlights the need for filtering the noise due to the small number problem and mapping results as continuous surfaces (isopleth maps) without subjective administrative boundaries.

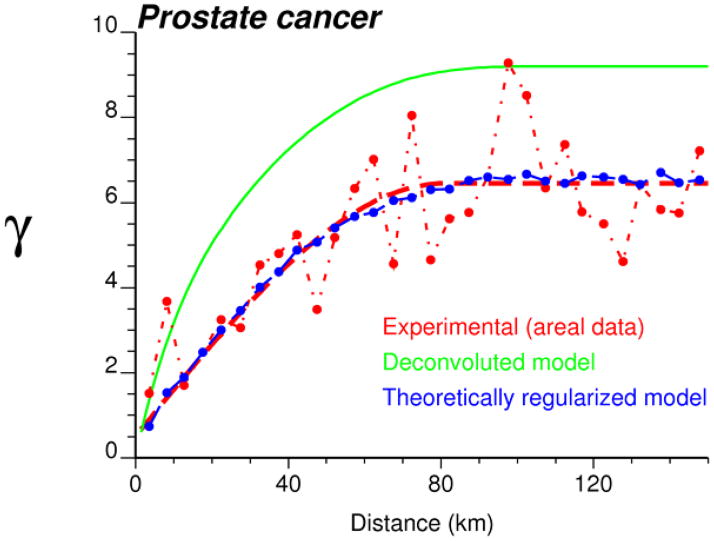
An important step in any geostatistical study is the estimation and modelling of the semivariogram which describes how the attribute under study varies in space. Figure 3 (dashed curve) shows the experimental semivariogram computed from ZIP code-level rates using the population-weighted estimator (equation 5). Since the spatial variability does not change with the direction, an omni directional semivariogram was computed and spherical model with a range of 81 km was fitted using least-square regression. This model was then deconvoluted using the iterative procedure described in Goovaerts (2008) and, as expected, the point-support model (solid curve) has a higher sill since the point process has a larger variance than its aggregated form. Its regularization (dotted line) yields a semivariogram model that is close to the one fitted to experimental values, which validates the consistency of the deconvolution.

Fig. 3.

Semivariogram of the risk of late-stage diagnosis computed from ZIP code-level rate data (dashed curve) using the population-weighted estimator (Equation 3), and the results of its deconvolution (top solid curve). The regularization of the point-support model yields a curve (dotted line) that is very close to the experimental one.

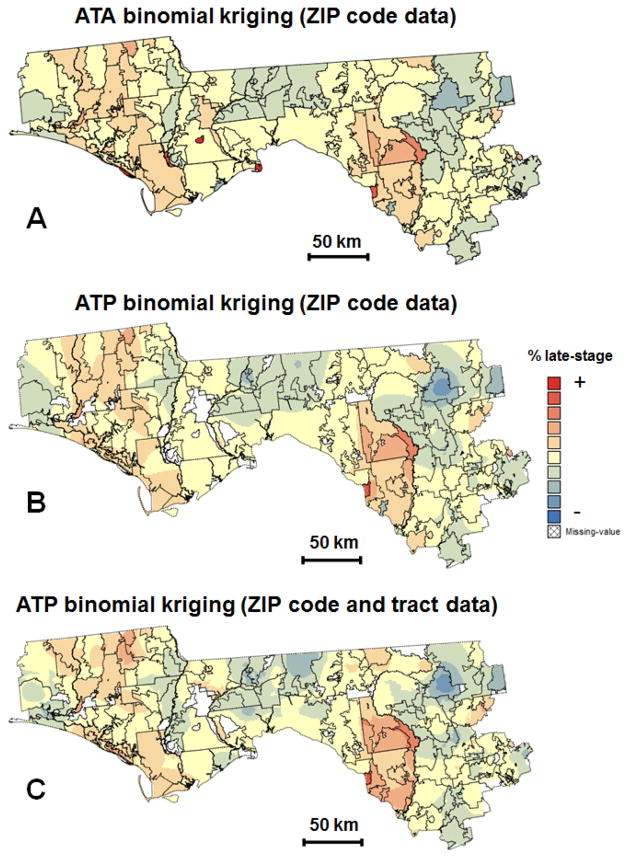
The deconvoluted model was used to estimate the risk of late-stage diagnosis at the ZIP code-level (ATA kriging) and to map the spatial distribution of that risk within the region (ATP kriging) using either ZIP code and census tract data (Fig. 4C) or only ZIP code data (Fig. 4B). In all cases, the geographical units were discretized using a regular grid with a spacing of 2km which is also used as interpolation grid for ATP kriging. The K′ neighbors in equations (2) and (6) are here defined as ZIP codes sharing a common border or vertex with the unit v_α′ (1-st order queen adjacencies). The map of ZIP code-level estimates (Fig. 4A) reveals two zones of high risk of late-stage diagnosis which stretch NS and correspond to the clusters of counties with higher percentage of late-stage diagnosis detected on Fig 2A. Interestingly, the ZIP codes with the highest percentages of late-stage diagnosis in Fig. 2B do not stand out after noise filtering using binomial kriging (Fig. 4A), which indicates that these rates were unreliable and likely based on a few cases. This illustrates a common pitfall of choropleth maps where unwarranted attention is devoted to a few oversized geographical units located in low population density areas.

Fig. 4.

Choropleth maps (ZIP code-level) and isopleth maps of the percentage of late-stage prostate cancer diagnosis estimated bybinomial kriging using: ZIP code-level rates (A,B) or ZIP code and census tract-level rates (C). All maps share the same legend that is not documented for confidentiality reasons.

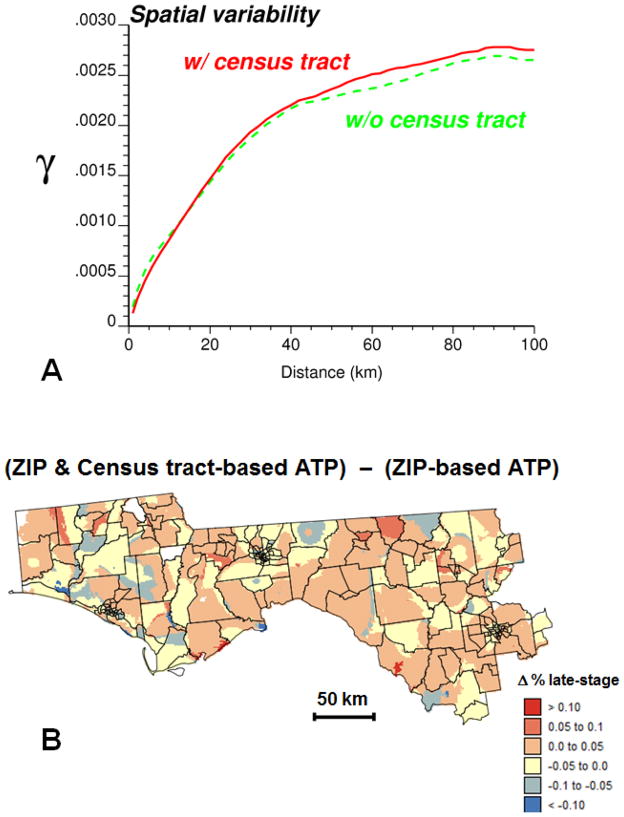
Area-to-point kriging allows the mapping of the risk of late-stage diagnosis across arbitrary ZIP code boundaries and increases the amount of details in the map (Figs. 4B–C). The impact of incorporating census tract data on the spatial variability of the isopleth map was explored using the semivariogram (Fig. 5A). The cross-over of the two curves indicates that this impact varies with the spatial scale. Whereas the map based on census tract and ZIP code data is globally more variable (i.e. higher sill of the semivariogram), the variability at distances shorter than 15 km is smaller than in the map created using only ZIP code data. The median extent of the census tracts in these 25 counties is approximately 17 km assuming a square shape. Thus, this greater spatial continuity at short distances is the direct result of the search strategy: the same census tract rate is used for interpolating all grid nodes within that tract.

Fig. 5.

Impact of incorporating census tract data into ATP kriging: (A) semivariograms of estimates based on ZIP code-level rates (dashed curve) or ZIP code and census tract-level rates (solid curve), (B) differences between estimates obtained with and without census tract-level rates.

Differences between the two sets of ATP kriging estimates are mapped in Fig. 5B, overlaid by the census tract boundaries. Positive differences are balanced by negative differences, resulting in a mean difference that is close to zero. Several spatial features in this map bear similarities with the patterns displayed by the choropleth maps of original rates (Fig. 2B–C). To quantify this similarity each grid node was assigned the original rates of the census tract and ZIP code in which it lies. The difference between these two rates was then correlated with the difference between ATP kriging estimates at these same nodes. The strong rank correlation coefficient (r=0.618) indicates that incorporating census tract data influences the most the risk estimate wherever ZIP code and census tract-level rates differ the most.

In absence of reference values, one cannot state that one map of estimated risks is more accurate than the other. However, following Zimmerman and Fang (2011) one should expect the incorporation of additional information to lead to better predictions. In addition, the incorporation of census tract data reduces the kriging variancebyan average of 10% (Figs. 6B-C). As expected, the smallest kriging variances are obtained for ZIP code-level estimates (Fig. 6A) since predictions are always more accurate at the area-level compared to the point-level.

Fig. 6.

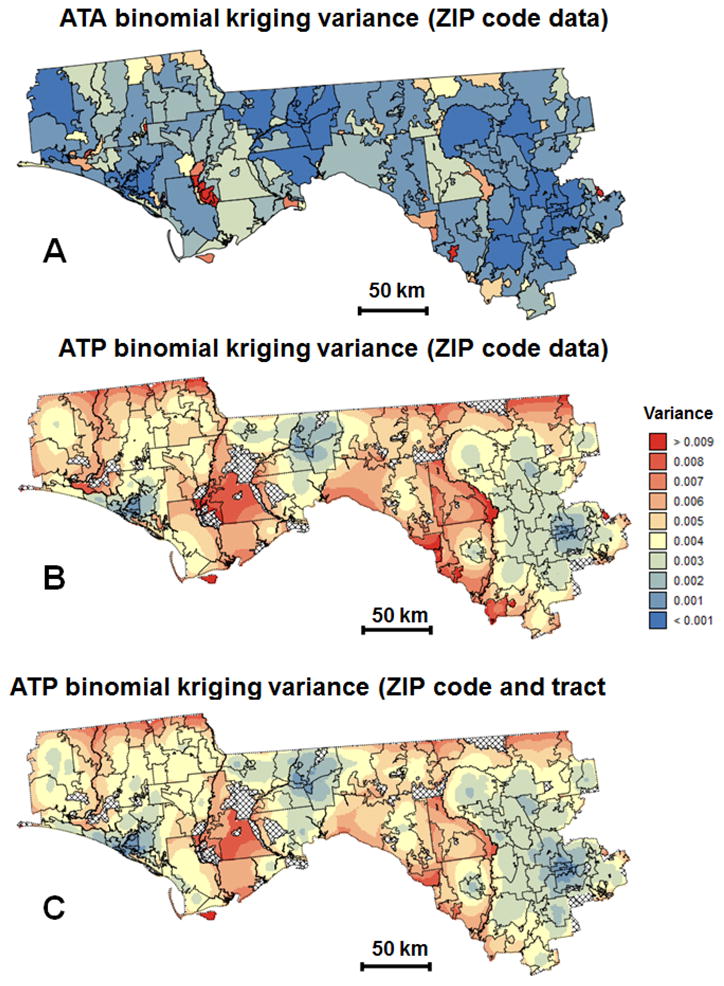
Maps of the binomial kriging variance corresponding to the choropleth and isopleth maps of Figure 4 that were createdusing: ZIP code-level rates (A,B) or ZIP code and census tract-level rates (C).

4. Conclusions

A common issue in spatial interpolation is the incorporation of data measured at various scales and over different spatial supports. This situation is frequently encountered in health studies where data are typically available over a wide range of scales, spanning from individual-level to different levels of aggregation. In particular this paper focused on the case where individual-level data are assigned to different types of geographical unit based on the success of the geocoding and the need to protect patient privacy. The objective was to combine both sources of information and create maps where disease rates vary continuously in space, reducing the visual bias associated with the interpretation of choropleth maps.

The analysis of prostate cancer data in Florida showed that incomplete geocoding is a widespread problem, in particular for cases diagnosed several decades ago and in rural communities. For example, in 1981 one fifth of cases were not geocoded and this percentage doubled in non-metropolitan counties. The allocation of these cases to ZIP codes, combined with the randomization of geocodes conducted by the cancer registry, created two sets of geographical units that can potentially lead to different conclusions when interpreted separately and without proper handling of the small number problem.

Geostatistics provides a framework to model the spatial correlation among health outcomes measured over geographic units of irregular size and population density, and to compute noise-free risk estimates over the same units or at much finer scales. A measure of the variance of prediction errors is also available to identify large and sparsely populated areas where risk estimates are less reliable. The noise-filtering accomplished by binomial kriging generated risk maps with a regional pattern that is closer to the one displayed by the more reliable county-level rates than by the original ZIP code-level rates. Incorporation of census tract information decreased the kriging variance and the within-tract spatial variability while increasing the global variability. The impact of using the two sets of rates was particularly marked wherever they differed the most. The greater accuracy of the risk maps produced by the proposed methodology will need to be confirmed by future simulation studies.