Abstract
This paper studies the Rayleigh-Plateau instability for co-flowing immiscible aqueous polymer solutions in a microfluidic channel. Careful vibration-free experiments with controlled actuation of the flow allowed direct measurement of the growth rate of this instability. Experiments for the well-known aqueous two phase system (ATPS, or aqueous biphasic systems) of dextran and polyethylene glycol solutions exhibited a growth rate of 1 s−1, which was more than an order of magnitude slower than an analogous experiment with two immiscible Newtonian fluids with viscosities and interfacial tension that closely matched the ATPS experiment. Viscoelastic effects and adhesion to the walls were ruled out as explanations for the observed behavior. The results are remarkable because all current theory suggests that such dilute polymer solutions should break up faster, not slower, than the analogous Newtonian case. Microfluidic uses of aqueous two phase systems include separation of labile biomolecules but have hitherto be limited because of the difficulty in making droplets. The results of this work teach how to design devices for biological microfluidic ATPS platforms.
INTRODUCTION
This paper describes the remarkable features of breakup into droplets, and lack of this breakup, of phase-separating polymer solutions. Cylindrical jets of one fluid inside another fluid are unstable and break up into droplets, as one can easily verify at the kitchen sink by running a thin liquid jet from the faucet. This fluid instability was first described by Plateau and Rayleigh,1, 2, 3 and there is a rich body of literature on the subject.4 Particularly relevant for this work is the breakup at low Reynolds number5 and the breakup of a jet that is confined by nearby walls.6, 7, 8, 9, 10 The understanding that emerges from the detailed analysis of these different cases is the following: perturbations of wavelength longer than the circumference of the jet grow with time (or distance traveled by the jet). The growth rate typically has a maximum for a certain wavelength, and except for the purely viscous case, decays to zero as the wavelength goes to infinity. Linear stability analysis of a thread of radius yields, for all these situations of varying complexity, dispersion relations that give the growth rate ω as a function of the perturbation wavenumber k, normalized on a characteristic time for small Reynolds-number flows.
Many biologically relevant fluids are non-Newtonian. By and large, complex rheology does not markedly change the linear instability on the thread, but it becomes important as the time scale of the flow approaches the relaxation time in the fluid just before pinch-off of droplets. In other words, viscoelasticity of a thread increases the growth rate slightly11 in the linear (small perturbation) regime, while non-linear terms that dominate when the perturbation has become large, slow down the growth, even suppressing satellite droplet formation and, characteristically, resulting in the longtime survival of thin threads that connect large droplets, much like water droplets on the thread of a spider web.4 More important is the fact that the threads under axial tension are stable.12 Unrelaxed axial tension (hereafter: tension) strongly stabilizes a jet for as long as the tension is larger than the capillary pressure in the thread, but after the tension has relaxed the instability kicks in, such that the overall effect is a delay in the onset of instability, not a slow down of the growth.
Aqueous two-phase systems (ATPS) constitute an especially relevant class of fluids for biological microfluidic applications.13, 14 Beijerinck15 showed over a century ago that solutions of starch and agar in water form two phases, and many other combinations of incompatible salt or polymer solutions have been found since. The discovery that many labile biomolecules prefer one aqueous phase over the other allows separation of such molecules without denaturation.16, 17 Use of these fluids in droplet microfluidics, in spite of their promise in biochemically relevant separations, has lagged significantly behind the use of aqueous droplets of biological materials surrounded by simpler oils and organic solvents.18, 19 One of the reasons is that controlled and reliable droplet formation has turned out to be difficult. Successful droplet formation in ATPS has, invariably, required external forcing, either mechanically as demonstrated recently by us20, 21 and others22 or by electrohydrodynamical actuation.23, 24 In other words, relying on the spontaneous formation of monodisperse droplets that is observed in oil/water microfluidic applications fails for aqueous two phase systems. Rather, we and others have observed either threads that survived indefinitely inside the channel without ever breaking up or more erratic droplet formation far downstream. Both are undesired flow behavior for droplet microfluidics.
The aim of this work is to quantify the growth rate of ATPS threads and to determine why they can survive without breaking up. On the one hand, we seek to characterize the instability in order to produce better droplet streams. On the other hand, the instability is markedly different from previous studies, and the experiments will guide further theoretical work. We first discuss flow of an analogous Newtonian system and then replace the Newtonian fluids, stepwise, with the aqueous polymer solutions, which by-and-large confirms existing knowledge. We then describe flow focussing of the well-known ATPS of dextran and polyethylene glycol solutions, and we quantify the break-up rate, which is much smaller than that of the equivalent Newtonian case. This is remarkable, because all current theory predicts that the growth rate should be larger. We also find that much more vigorous forcing is required to enhance break-up, compared to the Newtonian case. Finally, we show that eventually gravity becomes important. Even at the tiny density differences of ATPS, the thread sinks, touches the walls, and becomes stable indefinitely.
EXPERIMENTAL
Fluids used in the experiments
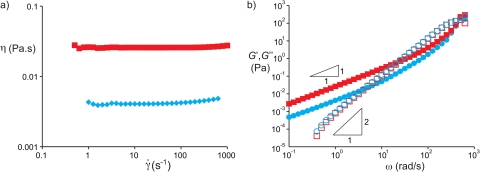
A dextran (dex) solution, 10% w/w (average molar mass 500 kg/mol, Aldrich) and a polyethylene glycol (PEG) solution, 7% w/w (average molar mass 10 kg/mol, Sigma) were prepared by dissolving the polymers in water using ultrasonication. Before injecting the solutions in the microfluidic devices, the solutions were filtered using filters having 0.45 μm pores. The interfacial tension of an ATPS is typically very low compared to the interfacial tension of an oil-water interface. For PEG and dextran, values typically range from several tens of for short polymers at low concentrations25 to several hundreds of for long polymers at high concentrations.26, 27, 28 For our system, the interfacial tension is at 25 °C, and almost independent of temperature in the range between 4 °C and 40 °C.26 The densities of the fluids were and . We characterized the rheological properties of the solutions29 using a rheometer with Couette geometry (TA Instruments AR-G2) at a temperature of 26 °C. The steady-state shear viscosities for the PEG and dextran solution were 4.4 mPas and 21.4 mPas, respectively, measured for shear rates in the range 1–100 s−1 as shown in Fig. 1a. The storage modulus and loss modulus are plotted in Fig. 1b for both solutions. From the crossover of and , we estimate relaxation times and .
Figure 1.
Rheological properties of the two aqueous polymer solutions: 10% w/w dextran in water (red squares) and 7% w/w polyethylene glycol in water (blue diamonds). (a) Steady shear viscosity versus shear rate. (b) Storage and loss moduli measured in small amplitude oscillatory shear.
As Newtonian analogs of the dextran and PEG solutions, we used a water/glycerol mixture with a viscosity of 22 mPas and pure hexadecane, using Tween 20 and Span 80 as surfactants to bring the interfacial tension down to closely match the value of the interfacial tension of the ATPS.30 The interfacial tension in such systems comprising a surfactant and a co-surfactant can be much lower compared to systems without a co-surfactant. Similar fluids and surfactants have previously been used by Guillot and co-workers6, 7, 8 to study the Rayleigh-Plateau instability of a confined thread of water in oil. High surfactant concentrations ensure that the characteristic time of diffusion near the interface, t, is small compared to the time scale of the breakup process. Estimating the diffusional distance, l, from the ratio of the interfacial concentration, Γ, and the bulk concentration, c, we find . For Span 80, the diffusion coefficient,31, the interfacial concentration,32, and the bulk concentration, , such that the diffusion time is of the order of , which is much shorter than the time to breakup. This explains why dynamic effects that occur at dilute () surfactant concentrations33 do not play a significant role in the breakup dynamics.
Chip fabrication and operation
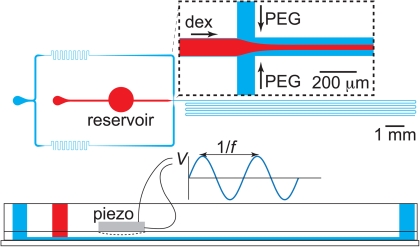
Fabrication of our microfluidic device was done using soft lithography. In brief, a 4-in. silicon wafer was patterned by exposing a layer of photo-resist (SU8-2050, Micro Resist Technology GmbH, Germany) to UV light through a high-resolution transparency mask containing the two-dimensional design of the microchannel network. This patterned wafer was subsequently used as a master to replicate the structure in poly(dimethylsiloxane) (PDMS). Our microfluidic devices were build up from two layers of PDMS that were prepared using a mixture of prepolymer and curing agent (Sylgard 184, Dow Corning) in a 10:1 ratio by weight. After curing the first 1 mm thin layer, a piezoelectric bending disc (0.5 in. diameter, Piezo Systems, Cambridge, MA) was placed on top of this layer and covered by a second thicker layer of PDMS. In this way, the piezo disc was embedded in the PDMS chip and separated from the fluid reservoir underneath it by an approximately 1 mm thin PDMS membrane, see Fig. 2. After curing this second layer, the PDMS structure was removed from the master. In the ATPS experiments, channels were sealed by irreversibly bonding a glass slide to the PDMS structure using an oxygen plasma treatment (Harrick PDC-002). In the oil-water experiments, sealing was done against a glass slide precoated with a thin layer of PDMS. After bonding, these devices were baked overnight at 120 °C to ensure hydrophobic recovery of PDMS.
Figure 2.
Top view sketch of the microfluidic device used to study the stability of fluid threads that form when coflowing the two immiscible streams. Both aqueous polymer solutions are injected through separate inlets and meet at a cross junction, after which they flow through a centimeters long channel. On top of the fluid reservoir that has been incorporated in the path between the inlet of the stream of dextran and the junction, a piezo-electric bending disc is positioned as shown in theside view in the bottom of the image. Applying a sinusoidal voltage with amplitude V and frequency f to the disc makes the disc periodically contract and relax, hereby pushing fluid in and out of the reservoir. In this way, the response of the jet to periodic perturbations was studied.
To study the interfacial dynamics under forcing, we actuated the piezo-electric bending disc by applying a sinusoidal voltage to the disc. As a result, the disc contracts and relaxes such that fluid is pushed out and pulled into the reservoir underneath the disc. The frequency of the forcing hence equals the frequency of the sinusoidal voltage. To verify that we can control the amplitude of perturbations applied to the thread as well, we measured how the voltage applied to the disc translates into movement inside the main channel. To this end, we placed a bubble inside the main channel that has a height and width of 100 μm and tracked the motion of this bubble under actuation of the piezo disc. We found that the displacement of the bubble is proportional to the amplitude of the AC voltage applied to the disc. Slight differences were observed in the proportionality constant when using different devices, which can be attributed to differences in thickness of the membrane between disc and fluid reservoir. Modulation of the thread velocity causes the modulation of the thread radius,34 thus allowing a precise analysis of growth rates from controlled perturbations, of known amplitude and frequency, instead of uncontrolled noisy perturbations.
To prevent any disturbances, other than the intentional ones through the piezo disc, special care was taken in the design of the setup. In particular, we were unable to dampen pulsations from syringe pumps. All experiments were performed on vibration-free optical tables, using gravity to feed the fluids from containers of adjustable height. As a result, the flow rates could not be set in an experiment and were only measured by video analysis after the experiments.
RESULTS AND DISCUSSION
Thread break-up of using immiscible Newtonian fluids
We first measure the growth of perturbations using two immiscible Newtonian fluids, which is well understood, before we discuss what happens in ATPS systems. In these experiments, care was taken to closely match conditions and fluid properties to the ATPS system. Figure 3a shows an aqueous thread composed of a solution of glycerol and water, which is focused by a stream of hexadecane. This thread breaks up into droplets 2 mm downstream the focusing section, or, equivalently, after 0.44 s. Before comparing this breakup time to that observed in ATPS systems in Sec. 3C, we first compare this value with the theoretical prediction of the growth rate in the Rayleigh-Plateau instability for confined threads in microchannels by Guillot et al.6 For a thread of radius and viscosity flowing through a cylindrical channel of radius R and focused by a stream of viscosity , the rate ω at which disturbances grow equals
| (1) |
In this equation, k is the dimensionless wavenumber of the perturbation, x is the dimensionless thread radius defined as is the viscosity ratio defined as and the function is equal to . Substituting the values of the fluid properties (), together with the values for the radii of the thread () and the channel (, x = 0.35), the dispersion relation (Eq. 1) predicts a maximum growth rate of for the tread shown in Fig. 3a. Assuming that perturbations at the entrance initially are of nanometer size and perturb the radius as until , we predict the break up at , clearly of the same order of magnitude as the experimentally observed value of t = 0.44 s.
Figure 3.
(a) Without forcing, a non-viscoelastic aqueous thread focused by an immiscible non-viscoelastic oil phase (hexadecane) breaks up into droplets 2 mm downstream of the cross junction in the channel with a square cross section of . This breakup length corresponds well with the theoretical prediction for a confined thread that has an undisturbed radius and flows at a velocity of ). Fluid properties: . (b) The same experiment with the piezo-electric bending disc operating at 100 mV.
We studied the stability of the thread for different dimensionless thread radii x by moving the feed container of the water/glycerol up and down. Thinner jets break up earlier and become even absolutely unstable (i.e., they immediately break up at the junction, as opposed to convectively unstable jets that are convected away while the perturbation grows), all in a good agreement with the analysis of confined Newtonian fluids.
The thread breakup in Fig. 3a occurred without applying external forcing. Figure 3b shows what happened when we applied a voltage of 100 mV to the piezo-electric disc. The focussing thread moved visibly in an oscillatory manner with a small amplitude of several micrometers. Note that the voltage is much smaller than the maximum voltage of 180 V. Nevertheless, this small disturbance in the thread velocity was sufficient to reduce the breakup time to less than 0.1 s such that droplets released at the junction as shown in Fig. 3b.
Strong viscoelasticity can have a marked influence on droplet formation. We measured the effect of viscoelasticity of each of the ATPS working fluids in combination with a Newtonian fluid. We both measured a thread of the dextran solution coflowing with hexadecane (), and with a thread of hexadecane surrounded by a PEG solution (). When PEG was the outer solution, we observed a little change with respect to the fully Newtonian case, and we observed direct droplet formation at the junction for small hexadecane flow rates. When a viscoelastic dextran thread was coflowing with hexadecane, we also observed break up directly at the junction, in agreement with recent reports that dripping at the junction is more prominent in viscoelastic flows.35 Also, we did not observe delayed dripping or slow necking that is such a distinctive feature of tension in the forming thread.36 The absence of these directly observable indicators of viscoelasticity leads us to conclude that for our ATPS fluids, the build up of tension in the thread is small relative to the capillary pressure.
Rayleigh-Plateau instability of the dextran-PEG system
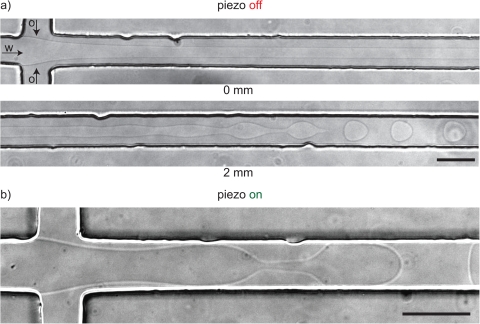
We now consider an experiment with the two aqueous solutions of dextran and PEG, as depicted in Fig. 4. A thread of dextran solution of radius is focussed in a microchannel of cross section , in the coflowing PEG solution at a velocity U = 5 mm/s. This is essentially the same experiment as the one we reported for water/glycerol and hexadecane in Fig. 3: the same (steady-shear) viscosities, similar interfacial tension, similar flow rates, and the same channel geometry. The difference is striking: ATPS threads did not break up at a distance comparable to the 2 mm observed in the analogous Newtonian case. The thread in this experiment does break up, erratically, as can be seen from the rough droplets in the channel at the bottom of the micrograph in Fig. 4a, after about 40 mm. It hence takes roughly 20 times as long as the Newtonian equivalent.
Figure 4.
(a) Without forcing, threads of dextran in PEG are stable over significant lengths, which exceed the theoretically predicted break up lengths by an order of magnitude. Droplets are visible in the bottom right of the micrograph as the channel meanders as indicated in Fig. 2. (b) Cross sectional view of the channel taken 2 mm downstream of the cross junction showing that the thread is centered and does not touch the walls.
We first rule out that the long delay of thread break-up is caused by sticking to the wall. When threads do stick to the wall, they are much more stable.37 To verify whether the thread touches the walls, we imaged the cross section of the channel using a confocal microscope by stacking images taken at different focal planes. We hereby used derivatives of PEG-rhodamine-B and dex-fluorescein to both label the thread and the surrounding fluid and recorded their fluorescence simultaneously. For the thread shown in Fig. 4, we found that it flows through the center of the channel and neither touches the top nor the bottom as evident from the inset. For the experiment described here, we rule out sticking of the thread to the wall as a stabilizing factor.
Another possible explanation for the enhanced stability would be the build up of elongational stresses during focussing of the thread. As we shall demonstrate below, the enhanced stability is not due to such stresses but is related to the lower growth rate of ATPS systems compared to oil/water systems.
Forced actuation of an ATPS thread
To better understand the observed stability for the ATPS threads, we study the evolution of the perturbations on the surface of the threads. Without applying any external forcing, the disturbances on the interface are not well defined leading to the break up of droplets of different sizes as shown in Fig. 4. Applying a mechanical forcing to the thread such that the fastest growing wavenumber is excited leads to perturbations on the interface with a well defined shape and wavelength that allows the measurement of growth rates. Before we show measured values of growth rates, we first discuss the effect of mechanical forcing of the thread. Fig. 5a shows four frames during one period of a 100-fold more forceful actuation than that in Fig. 3b. Clearly, the liquid-liquid interface moves in and out of the junction over considerable length. Fig. 5b shows the evolution of the thread downstream of the junction. In the first image, it is clear that the thread buckles a bit, similar in appearance to the buckling observed in expanding channels,38 and such an overdamped response is not uncommon for threads with strong flow-modulation.34
Figure 5.
(a) Actuating the piezo-electric disc using an AC voltage (f = 54 Hz, V = 12.5 V) results in dextran solution being pushed out and pulled into the fluid reservoir underneath the disc, which introduces perturbations on the interface of the thread. (b) Perturbations initially dampen and subsequently grow as shown in the series of micrographs taken at different distances from the inlet. (.)
In the first millimeter, the buckled thread straightens out and perturbations do not grow. We show now that this is due to tension in the thread. The tension directly at the junction can be estimated as the product of the extensional viscosity and the extension rate , where we estimate , based on the observation that the thread thins from w to r over a length of order w inside the junction. We were unable to measure the extensional viscosity, which may well be 1000-fold the steady-shear value, leading to a tension at the junction on the order of 100 Pa. This tension relaxes as . Growth of perturbations remains suppressed until , where the cross-over point is given by
| (2) |
As the extensional viscosity only appears in the logarithm of a large number, it is not important to know the value very precisely. For typical experiments, we find that is of the order of a millimeter. From the full dispersion relation of Ref. 12, we find that the transition from one regime to the next is quite abrupt, so we make little error by approximating that the upstream of , the growth of perturbations is essentially suppressed, whereas for distances downstream larger than , growth is unhindered by tension.
We now discuss the growth rate as determined from Fig. 5b. We measured the amplitude of the perturbation with t = z/U from the distance from the junction and U the centerline velocity. The amplitude increased exponentially with time over the range in which was larger than one pixel and small enough do not exhibit the bead-string non-linear effects. From images recorded between 3 mm and 18 mm from the junction, the growth rate was directly calculated as . We compare this measured growth rate with the theoretical prediction based on Eq. 1, . The difference is almost two orders of magnitude and cannot be explained by experimental error. Elastic tension in the line cannot explain the discrepancy between the theoretical value and the observed one. Indeed, previous account of the breakup of a viscoelastic jet in a Newtonian fluid shows that the growth rate is as predicted by linear theory after an initial delay.39 We did observe the same delay for our ATPS system. Strikingly, theory consistently predicts a small increase in the growth rate,4 whereas we observe the opposite.
One possible explanation for the observed slow growth is the thickness of the interface. Recent computational studies of free-boundary problems have proposed phase-field equations with diffuse interface models, based on the theory that goes back to van der Waals and Cahn and Hilliard.40, 41, 42 For computational efficiency, numerical computations introduce a mesoscale interface thickness that is much larger than realistic for common fluid-fluid interfaces. The thicker interface invariably results in slower growth of interfacial instabilities, compared with sharp interface limits, and recent numerical schemes correct for this.43, 44 Here, however, we know that the diffuse interface of an ATPS is much larger than that of an oil/water interface, at least of the order of the radius of gyration of the polymers, and this thick diffuse interface may explain the slow growth. Such an explanation has the advantage of explaining the lower growth rate, in agreement with the experiments, not a slightly higher one. It also agrees with the observation that the dextran thread readily breaks in hexadecane, where the interface will be sharp, but not in an aqueous PEG solution, where the interface will be diffuse. However, this hypothesis remains untested and is offered here only as a tentative explanation for the observations.
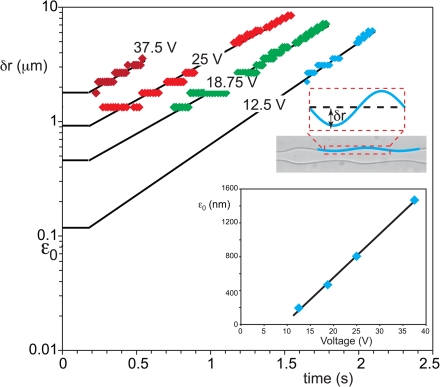
We now describe the effect of actuation amplitude on the growth. The amplitude in Fig. 5 was 12.5 V, and the forced buckling died out under tension before it could grow. The decay of the perturbation occurs on a viscous time scale,34 which we estimate as , where the wavelength is based on the thread velocity U and actuation frequency f as (U/f). This actual decay time, by this estimate, is on the order of several microseconds for our experiments and increases with increasing voltage. The decay time for tension, however, is longer, on the order of 10 or 100 ms. In other words, provided the perturbations are small, they die out before they can grow. Figure 6a shows the amplitude of perturbations on the interface obtained by taking pictures at different distances from the inlets and measuring the amplitude as shown on the inset. Increasing the amplitude V of the voltage applied to the piezo disc yields larger perturbations at the mixing section such that the thread breaks closer to the inlet. Importantly, the growth rate is independent of voltage. Voltages smaller than those used in Fig. 5 moved the break-up further downstream by only 2–3 mm, indicating that the actuation is dissipated before the tension has relaxed. For higher voltages on the piezo-electric bending disc, however, the break-up occurs faster, but this is only due to a higher initial disturbance, not due to a faster growth. The inset in Fig. 6 shows how the initial amplitude (obtained by extrapolating the growth curve to , i.e., to the end of the region under tension) increases linearly with applied voltage above a threshold value and has a minimum value of several tens of nanometers below that. It is striking that this length agrees with typical thicknesses of ATPS interfaces.45 Clearly, provided that the amplitude at the junction is large enough, the perturbations can outlive the viscous decay while the thread is under tension. It is this regime that is most useful for the production of monodisperse droplets.
Figure 6.
Amplitude of perturbations on the interface as a function of flow time for different actuation amplitudes. The lines are fitted to the experiments and are matched to horizontal lines that represent the zero-growth under tension immediately after the junction (). Inset: initial perturbation amplitude as a function of the amplitude of the voltage applied to the piezo-electric disc. (.)
Finally, downstream of the linear growth range, we find the typical beads-on-string pattern for viscoelastic fluids with the slow ultimate stage of breakup, which happens in Fig. 5b 28 mm downstream of the junction.
Long-time fate of the thread: Gravitational effects
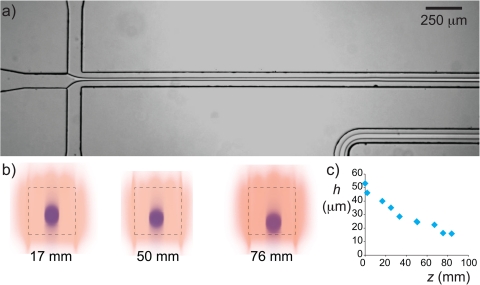
The growth rates recorded in Figs. 56 were measured under conditions that the thread did not touch the walls before break-up, as verified by confocal images similar to that in Fig. 4b. In our ATPS, the density difference between the two dilute aqueous polymer solutions is small, , such that the thread that was initially in the center of the channel does not sink quickly to the bottom of the channel. However, especially without actuation, the break-up time is so long that it competes with the settling time. In Fig. 7a, we show a micrograph of such a thread that touches the bottom wall far downstream of the cross junction. This stabilizes the thread, which runs from flow-focusing junction through the 160 mm long microfluidic channel all the way to the exit without breaking. We measured how fast the thread settles by taking confocal scans at different distances z from the inlet as shown in Fig. 7b. From those scans, we could measure the height of the center of the thread h, which we plot as a function of the distance z in Fig. 7c. The thread slowly settles and touches the bottom roughly z = 76 mm downstream of the inlet. The exact location where the thread touches the bottom depends on the thickness of the thread, as does the moment of breakup. For relatively thick threads (), we found that the thread always settled quicker than it breaks up, whereas for thin threads break up occurred before the thread touches the wall. From a practical point of view, the use of a mechanical actuator such as the piezo disc used in this work reduces the breakup length such that threads that would otherwise touch the walls can be broken up into droplets.
Figure 7.
(a) Micrograph showing a stable thread of dextran in PEG. The slightly larger density of the dextran solution results in settling of the thread as shown in the confocal scans in (b), which were taken at different distances downstream of the cross junction. The plot of the center of the thread h as a function of the distance away from the inlet shows that the thread sticks to the bottom roughly 76 mm downstream of the mixing section.
CONCLUSIONS
We have shown that aqueous two-phase systems have much slower interface dynamics in comparison with Newtonian oil/water mixtures. Careful vibration-free experiments with controlled actuation of the flow into a microfluidic flow focussing device allowed direct measurement of the growth of the Rayleigh-Plateau instability. Our experiments show that the growth rate of perturbations of a confined thread is two orders of magnitude smaller than predicted by theory. Experiments with all-Newtonian fluids of similar viscosity and interfacial tension show that this is not caused by fluid properties. The large discrepancy between theory and experiment, therefore, can only be explained by interfacial properties. Indeed, the interface of an ATPS is much more complex than the interface between oil and water and hence has a dynamic response on its own account that will require further theoretical analysis, for which the present work gives crucial experimental data. Comparison with experiments where a viscoelastic jet flows inside a hexadecane jet shows that viscoelasticity of the fluids also does not account for this difference, but viscoelasticity does explain the initial dampening of perturbations. From a more practical point of view, the results of this work are useful in the design of microfluidic devices that use parallel streams or droplet flows to exploit the separation possibilities of aqueous two-phase systems.
ACKNOWLEDGMENTS
The authors gratefully acknowledge NWO, NanoNed, and COST Action D43 for financial support and Piet Droppert and Ben Norder for technical assistance. We also thank John van der Schaaf, Stephen Picken, Hoang Ahn Duong, and Pouyan Boukany for fruitful discussions.
References
- Plateau J., Statique Expérimentale et Théoretique des Liquides Soumis aux Seules Forces Moléculaires (Gautier-Villars, Paris, 1873). [Google Scholar]
- Rayleigh L., Proc. R. Soc. London 29, 71 (1879). 10.1098/rspl.1879.0015 [DOI] [Google Scholar]
- Rayleigh L., Philos. Mag. 34, 145 (1892). [Google Scholar]
- Eggers J. and Villermaux E., Rep. Prog. Phys. 71, 036601 (2008). 10.1088/0034-4885/71/3/036601 [DOI] [Google Scholar]
- Tomotika S., Proc. R. Soc. London, Ser. A 150, 322 (1935). 10.1098/rspa.1935.0104 [DOI] [Google Scholar]
- Guillot P., Colin A., Utada A. S., and Ajdari A., Phys. Rev. Lett. 99, 104502 (2007). 10.1103/PhysRevLett.99.104502 [DOI] [PubMed] [Google Scholar]
- Guillot P., Colin A., and Ajdari A., Phys. Rev. E 78, 016307 (2008). 10.1103/PhysRevE.78.016307 [DOI] [PubMed] [Google Scholar]
- Herrada M. A., Gañán-Calvo A. M., and Guillot P., Phys. Rev. E 78, 046312 (2008). 10.1103/PhysRevE.78.046312 [DOI] [PubMed] [Google Scholar]
- Humphry K. J., Ajdari A., Fernández-Nieves A., Stone H. A., and Weitz D. A., Phys. Rev. E 79, 056310 (2009). 10.1103/PhysRevE.79.056310 [DOI] [PubMed] [Google Scholar]
- Son Y., Martys N. S., Hagedorn J. G., and Migler K. B., Macromolecules 36, 5825 (2003). 10.1021/ma0343986 [DOI] [Google Scholar]
- Goldin M., Yerushalmi J., Pfeffer R., and Shinnar R., J. Fluid Mech. 38, 689 (1969). 10.1017/S0022112069002540 [DOI] [Google Scholar]
- Goren S. L. and Gottlieb M., J. Fluid Mech. 120, 245 (1982). 10.1017/S0022112082002754 [DOI] [Google Scholar]
- Hardt S. and Hahn T., Lab Chip 12, 434 (2012). 10.1039/c1lc20569b [DOI] [PubMed] [Google Scholar]
- Frampton J. P., Lai D., Sriram H., and Takayama S., Biomed. Microdevices 13, 1043 (2011). 10.1007/s10544-011-9574-y [DOI] [PubMed] [Google Scholar]
- Beijerinck M. W., Zentralbl. Bakteriol. 2, 698 (1896). [Google Scholar]
- Albertsson P. A., Nature(London) 177, 771 (1956). 10.1038/177771a0 [DOI] [PubMed] [Google Scholar]
- Albertsson P. A., Partitioning of Cell Particles and Macromolecules (Wiley, New York, 1986). [Google Scholar]
- Vijayakumar K., Gulati S., deMello A. J., and Edel J. B., Chem. Sci. 1, 447 (2010). 10.1039/c0sc00229a [DOI] [Google Scholar]
- Yasukawa M., Kamio E., and Ono T., ChemPhysChem 12, 263 (2011). 10.1002/cphc.201000905 [DOI] [PubMed] [Google Scholar]
- Ziemecka I., van Steijn V., Koper G. J. M., Rosso M., Brizard A. M., van Esch J. H., and Kreutzer M. T., Lab Chip 11, 620 (2011). 10.1039/c0lc00375a [DOI] [PubMed] [Google Scholar]
- Ziemecka I., van Steijn V., Koper G. J. M., Kreutzer M. T., and van Esch J. H., Soft Matter 7, 9878 (2011). 10.1039/c1sm06517c [DOI] [Google Scholar]
- Lai D., Frampton J. P., Sriram H., and Takayama S., Lab Chip 11, 3551 (2011). 10.1039/c1lc20560a [DOI] [PubMed] [Google Scholar]
- Song Y. S., Choi Y. H., and Kim D. H., J. Chromatogr. A 1162, 180 (2007). 10.1016/j.chroma.2007.06.032 [DOI] [PubMed] [Google Scholar]
- Choi Y. H., Song Y. S., and Kim D. H., J. Chromatogr. A 1217, 3723 (2010). 10.1016/j.chroma.2010.04.015 [DOI] [PubMed] [Google Scholar]
- Ryden J. and Albertsson P. A., J. Colloid Interface Sci. 37, 219 (1971). 10.1016/0021-9797(71)90283-9 [DOI] [Google Scholar]
- Forciniti D., Hall C. K., and Kula M. R., J. Biotechnol. 16, 279 (1990). 10.1016/0168-1656(90)90042-A [DOI] [Google Scholar]
- Helfrich M. R., El-Kouedi M., Etherton M. R., and Keating C. D., Langmuir 21, 8478 (2005). 10.1021/la051220z [DOI] [PubMed] [Google Scholar]
- Liu Y., Lipowsky R., and Dimova R., Langmuir 28, 3831 (2012). 10.1021/la204757z [DOI] [PubMed] [Google Scholar]
- Larson R. G., The Structure and Rheology of Complex Fluids (Oxford University Press, USA, 1998). [Google Scholar]
- Hashimoto M., Garstecki P., Stone H. A., and Whitesides G. M., Soft Matter 4, 1403 (2008). 10.1039/b715867j [DOI] [PubMed] [Google Scholar]
- Campanelli J. R. and Wang X., J. Colloid Interface Sci. 213, 340 (1999). 10.1006/jcis.1999.6149 [DOI] [PubMed] [Google Scholar]
- Apenten R. K. O. and Zhu Q.-H., Food Hydrocolloids 10, 27 (1996). 10.1016/S0268-005X(96)80050-6 [DOI] [Google Scholar]
- Hansen S., Peters G. W. M., and Meijer H. E. H., J. Fluid Mech. 382, 331 (1999). 10.1017/S0022112098003991 [DOI] [Google Scholar]
- Bousfield D. W. and Denn M. M., Chem. Eng. Commun. 53, 61 (1987). 10.1080/00986448708911883 [DOI] [Google Scholar]
- Montanero J. M. and Ganan-Calvo A. M., J. Fluid Mech. 610, 249 (2008). 10.1017/S0022112008002681 [DOI] [Google Scholar]
- Arratia P. E., Gollub J. P., and Durian D. J., Phys. Rev. E 77, 036309 (2008). 10.1103/PhysRevE.77.036309 [DOI] [PubMed] [Google Scholar]
- Castro-Hernandez E., van Hoeve W., Lohse D., and Gordillo J. M., Lab Chip 11, 2023 (2011). 10.1039/c0lc00731e [DOI] [PubMed] [Google Scholar]
- Cubaud T., Jose B. M., and Darvishi S., Phys. Fluids 23, 042002 (2011). 10.1063/1.3573383 [DOI] [Google Scholar]
- Bousfield D. W., Keunings R., Marrucci G., and Denn M. M., J. Non-Newtonian Fluid Mech. 21, 79 (1986). 10.1016/0377-0257(86)80064-7 [DOI] [Google Scholar]
- Lowengrub J. and Truskinovsky L., Proc. R. Soc. London, Ser. A 454, 2617 (1998). 10.1098/rspa.1998.0273 [DOI] [Google Scholar]
- Lee H., Lowengrub J., and Goodman J., Phys. Fluids 14, 492 (2002). 10.1063/1.1425843 [DOI] [Google Scholar]
- Lee H., Lowengrub J., and Goodman J., Phys. Fluids 14, 514 (2002). 10.1063/1.1425844 [DOI] [Google Scholar]
- Folch R., Casademunt J., Hernandez-Machado A., and Ramirez-Piscina L., Phys. Rev. E 60, 1724 (1999). 10.1103/PhysRevE.60.1724 [DOI] [PubMed] [Google Scholar]
- Folch R., Casademunt J., Hernandez-Machado A., and Ramirez-Piscina L., Phys. Rev. E 60, 1734 (1999). 10.1103/PhysRevE.60.1734 [DOI] [PubMed] [Google Scholar]
- Lee S. H. S., Wang P., Yap S. K., Hatton T. A. and Khan S. A., Biomicrofluidics, 6, 022005 (2012). 10.1063/1.3694841 [DOI] [Google Scholar]