Performance of the M11-L density functional for bandgaps and lattice constants of unary and binary semiconductors

Abstract

The recently developed SOGGA11 and M11-L density functionals have been tested for the prediction of bandgaps and lattice constants by comparing to databases containing 31 bandgaps and 34 lattice constants. To make a comparative assessment we also test several other density functionals against the same databases; in particular, we test the local spin density approximation, PBE, PBEsol, SOGGA, TPSS, revTPSS, and M06-L local density functionals and the HSE screened-exchange hybrid nonlocal density functional; and for a subset of 13 lattice constants we also compare the mean errors to those of the AM05 and WC local density functionals and the HISS and HSEsol nonlocal density functionals. The tests show that, of the ten functionals tested against all 65 data, the SOGGA, PBEsol, and HSE functionals are the most accurate for lattice constants, whereas the HSE, M11-L, and M06-L density functionals are the most accurate for bandgaps. However, the SOGGA11 density functional is the most accurate generalized gradient approximation for bandgaps.

INTRODUCTION

Many years ago, semiconductors were defined as “rather poor conductors.”¹ But now they are recognized more positively as the materials at the heart of much modern technology. It is therefore essential to validate computational methodologies for materials design and evaluation in terms of their ability to predict the structural and electronic properties of semiconductors. The most central of these properties are lattice constants and bandgaps.

Bandgap is a critical property for understanding the optical and electrical properties of materials, for the design of semiconductor devices, and for the optimization of photocatalysis schemes. The accurate calculation of bandgaps is an active and important research area in solid-state physics and theoretical chemistry.^{2, 3, 4, 5} Although Kohn-Sham density functional theory (DFT) has been very successful in theoretical physics and quantum chemistry, local density functionals such as the local spin density approximation (LSDA) and generalized gradient approximations (GGAs) tend to underestimate bandgaps due to self-interaction errors. Self-interaction errors are also often largely responsible for the underestimation of chemical reaction barrier heights^{4, 6} and HOMO-LUMO gaps and for the overestimation of polarizabilities and hyperpolarizabilities of conjugated molecules. Hybrid functionals, which include a portion of nonlocal Hartree-Fock exchange, ameliorate the self-interaction problems, and they are much more accurate for bandgaps than the LSDA and GGAs.^{4, 7, 8} However, the computational cost for nonlocal exchange in solid-state physics calculations (or any calculations on spatially extended systems) is very high,^{4, 9, 10} and recently Heyd et al.^{4, 11, 12} developed a screened-exchange hybrid functional, called HSE, to ameliorate this problem.

Although on the one hand we want to develop the best density functionals regardless of their complexity and computational cost, the literature shows that in practice cost is still an important criterion for choosing a modeling method for applications to complex systems, and most computer programs for studying spatially extended systems such as solid-state materials either are restricted to local density functionals or are orders of magnitude more expensive when nonlocal functionals are employed. Therefore, there is great interest in testing and validating local functionals. Local functionals are those that depend on local properties such as electron density (the LSDA functionals), electron density and its reduced gradient (GGAs), or electron density, its reduced gradient, and the electronic local kinetic energy density (meta-GGAs). Local functionals do not include nonlocal Hartree-Fock exchange as required to fully eliminate self-interaction, nor do they include nonlocal correlation as required to model dispersion interactions between nonoverlapping subsystems. In the present study, we use databases of properties for 31 semiconductors to assess the performance of a large number of DFT functionals for lattice constants and bandgaps. The considered functionals include the nonlocal HSE (Refs. ^{4, 11, 12}) functional and nine local functionals: our recently proposed SOGGA11 (Ref. ¹³) and M11-L,¹⁴ their SOGGA (Ref. ¹⁵) and M06-L (Ref. ¹⁶) predecessors, and six other popular and high-performing functionals, in particular LSDA, PBE,¹⁷ PBEsol,^{18, 19} TPSS,²⁰ and the recent revTPSS.²¹ SOGGA11, SOGGA, PBE, and PBEsol are GGAs, and M11-L, M06-L, TPSS, and revTPSS are meta-GGAs.

Lattice constants are of key interest for solid-state applications and materials design. The performance for lattice constants of diverse solids of LSDA, five standard GGAs, one meta-GGA, and several unnamed variations of GGAs has been studied thoroughly by Haas et al.^{22, 23, 24} Their studies included five of the functionals studied here, and they ordered these functionals—from those that most underestimate lattice constants to those that most overestimate them—as LSDA, SOGGA, PBEsol, TPSS, and PBE.²² Their study did not include bandgaps, and here we study performance not only for lattice constants but also for bandgaps and a broad set of molecular properties with ten functionals including three very recent ones to obtain further perspective.

THEORY

Exchange-correlation functionals

The nine local density functionals studied here include a representative sampling of the most popular and most successful of the functionals in current use in solid-state physics and chemistry. We also consider one nonlocal functional, namely HSE, because—although nonlocal—it is designed to be more practical than local functionals for extended systems (although it is still more expensive). The cost reduction is accomplished by making use of range separation for the interelectronic coulomb repulsion

$$\frac{1}{r_{12}}=\underset{\mathrm{SR}}{\underbrace{\frac{\mathrm{erfc}\left(\omega r_{12}\right)}{r_{12}}}}+\underset{\mathrm{LR}}{\underbrace{\frac{\mathrm{erf}\left(\omega r_{12}\right)}{r_{12}}}}$$ (1)

in the exchange term, and then including nonlocality only in the short-range (SR) part. Thus HSE may be called a screened-exchange hybrid functional. This strategy retains some of the accuracy advantages of a nonlocal functional while avoiding at the same time the computationally expensive treatment of long-range (LR) nonlocal exchange.

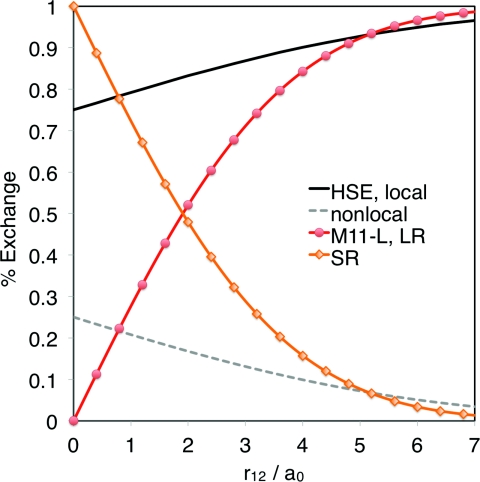
The local M11-L uses the range-separation of Eq. 1 but only at the local level. The M11-L exchange has a dual-range functional form that is composed of a meta-GGA functional with different parameters for SR and for LR. The differences between M11-L and HSE can be visualized by comparing the plot of the fraction of exchange as a function of the interelectronic distance r₁₂ for the two functionals, as in Figure 1.

Figure 1.

Range separation in the exchange functional: The black and grey curves are for the HSE screened-exchange hybrid (local is solid, nonlocal is dashed) and the red and orange curves are M11-L (LR is red with circles, SR is orange with diamonds).

Two of the GGA functionals studied here, namely SOGGA and PBEsol, were designed as specialized functionals, the former by imposing the correct second order coefficient (SO constraint) in the density gradient expansion and enforcing a tighter Lieb-Oxford bound while maintaining a simple functional form,¹⁵ and the latter by optimizing a parameter to solid-state lattice constants.^{18, 19} The SO constraint was also imposed on SOGGA11, which has a more flexible functional form that has been optimized to provide good across-the-board performance for chemical properties. The other considered functionals are the simple LSDA, which is widely used in solid-state calculations, the popular PBE GGA, and three meta-GGAs: TPSS, revTPSS (a modification of TPSS), and M06-L, which is a precursor (without range separation) of M11-L.

Lattice constants

Lattice constants are the distances between unit cells in a crystal lattice, and they are usually represented by three numbers a, b, and c, representing the distances in three directions of space. In this work, however, most semiconductors considered have simple isometric structures, such as diamond (A4), zincblende (B3), and rock salt (B1), that are completely specified by a single lattice constant, although we also consider a few wurtzite (B4) structures that require specifying two lattice constants. Lattice constants are usually measured and reported at room temperature; however in our database we used equilibrium values^{4, 22, 25, 26} obtained by removing the zero-point anharmonic expansion (ZPAE) contribution as described in Sec. 3A of this work; that is, the values correspond to experimentally based estimates of the geometry with the lowest Born–Oppenheimer electronic energy, including nuclear repulsion. In this way we can directly compare our calculated results with the experimental data, without having to estimate vibrational geometry shifts for each density functional.

Bandgaps

In discussing bandgaps, one should be very careful to distinguish optical bandgaps from fundamental bandgaps, as discussed elsewhere,^{27, 28} with the optical gap (the onset of optical absorption) being smaller by an amount equal to the exciton shift, which is often small in semiconductors. From a computational point of view, one often calculates neither the fundamental nor the optical gap, but rather the single-particle gap defined as the difference in the orbital energies of the highest occupied crystal orbital and the lowest unoccupied crystal orbital. Alternatively, one can attempt to calculate the optical gap by time-dependent density functional theory; these results can be quite different for general nonlocal functionals and molecular systems,²⁹ but in the macroscopic limit (which is the limit needed for the present study of solid-state semiconductors) and employing the adiabatic approximation for time-dependent density functional theory they are the same for local density functionals³⁰ and similar for the HSE density functional.⁵ Keeping these distinctions in mind so that we do not misinterpret the results, in the present article we follow the usual convention of comparing single-particle gaps from calculations to experimental optical gaps.

TEST SET AND COMPUTATIONAL DETAILS

The SLC34 and SBG31 databases and subsets

In the creation of the new databases we considered data from the SC/40 database by Heyd et al.⁴ and from the previously published³¹ DSBG9 database. SC/40 is an extensive database with bandgaps and lattice constants of 40 binary semiconductors, while DSBG9 is a smaller database of only 9 bandgaps. We trimmed the SC/40 database by deleting seven of the semiconductors for which there are no experimental values for either the lattice constant, the bandgap, or both and three semiconductors for which we had serious difficulties in obtaining converged self-consistent field solutions, even using a very high number of k points. This leaves 30 semiconductors, to which we added ZnO data^{32, 33} because of its importance in applications,^{34, 35, 36, 37, 38} and strong theoretical interest,^{39, 40, 41, 42, 43} for a total of 31 semiconductors. We then created two databases, SLC34 with 34 semiconductor lattice constants and SBG31 with 31 semiconductor bandgaps. Although both databases have data for the same 31 semiconductors, the lattice constant database has 34 data because there are two lattice constants each for the three semiconductors (GaN, InN, and ZnO) with wurtzite structures.

For a more detailed discussion and analysis of the results, we consider six subsets of the entire database. The first subset (S) is composed of semiconductors that have been widely used in previous studies; it is of particular interest for comparison of results with other published data. The second subset (D) is composed of difficult cases; in this subset are semiconductors for which LSDA and many popular GGA functionals are unable to predict a gap (the calculated gap is zero, incorrectly corresponding to a conductor). The semiconductors in the first two subsets are also included in one of the other four subsets, which are obtained by dividing the entire database into four nonoverlapping subsets organized according to the periodic table. The subset databases are identified as follows:

• S(13): thirteen semiconductors that have been widely used for testing density functionals: C, Si, Ge, SiC, BP, BAs, AlP, AlAs, β-GaN, GaP, GaAs, InP, InAs.

• D(6) and D(5): six lattice constants and five bandgaps for difficult semiconductors: Ge, GaSb, InN, InAs, InSb.

• G14(4): four unary semiconductors from group 14: C, Ge, Si, SiC.

• 2-16(6): six binary semiconductors from groups 2 and 16: MgS, MgSe, MgTe, BaS, BaSe, BaTe.

• 13-15(16) and 13-15(14): 16 lattice constants and 14 bandgaps for binary semiconductors from groups 13 and 15: BP, BAs, AlP, AlAs, AlSb, GaN, β-GaN, GaP, GaAs, GaSb, InN, InP, InAs, InSb.

• 12-16(8) and 12-16(7): eight lattice constants and seven bandgaps for binary semiconductors composed of a group 12 and an element from group 16: ZnO, ZnS, ZnSe, ZnTe, CdS, CdSe, CdTe.

For twelve of the lattice constants in S(13) we used the correction for ZPAE estimated by Hao et al., while the corrected experimental datum for InSb was taken from Schimka et al.²⁵ For the other semiconductors we corrected the data from the experimental references provided by Heyd et al.⁴ and the ZnO datum³² by estimating the ZPAE based on a statistical analysis of previous studies.^{22, 25, 26} We noticed that the value of the ZPAE correction for semiconductors with B3 structures is on average −0.010 Å (with the largest deviation being within 0.002 Å), and we applied this estimate of the correction to the remaining uncorrected experimental data of semiconductors with B3 structures. For the four remaining data with B1 structures we estimated from previous work an average ZPAE correction of −0.025 Å (with the largest deviation being within 0.010 Å), and we applied this to the uncorrected experimental data. The remaining three data are for B4 structures that have two lattice constants, and for these we estimate a B3-type correction of −0.010 Å for the smaller one, and a B1-type correction of −0.025 Å for the larger one; these ZPAE corrections are always smaller than 1% of the corresponding experimental lattice constants. The uncertainties in the equilibrium lattice constants due to the uncertainties in the estimated ZPAEs are small enough not to affect our conclusions.

For bandgaps there is much more agreement on the experimental data, and all the reference data were taken from Ref. 4, except for ZnO.³³

Software, basis sets, relativistic effects

All density functional calculations were carried out with the periodic-boundary-condition (PBC) methods⁴⁴ of a locally modified⁴⁵GAUSSIAN09 program,⁴⁶ using the ultrafine (99,590) Lebedev grid for density functional integrations. The calculated bandgaps were calculated at the optimized structures for each functional. Usually, we used 1000 k points, but in many cases we compared the results to calculations with 12 000 k points, and the results always agreed.

The basis sets and relativistic effective core potentials for the calculations SLC34 and SBG31 database were taken from the supporting information of Ref. 4. This involves using a modified 6-311G* basis (denoted m-6-311G* in Ref. 4) for lighter elements (B to S) and a small-core relativistic effective core potential with a polarized double zeta valence basis set (denoted m-cc-pVDZ-PP or m-Stuttgard-RSC-1997 in Ref. 4) for heavier elements (below the third period).

We will consider some additional databases in Sec. 4. For the calculations on those databases, we used the MG3S basis set⁴⁷ for main-group elements and the def2-TZVP basis set⁴⁸ for calculations that involve transition metals.

The convergence of the lattice constant results with respect to basis set size was carefully considered by Heyd et al.⁴ when they created the m-6-311G* basis, and we re-assessed it here by comparison of our results to those of more recent studies based on both Gaussians and plane waves. For this task we used the PBEsol functional and the S(13) subset as a representative enough combination for testing convergence. We found perfect agreement between our results and those obtained by Heyd et al.⁴ and more recently by Lucero et al.⁴⁹ These calculations all use the m-6-311G* Gaussian basis with periodic boundary conditions (G-PBC). Table 1 presents our results compared to those obtained by Haas et al.²² using the very accurate full-potential (linearized) augmented plane-wave and local orbitals [FP-(L)APW+lo] method, the results obtained by Schimka et al.²⁵ by using a plane-waves projector augmented wave (PW-PAW) method, and the results obtained by Hao et al.²⁶ by using a mix of Slater-type and numerical orbitals at the quadruple zeta plus quadruple polarization (STO+NO/QZQP) level; see references cited for the details of these methodologies and calculations.

Table 1.

Comparison of PBEsol results for the lattice constants of S(13) obtained with different numerical methods.

Solid	Expt.1	G-PBC2	FP-(L)APW+lo3	PW-PAW4	STO+NO/QZQP5
C	3.555	3.561	3.557	3.556	3.553
Si	5.422	5.442	5.438	5.436	5.432
Ge	5.644	5.692	5.684	5.674	5.679
SiC	4.348	4.380	4.360	4.359	4.356
BP	4.527	4.540	4.525	4.521	4.520
BAs	4.764	4.788	4.775	4.767	4.768
AlP	5.450	5.472	5.476	5.472	5.468
AlAs	5.649	5.682	5.681	5.683	5.676
β-GaN	4.523	4.519	4.502	4.494	4.499
GaP	5.441	5.468	5.447	5.438	5.439
GaAs	5.641	5.687	5.670	5.665	5.664
InP	5.858	5.891	5.890	5.882	5.882
InAs	6.048	6.099	6.098	6.094	6.089
MSE6		0.027	0.018	0.013	0.012
MUE6		0.028	0.021	0.019	0.017
Max |ɛ|7		0.051	0.050	0.046	0.041
Min |ɛ|7		0.004	0.002	0.001	0.002

¹The experimental results as corrected for ZPAE.

²Gaussian basis, periodic boundary conditions results obtained in this work, in agreement with similar results in Refs. ⁴ and ⁴⁹.

³Full-potential (linearized) augmented plane-wave and local orbitals results from Ref. 22.

⁴Plane-waves projector augmented wave results from Ref. 25.

⁵Slater-type and numerical orbitals at the quadruple zeta plus quadruple polarization level from Ref. 26.

⁶MSE and MUE denote mean signed error and mean unsigned error, respectively.

⁷Max |ɛ| and Min |ɛ| denote the largest unsigned error and the smallest unsigned error, respectively.

From the results presented in Table 1 we noticed that there is no general agreement between the methods, but the statistical parameters at the bottom of the table are similar. Although lattice constants obtained with a Gaussian basis are usually larger than those obtained with the other methods, the mean unsigned deviations all agree within 0.011 Å. According to these results, we can consider our results for mean unsigned errors to be accurate within a basis set uncertainty of about 0.011 Å, which is small enough that it will not affect our conclusions

Bandgaps are less sensitive to basis set size, and after a similar comparison of our results to those of Schimka et al.²⁵ we find agreement on both the signed and unsigned average errors of PBEsol and HSEsol within 0.06 eV between the two studies.

RESULTS

Lattice constants

Table 2 presents the results for the 34 lattice constants in SLC34. In all tables, the mean signed error is abbreviated MSE, and the mean unsigned error is abbreviated MUE. Functionals are listed in order of increasing MUE.

Table 2.

Lattice constants (Å) for SLC34.

Solid	Structure1	Expt.2	SOGGA	PBEsol	LSDA	HSE	revTPSS	M11-L	TPSS	M06-L	PBE	SOGGA11
C	A4	3.555	3.556	3.561	3.537	3.553	3.571	3.515	3.579	3.560	3.579	3.540
Si	A4	5.422	5.430	5.442	5.410	5.444	5.449	5.455	5.466	5.427	5.479	5.425
Ge	A4	5.644	5.672	5.692	5.634	5.701	5.698	5.593	5.744	5.752	5.776	5.723
SiC	B3	4.348	4.374	4.380	4.355	4.372	4.384	4.314	4.394	4.350	4.404	4.366
BP	B3	4.527	4.528	4.540	4.509	4.543	4.551	4.538	4.566	4.535	4.567	4.536
BAs	B3	4.764	4.774	4.788	4.750	4.794	4.797	4.763	4.821	4.805	4.829	4.797
AlP	B3	5.450	5.461	5.472	5.436	5.472	5.486	5.434	5.497	5.452	5.508	5.461
AlAs	B3	5.649	5.670	5.682	5.639	5.691	5.691	5.664	5.713	5.697	5.733	5.682
AlSb	B3	6.126	6.131	6.146	6.079	6.146	6.163	6.233	6.172	6.189	6.188	6.159
GaNc	B4	3.179	3.190	3.197	3.167	3.198	3.211	3.106	3.224	3.216	3.233	3.192
		5.160	5.221	5.233	5.165	5.204	5.253	5.073	5.244	5.261	5.272	5.218
β-GaN	B3	4.523	4.510	4.519	4.476	4.518	4.537	4.385	4.552	4.544	4.569	4.515
GaP	B3	5.441	5.452	5.468	5.418	5.484	5.494	5.386	5.522	5.498	5.534	5.494
GaAs	B3	5.641	5.668	5.687	5.626	5.705	5.703	5.607	5.745	5.753	5.771	5.726
GaSb	B3	6.086	6.092	6.111	6.043	6.140	6.134	6.111	6.183	6.211	6.208	6.254
InN3	B4	3.527	3.543	3.551	3.523	3.555	3.573	3.501	3.589	3.594	3.599	3.558
		5.679	5.787	5.801	5.684	5.729	5.831	5.702	5.765	5.867	5.807	5.801
InP	B3	5.858	5.869	5.891	5.839	5.909	5.928	5.903	5.961	5.947	5.970	5.955
InAs	B3	6.048	6.078	6.099	6.038	6.120	6.127	6.082	6.170	6.205	6.195	6.204
InSb	B3	6.473	6.489	6.501	6.430	6.535	6.524	6.554	6.585	6.644	6.608	6.712
ZnOc	B4	3.223	3.233	3.239	3.504	3.199	3.249	3.148	3.249	3.282	3.294	3.272
		5.194	5.267	5.277	5.211	5.275	5.320	5.109	5.325	5.331	5.352	5.328
ZnS	B3	5.399	5.367	5.383	5.319	5.432	5.437	5.399	5.465	5.448	5.467	5.440
ZnSe	B3	5.658	5.638	5.657	5.588	5.707	5.699	5.691	5.736	5.756	5.751	5.707
ZnTe	B3	6.079	6.064	6.089	6.017	6.150	6.128	6.233	6.174	6.235	6.195	6.130
CdS	B3	5.808	5.825	5.844	5.776	5.896	5.911	5.958	5.944	5.942	5.934	6.097
CdSe	B3	6.042	6.075	6.098	6.025	6.152	6.153	6.205	6.195	6.249	6.210	6.343
CdTe	B3	6.470	6.478	6.502	6.422	6.568	6.559	6.478	6.610	6.709	6.626	6.740
MgS	B3	5.612	5.665	5.676	5.618	5.681	5.710	5.797	5.719	5.649	5.721	5.816
MgSe	B1	5.375	5.458	5.477	5.417	5.499	5.504	5.600	5.520	5.520	5.532	5.504
MgTe	B3	6.410	6.419	6.432	6.381	6.478	6.479	6.462	6.517	6.478	6.517	6.646
BaS	B1	6.364	6.330	6.351	6.303	6.413	6.431	6.443	6.433	6.422	6.436	6.546
BaSe	B1	6.570	6.556	6.577	6.517	6.649	6.653	6.731	6.659	6.694	6.671	6.710
BaTe	B1	6.982	6.894	6.919	6.897	7.051	7.009	7.113	7.062	7.068	7.062	7.174
MSE4			0.014	0.029	−0.016	0.049	0.061	0.029	0.083	0.088	0.097	0.102
MUE5			0.027	0.035	0.037	0.051	0.061	0.071	0.083	0.088	0.097	0.104

¹The Strukturbericht symbols are used for the structures as follows: A4-diamond; B1-rock salt; B3-zincblende, B4-wurtzite.

²Experimental results are taken from Ref. 4 and corrected for ZPAE, except for ZnO which is taken from Ref. 32 and corrected for ZPAE.

³Wurtzite structures require the specification of two independent lattice constants.

⁴MSE denotes mean signed error.

⁵MUE denotes mean unsigned error.

Bandgaps

Table 3 presents the results for bandgaps. Functionals are again listed in order of increasing MUE. For all 34 semiconductors, if one density functional predicted that the gap is direct, then the other nine also predicted direct, and the same consistency holds for indirect; the result is indicated in the last column of the table.

Table 3.

Bandgaps (eV) results for SBG31.

Solid	Expt.1	HSE	M11-L	M06-L	TPSS	SOGGA11	PBE	revTPSS	LSDA	SOGGA	PBEsol	Type2
C	5.48	5.49	4.06	4.73	4.29	3.97	4.24	4.05	4.22	3.98	4.03	I
Si	1.17	1.28	1.24	1.04	0.80	0.26	0.72	0.63	0.62	0.45	0.53	I
Ge	0.74	0.83	0.90	0.16	0.32	0.09	0.13	0.14	0.00	0.02	0.00	I
SiC	2.42	2.40	2.28	1.59	1.42	1.22	1.46	1.23	1.42	1.16	1.27	I
BP	2.40	2.18	1.66	1.78	1.45	1.03	1.40	1.28	1.36	1.14	1.24	I
BAs	1.46	1.92	1.78	1.50	1.27	0.73	1.25	1.13	1.19	1.02	1.10	I
AlP	2.51	2.51	2.39	2.08	1.86	1.14	1.78	1.72	1.64	1.47	1.56	I
AlAs	2.23	2.21	2.22	1.86	1.66	0.99	1.55	1.57	1.43	1.28	1.37	I
AlSb	1.68	1.98	1.92	1.48	1.58	1.01	1.44	1.40	1.34	1.16	1.22	I
GaN	3.50	3.53	2.91	2.06	2.15	2.09	2.22	1.71	2.18	1.70	1.85	D
β-GaN	3.30	3.14	2.70	1.87	1.79	1.92	1.86	1.53	1.84	1.87	1.70	D
GaP	2.35	2.45	2.02	2.15	1.89	1.17	1.80	1.77	1.63	1.57	1.62	I
GaAs	1.52	1.12	1.64	0.89	0.60	0.72	0.36	0.73	0.04	0.55	0.42	D
GaSb	0.73	0.90	1.09	0.30	0.39	0.30	0.19	0.31	0.00	0.19	0.06	D
InN	0.69	0.76	0.51	0.01	0.00	0.13	0.00	0.01	0.00	0.00	0.00	D
InP	1.42	1.78	1.22	1.47	1.19	1.01	0.99	1.00	0.74	0.95	0.83	D
InAs	0.41	0.58	0.99	0.15	0.08	0.18	0.00	0.00	0.00	0.00	0.00	D
InSb	0.23	0.47	1.03	0.00	0.00	0.06	0.00	0.00	0.00	0.00	0.00	D
ZnO	3.40	2.90	2.55	0.98	0.94	0.94	0.88	0.77	0.91	0.79	0.83	D
ZnS	3.66	3.49	2.79	2.86	2.53	2.20	2.30	2.42	2.02	2.27	2.22	D
ZnSe	2.70	2.42	2.62	1.84	1.62	1.48	1.37	1.58	1.05	1.31	1.26	D
ZnTe	2.38	2.36	2.72	1.51	1.65	1.79	1.39	1.60	1.11	1.38	1.29	D
CdS	2.55	2.25	1.68	1.65	1.47	2.03	1.26	1.31	0.97	1.13	1.08	D
CdSe	1.90	1.51	1.74	0.98	0.85	1.46	0.63	0.77	0.31	0.50	0.45	D
CdTe	1.92	1.67	2.20	0.94	1.05	1.50	0.81	0.98	0.54	0.74	0.67	D
MgS	5.40	4.75	3.56	4.28	3.91	4.11	3.65	2.68	3.37	3.33	3.34	D
MgSe	2.47	2.75	3.14	2.35	2.21	2.02	1.90	2.03	1.74	1.67	1.70	I
MgTe	3.60	3.59	3.38	3.21	3.07	3.10	2.65	3.08	2.41	2.60	2.58	I
BaS	3.88	3.26	2.40	2.64	2.56	3.50	2.40	2.48	2.13	2.11	2.15	I
BaSe	3.58	2.81	2.42	2.27	2.18	2.59	2.05	2.17	1.84	1.79	1.83	I
BaTe	3.08	2.28	2.06	1.57	1.77	2.46	1.66	1.69	1.48	1.32	1.38	I
MSE		−0.10	−0.29	−0.73	−0.85	−0.89	−0.98	−1.00	−1.14	−1.14	−1.14
MUE		0.26	0.54	0.73	0.85	0.89	0.98	1.00	1.14	1.14	1.14

¹Experimental results are taken from Ref. 4, except for ZnO which is taken from Ref. 33.

²D = direct gap; I = indirect gap.

Performances for subsets and other databases

Although some density functionals (such as M06-L, SOGGA11, and M11-L) are designed as general-purpose functionals, others are tuned specifically for the solid state or solid–vapor interfaces. Among the latter group, in chronological order, the AM05 functional distinguishes between two separate regions in a real material, one type that is assumed to be well described by the uniform electron gas, and the other type assumed to be well described by a surface model system, an approximation that is very suitable for solids.⁵⁰ The WC functional is a modification of the PBE functional that provides better results for solids, at the price of compromising the performance for chemical systems.^{51, 52, 53} The HISS functional is a range-separated functional that has HF exchange only at the middle range of the electron-electron interaction (sometimes it is also referred as a three-range functional).⁵⁴ Finally, the HSEsol functional is a recent reparametrization of the original HSE functional specific for solid-state calculations.²⁵

Results for the four additional functionals mentioned in the previous paragraph are only available for comparison to the present results for the S(13) subset. In order to put the performances of the functionals considered in this work in perspective, in Table 4 we compare our results for the errors in the lattice constants of the S(13) subset to those for the four additional functionals mentioned in the previous paragraph.

Table 4.

Errors for the S(13) subset of lattice constants and comparison with other published results.

Functional	MUE	MSE	Max |ɛ|	Min |ɛ|
SOGGA	0.015	0.013	0.030	0.001
HSEsol1	0.015	−0.013	0.059	0.000
HISS2	0.016	0.007	0.040	0.000
LSDA	0.017	−0.016	0.047	0.007
WC3	0.022	0.019	0.052	0.001
AM053	0.025	0.020	0.063	0.002
PBEsol	0.028	0.027	0.051	0.004
HSE	0.035	0.034	0.072	0.002
M11-L	0.039	−0.018	0.138	0.001
revTPSS	0.042	0.042	0.079	0.014
SOGGA11	0.046	0.043	0.156	0.003
M06-L	0.050	0.050	0.157	0.002
TPSS	0.066	0.066	0.122	0.024
PBE	0.080	0.080	0.147	0.024

¹PW-PAW results from Ref. 25.

²G-PBC m-6-311G* results from Ref. 49.

³FP-(L)APW+lo results from Ref. 22.

In Table 5 we compare the MUEs for both lattice constants and bandgaps in SLC34 and SBG31, together with those of the five subsets of SLC34 and SBG31, and those of four more chemical databases: MGAE109/05 with 109 main group atomization energies,⁵⁵ DBH24/08 with 24 diverse barrier heights,⁵⁶ NCCE31/05 with 31 noncovalent complexation energies,^{57, 58} and TMBE15 with 15 transition metal bond energies. The TMBE15 database consists of all the systems that contain transition metals in the SRMBE13 and MRMBE5 databases.^{13, 14}

Table 5.

Mean unsigned errors for subsets of SLC34 AND SBG31 and for chemical databases and relative errors.

	M11-L	M06-L	TPSS	revTPSS	SOGGA11	HSE	PBE	PBEsol	SOGGA	LSDA
Lattice constants (Å)
S(14)	0.039	0.050	0.066	0.042	0.046	0.035	0.080	0.028	0.015	0.017
D(6)	0.040	0.136	0.096	0.072	0.132	0.054	0.123	0.050	0.034	0.019
G14(4)	0.039	0.030	0.054	0.033	0.029	0.026	0.067	0.027	0.016	0.012
2-16(6)	0.139	0.086	0.099	0.079	0.181	0.076	0.104	0.045	0.047	0.046
13-15(16)	0.048	0.081	0.074	0.054	0.072	0.039	0.091	0.035	0.022	0.021
12-16(8)	0.083	0.135	0.103	0.073	0.148	0.069	0.120	0.031	0.026	0.076
SLC341	0.071	0.088	0.083	0.061	0.104	0.051	0.097	0.035	0.027	0.037
Bandgaps (eV)
D(5)	0.42 (5)2	0.44 (4)2	0.40 (3)2	0.47 (3)2	0.41 (5)2	0.15 (5)2	0.50 (2)2	0.55 (1)2	0.52 (2)2	0.56 (0)2
G14(4)	0.45	0.57	0.75	0.94	1.07	0.06	0.82	1.00	1.05	0.89
2-16(6)	1.06	0.95	1.05	1.31	0.70	0.52	1.28	1.50	1.53	1.51
13-15(14)	0.40	0.63	0.73	0.86	0.96	0.21	0.81	0.94	0.94	0.90
12-16(7)	0.43	0.89	0.99	1.07	0.77	0.23	1.22	1.36	1.30	1.52
SBG313	0.54	0.73	0.85	0.99	0.89	0.26	0.98	1.14	1.14	1.14
Chemical databases (kcal/mol)
MGAE109/054	0.74	0.87	1.07	0.94	1.68	0.88	3.07	7.94	7.82	18.37
DBH24/08	2.56	4.05	8.20	8.14	5.14	3.77	8.18	10.3	10.2	13.3
NCCE31/05	0.56	0.58	1.17	1.14	1.28	0.75	1.24	1.79	1.84	3.31
TMBE15	4.43	7.74	7.58	8.06	11.67	14.99	9.62	14.53	14.96	27.94
Ave. other5	2.07	3.31	4.51	4.57	4.94	5.10	5.53	8.63	8.71	15.73

¹MUE from Table 2.

²The number of semiconductors that are correctly predicted to have a nonzero bandgap is reported in parenthesis.

³MUE from Table 3.

⁴As in all previous articles employing this database, the errors are given on a per bond basis.

⁵Average of the MUE of the other databases calculated as:

⁶[MUE(MGAE109/05)+MUE(DBH24/08)+MUE(NCCE31/05)+MUE(TMBE15)]/4.

The atomization energy and the barrier height databases test the performance of the functionals for two of the most central properties in chemistry, while the noncovalent interactions database is particularly interesting because of the high current activity in testing the ability of density functionals to predict noncovalent interaction energies, which are of high interest to both chemists and solid-state physicists. Finally, since all these chemical databases have no transition metals, the TMBE15 database is nicely complementary, and since compounds containing metals are an especially active and promising application area for local functionals, it is important to consider this category of systems.

The functionals in Table 5 are arranged in order of increasing average MUE for the four additional databases.

DISCUSSSION

Lattice constants

Table 2 is disappointing for the new density functionals, especially SOGGA11. As we shall see in the further discussion, this reflects the difficulty of obtaining good chemical properties and good lattice constant with the same functional. Whereas previous discussions^{15, 18, 19, 24} emphasized general connections between enforcing the second-order constraint and obtaining good results for lattice constants, the poor performance of SOGGA11 for lattice constants shows that those considerations were incomplete. If one has a simple functional form (such as that used in PBEsol or SOGGA or the unnamed variations of GGAs examined by Haas et al.²⁴), enforcing any one constraint has a more general effect on the density functional, since several global aspects of a density functional change when one changes any parameter in a simple functional form, whereas the very flexible form used in SOGGA11 allows the global behavior to be more independent of whether or not the second-order constraint is satisfied, and this shows that the previously apparent good correlation of accurate prediction of lattice constants with enforcing the second-order constraint was deceptive.

We note that revTPSS is a revised version of TPSS that was constructed²¹ based in part on the empirical realization that the TPSS functional does not give good solid-state lattice constants (just as PBEsol was designed to remedy this deficiency in PBE); thus it provides a good comparison to results for functionals that were not developed specifically with lattice constants in mind. Table 2 does show that revTPSS has smaller than average errors in lattice constants.

Table 2 suggests that it would be valuable to conduct further study to understand why some lattice constants are predicted more accurately than others. There are interesting differences not just between subgroups but also within subgroups. For example, it is not clear why density functional theory does much better for zinc chalcogenides than for Cd chalcogenides.

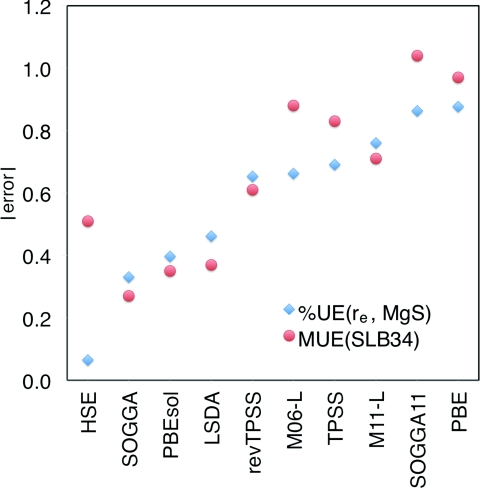
An interesting question is whether the performance of density functionals for molecular bond lengths is related to their performance for lattice constants.¹³ One consideration is that systems with extended structures in all three dimensions do not have exponentially vanishing tails in the electron density whereas molecules do. To gain insight into this question, we optimized the geometry of the MgS diatomic molecule for all the considered density functionals, using the same basis set as used for the solid. This diatomic was chosen because it appears in the 2–16 subset of SLC34, which is the subset with the largest average errors for lattice constants for M11-L, SOGGA11, PBEsol, and SOGGA (but not for the other six density functionals), and because the equilibrium internuclear distance r_e of MgS is well known^{59, 60} (2.143 Å). Note that the internuclear distances are different in ionic lattices than in molecules. For example, the lattice constant of 5.622 Å for MgS corresponds to a nearest neighbor Mg–S distance of 2.430 Å. Figure 2 compares the absolute percentage error in r_e for diatomic MgS to the mean unsigned error of the SLB34 database; we see that indeed there is a rough correlation, and the performance for the diatomic matches those of the lattice constant database for many functionals, including SOGGA, PBEsol, revTPSS, M11-L, and to a lesser extent also for LSDA, TPSS, and PBE. It would be interesting to further examine the relationship between the accuracy of density functionals for lattice constants and their accuracy for molecular bond lengths, but it is beyond the scope of the present work.

Figure 2.

Comparison of the absolute percentage error in the equilibrium distance of the MgS molecule (blue, diamonds, in Å) with MUE(SLB34) (red, circles, in percentage points) calculated with different density functional approximations.

When we broaden the discussion to include the four additional density functions introduced in Sec. 4C, we see from Table 4 that the HSEsol, HISS, WC, and AM05 functionals perform well for the lattice constants of S(13), all being better than PBEsol; in particular HSEsol provides results that are matched only by SOGGA. Note that HSEsol and HISS, like HSE, are nonlocal, whereas the other eleven functionals in Table 4 are local, but in some sense it is still “fair” to compare HSE, HSEsol, and HISS to the local functionals because they are local at long-range. However, since the HSEsol functional was optimized for improvement for solid-state systems, its performance for chemistry is similar to that of HSE at best.²⁵ Furthermore, we already showed that the WC functional deteriorates the performance for chemistry with respect to that of its PBE mother functional.⁵² Both the AM05 functional and the HISS functional seem promising from more than one point of view; however their complicated mathematical expressions present enough difficulties for their implementation in software packages that they have so far seen only limited use and circulation among users.

Bandgaps

All functionals in Table 3 underestimate the bandgaps on average, as shown by their negative MSE. For most functionals the magnitude of the MSE is the same as the MUE, which indicates that they underestimate all 31 bandgaps. HSE has the best performance for bandgaps, which illustrates how the inclusion of nonlocal short-range exchange removes a dominant part of the error. Among local functionals, M11-L is the best performer, with a remarkable gain of more than 25% over the performance of M06-L, which has the third best performance (second best among local functionals). The best GGA functional is SOGGA11, whose performance is midway between the TPSS and revTPSS meta-GGAs. Comparison of Tables 2, 3 shows that the functionals that provide the best performance for lattice constants (SOGGA, PBEsol, and LSDA) are the worst performers for bandgaps, which present a challenge for future functional development.

Comparison of M11-L with M06-L and the other meta-GGA functionals shows a clear advantage of the new dual-range exchange functional form that is used in M11-L. M11-L has about the same computational cost as M06-L and similar performance for lattice constants, but Table 5 shows that M11-L provides significant improvement not only for bandgaps but also for the three additional chemical databases. If we interpret poor performance for barrier heights and bandgaps as both coming mainly from self-interaction error, the good performance of M11-L for both the barrier heights database and the bandgaps shows that M11-L does a much better job in compensating the self-interaction error than any other previous local functional. Similarly, SOGGA11 does best for these databases of any GGA, with performance improved by about 50% for barrier heights and by about 10% for bandgaps as compared to the popular PBE functional.

For the difficult subgroup, Table 5 also presents the number of semiconductors for which the bandgap is predicted to be different than zero. M11-L, SOGGA11, and HSE are the only functionals that correctly predict all five semiconductors in this subgroup to have a gap. All functionals except HSE and M11-L yield a large underestimation of the gaps for these difficult cases (HSE and M11-L are the only functionals to have positive MSE, LSDA has the worst performance by predicting a zero bandgap for all five cases). Since most density functionals predict most of the difficult cases to be conductors, HSE and M11-L are the only suitable functionals for the study of these semiconductors, and if one restricts consideration to only local functionals, one is left with only M11-L.

The 2–16 semiconductors are a weakness for of M11-L in that both lattice constants and bandgaps are far from the average for the other subdatabases. However, this group is also the worst for HSE and many other functionals, which suggests another challenge for future functional development.

Overall analysis

In order to form a view of the overall performance of each of the density functionals, we need to consider all six databases; however, the errors for the different databases have different typical magnitudes and even different units. To allow a balanced comparison of the errors for the various databases, we first converted all the MUEs to relative errors. Averaged over the ten density functionals, the mean unsigned errors for the six databases, in the order that they appear in Table 5, are 0.065 Å, 0.87 eV, 4.34 kcal/mol, 7.38 kcal/mol, 1.37 kcal/mol, and 12.15 kcal/mol. Dividing each MUE by the average error for that database yields a unitless relative error. These are listed in Table 6, where the density functionals are arranged in order of increasing average relative error, which is given in the last row.

Table 6.

Relative errors.¹

	M11-L	HSE	M06-L	revTPSS	TPSS	SOGGA11	PBE	SOGGA	PBEsol	LSDA
	MGGA2	Nonlocal	MGGA	MGGA	MGGA	GGA	GGA	GGA	GGA	LSDA
SLB34	1.09	0.78	1.35	0.93	1.26	1.59	1.49	0.41	0.53	0.57
SBG31	0.62	0.30	0.84	1.14	0.98	1.03	1.13	1.32	1.32	1.32
MGAE109/05	0.17	0.20	0.20	0.22	0.25	0.39	0.71	1.80	1.83	4.23
DBH24/08	0.35	0.51	0.55	1.10	1.11	0.70	1.11	1.38	1.39	1.80
NCCE31/05	0.41	0.55	0.42	0.83	0.86	0.94	0.91	1.35	1.31	2.42
TMBE15	0.36	1.23	0.64	0.66	0.62	0.96	0.79	1.23	1.20	2.30
Ave. relative3	0.50	0.60	0.67	0.81	0.85	0.93	1.02	1.25	1.26	2.11

¹In each of the first six rows, the relative error is the MUE divided by the average MUE for that database.

²MGGA denotes meta-GGA.

³Averaged over all six relative errors.

Several interesting trends emerge when one arranges the results as in Table 6. First of all, we see that the nonlocal density functional has better performance than all but one of the local ones, all of the meta-GGAs perform better than any of the GGAs, and all of the GGAs perform better than LSDA. This is probably not too surprising, but the next observation is not as easy to explain. In particular the table shows that although the errors in bandgaps, main-group atomization energies, barrier heights, and noncovalent complexation energies all roughly correlate with one another (all four of these rows tend to show increasing errors, with only a few exceptions, as one proceeds left to right), there is basically no correlation with errors in lattice constants. The transition metal bond energies also do not correlate well with other properties. Clearly the features of density functionals that control semiconductor lattice constants and transition metal bond energies are distinct from those that control main-group energetic predictions.

Haas et al.²⁴ considered a more diverse set of solids than we do, but their conclusions and the trends in their paper are not all that different from ours for the density functionals and properties they considered. Haas et al.²⁴ concluded that “GGAs of the PBE form cannot describe well lattice parameters of solids and atomization energies of molecules simultaneously.” The present study allows for a more general conclusion, namely that even for more general forms of GGAs, atomization energies, barrier heights, noncovalent interaction energies, and bandgaps all improve or degrade together (at least on average), but performance for lattice constant of solids does not follow the same trends at all.

CONCLUDING REMARKS

In the present study, we tested the performances of our most recent functionals, SOGGA11 and M11-L, and compared them to those of other successful and popular density functionals for a large database of lattice constants and bandgaps of 31 semiconductors (SLC34 and SBG31). We considered ten functionals (nine local, one nonlocal) for bandgaps and 14 (11 nonlocal, three local) for lattice constants. We found that:

• For lattice constants the functionals that provide best performance are SOGGA and HSEsol; of these, the nonlocal HSEsol is a better general-purpose functional.

• M11-L provides reasonable results for lattice constants (better than M06-L), while SOGGA11 is the worst (of functionals tested) for this property.

• For bandgaps M11-L is the second best functional after HSE, and is the best local functional. SOGGA11 is the best GGA functional.

• A correct second order coefficient for the density gradient expansion is not sufficient to provide accurate results for lattice constants.

By construction, the average value (both the average for each row and the average for the whole table) of the relative errors in Table 6 is 1.0. Therefore, a relative error below 1.0 denotes better than average performance. Interestingly, among the ten functionals considered in this table, not a single one is better than average for all six databases, and none is worse than average for all six either. Thus, while it is possible to improve lattice constants of solids, it is very challenging to do so and to simultaneously achieve good performance for chemistry. The quest for a universally applicable density functional continues.