A Solution Study of Silica Condensation and Speciation With relevance to in vitro investigations of biosilicification

Abstract

With both mild synthesis conditions, a high level of organisation and functionality, biosilicas constitute a source of wonder and inspiration for both materials scientists and biologists. In order to understand how such biomaterials are formed and to apply this knowledge to the generation of novel bioinspired materials, a detailed study of the materials, as formed under biologically relevant conditions, is required. In this contribution, data from a detailed study of silica speciation and condensation using a model bio-inspired silica precursor (silicon catechol complex, SCC) is presented. The silicon complex quickly and controllably dissociates under neutral pH conditions to well-defined, metastable solutions of orthosilicic acid. The formation of silicomolybdous (blue) complexes was used to monitor and study different stages of silicic acid condensation. In parallel, the rates of silicomolybdic (yellow) complex formation, with mathematical modelling of the species present was used to follow the solution speciation of polysilicic acids. The results obtained from the two assays correlate well and monomeric silicic acid, trimeric silicic acids and different classes of oligomeric polysilicic acids and silica nuclei can be identified and their periods of stability during the early stages of silica condensation measured. For experiments performed at a range of temperatures (273–323K) an activation energy of 77kJ·mol⁻¹ was obtained for the formation of trimers. The activation energies for the forward and reverse condensation reactions for addition of monomers to polysilicic acids (273–293 ± 1K) were 55.0 and 58.6kJ·mol⁻¹ respectively. For temperatures above 293K, these energies were reduced to 6.1 and 7.3 kJ·mol⁻¹ indicating a probable change in the prevailing condensation mechanism. The impact of pH on the rates of condensation were measured. There was a direct correlation between the apparent third order rate constant for trimer formation and pH (4.7–6.9 ± 0.1) while values for the reversible first order rates reached a plateau at circumneutral pH. These different behaviours are discussed with reference to the generally accepted mechanism for silica condensation in which anionic silicate solution species are central to the condensation process. The results presented in this paper support the use of precursors such as silicon catecholate complexes in the study of biosilicification in vitro. Further detailed experimentation is needed to increase our understanding of specific biomolecule silica interactions that ultimately generate the complex, finely detailed siliceous structures we observe in the world around us.

Introduction

Silica formation in biological organisms has fascinated scientists for many years owing to the sophistication exhibited by organisms in structural and morphological control over the biosilica generated. Research on plant, animal and single celled organisms has shown that organic biomolecules are involved in biosilicification,^1–4 and associated model studies have been performed in vitro to try to understand the mechanisms by which these biomolecules act.^5–12 In natural aqueous systems, monosilicic acid is found at levels of a few tens to about one hundred ppm.^13–15 From this low precursor concentration reservoir, silicifying organisms are able to sequester and then deposit silica in a controlled manner. In vitro, aqueous monosilicic acid at levels above 100ppm and circumneutral pH will spontaneously condense to larger silicate oligomers followed by stable particles that will eventually form a gel network by a process occurring via well defined stages:¹³ (i) polymerisation of monomer to small particles, (ii) particle growth and finally (iii) formation of branched particle networks resulting in gelation. The earliest stages of condensation can be further described by distinct chemical reactions: the formation of dimers, then trimers and oligomers, that are kinetically distinct when monitored by molybdenum colorimetric complexation methods, such that changes in rate and mechanism during the condensation process can be monitored.^5,13 The formation of silica from solutions containing orthosilicic acid is thought to be activated by the formation of anionic silicate species that condense with uncharged monomers.^16,17 However pK_as ranging from 9.5 to 10.7 for small oligomeric species through to condensed particles^18–20 and 9.8 for the monomer²¹ suggest that concentrations of these anionic species are low when condensation occurs under circum-neutral pH conditions. The estimated population of Si(OH)₃O⁻ at pH 7 is 0.18%.²² In many studies a single reaction order/mechanism is assumed throughout the condensation process, but in respect of the complexity and number of competing species suggested by modelling and speciation studies this would appear naïve.²³ We would expect the observed kinetics to change throughout the condensation process to reflect the changing reactions and speciation at the molecular and colloidal levels.¹³ The orders of reaction observed during condensation have been determined for a range of precursors, concentrations and pH, with an initial zero order with respect to monomer (the so called induction period) being observed.^24,25 Subsequent condensation has been hypothesized to follow orders from 1 to 5,^25–30 sometimes showing transitional behaviour with pH^24,31,32 or degree of condensation.²⁴

When silica is formed within an organism the reaction environment includes biomolecules such as proteins,^2–4 polyamines^1,33 and carbohydrates.^34,35 If we are to understand the specific influence of such biomolecules on orthosilicic acid condensation then the effects of factors such as pH, temperature and precursor concentration of the model condensing system chosen must first be understood. In addition, the silicate species present must be known and controllable, especially if the early stages of the condensation process are to be studied. The ideal model system will consist exclusively of monomers at the beginning of the condensation process. Any other oligomeric or particulate species present will cause complications with data interpretation as re-dissolution of species and condensation with already formed silicates will exhibit varying kinetic behaviour.

Many silicic acid precusors have been used to investigate silicification in vitro including alkoxysilanes, ^3,7,9,11 glycol modified alkoxysilanes,^10,36 sodium silicate solutions,⁶ silica sols⁸ and silicon 1,2 dihydroxybenzene complexes.^5,37,38 However, the suitability of such model systems and their exact chemistries such as silicate speciation at a given pH, time and concentration are not always fully known. As examples, the use of alkoxysilanes is problematic as the initial stage involves the hydrolysis of alkoxysilane bonds resulting in a mixture of partially hydrolysed and partially condensed species in solution as well as varying amounts of additional alcohol generated by alkoxide hydrolysis;³⁹ the use of stabilised silica sols limits analysis to effects on aggregation; alkaline solutions of sodium silicate are known to contain stabilised oligomeric species,^40–43which upon initiation of the condensation process by pH reduction, dissociate to monomer at the same time as existing monomers begin to condense, thereby blurring the picture of the condensation process.

In contrast, silicon 1,2-dihydroxybenzene complexes are stable, forming mildly basic aqueous solutions (pH≈10), which upon neutralisation to pH≈7, rapidly form solutions of orthosilicic acid that are self-buffering above pH 6.5. In addition, such hypervalent silicon complexes have been implicated in the biosilicification process,^44,45 possibly as a means for the transport of silicon at concentrations exceeding the solubility of monosilicic acid, with the presence of 1,2-dihydroxybenzene being known to slightly increase the solubility of amorphous and crystalline silica.¹³ In previously reported studies and those described below, the concentration of free 1,2-dihydroxybenzene remains constant during the course of the condensation reaction. The increased solubility and any other effect of the free ligand can thus be taken into account using control experiments, enabling the effects of other experimental variables such as the concentration of a chosen additive to be studied.

Silicomolybdic acid methods, as used in this study are routinely used for the determination of silica content in aqueous solutions^46,47 and also in the measurement of rates of silica condensation^6,29 through the disappearance of molybdenum active species with time. A number of studies have been conducted attempting to differentiate between different silicate solution species with comparison to data acquired by inductively coupled plasma (ICP) methods and have been able to show that there are significant levels of monomeric silicic acid in sea water.⁴⁸ Measurement of the complexation rate of samples with the molybdenum containing compleximetric reagents has been used to differentiate between monomeric and particulate species in solutions and solids^49–52 and between molecular species in the dissolution of borosilicate glass.⁴⁸ Where mixtures of species have been monitored an empirical approach has been used to compare complexation rates during different stages of dissolution⁵³ and, to the best of our knowledge, no information is available distinguishing the early stages of silica condensation.

In this paper we report on the detailed study of a model silica precipitation system using dipotassium tris(1,2-benzenediolato-O,O’)silicate.2H₂O as the monosilicic acid precursor with titrimetric, ¹H NMR and colorimetric analytical (molybdenum yellow and blue) data being presented. The principal aims of the investigation were: (i) to confirm the rapid and controlled dissociation of the dipotassium tris(1,2-benzenediolato-O,O’)silicate.2H₂O to give initially pure supersaturated solutions of orthosilicic acid, making this complex an extremely desirable precursor for a model experimental silicifying system; (ii) to perform a kinetic analysis and study the effect of pH and temperature on the condensation process (to obtain rate constants and activation energies), and (iii) to use the rate of silicomolybdic acid complexation to implicate/identify the silicate species present at different times during the early stages of the condensation process.

Results and discussion

In order to confirm that the initial requirements of the model system were met, i.e. the only available source of condensable silicate present at the start of the reaction was orthosilicic acid at supersaturated concentrations, a study of the conditions and rate of precursor dissociation was performed.

Preparation of orthosilicic acid solutions – optimisation of conditions

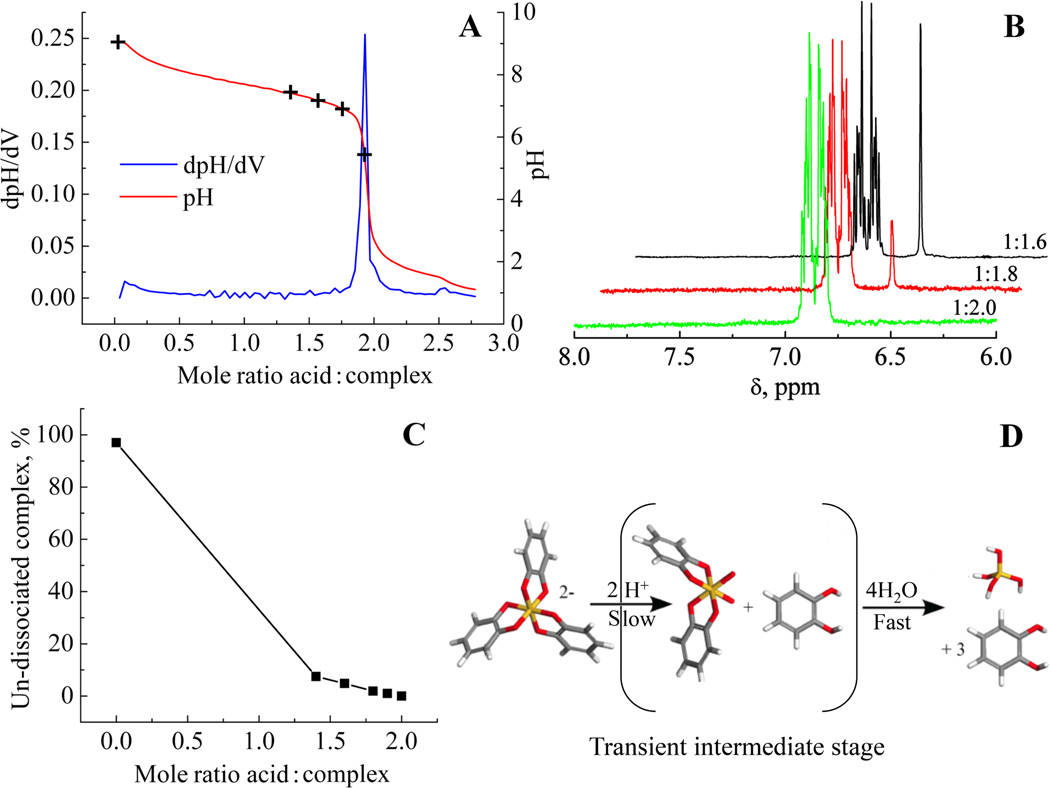
The results of a titrimetric study showed that stoichiometric additions of acid were required to fully dissociate the precursor complex at an acid to complex ratio of 2:1, Figure 1A. ¹H NMR at any of the levels of addition showed an absence of signals from species other than 1,2 dihydroxy benzene and the silicon tris 1,2-dihydroxybenzene complex (SCC) indicating, that at least in the time frame of the NMR experiment, no partial complexes containing only one or two 1,2 dihydroxybenzene molecules are generated during dissociation, Figure 1B. ¹H NMR analysis also showed that addition of acid ranging from 0–2 molar equivalents resulted in dissociation of the complex which was both rapid and controlled based on the amount of acid added, Figure 1C. The dissociation of the catecholate complex appears to proceed via 2 stages, Figure 1D: (i) removal of the first 1,2-dihydroxybenzene moiety by acid hydrolysis requiring 2 molar equivalents of acid that destabilises the hypervalent 6 coordinate state followed by (ii) removal of the now labile remaining 1,2-dihydroxybenzene moieties by hydrolysis. The overall reaction can be written as:

$$[{\mathrm{K}}_2\mathrm{S}\mathrm{i}{{\displaystyle ({\mathrm{C}}_6{\mathrm{H}}_4{\mathrm{O}}_2)}}_3+2{\mathrm{H}}^{+}+4{\mathrm{H}}_2\mathrm{O}\to \mathrm{S}\mathrm{i}{{\displaystyle (\mathrm{O}\mathrm{H})}}_4+3{\mathrm{C}}_6{\mathrm{H}}_4{{\displaystyle (\mathrm{O}\mathrm{H})}}_2+2{\mathrm{K}}^{+}]$$ (1)

This mechanism precludes the formation of any partially hydrolysed species as the rate determining step must be the first acid hydrolysis stage so only monomeric silicic acid or un-hydrolysed complex remains. At an acid to complex ratio lower than 2:1, any remaining undissociated complex in solution was also found to be stable and able to buffer the pH of the reaction system for more than 24 hours. The dissociation process for SCC is different to that observed for alkoxysilane precursors that require only catalytic amounts of acid for hydrolysis, and for which condensation and hydrolysis of partially and fully hydrolysed species compete during the early stages of silica formation.⁵⁴

Figure 1.

(A) Results of titrimetry with hydrochloric acid with markers representing the levels of molar ratio additions used in the ¹H NMR study. (B) Typical ¹H NMR spectra of partially and fully dissociated complex (singlet at 6.65ppm from complex, multiplet centred at 6.85 from dissociated 1,2 dihydroxybenzene). X:Y represents the mole ratios of Si:H⁺. (C) Plot of residual complex for samples treated with increasing amounts of acid. (D) Acid dissociation of silicon catecholate complex precluding the formation of partially hydrolysed species in the time frame of the NMR experiment.

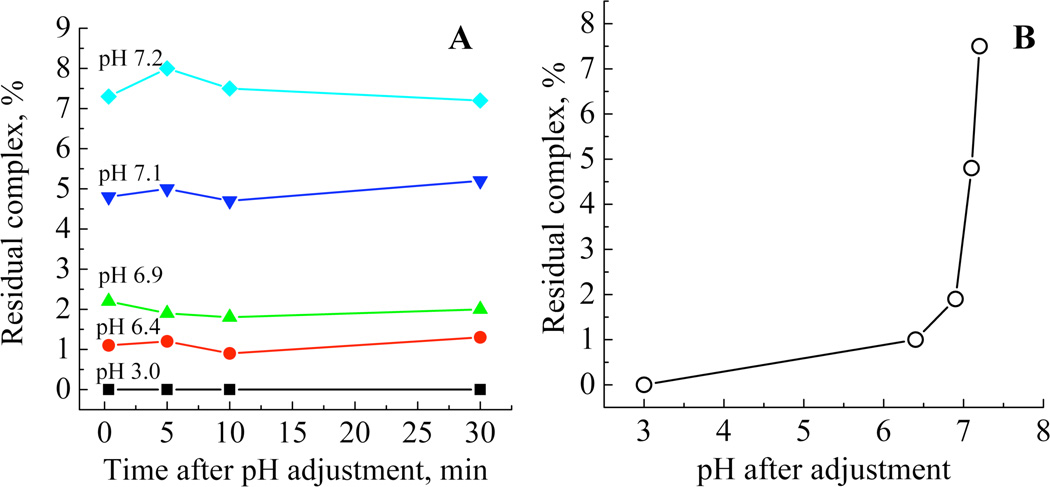
To measure the rate of complex dissociation upon pH adjustment, quenching experiments were carried out wherein after initial pH adjustment to values between 3.0–7.2, the pH was then raised back to 10 by the addition of potassium hydroxide solutions, limiting the time for dissociation to as little as 20 seconds. A typical spectrum of a quenched dissociated complex is given in the supporting information, Figure S1. The mol % of residual complex was calculated at each sample time and the data plotted as residual complex versus time after pH adjustment, Figure 2A or as residual complex versus pH after initial adjustment, Figure 2B. The data show that from as little as 20 seconds after mixing and pH adjustment the complex had dissociated to equilibrium values at all levels of acid addition.

Figure 2.

(A) Plot of residual complex with dissociation time for samples treated with increasing amounts of acid. (B) Relationship between pH and residual complex concentration. The pH values 7.2, 7.1, 6.9, 6.4 and 3.0 correspond to molar equivalents of acid to complex of 1.4, 1.6, 1.8, 1.9 and 2.0:1 respectively.

Based on the above data, the optimum conditions for the model system were chosen to be the addition of sufficient 2M hydrochloric acid to reduce the pH of a 30mM solution of the dipotassium tris(1,2-benzenediolato-O,O’)silicate·2H₂O to 6.8±0.05. This ensured that practically all the complex was dissociated (ca. 99%) and that the pH was not subject to significant variation due to any minor inaccuracies in acid addition. Although the level of orthosilicic acid selected is high in the context of natural reservoirs it does enable the complete condensation process from initiation to equilibrium to be observed within a 24 hour period. Any observed impact of additives compared with the control model should still be relevant to a biological system albeit on a longer time scale.

Speciation studies – correlation between molybdenum yellow and molybdenum blue analyses

In order to generate meaningful inferences from data generated from the model system, it is important that species present during the condensation process are known. Here we have, for the first time (to our knowledge) attempted to identify the silicate species present in a mixed silicate system at various stages of the condensation process using a combined analysis of the kinetics of condensation extracted from molybdenum blue data and the kinetics of species dissociation when silicate species are brought into contact with the molybdenum yellow reagent.

Speciation in 30mM condensing systems

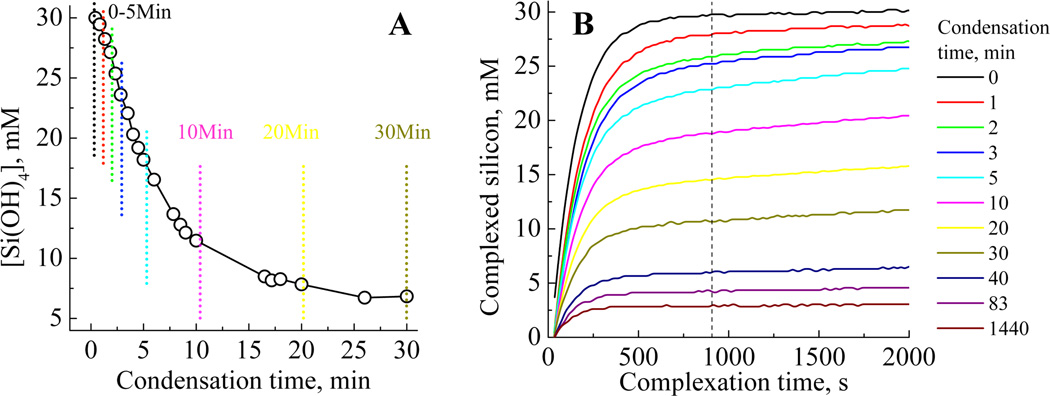
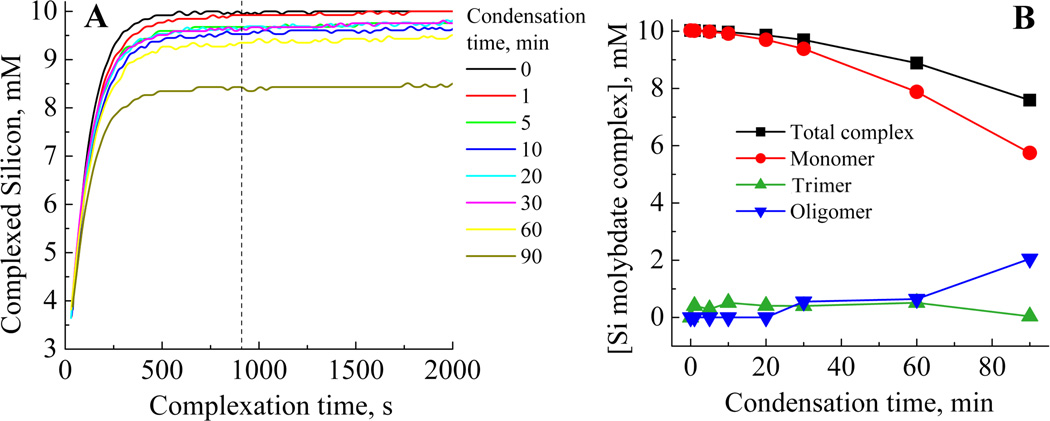
The molybdenum blue (silicomolybdous acid) colorimetric method when applied to the study of silica condensation yields data such as that shown in Figure 3A. From this can be extracted kinetic information and the effect of physicochemical parameters such as pH and temperature (data analysis from the study is presented below) and solution additives on the early stages of silica condensation. An alternative approach to the monitoring of silicic acid concentrations in solution is the molybdenum yellow (silicomolybdic acid) method where, for samples taken at time points identified by the vertical lines in Figure 3A the development of the yellow colour with time distinctly evolves, with both a decrease in the final silicon concentration detected and a visible change in the shape of the plots being observed, Figure 3B. The evolution suggests the presence of at least two types of molybdenum yellow-active species, together with a much slower reacting fraction, mostly made of highly condensed species such as silica particles. The mathematical modelling of this data with a three species model gave fits with R² values evolving from 0.9999 to 0.9704 during the 90min condensation period. As condensation proceeds, the first order law becomes unable to perfectly describe species breakdown. Indeed, the silica particles formed during the later stages of condensation, with sizes above the critical nucleus dimensions, behave as a solid phase as opposed to solution species, and therefore adopt specific kinetics of dissolution (Figure 4A).

Figure 3.

(A) The decrease in silicomolybdous acid (molybdenum blue) complex with time following pH reduction for 30 mM initial [Si(OH)₄] at pH 6.8, and (B) the formation of silicomolybdic acid yellow complex after increasing condensation times. The vertical lines in (A) represent a selection of the sampling times used to obtain the molybdenum yellow data presented in (B). The vertical line on (B) denotes the time at which the blue silicomolybdic acid complex is formed from species available in solution.

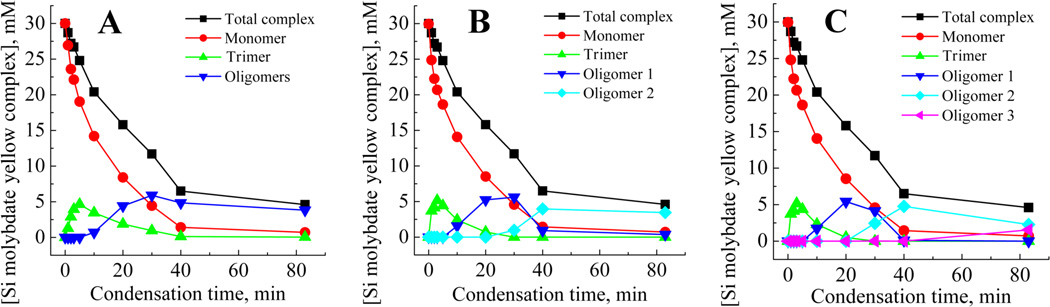
Figure 4.

Silicate speciation during the condensation process for 30mM initial [Si(OH)₄] at pH 6.8, with 3 (A), 4 (B) and 5 (C) species fits.

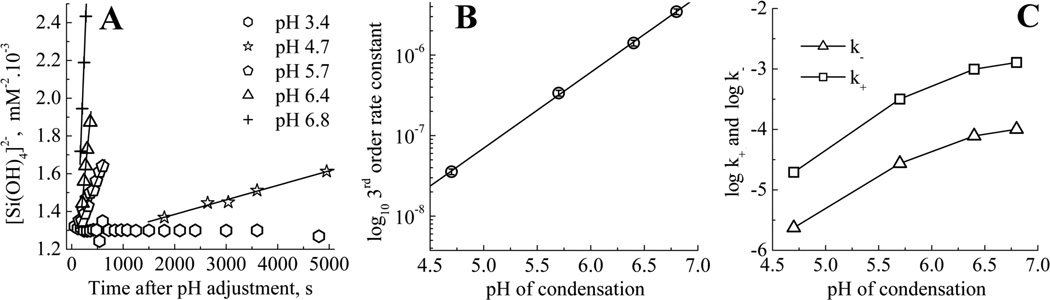
In the absence of a constraint over the composition of the system and for all the speciation models tested, the mathematical solution converges to the presence of only one species, the monomer, for t=0min (complexation rate of 0.42 min⁻¹). Applying a three species fit (Figure 4A) to the early stages of condensation (0–5 min) showed the presence of only one species in addition to the monomer. This second species exhibits a slower complexation rate (0.03min⁻¹), and begins to appear rapidly after pH adjustment. Over the time period 0 to 6 min, molybdenum blue data gave results consistent with a dominant third order process, e.g, the formation of trimeric species (Figure 6A and Table 1). In addition, a loss of around 45% of molybdenum blue active species from the system can be observed. This observation can be rationalised by the formation of trimers from the condensation of monomer and dimer, with the second species identified from molybdenum yellow analysis being assigned as trimers. The other possible species, dimers, are likely to be present only as an intermediate, low concentration fraction, even at this stage of the condensation process.

Figure 6.

(A) Apparent third order regions for condensation measured by the molybdenum blue assay. (B) Plot of the log of the apparent third order rate constants against pH and (C) Log of the forward and reverse of the first order rate constant variation with pH.

Table 1.

Apparent third order rate constants for the molybdenum blue [Si(OH)₄] assay.

pH of condensation	Apparent third order rate constant · 106/mM−2s−1
6.8	3.4 ± 0.24
6.4	1.41 ± 0.10
5.7	0.35 ± 0.03
4.7	0.04 ± 0.003
3.4	No measurable condensation

From 6 to 15 min condensation time, molybdenum blue data was found to fit to an expression for a reversible first order reaction (Figure 6C) suggesting that the favoured reaction is for monomer to condense on to already existing oligomers, starting from trimers.^5,55 The data obtained from the molybdenum yellow complexation experiments demonstrate that the fractions attributable to trimeric species and monomers disappear over time, with the concomitant formation of larger species having slower kinetics of complexation.

If the molybdenum yellow data is now subject to a fitting procedure using four or five species, the slow-complexing species fraction appears to split between different sub-classes of slower-reacting species. As condensation proceeds, the slower-reacting, smaller species fractions are progressively replaced by even more insoluble fractions. For a four species model (Figure 4B), a species showing reversibility with respect to the molybdic acid reagent was observed after 20min and increased in abundance with time to form a stable population. Increasing the species fit to 5 indicated that this species is further condensed to a slower dissociating entity (Figure 4C). The formation of this later species coincides with the detection of the first silica particles based on light scattering measurements on a similar model system.³⁷

Where these species are at low levels (post 3^rd order stage, 6–15 minutes), reversible 1^st order kinetics is still observed (see the in-depth kinetic analysis for details, Figure 7),⁵ with the addition of monomers to trimers and larger species being the prevailing reaction. The observed reversibility relates to silicate dissociation during condensation and not during molybdenum yellow complexation.

Figure 7.

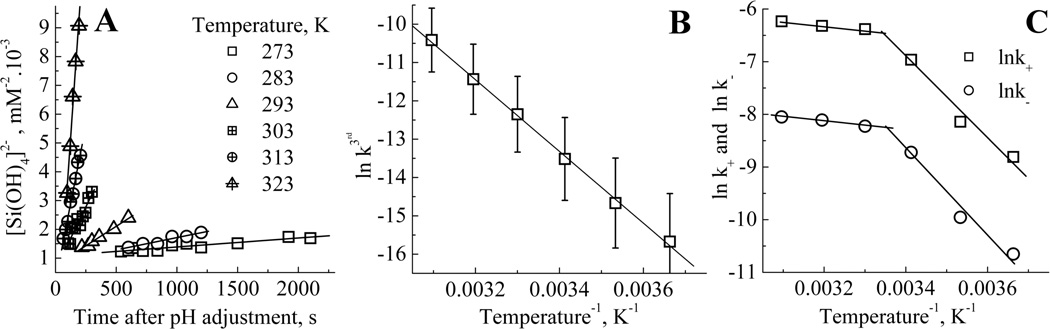
(A) apparent third order rate domains at 273 – 323K (B) Arrhenius plot of the apparent third order rates and (C) Arrhenius plot for the forward and reverse first order rate constants.

Speciation in 10mM condensing systems

In order to further differentiate molybdenum-active species of tetrameric or greater size during the early stages of condensation, the initial orthosilicic acid concentration was reduced to 10mM (Figure 5), with the aim of limiting the extent and speed of the conversion of oligomeric species to silica particulates. However, similarly to observations made for other metal ion systems, a lower [Si] will also reduce the proportion of such oligomers. At 10mM, the molybdenum blue activity remains virtually unaltered for about 10 minutes before measurable condensation occurs, Figure 5. Stable levels of total molybdenum active species were measured for 10 minutes after initiation of the condensation process. However, the rates of colour development of the samples did vary suggesting that the speciation pattern varied too. Fitting the molybdenum yellow complex data with three species representing monomer, trimer and larger oligomers gave R² values of 0.9991–0.9989. Fitting with a larger number of species gave rise to random fluctuations in the species concentrations, both due to the lower signal/noise ratio obtained for this concentration and to the inadequacy of the models using more than three species for this silicon concentration and condensation times analysed. The presence of a low level of trimer was detected even during the first minute of the reaction, the concentration of this species remaining fairly constant until the formation of a second condensed species (t = 30 min). For longer condensation times the trimer concentration decreased practically to zero whilst the level of the condensed oligomer continued to increase, this observation coinciding with the onset of a reduction in total molybdenum active species and is attributed to the formation of stable silicate oligomers not seen at a comparable stage in the condensation experiments performed at 30mM. According to modelling studies,^56,57 the formation of these more stable species is attributable to slow rearrangements and further condensation that is not allowed for in the faster condensing experiments performed at higher concentration.

Figure 5.

(A) Formation of silicomolybdic acid complex after increasing condensation times for 10mM initial [Si(OH)₄] at pH 6.8 and (B) Silicate speciation during the condensation process for 10mM initial [Si(OH)₄] at pH 6.8–3 species. The vertical line denotes the time at which corresponding molybdenum blue data was collected for the reactions.

In-depth kinetic analysis of the model system: Temperature and pH effects

Upon condensation, [Si₂O(OH)₆] dimers are formed as intermediate species, but do not seem to be observed from molybdenum yellow analysis. Moreover, these species, being able to dissociate into two equivalents of silicic acid during the complexation step of the assay, are not observed in the molybdenum blue assay. Further condensation of these species yields a trimer that is the first species not able to break down under the conditions of the assay. This stage is observed as the apparent loss of three equivalents of silicic acid and follows ‘apparent’ third order reaction kinetics. Although this process is reversible, the silicic acid concentration in solution lies well above the saturation level and the system is strongly driven towards condensation rather than redissolution. This is not the case for the addition of monomers to the trimer or larger oligomers that follows first order kinetics and rate constants for both the forward and the reverse reaction can be measured.

The effect of pH on the reaction process

The effect of pH on the rates of the early stages of silicic acid condensation was explored over the range 3.4–6.8 (measurements at higher pH were not made due to the presence of significant amounts of un-dissociated complex). Example raw data is given in the supporting information, Figure S2. The steep change in the apparent 3^rd order rate constant with pH (Table 1, Figure 6) reinforces the importance of carefully controlling acid addition to obtain meaningful data from model silicification experiments. E.g., an error of ±0.2 in pH from the model conditions would result in a discrepancy of ± 20% in the measured rate constant. The observed 3^rd order rate constants decreased sharply with pH, and at a pH of 3.4 no evidence of condensation was observed in the first 24 hours of measurement, although after 7 days the level of monosilicic acid had reduced by ca. 67% (data not shown). The log of the apparent third order rate constant shows a linear response with pH, i.e. with −log[H⁺], Figure 6B. Reversible first order rates also increased (both forward and reverse) with increasing pH but reached a limit for the highest pH values, this limit being absent from the apparent third order rate trend (Figure 6C). This difference in behaviour can be explained by considering the pK_as of monosilicic acid and particulate silica.² With a pK_a of 9.8, monosilicic acid has a weak tendency to deprotonate. The de-protonation of silanol groups on this species follows a linear trend between pH 5 and 8, with fewer than 2% of the silanols being deprotonated at pH 8. By comparison, colloidal silica particles are stronger acids with a pK_a of 6.8 and at a pH of 8, 94% of silanol groups are deprotonated. As the level of deprotonation increases so does the difficulty in removing more protons from the remaining silanol groups due to the increased charge density on the particles. Therefore the increase in the rate of condensation with pH is limited until at even higher pH (above 10) the silica will begin to re-dissolve. This behaviour is not observed for the 3^rd order rate domain as fewer than 1% of the orthosilicic acid molecules are anionic so there is no increased resistance to de-protonation with pH change. This data can be used to understand why additions of a range of molecules and ions to the model system significantly affects the reaction period where trimer formation is the dominant reaction as opposed to the time period where reversible 1^st order kinetics dominate.^37,38 A greater change in solution chemistry is required to influence the degree of ionisation of oligomers and particulate silica compared to monomer under the circumneutral pH conditions used for the in vitro studies of biosilicification.

The effect of temperature – calculation of activation energies

Experiments following the kinetics of silicic acid condensation were performed at temperatures between 273 and 323K. The increase in the apparent third order rate constant, k₃ with temperature highlights the need to conduct experiments with strict temperature control (Figure 7A and Table2).

Table 2.

Apparent third order rate constants derived from the appropriate domain data from the molybdenum blue [Si(OH)₄] assay.

Temperature of condensation/K	Apparent third order rate constant · 106/mM−2s−1
273	0.156
283	0.427
293	1.35
303	4.33
313	10.8
323	30.0

A discrepancy of only ±2°C results in approximately a ±20% variation in k₃. The beginning and end of the apparent third order domain were also shifted to earlier times upon temperature increase. The Arrhenius equation² was used to derive thermodynamic parameters from kinetic constants obtained at different temperatures:

$$k={{\displaystyle Ae}}^{\frac{-Ea}{RT}}$$ (2)

With k, the rate constant, T, the temperature, E_a the activation energy of the process and A, a term relating to the collisional frequency of the reacting species and the likelihood that they will be in the correct orientation to react. The plot of ln k₃ against T⁻¹ gave a linear trend (Figure 7B), emphasising the correct selection of the time intervals for determining the individual rate constants. The value for E_a obtained for the third order process was 77KJ·mol⁻¹. Similar treatment of the 1^st order domain data, Figure 7C gave activation energies for the forward and reverse condensation reactions of 55.0 and 58.6KJ·mol⁻¹ respectively. This is in good agreement with the results obtained by Harrison and Loton⁵ who measured an activation energy of 58KJ·mol⁻¹ over the 1^st order region but did not separate the forward and reverse rates. Activation energies for monomer condensation onto particles were also found to be of this order.⁵⁸ Activation energies of condensation reported elsewhere range from 13 to 85KJ·mol⁻¹.^{29,32,39,42–45,59–63} Activation energies determined for early condensation stages of a 1^st order process have been determined and range from 27KJ·mol⁻¹ for an apparent 1^st order reaction (using TEOS) up to 71KJ·mol⁻¹ calculated for monomer condensation on particles.⁶⁰ Variations of activation energies with pH^{32,42,44,45,61,62} and temperature²⁹ have been measured. Computational studies also give comparable values of 50KJ·mol⁻¹ for trimer formation and 95KJ·mol⁻¹ for dimer formation,⁶⁴ and demonstrated the effect of water on the reaction, with lower activation energies being obtained in excess water (55KJ·mol⁻¹), whereas higher values are obtained under anhydrous conditions (84KJ·mol⁻¹).⁶³

The activation energies obtained respectively for the forward and reverse processes reduce from 55 and 58.6 kJ·mol⁻¹ to 6.1 and 7.3 KJ·mol⁻¹ respectively for a temperature change between 20 and 30°C. At higher temperatures, both the duration and starting time of the first order condensation reaction stage decrease dramatically, making the transition between the kinetic domains difficult to isolate and may be the reason for the low activation energies found in this study. Therefore we only report here on the 1^st order kinetics at 303K and below where the apparent third order and first order regions are more easily isolable. The higher activation energy obtained for the apparent third order domain (77kJ·mol⁻¹) fits with the lower acidity of the silanol groups of monomers compared to equivalent groups on highly condensed species. This observation reinforces further the conclusions derived from the experiments performed under different pH conditions.

Discussion – relevance to biosilicification

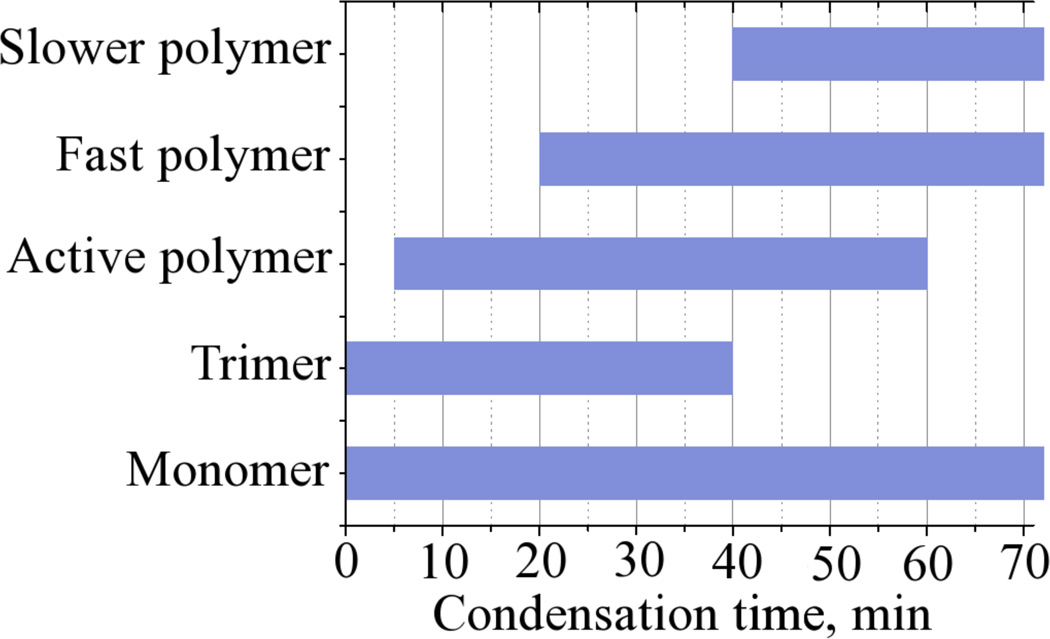
In this study we have analysed in detail a model system based on the hexa-coordinated silicon catechol complex, which has been central to our bio-inspired studies on silicification.^5,37,38,59 Upon pH adjustment, the system provides rapidly and stoichiometrically metastable solutions of monosilicic acid of controllable concentration. While the general methodology used for our previous studies included other aspects of analysis such as aggregation phenomena and the final materials properties, ^3,38,65 we focused here on the reaction kinetics and solution speciation pertinent to the early stages of the silicification process and identified time periods after which a range of oligomeric species were present in the condensing systems, Scheme 1.

Scheme 1.

Silicate species isolated by curve fitting of molybdenum yellow (silicomolybdic acid) data during the condensation of orthosilicic acid from an example 30mM condensing system

In order to understand mechanisms of biosilicification and to mimic biological silica formation, so called biomimetic and bioinspired in vitro model studies have been performed and reported in recent literature.^{6,7,9,37,65–73} Research into biological silicification has shown the involvement of catalytic biomolecules such as proteins and peptides.^1,22,74,75 In vitro model studies have used synthetic molecules (termed ’bioinspired additives’) which are derived from biomolecules identified to be responsible for biosilica formation. These model studies typically use a silica precursor and investigate the effects of the presence of a bioinspired additive, inorganic ions (e.g. phosphate), reaction pH, self-assembly of additives, etc. on silica formation.

Several aspects of silica formation have been investigated such as particle nucleation and growth, materials morphologies and porosities. However, the early stages of condensation involving monomeric, dimeric and oligomeric silicates have been rarely monitored. One possible reason for lack of understanding of initial condensation mechanisms is that not every chosen silica precursor can produce a pure solution of orthosilicic acid (rather a mixture of oligomeric silicates and partially hydrolysed/condensed precursor is formed). As a result, in vitro studies of biosilicification have predominantly focussed on additive-silica particle aggregation.^68,76,77 Exceptions are the studies of hydrolysis and condensation of monofunctional alkylalkoxysilanes where the precursor is allowed to form dimers while further reaction is restricted.^66,67

The use of a silicon-catecholate complex and the silicate speciation reported herein has allowed us to study closely the early stages of silicic acid condensation and selected examples are discussed. The amino acid lysine and its oligomers/polymers have been of great interest in silica formation and their presence in silica forming systems have produced spherical particles, granular gels and hexagonal plates.^8,9,69,78,79 However, these published reports did not probe the effect of lysine on the early stages of condensation and therefore concluded, based on the data available, that lysine promotes the aggregation of small silica particles in solution leading to silica precipitation under mild conditions.⁷⁶ In view of the results presented in this article, when the early stages of silicic acid condensation were studied in conjunction with particle growth, it was revealed that lysine (and its oligomers and polymers) increase the rates of silicic acid condensation (e.g. trimerisation). This effect became prominent as the chain length of lysine oligomers increased.³⁷ In addition to the effect of lysine on condensation rates, lysine was also found to promote aggregation of silica particles in solution³⁷ which supported the earlier findings reported in the literature.⁷⁶ The experimental approach described in this paper has allowed us to develop a greater understanding at the molecular level how polyamines inspired by those found in nature³³ are perfectly adapted to their function in the silicification process.^65,80 Furthermore, the mechanistic understanding of biological and bio-derived molecules in model studies of biosilica formation have enabled researchers to tailor the chemistry of additives and reaction conditions in order to generate materials with specified properties.⁸⁰ A further example is the role that hydroxyl-containing biomolecules (e.g. glycoproteins and proteins rich in amino acids such as serine and threonine) play in biosilicification. Previous studies suggested their involvement without any direct experimental evidence.^81,82 Using the approach outlined in this article a range of small molecules and proteins rich in hydroxyl groups have been shown to have little direct effect on the early stages of condensation in aqueous media.⁷¹

These examples clearly demonstrate the importance of the knowledge of silicate speciation in solutions with physiologically relevant pHs and the impact this knowledge can have on understanding biological silica formation.

Experimental

The following materials were purchased and used without further treatment: Dipotassium tris(1,2-benzene-diolato-O,O’)silicate (Silicon Catechol Complex, SCC) 97% (Sigma Aldrich); Oxalic acid dihydrate 99%, Ammonium Molybdate tetrahydrate 99%, 4-Methylaminophenol sulphate 99% (Acros organics); Hydrochloric acid 98%, Sodium Hydroxide 98%, Sodium Sulphite 99% (Fisher scientific); 1000ppm silica (as SiO₂) standard (BDH); Sodium-2,2-Dimethyl-2-Silapentane-5-Sulphonate (DSS) (MSD isotope).

Titrimetric / ¹H NMR study

Aqueous 30 mM·dm⁻³ solutions of SCC were titrated with freshly standardised 2 M·dm⁻³ solutions of hydrochloric acid by addition of 10µl aliquots and the pH monitored using a Radiometer PHM 240 pH meter fitted with a Mettler Toledo micro combination electrode. The stoichiometry of the acid dissociation was determined and then used to prepare solutions of SCC for ¹H NMR studies. The individually prepared samples (0–2.0 molar equivalents HCl) were monitored using a Jeol JNM-EX270 FT NMR spectrometer. The lock signal and chemical shift standard were supplied by use of an insert containing 1 mg·cm⁻³ 2,2-dimethyl-2-silapentane-5-sulphonate (DSS) in D₂O. Spectra were acquired using 32 scans and a relaxation delay of 1 second.

Molybdenum complexation studies

The molybdenum blue method routinely used by us and others to study the condensation of orthosilicic acid involves the formation of a yellow silicomolybdic acid complex which is then reduced to the more intensely coloured silicomolybdous acid complex, that is used for a more sensitive assay.⁹ The rate of formation of the yellow complex gives additional information on the silicate species present as the rate of dissociation of silicate oligomers to monomer is species dependent.¹³ In these studies the molybdenum yellow data was used for the first time to provide information on speciation changes with time during the condensation process. The molybdenum blue method was used to obtain information on changes in residual concentrations of orthosilicic acid with time and to obtain kinetic rate constants and activation energies for reactions occurring during the early stages of condensation. The required stock solutions (molybdic acid reagent and reducing reagent) were prepared as follows: Molybdic acid reagent stock: Ammonium molybdate·4H₂O (20g) and Hydrochloric acid (60cm³) were dissolved and made up to 1000cm³ with distilled and deionised water (ddH₂O). Working solutions were prepared by diluting 1.5cm³ of the stock solution with 15.0cm³ of ddH₂O. Reducing reagent (used for the molybdenum blue method): Oxalic acid (20g), 4-Methylaminophenolsulphate (6.67g) and sodium sulphite (4g) were dissolved in ddH₂O (500cm³). Concentrated sulphuric acid (100ml) was added and the solution made up to 1000cm³ with ddH₂O. 8.0cm³ of this solution was added after the silicomolybdic acid complex had been allowed to develop for 15 minutes.

Molybdenum yellow speciation studies

10µl of the condensing monosilicic acid solutions, (prepared by reduction of the pH of 10 and 30 mM·dm⁻³ solutions of dipotassium tris(1,2-benzenediolato-O,O’)silicate·2H₂O to 6.9±0.05 or where otherwise stated), were added to the working molybdic acid reagent solution at known time intervals between 0–24 hours. The formation of the yellow silicomolybdic acid complex was monitored at 370 and 410nm over a period of 30 minutes from the time of addition of the 10µl aliquot to the molybdic acid solution. Measurements made at 410nm gave far better results, for although the spectrometer response at 370nm was higher, the signal:noise ratio was much poorer due to interfering solution species contributing to the signal at the lower wavelength, Figure S3. Only the results of the 410nm measurements are presented in the main body of the paper.

The rate of silicomolybdic acid complexation is dependent on the rate of silicate oligomer dissociation in the molybdic acid reagent. Studies carried out using molybdic acid conditions of concentration and pH similar to here⁹ showed the complexation rate dependence on dissociation. Using calibration data obtained from solutions of known concentration, the curve of the silicic acid molybdenum yellow chelate concentration versus time was calculated from the A=f(t) curve (where A is the UV absorbance of the solution, t the time following mixing of the reagents and f, the relationship between A and t). The data was fitted with a theoretical function based on the assumption that the dissolution of all silicon species present obeys pseudo-first order kinetics and that the reaction of silicic acid with the reagent also obeys such a law. The fitting parameters comprise species concentrations together with their apparent rates of dissolution and the apparent rate of silicic acid reaction with the organic reagent.

Mathematical modelling of molybdenum yellow complexation

Speciation models of up to five species where tested during this study. When adding more species to the fitting model, the number of species was limited by : (a) Species which, during the fitting procedure, see their rates of dissolution converge to a similar value, indicating the existence of one species rather than two, and (b) The differentiation of slow-reacting species such as highly condensed oligomers, hampered by their very limited dissolution during the time of the assay. This limited dissolution leads to a low signal to noise ratio for such species, and random fluctuations in the speciation pattern as a result of uncertainties affecting the fitting process. For the fitting operation, a MatLab routine was used to limit the variation of apparent reaction rates for identical species present in different samples. The fitting algorithm uses a built-in nonlinear least-squares minimisation technique (MatLab curve-fitting toolbox) for the optimisation of curve-fitting parameters. The initial values of apparent rates were chosen on the basis of literature data (available with potassium as a counter ion)⁵ together with the analysis of pure samples of some of the species (monomer and highly condensed silica). The initial species concentrations were set equal to a fraction (10mM for three species) of the total concentration (30mM). The curves of the detected silicon concentration against time were then fitted a first time using an apparent first order model. The total silicon concentration for each sampling time was confirmed by digestion of sample portions with concentrated KOH and subsequent standard spectrophotometric measurement of the total digested silicon content using a standard molybdenum blue method. At the end of the initial fitting step, an apparent rate for each species reaction with the reagent was calculated as a average of the rates obtained for this species in the different samples analysed. To calculate this average rate for one species, the (silicon concentration, rate of complexation) parameter pairs obtained for the species in each sample after the first fit was used to calculate the average rate as a linear combination of the rates determined from different samples. New narrower boundaries for the variation of the kinetic constants were also determined, and the fitting/refinement operations reiterated until convergence of the parameters.

Molybdenum blue complexation studies

The molybdenum blue method was used to study the silicification process in model systems. The condensing systems used were prepared by adjustment of 30 mM SCC solutions to the desired pH (3.4–6.8±0.05) over a range of temperatures (0–50°C regulated by a thermostatically controlled water bath), and also using 10 mM SCC solutions adjusted to pH 6.8 and maintained at 25°C for slower condensation studies. 10µl aliquots of the condensing silicic acid solutions were added to the working molybdic acid reagent at known time intervals and left for 15 minutes before addition of the reducing reagent. Solutions were then left for at least 2 hours for the blue silicomolybdous acid complex to develop before measuring absorbance at 810nm. Levels of molybdenum active silicate species were determined against calibration standards prepared from dilutions of a stabilised 1000ppm SiO₂ standard.

Kinetic analysis of molybdenum blue data

Kinetic analysis of the orthosilicic acid condensation process was performed according to literature methods⁵ with data being fitted to [Si(OH)₄)]⁻² and ln([a]-[a_∞]) over appropriate time periods for apparent 3^rd and reversible 1^st order kinetics respectively (where a is the monomer concentration at time t, and a_∞ is the monomer concentration for an infinite condensation time. Four repeat determinations were carried out at 293±1K giving a number of degrees of freedom of n-1=3. For a 95% confidence with 3 degrees of freedom the t value is 3.182 and giving a confidence interval of 1.16·10⁻⁶±8.21·10⁻⁸ (≈9%) mM⁻²s⁻¹ for the apparent third order rate constant and 1.69·10⁻³±1.61·10⁻⁴ (≈7%)s⁻¹ for the overall reversible 1^st order. A sample analysed under the conditions used has therefore only 5% probability of falling outside of these intervals by systematic experimental error. Even relatively small changes observed in the determined rate constants can therefore be regarded as significant based on this analysis when using this model system.