Magnetorelaxometry Assisting Biomedical Applications of Magnetic Nanoparticles

Abstract

Due to their biocompatibility and small size, iron oxide magnetic nanoparticles (MNP) can be guided to virtually every biological environment. MNP are susceptible to external magnetic fields and can thus be used for transport of drugs and genes, for heat generation in magnetic hyperthermia or for contrast enhancement in magnetic resonance imaging of biological tissue. At the same time, their magnetic properties allow one to develop sensitive and specific measurement methods to non-invasively detect MNP, to quantify MNP distribution in tissue and to determine their binding state. In this article, we review the application of magnetorelaxometry (MRX) for MNP detection. The underlying physical properties of MNP responsible for the generation of the MRX signal with its characteristic parameters of relaxation amplitude and relaxation time are described. Existing single and multi-channel MRX devices are reviewed. Finally, we thoroughly describe some applications of MRX to cellular MNP quantification, MNP organ distribution and MNP-based binding assays. Providing specific MNP signals, a detection limit down to a few nanogram MNP, in-vivo capability in conscious animals and measurement times of a few seconds, MRX is a valuable tool to improve the application of MNP for diagnostic and therapeutic purposes.

Introduction

Physics of Magnetic Nanoparticles

Iron oxide nanoparticles represent a major class of particles used for novel magnetic applications in biomedicine, such as magnetic drug targeting, magnetic thermoablation, biosensors or molecular imaging. An overview over these applications is given in a number of review articles (1–8). Magnetic nanoparticles that are used for medical applications consist of a magnetite or maghemite core surrounded by a stabilizing and biocompatible coating. Due to the small core diameter of typically 4-30 nm, 10³–10⁴ atomic magnetic moments within one particle are coupled together resulting in a single domain of uniform magnetization with a total magnetic moment m given by

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ m = {M_{\text{p}}}{V_{\text{p}}} $$\end{document} 1

where M _p denotes the magnetization of the core material and V _p the core volume of the particle. Note that M _p is usually smaller than the saturation magnetization M _S of the bulk material.

Without an external field, the magnetic moments of an ensemble of magnetic nanoparticles in thermal equilibrium will be randomly oriented and no net magnetic moment will be seen in a distance from the assembly. In the presence of a magnetic field H, the magnetic moments of the nanoparticles will tend to align along the field direction, and a net magnetic moment will be generated. This phenomenon is commonly referred to by the notion superparamagnetism.

For isotropic and non-interacting particles in thermal equilibrium at a temperature T the fraction of the magnetic moments that are aligned give rise to the net magnetization M(H,T) that is described by the Langevin function relating the magnetic energy μ₀ H to the thermal energy k_B T

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ M(H,T) = {M_p}\left( {\coth \left( {\frac{{m{\mu_0}H}}{{{{\text{k}}_{\text{B}}}T}}} \right) - \frac{{{{\text{k}}_{\text{B}}}T}}{{m{\mu_0}H}}} \right) $$\end{document} 2

The equilibrium magnetization arising from a change of the external magnetic field H is not reached instantaneously but after a characteristic time τ _D by rotational diffusion of the magnetic moments within the particles, where (9).

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\tau_D} = \frac{{3{\eta_m}{V_p}}}{{{{\text{k}}_{\text{B}}}T}} $$\end{document} 3

The parameter \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\eta_m} = {M_S}/(6\alpha \gamma ) $$\end{document} denotes some kind of “magnetic” viscosity which hampers the rotational movement of the magnetic moments. The damping α and the gyromagnetic ratio γ are internal parameters characteristic of the particular nanoparticles’ crystal structure.

The actual magnetization behaviour of most magnetic nanoparticles is not isotropic, because of the presence of an effective magnetic anisotropy K, generally arising from a combination of magnetocrystalline and shape anisotropy. Due to this anisotropy, the magnetic moment has preferred orientations within the particle, along so-called easy axes representing local energy minima. For the simplest case of uniaxial anisotropy the energy barrier separating two minima is proportional to the volume of the particle, E _A = K V _p and the probability at a temperature T to surmount this energy barrier is given by the Néel relaxation time τ _Ν (10)

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\tau_{\text{N}}} = {\tau_0}\exp \left( {\frac{{K{V_p}}}{{{{\text{k}}_{\text{B}}}T}}} \right) $$\end{document} 4

where \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\tau_0} = 3{\eta_m}/K $$\end{document} is a damping or extinction time with values between 10⁻⁸ s and 10⁻¹² s (11) and k_B is the Boltzmann constant.

An additional relaxation mechanism appears if the magnetic nanoparticles are suspended in a carrier fluid of viscosity η, where the particles may rotate together with their magnetic moments. This is described by the Brownian relaxation time τ _B

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\tau_{\text{B}}} = \frac{{3\eta {V_h}}}{{{{\text{k}}_{\text{B}}}T}} $$\end{document} 5

with V _h denoting the hydrodynamic volume. Note that the rotating structure is not necessarily a single particle; it might be composed of several nanoparticles or of a magnetic nanoparticle bound to other colloidal objects. In any case, V _h in Eq. 5 refers to the overall hydrodynamic volume of the rotating colloidal structure.

If both relaxation mechanisms are present at the same time, the overall relaxation behaviour is described by an effective relaxation time τ _eff (12)

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\tau_{\text{eff}}} = \frac{{{\tau_{\text{N}}}{\tau_{\text{B}}}}}{{{\tau_{\text{N}}} + {\tau_{\text{B}}}}} $$\end{document} 6

with the shortest relaxation time prevailing. Figure 1 shows a logarithmic 2D plot of the effective relaxation time for different Néel and Brownian relaxation times according to Eq. 6 together with the corresponding core and hydrodynamic diameter assuming spherical magnetite MNP with an effective anisotropy K ~ 10⁴ J/m³. Additionally, the increase of relaxation time by increasing the shell thicknesses from 5 nm (white line) to 10 nm (red line) is visualized. This effect is much less pronounced when the total diameter is increased from 150 nm (orange line) to 160 nm (black line).

Fig. 1.

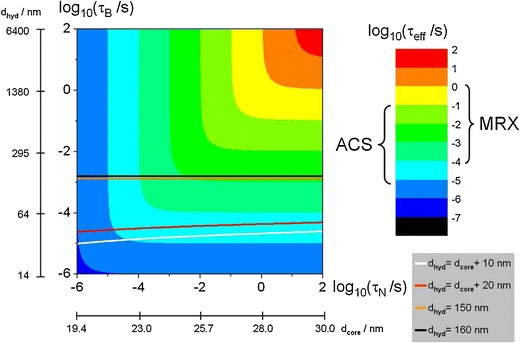
Logarithmic 2D plot of the effective relaxation time combining Néel (abscissa, Eq. 4) and Brownian relaxation (ordinate, Eq. 5) according to Eq. 6. Furthermore, the corresponding core and hydrodynamic diameter are displayed for magnetite MNP with an effective anisotropy K ~ 10⁴ J/m³. The straight lines have been added to show the influence of a fixed shell thickness of 5 nm (white line), 10 nm (red line) or a fixed hydrodynamic diameter of 150 nm (orange line) and 160 nm (black line) on the relaxation time with increasing core diameter.

Real nanoparticle systems usually exhibit a distribution of particle sizes and thereby also a distribution of relaxation times. Often, the log-normal distribution P _P(V _p) is taken to describe the particle core volume distribution

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {P_P}({V_P},{\mu_P},{\sigma_P}) = \frac{1}{{\sqrt {{2\pi }} \,{\sigma_P}\,{V_P}}}\exp \left( { - \frac{{{{\ln }^2}({V_P}/{\mu_p})}}{{2{\sigma_P^2}}}} \right) $$\end{document} 7

where μ _p is the median particle core volume and σ _p the standard deviation of the core volume distribution. Since according to Eq. 4 the Néel relaxation time depends on the core volume, the log-normal distribution of nanoparticle sizes also entails a log-normal distribution of relaxation times.

The distribution function P _h(V _h) of the hydrodynamic diameters is more variable and typically more complicated. An obvious lower bound is that for a given particle V _h > V _p.

Typical cases that can easily be modeled:

1. Single (spherical) nanoparticles with a fixed shell thickness d _s: V _h = π(d _P + 2d _s)³/6. In this case, V _h is still in the order of V _p.

2. Single nanoparticles where the shell thickness has another functional dependence on the particle diameter: V _h = f(V _P). Also in this case, V _h is typically in the order of V _p.

3. Aggregates of colloidal compartments with a lognormal distribution of aggregate volume characterized by its median μ _h and distribution width σ _h.

   \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {P_h}\left( {{V_h},{\mu_h},{\sigma_h}} \right) = \frac{1}{{\sqrt {{2\pi }} {\sigma_h}{V_h}}}\exp \left( { - \frac{{\ln^2 {{\left( {{V_h}/{\mu_h}} \right)}}}}{{2{\sigma_h}^2}}} \right) $$\end{document} 8

   In this case, V _h » V _p. The colloidal compartments might be magnetic, they might also consist of non-magnetic material. A special case of aggregates are so-called multicore particles, where a number of smaller magnetic cores are assembled within one organic shell. Due to the close distance between the different cores, the magnetic interaction between them can no longer be neglected for these multicore particles.

4. Immobilization of the nanoparticles to large or fixed objects: V _h = ∞ for all MNPs in the sample.

A superposition of these cases occurs in real world nanoparticle suspensions.

Due to the widely variable hydrodynamic diameter in colloidal dispersions, the effective relaxation time is only loosely dependent on the particle core volume as shown in Fig. 2.

Fig. 2.

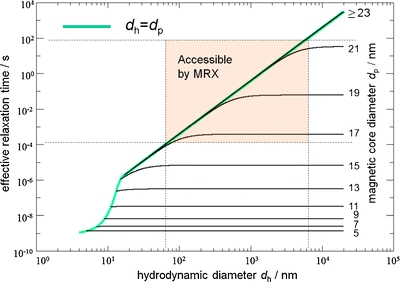
Effective relaxation time calculated by Eqs. (4–6) for different magnetic core diameters d _p as a function of the hydrodynamic diameter d _h for K _eff = 10⁴ J/m³, T = 290 K and η = 10⁻³ Pa·s. The shaded area is accessible by our MRX setup (10⁻⁴ s to 10² s), as determined by SQUID electronics dead time, sampling frequency and relaxation measurement interval. The green line indicates particles without a nonmagnetic shell layer where d _h = d _p. Immobilized particles are detectable only if they have a core diameter d _p of about 16 nm to 22 nm. If both Brownian and Néel relaxation are present, particles with d _p larger than 16 nm and at the same time d _h in the range from 50 nm to 5 μm are detectable by MRX. For particles with d _p ≥ 23 nm, only Brownian relaxation can be observed in the given time interval.

For a magnetic nanoparticle suspension, the overall distribution function of effective relaxation times is characterized by pairs of core volume and hydrodynamic volume:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ P = P\left( {{V_{\text{P}}},{V_{\text{h}}}} \right) $$\end{document} 9

Obviously, for a given particle formulation, the distribution of core diameters is independent of the binding state, whereas the hydrodynamic diameters and thus the effective relaxation times will be altered by a binding reaction or a cluster formation.

Magnetorelaxometry: Measurement Procedures and Experimental Implementation

The phenomenon of delayed magnetic response of ferri- or ferromagnetic materials to sudden changes of an external applied magnetic field has long been known and is commonly denoted as magnetic relaxation, magnetic viscosity or magnetic after effect (13). More recently, it was recognized that the measurement of this effect, i.e. in particular the measurement of the time dependent response of superparamagnetic nanoparticles to a sudden switch-off of the magnetic field, can be utilized to obtain specific information about the nanoparticles and their environment (14). Specific techniques and procedures of the measurement of these relaxation effects in magnetic nanoparticles are subsumed under the concept magnetorelaxometry.

As depicted in Fig. 3, a magnetorelaxometric measurement generally consists of two phases: A magnetizing phase when a magnetizing field of defined strength and duration partly aligns the MNP moments into the field direction, and a measurement phase, during which, shortly after the switching-off of the magnetizing field, the decaying magnetic field originating from the decay of the samples net magnetic moment is detected by a sensitive magnetic field sensors like SQUID, fluxgate (15) or optical magnetometer (16). The latter two sensor types enable even the observation of the magnetic nanoparticles during the magnetizing phase.

Fig. 3.

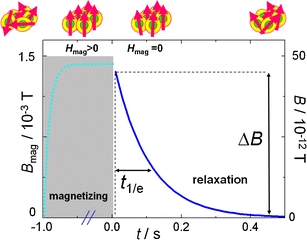
Magnetorelaxometry principle. The top line (from left to right) portrays a nanoparticle ensemble‘s behavior: initially in a disordered state without magnetization, partly rotated towards the field direction during magnetizing, and turning back into a randomly oriented distribution of magnetic moments leading to the detected magnetization relaxation. Typically a field of about 1.5 mT is applied for 1 s. After removal of the field and a short interval the SQUID amplifier needs to recover, the relaxation signals are acquired for 0.5 s.

The Magnetization of the Magnetic Nanoparticles

The net magnetization of a magnetic nanoparticle sample achieved at the end of the MRX magnetizing phase crucially depends on strength H _mag and duration t _mag of the externally applied magnetic field. Since a magnetic field reduces the barrier to reach the energy minimum in the Néel relaxation process and acts as a torque in the Brownian relaxation mechanism, we have to take into account the field influence on the magnetization time of the individual particles. For the Néel relaxation we have (17)

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\tau_{{{\text{mag,N}}}}}(H) = {\tau_{\text{N}}}\left( {1 - \frac{{0.82{\mu_0}H{M_S}}}{K}} \right) $$\end{document}

where τ _N is the Neel relaxation time as defined in Eq. 4. More sophisticated approaches for the field dependency of the Néel relaxation are discussed in (18) Accordingly, for Brownian relaxation the field dependency is found by simulations (19)

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\tau_{{{\text{mag,B}}}}}(H) = {\tau_{\text{B}}}{\left( {1 + 0.21{{\left( {\frac{{m{\mu_0}H}}{{{{\text{k}}_B}T}}} \right)}^2}} \right)^{{ - 1/2}}} $$\end{document}

If both mechanisms are present, the resulting effective relaxation time τ _mag(H) is given by Eq. 6 again. Thus, the initial magnetization amplitude M ₀ after a magnetization time t _mag is then

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {M_0}\left( {{t_{{mag}}}} \right) = \int\limits_{{{V_P}}} {\int\limits_{{{V_h}}} {M\left( {{V_p},{H_{{mag}}},T} \right)\left[ {1 - \exp \left( { - {t_{{mag}}}/{\tau_{{mag}}}\left( {{H_{{mag}}},{V_p},{V_h},T} \right)} \right)} \right]P\left( {{V_P},{V_h}} \right){\text{d}}{V_h}{\text{d}}{V_P}} } $$\end{document} 10

Here, M(V _p,H _mag,T) is the equilibrium value calculated according to Eq. 2. The total magnetic moment of the sample is the superposition of the magnetic moments of all single particles that were aligned by this procedure. Thus, the measurement of their subsequent relaxation by magnetorelaxometry represents an integral view on the ensemble of the magnetic nanoparticles in the sample.

The Relaxation of the Magnetic Nanoparticles

For a magnetic nanoparticle sample the relaxation process is described by

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ M(t) = \int\limits_{{{V_p}}} {\int\limits_{{{V_h}}} {{M_0}\left( {{V_p},{V_h}} \right)\exp \left( { - t/{\tau_{{eff}}}\left( {{V_p},{V_h}} \right)} \right)P\left( {{V_p},{V_h}} \right){\text{d}}{V_h}\,{\text{d}}{V_P}} } $$\end{document} 11

From the measured MRX relaxation curve two parameters can be extracted that describe its main features, the relaxation amplitude ΔB and a relaxation decay time t _1/e. The MRX relaxation amplitude is the magnetic field change between two selected time points within the recorded relaxation time interval. The MRX decay time t _1/e denotes the time after which the magnetic field value taken at a selected start point dropped by the factor e ≈ 2.718.

The appropriate number and type of magnetic field sensors for measuring the relaxation of the sample‘s effective magnetic moment is determined by the particular application. For several applications fluxgate and optical magnetometer having detection sensitivities down to 10⁻¹² T·Hz^−1/2 with a maximum bandwidth of about 10 kHz offer an acceptable way to apply magnetorelaxometry (15,16). At the cost of higher technical effort, the best sensitivity so far is reached by low T _c superconducting quantum interference devices (SQUIDs). These sensors enable the detection of magnetic fields as small as a few 10⁻¹⁵ T·Hz^−1/2, their bandwidth can reach several MHz. For measurement of samples at room temperature, the minimum distance between sample and SQUID is limited by the requirements of thermal insulation.

A sample of volume V containing a magnetization distribution M(r,t) originating from magnetic nanoparticles generates a magnetic flux density B(r,t) (hereafter simply termed magnetic field) outside the sample

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\mathbf{B}}({\mathbf{r}},t) = \frac{{{\mu_0}}}{{4\pi }}\int_V {\left( {\frac{{3{\mathbf{M}}({\mathbf{r}}\prime, t) \cdot ({\mathbf{r}} - {\mathbf{r}}\prime )({\mathbf{r}} - {\mathbf{r}}\prime )}}{{{{\left| {{\mathbf{r}} - {\mathbf{r}}\prime } \right|}^5}}} - \frac{{{\mathbf{M}}({\mathbf{r}}\prime, t)}}{{{{\left| {{\mathbf{r}} - {\mathbf{r}}\prime } \right|}^3}}}} \right)dV\prime } $$\end{document} 12

with the integration carried out over the sample volume V and with μ₀ (= 4π × 10⁻⁷ V·s/(A·m)) as the permeability of free space. Due to the relaxation of the MNP after turning off the magnetizing field, the magnetization M and hence the magnetic field B become time dependent. In cases where a magnetic nanoparticle accumulation can be assumed to be within a point-like region it can be described by a single magnetic moment m(r’,t) at r’. Eq. 12 simplifies then to the well-known formula describing the field of a magnetic dipole

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\mathbf{B}}({\mathbf{r}},t) = \frac{{{\mu_0}}}{{4\pi }}\left( {\frac{{{\mathbf{m}}({\mathbf{r}}\prime, t) \cdot ({\mathbf{r}} - {\mathbf{r}}\prime )({\mathbf{r}} - {\mathbf{r}}\prime )}}{{|{\mathbf{r}} - {\mathbf{r}}\prime {|^5}}} - \frac{{{\mathbf{m}}({\mathbf{r}}\prime, t)}}{{|{\mathbf{r}} - {\mathbf{r}}\prime {|^3}}}} \right) $$\end{document} 13

Equation 12 reflects the integral character of MRX: after magnetizing the sample volume, all magnetic nanoparticles in this volume contribute to the measured magnetic field signal at position r. As a consequence, MRX reflects all magnetic nanoparticles in the sample that exhibit a relaxation within the observation time window.

The observation time window is limited by the dead time of the SQUID sensor after the magnetizing field is switched off and the ending of the recording interval of the MRX signal. Particles having an effective relaxation time according to Eq. 6 that is much shorter than the dead time have decayed before they can be detected, thus they do not contribute to the MRX signal just as the time independent remanent magnetization. Further limiting factors of the magnetorelaxometric measurement technique are the upper limit of the signal bandwidth f _cutoff of the magnetic sensors and the sampling frequency f _s of the data acquisition system, only relaxation times with τ _eff > f ⁻¹_s and τ _eff > f _cutoff ⁻¹ can be resolved.

The detection parameters limit the range of particle sizes participating in the magnetorelaxometric measurement. The limits can be estimated by Eq. 3 as shown in Fig. 2. Assuming immobilized (Néel relaxation, solely) spherical iron oxide particles with a typical effective anisotropy of 10⁴ J/m³, only particles having a core diameter of about 16 nm to 22 nm are detectable in the time window of MRX (10⁻⁴ s to 10² s). If both Brownian and Néel relaxation are present, MNPs having core diameters larger than 16 nm and at the same time hydrodynamic diameters in the range from 50 nm to 5 μm are detectable by MRX. For particles with core diameters d _p ≥ 23 nm, only Brownian relaxation can be observed in the given time interval.

Magnetorelaxometry Measurement Devices

In order to meet the technical requirements for the two phases of a magnetorelaxometric measurement, an MRX device is composed of a magnetizing unit and one or more magnetic sensors that detect the relaxation. At present three different MRX systems all based on low T _c superconducting quantum interference device (SQUID) sensors are in use in our lab at PTB, as shown in Fig. 4. Low T_c SQUIDS have to be operated at low temperatures that usually are accomplished by housing the SQUIDs inside a Dewar cryostat filled with liquid Helium. Two of our SQUID based MRX devices are operated in a magnetically shielded room that suppresses environmental magnetic noise from outside, a third device has an integrated superconducting shield of its own. Due to the high performance of the PTB SQUID sensors and readout electronics, typically a bandwidth from dc to several megahertz and a dynamic range of over ±200 nT over a noise floor of 1.5 fT Hz^−1/2 can be achieved.

Fig. 4.

Magnetorelaxometry devices: a) single channel device, the inset draft shows the centre part of the system with the 150 μl sample container in the magnetizing coil about 12 mm below the SQUID sensor in the Dewar flask. b) 18 channel MRX scanner with integrated superconducting shield. The relaxation of samples and animals up to rabbit size are measured by circumferentially arranged 18 SQUID sensors (inset shows the sensor support chain) located midway of the horizontal warm bore. c) The PTB 304 channel vector magnetometer, the combination of this conventional biomagnetic measurement system operated inside a magnetically shielded room with a d) large Helmholtz coil system (d = 84 cm, located in front of the shielded room) allows MRX measurements on samples up to human size.

The single channel MRX system (1ch, Fig. 4a) used for high resolution MRX combines two SQUID sensors to form a spatial gradiometer arrangement for the suppression of magnetic far field distortions. At a distance of 12 mm below the nearest SQUID sensor located inside the tail of a liquid helium Dewar the samples of 150 μl volume (polyethylene microtiter vials) are placed inside the 10 mm bore of a twin coil (i.e. two parallel coils with opposite polarity to reduce their stray field at the SQUID location). Alternatively, larger samples up to 8 ml volume can be measured replacing the magnetizing coil by a larger twin coil of 27.5 mm bore diameter. Both twin coil systems can be energized by a magnetizing unit supplying magnetic fields up to 2 kA/m (2.5 mT).

In the first step, the sample is magnetized for 1 s. Following a 200 μs dead time interval after switching off the magnetic field that is required to recover the SQUID sensor electronics, the relaxation is recorded for typically 0.5 s, digitized at a 100 kHz sampling rate and 16 bit word length. The bandwidth of the MRX device is limited by the data acquisition unit. The short duration of one measurement makes repetitive measurements feasible, which may improve the signal-to-noise (SNR) ratio by signal averaging. For this setting, relaxation amplitudes ΔB down to 1 pT can be safely identified in an MRX measurement.

For MRX measurements of large sized samples up to human body dimensions, the PTB 304 SQUID vector magnetometer (Fig. 4c) is used—a home-made biomagnetic measurement system where the 304 SQUIDS are arranged in a large Dewar vessel in various orientations measuring the three magnetic field components that make up the magnetic field vector. For MRX applications this system is combined with a magnetizing unit composed of a gradient amplifier (Bruker) and a Helmholtz coil of 84 cm diameter (Fig. 4d). A DC current of 80 A is fed into the coil to provide a magnetizing field of 0.8 kA/m (1 mT). The large stray field of the Helmholtz coil requires the operation of the magnetizing coil outside the magnetically shielded room and the subsequent transport of the magnetized sample into the shielded room below the magnetometer. Since this transport is currently done manually, a dead time of 5 s to 10 s to record the relaxation after switching off the magnetizing field has to be taken into account. To compensate for this inevitably large dead time, the magnetizing field is applied for 60 s. According to Eq. 10 an extension of the magnetization time to 60 s gives also the large particles enough time to get aligned with the field so that the magnetization has reached its maximum value (for the given value of the magnetizing field). The data acquisition at a sampling rate of 250 Hz starts 10 s prior to switching off the magnetizing field by which the sample transport and start of the relaxation process are recorded. Thus the relaxation can be evaluated at the earliest moment when the sample has come to rest. The relaxation signals from the sample below the sensor are recorded for at least 75 s. During transport and measurements the door of the shielded room is kept open. This avoids further time loss and perturbations by the operation of the heavy sliding door, but admits the intrusion of low frequency magnetic noise signals of ±5 pT amplitude during the measurement phase, which limits the smallest detectable relaxation amplitude ΔB to about 10 pT for this setting.

In the third MRX device (Fig. 4b), 18 Helium cooled SQUIDs are arranged in a circle round a cylindrical horizontal warm bore, with 11 cm diameter being large enough to detect the relaxation signals from medium scale samples or animals up to rabbit size. This system enables MRX measurements in a typical laboratory environment, i.e. outside a shielded room. The necessary shielding is accomplished by a cylindrical superconducting Niobium shield which is integrated into this system. This magnetic shield is assembled within the liquid Helium tank of the Dewar vessel, but tightly aligned to the warm bore to keep environmental magnetic distortions from the SQUIDs. Sample magnetization can be performed either outside the warm bore, where a large variety of magnetic field sources can be used, or inside the warm bore at the sensor location by a Helmholtz coil with fields up to 4 mT. With this setup, the typical magnetizing duration amounts to 1 s followed by a 400 μs dead time interval, thus the relaxation data are acquired for 1 s at 100 kHz sampling rate and a 16 bit word length. For this device, a relaxation amplitude ΔB down to approximately 1 pT becomes detectable in an MRX measurement.

Applications

Exploiting the Relaxation Amplitude: Quantification and Localization of Magnetic Nanoparticles Administered to Organisms

The most relevant parameter for quantification and localization of MNP is the MRX relaxation amplitude ΔB. In addition, the relaxation curve should be assessed, because any changes in its shape may reflect changes of the particle size distribution during the MNP application and may add to the information of the quantification results. We classify the presented applications according to whether single channel or multi channel devices are used for MRX measurements.

Single Channel MRX: Quantification of Magnetic Nanoparticles in Tissue

Though of much less technical effort, single channel MRX provides a useful tool for quantifying MNP in tissue. A crucial issue in single channel MRX applications is the control of the distance between sample and detecting sensor, because the field of a magnetic dipole decays with the third power of the distance. As a consequence small sample sizes are preferred, with an extent that is much less than the distance to the sensor, so that a point-like magnetic source can be assumed. For larger sized samples a favourable relation between extent and distance can be achieved by increasing the distance between sensor and sample, but at the expense of reduced relaxation amplitude. To give a practical example, for measurements of tissue samples in a 8 ml container we usually increase this sample sensor distance to about 40 mm.

Our single channel device magnetizes m = (0,0,m _z) and detects relaxation signals B = (0,0,B _z) solely in z-direction. With the origin of the coordinate system at the sensor position and the sample position at r ’ = (0,0,z’) the magnetic field of a magnetic moment according to Eq. 12 is given by

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {B_z}(z) = \frac{{{\mu_0}}}{{2\pi }}\frac{{{m_z}}}{{|z - z\prime {|^3}}} $$\end{document} 14

A most efficient quantification procedure using single channel MRX is to refer the sample relaxation amplitude to the relaxation signal of a reference sample of known MNP content measured under the same conditions. By this we can bypass all peculiarities concerning the relaxation magnetization induced during the MRX magnetizing phase as described by Eq. 11.

Identical and Homogenous Sample Volumes

Typical applications are the quantification of the MNP content in blood samples, in small defined tissue samples supplied by a biopsy punch, or of MNP uptake by living cells (20). Here the samples are of identical shape and with a uniform magnetic nanoparticle distribution, so the nanoparticle amount of the sample X _MNP,sample is determined by the ratio of the relaxation curve amplitudes

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {X_{{MNP,sample}}} = \frac{{\Delta {B_{{z,sample}}}}}{{\Delta {B_{{z,reference}}}}}{X_{{MNP,reference}}} $$\end{document} 15

With X _MNP we denote either the total number N _MNP of MNP or the total iron mass m(Fe) in magnetic material depending on our knowledge of the reference sample. The iron amount of MNP reference samples is conveniently determined by photometry.

An important constraint noteworthy for any reliable MRX quantification is the congruence between sample and reference relaxation curve shape which assures that the MNP in sample and reference exhibit the same distribution of relaxation times. As an example Fig. 5a shows the relaxation curves of a small tissue sample together with the relaxation curves of two associated reference samples one with the MNP immobilized by freeze drying and the other in the original fluid state. The relaxation curve of the immobilized reference nearly perfectly matches the curve shape of the sample, thus being selected for the quantification.

Fig. 5.

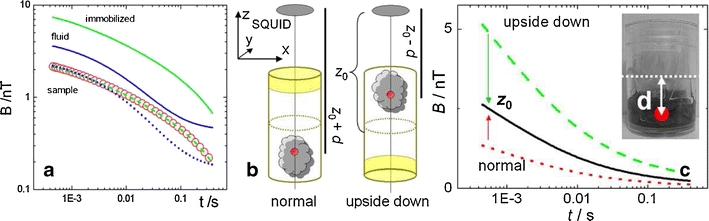
Quantifying the MNP amount of a small tissue sample by single channel MRX. (a) Relaxation curves of the sample piece together with immobilized and fluid MNP reference signals. An arbitrary constant offset B _ofs has been added to the relaxation curves solely for graphical representation. The blue dotted (fluid) and the green dashed (immobilized) curves are the reference signals normalized to match the sample curve. The normalization factor directly is proportional to the iron amount in the sample. (b) Determining the centre of a MNP accumulation in an irregularly shaped tissue sample by double MRX measurement reversing the sample. (c) Individual relaxation curves of an irregularly shaped pig lung sample (inset picture) containing MNP. Together with the relaxation curves of the sample measured in normal (dotted red curve) and upside down (dashed green) orientation the distance corrected relaxation curve (straight black) is displayed.

Quantification of Small Irregularly Shaped Samples

In many practical cases tissue samples show up in irregular shape. Thus, by simply applying the procedure described in "Identical and Homogenous Sample Volumes" quantification errors would emerge because the distance between MNP accumulation centre of the sample and SQUID sensor may differ from that of the homogeneous reference sample as illustrated in Fig. 5c. Examples are the quantification of uptake and clearance of MNP by a small tumor or inadvertently by different organs of small animals like mice, rats or rabbits.

In these cases the location of the magnetic source (assumed to be point like) inside the sample volume a priori is unknown, but can be determined by measuring the sample twice reversing the sample about the known distance d ₀ to the sensor, once in its normal posture and once again placing the sample upside down into the magnetizing coils as depicted in Fig. 5b.

Let z ₀ mark the distance between the center of the sample container to the sensor and thus the rotation axis for the sample reversion. Furthermore, d denotes the unknown displacement of the dipole location, depicted as a red circle in Fig. 5c, from position z ₀. So the dipole position is z’ = z ₀ + d for the normal and z’ = z ₀-d for the reversed sample position. Then, d = |z-z’| can be extracted from Eq. 14 introducing the ratio of the field amplitudes c = B _z,norm/B _z,rev

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ d = {z_0}\frac{{1 - {c^{{1/3}}}}}{{1 + {c^{{1/3}}}}} $$\end{document} 16

Conveniently, the absolute distance z ₀ between rotation axis and sensor is extracted from Eq. 16 by measuring the magnetic field of a small calibrated cylindrical coil with known magnetic moment supplied by a square-wave alternating current, which is positioned at the rotation point.

In our example a displacement of d = 9 mm was calculated using a rotation point distance z ₀ of 37 mm as determined by the calibration coil measurement. The quantification is then performed by means of Eq. 15 with the measured relaxation amplitudes of sample and reference first normalized to the distance z ₀ by \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {B_{{z,corr}}} = {B_{{z,norm}}}{({z_0} + d)^3}/z_0^3 = {B_{{z,rev}}}{({z_0} - d)^3}/{z_0}^3 $$\end{document}.

As an example of this scenario, the quantification of MNP in cell samples is described. In a cell culture experiment complexes of MNP with lentiviruses, carrying the test gene eGFP (for enhanced green fluoescent protein), were transduced to HUVECs (human umbilical vein endothelial cells) in a magnetic field gradient. For quantification of the MNP content within the cells after transduction, the HUVECs were harvested, fixated, counted and transferred in vials for the MRX measurement. The cells stacked at the bottom of the vial by gravity forces, so that the spatial distribution of the sample MNP distinguish from that of the reference sample, where the MNP were equally distributed. Thus, the cell samples were measured in up- and downward position and the center of gravity of MNP was estimated by (16). We found a deviation from the geometric center of the sample, 5 mm in height, of (2.2 ± 0.3) mm downwards. Accordingly, in the given setup, the quantification result was corrected by +35% compared to the result which would be obtained by (15) being valid for a homogeneous distribution of MNP in the measurement sample. The amount of MNP, quantified down to 1 pg/cell, correlated well with the gene expression, estimated by measurement of the green fluorescence light (20).

Reconstructing the MNP Distribution in a Sample of Larger Extension

The MRX approach based on "Quantification of Small Irregularly Shaped Samples" can be utilized for the spatially resolved quantitative reconstruction of a MNP distribution throughout an extended tissue sample. This was applied for ex-vivo quantification of MNP depositions in pig lungs after magnetic aerosol targeting (21). As shown in Fig. 6a the extracted lung lobe was first dissected into about 25 smaller pieces of about 2 cm³ volume. Each of these was quantified by MRX as described in "Quantification of Small Irregularly Shaped Samples" to obtain the absolute MNP content and then normalized to the corresponding tissue mass (leading to values for iron concentration in the tissue: μg Fe/g tissue). Finally, combining the single quantification results with the individual locations within the whole sample (see photography Fig. 6b), the MNP concentration distribution was reconstructed over the whole lung lobe with a centimetre spatial resolution. For the example shown the MNP were found nearly equally distributed over the whole lung lobe with a three-fold higher MNP uptake in the area of the main supplying bronchial tube. Additionally, the total absolute nanoparticle deposition within the whole lung and differences between individual lung lobes were determined.

Fig. 6.

Single channel MRX on dissected samples for quantitative reconstruction of a MNP distribution after magnetic aerosol targeting in a pig lung lobe (part. caudalis dorsalis, numbers indicate μg iron/g tissue. (a) MRX quantification results of each tissue piece normalized to tissue mass. (b) Reconstruction of the nanoparticle distribution superimposed onto a picture of the (intact) lung lobe.

For the type of MNP used and the tissue pieces dissected to fit into the 8 ml container, absolute iron amounts down to approximately m(Fe) = 200 ng could safely be detected. By refining the sample dissection and using 150 ml sample containers at the closest possible sample sensor distance even a millimeter spatial resolution becomes feasible, with the detection limit lowered to some 10 ng iron absolute. Note that this can only be regarded a rough estimation since the particular detection limit is to a large extent dependent on type and size parameters of the individual MNP used in an application.

Multi Channel MRX: Localization and Quantification of Magnetic Nanoparticle Accumulations in Tissue

The application of the dissection procedure described in "Reconstructing the MNP Distribution in a Sample of Larger Extension" often becomes impractical for larger sized samples or even impossible for in-vivo studies. In this situation, often spatial information in terms of the magnetic field distribution is of interest, because these data may help to reconstruct the distribution of the nanoparticle density within the tissue. This information can be obtained by scanning a single channel SQUID system across the object, or, more effectively, by using a multi-channel SQUID system. In a multi-channel system a number of magnetic field sensors are located at different sites in a large Dewar cryostat, which is positioned close to the sample. Depending on the distance and orientation of the sensor with respect to the object, the relaxation amplitude is different for each sensor, while the detected time dependent relaxation curve has the same shape (Fig. 7a). For a fixed sample, a multi-channel system registers a steady magnetic field pattern which decays monotonously in time (Fig. 7b).

Fig. 7.

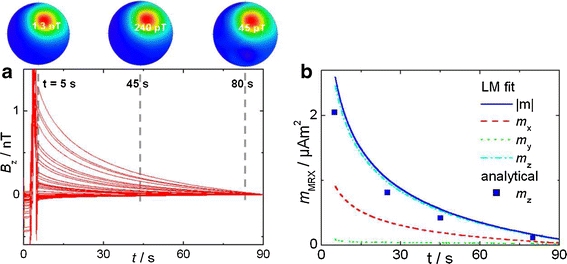
Multi channel MRX of a point-like MNP reference sample. Left) Relaxation curves (57 B _z-sensors) and corresponding magnetic field patterns at t = 5 s, 45 s, 80 s. Right) Decay of magnetic moments (m _x,m _y,m _z) of the MNP determined by Levenberg-Marquardt fitting and analytically for m _z from the magnetic field pattern.

A Single Point-Like MNP Accumulation

A single point-like MNP accumulation is the simplest case of a nanoparticle distribution, which is relatively easy to reconstruct from multichannel MRX data. Even if the real situation is more complicated, a point-like accumulation may be a useful model that may help to obtain a first overview. Mathematically, the determination of location and amount of a point-like magnetic nanoparticle accumulation from a measured relaxation field pattern at a given time point t means the inversion of Eq. 13.

This can be performed analytically if the direction of the magnetic field during the magnetizing phase coincides with the x-, y-, or z-direction, so that the localization of a point-like MNP accumulation can directly be read off from a magnetic field pattern (22). With the magnetizing field along the z-direction (x-direction) the lateral x,y position is located at the maximum B ₊ of the magnetic field pattern. The depth or z location is determined by the radius R of the zero line circle surrounding the field pattern, z = 2^−1/2 R, and the magnetic moment follows as m_z = (2π/μ₀)z³B₊ (m_x = (5^5/2π/(12μ₀))d³B₊). With the magnetizing field applied along the x-direction the lateral x,y-position is located half way between the two extreme values B ₊ and B ₋. The depth or z location is determined by the distance between B ₊ and B ₋, while the magnetic moment follows as m _x = 25/12 5^1/2 π/μ ₀  d ³ B ₊.

From four magnetic field patterns at t = 5 s, 25 s, 45 s, and 80 s we determined a MNP accumulation localized at x = 22 mm, y = 44 mm, and z = −68 mm) with the magnetic moment decaying with time as displayed in Fig. 7b. When magnetizing along z-direction the MNP accumulation centred below the 304ch device should be closer than 7 cm to the sensor area (of radius 11 cm) since otherwise the zero line of the field pattern would lie outside.

For an arbitrary magnetizing direction we use a non-linear Levenberg-Marquardt algorithm for fitting the three location parameters (x’,y’,z’) together with three magnetic moment (m _x(t),m _y(t),m _z(t)) parameters of the MNP accumulation describing best the corresponding magnetic field pattern of each relaxation time point according to Eq. 13. In this case, the location parameters x’,y’,z’ can be kept fixed in the fitting procedure, because the object does not move with respect to the sensor system. These results are displayed for the moments in Fig. 7.

Similar to the single channel situation of "Identical and Homogenous Sample Volumes", the absolute MNP amount then follows by normalizing the magnetic moment to the moment of a reference sample of known MNP content measured and analyzed under same conditions. Though strongly depending on particular MNP type and sample properties MNP accumulations down to some μg iron can reliably be quantified and the localization accuracy often lies below one millimetre.

In-Vivo Localization and Quantification of a Magnetic Point-Like MNP Accumulation

For in-vivo MRX measurements on animals (or even humans), additional signals from the respiration and muscle motion are superimposed to the relaxation signals even if the animal is kept fixed. An even greater challenge is the recording of a free moving conscious animal, where the location of magnetic moment of the MNP accumulation cannot be assumed constant for the fitting procedure.

As an example we present the in-vivo localization and quantification of a point like MNP accumulation in a carcinoma mouse model in a magnetic thermoablation treatment investigation (23) In this study, MNP were injected into the tumor and subjected to an alternating magnetic field which is absorbed by the particles and dissipated by delivering heat to the surrounding tissue. To assure an adequate heat production that kills the tumor cells, quantity and position of the MNP need to be continuously controlled. To this end, the location and amount of the MNP accumulation were repeatedly determined by 304ch MRX measurements of the conscious mouse, which was housed in a small cylindrically box.

Figure 8a shows the relaxation signal of a conscious mouse after MNP injection recorded by a central SQUID of the 304ch system together with corresponding field patterns (Fig. 8a top) at selected time points. The movement of the mouse becomes nicely visible in the field patterns, while the relaxation curves of the individual sensors detecting the magnetic field seem to be strongly distorted (Fig. 8a). However, fitting the field patterns at each time instant with the magnetic point dipole model Eq. 13 allows the identification of the spatial movement of the mouse (Fig. 8b) and the quantification of the magnetic moment relaxation of the nanoparticles (Fig. 8c).

Fig. 8.

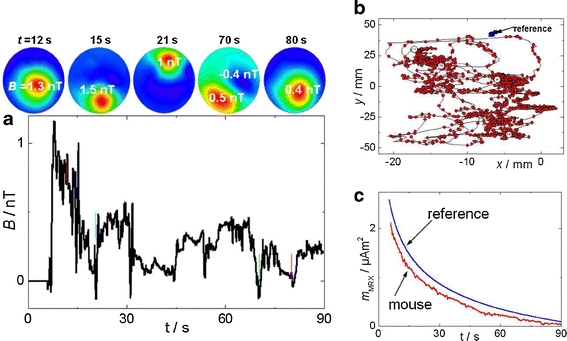
304ch-MRX quantification of a magnetic nanoparticle accumulation in a conscious mouse: a) the relaxation curve detection by the central SQUID sensor starts some 10 s after switching off the magnetizing field and transporting the conscious mouse housed in a plastic tube beneath the MRX device. Magnetic field pattern snapshots (top row) at time points t = 16 s, 19 s, 24 s, 71 s, 86 s display the point-like dipolar character of a nanoparticle accumulation moving relatively to the sensor positions. Fitting the field patterns for each point in time with the magnetic point dipole model Eq. 13 allows b) the identification of the spatial movement of the mouse and c) the detection of magnetic moment relaxation of the nanoparticles. For comparison the results for a fixed reference sample is added

Reconstruction of Extended MNP Accumulations

For the quantification and localization of magnetic nanoparticles distributed over larger extended tissue areas the magnetic point dipole is an inadequate model. Nonetheless, a quantification and localization still can be accomplished with appropriate adopted forward models. So far we have two different approaches implemented for magnetorelaxometry. As a straightforward expansion the multiple point dipoles model uses a number of point dipoles at predefined locations within a sample for the description of the measured magnetic relaxation field pattern (24). Additionally, adjusting the direction of the magnetizing field, only one parameter, the magnetic moment component pointing into that direction, remains free for each of the dipoles.

Alternatively, at somewhat higher computational cost, the measured magnetic relaxation field pattern can be analyzed by means of a multipole expansion (25). The resulting set of multipole coefficients in combination with an appropriate choice of a magnetization distribution model enables extracting important quantities like the total magnetic moment, the location and even the extension of an accumulation.

Investigating the Relaxation Curve Shape: Interactions of Magnetic Nanoparticles with Their Biological Environment

MNPs as Probes of the Local Hydrodynamic Environment

Magnetorelaxometry displays the superposition of signals from all individual nanoparticles that are suspended in the liquid of the sample. Even though this is an integral approach to monitor the behaviour of magnetic nanoparticles, MNPs may serve as probes of the local hydrodynamic environment. As it was pointed out in the introduction, the Brownian relaxation time of a given nanoparticle suspended in a fluid medium depends on its hydrodynamic volume, which includes the nonmagnetic (e.g. polymeric) shell surrounding the magnetic core as well as possibly a hydration layer. The shape of the magnetic relaxation curve reflects the local hydrodynamic environment of the MNP.

The organic molecules of the nanoparticle shell can be covalently or ionically bound to reactive biomolecules. Any conformational change or chemical reaction of these biomolecules with analytes in the suspension will alter the hydrodynamic shape of the MNP. By this mechanism, the binding reaction of a biomolecule and an analyte can be monitored in terms of a change of the relaxation behaviour, so that MRX measurement data may even provide insight into the microscopic behaviour of biochemical reactions.

A number of applications have been suggested that utilize this mechanism, among them the so-called magnetic relaxation immunoassay (MARIA) (26). In addition to the liquid phase MRX immunoassay there are various assay layouts where the analyte is not dissolved in the carrier medium (Fig. 9a) but immobilized, e.g., by attaching it to a rigid surface (Fig. 9b) or to the surface of latex beads of much larger dimensions than that of the MNP, say, with diameters of around a micrometer. In such a setting, the Brownian relaxation is fully suppressed by the binding reaction, so that only the Néel mechanism is active, leading to a slower effective relaxation. In Fig. 9c, a bead based assay is depicted, where the analyte is fixed to large beads in the range 0.1.1 μm leading to a distinct change in hydrodynamic size (27).

Fig. 9.

Different kinds of MNP based binding-assays for biomolecule detection by MRX: (a) solid phase, (b) liquid phase, (c) bead based, (d) agglutination assay

Yet another type of assay (Fig. 9d) is the agglutination assay, which was recently suggested (28). In the agglutination assay, both the MNP and the analyte exhibit multiple binding sites so that at a certain concentration ratio the analytes give rise to multiple cross-linking between the particles. This results in the formation of large agglomerates, consisting of networks having relatively large hydrodynamic diameters.

In general, a series of MRX measurements is necessary to interpret the relaxation measurements in terms of changes in the local hydrodynamic environment. The first step is an MRX measurement that documents the initial state of the MNP system under investigation. Then, the physical parameters or the chemical composition of the sample is altered eventually leading to a change in the hydrodynamic behaviour of the MNPs, which is reflected by changes of the MRX relaxation curve over subsequent measurements. Control measurements with removed or saturated binding sites both on MNPs and on the analyte are in most cases appropriate to demonstrate the specificity of the hydrodynamic changes.

In the following, three practical approaches that quantify MRX curve shape changes are discussed: 1) the comparison to reference curves for the relaxation of bound and unbound nanoparticles, 2) the parameterization of the relaxation curve by a typical relaxation time t _1/e and 3) modelling of the relaxation curve by assuming a special distribution function for the hydrodynamic diameters.

Characterization of the Relaxation Curve by Reference Curves

In the case of the solid phase assay layout where the rotational diffusion of the bound particles is fully suppressed, the relaxation behavior of an individual particle changes only upon the binding process, but remains unchanged as long as the nanoparticle is in its initial state. Thus, the task is to discriminate the signal contributions of bound and unbound particles, where both fractions are characterized by a well defined relaxation behavior. The most effective way to obtain reference data for the discrimination task is by measuring separately MRX curves of nanoparticles in the bound and in the unbound state. This is easily done by using samples of the nanoparticle preparations in solution for the reference signal B _ub(t) of unbound particles and freeze-dried samples for the reference signal B _b(t) of bound and immobilized particles.

The measured relaxation curve B(t) is modelled as the superposition \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \hat{B}(t) $$\end{document} of the reference curves B _b(t) for bound and B _ub(t) for unbound MNP, complemented by an arbitrary constant offset B _offs that cannot be avoided in measurements using SQUIDs:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \hat{B}(t) = a[\beta {B_{\text{b}}}(t) + (1 - \beta ){B_{\text{ub}}}(t)] + {B_{{offs}}} $$\end{document} 17

The parameter a describes the iron content of the measured sample in relation to that of the reference sample, and β describes the fraction of bound MNP. In matrix notation, Eq. 17 is written as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\mathbf{\hat{B}}} = {\mathbf{Pz}}\;{\text{with}}\;{\mathbf{P}} = \left[ {\begin{array}{*{20}{c}} {{{\mathbf{B}}_{{\mathbf{b}}}}} & {{{\mathbf{B}}_{{\mathbf{u}{\mathbf{b}}}}}} & 1 \\ \end{array} } \right]\;{\text{and}}\;{\mathbf{z}}\left[ {\begin{array}{*{20}{c}} {a\beta } \\ {a(1 - \beta )} \\ {{B_{\text{offs}}}} \\ \end{array} } \right] $$\end{document} 18

The model is related to the vector of measured data B by introducing a vector of model deviations u:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\mathbf{B}} = {\mathbf{\hat{B}}} + {\mathbf{u}} = {\mathbf{Pz}} + {\mathbf{u}}\quad {\text{with}}\quad {\mathbf{u}} = \left[ {\begin{array}{*{20}{c}} {{B_1} - {{\hat{B}}_1}} \\ \vdots \\ {{B_K} - {{\hat{B}}_K}} \\ \end{array} } \right] $$\end{document} 19

The unknown parameter vector z is found by minimizing the variance of u which is satisfied for the ordinary least square estimator z _OLS:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {{\mathbf{z}}_{\text{OLS}}} = \left[ {\begin{array}{*{20}{c}} {a\beta } \\ {a\left( {1 - \beta } \right)} \\ {{B_{\text{offs}}}} \\ \end{array} } \right] \equiv \left[ {\begin{array}{*{20}{c}} {{k_1}} \\ {{k_2}} \\ {{B_{{offs}}}} \\ \end{array} } \right] = {{\mathbf{P}}^{ + }}{\mathbf{B}} = {\left( {{{\mathbf{P}}^{{\mathbf{T}}}}{\mathbf{P}}} \right)^{{ - 1}}}{{\mathbf{P}}^{{\mathbf{T}}}}{\mathbf{B}} $$\end{document} 20

Here, P ⁺ denotes the Moore-Penrose pseudoinverse of P. The fraction of bound magnetic nanoparticles is then easily calculated as \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\beta} = {k_{{1}}}/\left( {{k_{{1}}} + {k_{{2}}}} \right) $$\end{document} and the relative iron content follows as \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ a = {k_{{1}}} + {k_{{2}}} $$\end{document}.

Since an MRX measurement can be repeated in intervals of a few seconds and washing steps are not necessary, β can be updated with a temporal resolution of a few seconds. Thus, the method may be used as a tool to monitor the binding kinetics of a reaction that proceeds within a corresponding time interval.

Characterization of the Relaxation Curves by t_1/e

In some assay types, e.g. in the agglutination assay (Fig. 9d), the distribution of hydrodynamic diameters of the colloidal entities containing nanoparticles is permanently changing throughout the binding process. Consequently, while the distribution of magnetic core diameters will remain constant, the distribution P(d _h) of hydrodynamic diameters at a specific time instant t is not known. In this case, it is impossible to use reference curves for quantification of the binding process as it was proposed in section "Characterization of the Relaxation Curve by Reference Curves". A pragmatic way to document a change in curve shape is given by computing t _1/e, i.e. the time when the amplitude of the relaxation signal has reached 1/e of its initial value. The total signal is the superposition of all relaxation processes occurring with τ _eff = τ _eff(d _p,d _h) in the suspension. Especially for larger so-called “blocked” particles, where τ _N > > t _meas, the effective relaxation time τ _eff is direct proportional to the hydrodynamic volume V _h and all changes in the hydrodynamic volume V _h are reflected in t _1/e.

A significant rise in t _1/e means increased hydrodynamic diameters of the colloidal compartments and may indicate aggregation processes. Thus, this method can provide an efficient quality check of MNP suspensions.

Parameter Estimation for the Distribution of Hydrodynamic Diameters

Under the assumption of a special distribution function for the hydrodynamic diameters, the parameters of this distribution can be estimated from the relaxation data. A typical example is the assumption of a lognormal distribution of hydrodynamic diameters d _h, as in Eq. 8. By fitting this model to the measurement data via a nonlinear fitting routine, the mean hydrodynamic diameter μ _h and the distribution width σ _h can be estimated.

Conclusion

Magnetic nanoparticles have a wide range of applications in medicine and biomedical research. Their physical properties enable the measurement of a magnetic relaxation signal after a rapid change of an external magnetic field. The relaxation signal depends on core sizes and hydrodynamic volumes of the MNPs. Because neither the surrounding biological environment nor any remanent magnetic material in the vicinity will generate such relaxation signals, magnetorelaxometry is highly specific for MNPs.

Thus the quantification of MNP in living conscious animals is feasible. The temporal decoupling from the large change in excitation field allows one the use of ultrasensitive SQUID sensors for readout of the magnetic relaxation signals. This technique together with the high specificity of MRX measurements make the quantitative determination of the MNP content in large tissue samples down to a few picogram possible. The analysis of the MNP relaxation curves enables the observation of colloidal structure changes.