FAST WAVELET-BASED SINGLE-PARTICLE RECONSTRUCTION IN CRYO-EM

Abstract

This paper presents a novel algorithm for the 3D tomographic inversion problem that arises in single-particle electron cryo-microscopy (Cryo-EM). It is based on two key components: 1) a variational formulation that promotes sparsity in the wavelet domain and 2) the Toeplitz structure of the combined projection/back-projection operator. The first idea has proven to be very effective for the recovery of piecewise-smooth signals, which is confirmed by our numerical experiments. The second idea allows for a computationally efficient implementation of the reconstruction procedure, using only one circulant convolution per iteration.

1. INTRODUCTION

Together with X-ray crystallography and nuclear magnetic resonance (NMR) spectroscopy, electron cryo-microscopy (Cryo-EM) is one of the key techniques for determining the structure of biological macromolecules. Cryo-EM can achieve resolutions in the nanometer range and can be used for imaging a variety of subcellular components [1]. While X-ray crystallography can provide sub-atomic resolutions, Cryo-EM has the advantage of a simpler specimen preparation, as it does not require crystallization. It is also more suitable for imaging large molecules than NMR.

One of the main challenges of Cryo-EM lies in the high radiation sensitivity of biological samples. Even when using a low-dose mode, imaging a sample ultimately leads to its destruction. The maximum tolerance is on the order of 5 to 10 electrons per square Ångström, leading to signal-to-noise ratios (SNR) that are sometimes well below unity [2].

3D cryo-EM imaging techniques can be divided into two main categories: 1) electron tomography, where the specimen is physically tilted along a single axis and imaged several times, and 2) “single-particle” reconstruction, where the sample contains multiple copies of the same molecule under different orientations, which are imaged only once. The first category has the advantage that the projection angles are known, thus allowing for standard tomographic inversion procedures. For the second category, the orientations of the molecules are usually unknown. While this requires a broader computational framework for the reconstruction, it potentially allows for improved SNRs (through data averaging) and higher resolutions (thanks to the lower radiation and absence of a “missing-frequency wedge”).

The main steps of a full single-particle reconstruction procedure can be summarized as follows.

1. Preprocessing: the individual molecules are detected and extracted from the acquired data.

2. Class averaging: images with high correlation are averaged together to improve their SNR.

3. Orientation estimation: this is done either via finding common lines in the frequency domain (based on the projection-slice theorem stated below) or via reprojection (based on a correlation measurement with templates generated from a previous reconstruction). This step may also include a shift estimation.

4. Reconstruction: a 3D image is generated by a tomographic inversion algorithm.

5. Iterative refinement: the whole procedure is repeated from step 3, using the outcome of the most recent reconstruction to improve the results.

The diversity of pattern-recognition and image-processing problems that need to be solved at each of these steps constitutes very fertile grounds for algorithm development. Here we will focus on the reconstruction step.

The reconstruction algorithms that are most commonly found in the literature—see [3] for a recent review—are either based on a direct inversion in the frequency-domain (filtered back-projection, gridding) or on a quadratic variational formulation. In particular, least squares and regularized least squares formulations are still very much in use, typically leading to linear reconstruction procedures such as the Landweber algorithm or the Kaczmarz (ART) method.

The present work has two main aspects. First, we use a non-quadratic regularization that favors estimates with a sparse wavelet expansion. Wavelet-domain sparsity has proven to be successful paradigm for a wide range of other inverse problems—see e.g. [4] for a recent application to optical microscopy. It leads to a non-linear variant of the Landweber algorithm that incorporates a wavelet-domain thresholding operation at every iteration.

Second, we take advantange of the Toeplitz structure of the iteration operator, which allows for a computationally effective implementation of the algorithm. Furthermore, we precompute recurring quantities using non-uniform FFTs [5]. The Toeplitz property appears in [5] and has been used e.g. for 2D magnetic-resonance imaging [6, 7, 8], but to our knowledge it is not commonly exploited in the context of 3D Cryo-EM.

2. STRUCTURE OF THE IMAGING MODEL

2.1. Fourier-transform conventions

We will use the following definition for the Fourier transform of a D-dimensional function f(x) = f(x₁, …, x_D):

$$\mathrm{f̂}({\omega }_1,\dots ,{\omega }_D)=\mathrm{f̂}(\mathit{\omega })={\displaystyle {\int }_{{ℝ}^D}}f(\mathbf{x})e^{-i{\mathit{\omega }}^T\mathbf{x}}\mathrm{d}\mathbf{x}.$$

Given an even integer N > 0, we define S_N = {−N/2, …, N/2 − 1}. In this paper we will consider D-dimensional discrete signals indexed in $S_N^D$. To distinguish them from functions, we will use square brackets, such as in f[n] = f[n₁, …, n_D]. With these conventions, the Discrete Fourier Transform (DFT) is defined as

$$\mathrm{f̂}[k_1,\dots ,k_D]=\mathrm{f̂}[\mathbf{k}]={\displaystyle \sum _{\mathbf{n}\in S_N^D}}f[\mathbf{n}]e^{-i2\pi {\mathbf{k}}^T\mathbf{n}/N}.$$

2.2. The projection-slice theorem

In the context of electron microscopy, a molecule is characterized by its Coulomb potential, a function of the three spatial coordinates f(x) = f(x₁, x₂, x₃). A simple model for Cryo-EM imaging is a projection along the axial direction of the microscope, say x₃:

$$𝒫f(x_1,x_2)={\displaystyle {\int }_{ℝ}}f(x_1,x_2,x_3)\mathrm{d}{x}_3.$$

In practice we observe a large number of projections of the same molecule under different (random) orientations. Each orientation is associated with a certain rotation matrix R and its corresponding rotation operator ℛf(x) = f(Rx). With the above definition of the Fourier transform, we have:

Property 1 (Projection-slice theorem).

$$\widehat{𝒫ℛf}({\omega }_1,{\omega }_2)=ℛ\mathrm{f̂}({\omega }_1,{\omega }_2,0)$$

In the sequel we will index the rotation operators and matrices corresponding to the different orientations of the molecule by p ∈ {1, …, P}.

2.3. Discretization

Let us assume that f(x) is supported in the open ball B(r) = {x ∈ ℝ³ | ‖x‖ < r}, and that we measure the samples

$$g_p[\mathbf{n}]=𝒫{ℛ}_{p}f(2r\mathbf{n}/N)\text{ for }\mathbf{n}\in S_N^2.$$

From these measurements, our goal will be to reconstruct the samples

$$f[\mathbf{n}]=f(2r\mathbf{n}/N)\text{ for }\mathbf{n}\in S_N^3.$$

When N is sufficiently large, the continuous Fourier transforms in the projection-slice theorem can be approximated using Riemann sums. This leads to the following model (which is in terms of the DFTs of the measurements).

Property 2 (Discretized imaging model).

For $\mathbf{k}=[k_1,k_2]\in S_N^2$, define ω_p,k = 2πR_p[k₁ k₂ 0]^T/N. Then ĝ = Af + b̂, where the operator A is defined as

$${(\mathit{\text{Af}})}_p[\mathbf{k}]=\frac{r}{N}{\displaystyle \sum _{\mathbf{n}\in S_N^3}}f[\mathbf{n}]e^{-i{\mathit{\omega }}_{p,\mathbf{k}}^T\mathbf{n}.}$$

and b̂_p[k] represents measurement and discretization errors.

In the remainder of this paper, the symbol f will refer to the discrete signal f[n].

3. WAVELET-REGULARIZED RECONSTRUCTION

Standard variational approaches to single-particle reconstruction are based on the minimization of a cost functional of the form

$$𝒞(f)={\Vert ĝ-\mathit{\text{Af}}\Vert }_{{\ell }_2}^2+\lambda 𝒬(f),$$

where 𝒬(f) is a quadratic regularization term. A typical choice is the squared ℓ₂ norm of a discretized Laplacian applied to f, which favors smooth solutions as λ increases.

In this paper we will set 𝒬(f) = ‖W f‖_ℓ1, where W represents a wavelet decomposition operator (for simplicity, we will assume that the wavelet basis is orthonormal). The key idea is that, compared to a standard ℓ₂ norm, the ℓ₁ norm behaves as follows: small coefficients are more penalized and large coefficients are less penalized. Thus we favor solutions whose energy is concentrated in a small number of large wavelet coefficients.

3.1. The thresholded Landweber algorithm

Using results from the theory of non-smooth convex optimization [9], it can be shown that f is a minimizer if and only if it is a fixed point of the non-linear operator

$$U\{f\}=W^{*}{T}_{\lambda \tau /2}\{W(f-\tau A^{*}\mathit{\text{Af}}+\tau A^{*}ĝ)\}.$$

Here τ is a step-size parameter, A* is the adjoint of A and T_λτ/2 denotes the a soft-thresholding operation (see e.g. [4]). This leads to a non-linear iterative reconstruction procedure defined by f^(k+1) = U{f^(k)}. Note that without thresholding (λ = 0), one recovers the standard Landweber iteration.

An important observation is that the computation of h = A*ĝ can be done once and for all in the beginning and thus the iteration essentially boils down to the application of the symmetrized operator A*A. The adjoint of A can be expressed as

$$h[\mathbf{n}]=A^{*}ĝ[\mathbf{n}]=\frac{r}{N}{\displaystyle \sum _{p,\mathbf{k}}}{ĝ}_p[\mathbf{k}]e^{i{\mathit{\omega }}_{p,\mathbf{k}}^T\mathbf{n}.}$$ (1)

For the operator A*A, we will use the following result:

Property 3 (Toeplitz structure of the symmetrized operator).

$$A^{*}\mathit{\text{Af}}[\mathbf{n}]={\displaystyle \sum _{\mathbf{k}\in S_N^3}}f[\mathbf{k}]c[\mathbf{n}-\mathbf{k}],$$

where, for $\mathbf{n}\in S_{2N}^3$,

$$c[\mathbf{n}]=\frac{r^2}{N^2}{\displaystyle \sum _{p,\mathbf{k}}}{e}^{i{\mathit{\omega }}_{p,\mathbf{k}}^T\mathbf{n}}.$$ (2)

This property allows for a fast implementation of the symmetrized operator: once the convolution kernel c[n] has been precomputed, it is sufficient to extend f[n] to the domain $S_{2N}^3$ by zero-padding, to perform a circular convolution with c[n], and to restrict the result back to $S_N^3$. The circulant convolution can be computed efficiently in the frequency domain using the FFT algorithm.

3.2. Back-projection and kernel computation

It remains to explain how to compute the back-projection h[n] and the kernel c[n] efficiently. Formula (1), as well as its particular case (2), is not a standard DFT because the frequencies ω_p,k do not necessarily lie on the grid $\frac{2\pi }{N}{S}_N^3$. We thus use the (type-1) non-uniform FFT algorithm [5], which is based on the following steps:

1. interpolate the frequency coefficients on a (usually finer-resolution) uniform grid (Cost: 𝒪(N²P));

2. apply a uniform FFT algorithm (Cost: 𝒪(N³ log N));

3. compensate for the effect of the interpolation procedure by a coefficient-wise division (Cost: 𝒪(N)).

In practice the interpolation step often has the dominant computational cost. It requires choosing a window function whose spatial expression w(x) and Fourier transform ŵ(ω) are known analytically (typically a Gaussian). To compute (1) we can then define

$$â(\mathit{\omega }){\displaystyle \sum _{p,\mathbf{k}}}{ĝ}_p[\mathbf{k}]ŵ(\mathit{\omega }-{\mathit{\omega }}_{p,\mathbf{k}}),$$

whose inverse Fourier transform is

$$\frac{1}{{(2\pi )}^D}{\displaystyle {\int }_{{ℝ}^D}}â(\mathit{\omega })e^{i{\mathit{\omega }}^T\mathbf{n}}d\mathit{\omega }=w(\mathbf{x}){\displaystyle \sum _{p,\mathbf{k}}}{ĝ}_p[\mathbf{k}]e^{i{\mathit{\omega }}_{p,\mathbf{k}}^T\mathbf{x}}.$$

In particular, for x = n ∈ S^D, we can write that

$$\frac{1}{{(2\pi )}^D}{\displaystyle {\int }_{{[-\pi ,\pi ]}^D}}ã(\mathit{\omega })e^{i{\mathit{\omega }}^T\mathbf{n}}d\mathit{\omega }=w(\mathbf{n})h[\mathbf{n}],$$

where ã(ω) = ∑_k∈ℤ^D ã(ω − 2πk).

Replacing the last integral by a Riemann sum leads to

$$h[\mathbf{n}]\approx \frac{1}{w(\mathbf{n})M^D}{\displaystyle \sum _{\mathbf{m}\in S_M^3}}ã(2\pi \mathbf{m}/M)e^{i2\pi {\mathbf{m}}^T\mathbf{n}/M},$$

where M is a (small) multiple of N that can be freely chosen. The above sum is an inverse DFT of the coefficients ã[m] = ã(2πm/M), which are obtained through a non-uniform interpolation procedure (with periodic boundary conditions).

4. NUMERICAL EXPERIMENTS

We now present the results of two numerical experiments on synthetic data of size N³ = 64³. To simulate measurements, the forward imaging model was implemented using a type-2 non-uniform FFT algorithm (see [5]). We used P = 500 projections and Gaussian white noise of variance σ² was added to each of them. To have a relative measure of the noise level, we define the signal-to-noise ratio (SNR) as (Variance of the projections)/σ².

In the first experiment, we used a 3D modified Shepp-Logan phantom as the original data f. We compared the performance of the thresholded Landweber (TL) algorithm with a simple least-squares (LS) formulation obtained for λ = 0, as well as a regularized least-squares (RLS) formulation with a Laplacian regularization. The latter was implemented using the steepest-descent algorithm described by Penczek in [3]. The initial estimate f⁽⁰⁾ was set to zero for all algorithms. We assigned a fixed budget of 50 iterations to each algorithm and kept the estimate f^(k) for which the SNR improvement 20 log₁₀ (‖f⁽⁰⁾ − f‖/‖f^(k) − f‖) was the highest. For the RLS and TL algorithms, λ was adjusted so as to maximize this quantity. For TL, we used Haar wavelets with three decomposition levels, combined with the random-shift technique described in [4]. Table 1 lists the results for three different input SNRs. It is seen that the TL algorithm consistently yields better estimates.

Table 1.

SNR improvements for Experiment 1.

Input SNR	LS	RLS	TL
1/1	8.19 dB	8.42 dB	9.54 dB
1/8	4.74 dB	5.36 dB	7.27 dB
1/64	2.82 dB	3.66 dB	4.66 dB

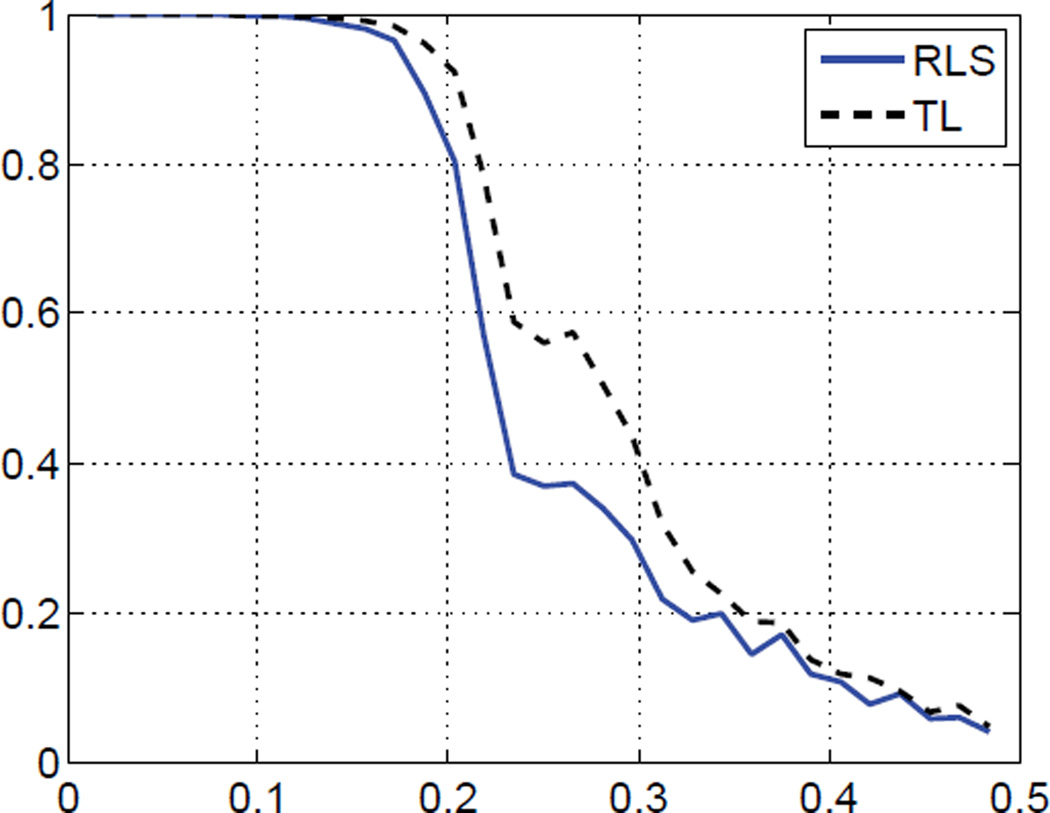
In the second experiment, we used the 3D image of a ribosome as the original data, and the input SNR was set to 1/8. This time we used Symlet4 wavelets for regularization. Visually the result of the TL algorithm contains less background noise than the one obtained with RLS. This is illustrated in Fig. 1, which shows cross-sections through the different data volumes. The SNR improvements confirm this impression (RLS: 13.17 dB; TL: 14.26 dB). In Fig. 2, a plot of the Fourier shell correlation (FSC) for this experiment suggests that the TL algorithm achieves a slightly better resolution (see e.g. [2] for a discussion of the FSC).

Fig. 1.

Results of Experiment 2.

Fig. 2.

Fourier-shell correlation for Experiment 2.

5. CONCLUSION

We have presented an efficient implementation of the thresholded Landweber algorithm using the specific structure of the single-particle reconstruction problem in Cryo-EM. It requires only two initial non-uniform FFTs for computing the back-projection and the Toeplitz kernel associated with the symmetrized operator appearing in the iteration. The actual iterations are performed with standard FFTs.

The first results obtained here confirm the potential of wavelet regularization for 3D Cryo-EM imaging. The algorithmic refinements that we have used carry over to the case where the Contrast Transfer Function (CTF) of the system must be taken into account.

In the future we plan to perform more extensive comparisons with standard single-particle-reconstruction software packages. Ultimately the goal is to incorporate the algorithm into a full iterative-refinement loop. In this framework it is certainly worth investigating further acceleration methods such as preconditioning or the multilevel scheme described in [4].