Three-Dimensional Structure Determination from Common Lines in Cryo-EM by Eigenvectors and Semidefinite Programming

Abstract

The cryo-electron microscopy reconstruction problem is to find the three-dimensional (3D) structure of a macromolecule given noisy samples of its two-dimensional projection images at unknown random directions. Present algorithms for finding an initial 3D structure model are based on the “angular reconstitution” method in which a coordinate system is established from three projections, and the orientation of the particle giving rise to each image is deduced from common lines among the images. However, a reliable detection of common lines is difficult due to the low signal-to-noise ratio of the images. In this paper we describe two algorithms for finding the unknown imaging directions of all projections by minimizing global self-consistency errors. In the first algorithm, the minimizer is obtained by computing the three largest eigenvectors of a specially designed symmetric matrix derived from the common lines, while the second algorithm is based on semidefinite programming (SDP). Compared with existing algorithms, the advantages of our algorithms are five-fold: first, they accurately estimate all orientations at very low common-line detection rates; second, they are extremely fast, as they involve only the computation of a few top eigenvectors or a sparse SDP; third, they are nonsequential and use the information in all common lines at once; fourth, they are amenable to a rigorous mathematical analysis using spectral analysis and random matrix theory; and finally, the algorithms are optimal in the sense that they reach the information theoretic Shannon bound up to a constant for an idealized probabilistic model.

1. Introduction

Cryo-electron microscopy (cryo-EM) is a technique by which biological macromolecules are imaged in an electron microscope. The molecules are rapidly frozen in a thin (~ 100nm) layer of vitreous ice, trapping them in a nearly physiological state [1, 2]. Cryo-EM images, however, have very low contrast due to the absence of heavy-metal stains or other contrast enhancements, and have very high noise due to the small electron doses that can be applied to the specimen. Thus, to obtain a reliable three-dimensional (3D) density map of a macromolecule, the information from thousands of images of identical molecules must be combined. When the molecules are arrayed in a crystal, the necessary signal-averaging of noisy images is straightforwardly performed. More challenging is the problem of single-particle reconstruction (SPR), where a 3D density map is to be obtained from images of individual molecules present in random positions and orientations in the ice layer [1].

Because it does not require the formation of crystalline arrays of macromolecules, SPR is a very powerful and general technique, which has been successfully used for 3D structure determination of many protein molecules and complexes roughly 500 kDa or larger in size. In some cases, sufficient resolution (~ 0.4nm) has been obtained from SPR to allow tracing of the polypeptide chain and identification of residues in proteins [3, 4, 5]; however, even with lower resolutions many important features can be identified [6].

Much progress has been made in algorithms that, given a starting 3D structure, are able to refine that structure on the basis of a set of negative-stain or cryo-EM images, which are taken to be projections of the 3D object. Datasets typically range from 10⁴ to 10⁵ particle images, and refinements require tens to thousands of CPU-hours. As the starting point for the refinement process, however, some sort of ab initio estimate of the 3D structure must be made. If the molecule is known to have some preferred orientation, then it is possible to find an ab initio 3D structure using the random conical tilt method [7, 8]. There are two known solutions to the ab initio estimation problem of the 3D structure that do not involve tilting. The first solution is based on the method of moments [9, 10] that exploits the known analytical relation between the second order moments of the 2D projection images and the second order moments of the (unknown) 3D volume in order to reveal the unknown orientations of the particles. However, the method of moments is very sensitive to errors in the data and is of rather academic interest [11, section 2.1, p. 251]. The second solution, on which present algorithms are based, is the “angular reconstitution” method of Van Heel [12] in which a coordinate system is established from three projections, and the orientation of the particle giving rise to each image is deduced from common lines among the images. This method fails, however, when the particles are too small or the signal-to-noise ratio is too low, as in such cases it is difficult to correctly identify the common lines (see section 2 and Figure 2 for a more detailed explanation about common lines).

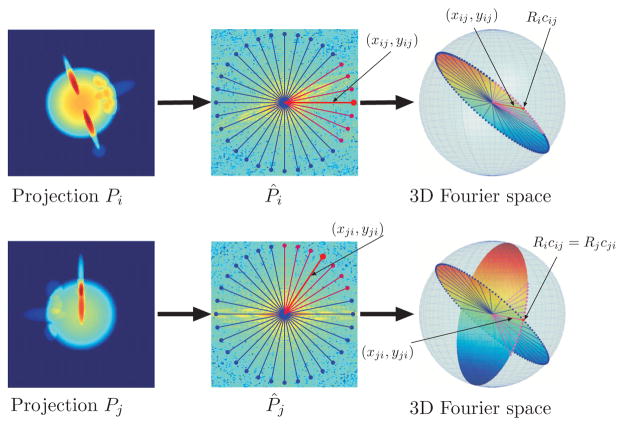
Figure 2.

Fourier projection-slice theorem and common lines.

Ideally one would want to do the 3D reconstruction directly from projections in the form of raw images. However, the determination of common lines from the very noisy raw images is typically too error-prone. Instead, the determination of common lines is performed on pairs of class averages, namely, averages of particle images that correspond to the same viewing direction. To reduce variability, class averages are typically computed from particle images that have already been rotationally and translationally aligned [1, 13]. The choice of reference images for the alignment is, however, arbitrary and can represent a source of bias in the classification process. This therefore sets the goal for an ab initio reconstruction algorithm that requires as little averaging as possible.

By now there is a long history of common-line–based algorithms. As mentioned earlier, the common lines between three projections uniquely determine their relative orientations up to handedness (chirality). This observation is the basis of the angular reconstitution method of Van Heel [12], which was also developed independently by Vainshtein and Goncharov [14]. Other historical aspects of the method can be found in [15]. Farrow and Ottensmeyer [16] used quaternions to obtain the relative orientation of a new projection in a least squares sense. The main problem with such sequential approaches is that they are sensitive to false detection of common lines, which leads to the accumulation of errors (see also [13, p. 336]). Penczek, Zhu, and Frank [17] tried to obtain the rotations corresponding to all projections simultaneously by minimizing a global energy functional. Unfortunately, minimization of the energy functional requires a brute force search in a huge parametric space of all possible orientations for all projections. Mallick et al. [18] suggested an alternative Bayesian approach, in which the common line between a pair of projections can be inferred from their common lines with different projection triplets. The problem with this particular approach is that it requires too many (at least seven) common lines to be correctly identified simultaneously. Therefore, it is not suitable in cases where the detection rate of correct common lines is low. In [19] we introduced an improved Bayesian approach based on voting that requires only two common lines to be correctly identified simultaneously and can therefore distinguish the correctly identified common lines from the incorrect ones at much lower detection rates. The common lines that passed the voting procedure are then used by our graph-based approach [20] to assign Euler angles to all projection images. As shown in [19], the combination of the voting method with the graph-based method resulted in a 3D ab initio reconstruction of the E. coli 50S ribosomal subunit from real microscope images that had undergone only rudimentary averaging.

The two-dimensional (2D) variant of the ab initio reconstruction problem in cryo-EM, namely, the reconstruction of 2D objects from their one-dimensional (1D) projections taken at random and unknown directions, has a somewhat shorter history, starting with the work of Basu and Bresler [21, 22], who considered the mathematical uniqueness of the problem as well as the statistical and algorithmic aspects of reconstruction from noisy projections. In [23] we detailed a graph-Laplacian based approach for the solution of this problem. Although the two problems are related, there is a striking difference between the ab initio reconstruction problems in 2D and 3D. In the 3D problem, the Fourier transforms of any pair of 2D projection images share a common line, which provides some non-trivial information about their relative orientations. In the 2D problem, however, the intersection of the Fourier transforms of any 1D projection sinograms is the origin, and this trivial intersection point provides no information about the angle between the projection directions. This is a significant difference, and, as a result, the solution methods to the two problems are also quite different. Hereafter we solely consider the 3D ab initio reconstruction problem as it arises in cryo-EM.

In this paper we introduce two common-line–based algorithms for finding the unknown orientations of all projections in a globally consistent way. Both algorithms are motivated by relaxations of a global minimization problem of a particular self-consistency error (SCE) that takes into account the matching of common lines between all pairs of images. A similar SCE was used in [16] to assess the quality of their angular reconstitution techniques. Our approach is different in the sense that we actually minimize the SCE in order to find the imaging directions. The precise definition of our global SCE is given in section 2.

In section 3, we present our first recovery algorithm, in which the global minimizer is approximated by the top three eigenvectors of a specially designed symmetric matrix derived from the common-line data. We describe how the unknown rotations are recovered from these eigenvectors. The underlying assumption for the eigenvector method to succeed is that the unknown rotations are sampled from the uniform distribution over the rotation group SO(3), namely, that the molecule has no preferred orientation. Although it is motivated by a certain global optimization problem, the exact mathematical justification for the eigenvector method is provided later in section 6, where we show that the computed eigenvectors are discrete approximations of the eigenfunctions of a certain integral operator.

In section 4, we use a different relaxation of the global optimization problem, which leads to our second recovery method based on semidefinite programming (SDP) [24]. Our SDP algorithm has similarities to the Goemans–Williamson max-cut algorithm [25]. The SDP approach does not require the previous assumption that the rotations are sampled from the uniform distribution over SO(3).

Compared with existing algorithms, the main advantage of our methods is that they correctly find the orientations of all projections at amazingly low common line detection rates as they take into account all the geometric information in all common lines at once. In fact, the estimation of the orientations improves as the number of images increases. In section 5 we describe the results of several numerical experiments using the two algorithms, showing successful recoveries at very low common-line detection rates. For example, both algorithms successfully recover a meaningful ab initio coordinate system from 500 projection images when only 20% of the common lines are correctly identified. The eigenvector method is extremely efficient, and the estimated 500 rotations were obtained in a matter of seconds on a standard laptop machine.

In section 6, we show that in the limit of an infinite number of projection images, the symmetric matrix that we design converges to a convolution integral operator on the rotation group SO(3). This observation explains many of the spectral properties that the matrix exhibits. In particular, this allows us to demonstrate that the top three eigenvectors provide the recovery of all rotations. Moreover, in section 7 we analyze a probabilistic model which is introduced in section 5 and show that the effect of the misidentified common lines is equivalent to a random matrix perturbation. Thus, using classical results in random matrix theory, we demonstrate that the top three eigenvalues and eigenvectors are stable as long as the detection rate of common lines exceeds $\frac{6\sqrt{2}}{5\sqrt{N}}$, where N is the number of images. From the practical point of view, this result implies that 3D reconstruction is possible even at extreme levels of noise, provided that enough projections are taken. From the theoretical point of view, we show that this detection rate achieves the information theoretic Shannon bound up to a constant, rendering the optimality of our method for ab initio 3D structure determination from common lines under this idealized probabilistic model.

2. The global self-consistency error

Suppose we collect N 2D digitized projection images P₁, …, P_N of a 3D object taken at unknown random orientations. To each projection image P_i (i = 1, …, N) there corresponds a 3 × 3 unknown rotation matrix R_i describing its orientation (see Figure 1). Excluding the contribution of noise, the pixel intensities correspond to line integrals of the electric potential induced by the molecule along the path of the imaging electrons, that is,

Figure 1.

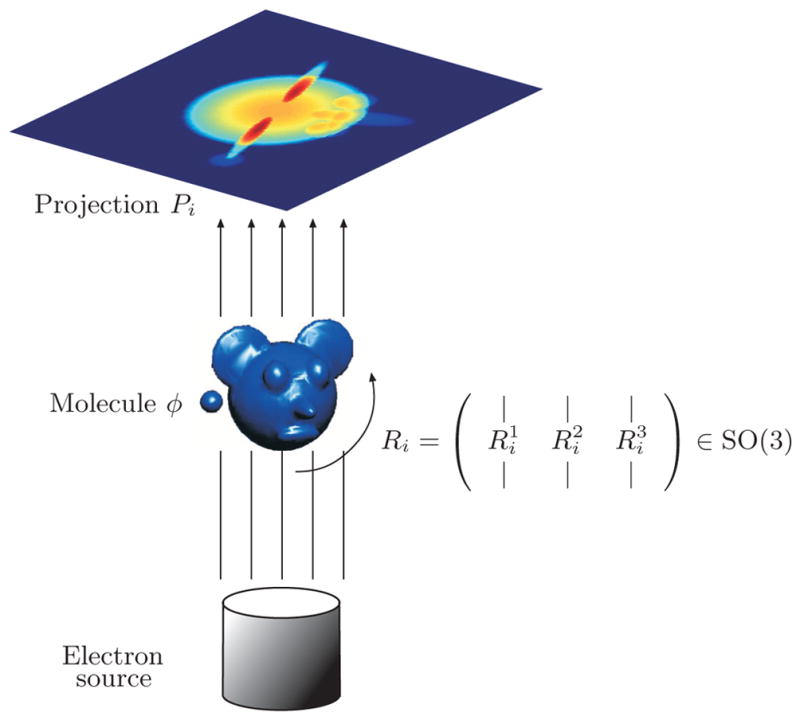
Schematic drawing of the imaging process: every projection image corresponds to some unknown 3D rotation of the unknown molecule.

$$P_i(x,y)={\int }_{-\infty }^{\infty }{\phi }_i(x,y,z)dz,$$ (2.1)

where φ(x, y, z) is the electric potential of the molecule in some fixed “laboratory” coordinate system and ${\phi }_i(r)=\phi (R_i^{-1}r)$ with r = (x, y, z). The projection operator (2.1) is also known as the X-ray transform [26]. Our goal is to find all rotation matrices R₁, …, R_N given the dataset of noisy images.

The Fourier projection-slice theorem (see, e.g., [26, p. 11]) says that the 2D Fourier transform of a projection image, denoted P̂, is the restriction of the 3D Fourier transform of the projected object φ̂ to the central plane (i.e., going through the origin) θ^⊥ perpendicular to the imaging direction, that is,

$$\widehat{P}(\eta )=\widehat{\phi }(\eta ),\eta \in {\theta }^{\perp }.$$ (2.2)

As every two nonparallel planes intersect at a line, it follows from the Fourier projection- slice theorem that any two projection images have a common line of intersection in the Fourier domain. Therefore, if P̂_i and P̂_j are the 2D Fourier transforms of projections P_i and P_j, then there must be a central line in P̂_i and a central line in P̂_j on which the two transforms agree (see Figure 2). This pair of lines is known as the common line. We parameterize the common line by (ωx_ij, ωy_ij) in P̂_i and by (ωx_ji, ωy_ji) in P̂_j, where ω ∈ ℝ is the radial frequency and (x_ij, y_ij) and (x_ji, y_ji) are two unit vectors for which

$${\widehat{P}}_i({\omega x}_{ij},{\omega y}_{ij})={\widehat{P}}_j({\omega x}_{ji},{\omega y}_{ji})\text{for}\text{all}\omega \in \mathbb{R}.$$ (2.3)

It is instructive to consider the unit vectors (x_ij, y_ij) and (x_ji, y_ji) as 3D vectors by zero-padding. Specifically, we define c_ij and c_ji as

$$c_{ij}={(x_{ij},y_{ij},0)}^T,$$ (2.4)

$$c_{ji}={(x_{ji},y_{ji},0)}^T.$$ (2.5)

Being the common line of intersection, the mapping of c_ij by R_i must coincide with the mapping of c_ji by R_j:

$$R_i{c}_{ij}=R_j{c}_{ji}\text{for}1\le i<j\le N.$$ (2.6)

These can be viewed as $\left(\begin{array}{c}N\\ 2\end{array}\right)$ linear equations for the 6N variables corresponding to the first two columns of the rotation matrices (as c_ij and c_ji have a zero third entry, the third column of each rotation matrix does not contribute in (2.6)). Such overdetermined systems of linear equations are usually solved by the least squares method [17]. Unfortunately, the least squares approach is inadequate in our case due to the typically large proportion of falsely detected common lines that will dominate the sum of squares error in

$$\underset{R_1,\dots ,R_N}{min}\sum _{i\ne j}{\left|\right|R_i{c}_{ij}-R_j{c}_{ji}\left|\right|}^2.$$ (2.7)

Moreover, the global least squares problem (2.7) is nonconvex and therefore extremely difficult to solve if one requires the matrices R_i to be rotations, that is, when adding the constraints

$$R_i{R}_i^T=I,det(R_i)=1\text{for}i=1,\dots ,N,$$ (2.8)

where I is the 3 × 3 identity matrix. A relaxation method that neglects the constraints (2.8) will simply collapse to the trivial solution R₁ = · · · = R_N = 0 which obviously does not satisfy the constraint (2.8). Such a collapse is easily prevented by fixing one of the rotations, for example, by setting R₁ = I, but this would not make the robustness problem of the least squares method go away. We therefore take a different approach for solving the global optimization problem.

Since ||c_ij|| = ||c_ji|| = 1 are 3D unit vectors, their rotations are also unit vectors; that is, ||R_ic_ij|| = ||R_jc_ji|| = 1. It follows that the minimization problem (2.7) is equivalent to the maximization problem of the sum of dot products

$$\underset{R_1,\dots ,R_N}{max}\sum _{i\ne j}{R}_i{c}_{ij}·R_j{c}_{ji},$$ (2.9)

subject to the constraints (2.8). For the true assignment of rotations, the dot product R_ic_ij · R_jc_ji equals 1 whenever the common line between images i and j is correctly detected. Dot products corresponding to misidentified common lines can take any value between −1 to 1, and if we assume that such misidentified lines have random directions, then such dot products can be considered as identically independently distributed (i.i.d.) zero-mean random variables taking values in the interval [−1, 1]. The objective function in (2.9) is the summation over all possible dot products. Summing up dot products that correspond to misidentified common lines results in many cancelations, whereas summing up dot products of correctly identified common lines is simply a sum of ones. We may consider the contribution of the falsely detected common lines as a random walk on the real line, where steps to the left and to the right are equally probable. From this interpretation it follows that the total contribution of the misidentified common lines to the objective function (2.9) is proportional to the square root of the number of misidentifications, whereas the contribution of the correctly identified common lines is linear. This square-root diminishing effect of the misidentifications makes the global optimization (2.9) extremely robust compared with the least squares approach, which is much more sensitive because its objective function is dominated by the misidentifications.

These intuitive arguments regarding the statistical attractiveness of the optimization problem (2.9) will later be put on firm mathematical ground using random matrix theory as elaborated in section 7. Still, in order for the optimization problem (2.9) to be of any practical use, we must show that its solution can be efficiently computed. We note that our objective function is closely related to the SCE of Farrow and Ottensmeyer [16, eq. (6), p. 1754] given by

$$\mathit{SCE}=\sum _{i\ne j}arccos(R_i{c}_{ij}·R_j{c}_{ji}).$$ (2.10)

This SCE was introduced and used in [16] to measure the success of their quaternion-based sequential iterative angular reconstitution methods. At the small price of deleting the well-behaved monotonic nonlinear arccos function in (2.10), we arrive at (2.9), which, as we will soon show, has the great advantage of being amenable to efficient global nonsequential optimization by either spectral or semidefinite programming relaxations.

3. Eigenvector relaxation

The objective function in (2.9) is quadratic in the unknown rotations R₁, …, R_N, which means that if the constraints (2.8) are properly relaxed, then the solution to the maximization problem (2.9) would be related to the top eigenvectors of the matrix defining the quadratic form. In this section we give a precise definition of that matrix and show how the unknown rotations can be recovered from its top three eigenvectors.

We first define the four N × N matrices S¹¹, S¹², S²¹, and S²² using all available common-line data (2.4)–(2.5) as

$$S_{ij}^{11}=x_{ij}{x}_{ji},S_{ij}^{12}=x_{ij}{y}_{ji},S_{ij}^{21}=y_{ij}{x}_{ji},S_{ij}^{22}=y_{ij}{y}_{ji}$$ (3.1)

for 1 ≤ i ≠ j ≤ N, while their diagonals are set to zero:

$$S_{ii}^{11}=S_{ii}^{12}=S_{ii}^{21}=S_{ii}^{22}=0,i=1,\dots ,N.$$

Clearly, S¹¹ and S²² are symmetric matrices (S¹¹ = S^11T and S²² = S^22T), while S¹² = S^21T. It follows that the 2N × 2N matrix S given by

$$S=\left(\begin{array}{cc}{S}^{11}& S^{12}\\ S^{21}& S^{22}\end{array}\right)$$ (3.2)

is symmetric (S = S^T) and stores all available common line information. More importantly, the top eigenvectors of S will reveal all rotations in a manner we describe below.

We denote the columns of the rotation matrix R_i by $R_i^1,R_i^2$, and $R_i^3$, and write the rotation matrices as

$$R_i=\left(\begin{array}{ccc}\mid & \mid & \mid \\ R_i^1& R_i^2& R_i^3\\ \mid & \mid & \mid \end{array}\right)=\left(\begin{array}{ccc}{x}_i^1& x_i^2& x_i^3\\ y_i^1& y_i^2& y_i^3\\ z_i^1& z_i^2& z_i^3\end{array}\right),i=1,\dots ,N.$$ (3.3)

Only the first two columns of the R_i’s need to be recovered, because the third column is given by the cross product: $R_i^3=R_i^1\times R_i^2$. We therefore need to recover the six N-dimensional coordinate vectors x¹, y¹, z¹, x², y², z² that are defined by

$$x^1={(x_1^1{x}_2^1\cdots x_N^1)}^T,y^1={(y_1^1{y}_2^1\cdots y_N^1)}^T,z^1={(z_1^1{z}_2^1\cdots z_N^1)}^T,$$ (3.4)

$$x^2={(x_1^2{x}_2^2\cdots x_N^2)}^T,y^2={(y_1^2{y}_2^2\cdots y_N^2)}^T,z^2={(z_1^2{z}_2^2\cdots z_N^2)}^T.$$ (3.5)

Alternatively, we need to find the following three 2N-dimensional vectors x, y, and z:

$$x=\left(\begin{array}{c}{x}^1\\ x^2\end{array}\right),y=\left(\begin{array}{c}{y}^1\\ y^2\end{array}\right),z=\left(\begin{array}{c}{z}^1\\ z^2\end{array}\right).$$ (3.6)

Using this notation we rewrite the objective function (2.9) as

$$\sum _{i\ne j}{R}_i{c}_{ij}·R_j{c}_{ji}=x^{T}Sx+y^{T}Sy+z^{T}Sz,$$ (3.7)

which is a result of the following index manipulation:

$$\begin{array}{l}\sum _{i\ne j}{R}_i{c}_{ij}·R_j{c}_{ij}=\sum _{i\ne j}{x}_{ij}{x}_{ji}{R}_i^1·R_j^1+x_{ij}{y}_{ji}{R}_i^1·R_j^2+y_{ij}{x}_{ji}{R}_i^2·R_j^1+y_{ij}{y}_{ji}{R}_i^2·R_j^2\\ =\sum _{i\ne j}{S}_{ij}^{11}{R}_i^1·R_j^1+S_{ij}^{12}{R}_i^1·R_j^2+S_{ij}^{21}{R}_i^2·R_j^1+S_{ij}^{22}{R}_i^2·R_j^2\end{array}$$ (3.8)

$$\begin{array}{l}=\sum _{i,j}{S}_{ij}^{11}(x_i^1{x}_j^1+y_i^1{y}_j^1+z_i^1{z}_j^1)+S_{ij}^{11}(x_i^1{x}_j^2+y_i^1{y}_j^2+z_i^1{z}_j^2)\\ +S_{ij}^{21}(x_i^2{x}_j^1+y_i^2{y}_j^1+z_i^2{z}_j^1)+S_{ij}^{22}(x_i^2{x}_j^2+y_i^2{y}_j^2+z_i^2{z}_j^2)\\ =x^{1^T}{S}^{11}{x}^1+y^{1^T}{S}^{11}{y}^1+z^{1^T}{S}^{11}{z}^1\\ +x^{1^T}{S}^{12}{x}^2+y^{1^T}{S}^{12}{y}^2+z^{1^T}{S}^{12}{z}^2\\ +x^{2^T}{S}^{21}{x}^1+y^{2^T}{S}^{21}{y}^1+z^{2^T}{S}^{21}{z}^1\\ +x^{2^T}{S}^{22}{x}^2+y^{2^T}{S}^{22}{y}^2+z^{2^T}{S}^{22}{z}^2\\ =x^{T}Sx+y^{T}Sy+z^{T}Sz.\end{array}$$ (3.9)

The equality (3.7) shows that the maximization problem (2.9) is equivalent to the maximization problem

$$\underset{R_1,\dots ,R_N}{max}{x}^{T}Sx+y^{T}Sy+z^{T}Sz,$$ (3.10)

subject to the constraints (2.8). In order to make this optimization problem tractable, we relax the constraints and look for the solution of the proxy maximization problem

$$\underset{\left|\right|x\left|\right|=1}{max}{x}^{T}Sx.$$ (3.11)

The connection between the solution to (3.11) and that of (3.10) will be made shortly. Since S is a symmetric matrix, it has a complete set of orthonormal eigenvectors {v¹, …, v^2N} satisfying

$${Sv}^n={\lambda }_n{v}^n,n=1,\dots ,2N,$$

with real eigenvalues

$${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_{2N}.$$

The solution to the maximization problem (3.11) is therefore given by the top eigenvector v¹ with largest eigenvalue λ₁:

$$v^1=\underset{\left|\right|x\left|\right|=1}{\text{argmax}}{x}^{T}Sx.$$ (3.12)

If the unknown rotations are sampled from the uniform distribution (Haar measure) over SO(3), that is, when the molecule has no preferred orientation, then the largest eigenvalue should have multiplicity three, corresponding to the vectors x, y, and z, as the symmetry of the problem in this case suggests that there is no reason to prefer x over y and z that appear in (3.10). At this point, the reader may still wonder what is the mathematical justification that fills in the gap between (3.10) and (3.11). The required formal justification is provided in section 6, where we prove that in the limit of infinitely many images (N → ∞) the matrix S converges to an integral operator over SO(3) for which x, y, and z in (3.6) are eigenfunctions sharing the same eigenvalue. The computed eigenvectors of the matrix S are therefore discrete approximations of the eigenfunctions of the limiting integral operator. In particular, the linear subspace spanned by the top three eigenvectors of S is a discrete approximation of the subspace spanned by x, y, and z.

We therefore expect to be able to recover the first two columns of the rotation matrices R₁, …, R_N from the top three computed eigenvectors v¹, v², v³ of S. Since the eigenspace of x, y, and z is of dimension three, the vectors x, y, and z should be approximately obtained by a 3×3 orthogonal transformation applied to the computed eigenvectors v¹, v², v³. This global orthogonal transformation is an inherent degree of freedom in the estimation of rotations from common lines. That is, it is possible to recover the molecule only up to a global orthogonal transformation, that is, up to rotation and possibly reflection. This recovery is performed by constructing for every i = 1, …, N a 3 × 3 matrix

$$A_i=\left(\begin{array}{ccc}\mid & \mid & \mid \\ A_i^1& A_i^2& A_i^3\\ \mid & \mid & \mid \end{array}\right)$$

whose columns are given by

$$A_i^1=\left(\begin{array}{c}{v}_i^1\\ v_i^2\\ v_i^3\end{array}\right),A_i^2=\left(\begin{array}{c}{v}_{N+i}^1\\ v_{N+i}^2\\ v_{N+i}^3\end{array}\right),A_i^3=A_i^1\times A_i^2.$$ (3.13)

In practice, due to erroneous common lines and deviations from the uniformity assumption, the matrix A_i is approximately a rotation, so we estimate R_i as the closest rotation matrix to A_i in the Frobenius matrix norm. This is done via the well-known procedure [27] $R_i=U_i{V}_i^T$, where $A_i=U_i{\mathrm{\sum }}_i{V}_i^T$ is the singular value decomposition of A_i. A second set of valid rotations R̃_i is obtained from the matrices Ã_i whose columns are given by

$${\stackrel{\sim }{A}}_i^1=\left(\begin{array}{rrr}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\\ \hfill 0\hfill & \hfill 0\hfill & \hfill -1\end{array}\right)A_i^1,{\stackrel{\sim }{A}}_i^2=\left(\begin{array}{rrr}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\\ \hfill 0\hfill & \hfill 0\hfill & \hfill -1\end{array}\right)A_i^2,{\stackrel{\sim }{A}}_i^3={\stackrel{\sim }{A}}_i^1\times {\stackrel{\sim }{A}}_i^2,$$ (3.14)

via their singular value decomposition, that is, ${\stackrel{\sim }{R}}_i={\stackrel{\sim }{U}}_i{\stackrel{\sim }{V}}_i^T$, where ${\stackrel{\sim }{A}}_i={\stackrel{\sim }{U}}_i{\mathrm{\sum }^{\sim }}_i{\stackrel{\sim }{V}}_i^T$. The second set of rotations R̃_i amounts to a global reflection of the molecule; it is a well-known fact that the chirality of the molecule cannot be determined from common-line data. Thus, in the absence of any other information, it is impossible to prefer one set of rotations over the other.

From the computational point of view, we note that a simple way of computing the top three eigenvectors is using the iterative power method, where three initial randomly chosen vectors are repeatedly multiplied by the matrix S and then orthonormalized by the Gram–Schmidt (QR) procedure until convergence. The number of iterations required by such a procedure is determined by the spectral gap between the third and forth eigenvalues. The spectral gap is further discussed in sections 5–7. In practice, for large values of N we use the MATLAB function eigs to compute the few top eigenvectors, while for small N we compute all eigenvectors using the MATLAB function eig. We remark that the computational bottleneck for large N is often the storage of the 2N × 2N matrix S rather than the time complexity of computing the top eigenvectors.

4. Relaxation by a semidefinite program

In this section we present an alternative relaxation of (2.9) using semidefinite programming (SDP) [24], which draws similarities with the Goemans–Williamson SDP for finding the maximum cut in a weighted graph [25]. The relaxation of the SDP is tighter than the eigenvector relaxation and does not require the assumption that the rotations are uniformly sampled over SO(3).

The SDP formulation begins with the introduction of two 3 × N matrices R¹ and R² defined by concatenating the first columns and second columns of the N rotation matrices, respectively,

$$R^1=\left(\begin{array}{cccc}\mid & \mid & & \mid \\ R_1^2& R_2^1& \cdots & R_N^1\\ \mid & \mid & & \mid \end{array}\right),R^2=\left(\begin{array}{cccc}\mid & \mid & & \mid \\ R_1^2& R_2^2& \cdots & R_N^2\\ \mid & \mid & & \mid \end{array}\right).$$ (4.1)

We also concatenate R¹ and R² to define a 3 × 2N matrix R given by

$$R=(R^1{R}^2)=\left(\begin{array}{cccccccc}\mid & \mid & & \mid & \mid & \mid & & \mid \\ R_1^1& R_2^1& \cdots & R_N^1& R_1^2& R_2^2& \cdots & R_N^2\\ \mid & \mid & & \mid & \mid & \mid & & \mid \end{array}\right).$$ (4.2)

The Gram matrix G for the matrix R is a 2N × 2N matrix of inner products between the 3D column vectors of R, that is,

$$G=R^{T}R.$$ (4.3)

Clearly, G is a rank-3 semidefinite positive matrix (G ≽ 0), which can be conveniently written as a block matrix

$$G=\left(\begin{array}{cc}{G}^{11}& G^{12}\\ G^{21}& G^{22}\end{array}\right)=\left(\begin{array}{cc}{R}^{1^T}{R}^1& R^{1^T}{R}^2\\ R^{2^T}{R}^1& R^{2^T}{R}^2\end{array}\right).$$ (4.4)

The orthogonality of the rotation matrices ( $R_i^T{R}_i=I$) implies that

$$G_{ii}^{11}=G_{ii}^{22}=1,i=1,2,\dots ,N,$$ (4.5)

and

$$G_{ii}^{12}=G_{ii}^{21}=0,i=1,2,\dots ,N.$$ (4.6)

From (3.8) it follows that the objective function (2.9) is the trace of the matrix product SG:

$$\sum _{i\ne j}{R}_i{c}_{ij}·R_j{c}_{ji}=\text{trace}(SG).$$ (4.7)

A natural relaxation of the optimization problem (2.9) is thus given by the SDP

$$\underset{G\in {\mathbb{R}}^{2N\times 2N}}{max}\text{trace}(SG)$$ (4.8)

$$\text{subject}\text{to}G\succcurlyeq 0,$$ (4.9)

$$G_{ii}^{11}=G_{ii}^{22}=1,G_{ii}^{12}=G_{ii}^{21}=0,i=1,2,\dots ,N.$$ (4.10)

The only constraint missing in this SDP formulation is the nonconvex rank-3 constraint on the Gram matrix G. The matrix R is recovered from the Cholesky decomposition of the solution G of the SDP (4.8)–(4.10). If the rank of G is greater than 3, then we project the rows of R onto the subspace spanned by the top three eigenvectors of G and recover the rotations using the procedure that was detailed in the previous section in (3.13). We note that except for the orthogonality constraint (4.6), the semidefinite program (4.8)–(4.10) is identical to the Goemans–Williamson SDP for finding the maximum cut in a weighted graph [25].

From the complexity point of view, SDP can be solved in polynomial time to any given precision, but even the most sophisticated SDP solvers that exploit the sparsity structure of the max cut problem are not competitive with the much faster eigenvector method. At first glance it may seem that the SDP (4.8)–(4.10) should outperform the eigenvector method in terms of producing more accurate rotation matrices. However, our simulations show that the accuracy of both methods is almost identical when the rotations are sampled from the uniform distribution over SO(3). As the eigenvector method is much faster, it should also be the method of choice whenever the rotations are a priori known to be uniformly sampled.

5. Numerical simulations

We performed several numerical experiments that illustrate the robustness of the eigenvector and the SDP methods to false identifications of common lines. All simulations were performed in MATLAB on a Lenovo Thinkpad X300 laptop with Intel Core 2 CPU L7100 1.2GHz with 4GB RAM running Windows Vista.

5.1. Experiments with simulated rotations

In the first series of simulations we tried to imitate the experimental setup by using the following procedure. In each simulation, we randomly sampled N rotations from the uniform distribution over SO(3). This was done by randomly sampling N vectors in ℝ⁴ whose coordinates are i.i.d. Gaussians, followed by normalizing these vectors to the unit 3D sphere S³ ⊂ ℝ⁴. The normalized vectors are viewed as unit quaternions which we converted into 3 × 3 rotation matrices R₁, …, R_N. We then computed all pairwise common-line vectors $c_{ij}=R_i^{-1}\frac{R_i^3\times R_j^3}{\left|\right|R_i^3\times R_j^3\left|\right|}$ and $c_{ji}=R_j^{-1}\frac{R_i^3\times R_j^3}{\left|\right|R_i^3\times R_j^3\left|\right|}$ (see also the discussion following (6.2)). For each pair of rotations, with probability p we kept the values of c_ij and c_ji unchanged, while with probability 1 − p we replaced c_ij and c_ji by two random vectors that were sampled from the uniform distribution over the unit circle in the plane. The parameter p ranges from 0 to 1 and indicates the proportion of the correctly detected common lines. For example, p = 0.1 means that only 10% of the common lines are identified correctly, and the other 90% of the entries of the matrix S are filled in with random entries corresponding to some randomly chosen unit vectors.

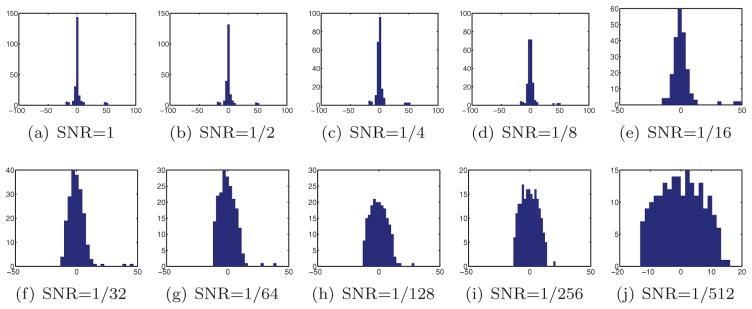
Figure 3 shows the distribution of the eigenvalues of the matrix S for two different values of N and four different values of the probability p. It took a matter of seconds to compute each of the eigenvalue histograms shown in Figure 3. Evident from the eigenvalue histograms is the spectral gap between the three largest eigenvalues and the remaining eigenvalues, as long as p is not too small. As p decreases, the spectral gap narrows down, until it completely disappears at some critical value p_c, which we call the threshold probability. Figure 3 indicates that the value of the critical probability for N = 100 is somewhere between 0.1 and 0.25, whereas for N = 500 it is bounded between 0.05 and 0.1. The algorithm is therefore more likely to cope with a higher percentage of misidentifications by using more images (larger N).

Figure 3.

Eigenvalue histograms for the matrix S for different values of N and p.

When p decreases, not only does the gap narrow, but also the histogram of the eigenvalues becomes smoother. The smooth part of the histogram seems to follow the semicircle law of Wigner [28, 29], as illustrated in Figure 3. The support of the semicircle gets slightly larger as p decreases, while the top three eigenvalues shrink significantly. In the next sections we will provide a mathematical explanation for the numerically observed eigenvalue histograms and for the emergence of Wigner’s semicircle.

A further investigation into the results of the numerical simulations also reveals that the rotations that were recovered by the top three eigenvectors successfully approximated the sampled rotations, as long as p was above the threshold probability p_c. The accuracy of our methods is measured by the following procedure. Denote by R̂₁, …, R̂_N the rotations as estimated by either the eigenvector or SDP methods, and by R₁, …, R_N the true sampled rotations. First, note that (2.6) implies that the true rotations can be recovered only up to a fixed 3 × 3 orthogonal transformation O, since if R_ic_ij = R_jc_ji, then also OR_ic_ij = OR_jc_ji. In other words, a completely successful recovery satisfies ${\widehat{R}}_i^{-1}{R}_i=O$ for all i = 1, …, N for some fixed orthogonal matrix O. In practice, however, due to erroneous common lines and deviation from uniformity (for the eigenvector method), there does not exist an orthogonal transformation O that perfectly aligns all the estimated rotations with the true ones. But we may still look for the optimal rotation Ô that minimizes the sum of squared distances between the estimated rotations and the true ones:

$$\widehat{O}=\underset{O\in \text{SO}(3)}{\text{argmin}}\sum _{i=1}^N{\left|\right|R_i-{O\widehat{R}}_i\left|\right|}_F^2,$$ (5.1)

where ||·||_F denotes the Frobenius matrix norm. That is, Ô is the optimal solution to the registration problem between the two sets of rotations in the sense of minimizing the mean squared error (MSE). Using properties of the trace, in particular tr(AB) = tr(BA) and tr(A) = tr(A^T), we notice that

$$\begin{array}{l}\sum _{i=1}^N{\left|\right|R_i-{O\widehat{R}}_i\left|\right|}_F^2=\sum _{i=1}^N\text{tr}\left[\left(R_i-{O\widehat{R}}_i\right){\left(R_i-{O\widehat{R}}_i\right)}^T\right]=\sum _{i=1}^N\text{tr}\left[2I-2{O\widehat{R}}_i{R}_i^T\right]\\ =6N-2\text{tr}\left[O\sum _{i=1}^N{\widehat{R}}_i{R}_i^T\right].\end{array}$$ (5.2)

Let Q be the 3 × 3 matrix

$$Q=\frac{1}{N}\sum _{i=1}^N{\widehat{R}}_i{R}_i^T;$$ (5.3)

then from (5.2) it follows that the MSE is given by

$$\frac{1}{N}\sum _{i=1}^N{\left|\right|R_i-{O\widehat{R}}_i\left|\right|}_F^2=6-2\text{tr}(OQ).$$ (5.4)

Arun, Huang, and Bolstein [27] proved that tr(OQ) ≤ tr(VU^TQ) for all O ∈ SO(3), where Q = UΣV^T is the singular value decomposition of Q. It follows that the MSE is minimized by the orthogonal matrix Ô = VU^T, and the MSE in such a case is given by

$$\mathit{MSE}=\frac{1}{N}\sum _{i=1}^N{\left|\right|R_i-\widehat{O}{\widehat{R}}_i\left|\right|}_F^2=6-2\text{tr}({VU}^{T}U\mathrm{\sum }{V}^T)=6-2\sum _{r=1}^3{\sigma }_r,$$ (5.5)

where σ₁, σ₂, σ₃ are the singular values of Q. In particular, the MSE vanishes whenever Q is an orthogonal matrix, because in such a case σ₁ = σ₂ = σ₃ = 1.

In our simulations we compute the MSE (5.5) for each of the two valid sets of rotations (due to the handedness ambiguity, see (3.13)–(3.14)) and always present the smallest of the two. Table 1 compares the MSEs that were obtained by the eigenvector method with the ones obtained by the SDP method for N = 100 and N = 500 with the same common-line input data. The SDP was solved using SDPLR, a package for solving large-scale SDP problems [30] in MATLAB.

Table 1.

The MSE of the eigenvector and SDP methods for N = 100 (left) and N = 500 (right) and different values of p.

(a) N = 100
p	MSE(eig)	MSE(sdp)
1	0.0055	4.8425e-05
0.5	0.0841	0.0676
0.25	0.7189	0.7140
0.15	2.8772	2.8305
0.1	4.5866	4.7814
0.05	4.8029	5.1809

(b) N = 500
p	MSE(eig)	MSE(sdp)
1	0.0019	1.0169e-05
0.5	0.0166	0.0143
0.25	0.0973	0.0911
0.15	0.3537	0.3298
0.1	1.2739	1.1185
0.05	5.4371	5.3568

5.2. Experiments with simulated noisy projections

In the second series of experiments, we tested the eigenvector and SDP methods on simulated noisy projection images of a ribosomal subunit for different numbers of projections (N = 100, 500, 1000) and different levels of noise. For each N, we generated N noise-free centered projections of the ribosomal subunit, whose corresponding rotations were uniformly distributed on SO(3). Each projection was of size 129 × 129 pixels. Next, we fixed a signal-to-noise ratio (SNR), and added to each clean projection additive Gaussian white noise¹ of the prescribed SNR. The SNR in all our experiments is defined by

$$\text{SNR}=\frac{\text{Var}(\mathit{Signal})}{\text{Var}(\mathit{Noise})},$$ (5.6)

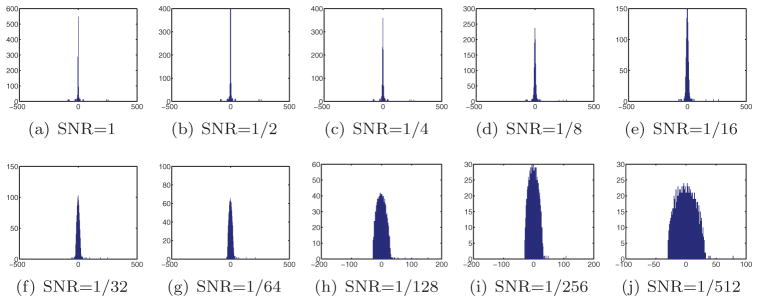
where Var is the variance (energy), Signal is the clean projection image, and Noise is the noise realization of that image. Figure 4 shows one of the projections at different SNR levels. The SNR values used throughout this experiment were 2^−k with k = 0, …, 9. Clean projections were generated by setting SNR = 2²⁰.

Figure 4.

Simulated projection with various levels of additive Gaussian white noise.

We computed the 2D Fourier transform of all projections on a polar grid discretized into L = 72 central lines, corresponding to an angular resolution of 360°/72 = 5°. We constructed the matrix S according to (3.1)–(3.2) by comparing all $\left(\begin{array}{c}N\\ 2\end{array}\right)$ pairs of projection images; for each pair we detected the common line by computing all L²/2 possible different normalized correlations between their Fourier central lines, of which the pair of central lines having the maximum normalized correlation was declared as the common line. Table 2 shows the proportion p of the correctly detected common lines as a function of the SNR (we consider a common line as correctly identified if each of the estimated direction vectors (x_ij, y_ij) and (x_ji, y_ji) is within 10° of its true direction). As expected, the proportion p is a decreasing function of the SNR.

Table 2.

The proportion p of correctly detected common lines as a function of the SNR. As expected, p is not a function of the number of images N.

(a) N = 100
SNR	p
clean	0.997
1	0.968
1/2	0.930
1/4	0.828
1/8	0.653
1/16	0.444
1/32	0.247
1/64	0.108
1/128	0.046
1/256	0.023
1/512	0.017

(b) N = 500
SNR	p
clean	0.997
1	0.967
1/2	0.922
1/4	0.817
1/8	0.639
1/16	0.433
1/32	0.248
1/64	0.113
1/128	0.046
1/256	0.023
1/512	0.015

(c) N = 1000
SNR	p
clean	0.997
1	0.966
1/2	0.919
1/4	0.813
1/8	0.638
1/16	0.437
1/32	0.252
1/64	0.115
1/128	0.047
1/256	0.023
1/512	0.015

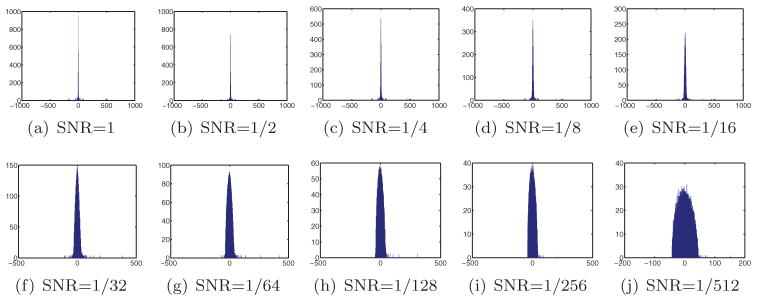
We used the MATLAB function eig to compute the eigenvalue histograms of all S matrices as shown in Figures 5–7. There is a clear resemblance between the eigenvalue histograms of the noisy S matrices shown in Figure 3 and those shown in Figures 5–7. One noticeable difference is that the top three eigenvalues in Figures 5–7 tend to spread (note, for example, the spectral gap between the top three eigenvalues in Figure 5(e)), whereas in Figure 3 they tend to stick together. We attribute this spreading effect to the fact that the model used in section 5.1 is too simplified; in particular, it ignores the dependencies among the misidentified common lines. Moreover, falsely detected common lines are far from being uniformly distributed. The correct common line is often confused with a Fourier central line that is similar to it; it is not just confused with any other Fourier central line with equal probability. Also, the detection of common lines tends to be more successful when computed between projections that have more pronounced signal features. This means that the assumption that each common line is detected correctly with a fixed probability p is too restrictive. Still, despite the simplified assumptions that were made in section 5.1 to model the matrix S, the resulting eigenvalue histograms are very similar.

Figure 5.

Eigenvalue histograms of S for N = 100 and different levels of noise.

Figure 7.

Eigenvalue histograms of S for N = 1000 and different levels of noise.

From our numerical simulations it seems that increasing the number of projections N separates the top three eigenvalues from the bulk of the spectrum (the semicircle). For example, for N = 100 the top eigenvalues are clearly distinguished from the bulk for SNR = 1/32, while for N = 500 they can be distinguished for SNR = 1/128 (maybe even at SNR = 1/256), and for N = 1000 they are distinguished even at the most extreme noise level of SNR = 1/512. The existence of a spectral gap is a necessary but not sufficient condition for a successful 3D reconstruction, as demonstrated below. We therefore must check the resulting MSEs in order to assess the quality of our estimates. Table 3 details the MSE of the eigenvector and SDP methods for N = 100, N = 500, and N = 1000. Examining Table 3 reveals that the MSE is sufficiently small for SNR ≥ 1/32, but is relatively large for SNR ≤ 1/64 for all N. Despite the visible spectral gap that was observed for SNR = 1/64 with N = 500 and N = 1000, the corresponding MSE is not small. We attribute the large MSE to the shortcomings of our simplified probabilistic Wigner model that assumes independence among the errors.

Table 3.

The MSE of the eigenvector and SDP methods for N = 100, N = 500, and N = 1000.

(a) N = 100
SNR	MSE(eig)	MSE(sdp)
1	0.0054	3.3227e-04
1/2	0.0068	0.0016
1/4	0.0129	0.0097
1/8	0.0276	0.0471
1/16	0.0733	0.1951
1/32	0.2401	0.6035
1/64	2.5761	1.9509
1/128	3.2014	3.1020
1/256	4.0974	4.1163
1/512	4.9664	4.9702

(b) N = 500
SNR	MSE(eig)	MSE(sdp)
1	0.0023	2.4543e-04
1/2	0.0030	0.0011
1/4	0.0069	0.0071
1/8	0.0203	0.0414
1/16	0.0563	0.1844
1/32	0.1859	0.6759
1/64	1.7549	1.3668
1/128	2.6214	2.4046
1/256	3.4789	3.3539
1/512	4.6027	4.5089

(c) N = 1000
SNR	MSE(eig)	MSE(sdp)
1	0.0018	2.3827e-04
1/2	0.0030	0.0011
1/4	0.0072	0.0067
1/8	0.0208	0.0406
1/16	0.0582	0.1899
1/32	0.1996	0.7077
1/64	1.7988	1.5370
1/128	2.5159	2.3243
1/256	3.5160	3.4365
1/512	4.6434	4.6013

To demonstrate the effectiveness of our methods for ab initio reconstruction, we present in Figure 8 the volumes estimated from N = 1000 projections at various levels of SNR. For each level of SNR, we present in Figure 8 four volumes. The left volume in each row was reconstructed from the noisy projections at the given SNR and the orientations estimated using the eigenvector method. The middle-left volume was reconstructed from the noisy projections and the orientations estimated using the SDP method. The middle-right volume is a reference volume reconstructed from the noisy projections and the true (simulated) orientations. This enables us to gauge the effect of the noise in the projections on the reconstruction. Finally, the right column shows the reconstruction from clean projections and orientations estimated using the eigenvector method. It is clear from Figure 8 that errors in estimating the orientations have far more effect on the reconstruction than high levels of noise in the projections. All reconstructions in Figure 8 were obtained using a simple interpolation of Fourier space into the 3D pseudopolar grid, followed by an inverse 3D pseudopolar Fourier transform, implemented along the lines of [31, 32].

Figure 8.

Reconstruction from N = 1000 noisy projections at various SNR levels using the eigenvector method. Left column: reconstructions generated from noisy projections and orientations estimated using the eigenvector method. Middle-left column: reconstructions generated from noisy projections and orientations estimated using the SDP method. Middle-right column: reconstructions from noisy projections and the true orientations. Right column: reconstructions from estimated orientations (using the eigenvector method) and clean projections.

As mentioned earlier, the usual method for detecting the common-line pair between two images is by comparing all pairs of radial Fourier lines and declaring the common line as the pair whose normalized cross-correlation is maximal. This procedure for detecting the common lines may not be optimal. Indeed, we have observed empirically that the application of principal component analysis (PCA) improves the fraction of correctly identified common lines. More specifically, we applied PCA to the radial lines extracted from all N images, and linearly projected all radial lines into the subspace spanned by the top k principal components (k ≈ 10). As a result, the radial lines are compressed (i.e., represented by only k feature coefficients) and filtered. Table 4 shows the fraction of correctly identified common lines using the PCA method for different numbers of images. By comparing Table 4 with Table 2 we conclude that PCA improves the detection of common lines. The MSEs shown in Table 3 correspond to common lines that were detected using the PCA method.

Table 4.

The fraction of correctly identified common lines p using the PCA method for different numbers of images: N = 100, N = 500, and N = 1000.

SNR	p(N = 100)	p(N = 500)	p(N = 1000)
1	0.980	0.978	0.977
1/2	0.956	0.953	0.951
1/4	0.890	0.890	0.890
1/8	0.763	0.761	0.761
1/16	0.571	0.565	0.564
1/32	0.345	0.342	0.342
1/64	0.155	0.167	0.168
1/128	0.064	0.070	0.072
1/256	0.028	0.032	0.033

In summary, even if ab initio reconstruction is not possible from the raw noisy images whose SNR is too low, the eigenvector and SDP methods should allow us to obtain an initial model from class averages consisting of only a small number of images.

6. The matrix S as a convolution operator on SO(3)

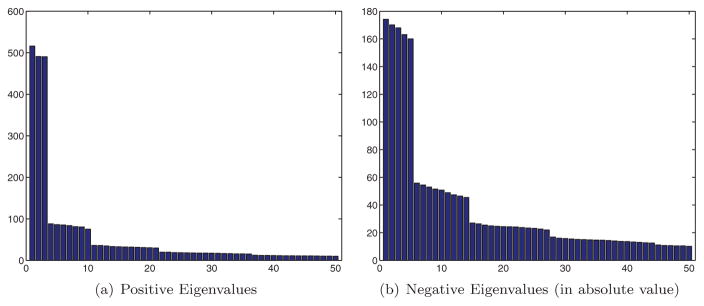
Taking an even closer look into the numerical distribution of the eigenvalues of the “clean” 2N × 2N matrix S^clean corresponding to p = 1 (all common lines detected correctly) reveals that its eigenvalues have the exact same multiplicities as the spherical harmonics, which are the eigenfunctions of the Laplacian on the unit sphere S² ⊂ ℝ³. In particular, Figure 9(a) is a bar plot of the 50 largest eigenvalues of S^clean with N = 1000 and clearly shows numerical multiplicities of 3, 7, 11, … corresponding to the multiplicity 2l + 1 (l = 1, 3, 5, …) of the odd spherical harmonics. Moreover, Figure 9(b) is a bar plot of the magnitude of the most negative eigenvalues of S. The multiplicities 5, 9, 13, … corresponding to the multiplicity 2 l + 1 (l = 2, 4, 6, …) of the even spherical harmonics are evident (the first even eigenvalue corresponding to l = 0 is missing).

Figure 9.

Bar plot of the positive (left) and the absolute values of the negative (right) eigenvalues of S with N = 1000 and p = 1. The numerical multiplicities 2l + 1 (l = 1, 2, 3, …) of the spherical harmonics are evident, with odd l values corresponding to positive eigenvalues, and even l values (except l = 0) corresponding to negative eigenvalues.

The numerically observed multiplicities motivate us to examine S ^clean in more detail. To that end, it is more convenient to reshuffle the 2N × 2N matrix S defined in (3.1)–(3.2) into an N × N matrix K whose entries are 2 × 2 rank-1 matrices given by

$$K_{ij}=\left(\begin{array}{cc}{x}_{ij}{x}_{ji}& x_{ij}{y}_{ji}\\ y_{ij}{x}_{ji}& y_{ij}{y}_{ji}\end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right)c_{ij}{c}_{ji}^T{\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right)}^T,i,j=1,\dots ,N,$$ (6.1)

with c_ij and c_ji given in (2.4)–(2.5). From (2.6) it follows that the common line is given by the normalized cross product of $R_i^3$ and $R_j^3$, that is,

$$R_i{c}_{ij}=R_j{c}_{ji}=\pm \frac{R_i^3\times R_j^3}{\left|\right|R_i^3\times R_j^3\left|\right|},$$ (6.2)

because R_ic_ij is a linear combination of $R_i^1$ and $R_i^2$ (perpendicular to $R_i^3$), while R_jc_ji is a linear combination of $R_j^1$ and $R_j^2$ (perpendicular to $R_j^3$); a unit vector perpendicular to $R_i^3$ and $R_j^3$ must be given by either $\frac{R_i^3\times R_j^3}{\left|\right|R_i^3\times R_j^3\left|\right|}$ or $-\frac{R_i^3\times R_j^3}{\left|\right|R_i^3\times R_j^3\left|\right|}$. Equations (6.1)–(6.2) imply that K_ij is a function of R_i and R_j given by

$$K_{ij}=K(R_i,R_j)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right)R_i^{-1}\frac{(R_i^3\times R_j^3){(R_i^3\times R_j^3)}^T}{{\left|\right|R_i^3\times R_j^3\left|\right|}^2}{R}_j{\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right)}^T,$$ (6.3)

for i ≠ j regardless of the choice of the sign in (6.2), and $K_{ii}=\left(\begin{array}{cc}0& 0\\ 0& 0\end{array}\right)$.

The eigenvalues of K and S are the same, with the eigenvectors of K being vectors of length 2N obtained from the eigenvectors of S by reshuffling their entries. We therefore try to understand the operation of matrix-vector multiplication of K with some arbitrary vector f of length 2N. It is convenient to view the vector f as N vectors in ℝ² obtained by sampling the function f: SO(3) → ℝ² at R₁, …, R_N, that is,

$$f_i=f(R_i),i=1,\dots ,N.$$ (6.4)

The matrix-vector multiplication is thus given by

$${(Kf)}_i=\sum _{j=1}^N{K}_{ij}{f}_j=\sum _{j=1}^{N}K(R_i,R_j)f(R_j),i=1,\dots ,N.$$ (6.5)

If the rotations R₁, …, R_N are i.i.d. random variables uniformly distributed over SO(3), then the expected value of (Kf)_i conditioned on R_i is

$$\mathbb{E}[{(Kf)}_i\mid R_i]=(N-1){\int }_{\text{SO}(3)}K(R_i,R)f(R)dR,$$ (6.6)

where dR is the Haar measure (recall that by being a zero matrix, K(R_i, R_i) does not contribute to the sum in (6.5)). The eigenvectors of K are therefore discrete approximations to the eigenfunctions of the integral operator given by

$$(\mathcal{K}f)(R_1)={\int }_{\text{SO}(3)}K(R_1,R_2)f(R_2){dR}_2,$$ (6.7)

due to the law of large numbers, with the kernel K: SO(3) × SO(3) → ℝ^2×2 given by (6.3). We are thus interested in the eigenfunctions of the integral operator given by (6.7).

The integral operator 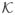is a convolution operator over SO(3). Indeed, note that K given in (6.3) satisfies

$$K({gR}_1,{gR}_2)=K(R_1,R_2)\text{for}\text{all}g\in \text{SO}(3),$$ (6.8)

because $({gR}_1^3)\times ({gR}_2^3)=g(R_1^3\times R_2^3)$ (and gg⁻¹ = g⁻¹g = I. It follows that the kernel K depends only upon the “ratio” $R_1^{-1}{R}_2$, because we can choose $g=R_1^{-1}$ so that

$$K(R_1,R_2)=K(I,R_1^{-1}{R}_2),$$

and the integral operator 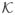of (6.7) becomes

$$(\mathcal{K}f)(R_1)={\int }_{\text{SO}(3)}K(I,R_1^{-1}{R}_2)f(R_2){dR}_2.$$ (6.9)

We will therefore define the convolution kernel K̃: SO(3) → ℝ^2×2 as

$$\stackrel{\sim }{K}(U^{-1})\equiv K(I,U)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right)\frac{(I^3\times U^3){(I^3\times U^3)}^T}{{\left|\right|I^3\times U^3\left|\right|}^2}U{\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right)}^T,$$ (6.10)

where I³ = (0 0 1)^T is the third column of the identity matrix I. We rewrite the integral operator 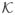from (6.7) in terms of K̃ as

$$(\mathcal{K}f)(R_1)={\int }_{\text{SO}(3)}\stackrel{\sim }{K}(R_2^{-1}{R}_1)f(R_2){dR}_2={\int }_{\text{SO}(3)}\stackrel{\sim }{K}(U)f(R_1{U}^{-1})dU,$$ (6.11)

where we used the change of variables $U=R_2^{-1}{R}_1$. Equation (6.11) implies that 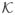is a convolution operator over SO(3) given by [33, p. 158]

$$\mathcal{K}f=\stackrel{\sim }{K}\ast f.$$ (6.12)

Similar to the convolution theorem for functions over the real line, the Fourier transform of a convolution over SO(3) is the product of their Fourier transforms, where the Fourier transform is defined by a complete system of irreducible matrix-valued representations of SO(3) (see, e.g., [33, Theorem (4.14), p. 159]).

Let ρ_θ ∈ SO(3) be a rotation by the angle θ around the z-axis, and let ρ̃_θ ∈ SO(2) be a planar rotation by the same angle:

$${\rho }_{\theta }=\left(\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right),{\stackrel{\sim }{\rho }}_{\theta }=\left(\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right).$$

The kernel K̃ satisfies the invariance property

$$\stackrel{\sim }{K}({({\rho }_{\theta }U{\rho }_{\alpha })}^{-1})={\stackrel{\sim }{\rho }}_{\theta }\stackrel{\sim }{K}(U^{-1}){\stackrel{\sim }{\rho }}_{\alpha }\text{for}\text{all}\theta ,\alpha \in [0,2\pi ).$$ (6.13)

To that end, we first observe that ρ_θI³ = I³ and (Uρ_α)³ = U³, so

$$I^3\times {({\rho }_{\theta }U{\rho }_{\alpha })}^3=({\rho }_{\theta }{I}^3)\times {({\rho }_{\theta }U{\rho }_{\alpha })}^3={\rho }_{\theta }(I^3\times {(U{\rho }_{\alpha })}^3)={\rho }_{\theta }(I^3\times U^3),$$ (6.14)

from which it follows that

$$\left|\right|I^3\times {({\rho }_{\theta }U{\rho }_{\alpha })}^3\left|\right|=\left|\right|{\rho }_{\theta }(I^3\times U^3)\left|\right|=\left|\right|I^3\times U^3\left|\right|,$$ (6.15)

because ρ_θ preserves length, and it also follows that

$$(I^3\times {({\rho }_{\theta }U{\rho }_{\alpha })}^3){(I^3\times {({\rho }_{\theta }U{\rho }_{\alpha })}^3)}^T={\rho }_{\theta }(I^3\times U^3){(I^3\times U^3)}^T{\rho }_{\theta }^{-1}.$$ (6.16)

Combining (6.15) and (6.16) yields

$$\frac{(I^3\times {({\rho }_{\theta }U{\rho }_{\alpha })}^3){(I^3\times {({\rho }_{\theta }U{\rho }_{\alpha })}^3)}^T}{{\left|\right|I^3\times {({\rho }_{\theta }U{\rho }_{\alpha })}^3\left|\right|}^2}{\rho }_{\theta }U{\rho }_{\alpha }={\rho }_{\theta }\frac{(I^3\times U^3){(I^3\times U^3)}^T}{{\left|\right|I^3\times U^3\left|\right|}^2}U{\rho }_{\alpha },$$ (6.17)

which together with the definition of K̃ in (6.10) demonstrates the invariance property (6.13).

The fact that 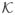is a convolution satisfying the invariance property (6.13) implies that the eigenfunctions of 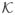are related to the spherical harmonics. This relation, as well as the exact computation of the eigenvalues, will be established in a separate publication [34]. We note that the spectrum of 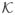would have been much easier to compute if the normalization factor ||I³ × U³||² did not appear in the kernel function K̃ of (6.10). Indeed, in such a case, K̃ would have been a third order polynomial, and all eigenvalues corresponding to higher order representations would have vanished.

We note that (6.6) implies that the top eigenvalue of S^clean, denoted λ₁(S^clean), scales linearly with N; that is, with high probability,

$${\lambda }_1(S^{\mathit{clean}})=N{\lambda }_1(\mathcal{K})+O(\sqrt{N}),$$ (6.18)

where the $O(\sqrt{N})$ term is the standard deviation of the sum in (6.5). Moreover, from the top eigenvalues observed in Figures 3(a), 3(e), 5(a), 6(a), and 7(a) corresponding to p = 1 and p values close to 1, it is safe to speculate that

Figure 6.

Eigenvalue histograms of S for N = 500 and different levels of noise.

$${\lambda }_1(\mathcal{K})=\frac{1}{2},$$ (6.19)

as the top eigenvalues are approximately 50, 250, and 500 for N = 100, 500, and 1000, respectively.

We calculate λ₁( 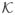) analytically by showing that the three columns of

$$f(U)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right)U^{-1}$$ (6.20)

are eigenfunctions of 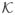. Notice that since U⁻ = U^T, f(U) is equal to the first two columns of the rotation matrix U. This means, in particular, that U can be recovered from f(U). Since the eigenvectors of S, as computed by our algorithm (3.6), are discrete approximations of the eigenfunctions of 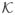, it is possible to use the three eigenvectors of S that correspond to the three eigenfunctions of 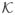given by f(U) to recover the unknown rotation matrices.

We now verify that the columns f(U) are eigenfunctions of 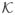. Plugging (6.20) into (6.11) and employing (6.10) give

$$(\mathcal{K}f)(R)={\int }_{\text{SO}(3)}\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right)\frac{(I^3\times U^3){(I^3\times U^3)}^T}{{\left|\right|I^3\times U^3\left|\right|}^2}U\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right)U^{-1}{R}^{-1}dU.$$ (6.21)

From UU⁻¹ = I it follows that

$$U\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right)U^{-1}={\mathit{UIU}}^{-1}-U\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right)U^{-1}=I-U^3{U}^{3^T}.$$ (6.22)

Combining (6.22) with the fact that (I³ × U³)^T U³ = 0, we obtain

$$\frac{(I^3\times U^3){(I^3\times U^3)}^T}{{\left|\right|I^3\times U^3\left|\right|}^2}U\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right)U^{-1}=\frac{(I^3\times U^3){(I^3\times U^3)}^T}{{\left|\right|I^3\times U^3\left|\right|}^2}.$$ (6.23)

Letting U³= (x y z)^T, the cross product I³× U³ is given by

$$I^3\times U^3={(-yx0)}^T,$$ (6.24)

whose squared norm is

$${\left|\right|I^3\times U^3\left|\right|}^2=x^2+y^2=1-z^2,$$ (6.25)

and

$$(I^3\times U^3){(I^3\times U^3)}^T=\left(\begin{array}{ccc}{y}^2& -xy& 0\\ -xy& x^2& 0\\ 0& 0& 0\end{array}\right).$$ (6.26)

It follows from (6.21) and identities (6.23)–(6.26) that

$$(\mathcal{K}f)(R)={\int }_{\text{SO}(3)}\frac{1}{1-z^2}\left(\begin{array}{ccc}{y}^2& -xy& 0\\ -xy& x^2& 0\end{array}\right)dU{R}^{-1}.$$ (6.27)

The integrand in (6.27) is only a function of the axis of rotation U³. The integral over SO(3) therefore collapses to an integral over the unit sphere S² with the uniform measure dμ (satisfying ∫_S²dμ = 1) given by

$$(\mathcal{K}f)(R)={\int }_{S^2}\frac{1}{1-z^2}\left(\begin{array}{ccc}{y}^2& -xy& 0\\ -xy& x^2& 0\end{array}\right)d\mu R^{-1}.$$ (6.28)

From symmetry it follows that ${\int }_{S^2}\frac{xy}{1-z^2}d\mu =0$ and that ${\int }_{S^2}\frac{x^2}{1-z^2}d\mu ={\int }_{S^2}\frac{y^2}{1-z^2}d\mu$. As $\frac{x^2}{1-z^2}+\frac{y^2}{1-z^2}=1$ on the sphere, we conclude that ${\int }_{S^2}\frac{x^2}{1-z^2}d\mu ={\int }_{S^2}\frac{y^2}{1-z^2}d\mu =\frac{1}{2}$ and

$$(\mathcal{K}f)(R)=\frac{1}{2}\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right)R^{-1}=\frac{1}{2}f(R).$$ (6.29)

This shows that the three functions defined by (6.20), which are the same as those defined in (3.6), are the three eigenfunctions of 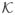with the corresponding eigenvalue ${\lambda }_1(\mathcal{K})=\frac{1}{2}$, as was speculated before in (6.19) based on the numerical evidence.

The remaining spectrum is analyzed in [34], where it is shown that the eigenvalues of 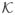are

$${\lambda }_l(\mathcal{K})=\frac{{(-1)}^{l+1}}{l(l+1)},$$ (6.30)

with multiplicities 2l + 1 for l = 1, 2, 3, …. An explicit expression for all eigenfunctions is also given in [34]. In particular, the spectral gap between the top eigenvalue ${\lambda }_1(\mathcal{K})=\frac{1}{2}$ and the next largest eigenvalue ${\lambda }_3(\mathcal{K})=\frac{1}{12}$ is

$$\mathrm{\Delta }(\mathcal{K})={\lambda }_1(\mathcal{K})-{\lambda }_3(\mathcal{K})=\frac{5}{12}.$$ (6.31)

7. Wigner’s semicircle law and the threshold probability

As indicated by the numerical experiments of section 5, false detections of common lines due to noise lead to the emergence of what seems to be Wigner’s semicircle for the distribution of the eigenvalues of S. In this section we provide a simple mathematical explanation for this phenomenon.

Consider the simplified probabilistic model of section 5.1 that assumes that every common line is detected correctly with probability p, independently of all other common lines, and that with probability 1 − p the common lines are falsely detected and are uniformly distributed over the unit circle. The expected value of the noisy matrix S, whose entries are correct with probability p, is given by

$$\mathbb{E}S={pS}^{\text{clean}},$$ (7.1)

because the contribution of the falsely detected common lines to the expected value vanishes by the assumption that their directions are distributed uniformly on the unit circle. From (7.1) it follows that S can be decomposed as

$$S={pS}^{\text{clean}}+W,$$ (7.2)

where W is a 2N × 2N zero-mean random matrix whose entries are given by

$$W_{ij}=\{\begin{array}{cc}(1-p)S_{ij}^{\text{clean}}& \text{with}\text{probability}p,\\ -{pS}_{ij}^{\text{clean}}+X_{ij}{X}_{ji}& \text{with}\text{probability}1-p,\end{array}$$ (7.3)

where X_ij and X_ji are two independent random variables obtained by projecting two independent random vectors uniformly distributed on the unit circle onto the x-axis. For small values of p, the variance of W_ij is dominated by the variance of the term X_ijX_ji. Symmetry implies that $\mathbb{E}{X}_{ij}^2=\mathbb{E}{X}_{ji}^2=\frac{1}{2}$, from which we have that

$$\mathbb{E}{W}_{ij}^2=\mathbb{E}{X}_{ij}^2{X}_{ji}^2+O(p)=\frac{1}{4}+O(p).$$ (7.4)

Wigner [28, 29] showed that the limiting distribution of the eigenvalues of random n × n symmetric matrices (scaled down by $\sqrt{n}$), whose entries are i.i.d. symmetric random variables with variance σ² and bounded higher moments, is a semicircle whose support is the symmetric interval [−2σ, 2σ]. This result applies to our matrix W with n = 2N and $\sigma =\frac{1}{2}+O(p)$, since the entries of W are bounded zero-mean i.i.d. random variables. Reintroducing the scaling factor $\sqrt{n}=\sqrt{2N}$, the top eigenvalue of W, denoted λ₁(W), is a random variable fluctuating around $2\sigma \sqrt{n}=\sqrt{2N}(1+O(p))$. It is known that λ₁(R) is concentrated near that value [35]; that is, the fluctuations are small. Moreover, the universality of the edge of the spectrum [36] implies that λ₁(W) follows the Tracy–Widom distribution [37]. For our purposes, the leading order approximation

$${\lambda }_1(W)\approx \sqrt{2N}$$ (7.5)

suffices, with the probabilistic error bound given in [35].

The eigenvalues of W are therefore distributed according to Wigner’s semicircle law whose support, up to small O(p) terms and finite sample fluctuations, is [ $-\sqrt{2N},\sqrt{2N}$]. This prediction is in full agreement with the numerically observed supports in Figure 3 and in Figures 5–7, noting that for N = 100 the right edge of the support is located near $\sqrt{200}\approx 14.14$, for N = 500 near $\sqrt{1000}\approx 31.62$, and for N = 1000 near $\sqrt{2000}\approx 44.72$. The agreement is striking especially for Figures 5–7 that were obtained from simulated noisy projections without imposing the artificial probabilistic model of section 5.1 that was used here to actually derive (7.5).

The threshold probability p_c depends on the spectral gap of S^clean, denoted Δ(S^clean), and on the top eigenvalue λ₁(W) of W. From (6.31) it follows that

$$\mathrm{\Delta }(S^{\text{clean}})=\frac{5}{12}N+O(\sqrt{N}).$$ (7.6)

In [38, 39, 40] it is proved that the top eigenvalue of the matrix A + W, composed of a rank-1 matrix A and a random matrix W, will be pushed away from the semicircle with high probability if the condition

$${\lambda }_1(A)>\frac{1}{2}{\lambda }_1(W)$$ (7.7)

is satisfied. Clearly, for matrices A that are not necessarily of rank-1, the condition (7.7) can be replaced by

$$\mathrm{\Delta }(A)>\frac{1}{2}{\lambda }_1(W),$$ (7.8)

where Δ(A) is the spectral gap. Therefore, the condition

$$p\mathrm{\Delta }(S^{\text{clean}})>\frac{1}{2}{\lambda }_1(W)$$ (7.9)

guarantees that the top three eigenvalues of S will reside away from the semicircle. Substituting (7.5) and (7.6) in (7.9) results in

$$p\left(\frac{5}{12}N+O(\sqrt{N})\right)>\frac{1}{2}\sqrt{2N}(1+O(p)),$$ (7.10)

from which it follows that the threshold probability p_c is given by

$$p_c=\frac{6\sqrt{2}}{5\sqrt{N}}+O(N^{-1})$$ (7.11)

For example, the threshold probabilities predicted for N = 100, N = 500, and N = 1000 are p_c ≈ 0.17, p_c ≈ 0.076, and p_c ≈ 0.054, respectively. These values match the numerical results of section 5.1 and are also in good agreement with the numerical experiments for the noisy projections presented in section 5.2.

From the perspective of information theory, the threshold probability (7.11) is nearly optimal. To that end, notice that to estimate N rotations to a given finite precision requires O(N) bits of information. For p ≪ 1, the common line between a pair of images provides O(p²) bits of information (see [41, section 5, eq. (82)]). Since there are N(N − 1)/2 pairs of common lines, the entropy of the rotations cannot decrease by more than O(p²N²). Comparing p²N² to N, we conclude that the threshold probability p_c of any recovery method cannot be lower than $O(\frac{1}{\sqrt{N}})$. The last statement can be made precise by Fano’s inequality and Wolfowitz’s converse, also known as the weak and strong converse theorems to the coding theorem that provide a lower bound for the probability of the error in terms of the conditional entropy (see, e.g., [42, Chapter 8.9, pp. 204–207] and [43, Chapter 5.8, pp. 173–176]). This demonstrates the near-optimality of our eigenvector method, and we refer the reader to section 5 in [41] for a complete discussion about the information theory aspects of this problem.

8. Summary and discussion

In this paper we presented efficient methods for computing the rotations of all cryo-EM particles from common-line information in a globally consistent way. Our algorithms, one based on a spectral method (computation of eigenvectors), and the other based on SDP (a version of max-cut), are able to find the correct set of rotations even at very low common-line detection rates. Using random matrix theory and spectral analysis on SO(3), we showed that rotations obtained by the eigenvector method can lead to a meaningful ab initio model as long as the proportion of correctly detected common lines exceeds $\frac{6\sqrt{2}}{5\sqrt{N}}$ (assuming a simplified probabilistic model for the errors). It remains to be seen how these algorithms will perform on real raw projection images or on their class averages, and to compare their performance to the recently proposed voting recovery algorithm [19], whose usefulness has already been demonstrated on real datasets. Although the voting algorithm and the methods presented here try to solve the same problem, the methods and their underlying mathematical theory are different. While the voting procedure is based on a Bayesian approach and is probabilistic in its nature, the approach here is analytical and is based on spectral analysis of convolution operators over SO(3) and random matrix theory.

The algorithms presented here can be regarded as a continuation of the general methodology initiated in [41], where we showed how the problem of estimating a set of angles from their noisy offset measurements can be solved using either eigenvectors or SDP. Notice, however, that the problem considered here of recovering a set of rotations from common-line measurements between their corresponding images is different and more involved mathematically than the angular synchronization problem that is considered in [41]. Specifically, the common-line-measurement between two projection images P_i and P_j provides only partial information about the ratio $R_i^{-1}{R}_j$. Indeed, the common line between two images determines only two out of the three Euler angles (the missing third degree of freedom can be determined only by a third image). The success of the algorithms presented here shows that it is also possible to integrate all the partial offset measurements between all rotations in a globally consistent way that is robust to noise. Although the algorithms presented in this paper and in [41] seem to be quite similar, the underlying mathematical foundation of the eigenvector algorithm presented here is different, as it crucially relies on the spectral properties of the convolution operator over SO(3).

We would like to point out two possible extensions of our algorithms. First, it is possible to include confidence information about the common lines. Specifically, the normalized correlation value of the common line is an indication for its likelihood of being correctly identified. In other words, common lines with higher normalized correlations have a better chance of being correct. We can therefore associate a weight w_ij with the common line between P_i and P_j to indicate our confidence in it, and multiply the corresponding 2 × 2 rank-1 submatrix of S by this weight. This extension gives only a little improvement in terms of the MSE as seen in our experiments, which will be reported elsewhere. Another possible extension is to include multiple hypotheses about the common line between two projections. This can be done by replacing the 2 × 2 rank-1 matrix associated with the top common line between P_i and P_j by a weighted average of such 2 × 2 rank-1 matrices corresponding to the different hypotheses. On the one hand, this extension should benefit from the fact that the probability that one of the hypotheses is the correct one is larger than that of just the common line with the top correlation. On the other hand, since at most one hypothesis can be correct, all hypotheses except maybe one are incorrect, and this leads to an increase in the variance of the random Wigner matrix. Therefore, we often find the single hypothesis version favorable compared to the multiple hypotheses version. The corresponding random matrix theory analysis and the supporting numerical experiments will be reported in a separate publication.

Finally, we note that the techniques and analysis applied here to solve the cryo-EM problem can be translated to the computer vision problem of structure from motion, where lines perpendicular to the epipolar lines play the role of the common lines. This particular application will be the subject of a separate publication.