Single-Cell Growth Probability of Listeria monocytogenes at Suboptimal Temperature, pH, and Water Activity

Abstract

The single-cell growth probability of Listeria monocytogenes was characterized in tryptone soy broth supplemented with 0.6% yeast extract at temperature ranging from 5 to 25°C, pH ranging from 4.4 to 6.5, and water activity ranging from 0.919 to 0.989. Growth was monitored visually in 96-microwell plates and the growth probability was deduced from concentrations estimated with the MPN calculation. Models were proposed to describe the increase of the probability from 0 to 1 with increasing values of environmental factors. An exponential model was used for the temperature and the individual minimal temperature for growth ranged from −3.6°C [−4.5°C, −2.7°C] to 17.3°C [16.0°C, 18.6°C]. An inverse exponential model was convenient for the pH and the minimal pH for growth of individual cells ranged from 4.34 [3.93, 4.75] to 5.93 [4.85, 7.01]. A linear model was used for the water activity and the minimal value for growth of individual cells ranged from 0.917 [0.909, 0.925] to 0.988 [0.966, 1]. In spite of the great between-experiment variability, the minimal values estimated for the growth limits of individual cells were in accordance with values usually proposed for L. monocytogenes populations. This study provides models allowing the prediction of the growth probability of a few cells contaminating chilled foods with suboptimal pH and water activity improving thus the assessment of the behavior of L. monocytogenes cells naturally contaminating foods.

Introduction

Listeria monocytogenes is a well-known foodborne pathogen and constitutes a kind of paragon for quantitative microbiology since its ubiquitous nature leading to a frequent contamination of food and its ability to multiply in many foods during chilled storage encouraged the development of predictive modeling and quantitative microbial risk assessment. Many risk assessments were thus published aiming at assessing the probability of severe listeriosis when eating ready-to-eat foods (Anonymous, 2003, 2004; Pouillot et al., 2009; Ross et al., 2009a; Mataragas et al., 2010), ranking the most risky foods (Anonymous, 2003; Ross et al., 2009a), or assessing the impact of management options on the listeriosis probability (Anonymous, 2003, 2004; Pouillot et al., 2009; Ross et al., 2009b; Mataragas et al., 2010). The assessment of the microbial behavior of the pathogen is of the highest importance when performing these assessments since the listeriosis cases are predominantly linked to the consumption of highly contaminated foods (Anonymous, 2004) and considering the variability of this behavior is of paramount in the context of risk analysis framework (Anonymous, 2008). The major sources of variability affecting microbial responses in foods are the initial contamination level, the variability in processing factors, the variability in the food characteristics, in the storage conditions, and the biological variability, i.e., the variability of microbial behavior. For several years, it is accepted that the accurate behavior prediction of L. monocytogenes in food requires a single-cell approach taking into account the physiological state of cells initially contaminating foods since this will strongly influence the lag phase duration of the bacterial population. Theoretical developments (Baranyi, 1998) and experimental results (Elfwing et al., 2004; Guillier et al., 2005; Pin and Baranyi, 2006; Métris et al., 2008) describing the variability of single-cell lag times among clonal bacterial populations and showing the increase of this variability when inimical treatments are applied to bacterial cells were published. It is also known for decades that bacterial injury can inhibit the growth initiation of some cells in a population and this is of first importance when studying the resuscitation of stressed cells in selective culture media (Wu, 2008). It was shown that it is possible to characterize the single-cell growth probability corresponding to the probability for an individual cell to initiate growth in a given culture medium (Dupont and Augustin, 2009). Some experiments have also suggested the possibility that minimal values of environmental factors allowing the multiplication of individual cells can vary from one cell to another. Pascual et al. (2001) observed an increase of the inoculum size needed to initiate growth of L. monocytogenes when increasing the NaCl concentration in the growth medium or when decreasing its pH. Koutsoumanis and Sofos (2005) observed that the growth boundaries of L. monocytogenes according to the temperature, the pH, and the water activity were affected by the inoculum size and that higher numbers of cells increased the growth probability. Koutsoumanis (2008) reported similar observations with Salmonella.

The aim of this study was to characterize the single-cell growth probability of L. monocytogenes according to the three major environmental factors, i.e., the temperature, the pH, and the water activity, and then to characterize the variability of the individual minimal temperature, pH, and water activity for growth of a strain of this pathogen.

Materials and Methods

Strain and inoculum preparation

Listeria monocytogenes LM14 (serotype 4b, environment of meat industry isolate) was maintained at −20°C on cryobeads (AES Laboratoire, Combourg, France). The strain LM14 is the reference strain of the French program in predictive microbiology Sym’Previus¹.

Cryobeads were incubated at 30°C for 24 h in tryptone soy broth supplemented with 0.6% yeast extract (TSBye, LEB Oxoid, Unipath Ltd., Basingstoke, UK). The first bacterial culture was diluted to obtain an initial bacterial concentration of approximately 10³ cells ml⁻¹ in TSBye. This bacterial suspension was then incubated in TSBye for 18 h at 25°C to obtain 10⁸ cells ml⁻¹ in the exponential growth phase. TSBye was eliminated by centrifugation (3,000 × g, 10 min, 4°C), cells were washed in 0.85% NaCl (AES Laboratoire), and centrifuged again. The supernatant was discarded and the cells were recovered in tryptone salt broth (TS, AES Laboratoire). Aliquots of 1 ml of TS containing 10⁸ cells were stored at −20°C for 48 h to 6 months.

Impact of temperature, pH, and water activity on the single-cell growth probability

The probability for individual cells of L. monocytogenes to initiate growth was studied in TSBye adjusted to different suboptimal temperatures, pH, or water activities. TSBye incubated at 37°C was the reference condition assumed to be the most favorable condition for growth allowing the growth of all the viable cells. The tested conditions for temperature were 5, 7.5, 10.5, 13, 15, and 20.5°C, pH of TSBye was adjusted to 7 and no salt was added (i.e., water activity equal to 0.997). The tested conditions for pH were 4.4, 4.5, 4.6, 4.7, 4.8, 4.9, 5.0, 5.1, 5.2, 5.3, 5.5, 6.0, and 6.5 by adding HCl (Prolabo, Paris, France) to TSBye and incubation was performed at 15 and 37°C. The tested conditions for water activity were 2, 3, 4, 5, 6, 7, 8, 8.5, 9, 9.5, 10, 10.5, 11, and 12% (wt/vol) of added NaCl to pH 7 TSBye incubated at 15 and 37°C. The corresponding water activities, a_w, were calculated according the relationship published by Chirife and Resnik (1984):

$${\text{a}}_{\text{w}}=\text{1}-\text{0}\text{.0052471}\cdot \text{WPS}-\text{0}\text{.00012206}\cdot \text{WP}{\text{S}}^2$$ (1)

where WPS is the percentage of water phase salt.

The deduced a_w were 0.989, 0.983, 0.977, 0.971, 0.964, 0.957, 0.950, 0.947, 0.943, 0.939, 0.935, 0.931, 0.928, and 0.919, respectively. Each tested condition was replicated between 3 and 18 times (10 times on average).

Estimation of single-cell growth probability

Aliquots of cells stored at −20°C were thawed at room temperature and diluted in TSBye. Two 96-microwell plates were filled with dilutions adjusted to obtain between 10 and 90% of wells showing growth in reference and tested conditions or 24 wells were each filled with three successive 10-fold dilutions of cell suspensions. The microplates were covered with parafilm to avoid dehydration and then incubated at 37°C for 48 h for reference condition and for up to 3 months for tested conditions. Wells exhibiting turbidity in TSBye were considered as positive for growth.

Assuming a Poisson distribution of cells in the wells, the cell concentrations in reference and tested conditions were calculated with the BAM-MPN Excel spreadsheet developed by Garthright and Blodgett (2003) from the observed proportion of positive wells obtained for each inoculated dilutions. The Excel spreadsheet is freely available on the US Food and Drug Administration website².

The probability for a single-cell to initiate growth, p, is equal to (Dupont and Augustin, 2009):

$$p=c_{\text{i}}\text{/}{c}_{\text{ref}}$$ (2)

where c_i is the cell concentration in tested conditions i and c_ref is the concentration in reference conditions. Strictly speaking, the single-cell growth probability, p, is effectively related to the ability for an individual cell to multiply but also to the multiplication ability of its daughter cells.

Development of models describing the evolution of the single-cell growth probability with temperature, pH, and water activity

The single-cell growth probability, p, increase from 0 to 1 when environmental factors values increases to more favorable conditions. We thus define two theoretical parameters X_inf and X_sup where X represents the temperature, T, the pH, or a_w. When X is smaller than X_inf, p is equal to 0 and when X is greater than X_sup, p is equal to 1. The increase of p when X increased from X_inf to X_sup was exponential for T, inverse exponential for pH, and linear for a_w.

The following models were used to describe these trends:

$$\begin{array}{rcll}p\left(T\right)& =\left\{\begin{array}{cc}0,\hfill & T\le T_{inf}\hfill \\ & \\ \frac{exp\left(T∕c\right)-exp\left(T_{inf}∕c\right)}{exp\left(T_{sup}∕c\right)-exp\left(T_{inf}∕c\right)},\hfill & T_{inf}<T<T_{sup}\hfill \\ & \\ 1,\hfill & T\ge T_{sup}\hfill \\ \hfill \end{array}\right.& & \text{(3)}\\ p\left(\text{pH}\right)& =\left\{\begin{array}{cc}0,\hfill & \text{pH}\le \text{p}{\text{H}}_{inf}\hfill \\ & \\ \frac{exp\left(-\text{pH}\right)-exp\left(-\text{p}{\text{H}}_{inf}\right)}{exp\left(-\text{p}{\text{H}}_{sup}\right)-exp\left(-\text{p}{\text{H}}_{inf}\right)},\hfill & \text{p}{\text{H}}_{inf}<\text{pH}<\text{p}{\text{H}}_{sup}\hfill \\ & \\ 1,\hfill & \text{pH}\ge \text{p}{\text{H}}_{sup}\hfill \\ \hfill \end{array}\right.& & \text{(4)}\\ p\left({\text{a}}_{\text{w}}\right)& =\left\{\begin{array}{cc}0,\hfill & {\text{a}}_{\text{w}}\le {\text{a}}_{\text{w},inf}\hfill \\ & \\ \frac{{\text{a}}_{\text{w}}-{\text{a}}_{\text{w},inf}}{{\text{a}}_{\text{w},sup}-{\text{a}}_{\text{w},inf}},\hfill & {\text{a}}_{\text{w},inf}<{\text{a}}_{\text{w}}<{\text{a}}_{\text{w},sup}\hfill \\ & \\ 1,\hfill & {\text{a}}_{\text{w}}\ge {\text{a}}_{\text{w},sup}\hfill \\ \hfill \end{array}\right.& & \text{(5)}\end{array}$$

T, pH, and a_w were assumed to have independent effects on the single-cell growth probability and the following model was proposed to describe the combined effect of the three environmental factors:

$$p\left(T,\text{pH},a_w\right)=p\left(T\right)\cdot p\left(\text{pH}\right)\cdot p\left({\text{a}}_{\text{w}}\right)$$ (6)

This equation was used to correct single-cell growth probabilities observed at 15°C in pH and a_w experiments.

Model fitting and single-cell growth probability prediction

Since great between-experiments variability was observed, we used a non-linear mixed effects model to model the random effects corresponding to the between-experiments variability. The normal distributions describing the parameter variability were estimated using the Monolix software³.

Monte Carlo simulations were performed to predict the single-cell growth probability distribution according to the environmental factors. Parameters values were independently and randomly selected from their respective normal distributions and 10⁴ iterations were performed with the Matlab software R2010 (The MathWorks Inc., Natick, MA, USA). These simulations allowed defining variation or credibility intervals for estimated probabilities.

Results and Discussion

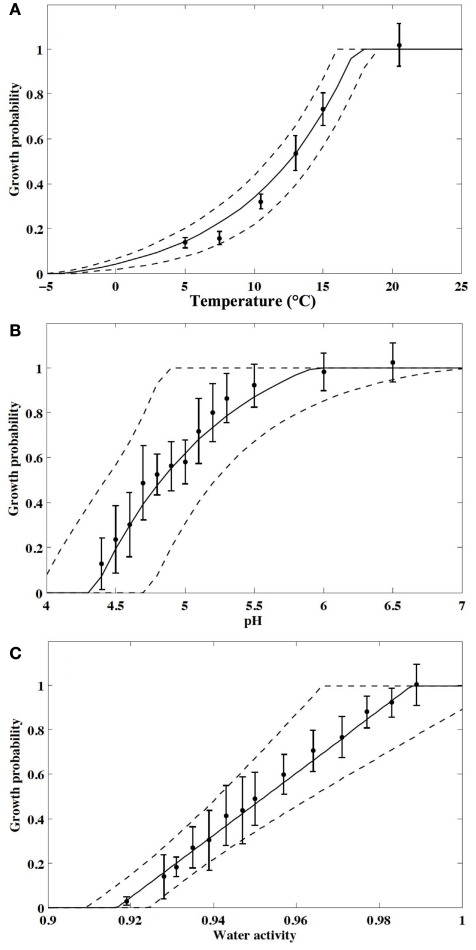
Evolutions of the single-cell growth probability, p, according to T, pH, and a_w are presented in Figure 1. The observed between-experiment variability was large and, for instance, p-values ranged from 0.52 to 0.94 at 15°C, from 0.27 to 0.97 at pH 5, and from 0.19 to 0.79 at a_w 0.95. This variation is unexplained. It is partly due to the great uncertainty of concentrations estimated with the MPN method and also perhaps to the variability in physiological state of microbial populations used in experiments. This great between-experiment variability in single cell growth probability was already observed by Dupont and Augustin (2009) and can be partly explained by the difficulty to experimentally reproduce specific microbial physiological states. In this study, we chose 48 h to six months frozen storage to standardize the microbial population, but despite an approximately stable cell viability observed on non-selective culture media during the storage length, no trend in the single cell growth probability with the storage duration, and the great variability observed for same aged aliquots experimentally used the same day, we can imagine that the observed variability is essentially linked to physiological heterogeneity of bacterial aliquots.

Figure 1.

Evolution of the single-cell growth probability of L. monocytogenes in TSBye according to (A) the temperature, (B) the pH, (C) the water activity. Points represent the mean of the observed probabilities and vertical bars represent the SD. Lines are the fitted models, solid lines correspond to the median behavior and dashed lines represent the 2.5th and 97.5th percentiles of variation.

The estimated model parameters are presented in Table 1. The proposed models described satisfactorily the observed increases in probability with environmental factors and the random effects quantified by σ_experiment allowed the prediction of a variation region in accordance with observed probabilities (Figure 1).

Table 1.

Parameters of the models describing the evolution of the single-cell growth probability of L. monocytogenes with environmental factors.

Environmental factors	Parameters	Value	σexperiment
Temperature	Tinf (°C)	−3.6	0.46
	Tsup (°C)	17.3	0.67
	c	7.6	1.21
pH	pHinf	4.34	0.21
	pHsup	5.93	0.55
Water activity	aw,inf	0.917	0.004
	aw,sup	0.988	0.011

The theoretical cellular minimal temperature for growth varied from −3.6 to 17.3°C with a 95% variation interval for −3.6°C ranging from −4.5 to −2.7°C. The interval for the upper value is [16.0°C, 18.6°C]. These values match the usual minimal temperatures estimated for L. monocytogenes populations which classically vary between −4 and 2°C (Anonymous, 2004; Augustin et al., 2005; Couvert et al., 2010; Mejlholm et al., 2010). For the pH, the cellular minimal value for growth varied from 4.34 to 5.93 and the 95% variation interval for 4.34 ranged from 3.93 to 4.75. The interval for the upper value is [4.85, 7.01]. These values also match the usual population estimations for minimal pH adjusted with HCl allowing the growth of L. monocytogenes which are located between 4.2 and 4.3 (Anonymous, 2004; Augustin et al., 2005; Couvert et al., 2010; Mejlholm et al., 2010). For the water activity, the cellular minimal value for growth ranged from 0.917 to 0.988 with a 95% variation interval ranging from 0.909 to 0.925 for the lower value. The interval for the upper value is [0.966, 1]. The classical estimations for the minimal population water activity ranged from 0.91 to 0.93 (Anonymous, 2004; Augustin et al., 2005; Couvert et al., 2010; Mejlholm et al., 2010). Aguirre and Koutsoumanis (2011) studied the a_w growth limits of individual cells of another strain of L. monocytogenes on tryptone soy agar (TSA). They observed a distribution of individual limits varying from 0.937 to 0.997. These higher values obtained on TSA in comparison with those observed in our study in TSBye are not surprising since Koutsoumanis et al. (2004) already observed a significant difference between the growth limits in broth and agar with a substantial increase in growth limits on agar.

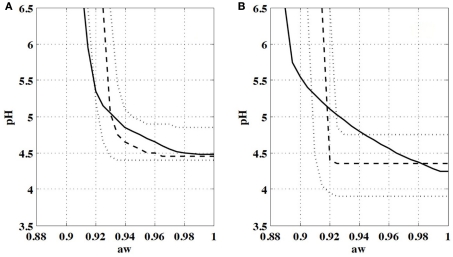
The model proposed in Eq. 6 can then be used to estimate the growth probability of a L. monocytogenes population in suboptimal conditions for the environmental factors, temperature, pH, and water activity according to the number of cells present in the population. In this case the growth probability is equal to 1 − (1 − p)ⁿ with n the number of cells. The model was applied to predict the evolution of the growth probability of L. monocytogenes with the inoculum size. Figure 2 shows examples of predicted growth/no growth interfaces in the same conditions as Koutsoumanis and Sofos (2005) used for L. monocytogenes in tryptic soy broth at 15°C. The growth/no growth interface logically moved with the inoculum size and, for instance, the water activity corresponding to a growth probability of 0.5 for pH 5 was 0.93 with a 95% credibility interval between 0.92 and 0.945 for an initial population of 0.9 log cells (Figure 2A), this minimal water activity decreased to 0.92 (with a 95% credibility interval between 0.91 and 0.925) when the initial population increased to 4.2 log cells (Figure 2B). Although the minimal values for growth seemed different (mainly the minimal water activity), the growth/no interfaces were close for a small initial population (Figure 2A). On the other hand, a significant gap was observed between the interfaces describing the limits of a large population (Figure 2B). This gap was partly linked to the very low water activity allowing growth of high inoculum obtained by Koutsoumanis and Sofos (2005). They observed a value of approximately 0.89 (Figure 2B) significantly lower than our mean estimation for minimal water activity of 0.917. Moreover, the shape of the growth/no growth interface observed by Koutsoumanis and Sofos (2005) for low pH potentially indicated synergistic effects of environmental factors that are not taken into account in the model Eq. 6.

Figure 2.

Comparison of growth/no growth interfaces observed by Koutsoumanis and Sofos (2005) for L. monocytogenes in tryptic soy broth at 15°C with interfaces predicted with the single-cell growth probability model for population of (A) 0.9 log cells and (B) 4.2 log cells. Solid lines are interfaces observed by Koutsoumanis and Sofos (2005) for a growth probability of 0.5. Dashed and dotted lines are interfaces predicted with the model for a growth probability of 0.5. Dashed lines correspond to the median behavior and dotted lines represent the 2.5th and 97.5th percentiles of variation or credibility.

Although supplementary experiments are necessary to investigate the potential effect of interactions between the environmental factors on the single-cell growth probability, the results presented in this paper, and the provided models are useful to assess the behavior of a few L. monocytogenes cells contaminating a food. The complementary use of this model with models describing the variability of individual cell lag time of growing cells should undeniably improve the prediction of microbial load of contaminated foodstuffs.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.