ON THE CHEMICAL SYNTHESIS OF NEW TOPOLOGICAL STRUCTURES

1. Introduction

During the last 20–30 years major advances have been made in the chemical synthesis and assembly of geometric and topological structures. A basic idea is to use a topological or mechanical bond in the sense that the two molecules are being mechanically interlocked or linked. In such a process the molecules are roughly being thought of as curves in 3 dimensional space. From a geometric and topological point of view, knots and links (knots with several components) are very interesting structures. Knots have been studied a lot with associated invariants. Links have been studied less.

A very natural question is how to realize or synthesize topological structures, such as knots and links as assemblies of molecules. In particular can one synthesize well-known knots and links, for example, the trefoil knot and the Borromean rings? This has successfully been done, see [2, 4, 11, 14, 15].

2. New geometric and topological structures

In the papers [1, 2], the first author has introduced a general framework for higher order structures called hyperstructures. Some of the geometric and topological aspects of these were developed in [2, 3] with suggestions for new applications as for example the synthesis of new materials. Let us recall some of these ideas when applied to knots and links. We basically follow the presentation in [3], to illustrate the chemical constructions we have in mind.

A topological link is an embedding of circles in three dimensional space which may be linked together. A knot is a link with just one component.

Example:

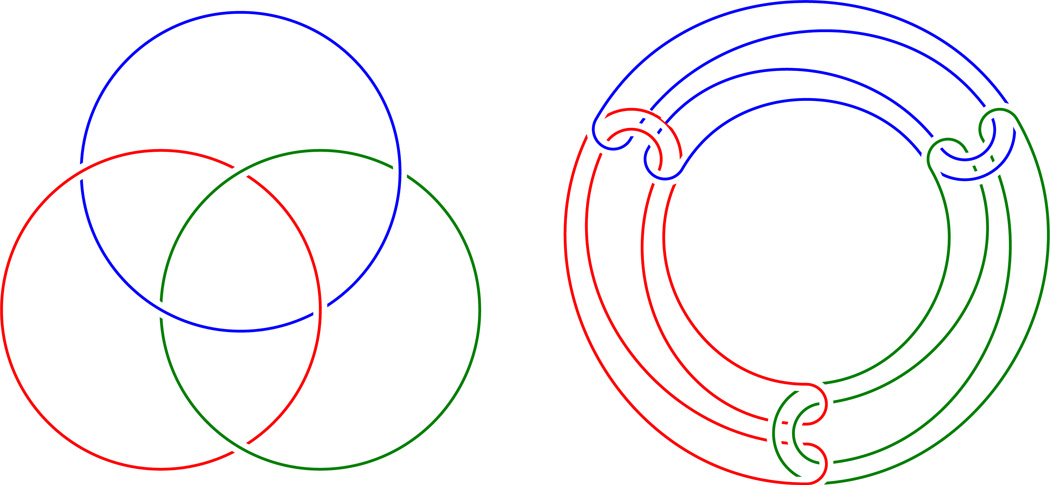
Borromean and Brunnian rings:

Both links in Figure 1 have the property that if any one component (ring) is removed the other two are unlinked. These two versions of Borromean and Brunnian rings are not equivalent (isotopic), see [3].

Figure 1.

Borromean rings to the left and Brunnian rings (of type 1B(3)) to the right

The notion of Borromean rings has been extended to Brunnian rings as follows.

Definition 2.1. n rings in three dimensional space form a Brunnian ring of length n if and only if they are linked in such a way that if any component is removed the (n − 1) remaining ones are unlinked, or in other words, every sublink is trivial.

Hence Borromean rings are Brunnian of length 3. We shall refer to them all as B-structures, see the figure in Example 2 in Section 4.

The classical Borromean rings have 3 components. We may also introduce Borromean rings of length n:

Definition 2.2. n rings in three dimensional space form a Borromean ring of length n if and only if any two components are unlinked.

For more examples see [3].

3. Higher Order Structures

Often in science one has to consider structures of structures: sets of sets, vector spaces of vector spaces, forms of forms, links of links, etc.

In [1, 2] we introduced a general framework for dealing with higher order structures, namely what we call Hyperstructures.

In the present paper we will present some geometrical and topological hyperstructures, namely what we get when we consider links of links of links …

4. New Higher Order Topological Structures

All links considered are in three dimensional space.

Before giving the general construction let us give some examples to indicate the idea.

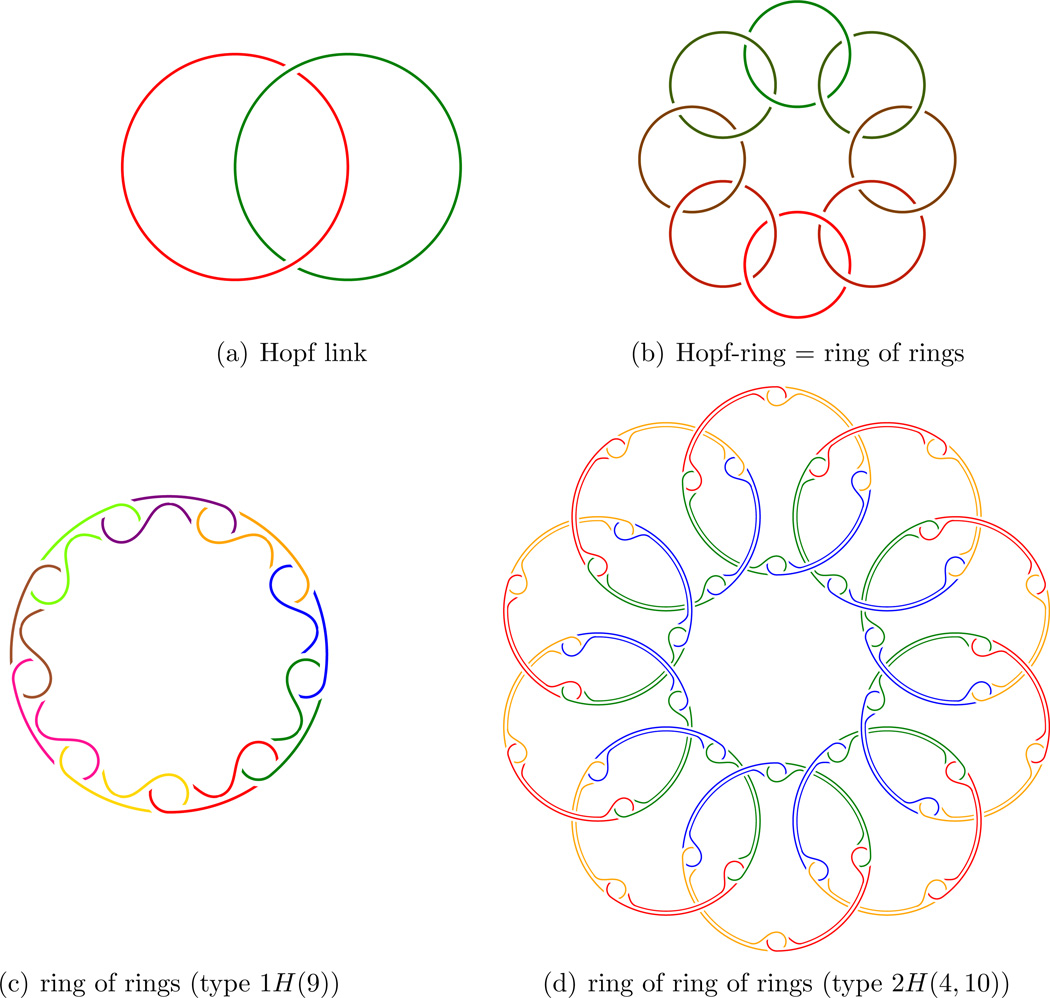
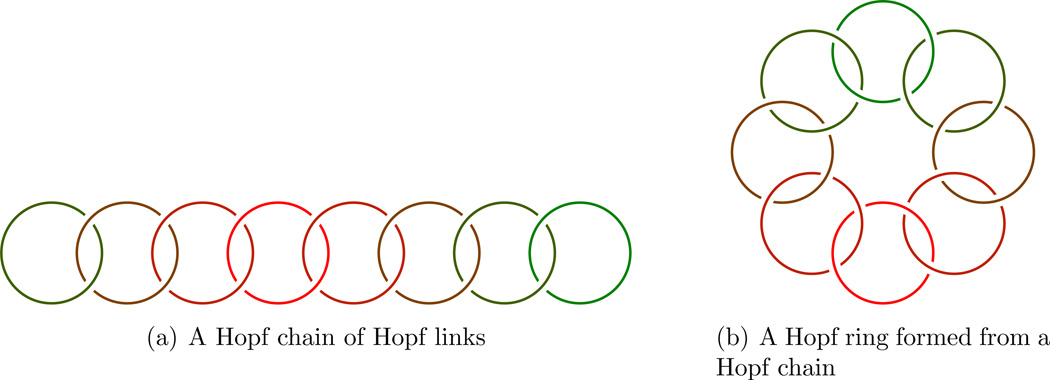
Example: From rings we may form a ring of rings based on the Hopf link:

From Hopf-rings we may in the same way form a Hopf-ring of Hopf-rings as illustrated in Figure 2.

Figure 2.

Clearly they are topologically “ring-like” in the sense that they have been formed by chains being made into loops.

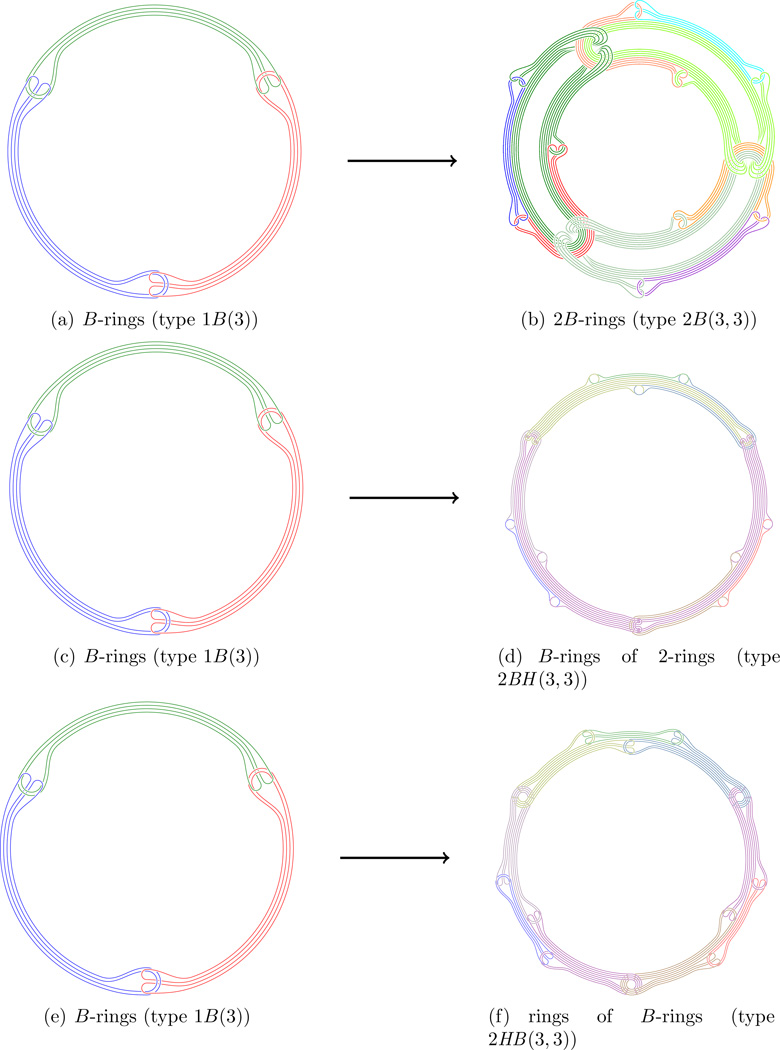
But then from these B-rings we may form B-rings of B-rings to be called 2B-rings. This process clearly iterates to nB-rings, and they are truly n-th order B-rings.

Just from rings and B-rings there are many interesting combinations of second order structures to be formed:

rings → 2-rings	(see Figure 2)
B-rings → 2B-rings	(see Figure 3)
B-rings → B-rings of 2-rings	(see Figure 3)
B-rings → rings of B-rings	(see Figure 3).

Figure 3.

The geometric and topological properties of these new links are measured by their complement in three dimensional space:

$$\mathit{\text{nK}}={ℝ}^3-(\mathit{\text{nB}}).$$

The topology of this is surprisingly complicated even for n = 2 as pointed out in [2]. One needs a form of higher order cohomology operations (Massey products) in order to study them for n = 2. For n > 2 and other links they have not been studied at all.

Higher order links in this new sense have not even been defined nor studied systematically in the literature prior to [2], see also [8]. Let us now explicate the general link construction that follows from the hyperstructure idea.

5. The General Idea

We follow [3]. Let ℒ₁ be a family of links in ℝ³, for example rings or Borromean rings or both.

Pick a finite number of links from ℒ₁ and link or arrange them together in a chain.

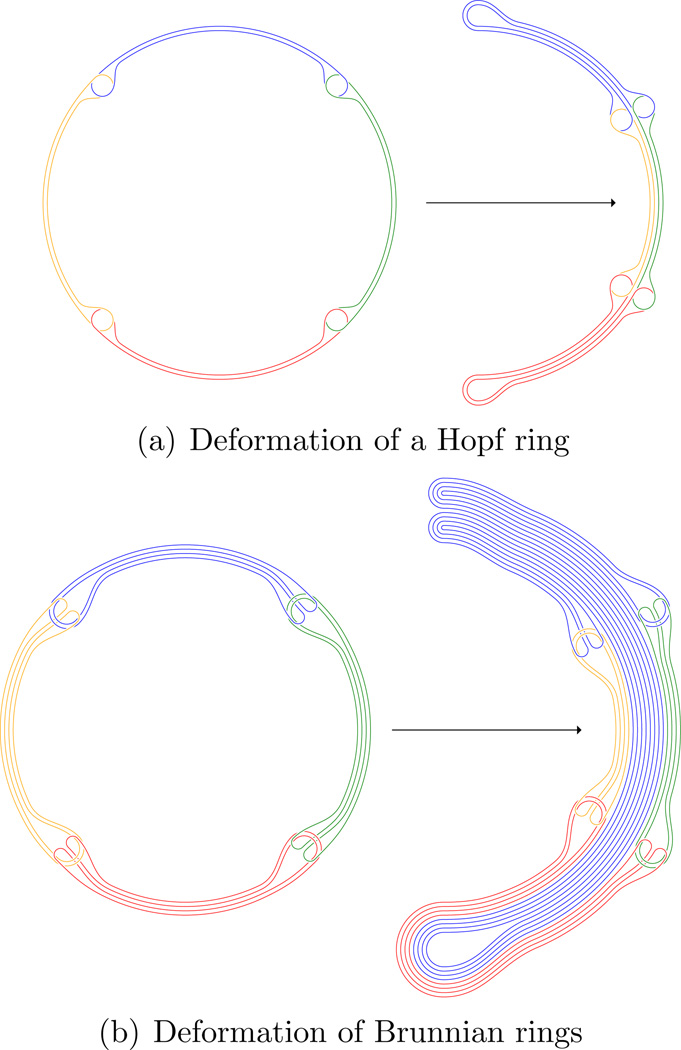
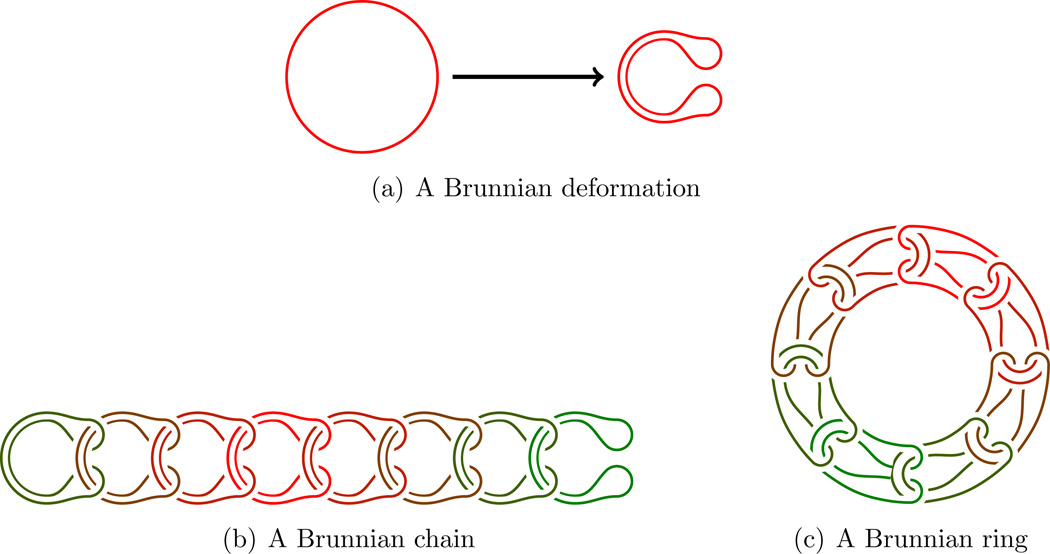
Using the general deformation principle of rings (O) into U-shaped figures as follows:

Then form loops (possibly knotted) of such chains in such a way that they become interlocked.

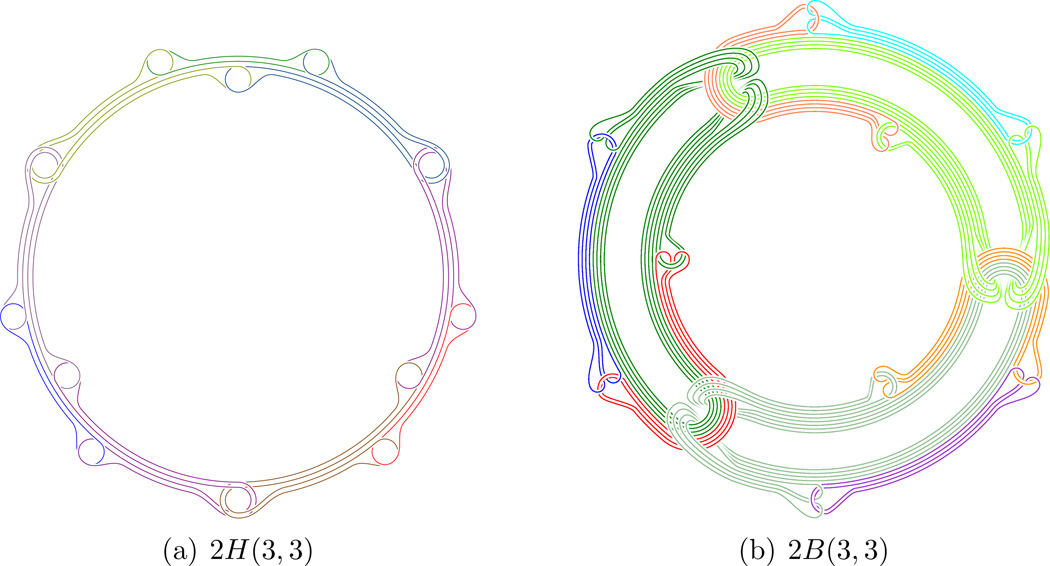
Leading to 2H(3, 3) and 2B(3, 3):

New links are then formed of these loops (knots) or rings using the same deformation principle. We will call these second order links based on ℒ₁ and denote them by

$${ℒ}_1\int {ℒ}_2.$$

Links are formed from the given family ℒ₁. Of course we could have chosen one family or alphabet of links at each level, but it is notationally simpler if we keep them all in one family.

Next we apply the same procedure to the family of links ℒ₁ ∫ ℒ₂, for short ℒ₂, but the notation indicate the dependence on ℒ₁, form chains, loops (knots) and new links. We denote the new family coming from the constructions

$${ℒ}_1\int {ℒ}_2\int {ℒ}_3.$$

This process is then iterated to form

$${ℒ}_1\int {ℒ}_2\int \cdots \int {ℒ}_n,$$

abbreviated ℒ_n when no confusion may arise.

Definition 5.1. An n-th order link is an element of some family ℒ_n.

Clearly our previous examples of n-rings and nB-rings are n-th order links. The following definition makes a distinction between them.

Definition 5.2. The elements of a family of n-th order links

$${ℒ}_1\int {ℒ}_2\int \cdots \int {ℒ}_n$$

are called (n, i)B links, if: removing an ℒ_i link from an ℒ_n link gives just a collection of unlinked ℒ_i links.

Clearly nB-rings as we have defined them would be (n, n − 1)B links, but n-rings would not be. Rings (closed loops) in ℝ³ will be 1-links.

Let us conclude with some examples. If ℒ₁ = {unknotted rings} then

$$\begin{array}{c}\text{ring of rings}=2-\text{ring}\in {ℒ}_1\int {ℒ}_2,\\ B-\text{rings}\in {ℒ}_1\int {ℒ}_2\end{array}$$

and

$$\begin{array}{c}\hfill 2B-\text{rings}\in {ℒ}_1\int {ℒ}_2\int {ℒ}_3,\\ \hfill \text{ring of}B-\text{rings}\in {ℒ}_1\int {ℒ}_2\int {ℒ}_3,\\ \hfill B-\text{rings of}2-\text{rings}\in {ℒ}_1\int {ℒ}_2\int {ℒ}_3.\end{array}$$

If ℒ₁ = {unknotted rings, B-rings}, then 2B-rings ∈ ℒ₁ ∫ ℒ₂.

The following notation will be useful later on.

Let ℒ₁ = {unknotted rings} and let

$${ℒ}_1^H(n_1)=\{\text{Hopf}-\text{rings of length}{n}_1\},$$

we call these type 1H(n₁) links. Then ${ℒ}_1^H\int {ℒ}_2^H(n_1,n_2)$ will represent Hopf-rings of Hopf-rings, we call these type 2H(n₁, n₂) links and we proceed to form kH(n₁, …, n_k) links.

Similarly let

$${ℒ}_1^B(n_1)=\{\text{Brunnian rings of length}{n}_1\},$$

we call these type 1B(n₁) links. Then ${ℒ}_1^B\int {ℒ}_2^B(n_1,n_2)$ will represent Brunnian rings of length n₂ of Brunnian rings of length n₁, we call these type 2B(n₁, n₂) links and we proceed to form kB(n₁, …, n_k) links.

For illustrations of all these types of links as for example 2H(3, 3, 3) and 2B(3, 3, 3), see [3].

Finally, there is an enormous variety of possibilities of forming new higher order links using the linking and bending (folding) principle that we have introduced. Our main purpose has just been to introduce and illustrate the general principle, and illustrate a few cases.

For example, the bending procedure in Figure 6 may be iterated one more time (or several), then forming new types of chains and rings for further iteration, see [3] for more details.

Figure 6.

6. Chemical synthesis and assembly

As pointed out in the introduction various types of non-trivial knots (trefoil) and links (Borromean rings) have been synthesized by chemical techniques, see [3, 11, 14, 15], but surprisingly enough not Brunnian links of length 3 or more, and Hopf-links of order 1 as well. These ought to be considered first. Then the natural question following our introduction to higher order (or hyperstructured) links, is if it is possible to synthesize these as well.

Which higher order links would be reachable?

Natural candidates would be kB(n₁, n₂, …, n_k)-rings and kB(n₁, n₂, …, n_k)-rings for k ≤ 3 and n_i ≤ 3. We think that it is useful and important to introduce and present the general construction of higher order links even if one must stick to the lower levels with respect to synthesis at the beginning.

Will this be possible by existing techniques or their extensions? Or may entirely new techniques be required?

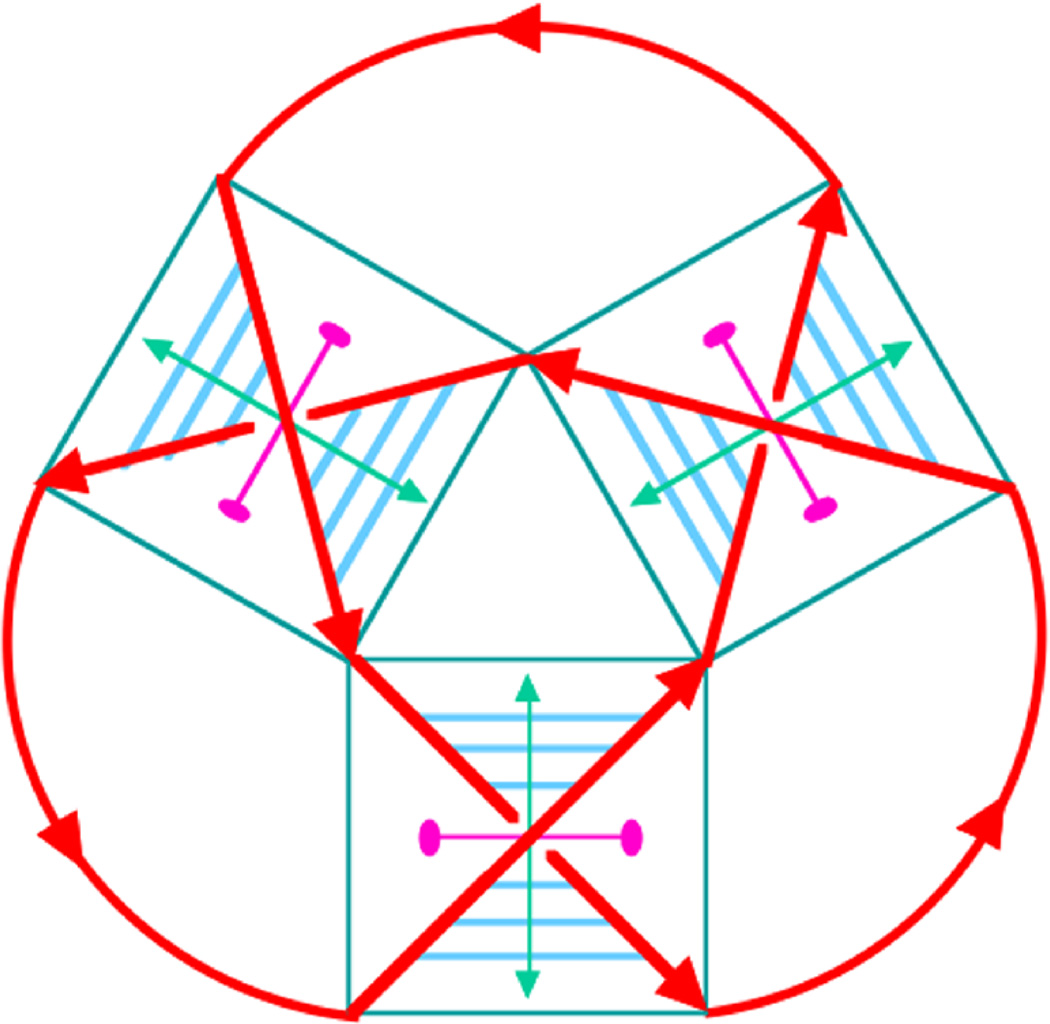
The most convenient system with which to approach these targets is likely to be double helical nucleic acids, particularly DNA. It has been shown [13] that a half-turn of DNA (about 6 base pairs of classical B-DNA) is equivalent to a crossing in a knot or a link. This notion is illustrated in Figure 8, for a trefoil knot with negative nodes.

Figure 8.

The backbone is shown as a red curve with polarity, reflecting the polarity of the DNA backbone. Boxes have been drawn around each of the nodes. The parts of the backbone inside the boxes become the diagonals, dividing the boxes into four quadrants, two between parallel diagonals and two between antiparallel diagonals. The backbones in the DNA double helix are antiparallel, so base pairs (shown as six blue lines connecting diagonals) are drawn between them. The double helix axis is drawn as a double-headed arrow in green, and a dyad axis relating the two segments of the backbone is drawn as a magenta line perpendicular to the helix axis terminating in ellipses. A trefoil knot has been constructed using this approach [6].

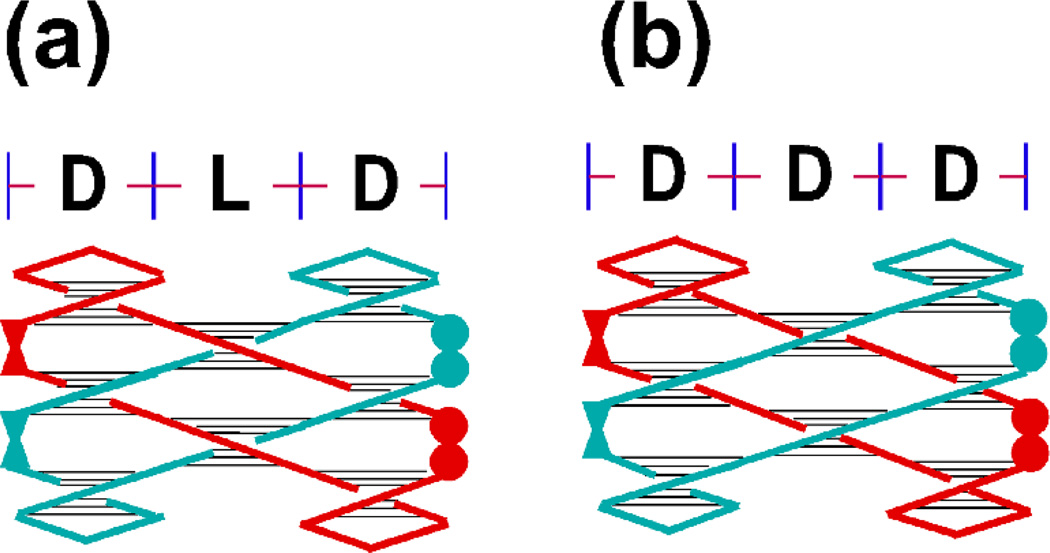
Regular B-DNA is a ’right-handed’ structure, meaning that these nodes would all have the sign −1. This is a consequence, among other things, of the fact that its backbone contains D-sugar groups. In the past, the way that nodes with a +1 sign were constructed was to use a left-handed conformation of DNA, called Z-DNA [12]. This approach has worked in simple cases [5, 7, 11], but is not entirely satisfactory, because Z-DNA has somewhat different geometrical features from B-DNA, is not exactly the mirror image of DNA, and is reliably made only from a somewhat limited set of sequences. Very recently, the synthetic building blocks for L-sugar groups (the mirror image of D-sugar groups) have become conveniently available. Consequently, it is as easy (if not as inexpensive) to make positive nodes today as it is to make negative nodes. Recently, this method has been used to build a small woven structure that is shown in Figure 9.

Figure 9.

Panel (a) shows the woven structure and panel (b) illustrates a control structure made exclusively from nucleotides containing D-sugars. Each structure in (a) and (b) contains 3 domains, and types of sugars in the domains are indicated at the top. To demonstrate that the structures have been made, it is necessary to turn each strand into a cycle. In addition, to make sure that the strands are antiparallel, each strand needs to contain a 5’, 5’ linkage (shown by the fused filled circles on the right of each image) and a 3’, 3’ linkage (shown by the bowtie-like structures on the left), rather than the conventional 5’, 3’ linkages.

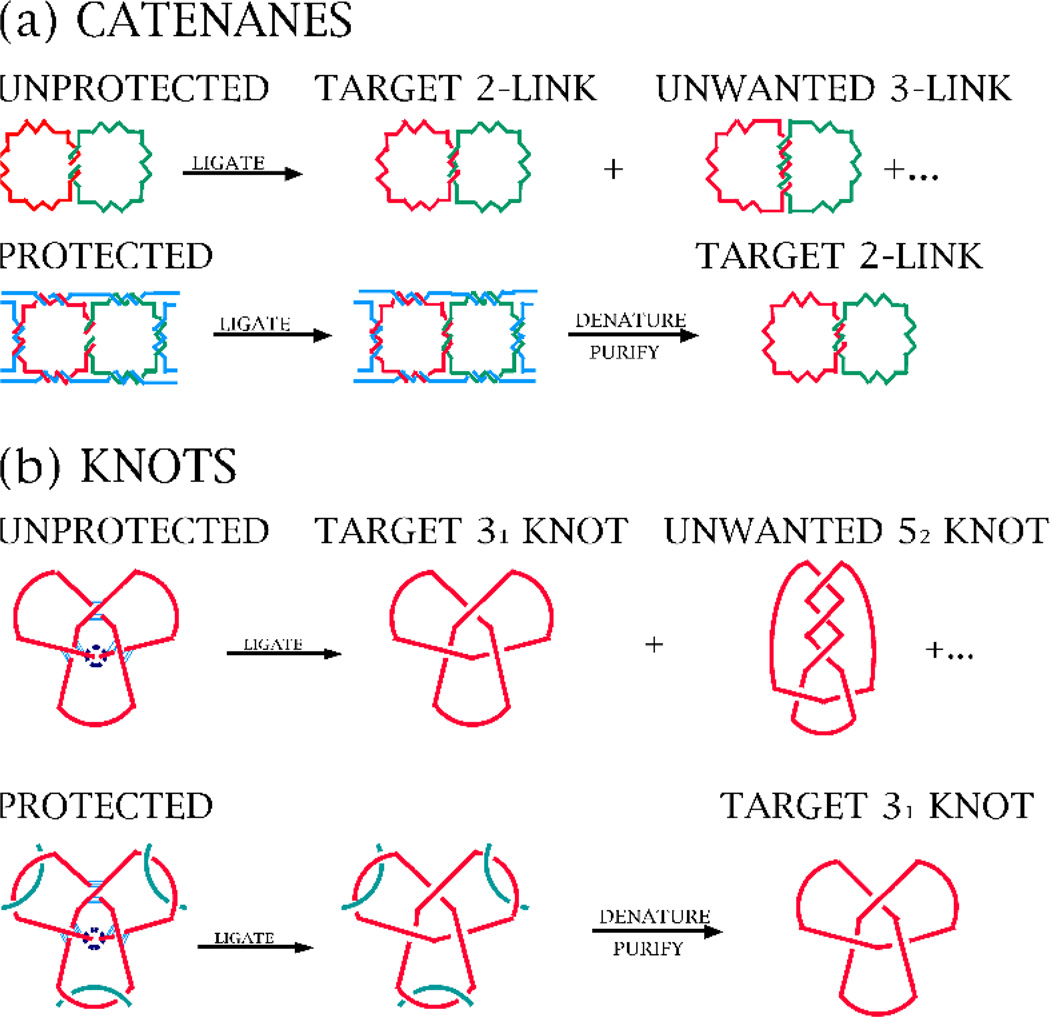
The third aspect of chemical synthesis of DNA molecules with complex topology is topological protection. The key issue here is that unwanted crossings can occur in a single-stranded DNA molecule just sitting in a vessel waiting to be ligated into a closed cyclic molecule. This concept is shown in Figure 10.

Figure 10.

Panel (a) shows that the wrong catenane can result if strands targeted to unpaired strands in the product are left unpaired when ligation is performed, but that the target product can be obtained those strands that are transiently put into a double stranded state. The bottom panel shows the same notion for knots. In the past, topological protection has been used successfully to build a series of differently-linked catenanes from the same strands [9]. It has been less successful in protecting knots from forming undesired crossings, possibly because knots have usually had oligo-dT units as their linkers. The protecting group would be an oligo-dA unit, leading two oligo-dT segments to wind around each other to form a triple helix. The topological protecting group is readily removed by either denaturation or, possibly by Yurke et al. [16] methods of strand removal.

It seems like 2H- and 2B-rings may be an interesting and natural structures to start with, and that the second author’s DNA techniques may be suitable for this. The illustrations in this paper are based on algorithms putting local pieces together like local motifs in chemistry. This may be useful in the process of synthesizing them.

7. Conclusion

We have introduced some new topological structures coming from [2] — higher order links — and we raise the question of how they possibly may be synthesized. In general this is a daunting task, but some low order links seem possible to start with.

If successful it is a very interesting question (as pointed out in [2]) what kind of new properties (electrical, optical, mechanical) these new molecules and materials may have. In [3] the first author discussed how the new higher order links suggest new states of matter in cold gas, nuclei, etc.

The fact that these higher order topological links have a highly non-trivial topological structure with increasing complexity for each level may indicate new emergent properties.

Figure 4.

Figure 5.

Figure 7.