Adaptation at the output of the chemotaxis signalling pathway

Abstract

In the bacterial chemotaxis network, receptor clusters process input^1–3, and flagellar motors generate output⁴. Receptor and motor complexes are coupled by the diffusible protein CheY-P. Receptor output (the steady-state concentration of CheY-P) varies from cell to cell⁵. However, the motor is ultrasensitive, with a narrow [CheY-P] operating range⁶. How might the match between receptor output and motor input be optimized? Here we show that the motor can shift its operating range by changing its composition. The number of FliM subunits in the C-ring increases in response to a decrement in the concentration of CheY-P, increasing motor sensitivity. This shift in sensitivity explains the slow partial adaptation observed in mutants that lack the receptor methyltransferase and methylesterase^7–8 and why motors exhibit signal-dependent FliM turnover⁹. Adaptive remodelling is likely to be a common feature in the operation of many molecular machines.

The chemotaxis signalling pathway allows bacterial cells to sense and respond to changes in concentrations of chemical attractants or repellents^1–2. Binding of chemicals by receptors modulates the activity of an associated histidine kinase, CheA, thereby changing the level of phosphorylation of the response regulator, CheY. CheY-P binds to FliM, a component of the switch complex at the base of the flagellar motor and modulates the direction of motor rotation. A phosphatase, CheZ, dephosphorylates CheY-P. The chemotaxis pathway is well known for its high gain^8,10–11, wide dynamic range^11–12, and robust adaptation^5,13, mediated by receptor methylation and demethylation (by CheR and CheB).

The output of the chemotaxis pathway, the flagellar motor, is ultrasensitive to the intracellular concentration of CheY-P, with a Hill coefficient of about 10, imposing a narrow operational range for [CheY-P]⁶. While precise adaptation is a robust property of the chemotaxis pathway for certain attractants, e.g., aspartate, the steady-state concentration of CheY-P is not⁵. Given cell-to-cell variations in the concentration of CheY-P and the fact that different cells can maintain their chemotactic sensitivity¹⁴, it has been suggested that cells might have additional molecular mechanisms to adjust the CheY-P concentration around the operational value of ~3 μM⁶. One possibility is a feedback mechanism that allows a cell to adjust its kinase activity in response to motor output. This mechanism would increase the kinase activity if cells only ran, and would decrease the kinase activity if cells only tumbled. In earlier work, we looked for such a mechanism by monitoring the kinase activity with a FRET technique¹⁵ while jamming flagellar bundles with an anti-filament antibody. Stopping motors had no effect on kinase activity¹⁶.

Here, we report that the motor itself adapts, shifting its response function according to the steady-state concentration of CheY-P. It does this by increasing the complement of FliM when the concentration of CheY-P is low. Motor remodeling is well known for the stator elements MotA and MotB, which if defective, can be replaced by wild-type protein, as evidenced by stepwise increments in motor torque^17–18. Such exchange also has been visualized by TIRF microscopy of GFP-labeled protein¹⁹, and a similar technique has been used to demonstrate FliM⁹ and FliN²⁰ exchange in cells containing CheY-P. The present work addresses the functional consequences of FliM exchange. We studied cheR cheB cells, which are defective in methylation and demethylation, and monitored motor and kinase responses to step-addition of the non-metabolisable attractant α-methylaspartate (MeAsp), using bead²¹ and FRET¹⁵ assays. One cannot do these experiments with wild-type cells, because their adaptation to aspartate is robust, so that the steady-state concentration of CheY-P does not change. Motor adaptation occurs on a minute rather than on a second timescale and does not play a direct role in sensing temporal gradients. Instead, it helps to match the operating point of the motor to the output of the chemotaxis receptor complex, obviating the requirement for fine tuning of that output.

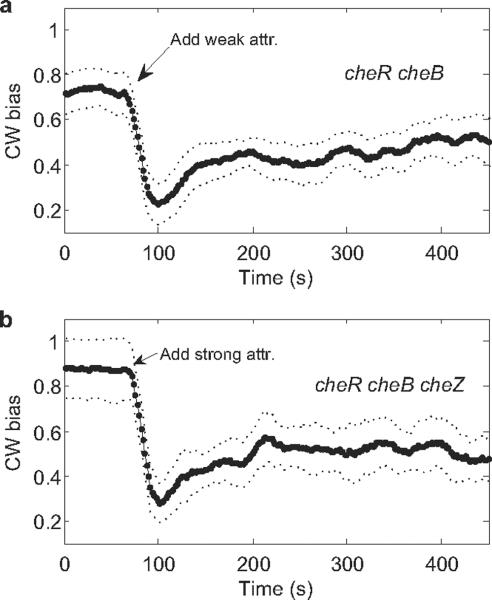
Using a bead assay, we found partial adaptation in cheR cheB cells within 1 min following the initial response, Fig. 1 a, which shows the averaged responses of 7 motors on different cells to stepwise addition of 1 mM MeAsp. These results are similar to those obtained previously with tethered cells^7–8. A recent model suggests that partial adaptation might be due to dynamic localization of CheZ²². To test this hypothesis, we repeated the bead experiments using cheR cheB cheZ cells. The results were essentially the same, Fig. 1b, which shows the averaged responses of 4 motors on different cells of a cheR cheB cheZ strain to stepwise addition of 2 mM MeAsp + 0.5 mM L-serine (a stronger stimulus needed because of the lower sensitivity of cheZ strains). So CheZ is not required for this partial adaptation.

Fig. 1.

Motor responses to stepwise addition of chemical attractants monitored by the bead assay. The attractants were applied at the times indicated by the arrows. Error bounds for standard errors of the mean are shown as dotted lines. (a) Averaged responses of 7 cheR cheB cells (JY35 carrying pKAF131) to 1 mM MeAsp (weak attractant). (b) Averaged responses of 4 cheR cheB cheZ cells (JY32 carrying pVS7 and pKAF131) to 2 mM MeAsp + 0.5 mM L-serine (strong attractant).

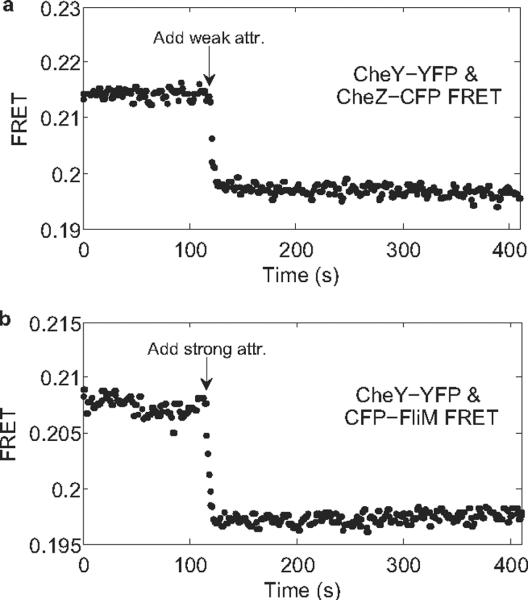
CheY-P concentrations were monitored by measuring FRET between CheZ-CFP and CheY-YFP. We measured responses in cheR cheB cells to stepwise addition of 1mM MeAsp, Fig. 2a. The response shown in Fig. 2a is similar to that obtained previously¹¹. No adaptation is apparent. To rule out possible complications due to CheZ oligomerization²³, we also measured CFP-FliM/CheY-YFP FRET²⁴ in cheR cheB cells following stepwise addition of 2 mM MeAsp + 0.5 mM L-serine (a stronger stimulus needed because of the lower sensitivity of CFP-FliM/CheY-YFP FRET), as shown in Fig. 2b. No adaptation is apparent in either panel of Fig. 2, so the partial adaptation shown in Fig. 1 does not occur upstream of CheY-P. It must occur at the level of the flagellar motor.

Fig. 2.

FRET responses (Y/C ratio) of cheR cheB cells to stepwise addition of chemical attractants. The attractants were added at the times indicated by the arrows. (a) CheY-YFP/CheZ-CFP FRET responses to 1 mM MeAsp (weak attractant). (b) CheY-YFP/CFP-FliM FRET responses to 2 mM MeAsp + 0.5 mM L-serine (strong attractant).

Clockwise (CW) biases of motors were measured before addition of attractant, immediately after addition of attractant, and after time was allowed for partial adaptation. We focused on motors with pre-stimulus CW biases around 0.8 (ranging from 0.70 to 0.95). Due to cell-to-cell variation, the lowest biases following stimulation ranged from 0 to 0.75. The concentration of CheY-P in a given cell was estimated from its CW bias at the time of the lowest bias, using the response curve measured previously by Cluzel et al.⁶, shown by the red line in Fig. 3 (Hill coefficient N_H=10.3, CheY-P dissociation constant K=3.1 μM). Then the CW bias found after that cell had adapted was plotted as a function of this concentration, as shown by the blue data points in Fig. 3. The measurements were carried out for 49 motors on different cheR cheB cells with stepwise addition of 0.5 or 1 mM MeAsp. Following adaptation, the relationship between the CW bias and the concentration of CheY-P shifted to lower concentrations of CheY-P, increasing motor sensitivity to CheY-P.

Fig. 3.

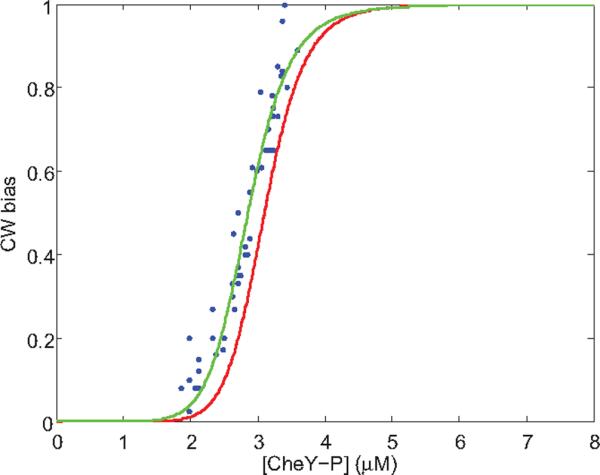
CW bias as a function of CheY-P concentration. The red curve is for pre-stimulus wild-type motors, as measured by Cluzel et al.⁶ and fit with an MWC model with 34 FliM units²⁶. The blue dots are data for motors that have partially adapted to stepwise addition of attractant, with a two-parameter fit to the MWC model with N_av = 36 FliM units shown by the green curve; see text.

How the motor accomplishes this shift is intriguing. We sought to explain the shift in the motor response curve by using an MWC type model^25–26, which has been used previously to explain the motor switching kinetics²⁶. In this model, the C-ring is considered to be an allosteric switch, stochastically switching between two conformational states, CCW and CW, with N independent binding sites for CheY-P, corresponding to N units of FliM in the C-ring. The CW state has a higher affinity to CheY-P than the CCW state. The CW bias of the motor is given by: B_CW=(1+[CheY-P]/K)^N/((1+[CheY-P]/K)^N+L(1+[CheY-P]/(KC))^N), where L is the ratio of the probability that the motor is in the CCW state to the probability that it is in the CW state in the absence of CheY-P, K is the CheY-P dissociation constant for the CW state, and C is the ratio of dissociation constants for the CCW and CW states, respectively²⁶. With reasonable values for the parameters, e.g., N=34, L=10⁷, and K=3.1 μM^6,27, the model can be fit to the ultrasensitivity data of Cluzel et al. with a best-fit value of C of 4.1, as shown by the red curve in Fig. 3. With these values for the parameters L, K, and C, and assuming that the number of FliM units N varies with [CheY-P], we can fit the data measured for the adapted motor using the MWC model with N = N_av + α([CheY-P] − 2.7), where N is written as a Taylor expansion about the average value of [CheY-P], 2.7 μM. We obtain a two-parameter fit with N_av = 36 and α = −1.2 μM⁻¹, shown by the green curve in Fig. 3. The average value of N has increased from 34 to 36. Sensitivity of an MWC complex is known to increase with N for fixed values of L, K, and C²⁸. Equivalently, the motor bias versus [CheY-P] curve shifts to smaller [CheY-P] with larger N as shown in Fig. 3. Intuitively, the fact that increasing the number of FliM units causes an increase in CW bias can be understood by considering the energetics of the switch. Each CheY-P binding decreases the energy level of CW state by a specific amount. With the values for parameters L, K and C fixed, increasing the number of FliM, i.e. CheY-P binding sites, increases the number of CheY-P bound to the motor. This decreases the energy level of the CW state, thereby increasing the CW bias.

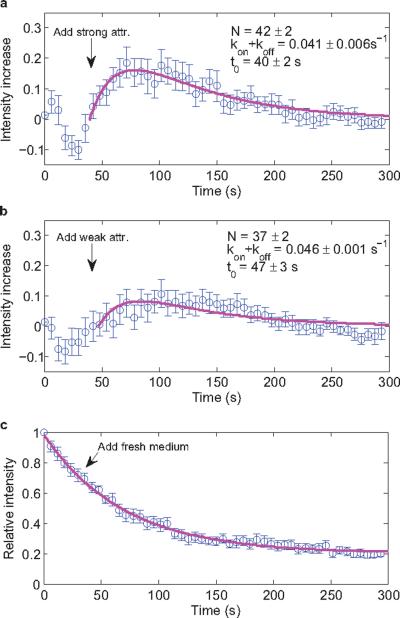
To directly test for this increase of the number of FliM units, we fused YFP to the C-terminus of FliM and monitored the fluorescence intensity of single motors using total internal reflection fluorescence (TIRF) microscopy. To minimize shifts in motor position, we tethered a cheR cheB strain that lacks the flagellar filament to glass via single hooks with anti-hook antibody. Changes in fluorescence were measured upon addition of 2 mM MeAsp + 0.5 mM L-serine, which should saturate the chemoreceptors and eliminate CheY-P, or of 1 mM MeAsp, which should simply reduce the concentration of CheY-P. The results are shown in Fig. 4. Fig. 4a is the averaged response of 20 motors to the strong attractant, and Fig. 4b is the averaged response of 22 motors to the weak attractant. In either case, the fluorescence intensity increased following the addition of attractant on a time scale consistent with partial adaptation, by a larger amount for the stronger attractant. We compensated for fluorescence bleaching by subtracting a control curve (Fig. 4c) and fitting the results to a model in which the FliM off rate decreases when the CheY-P concentration decreases; see Methods. Steady state is reached when Nk_off =(M− N)k_on, where N is the number of FliM molecules in the motor, and M is the maximum number of FliM binding sites in the motor. The fits are shown in magenta and the final values for N are given in each panel (assuming an initial value of 34). These values agree with those presented in Fig. 3. So the motor increases the number of FliM units as it partially adapts to a decrement in the concentration of CheY-P. By doing so, it increases its dynamic range.

Fig. 4.

Changes in single-motor FliM-YFP fluorescence intensities in cheR cheB cells tethered by hooks and stimulated by addition of attractant (at time t₀, arrow). The intensity for a given motor was normalized by its intensity at time 0, intensities for different motors were averaged, and the fit to the control of panel c was subtracted. Fits with the model are shown in magenta and the parameters for these fits are given. Error bars are standard errors of the mean. (a) Responses of 20 motors to addition of 2 mM MeAsp + 0.5 mM L-serine. (b) Responses of 22 motors to addition of 1 mM MeAsp. (c) Responses of 15 motors without addition of attractant, fit with an exponential decay function plus a constant.

We eliminated the concern that binding of CheY-P to FliM-YFP might be different than binding to wild-type FliM by using the bead assay to compare the biases, switching rates, and speeds for motors of cheR cheB cells expressing FliM-YFP or wild-type FliM: the biases were 61±16% or 58±19%, the switching rates were 3.8±1.2 or 3.4±1.0 s⁻¹, and the speeds were 50.4±8.4 or 51.5±8.2 Hz, respectively.

The motor adaptation mechanism observed here is related to the turnover of motor C-ring components discovered recently ^9,20, where exchange of FliM was found to be signal dependent and exhibited a similar timescale ⁹. The detailed mechanism should involve changes in FliM on/off rates dependent upon either CheY-P binding or rates of motor switching. As noted earlier, the timescale for motor adaptation (1 min) is much slower than that for receptor methylation/demethylation (1 s), which enables cells to make rapid temporal comparisons; thus, motor adaptation does not play a critical role in that aspect. Instead, it helps match the operating point of the motor to the output of the chemotaxis receptor complex.

Methods summary

All strains used in this study were derivatives of E. coli K12 strain RP437. Cells were grown at 33 °C in 10 ml T-broth supplemented with the appropriate antibiotics and inducers to an OD₆₀₀ of 0.45 to 0.50. Cells were collected by centrifugation (10 min at 1300 × g), washed twice in 10 ml of motility medium (10 mM potassium phosphate/0.1 mM EDTA/1 μM methionine/10 mM lactic acid, pH 7.0), and resuspended in 10 ml of this medium. They were used immediately for experiments or stored at 4 °C for up to 2 h. All experiments were carried out with a custom-made flow chamber at room temperature.

For the bead assay, cells were sheared to truncate flagella, and 1.0-μm-diameter polystyrene latex beads were attached to the filament stubs. Rotation of the bead was monitored with a laser dark-field setup described previously ²⁹. Rotational velocity as a function of time was determined for each motor and smoothed with a 25-point running average. CW bias was calculated over a 20-s interval every 2 s, leading to a plot of CW bias versus time.

FRET measurements of bacterial populations were carried out as described previously ³⁰.

For TIRF measurements, cells were tethered to the bottom window of the flow chamber by single hooks using anti-FlgE antibody, following a protocol adapted from Yuan & Berg ²¹. The fluorescence intensity of the motors was monitored with a TIRF microscope (Nikon Eclipse Ti-U), and images were recorded with a back-illuminated, cooled (−55 °C), electron-multiplying CCD camera (DV887ECS-BV, Andor Technology). Image analysis of the motor spots was carried out using a Gaussian mask method described previously ¹⁹.

Methods

Strains and plasmids

All strains used in this study are derivatives of E. coli K12 strain RP437 ³¹: JY32 [cheR cheB cheY cheZ fliC], JY35 [cheR cheB fliC], RP2893 [Δ2206(tap-cheZ)] ¹¹, JY37 [cheR cheB cheY fliM], and JY40 [cheR cheB fliM fliC]. The fliM-eyfp^A206K fusion with a 3× glycine linker was cloned into pTrc99A ³² under an IPTG-inducible promoter, yielding pRWB7. pDFB72 carrying wild-type fliM on pTrc99A was a gift from David Blair. pVS7 carrying wild-type cheY on a pBAD18-Kan ³³ vector was a gift from Victor Sourjik. pVS18 carrying cheY-eyfp on pTrc99A, pVS31 carrying ecfp-fliM on pBAD33 ³³, and pVS54 carrying cheZ-ecfp on pBAD33, were described previously ^11,24. pKAF131 carrying the sticky fliC allele under control of the native fliC promoter, was described previously ³⁴. For studies of cheR cheB cells with the bead assay, JY35 carrying pKAF131 was used. For studies of cheR cheB cheZ cells with the bead assay, JY32 carrying pVS7 and pKAF131 was used. For CheZ-CFP/CheY-YFP FRET studies of cheR cheB cells, RP2893 carrying pVS18 and pVS54 was used. For CFP-FliM/CheY-YFP FRET studies of cheR cheB cells, JY37 carrying pVS18 and pVS31 was used. For the TIRF studies of single motors, JY40 carrying pRWB7 was used. For comparison of motors with wild-type FliM and FliM-YFP, JY40 carrying pDFB72 and pKAF131, and JY40 carrying pRWB7 and pKAF131 were used. Cells were grown at 33 °C in 10 ml T-broth (1% tryptone and 0.5% NaCl) supplemented with the appropriate antibiotics (Amp: 100 μg/ml, Kan: 50 μg/ml, Cam: 34 μg /ml) and inducers (0.005% arabinose for the bead assay, 0.01% arabinose and 50 μM IPTG for the FRET studies, 100 μM IPTG for the TIRF studies) to an OD₆₀₀ of 0.45 to 0.50. Cells were collected by centrifugation (10 min at 1300 × g), washed twice in 10 ml of motility medium (10 mM potassium phosphate/0.1 mM EDTA/1 μM methionine/10 mM lactic acid, pH 7.0), and resuspended in 10 ml of this medium. They were used immediately for experiments or stored at 4 °C for up to 2 h.

The bead assay and data analysis

Cells were sheared to truncate flagella by passing 1 ml of the washed-cell suspension 50 times between two syringes equipped with 23-gauge needles and connected by a 7-cm length of polyethylene tubing (0.58 mm i.d., catalog no. 427411; Becton Dickinson, Waltham, MA). The sheared cell suspension was centrifuged and resuspended in 0.5 ml of motility medium. 50 μl of this suspension was placed on a glass coverslip coated with poly-L-lysine (0.01%, catalog no. P4707; Sigma, St. Louis, MO) and allowed to stand for 2 min, then 5 μl of 1.0-μm-diameter polystyrene latex beads (2.69%, catalog no. 07310; Polysciences, Warrington, PA) was added, mixed by gentle pipetting, and allowed to stand for 2 min. The coverslip was installed as the top window of a flow chamber ³⁵ and rinsed with motility medium. The chamber was kept under a constant flow of buffer (400 μl/min) by a syringe pump (Harvard Apparatus, Holliston, MA). Rotation of the bead was monitored with a laser dark-field setup described previously ³⁶. Outputs from the photomultiplier tubes were DC-coupled to an 8-pole low-pass Bessel filter (3384, Krohn-Hite) with a cutoff frequency of 200 Hz and sampled at 500 Hz using LabView. For each experiment, the rotation of the bead was monitored for 70 s, then the medium was switched to attractants, and the rotation was monitored further for about 400 s.

Rotational velocity as a function of time was determined for each motor as described previously ³⁶ and smoothed with a 25-point running average. CW bias was calculated over a 20-s interval every 2 s, leading to a plot of CW bias versus time.

FRET measurements

FRET measurements of bacterial populations were carried out as described previously ^15,30, except that the epifluorescent illumination was provided by a LED white light source (MCWHL2-C3, Thorlabs) through an excitation bandpass filter (FF01-438/24–25, Semrock). For each experiment, 4 ml of the washed-cell suspension was centrifuged and resuspended in 55 μl of motility medium, which was placed on a glass coverslip coated with poly-L-lysine (0.1% , catalog no. P8920, Sigma) and allowed to stand for 5 min. The coverslip was installed as the top window of a flow chamber ³⁵ and rinsed with motility medium. The chamber was kept under a constant flow of buffer (500 μl/min). Epifluorescent emission was split into donor (cyan, C) and acceptor (yellow, Y) channels and collected by photon-counting photomultipliers (H7421-40, Hamamatsu). Signal intensities of these two channels were recorded by a computer running LabView, and the ratio between them (R=Y/C) provided an indicator of FRET activity. The FRET traces were smoothed with a median filter of rank 3.

TIRF measurements, data analysis, and fits to the model

Cells were tethered to glass by hooks using anti-FlgE antibody, following a protocol adapted from Yuan & Berg ²¹: 350 μl of the washed-cell suspension was centrifuged and resuspended in 100 μl of motility medium; 10 μl of anti-FlgE antibody (0.1 mg/ml) was added, and the mixture was incubated at 23 °C for 25 min. The antibody-treated cells were washed twice with 350 μl of motility medium and gently resuspended in 55 μl of motility medium. This cell suspension was placed on the bottom coverslip of a flow chamber (which was washed earlier with ethanol and dH₂O and air-dried for 2 h) and allowed to stand for 15 min. The top coverslip of the flow chamber was then installed and rinsed with motility medium. The chamber was kept under a constant flow of buffer (100 μl/min). For each experiment, the flow was switched to attractants at 1 min before the start. It took about 1 min and 30 s for the attractant to reach the flow chamber and about 30 s to replace the medium, so effectively the medium reached the cells at between 30 s to 60 s after the start of each experiment. Only stably rotating and switching motors were monitored. The motors observed usually started with high CW bias; upon addition of strong attractant, they changed to exclusively CCW and remained 100% CCW throughout the observation time; upon addition of weak attractant, their CW bias reduced and later partially recovered; upon addition of motility medium, their CW bias did not change. The fluorescent intensity of the motors was monitored with a TIRF microscope (Nikon Eclipse Ti-U), and images were recorded at 65 nm/pixel with a back-illuminated, cooled (−55 °C), electron-multiplying CCD camera (DV887ECS-BV, Andor Technology). The camera was controlled by Andor Solis software running on a desktop computer. Image acquisition was under Andor Solis `kinetic' mode, with 200 ms exposures every 6 s for 50 exposures for each motor. The laser illumination was blocked in between exposures.

Images of the motor spots showed radially symmetric and approximately Gaussian intensity profiles. The width of these spots was about 5 pixels (325 nm). The fluorescent intensity centroid for each motor was calculated using a Gaussian mask method described previously^19,37. Specifically, an initial estimate was made based on the peak pixel intensity, a 9×9 pixel region of interest (ROI) was defined centring on the initial motor centroid, and the motor centroid was calculated as follows: Firstly, a circular motor mask of diameter 300 nm was applied to the ROI centring on the current motor centroid. Secondly, pixel intensities within the motor mask were multiplied by a radially symmetric 2-dimensional Gaussian mask of fixed half-width 170 nm, and a revised estimate for the motor centroid was calculated using a weighted average. Lastly, the previous two steps were iterated either 150 times or until the motor mask began clipping the side of the ROI. We also calculated the motor centroid with a 2-dimensional Gaussian fitting, and both methods yielded comparable results. After the centroid was calculated, the background intensity was defined as the mean pixel intensity within the ROI but external to the final motor mask, and the motor intensity was calculated as the sum of all pixel intensities within the motor mask after subtraction of the background intensity from each pixel value.

The model assumes that CheY-P binding destabilizes FliM, so that when [CheY-P] suddenly decreases due to addition of attractant, k_off (the off rate of each FliM unit) decreases, while k_on remains the same. When the number of FliM units (N) in the C-ring reaches a new steady state, Nk_off=(M−N)k_on, where M is the maximum number of FliM binding sites in a motor. The pre-stimulus N is assumed to be 34. During the response to the attractant step, the increment of N satisfies dn=((M−(n+34))k_on−(n+34)k_off)dt, while the increment of the normalized motor intensity satisfies df=dn/a−λfdt, where a is the normalization factor that converts the number of FliM units to fluorescence intensity, and λ is the fluorescence bleaching rate obtained by fitting the control curve (Fig. 4c). Solving these two differential equations with the initial conditions: n(0)=0, f(0)=0 leads to:

$$\begin{array}{c}\hfill f=\frac{(k_{\mathit{on}}M-34(k_{\mathit{on}}+k_{\mathit{off}}))}{a(k_{\mathit{on}}+k_{\mathit{off}}-\lambda )}(e^{-\lambda t}-e^{-(k_{\mathit{on}}+k_{\mathit{off}})t})\hfill \\ \hfill =\frac{(N-34)(k_{\mathit{on}}+k_{\mathit{off}})}{a(K_{\mathit{on}}+k_{\mathit{off}}-\lambda )}(e^{-\lambda t}-e^{-(k_{\mathit{on}}+k_{\mathit{off}})t})\hfill \end{array}$$

If the time of arrival of the attractant at the cell is t₀ instead of 0, change t in the above equations to t−t₀.