Clinical application of pharmacokinetic analysis as a biomarker of solitary pulmonary nodules: Dynamic contrast enhanced MR imaging

Abstract

The purpose of this study is to evaluate perfusion indices and pharmacokinetic parameters in solitary pulmonary nodules (SPNs). Thirty patients of 34 enrolled with SPNs (15–30 mm) were evaluated in this study. T1 and T2-weighted structural images and 2D turbo FLASH perfusion images were acquired with shallow free breathing. B-spline non-rigid image registration and optimization by χ² test against pharmacokinetic model curve were performed on dynamic contrast enhanced (DCE) MRI. This allowed pixel-by-pixel calculation of k_ep, the rate constant for tracer transport to and from plasma and the extravascular extracellular space (EES). Mean transit time (MTT), time-to-peak (TTP), initial slope (IS), and maximum enhancement (E_max) were calculated from time-intensity curves fitted to a gamma variate function. After blinded data analysis, correlation with tissue histology from surgical resection or biopsy samples was performed. Histologic evaluation revealed 25 malignant and 5 benign SPNs. All benign SPNs had k_ep <1.0 min⁻¹. Nineteen of 25 (76%) malignant SPNs showed k_ep > 1.0 min⁻¹. Sensitivity to diagnose malignant SPNs at a cutoff of k_ep = 1.0 min⁻¹ was 76%, specificity was 100%, positive predictive value (PPV) was 100%, negative predictive value (NPV) was 45%, and accuracy was 80%. Of all indices studied, k_ep was the most significant in differentiating malignant from benign SPNs.

Introduction

Lung cancer is the most common cause of cancer death in both men (30%) and women (26%) in the United States and world [1–3]. Five-year survival rate of all patients with lung cancer ranges from 13% to 18% [2]; however, early detection and resection of Stage I tumors less than 30 mm in size result in 5-year survival rates as high as 70–75% [4–6]. The National Lung Screening Trial recently reported that low-dose helical CT screening for lung cancer could reduce cancer death by 20% among smokers compared with chest x-ray screening, pointing to the importance of early diagnosis in improving survival [7].

As utilization of CT for evaluation of lung abnormalities in general is becoming more common, in addition to CT screening for lung cancer [8, 9, 10], the number of small lung nodules detected on CT has noticeably increased. Once a nodule is found, it is necessary to be analyzed by both qualitative and quantitative methods. The current accepted approach for an incidentally found small lung nodule is CT follow-up at 3–6 months or 6–12 months, depending on the patient's risk level, to monitor growth of the nodules [11]. When the risk level is high, e.g. for nodules larger than 10 mm and of indeterminate morphology, or the nodule has grown on follow-up CT, it often requires an invasive surgical procedures such as CT-guided needle or core biopsy and video assisted thoracic surgery (VATS) to confirm diagnosis. Major complications after CT-guided biopsy are pneumothorax (8–46%) and hemorrhage (2–10%) [12, 13], and after VATS include pulmonary complication (10–14%), cardiac arrhythmia (14–17%), and hemorrhage (3–5%) [14], only to find most of the small nodules were benign [15, 16]. Therefore, it is important to investigate a non-surgical technique to diagnose these small nodules.

Dynamic contrast CT [17, 18], positron emission tomography (PET) [19, 20], and dynamic contrast enhanced (DCE) MRI [21, 22] are examples of non-surgical techniques to quantitatively evaluate a pulmonary nodule. While each technique gives a certain level of reliable results to diagnose a malignant solitary pulmonary nodule (SPN), DCE-MRI offers a radiation-free non-invasive option to patients. Recent advances in MRI technology have made lung imaging much more acceptable and desirable for detailed analysis [23, 24]. Several studies have been published on DCE-MRI in lung cancer discussing the diagnostic role of perfusion indices derived from the time-intensity curves (commonly using curve fitting to a gamma variate function) [25– 27]. More recently, attention has been given to the investigation of pharmacokinetic parameters [28], such as the trans-endothelial transfer constant (K^trans), the fractional volume vp in the plasma, and the fractional volume v_e in the extravascular extracellular space (EES). The characteristic rate of transfer of contrast tracer to and from plasma and the EES is given by k_ep, which is equal to the ratio K^trans / v_e; it is this parameter which is the focus of the current study, being dependent on both endothelial permeability and the EES volume fraction.

This study comprises two major points: The first is a new analysis of the Tofts model for tracer transport between plasma and the extravascular extracellular space (EEC). In particular, we focus on the interpretation of the model in terms of compartmental analysis, and pay particular attention to the role of characteristic transport times compared with hemodynamically determined characteristic times that influence the concentration profile delivered to the region of interest. We argue that, physiologically, the Tofts model is not a true two-compartment model; rather, it is a one compartment model with external source term. We further argue that, absent independent measurement of the EES volume fraction v_e, the tracer transport rate constant k_ep is the only quantitative measure that can be measured. Second, we discuss the clinical application of k_ep analysis as a biomarker in differential diagnosis in early stage lung cancer, and in particular, the extent to which it distinguishes between benign and malignant SPNs. We hypothesize that k_ep analysis is a simple estimator that distinguishes between malignant and benign histology, as it focuses specifically on the dynamics of contrast material transport into and out of the EES. It thus represents a feature that is specific to the tissue's permeability and volume fractionation. As a single parameter, its simplicity adds to the power of this approach as well. Importantly, we emphasize that compared with CT or nuclear medicine modalities, the absence of non-ionizing radiation in MRI based approaches is a clear clinical advantage in the ability to manage patients longitudinally in terms of tumor growth and individual response to therapy.

Materials and Methods

All data analyses were performed blindly without knowledge of the histology result. After all data analyses were done, correlation with tissue histology was performed.

Patients

Thirty-four patients (9 males, 25 females, 26–87 years old, average 65 years old) with an SPN from 15 to 30mm in size entered this study. The study was conducted under the guideline of the Institutional Review Board and written informed consent was obtained from all the participants. The initial diagnosis of an SPN was made by chest x-ray and CT. Four patients had a follow-up CT scan without resection or biopsy because they were considered clinically benign; they were excluded from the data analysis.

MRI protocol

All MRI studies were performed in a 3T-whole body magnet using a body array coil. All patients underwent T2-weighted axial half-Fourier acquisition single-shot turbo spin-echo (HASTE) imaging, pre and post contrast T1-weighed axial, sagittal, and coronal volumetric interpolated breath-hold examination (VIBE) imaging, and 2D turbo FLASH perfusion imaging with shallow free breathing. Figure 1 shows representative axial T2 and post contrast T1-weighted images. The MRI parameters were as follows: T2-weighted HASTE (TR/TE=1200/100 msec, FOV=400 mm, 320×320, 1 excitation, BW=780 kHz, FA=150, ETL=256, 5.5-mm slice thickness/1.6-mm inter slice gap, scan time=6 min); T1-weighted VIBE (TR/TE=3.4/1.3 msec, FOV=400 mm, 260×320, 1 excitation, BW=505 kHz, FA=10, 4-mm slice thickness/0-mm inter slice gap, scan time=1.7 min, pre and post Gd-DTPA 0.1 mmol/kg bolus injection); 2D turbo FLASH perfusion (TR/TE=500/1.6 msec, FOV=400 mm, 192×180, 1 excitation, BW=360kHz, FA=10, 5-mm slice thickness, oblique sagittal orientation, 124 frames, 2 sec/frame, scan time=4 min, Gd-DTPA iv. 0.1 mmol/kg).

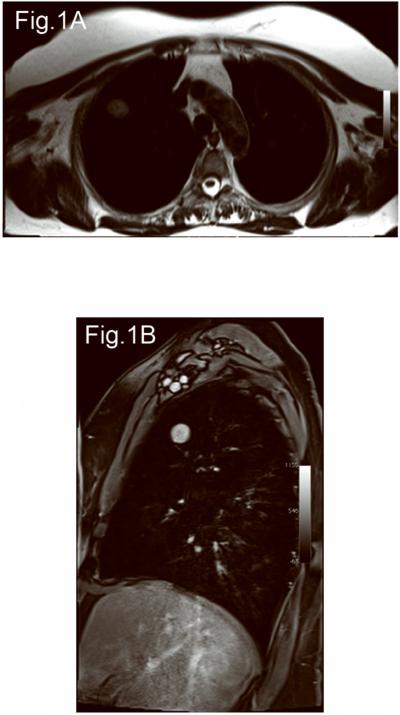
Figure 1.

A 65 years old, male. Left upper lobe adenocarcinoma with Type A curve and k_ep 3.2 min⁻¹. (A) Axial T2-weighted HASTE image, (B) Post contrast sagittal T1-weighted VIBE image.

Image registration and averaging procedure

Misalignments of the SPNs among the image frames in the free-breathing DCE-MRI series were corrected by registering each frame to a reference image frame selected from the same series. Prior to the image registration process, a rectangular region of interest (ROI) in the image was manually cropped and masked so that anatomical structures that moved independently from the target nodules were excluded from the ROI. The same ROI and the mask were applied to the all images in the same series of DCE-MRI. The image registration process consisted of rigid image registration as initial alignment followed by non-rigid B-spline registration [29] with maximization of mutual information [30]. B-spline registration algorithm parameterizes a deformation field of the image by a grid of control points, where displacements of points between the control points are obtained by interpolating the displacements of the adjacent control points using B-spline. The displacements of control points are optimized so that the mutual information, which serves as a similarity measure of two images, is maximized. The cropping, masking, and registration were performed using 3D Slicer [31], a medical image processing and visualization software package, on a Linux-based workstation (OS: Fedora 10; 4 Xeon E7440 quad-core 2.4 GHz CPUs (total 16 cores); 128 GB memory).

After image registration, we fit model time-intensity curves described below to data in each pixel and examined the `goodness-of-fit' between the measured time-intensity curve and the pharmacokinetic model curve by a χ² test [32, 33]. This is used to evaluate the null hypothesis stating that the measured curve is consistent with the theoretical model curve. It was tested against pharmacokinetic prediction curves. The time-intensity curve in a given pixel was considered to be reliable only if the confidence level was more than 50 % in the χ² test. The representative k_ep value was calculated by averaging k_ep from the pixels with reliable time-intensity curves [34]. Parametric maps of a representative nodule are shown in Figure 2.

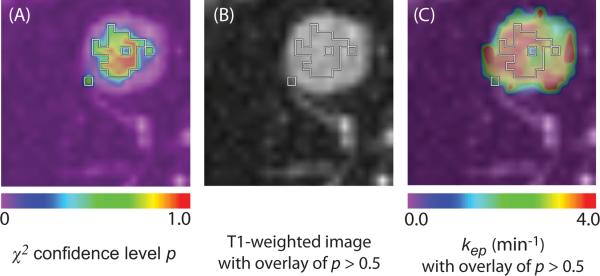
Figure 2.

Representative parametric maps of tumor area in the same case from Figure 1. (A) Goodness-of-fit map color-coded according to confidence level of χ² test overlaid on a T1-weighted image. (B) Boundaries of voxels with more than 50% confidence level of χ² test are superimposed on the T1 image. (C) Color-coded k_ep map. The map shows k_ep values of the entire tumor area. k_ep values within the boundaries of panel B was used for the evaluation. The isolated voxel at the edge of the tumor is a single voxel.

Time-intensity curves

Time-intensity curves I(t) were characterized by three methods.

• (1)
  The first method comprises 4 simple indices: The first index is the initial slope (IS), computed numerically directly from the data. The other three (mean transit time MTT, time to peak TTP, and maximum enhancement (E_max) are all derived analytically from a least squares best fit of the data to a gamma variate function, defined by γ (t) = At^k−1e^−αtα^k / Γ(k), where A is an overall scaling parameter to account for amplitude dependence and Γ(k) is the Legendre gamma function. Specifically, these four indices are defined as follows:

  IS = (I(t₉₀) − I(t₁₀))/(t₉₀ − t₁₀) where t₁₀ and t₉₀ are the times at 10% and 90% enhancement, respectively.

  MTT = k / α, where k and α are obtained from the gamma variate fit. The first moment of this distribution is given simply by k / α. However, the interpretation of this as a “mean transit time” is problematic and largely misleading; see the Discussion for a correct view of this.

  TTP = (k − 1) / α, where k and α are obtained from the gamma variate fit.

  E_max = Aα(k − 1)^k−1e^1−k / Γ(k), where A, k and α are obtained from the gamma variate fit.

• (2)The curves were analyzed specifically with respect to the pharmacokinetic rate constant k_ep characterizing tracer transport between plasma and the extravascular extracellular space (EES). Details of this procedure are described below.
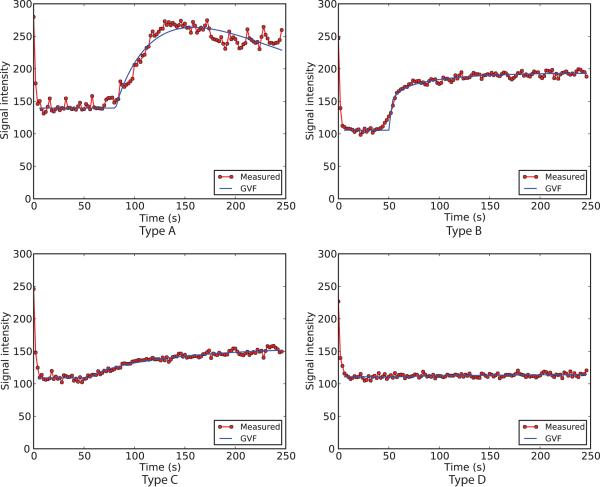
• (3)Time-intensity curves were classified into 4 patterns: Type A, B, C, and D; representatives of these types are shown in Fig. 3. These types are defined as follows. Type A: I(t) reaches peak enhancement within the 4-minute scan time and washes out more than 50% of peak intensity by 4 minutes. Type B: I(t) rises to a peak within 4 minutes, but the decrease of intensity during washout is less than 50% of peak intensity by 4 minutes. Type C: Slow continuous increase of intensity, without reaching a peak within the 4-minute scan time. Type D: No enhancement or signal increase.

Figure 3.

Four representative examples of time-intensity curves are shown. The red dots indicate mean intensity of manually countered nodules at each time point. The blue lines indicate gamma variate functions (GVF) fitted to the time-intensity curves.

Pharmacokinetic parameter estimation

The tracer transport rate constant (k_ep) between plasma and the extravascular extracellular space (EES) is defined beginning with the diffusive mass transport between these spaces, v_edC_e / dt = PS(C_p − C_e), where C_p and C_e are tracer concentrations in the plasma and EES respectively. v_e is the EES volume density, P and S are the permeability and surface area densities of the plasma/EES interface. Combining constants yields the fundamental equation for the transport process,

$${\mathit{dC}}_e∕\mathit{dt}=k_{\mathit{ep}}(C_p-C_e)$$ (1)

where k_ep = PS / v_e. The product PS is often denoted K^trans, a volume density independent rate constant. Note that we explicitly assume tracer transport symmetry, meaning that the transport is passive and indifferent to directionality. In this formulation, plasma concentration is taken as a source term for the single EES compartment. The solution to Eq. (1) is elementary, C_e = G ⊗C_p, i.e. the convolution of the impulse response with the driving or source term. Here G(t) = exp(−k_ept), representing the EES tracer concentration following a single bolus. For the source term, we adopt that given by Tofts [35] as measured in control normals: $C_p\left(t\right)=D\sum _{i=1,2}{a}_i\text{exp}(-m_{i}t)$, where D is the dose. This is a biexponential curve fit, which results in parameter values of (a₁,a₂) = (3.99,4.78)kg/l for a dose normalized to unit amplitude, and (m₁,m₂) = (0.144,0.0111) min⁻¹ for rate constants. These are empirical relations assumed to hold across all individuals. With this source term, the solution to Eq. (1) becomes, explicitly,

$$C_e\left(t\right)={\mathit{Dk}}_{\mathit{ep}}\sum _{i=1,2}\frac{a_i}{m_i-k_{\mathit{ep}}}[\text{exp}(-k_{\mathit{ep}}t)-\text{exp}(-m_{i}t)].$$ (2)

Now what is pertinent to the measurement is not C_e directly, but rather the volume weighted average of concentration in the EES and plasma compartments. That is, C_t = v_eC_e + v_pC_p, where C_t is the volume weighted mean concentration, and v_e and v_p are the EES and plasma volume densities respectively. Substituting the above expression for C_e into this weighted expression for C_t is precisely Eq. (12) of Tofts [35]. We now approximate the physiology by the explicit assumption that v_p is small and may be neglected. This amounts to approximating the mean tissue concentration by C_t(t) = v_eC_e (t).

Finally, the actual MRI signal is proportional to, but not a direct measure of concentration; there is further a background pre-contrast intensity present. We therefore define an enhancement curve by E(t) = S(t) / S(t₀) −1, where S(t) is the time-intensity curve and t₀ is the time of tracer appearance. S(t₀) is estimated by the average value of S(t) over a time window 6 to 176 sec prior to t₀. From the proportionality assumption, we therefore take E(t) = BC_t(t), where C_t(t) is given by the equation above. We then fit the data to this by minimizing least squares deviation, with three free parameters t₀, k_ep, and the overall prefactor to the sum in Eq. (2). This factor is given by Bv_eDk_ep, and as the concentration/MRI signal constant of proportionality B is unknown, the recovered prefactor was ignored as having no meaning. We recognize that our approach is based on linear pharmacokinetics, and a linear relation between the MRI enhancement and tracer concentration. This may be compromised especially during the first pass at early times, but following this, concentrations are sufficiently low that the relationship between signal intensity and contrast concentration can be considered linear [36, 37]. Our estimation of k_ep (the parameter of interest) is taken from the entire curve over all time of measurement; it is not dominated by the early portion of the time-intensity curve, where nonlinearities in the enhancement/concentration relationship may obtain. Note that this stands in contrast to indices such as the initial slope or initial area under the curve, which by definition are sensitive to early time points, and hence to departures from linearity.

Statistical analysis

A Mann-Whitney U test was performed for each perfusion index and pharmacokinetic parameter to see if there were statistically significant differences between malignant and benign SPNs.

Results

Of 30 patients, 27 underwent surgical resection, and 3 underwent CT-guided needle biopsy. The histology included 17 adenocarcinomas, 5 squamous cell carcinomas (SCC), 3 carcinoid tumors, 1 benign solitary fibrous tumor, 1 sclerosing pneumocytoma, 1 hamartoma, 1 reactive nodule, and 1 mycobacterial granuloma.

Average k_ep for malignant SPNs was 1.80±0.85 min⁻¹, for benign SPNs was 0.61±0.36 min⁻¹, which difference in values was the most significant (p=0.005) among all the indices and the parameters. Nineteen of 25 (76%) malignant SPNs demonstrated k_ep greater than 1.0 min⁻¹, and 6 demonstrated k_ep less than 1.0 min⁻¹. All benign SPNs had k_ep less than 1.0 min⁻¹. Sensitivity for diagnosing malignant SPNs by k_ep at cutoff value of 1.0 min⁻¹; 76%, specificity; 100%, PPV; 100%, NPV; 45%, and accuracy: 80%. Fig. 4 shows the distribution of values for malignant vs. benign SPNs.

Figure 4.

Box and whiskers graphs of perfusion parameter values, malignant vs. benign SPNs. Majority of malignant SPNs showed k_ep >1.0 min⁻¹, and benign SPNs showed k_ep <1.0 min⁻¹. Other perfusion parameters did not separate malignant from benign SPNs with wide range of value overlaps.

Average values of perfusion indices (MTT, TTP, IS, E_max) and pharmacokinetic parameter k_ep are given in Table 1. We analyzed each value by histology type, malignant vs. benign. Average MTT was slightly higher in malignant SPNs than benign SPNs (p=0.037). Average TTP was slightly shorter in malignant SPNs than benign SPNs (p=0.011). Average IS was steeper (p=0.032) and E_max was larger (not statistically significant, p=0.062) in malignant SPNs than benign SPNs.

Table 1.

Mean values of perfusion indices and pharmacokinetic parameters by histology (malignant vs. benign)

Histology	MTT (min)	TTP (min)	IS (min−1)	Emax	kep (min−1)
Malignant (25 cases)	6.68±1.63	3.59±1.00	55.4±32.8	72.9±30.5	1.80±0.85
Benign (5 cases)	8.98±2.09	10.2±6.92	18.4±20.2	52.8±18.2	0.61±0.36
M-W p-value	0.037	0.011	0.032	0.062	0.005

MTT: Mean transit time, TTP: Time to peak, E_max: Maximum enhancement intensity, IS: Initial slope. M-W p-value: Mann-Whitney U-test, Two-sided p-value for Malignant not equal to Benign. p<0.05 was defined statistically significantly different.

Two out of 30 SPNs demonstrated Type A curve pattern (both malignant), 19 SPNs (2 benign and 17 malignant) showed Type B curve, 6 SPNs (1 benign and 5 malignant) showed Type C curve, and 3 SPNs (2 benign and 1 malignant) showed Type D curve.

Discussion

Pharmacokinetic analysis

Several points are important to appreciate in the pharmacokinetic analysis. Perhaps most important is its foundation in compartmental theory. It is widely thought that the approach outlined above under Methods is a classical two compartment analysis. This is misleading. As noted in the comments following Eq. (1), plasma concentration serves as a given source (and sink) term for tracer transport into and out of the EES. The plasma space is therefore an independent variable, and not one that has its own equation of temporal evolution dependent on other convective and diffusive source and sink terms. Indeed, inspection of the foundations laid down in Eq. (9) of Tofts [35] reveals a conspicuous absence of a conservation of mass equation for the evolution of plasma concentration. A true two compartment analysis would involve an independent equation of conservation of mass for the plasma. This would rest on equality between the difference in mass flux into the space from the arterial side less that on the venous side and the transport to the EES. Absent this, the model is fundamentally a one compartment model with a source term.

A correct and thorough treatment of the full two-compartment model has recently appeared in an important paper [28]. In that work, careful attention is paid to the consequences of conservation of mass in both the plasma space and in the EES, and importantly, the work gives a number of limiting cases of interest, depending on the degree of perfusion, vascularization, and tracer exchange times. In the particular case of solitary pulmonary nodules treated here, we argue that this corresponds to weakly vascularized and highly perfused tissue. It is precisely in this limit that the concept of an independent vascular space or compartment fails; it rather comprises a source/sink term for the single EES compartment.

To what extent is this reduction of the full Tofts or extended Tofts model a limitation, and to what extent is this justified? The answer to this depends on the relative rates, or equivalently characteristic times for transport. Mass flux into and out of the plasma compartment due to perfusion is governed by a characteristic convection time given by the ratio of local plasma volume density to local blood flow density. This is on the order of seconds. By contrast, the characteristic times for diffusive transport between plasma and the EES are governed by permeability, surface area density, and volume of the EES; these times are on the order of minutes. In such a circumstance, tracer transport is said to be diffusion limited as distinct from perfusion limited. The idea of characterizing transport by diffusion limited or perfusion limited mechanisms is important in a variety of applications, including the diffusive component in ventilation/perfusion relationships [38] as well as in gas resorption from closed body cavities [39]. It is known from these studies that to the extent transport is diffusion limited, the convective component can indeed be taken as a source term, in which case the governing differential equations reduce to one (the slow compartment, here the EES) of first order.

Note that this reduction to a single compartment with source term does not depend on assuming the volume density of plasma is negligible (though that is sufficient); rather it depends on the observation that characteristic diffusion times for transport are much longer than convective transport times.

Finally, we note that in the present study, there is only one independent parameter of physiologic importance that can be measured, namely the plasma/EES rate constant k_ep. Since k_ep = K^trans / v_e, it follows that if v_e can be independently measured with say T1 measurements, then the more fundamental pharmacokinetic parameter K^trans can be estimated, but absent this, k_ep remains as the only parameter accessible to measurement.

We did not measure absolute T1 values for two reasons: 1. Given that our approach is targeted to the clinical setting with a 45 minute examination time, it is not practical to add the relatively long sequence required to measure absolute T1 values. 2. As described above, the only parameter of interest in this study was k_ep, and the fact that it is a tracer transport rate constant means it does not require an absolute T1 value for calculation. On the surface, this would seem a major disadvantage, but it is balanced by a commensurate reduction in the number of parameters to be estimated. Models that attempt to be more inclusive of more complex physiologic features suffer from the fact that, with multiple parameters, the confidence in each is correspondingly reduced. A more serious issue with more complex models arises from motion artifact associated with the free-breathing imaging we used here. This distorts the underlying time-intensity curve and would be excluded by the goodness of fit test used in the simple model, but complex models with multiple parameters can often fit even artifactual data well, and would not be excluded by a goodness of fit test, even though the results are clearly spurious. In this case the combination of a complex model and good fit is particularly poor precisely because it may fail to detect poor data contaminated by artifact. This is exactly what we wish to avoid. Similar considerations apply in cases of profound intravoxel inhomogeneity in histology, e.g., partial tumor necrosis. The fact that we are using the simple tracer transport rate constant k_ep as a sole descriptor of the pharmacokinetic dynamics thus avoids confounding variables; its simplicity in differential diagnosis contributes to its power.

Mean transit time

As noted in Methods, the interpretation of the first moment of the time-intensity curves (above the background) as a mean transit time is problematic. This has serious consequences to the use of this parameter in differentially characterizing tissue properties in tumors. In particular, note first that the EES concentration/time curve, which is the quantity measured, is by Eq. (2) a convolution of the source term (here given by the Tofts result in equation (12) of ref [35]) with the impulse response of the EES. It is elementary to show that the first moment of a convolution is the simple additive sum of the first moments of the convolving partners. That means that the MTT as defined in Methods, and as used in e.g. [40–43] is the sum of two parts. The first part is the mean transit time from the site of injection of tracer, mixing and distributed through its transit in the great veins, the right heart, and finally to the pulmonary artery and distributed arterioles and capillaries. (A small point: since the measurement of MTT takes as its zero of time the first appearance of tracer, any pure time delay secondary to pure bulk transport is neglected.) The second part contributing to the measured MTT is the mean residence time of the tracer in the EES. Note that this is not a transit time in any sense; it is a residence time in a particular compartment, that in turn modulates the transit time of the combined system. Following this line of reasoning, therefore, we now define a new quantity; the EES mean residence time (MRT), given by MRT = MTT−<t>_source, where <t>_source is the first moment of the source distribution.

For the Tofts parameters given in Methods, and for the biexponential form given there, <t>_source is easy to compute. Explicitly, it is given by $<t{>}_{\mathit{source}}=\raisebox{1ex}{$\sum _{i=1,2}{a}_i∕{m_i}^2$}\!\left/ \!\raisebox{-1ex}{$\sum _{i=1,2}{a}_i∕m_i$}\right.$. With the Tofts parameters given in Methods, this results in <t>_source =85.1 min, which represents a lower bound on the possible measured MTT. By contrast, the data shown in Table 1 reveal that the overall MTT as measured by the fitted gamma variate is on the order of 6–10 min, significantly less than the lower bound that necessarily obtains with the Tofts parametrization of the plasma source. How can this wide discrepancy be resolved? The answer lies in an appreciation of the relative magnitudes of the physiologic characteristic times compared with the experimental time window. The Tofts biexponential form has two terms with rate constants of (m₁,m₂) = (0.144,0.0111)min⁻¹. The first component (rate constant of 0.144 min⁻¹) is equivalent to a characteristic time of around 7 min; the second component (rate constant of 0.0111 min⁻¹) is equivalent to a characteristic time of around 90 min. In comparison to these characteristic times, the experimental time window in the studies reported here is 4 min, which is comparable to the first source component, but more than one log shorter than the second component.

There are two conclusions from this observation, one with respect to data analysis and one with respect to physiology: (1) To the extent that this second component is very long compared to the experimental time window, its existence is essentially “invisible” to data collected within that window. (2) This very long component cannot represent anything physiologic in the sense of transit time. Mean systemic circulation times are on the order of 1 min, so multiple mixing and spreading of the initial bolus, especially in the heart and parallel pathways throughout both the pulmonary and systemic circulations masquerade as a spreading transit time. Moreover, renal clearance is an important contributor to concentration decay over this time period. These physiologic features are particularly important insofar as none of these mechanisms pertain to the central question of identifying tumor specific characteristics in the pulmonary nodules. For all these reasons, there is little to be gained, and much to be lost through misinterpretation by including this confounding component of the source term. Simplifying the Tofts source to the single fast exponential term would seem like a solution to this problem, but even here there are difficulties. The first order moment of the fast Tofts source is 1/m₁ = 6.9 min, fully consistent with our data showing overall first moments within a few minutes of this. In principle, a simple subtraction of the first moment of the arterial source term would lead to a measurement of the mean residence time in the SPN. However, to the extent that the arterial source term itself has a moment that is much longer than the mean residence time, such a subtraction is prone to excessive error and cannot be trusted. Indeed, our mean values for benign tumors is 8.6 min, and for malignant tumors 6.7 min. These values must be compared with the Tofts source term moment of 6.9 min. The fact that the subtraction in the case of malignant tumors results in a negative residence time is sufficient evidence for the unreliability of any such characterization of time-intensity curves as being meaningful. Of course, if the arterial input function can be independently measured, then again, in principle, such a subtraction of moments is possible. But importantly, to the extent that these moments are dominated by blood circulatory mixing and clearance, and are only modulated by tumor tissue residence times to a small extent, the implication is that any such attempt to characterize SPNs on the basis of measurements of “MTT” (independent of how that is interpreted) is likely to be of little value.

We explicitly use the Tofts biexponential function for the source term (or arterial input function); we do not independently measure it because we used oblique sagittal sections through an SPN, and the pulmonary artery or a bronchial artery could not be always included in the section. Moreover, pulmonary nodules are mostly fed by bronchial arteries and their direct supply to the nodule is often difficult to locate. The specific parameter values given by Tofts are population averages, and raises the question: for which patient subgroups is this an appropriate approach. We argue that this depends on the patient status. We are explicitly interested in differential diagnosis of solitary pulmonary nodules early in disease, in patients without serious comorbidities. In these individuals, without cardiac myopathies or other hemodynamic pathologies and without severe ventilation/perfusion mismatches, the mixing mechanisms referred to above and therefore the structure of the source term are likely to be near normal. By contrast, in patients with significant hemodynamic compromise or pulmonary dysfunction, the use of population-averaged parameters is likely to be in error; these cases of advanced disease are beyond the scope of our simplified analysis.

Clinical interpretation of parameters

Among the various indices studied, we found k_ep to be a biomarker that to a significant extent separates malignant from benign tumors. The average k_ep value of pixels within the ROI located over the SPN was less than 1.0 min⁻¹ in all benign SPNs. Seventy-six percent of malignant SPNs (19 of 25) had k_ep greater than 1.0 min⁻¹. The exceptions to this differentiation based on pharmacokinetic analysis deserve comment. Specifically, six malignant SPNs that showed k_ep < 1.0min⁻¹ included a poorly differentiated SCC, two acinar-pattern adenocarcinomas, and three mixed-type adenocarcinoma. The average size of these tumors was 18.5 mm (ranged from 17–21 mm). On the other hand, the average size of 21 malignant SPNs with k_ep > 1.0 min⁻¹ was 20.4 mm (range 19–28 mm), significantly larger than those with k_ep <1.0min⁻¹. This size difference is consistent with the idea that smaller tumors with fewer vessels have less surface area, with commensurately smaller K^trans and k_ep. Conversely, as the tumor grows, angiogenesis leads to increased surface area, increased K^trans and k_ep, in turn permitting higher contrast transport directly accessible to measurement.

Investigating perfusion indices such as MTT, TTP, IS, E_max, and time-intensity curve by DCE-MRI gives a different perspective from evaluating k_ep. We observed 4 different types of time-intensity curves in this study, consistent with previous work by Schaefer et al [25]. According to their findings of micro-vascular density and time-intensity curves, malignant SPNs tended to have higher micro-vascular density with Type A curves, which demonstrated short MTT and TTP. Our result that Type A curves included only malignant SPNs is in agreement with previous findings [25], presumably as a consequence of high microvascularity. Furthermore, E_max was the largest in this group and washout was faster than other types. This is also consistent for the tumors with high microvascular density. Acute inflammation cases; however, may also demonstrate Type A curve as well since, such pathology develops neovascular proliferations, as reported previously [25–27]. It seems that unless the lesion is clinically suspicious of acute active inflammation, and if inflammatory diseases can be ruled out clinically and by other modalities, we should consider an SPN with Type A time-intensity curve as likely to be a malignant tumor. We included carcinoid tumors in the malignant category in this study, since it is treated as clinically malignant. On the other hand, when the lesion has very limited vascularity, time-intensity curves may show an extremely small change in intensity over time (Type D). The histologic diagnoses of the two lesions with Type D curve in this study were a reactive nodule and a hamartoma, which did not have tumor vessels within the lesions. Another SPN with Type D curve was an invasive SCC. It demonstrated thin ring-enhancement on post-contrast T1-weighted images as well as on DCE-MRI, which suggested necrosis or little neovascularity in the majority of the tumor.

We conclude that pharmacokinetic analysis by DCE-MRI is important and practical: its importance lies in the fact that it does not utilize ionizing radiation; its practicality lies in the fact that one can obtain equivalent results to those obtainable from dynamic CT. DCE-MRI also provides additional information with its better soft tissue contrast. From the clinical perspective, this simple and practical approach may reduce the number of invasive surgical biopsies, e.g., needle biopsy and VATS, often only to prove the nodule is benign, and thus contribute to overall better management of patients.

Future plans

Tumor vascularity has been shown to correlate with vascular endothelial growth factor (VEGF) receptor expression in non-small cell lung carcinomas. Expression of VEGF receptor is reported in 77% of adenocarcinomas and 75% of SCC [44]. Furthermore, 9% of non-small cell lung carcinomas do not have neovascularization [45]. Even though VEGF receptor expression alone does not uniquely determine tumor vascularity, observation of VEGF receptor expression as well as CD 31 stain for vascular endothelium, particularly in the exceptional cases of malignant tumors with k_ep. 1.0min⁻¹, would be important to investigate in the future. Similarly, tracking pharmacokinetic parameters such as k_ep during the course of therapeutic interventions including chemotherapy and radiation therapy is a clear area where intense follow up studies in larger cohorts would be helpful. This idea is particularly acute in the context of the extent to which these therapies change tumor vessel permeability and perfusion patterns, especially with the use of anti-neovascularization agents.

Summary

Pharmacokinetic parameters such as K_trans require independent measurement of extravascular extracellular volume fractions in addition to the simple rate constant governing transport between plasma and the EES, and this is more difficult in free breathing patients. The concept of “mean transit time” requires careful interpretation, as it depends on the temporal character of the arterial input function. We believe these should not be used without a critical assessment of the assumptions that underlie their interpretations. By contrast, the pharmacokinetic parameter k_ep, which governs the rate at which plasma communicates with the extravascular extracellular space in SPNs, is a clear biomarker distinguishing benign from malignant SPNs. Use of this measure in differential diagnosis will promote increased specificity in patient management and follow-up, as well as in indications for surgical interventions.