Motivation and timing: Clues for modeling the reward system

Abstract

There is growing evidence that a change in reward magnitude or value alters interval timing, indicating that motivation and timing are not independent processes as was previously believed. The present paper reviews several recent studies, as well as presenting some new evidence with further manipulations of reward value during training vs. testing on a peak procedure. The combined results cannot be accounted for by any of the current psychological timing theories. However, in examining the neural circuitry of the reward system, it is not surprising that motivation has an impact on timing because the motivation/valuation system directly interfaces with the timing system. A new approach is proposed for the development of the next generation of timing models, which utilizes knowledge of the neuroanatomy and neurophysiology of the reward system to guide the development of a neurocomputational model of the reward system. The initial foundation along with heuristics for proceeding with developing such a model is unveiled in an attempt to stimulate new theoretical approaches in the field.

Historically, factors that affect motivation vs. timing have been viewed as independent. For example, Roberts (e.g., 1981) proposed a simple timing model in which the time of food impinged on the clock and the comparison (of perceived and expected time), whereas the probability of food affected other processes such as motivation. Effects on the clock were proposed to alter the position of the response function and effects on other processes were proposed to alter response rate. However, even in Roberts‘ paper, there was an indication of an effect of motivation on timing. In his Experiment 3, the rats were pre-fed prior to the onset of peak-procedure testing (see Section 1.1). During the initial few sessions of testing, there was a noticeable rightward shift in the peak time coupled with a decrease in response rate, suggesting that the pre-feeding manipulation had altered timing. More recently, a number of studies have shown effects of motivational variables on timing processes, indicating that motivation and timing are not independent. Recently published research from our laboratory is reviewed along with presenting some new evidence that provides further insight into the nature of the motivational effects on timing. The results are interpreted in relation to quantitative models of timing and current neurobiological evidence.

1.1. Motivation and timing are not independent

In the peak procedure (Roberts 1981; Catania 1970), subjects receive intermixed reinforced fixed interval (FI) and non-reinforced peak interval (PI) trials, typically three to four times the duration of the FI. On individual PI trials, subjects normally produce a burst (high state) of responding that surrounds the expected time of reward availability (e.g., Church, Meck, and Gibbon 1994). When averaged over a number of trials typical PI response functions are characterized by a gradual increase in response rate until the expected time of food delivery followed by a decrease in response rate. Using the peak procedure, Galtress and Kirkpatrick (2009) demonstrated that increasing reward magnitude from 1 to 4 food pellets led to a steeper response function that was shifted to the left and was sustained over many sessions of training. A subsequent reduction in reward magnitude from 4 to 1 food pellet(s) resulted in the response function shifting back to the right. The observed shifts in the peak location were a result of the contrast between the two reward magnitudes, rather than a consequence of absolute reward magnitude. Initial peak procedure training for 1 or 4 food pellets in separate groups of rats produced steeper PI response functions for the 4 pellet reward, but no differences were found between the two groups in the location of the response peak. Similar results have also been reported using changes in the magnitude of brain stimulation in rats (Ludvig, Conover, and Shizgal 2007) and alterations in the magnitude of grain reward in pigeons (Ludvig, Balci, and Spetch 2011), with increases in reward magnitude resulting in a leftward shift in the peak and decreases in reward magnitude resulting in a rightward shift in the peak.

Further experiments by Galtress and Kirkpatrick (2009) showed that alterations in the motivational state of the rat by either pre-feeding or reducing reward palatability through pairing the reward with nausea-inducing lithium chloride dramatically shifted the peak to the right and decreased response rates. By examining the effect of devaluation on the peak shift to two different durations (30 s and 60 s), it was determined that the shifts in the peak function were neither additive (a constant duration) nor multiplicative (proportional to the delay to reinforcement).

In an additional series of experiments, Galtress and Kirkpatrick (2010a) employed a bisection procedure (Church and Deluty 1977) to further investigate the nature of the effect of reward magnitude on timing. Rats were trained to discriminate a short (2 s) from a long duration (8 s) and tested on intermediate durations to produce a psychophysical function. In initial training, a single food pellet was delivered following correct responses to both the short and long durations, followed by an increase to 4 food pellets for one of the durations in a subsequent phase. The increase in reward magnitude resulted in an overall flattening of the psychophysical function, but the point of subjective equality (PSE) remained at the geometric mean of the short and long durations. Flattening of the response function with an unaltered PSE was also found when the rats were trained on the two different magnitudes (1 vs. 4) initially compared to an equal magnitude (1 vs. 1) control group. The results concur with a previous report by Ward and Odum (2006) in which pre-feeding flattened the psychophysical function during temporal discrimination. However, Galtress and Kirkpatrick (2010a) controlled for any effects of satiety through increased reward magnitude and found that the flattening of the function was not due to a change in motivational state due to satiety, but as a result of possible within- and between-phase reward magnitude contrast.

1.2. State-dependency and timing

More recent studies in our laboratory have produced satiety through pre-feeding to further investigate the effect of contrasting motivational state on the peak procedure by inducing either reward devaluation through deprivation during training and pre-feeding prior to the test phase or inducing reward inflation through prefeeding during training and testing in a deprived state.

1.2.1. Experiment 1

Experiment 1 aimed to further understand if the effect of changes in motivational state due to satiety devaluation on timing (Galtress and Kirkpatrick 2009) would be altered depending on the direction of the change. Manipulations of reward magnitude appear to have directionally specific effects on timing in the peak procedure. Increases in magnitude shifted the response function to the left, and decreases shifted the response function to the right. The present experiment examined a comparable manipulation in which the change in motivational state resulted in either reward devaluation or reward inflation. Directional specificity would result in a rightward shift in the peak with reward devaluation and a leftward shift with reward inflation.

1.2.1.2. Method

Two groups of rats (n = 12) were given peak-interval training, following initial lever-press training. Within each group, half of the rats received a houselight cue (onset for trial initiation and offset for trial termination) during both FI and PI trials, and the other half received lever insert to cue trial onset and lever retraction to cue trial termination. The cue manipulation was conducted to check for any differences in the nature of the cues in response initiation, which could presumably interact with motivational manipulations. The cue manipulation did not produce any effects on any measures of responding, so from here forward all aspects of the procedure and results will be described without reference to differences in cues.

Both groups of rats (Non-fed and Pre-fed) were given an FI 60-s, PI 240-s peak procedure. On FI trials, food was primed after 60 s, and the first lever press resulted in the termination of the trial cue (light or lever), delivery of a single food pellet, and initiation of the intertrial interval (ITI) of 120 s. PI 240-s trials ended without food delivery. In the Non-fed group, lever-press training and peak-procedure training were carried out under food-deprivation conditions (approximately 21 hr of food restriction); however, in the Pre-fed group, satiety levels were manipulated by pre-feeding the rats 15 g of food pellets per pair in their home cages for 30 min prior to the experimental sessions. Rats were maintained at 85% of their free-feeding weights in both groups. In all cases, peak-interval training sessions consisted of 14 FI 60-s trials and 7 PI 240-s trials and lasted for a total of 30 sessions. In a subsequent test session, all rats were given 14 PI 240-s trials (ITI 120 s) under the opposite pre-feeding manipulation to peak-interval training, so that the Non-fed group received pre-feeding, whereas the Pre-fed group was tested under food-deprivation. There were no FI trials in this stage so as to eliminate any interaction between deprivation state and food consumption (see Galtress and Kirkpatrick 2009).

1.2.1.2. Results

An individual trials low-high-low algorithm (LHL; Church, Meck, and Gibbon 1994) was conducted on the PI trials during the last session of training and during the test session. On each trial, the start and end times of high state responding were determined by locating the best-fitting transition between low-high and high-low levels of responding, while high state response rate was calculated as mean responses per minute within the high state of responding.

Figure 1 displays the start and end times and the response rate in the high state as a function of group during the baseline and test phases. As seen in the figure, the start and end times were later during the test phase in both groups, and the difference was more pronounced for start times. In addition, response rates were higher during training than during the test phase, due in part to the absence of reinforcement in the test phase. Also, the response rate was higher in the Non-fed group than the Pre-fed group during the baseline phase. Separate ANOVAs were conducted on each dependent measure with the factors of Phase (Training vs. Test) and Group (Non-fed vs. Pre-fed). The analysis revealed an effect of Phase on start times, F(1,22) = 13.0. For the high state response rate, there was an effect of Phase, F(1,22) = 26.7, and a Phase × Group interaction, F(1,22) = 8.9. There were no effects on end times, and there was no main effect of Group on any measure.

Figure 1.

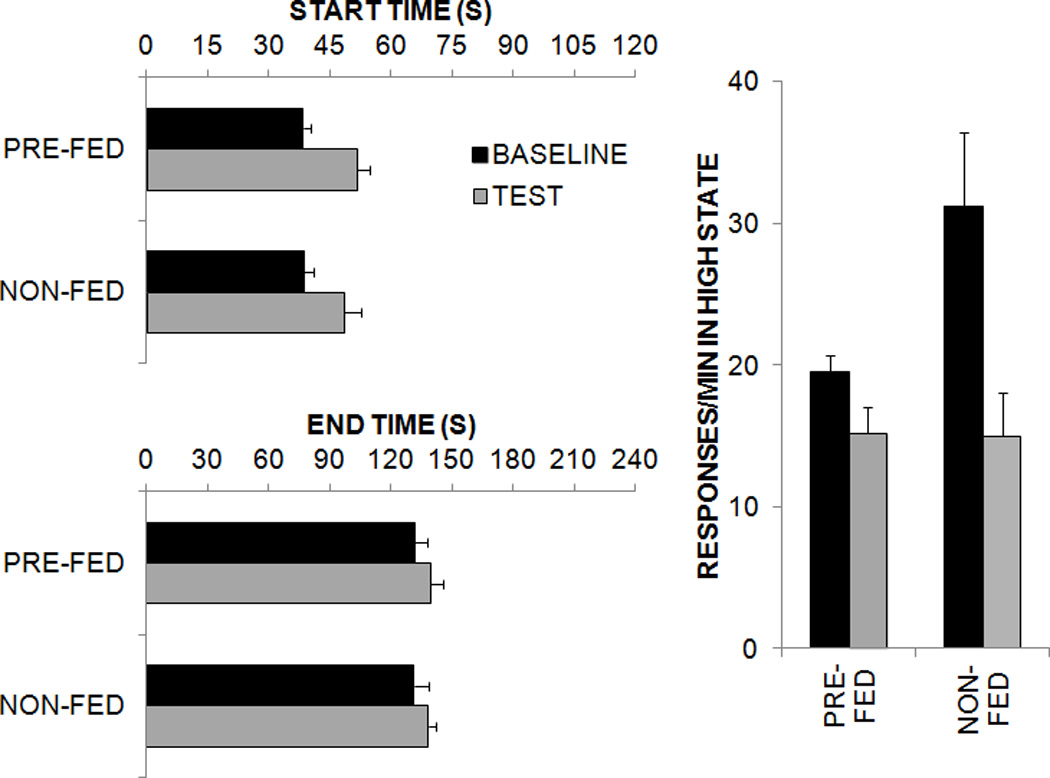
Results of the low-high-low analyses (start times, end times, and responses/min in the high state) conducted on individual peak trials during baseline and test phases in Experiment 1.

1.2.1.3. Discussion

These results indicate that both the Non-fed and the Pre-fed groups produced comparable temporal behavior in the baseline phase of the experiment suggesting that the current motivational state did not affect timing. However, responding for reward, especially response initiation, was shifted to the right when comparing baseline and test phases in both groups. While the effect on timing was the same in both groups, the Phase × Group interaction on the response rate in the high state confirmed that the rats were sensitive to the effects of pre-feeding in their baseline response rates. Both groups displayed a reduction during testing due to modest extinction of responding, which appeared to mask any group differences during the test phase. Therefore, the effect of satiety on rate was a product of the current motivational state, whereas the effect on timing was a product of a change in motivational state.

1.2.2. Experiment 2

In Experiment 2, two qualitatively different rewards were used to investigate any sensory-specific effect of motivational state on timing behavior. Specifically, this experiment was designed to test whether overall motivational contrast between food deprivation and satiety had an effect on any to-be-timed interval, or alternatively whether the process was reward-specific. As the prior experiment indicated that the shift in motivational state between food-deprivation and satiety produced similar effects regardless of the direction of change, the present experiment employed the use of food-deprivation followed by a subsequent satiety procedure.

1.2.2.1. Method

Four groups (n = 6) of food-deprived rats were pre-trained to press two levers for a food pellet reward (Group FF), a sucrose pellet reward (Group SS), or both rewards (one reward per lever; Groups FS and SF) and then subsequently trained on a two-lever discrete-trials peak procedure. Here, both levers were trained in randomly intermixed trials with one lever delivering reinforcement on an FI 30-s, PI 120-s schedule, while the second lever delivered reinforcement on an FI 60-s, PI 240-s schedule. There were 24 FI and 8 PI trials per session (12 FI and 4 PI trials per lever) and initial training lasted 20 sessions. During training, Group FS received a food pellet reward following the FI 30-s delay and a sucrose pellet reward following the FI 60-s delay; Group SF received a sucrose pellet reward following the FI 30-s delay and food pellet reward following the FI 60-s delay, Groups FF and SS received a food pellet or a sucrose pellet reward for both durations, respectively.

Following initial training, all groups were given two test phases with food or sucrose in a counterbalanced order. The test sessions for each phase consisted of 12 PI 240-s (for the 60-s lever) and 12 PI 120-s trials (for the 30-s lever), randomly intermixed. Immediately prior to each test session, the rats were pre-fed with food pellets (Food test) or sucrose pellets (Sucrose test). The three baseline sessions prior to the Food test comprised the Food baseline and the three prior to the Sucrose test were considered as the Sucrose baseline. The procedure involved pre-feeding of a novel reward for Groups FF and SS (Sucrose test and Food test, respectively) in addition to pre-feeding the familiar reward in the opposite test condition. For Groups FS and SF, the pre-fed reward was familiar in both cases but may produce selective devaluation only to the schedule of reinforcement that delivered the devalued reward, if the devaluation effect is sensory specific. In other words, food devaluation should affect responses on the food-rewarded schedule and sucrose devaluation on the sucrose-rewarded schedule.

1.2.2.2. Results

Individual-trial LHL analyses determined the start and end times and high state response rate for the high response state over the last 24 PI trials of each phase for the 30-s (Figure 2) and 60-s (Figure 3) schedules. An ANOVA including the factors Phase (Food baseline, Food test, Sucrose baseline, and Sucrose test), Duration (FI 30 and FI 60), and Group (FF, SS, FS and SF) was conducted on each dependent measure. Both figures show an overall increase in start times during the Food test and the Sucrose test phases when compared to baseline. This effect was more pronounced on the 60 s duration. There is a similar overall increase in end times between baseline and test. For the high state response rate measure, there was an overall reduction in responding between baseline and test sessions for all the groups.

Figure 2.

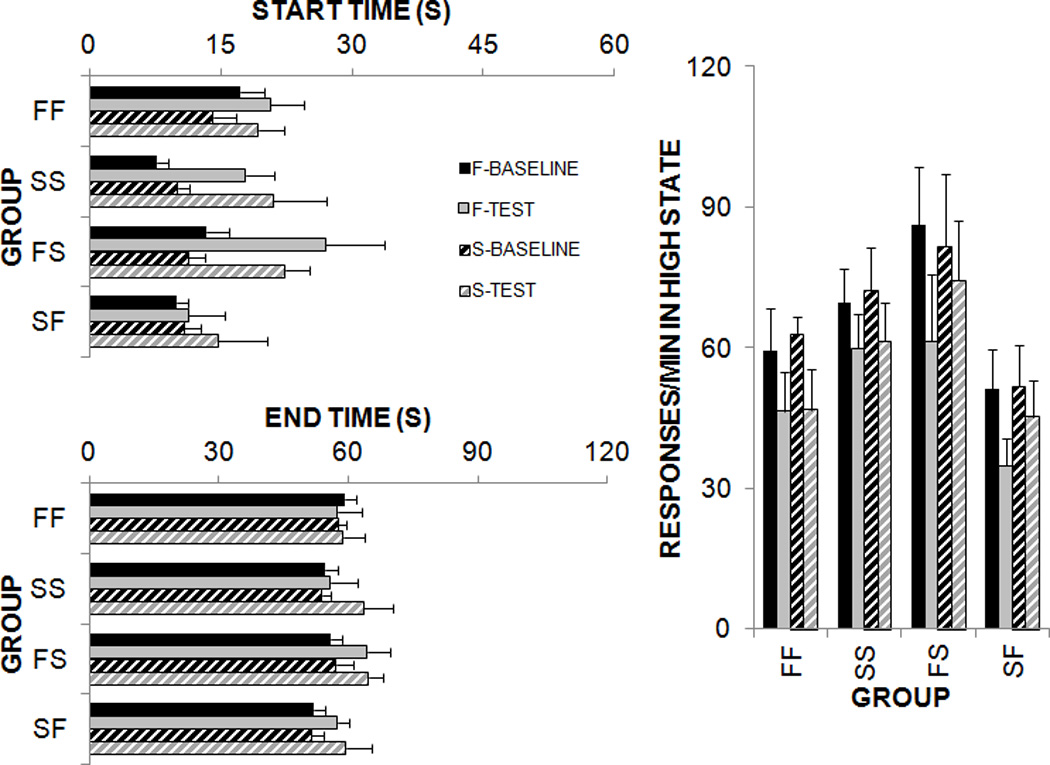
Start times, end times, and responses/min in the high state from the low-high-low analyses conducted on individual peak trials on the 30-s schedule during baseline and phases in Experiment 2. The F-baseline and S-baseline refer to responding on the 30-s schedule during the sessions prior to the food or sucrose pre-feeding test. The F-test and S-test refer to responding on the 30-s schedule during the food or sucrose satiety test.

Figure 3.

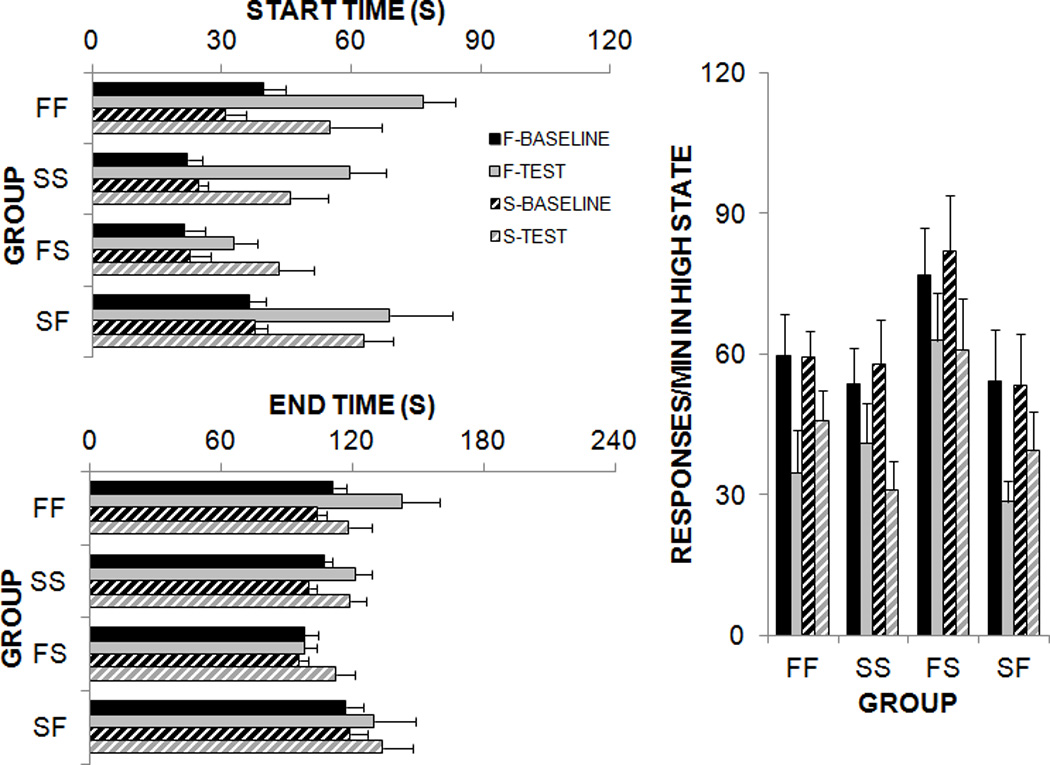
Results of the low-high-low analyses conducted on individual peak trials on the 60-s schedule during baseline and test phases in Experiment 2. The F-baseline and S-baseline refer to responding on the 60-s schedule during the sessions prior to the food or sucrose pre-feeding test. The F-test and S-test refer to responding on the 60-s schedule during the food or sucrose satiety test.

An analysis of start times revealed main effects of Phase, F(3,60) = 24.6, Duration, F(1,20) = 271.7, and Group, F(3,20) = 3.6 with significant interactions between Duration × Group, F(3,20) = 13.8, and Duration × Phase, F(3,60) = 8.4. An analysis of end times revealed main effects of Phase, F(3,60) = 5.7 and Duration, F(1,20) = 1262.6 and a significant interaction between Duration × Group, F(3,60) = 15.1. For the high state response rate, there were main effects of Phase, F(3,60) = 24.4, and Duration, F(1,20) = 5.8, and a significant Duration × Phase interaction, F(3,60) = 2.9.

Post-hoc analyses of the Duration × Group interactions were conducted using Tukey pairwise comparisons. These revealed group differences in timing of the FI 60-s schedule. The two groups that received food on the FI 60-s schedule (FF and SF) produced later start and end times than the two groups that received sucrose (SS and FS). In addition, Group FS produced earlier start and end times than the other three groups. These results indicated that, at least for the FI 60-s schedule, the sucrose reward resulted in earlier start and end times than the food reward. The same pattern of results was observed for the FI 30-s schedule, but these effects did not reach statistical significance. Duration × Phase interactions were also investigated. Here, there was an overall increase in the start times between baseline and test on the 60 s duration, but there were no significant differences between baseline and test for the 30 s duration. In the high state response rate, both the baseline levels of responding on the 30 s and the 60 s durations were comparable and there was a significant reduction in response rate between baseline and test, especially for the 60 s duration. These combined results suggested that pre-feeding affected response initiation, rather than an overall shift the response function and that this effect was more apparent on the 60-s schedule. Overall, the effect of satiety was not specific to reward type or previous experience with the reward.

An additional comparison was made between the FI 30-s and FI 60-s schedules to determine the nature of the effects of pre-feeding on the response function. Galtress and Kirkpatrick (2009) found that the effects of pre-feeding were neither additive, nor multiplicative in nature and so did not support either a clock-speed or response-threshold interpretation; rather the authors concluded that the attention to the to-be-timed interval was disrupted by satiety (see Section 1.3). In this experiment there is a further opportunity for a within-subjects comparison of satiety effects over two durations. Following the method used by Galtress and Kirkpatrick (2009), measures of the difference, ratio, and relative spread of the two durations were taken from the individual-trials analysis for the Food and Sucrose baseline and test conditions for all rats. The analysis was conducted on the data from the LHL algorithm, but here the data were collapsed across groups to increase statistical power, as there were comparable effects of satiety in all groups in the previous analysis. For the difference measure, the baseline was subtracted from the test for the start and end times of the high response state. Similar difference scores for the 30 s and the 60 s duration would be indicative of an additive effect of pre-feeding on responding; for example there might be a constant 15 s shift in start and end times in both cases. For the ratio measure, the test start and end times were divided by the baseline values. Similar ratio scores between the 30 s and the 60 s duration would suggest a multiplicative effect of pre-feeding indicating that the start and end times had increased by the same factor. Table 1 shows the mean values for the difference and the ratio scores for the start and end times. The difference scores in the Food and the Sucrose conditions, as well as in the baseline vs. test conditions appear larger on the 60 s lever than the 30 s lever and this effect was larger for start times than end times. In the ratio scores, there were somewhat lower scores for the end times compared to the start times, but there were no clear differences across durations or in comparing food and sucrose. Separate ANOVAs examined the effect of duration on the difference and ratio scores for start and end times for the food and the sucrose conditions. For the difference scores, there was an effect of Duration on the difference scores for the start times for both the Food condition, F (1,23) = 12.0, and the Sucrose condition, F (1,23) = 15.3, but there was no effect of Duration on the end times in either condition. No effect of Duration was found for the ratio scores.

Table 1.

Top: Difference and ratio scores between baseline and test phases for the 30- and 60-s schedules under sucrose and food devaluation phases. The scores were calculated separately for the start and end times during the food and sucrose tests across the 30-s and the 60-s lever durations. Bottom: The relative spread (middle time / high state duration) for the 30-s and the 60-s schedules during the baseline and test phases.

		START 30 S	START 60 S	END 30 S	END 60 S
DIFFERENCE SCORES	FOOD	7.12	29.60	3.37	14.66
	SUCROSE	7.76	22.77	6.61	16.17
RATIO SCORES	FOOD	1.85	2.16	1.00	.98
	SUCROSE	1.67	1.20	1.13	1.66
		BASE 30 S	BASE 60 S	TEST 30 S	TEST 60 S
RELATIVE SPREAD	FOOD	1.31	1.16	1.09	.77
	SUCROSE	1.32	1.15	1.10	.83

The relative spread was calculated by subtracting the start time from the end time of the high state to determine the high state duration. The high state duration was then divided by the middle point (end-start/2) to give a measure of the relative spread of the response function. A similar relative spread between the baseline and the test functions would suggest a multiplicative effect of pre-feeding on the shift in responding whereas a similar relative spread between the 30 s and the 60 s durations, particularly on baseline, would indicate that the spread of the response functions was scalar for the two durations. Table 1 shows the relative spread scores over the four phases of the experiment. For both the Food and the Sucrose conditions, the relative spread of the 30 s function appears larger than that of the 60 s function and the spread of both the 30 s and the 60 s function appears larger on baseline than test. Separate ANOVAs were conducted between the baseline and test phases for the Food and Sucrose devaluation phases. In the Food condition, there was an effect of Phase on the relative spread measure from the 30 s function, F(1,23) = 11.1, and the 60 s function, F(1,23) = 61.2. In the Sucrose devaluation phase, there was an effect of Phase on the relative spread measure from the 30 s function, F(1,23) = 13.1, and the 60 s function, F(1,23) = 34.0. Separate ANOVAs were also calculated on the relative spread measure between the 30 s and 60 s durations for both the Food and Sucrose conditions. There was an effect of Duration in the Food baseline phase, F(1,23) = 8.2, the Food test phase, F(1,23) = 11.5, the Sucrose baseline phase, F(1,23) = 12.5, and the Sucrose test phase, F(1,23) = 15.4. In all cases the 30-s response function was relatively wider than the 60-s response function. These results suggest that the spread of the response functions did not show scalar variance when comparing the two schedules (30 s vs. 60 s) or the two conditions (baseline vs. test).

1.2.2.3. Discussion

The pattern of results in Experiment 2 indicated that the effects of pre-feeding were the same regardless of the type of reward and not dependent on a prior association with the test duration, suggesting that the effect of motivational state was not reward-specific. When comparing the test to the baseline phase, the high state response rate was lower for both durations, and for the FI 60-s schedule, the start times were later. This suggests that the rats were sensitive to the motivational effects of satiety and, for the FI 60-s schedule, this resulted in a rightward shift in response function between baseline and test, with the effect being greater for response initiation than for response cessation.

The effect of Duration on the start time difference scores plus the lack of an effect of Duration on the ratio scores indicate that the shift in response initiation under pre-feeding is not wholly additive. However, as the relative spread between the 30-s and the 60-s response functions is significantly different overall, then in this case, the two durations do not have scalar variance. This may have affected the ability to measure the effects of satiety on the 30-s duration if this duration was timed with relative imprecision compared to the 60-s duration, which could explain the overall greater sensitivity to detect differences for the 60-s duration. As both the baseline and test comparisons were also not proportional, it was not pre-feeding alone that was producing a lack of scalar variance. It could be the case that there was some interference effect between the two schedules and that the relatively wider spread of the 30-s response function was due to the rats' persistent responding on that schedule. The relative spread results also indicated that the effect of satiety was not entirely proportional. Therefore, as was found previously, there is mixed evidence indicating shifts that were neither additive or proportional.

There also appears to be an effect of sucrose reward on the response function that is independent of pre-feeding effects, particularly on the 60 s duration. The earlier overall start and end times for responding for sucrose reward may reflect a higher preference for sucrose translating into an increased motivation to respond early. The leftward shift in the response function in Group FS may have been a result of contrasting reward value as found previously (Galtress and Kirkpatrick 2009). However, a within-session contrast with food cannot fully explain the results as the effect is apparent not only in Group FS but also to a lesser extent in Group SS prior to any experience with food reward.

1.3. Theoretical interpretations based on quantitative timing models

Interpretation of the effects of motivation on timing may be aided by the extant computational models of timing behavior. Such theories can potentially guide our understanding of the effects of motivation on timing. Models that explicitly incorporate reward processing/motivation are considered as well as those that do not.

1.3.1. Scalar timing theory

Scalar expectancy theory (SeT; Gibbon and Church 1984; Gibbon, Church, and Meck 1984) is the most frequently applied timing model. It consists of a pacemaker-accumulator system, a memory system, and a comparator decision process. The pacemaker-accumulator system contains a pacemaker that emits pulses at a constant rate within a trial; the pacemaker rate is sampled from a Gaussian distribution, and thus varies across trials. When timing is initiated by presentation of a time marker, a switch between the pacemaker and accumulator closes and the accumulator begins to linearly accumulate pulses received from the pacemaker. At the time of reinforcement, the number of pulses in the accumulator is stored in reference memory, which contains a collection of the number of pulses from previously reinforced durations. Because the clock speed varies according to a Gaussian distribution (with a determined mean and a standard deviation that is proportional to the mean) from trial to trial, the variance in reference memory reflects the scalar variation in the pacemaker. The contents of reference memory can be modified with a multiplicative parameter k* that can distort the remembered time of reinforcement (either shorter or longer than the actual time). The decision process uses a random sample from reference memory as a target, continuously comparing the current number of pulses in the accumulator with the target. When the current number is sufficiently close to the target, as determined by a decision threshold that varies trial to trial according to a Gaussian distribution, then responding will occur. In regards to the peak procedure, separate decision thresholds have been proposed for the initiation and cessation of responding within individual trials (Gibbon and Church 1990).

The elements of scalar timing theory offer several potential mechanisms for explaining motivational effects on timing. For instance, pacemaker rate has been suggested to vary with changes in arousal level (e.g., Wearden, Philpott, and Win 1999). Additionally, the times of the closing and opening of the switch on each trial have been proposed to fluctuate with variations in attention within each trial (Fortin 2003; Fortin and Massé 2000; Thomas and Weaver 1975; Zakay 1989), consequently producing alterations of perceived durations; attention may be affected by levels of motivation. Furthermore, motivation could affect the location of the decision threshold(s), thereby producing effects on timing performance.

In examining the set of results discussed above, it does not appear that any single process in scalar timing theory can account for the pattern of outcomes. At first glance, alterations in pacemaker speed would appear to be the most obvious mechanism to consider due to the history of use of this component of the model in explaining the effects of drugs (Maricq and Church 1983; Maricq, Roberts, and Church 1981; Matell, Bateson, and Meck 2006; Meck 1996, 1983; Buhusi and Meck 2002; Cevik 2003) and arousing stimuli (Wearden, Philpott, and Win 1999) on timing. However, there are several observations that do not fit with a clock speed interpretation, at least not as the sole mechanism: (1) the effects of reward magnitude shifts were long-lasting (Galtress and Kirkpatrick 2009) – clock speed effects are transient due to the updating of the reference memory with samples that reflect the new clock rate; (2) the devaluation effects on the peak were not multiplicative/proportional (Galtress and Kirkpatrick 2009; see also Experiment 2 above), as predicted by a change in pacemaker rate; (3) reward changes in a bisection task flattened the psychophysical function, as opposed to shifting the function to the left or right (Galtress and Kirkpatrick 2010a); and (4) training under satiety followed by testing in a deprived state produced the same rightward shift as training under deprivation and testing under satiety (Experiment 1, Section 1.2.1) – an arousal-induced clock speed change should result in a leftward shift in the former condition and a rightward shift in the latter.

Galtress and Kirkpatrick (2009, 2010a) proposed that both between- and within-session reward contrast effects operated to modify attention to time, thereby producing effects on the operation of the switch in the pacemaker-accumulator component of scalar timing theory. The effects on switch operation would contribute both additive (switch closure/opening) and multiplicative (switch fluctuation) components, would result in a flattening of the psychophysical function, and could explain the effects of satiety devaluation in training vs. testing by assuming a state-dependent modulation of attention. A delay in switch closure could also explain the stronger effect of the reward magnitude/value changes on the initiation of responding compared to the cessation of responding following reward omission (Ludvig, Balci, and Spetch 2011; Ludvig, Conover, and Shizgal 2007). However, attention effects within scalar timing are not entirely consistent with the pattern of results as these effects should be transient in a similar fashion to the pacemaker rate effects (due to the populating of memory with a new set of samples reflecting the change in attention).

Finally, changes in the decision threshold could account for the results. It is possible that changes in the decision threshold are responsible for the absolute effects of reward magnitude on the precision of timing. Exposure to 4 pellets on a peak procedure produced sharper timing functions both in initial training and also following a shift from 1 to 4 pellets (Galtress and Kirkpatrick 2009). These results are consistent with a decrease in the mean and/or the standard deviation of the decision threshold that increased the precision of timing. In addition, a change in decision threshold could account for the stronger effects of reward magnitude changes on the initiation of responding compared to response cessation, as was found in the present studies, by assuming that motivation produced a stronger effect on the start threshold. Furthermore, changes in the decision threshold could persist over time. In the timing literature, much less attention has been paid to understanding the effects of decision thresholds on bisection performance (Wearden 2004), but changes in the mean threshold (for identifying a short vs. long) should affect primarily the PSE, whereas changes in the variation of the decision threshold would affect the slope (DL) of the bisection function. Therefore, changes in variability of the threshold could potentially account for motivational effects on bisection performance. However, it is not clear how this change in threshold would be related to the involvement of decision thresholds in the peak procedure, where the most likely effects would be on the overall mean and, most particularly, on the mean of the start threshold.

Overall, it appears that no single process within scalar timing theory can account for the pattern of results. This may be due to the effect of motivation on multiple aspects of timing, thereby requiring the contribution of more than one component of the model. Most importantly, however, is the problem that scalar timing theory does not contain any rules for determining how motivation or arousal should change its parameters. The assumptions applied here are entirely ad hoc interpretations of motivational effects on individual parameters of the model. There is no basis for determining a priori predictions derived from the original model. It is also worth noting that this problem applies to other timing models such as the multiple oscillator model (Church and Broadbent 1990), packet theory (Kirkpatrick 2002), the modular theory of timing (Guilhardi, Yi, and Church 2007) and the striatal beat frequency model (Matell and Meck 2004; Miall 1989; Matell and Meck 2000). Therefore, other models that explicitly incorporate reward properties are now considered.

1.3.2. Other timing models

The main alternatives that explicitly incorporate reward properties within the framework of a timing model are: the behavioral theory of timing (BeT; Killeen and Fetterman 1988), the learning to time model (LeT; Machado 1997), the behavioral economic model (BEM; Jozefowiez, Staddon, and Cerutti 2009), and the multiple time scales model (MTS; Staddon and Higa 1996). In both BeT and LeT, the primary role of reinforcement is to set the pacemaker rate. Higher rates of reinforcement (and presumably higher magnitudes) increase the pacemaker rate. This would produce an effect of temporarily shifting the peak to the left when the reward magnitude increased. However, this effect would be transient. The long-lasting nature of the observed effects of reward magnitude on performance argues against this mechanism. In addition, in the bisection procedure, the increase in magnitude would sharpen the psychophysical function due to the faster pacemaker speed, rather than flattening the function as was observed, so the bisection results are in the opposite direction to the predictions of both models.

BEM is a relatively new timing model that aims to explicitly couple reward/motivational variables with timing processes. This model does predict reward magnitude and value effects on timing that generally accord with the previous results of Galtress and Kirkpatrick (2009). However, BEM does not correctly account for the results in the bisection task. This model proposes that the increase in reward magnitude for one of the choices would result in an overall bias to choose that sample, which would shift the psychophysical function upward (for biases to the long sample) or downward (for biased to the short sample) rather than flattening the function as was observed.

The MTS model includes the explicit assumption that a sudden increase or decrease in reward magnitude will produce a short-lived effect on anticipatory timing of the subsequent reward(s). However, the prediction here is that smaller rewards result in earlier responding than larger rewards, which is the opposite of the results discussed in the present report. The brief effect of changes in reward magnitude or value is likely due to different mechanisms from the more chronic effects that are discussed above. Some consideration of the relationship between the transient and chronic effects of reward magnitude changes would be valuable for future model development. Another valuable contribution of the MTS model is the correct prediction of the reward omission effect, which is the short-lived reduction in pausing on fixed interval schedules following sudden reward omission (Staddon and Innis 1966). Although this effect is not directly relevant to an interpretation of the present results, this should be considered when developing the next generation of timing models.

Overall, in considering the pattern of data in relation to model predictions, it is apparent that none of the current models are able to incorporate the effects of motivational variables on timing. Growing evidence indicates the importance of motivation in the timing process (Doughty and Richards 2002; Galtress and Kirkpatrick 2009, 2010a; Galtress and Kirkpatrick 2010b; Grace and Nevin 2000; Kacelnik and Brunner 2002; Ludvig, Balci, and Spetch 2011; Roberts 1981; Ludvig, Conover, and Shizgal 2007), leading to the realization that new timing models (or modifications of existing models) that explicitly incorporate motivational variables are needed. The subsequent sections provide a basis for guiding future theoretical developments.

1.4. Reward system circuitry

The psychological models discussed above have been critical to our understanding of behavioral phenomena in the timing field. However, such models have been criticized for failing the “neural plausibility” test (Bhattacharjee 2006). For instance, while scalar expectancy theory (Gibbon 1977) has contributed to the explanation of the increase in timing variability with increases in duration, the neural implementation of this model in the form of the striatal beat frequency (SBF) model is not completely physiologically plausible (Matell and Meck 2004). Furthermore, psychological timing models do not accurately account for the effects of motivation on timing, even when considering models that explicitly incorporate motivational aspects of reward (Section 1.3.2). However, the motivation-timing interactions are not surprising because reward processing and time processing circuits are so intricately interconnected. A consideration of the structure and function of these circuits may aid in guiding the development of new timing models that may more readily incorporate the present results.

The reward system consists of three main components, each with its own circuitry: reward processing, interval timing, and decision-making. The components and interconnections of these systems are diagrammed in Figures 4–6. While there is considerable evidence that implicates different neural structures in reward prediction and valuation (e.g., Peters and Büchel 2010, 2011), interval timing (e.g., Coull, Cheng, and Meck 2011), and decision-making (e.g., Doya 2008), the following sections summarize such evidence to support the interaction and integration of the reward-processing, interval-timing, and decision-making sub-systems.

Figure 4.

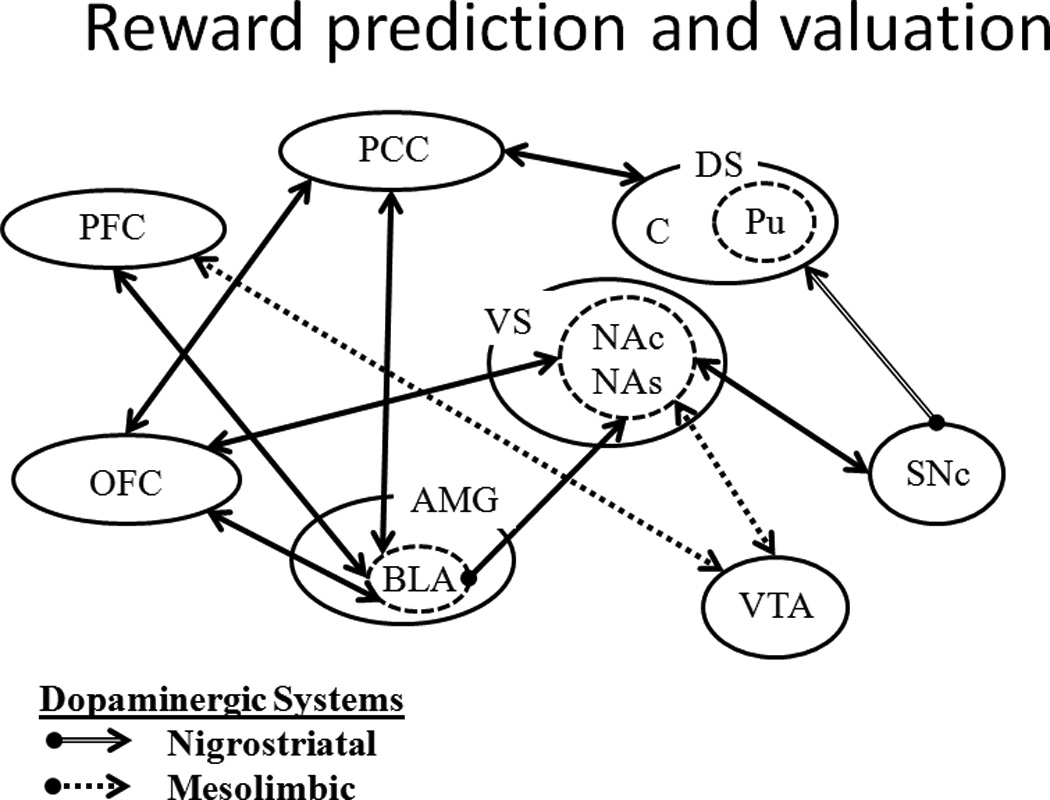
A diagram of the neural circuitry involved in the reward prediction and valuation component of the reward system. The nigrostriatal system consists of the substantia nigra pars compacta (SNc) projections the dorsal striatum (DS), which is composed of the caudate nucleus (C) and the putamen (Pu). The mesolimbic system is composed of the ventral tegmental area (VTA) projections to the ventral striatum (VS)/Nucleus accumbens (NA) and pre-frontal cortex (PFC). The NA is subdivided into core (NAc) and shell (NAs) components. Other important components of this system include the amygdala (AMG), particularly the basolateral nucleus (BLA), the posterior cingulate cortex (PCC) and the orbitofrontal cortex (OFC).

Figure 6.

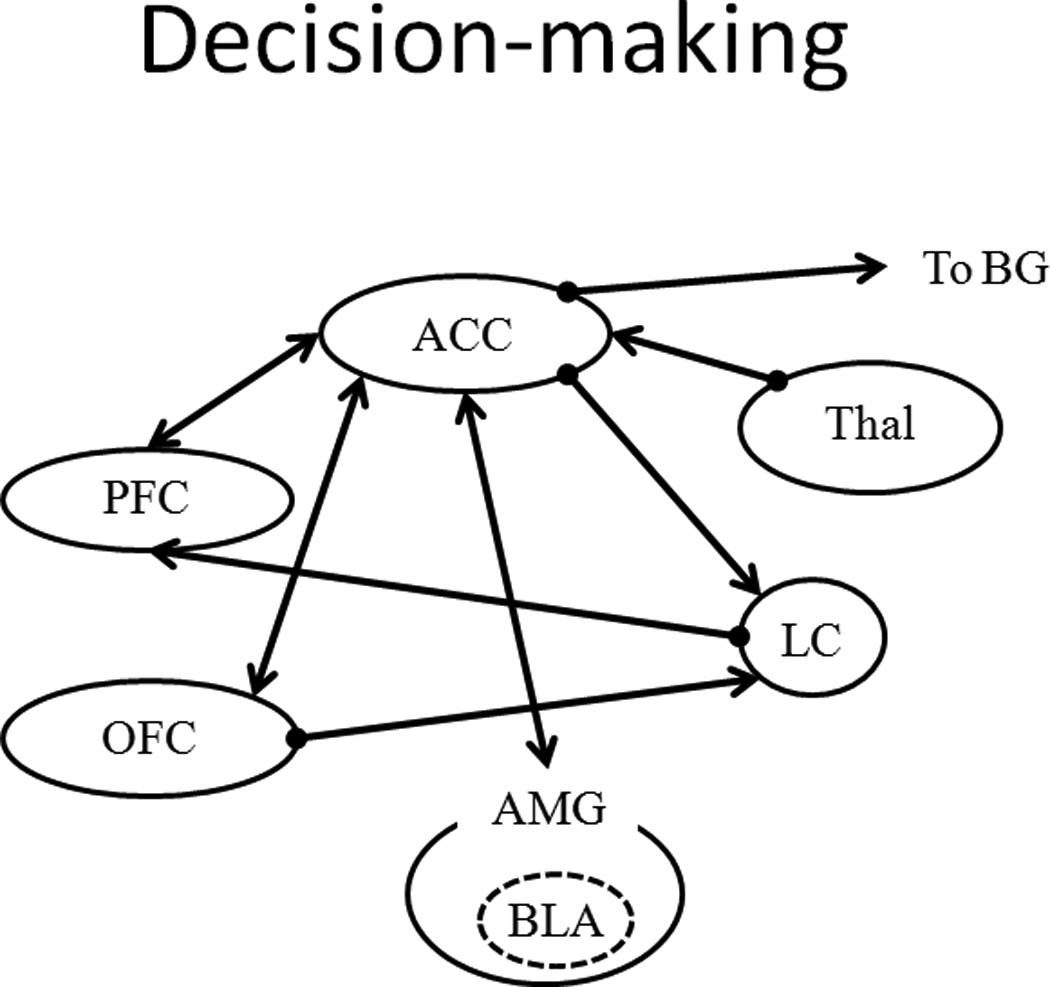
A diagram of the neural circuitry involved in the decision-making component of the reward system. Input from the thalmus (Thal) is sent to the anterior cingulate cortex (ACC), which connects to the locus coerulus, amygdala (AMG, particularly the basolateral nucleus, BSA), orbitofrontal cortex (OFC), and prefrontal cortex (PFC). Output from the ACC is sent to the basal ganglia (BG).

1.4.1. Reward prediction and valuation

The primary components of the reward prediction and valuation sub-system are situated in the mid-brain dopamine system (Figure 4). The reward prediction and valuation system is involved in reward learning and decision-making and in Pavlovian and instrumental conditioning. For example, the dopaminergic neurons in the ventral tegmental area (VTA) and substantia nigra pars compacta (SNc) have been implicated in the comparison between expected and actual rewards, or prediction error (Bayer and Glimcher 2005; Schultz 1998; Schultz, Dayan, and Montague 1997; Waelti, Dickinson, and Schultz 2001). The VTA and SNc share projections to the nucleus accumbens core (NAc) / ventral striatum (VS) which has been associated with the processing of overall reward value (e.g., Gregorios-Pippas, Tobler, and Schultz 2009) and the incentive motivational value of rewards (Galtress and Kirkpatrick 2010b; Peters and Büchel 2011). The incentive motivational valuation of rewards has also been linked to the orbitofrontal cortex (OFC; Kable and Glimcher 2009; Peters and Büchel 2010, 2011), which has bilateral connections with the NAc and areas that are associated with acquiring representations of reward value (basolateral amygdala, BLA; Frank and Claus 2006), and processing the subjective value of delayed rewards (posterior cingulate cortex, PCC; Kable and Glimcher 2007; Peters and Büchel 2009, 2011). The timing system (Figure 5) is strongly interwoven with prediction error/reward learning and has been proposed in some models to contribute directly to prediction error learning through a rate estimation process (Gibbon and Balsam 1981; Gallistel and Gibbon 2000). Furthermore, considering the connections between the OFC and the anterior cingulate cortex (ACC) and locus coeruleus (LC; Figure 6), the areas that represent the incentive motivational valuation of rewards (OFC) are also connected to the areas that are associated with decision-making (e.g., ACC, LC), which is not surprising given that decision making relies heavily on outcome valuation (or utility).

Figure 5.

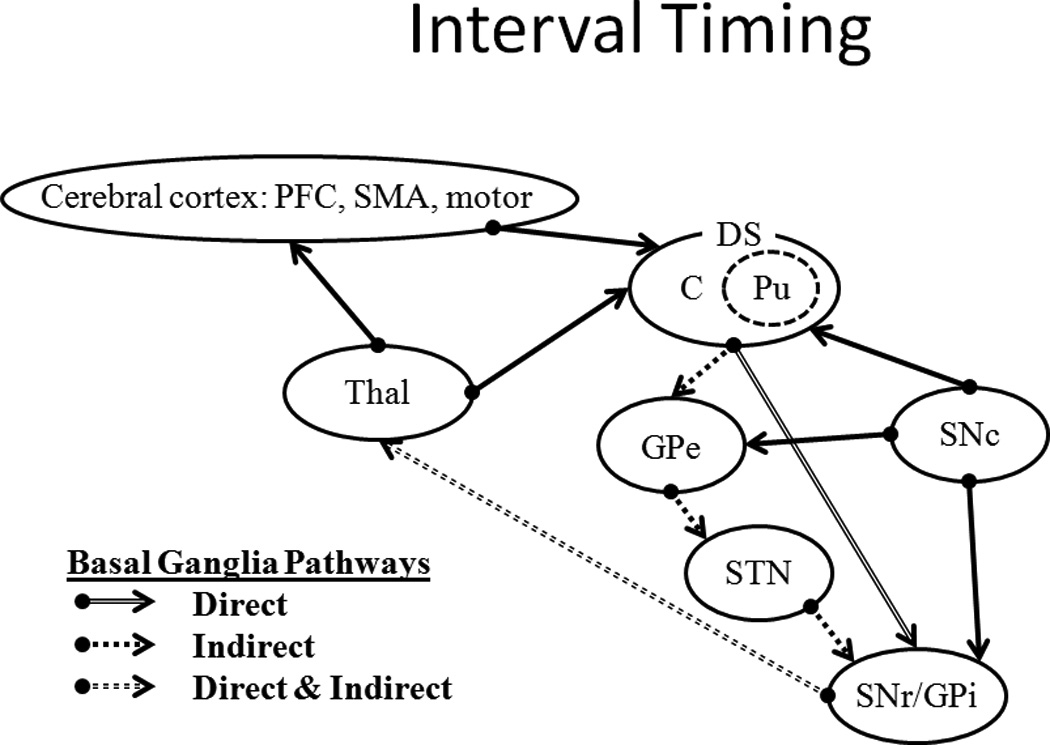
A diagram of the neural circuitry involved in the interval timing component of the reward system. Multiple areas of the cerebral cortex, including the pre-frontal cortex (PFC) and supplementary motor area (SMA) connect with the dorsal striatum (DS; both caudate, C, and putamen Pu). This system also contains the nigrostriatal connections from the substantia nigra pars compacta (SNc) to the DS. The DS sends output through a direct and an indirect pathway to the thalamus (Thal) and then onto the motor cortex. The direct pathway carries straight through the substantia nigra pars compacta/internal segment of the globus pallidus (SNr/GPi) complex to the Thal. The indirect pathway passes through the external segment of the globus pallidus (GPe) and the subthalamic nucleus (STN) before joining with the SNr/GPi complex. The SNc connects to both the GPe and SNr/GPi.

1.4.2. Interval Timing

The cortico-striatal-thalamic network is the primary system that is involved in anticipatory interval timing (Coull et al. 2004; Coull, Nazarian, and Vidal 2008; Morillon, Kell, and Giraud 2009; Nenadic et al. 2003; Rao, Mayer, and Harrington 2001; Buhusi and Meck 2005; Matell and Meck 2004; Meck 1996). The interval timing system interfaces to the reward prediction and valuation system through the shared substrates of the SNc and dorsal striatum (DS; i.e., nigrostriatal pathway), which are involved in the encoding of prediction error (e.g., Schultz 1998). The putamen (Pu) in the DS has been proposed to function as a "supramodal timer" (Coull, Cheng, and Meck 2011) that is involved in encoding temporal durations (Meck 2006; Matell, Meck, and Nicolelis 2003; Coull and Nobre 2008; Meck, Penney, and Pouthas 2008). The two pathways from the DS to the thalamus (Thal) via the basal ganglia (BG) – the direct pathway and the indirect pathway (see Figure 5) – transmit excitatory and inhibitory information, respectively, to the motor cortex. These pathways are modulated by the SNc, which results in a balance of excitation and inhibition that is important for motor timing (see Coull, Cheng, and Meck 2011, for a review). This suggests a strong relationship between temporal prediction and reward prediction, which is not surprising given that both co-occur in many Pavlovian and instrumental conditioning procedures. Pavlovian and instrumental conditioning procedures typically involve events that unfold over time, with an earlier event (stimulus or response) predicting or producing a later event (outcome/reward). Furthermore, given the role of the PFC in the updating of temporal expectations (Macar, Vidal, and Casini 1999; Morillon, Kell, and Giraud 2009; Genovesio, Tsujimoto, and Wise 2009; Coull, Nazarian, and Vidal 2008) and the connections between the PFC and ACC (Figure 6), integration of temporal information and decision-making may be associated with the ACC (e.g., Doya 2008).

1.4.3. Decision-making

Decisions are primarily accomplished by the cognitive control network (Figure 6). The ACC has bilateral connections with reward valuation substrates (see Section 1.4.1). The ACC has been implicated in a variety of different elements of decision-making including sustaining rewarded actions (Doya 2008; Kennerley et al. 2006), guiding decisions in conflict situations (Peters and Büchel 2011; Pochon et al. 2008), encoding the effort associated with rewarded responses (Doya 2008), and the adaptive adjustment of behavior (Hayden et al. 2011). Prediction error reflecting the size and probability of expected vs. obtained reward is also associated with this structure (Hayden et al. 2011), as is the encoding of the costs of responses (Cohen, McClure, and Yu 2007). Thus, it appears that the ACC is involved in many different aspects of decision-making and adjustment of behavior in reward-based learning tasks.

Given the additional thalamus-ACC and ACC-BG connections, there appears to be considerable interaction and integration of the systems involved in reward processing, interval timing, and decision making. For example, the OFC is a candidate structure for integration of information across multiple components of these systems, given its involvement in reward valuation and the connections between it and components of the interval-timing and decision-making systems. Therefore, the interaction between the systems that have been associated with motivation and timing (and, consequently, decision making) provides the foundation for the development of a psychological and neurocomputational model of the reward system that would conceivably pass the “neural plausibility” test mentioned above (Bhattacharjee 2006).

1.5. Interpretations derived from reward system circuitry

As noted in Section 1.3, current psychological timing models cannot easily account for the pattern of reward value effects on timing behavior. However, in examining the neural circuitry (see Figures 4 and 5, Sections 1.4.1 and 1.4.2), an interaction of motivation and timing is hardly surprising. Although the motivation/valuation and timing systems are separate circuits, they are heavily interconnected, so there is ample opportunity for signal information from one system to interact with processing that is occurring within the other system.

The candidate areas for involvement in the reward magnitude contrast effects on timing would be the BLA, which is associated with detection of the sensory properties of rewards (Blundell, Hall, and Killcross 2001), and the NAc which has been demonstrated to code the overall value of reward (Cardinal et al. 2001; Galtress and Kirkpatrick 2010b; Bezzina et al. 2007; Bezzina et al. 2008; Pothuizen et al. 2005; Winstanley et al. 2005; Peters and Büchel 2010, 2011). The NAc shares bi-directional connections with the SNc, the origin of the nigrostriatal pathway. The SNc projections to DS have been postulated to be one source of processing of prediction errors (Schultz, Dayan, and Montague 1997). Prediction errors are important for detection of a violation of expectancy in outcome, and would presumably be an important contributor to the reward magnitude on timing as these effects are driven by a contrast in reward magnitude than the absolute reward magnitude (Galtress and Kirkpatrick 2009). In the present studies, the prediction error signal would code the difference between expected reward magnitude and received reward magnitude. Through its bidirectional connections with the DS, the SNc provides a route for the prediction error signal to influence timing. Changes in reward magnitude could shift the peak through the SNc altering the balance of excitation and inhibition in the direct and indirect motor output pathways on a moment-to-moment basis.

The alteration of timing due to satiety manipulations appears, at least in part, to operate through a different route. Regardless of whether the test phase involved an increase in reward value (release from satiety) or decrease in reward value (induction of satiety), there was a rightward shift in the response function (see Section 1.2.1). This indicates that a change in internal motivational state produced a qualitatively different outcome from a change in reward magnitude (where increases in magnitude shift the peak to the left and decreases shift the response function to the right). This difference in pattern of results suggests that separate pathways must be responsible for reward magnitude vs. reward value changes. For the reward value changes, the most likely pathway leads through the OFC, which has been linked with processing changes in the incentive motivational value of rewards under devaluation conditions (Gottfried, O'Doherty, and Dolan 2003). The OFC would then transmit the altered reward value to the NAc, which would then send this information to the SNc, which could then regulate the timing of responding through modulation of excitation/inhibition of the BG output pathways to the Thal. Sucrose also appears to exert somewhat different effects on responding compared to food, with sucrose producing earlier start and end times even in the baseline condition. This effect is different from the baseline effect of higher magnitude reward, which produces sharper timing functions. The NAc has been implicated in sensitivity to sucrose through changes in dopamine (Hajnal, Smith, and Norgren 2004), so the effects of sucrose may bypass the OFC and operate more directly on the NAc. From that point, the NAc would alter signaling of the SNc which would regulate motor output through the DS/BG to Thal pathways. Although the proposed terminal pathways are the same in all of the reward manipulations, the input to the system would occur through different routes, thereby providing the opportunity for a qualitatively different effect of magnitude, reward preference, and reward value on responding.

The present interpretation of the results in the framework of the neural circuitry requires further refinement to determine the finer-grained mechanisms that are at work within this system that produce the motivational effects on timing. However, it seems that using the neural circuitry as a guide for interpreting results can be fruitful. In addition, it also suggests that future timing models should interface more directly with the neurobiological literature in developing the general framework for the next generation of computational models. Section 1.8 presents an approach for developing a neurobiological-based computational model of the reward system and will provide some examples where this general approach has proven successful on a smaller scale.

1.6. Extinction and the reward system

The procedure of extinction involves the omission of an expected reward following a cue (or response) that has previously preceded the reward. Therefore, in conjunction with the theme of this special issue of Behavioural Processes, it is worth considering how the neural structures associated with the presentation and timing of reinforcement relate to the brain regions corresponding to the processing of and behavior reflecting the absence of expected reinforcement.

With regard to the role of the reward system circuitry in extinction, the BLA may contribute to the encoding of an omitted reward and subsequently project this information to the OFC (Frank 2006). The absence of an expected reinforcer should result in a negative prediction error, which has been affiliated with the lateral habenula (lHAB), which is more active following the omission of an expected reward (i.e., negative prediction error) than following the presentation of reward (Matsumoto and Hikosaka 2007). On omitted-reward trials, the activity of the lHAB preceded that of the SNc, suggesting that the negative prediction errors detected in the SNc and VTA (e.g., Schultz, Dayan, and Montague 1997) may be due to the earlier activity in the lHAB (Matsumoto and Hikosaka 2007). This suggests that this neural substrate should be included in future models of reward learning and extinction. Interestingly, in connection with the present results, although extinction is another form of value change, it does not appear to alter timing in a peak procedure (Galtress and Kirkpatrick 2009; Ohyama et al. 1999). This further suggests that a different subcircuit within the reward system (most likely involving the lHAB) is responsible for the detection of and response to reward omission compared to the effects of changes in reward magnitude or motivational state. It is expected, however, that reward omission signals should still involve the same final common pathway as the other reward effects, through the NAc, SNc and BG. The involvement of the NAc in reward omission and timing is briefly discussed in the following section.

1.7. Nucleus accumbens, incentive value, and timing

When considering the neural pathways involved in reward processing (see Section 1.4), in combination with the interpretations based on the neural circuitry of the reward system in Section 1.5, the nucleus accumbens core (NAc) is a likely candidate for involvement in the motivation-timing interactions due to its purported role in determining overall reward value. Using a peak procedure task, Galtress and Kirkpatrick (2010b) demonstrated that NAc-lesioned rats did not show the leftward shift in the peak with an increase in reward magnitude found in controls and previously observed in intact animals by Galtress and Kirkpatrick (2009). There was also evidence of a deficit in response cessation as a result of reward omission during non-reinforced PI trials. This deficit in cessation of responding following expected reward on peak trials was evident in rats trained both prior to and following NAc lesions.

Additionally, Galtress and Kirkpatrick (2010b) found that NAc-lesioned rats, although not inherently impulsive when trained on a delay discounting task, did not modify choice behavior when reward magnitude was increased, resulting in a steeper discounting rate than controls. Yet, the NAc-lesioned rats did produce appropriate alterations in choice behavior when the delay to reward was decreased. Using a reward magnitude contrast procedure, it was discovered that the failure of the NAc-lesioned rats to modify behavior in response to reward magnitude change was not due to an inability to perceive the change in reward magnitude, but rather was due to impairments in incentive motivational changes in response to increases in reward magnitude.

The results of Galtress and Kirkpatrick (2009, 2010a; 2010b) coupled with Experiments 1 and 2 of the present report (see Section 1.2) indicate that a change in incentive motivational state from satiety, reward devaluation, or resulting from differing levels of reward magnitude produced effects on the timing of a delay associated with reinforcement. This interaction was evident in shifts in responding for delayed reward and reduced accuracy in temporal discrimination. The effects of reward magnitude appear to be qualitatively different from the effects of reward devaluation/inflation in that reward magnitude increase shifted the peak to the left, whereas reward inflation through release from satiety shifted the peak to the right, and satiety effects were not specific to a particular food type. At the neural level, lesions of the NAc led to deficits in behavior associated with reward value and timing (Meck 2006), impulsive choice and reward omission indicating that all of these processes are reliant on the reward valuation mechanism of the NAc. Further examinations of the neural substrates involved in the motivation-timing interactions can guide the development of future timing models. The following section provides some foundation for these future developments.

1.8. Foundations of a neurocomputational model of the reward system

An alternative approach to developing quantitative timing models is through using neurophysiological and neurochemical evidence to guide model development. This approach to modeling represents a sort of paradigm shift that is currently underway in the field, with a change in focus from models that rely on metaphors for psychological/cognitive processes to models that develop equations that embody the neural computations present within the system. There are three pieces of evidence that have featured thus far in the neurocomputational modeling toolkit to confirm existing models or develop new computational models: (1) the neurophysiology of cells within nuclei; (2) the neurotransmitter function of cells within nuclei; and (3) neuroanatomical evidence of the connections/interconnections of nuclei.

One of the most compelling examples of this approach stems from Schultz and colleagues' (Schultz 1998; Schultz, Dayan, and Montague 1997) examination of prediction error computations within the brain. In their seminal paper (Schultz, Dayan, and Montague 1997), they reported that dopamine neurons in the VTA and SNc fired in a manner consistent with encoding of a prediction error signal proposed by temporal difference models such as the Sutton-Barto model (1981), derived from more foundational linear operator models such as the Rescorla-Wagner model (Rescorla and Wagner 1972). These neurons fire immediately following unpredictable reward delivery and following the onset of a stimulus that has been previously associated with a predictable reward (but not after reward delivery if the reward is predicted). These neurons also show suppression of activity following the omission of an expected reward. Schultz and colleagues proposed a simple model in which sensory information arrives in the VTA in the form of a temporal derivative, which is the difference between the current sensory conditions and the expected conditions based on past experience -- this is the essence of prediction error. Reward information is also sent to the VTA, so that stimulus and outcome encoding are simultaneously available. The output from the VTA was proposed to consist of a sum of the reward signal and the prediction error signal on a moment-to-moment basis. Simulations based on the prediction error model matched the behavior of the dopamine neurons and also produced results consistent with behavioral outcomes in both blocking and secondary conditioning procedures.

Another interesting example is the Frank neural network model (Frank and Claus 2006; Frank 2005, 2006), a neurocomputational model of reward learning and decision-making. This model focused on neurobiological evidence to guide the construction of a neural network model that produces responses that are designed to lead to positive outcomes, while avoiding negative outcomes. The BG system is responsible for modulating responses to input stimuli. The striatum contains representations of the possible response-outcome associations for a given task and these representations compete within the internal segment of the globus pallidus. Stronger "go" representations lead to disinhibition within the Thal, which then enhances the response output in the pre-motor cortex, while also suppressing alternative response(s). The striatal responses are acquired through changes in SNc dopamine as a product of positive or negative outcomes for particular responses. The augmented model, described in Frank and Claus (2006) adds the contribution of the OFC, with the medial lateral OFC representing current outcome expectancy and biasing response selection in the pre-motor cortex. They also proposed separate sub-areas of the OFC that encode contextual information relating to previous gains and losses in a particular setting, providing a working memory representation of expectancy of outcomes that is situational-specific. This model has been shown to correctly predict behavioral outcomes in decision-making situations such as simple gambling tasks and provides a strong initial foundation for further developments of neurocomputational models of the motivation/valuation system.

While the two above examples have focused in modeling reward learning and reinforcement based decision-making, there are also timing models that have been developed using this neurocomputational approach. Two noteworthy examples are the spectral theory of timing and the SBF model. The representation of time in the spectral theory of timing (Grossberg and Schmajuk 1989) was derived from the neural response rates of dopamine neurons that results in a series of functions that increase during a timed duration at different rates. The functions mimic the accumulation of synaptic neurotransmitter levels from neurons firing at different rates coupled with habituation in the post-synaptic neuron so that the final gated signal is the sum of these two processes. Reinforcement results in the storage of a pattern of strengths of activation of each signal function, with some distortion, according to a Hebbian learning rule. The perceptual and memory functions are combined multiplicatively to translate into a graded tendency to respond. While this model has been shown to produce correct patterns of results from basic timing procedures such as the peak procedure, it does not function very effectively with temporal durations in the multi-seconds range (see, for example, Church and Kirkpatrick 2001).

The SBF model proposes that timing is accomplished by a group of pacemaker neurons/oscillators of different frequencies, spiking for brief periods in each cycle (Miall 1989). This model has been developed to serve as a biologically plausible version of SET (Matell and Meck 2004). The beat frequency of a pair of oscillators is the frequency of co-occurrence of spiking. For a group of cells, the beat frequency is the lowest common multiple of the periods of the oscillators, giving an index of the rate of coincidence. The set of oscillators are fired together at stimulus onset (the beginning of the temporal duration), but because they are all oscillating at different frequencies will quickly become desynchronized. Oscillators that are spiking at the time of reinforcement result are strengthened via a Hebbian learning rule. While this model can produce realistic timing functions, it has been criticized for lack of plausibility due to the absence of noise in the oscillator periods (but see Hab et al. 2008 for recent attempts at resolving the scalar variance problem; Almeida and Ledberg 2010), and it has been noted that it does not adequately time durations over 20 s (Matell and Meck 2004). In addition, single- and multiple-neuron recordings of striatal and cortical neurons during a two-duration temporal generalization task (Matell, Meck, and Nicolelis 2003) revealed that some cells were more responsive to the shorter duration signal (10 s) and some to the longer duration signal (40 s), suggesting that there may be encoding specialization for different durations. Subsets of neurons in the dorsolateral anterior striatum and ACC showed the greatest sensitivity to specific durations. These results suggest the need for development of modeling approaches/expansion of the SBF model to incorporate new neuroanatomical and neurophysiological evidence.

It is apparent from the examination of the neural circuitry (Figures 4–6, Section 1.4) that the reward processing, timing, and decision-making processes are heavily interconnected and form a larger integrated network that serves the function of learning about gains and losses of rewards and the stimuli that predict those outcomes (through Pavlovian and instrumental conditioning); determines the probability of reward, the overall value of reward, and the delay to reward; makes choices for gaining rewards; sustains reward-related actions; and encodes the cost and effort associated with responses for rewards, among other things. In addition, to account for the effect of motivational variables on timing, one must seek a more comprehensive modeling approach that incorporates motivation/reward processing/valuation and timing within a single theoretical framework. Successful modeling of pieces of the reward system is already underway, but it is imperative that future modeling efforts take a broader approach towards modeling the entirety of the system. As the knowledge of neuroanatomy, neurochemistry, and neurophysiology takes shape, so too will the model. There already is sufficient knowledge of the function of the circuitry of the reward system for an initial attempt at developing a computational model of the whole system. And such a model will provide a framework for integrating a wide range of phenomena within a single theoretical framework, a feat which has not been previously attempted. In addition, the development of a comprehensive model of the reward system will stimulate future behavioral and neurobiological research and will represent a major advancement of the field.

Highlights.

• *Changes in reward magnitude or value impact on interval timing
• *Current computational timing theories do not adequately account for motivational effects on timing
• *Motivational effects on timing are not surprising given the nature of connectivity within the reward system
• *A neurocomputational approach is proposed for developing a new computational model of the reward system