Extinction under a Behavioral Microscope: Isolating the Sources of Decline in Operant Response Rate

Abstract

Extinction performance is often used to assess underlying psychological processes without the interference of reinforcement. For example, in the extinction/reinstatement paradigm, motivation to seek drug is assessed by measuring responding elicited by drug-associated cues without drug reinforcement. Nonetheless, extinction performance is governed by several psychological processes that involve motivation, memory, learning, and motoric functions. These processes are confounded when overall response rate is used to measure performance. Based on evidence that operant responding occurs in bouts, this paper proposes an analytic procedure that separates extinction performance into several behavioral components: 1) the baseline bout initiation rate, within-bout response rate, and bout length at the onset of extinction; 2) their rates of decay during extinction; 3) the time between extinction onset and the decline of responding; 4) the asymptotic response rate at the end of extinction; 5) the refractory period after each response. Data that illustrate the goodness of fit of this analytic model are presented. This paper also describes procedures to 1) isolate behavioral components contributing to extinction performance; 2) make inferences about experimental effects on these components. This microscopic behavioral analysis allows the mapping of different psychological processes to distinct behavioral components implicated in extinction performance, which may further our understanding of the psychological effects of neurobiological treatments.

1. Introduction

Operant extinction refers to the substantial reduction in response rate that results from the discontinuation of a response-outcome contingency, which typically involves the elimination of the outcome. The term is often used interchangeably to refer to the change in response rate and to the discontinuation of reinforcement. The performance component of extinction—the change in response rate—is of theoretical interest, because it may express critical learning and memory processes (Bouton 2004; Killeen et al. 2009). The procedural component of extinction—the discontinuation of reinforcement—is often implemented to test the effects of treatments on behavior without the interference of reinforcement. For instance, in the extinction/reinstatement paradigm (Stewart and de Wit 1987), the ability of drug-associated cues to elicit a drug-seeking response is assessed in the absence of drug reinforcement (Pentkowski et al. 2010; Pockros et al. 2011). Extinction is also often implemented in concert with reinforcer-devaluation to establish whether responding is goal-directed or habitual (Dickinson and Balleine 1994; Dickinson et al. 1995; Olmstead et al. 2001).

Despite decades of research on operant extinction, it is yet unclear how the elimination of a reinforcing outcome causes a decline in response rate. The absence of the reinforcer has been interpreted to imply the absence of reinforcer-elicited arousal (Killeen et al. 1978; Killeen 1998); the absence of the response-outcome contingency has been interpreted to imply the acquisition of a new response-no outcome association (Bouton 2004; Rescorla 2001). How each of these psychological processes, de-motivation and extinction learning, contribute to the decline in response rate is fundamental to the construction of learning models (Podlesnik and Sanabria 2010).

The causes of extinction performance are even less clear when behavior is observed in the context of an experimental treatment. Treatment-induced reductions in cue reinstatement of extinguished responding, for example, are often interpreted as de-motivating drug-seeking behavior (Epstein et al. 2006; Fuchs et al. 1998). However, a treatment may yield similar results by interfering with the retrieval of memories linking response, cue, and drug (See 2005), by accelerating extinction learning (Leslie et al. 2004; Quirk and Mueller 2008), or by compromising the motoric ability to produce the operant response (Johnson et al. 2011).

The fact that extinction performance can be affected by several distinct psychological processes highlights the problem of using overall response rate as a unitary dependent measure. This measure is an oversimplification for two reasons. First, extinction performance is governed by a process that generates an initial response rate, and a potentially independent process that causes its decline (Clark 1959; Nevin and Grace 2000; Tonneau et al. 2000). Overall response rate confounds these two processes. Second, there is extensive evidence that operant behavior, even during reinforcement, is not unitary, but is instead organized into bouts of responses separated by relatively long pauses (Gilbert 1958). This is evident across operants (Johnson et al. 2011; Johnson et al. 2009; Shull and Grimes 2003; Shull et al. 2004), reinforcers (Conover et al. 2001; Johnson et al. 2011), schedules of reinforcement (Reed 2011), and species (Johnson et al. 2011; Johnson et al. 2009; Machlis 1977; although see Bennett et al. 2007; Bowers et al. 2008; Podlesnik et al. 2006). Operant performance is therefore determined by the rate at which bouts are initiated, the response rate within bouts, and the length of bouts. Using overall response rate as a unitary measure confounds these dissociable behavioral components.

In contrast, a microscopic behavioral analysis separates performance into its behavioral components by decomposing overall response rate into several elementary measures. This analysis allows the potential mapping of different psychological processes to distinct behavioral components. Such mapping may be accomplished, for example, by experimentally manipulating psychological variables and quantifying the resultant effects on each behavioral component (Brackney et al. 2011; Reed 2011; Shull 2004; Shull et al. 2001). Given this mapping, the effect of a neurobiological treatment on different psychological processes may then be inferred by examining its effect on the behavioral components (Johnson et al. 2011). The mapping of psychological processes to dissociable aspects of behavior is an important goal in experimental psychology and behavioral neuroscience (e.g., Ho et al. 1999; Killeen 1994; Olton 1987; Robbins 2002).

The present paper proposes an analytic procedure to dissociate the behavioral components that underlie extinction performance. The organization of reinforced behavior into bouts will serve as the starting point for a descriptive model of extinction performance; goodness of fit will be illustrated with data. The paper then describes the appropriate procedures for 1) identifying the relevant behavioral processes that contribute to the decline of response rate during extinction, 2) estimating parameter values for individual subjects and for experimental groups, and 3) establishing the credibility of differences in parameters between experimental groups.

2. The Bi-exponential Refractory Model (BERM) of Operant Performance

Empirical evidence suggests that the distribution of inter-response times (IRTs) is a mixture of two exponential distributions. This is consistent with the notion that responses are organized into bouts: one exponential distribution describes long IRTs separating bouts, and the other describes short IRTs separating responses within bouts (Shull 2004; Shull et al. 2001; Shull and Grimes 2003; Shull et al. 2004). Adding a refractory period between responses (Brackney et al. 2011; Killeen et al. 2002), the bi-exponential distribution may be expressed as

$$\begin{array}{l}Pr(\text{IRT}=\tau \mid \tau <\delta )=0\\ Pr(\text{IRT}=\tau \mid \tau \ge \delta )={\mathit{pwe}}^{-w(\tau -\delta )}+(1-p){be}^{-b(\tau -\delta )},w>b,\end{array}$$ (1)

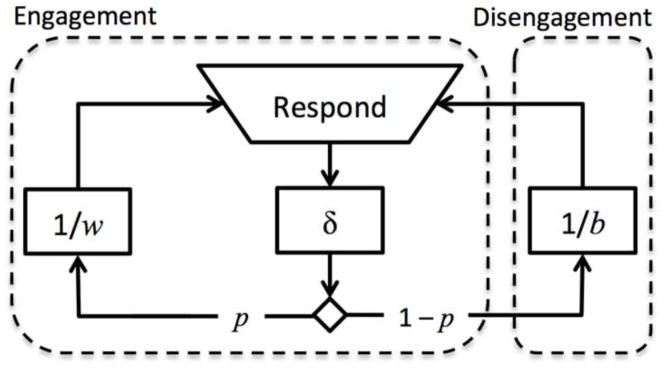
where b is the bout-initiation rate, w is the within-bout response rate, and δ is the refractory period. The necessity of δ is justified both theoretically, because each response takes a finite amount of time to complete, and empirically (Brackney et al. 2011). Because the mean IRT is the reciprocal of response rate, 1/b + δ is the mean time between bouts and 1/w + δ is the mean time between responses within bouts. p is the proportion of IRTs within bouts and 1 − p is the complementary proportion of IRTs between bouts. p is also the probability of continuing in a bout after a response¹. The mean number of responses per bout, excluding the bout-initiating response, is the bout length L, where L = p/(1 − p) (see Appendix A). Eq. 1 is called the bi-exponential refractory model (BERM) of operant performance. BERM can also be expressed as a flow chart, representing the subject cycling between states of engagement and disengagement (Fig. 1).

Fig. 1.

Flow-chart illustration of the bi-exponential refractory model (BERM) underlying Eq. 1. Solid square boxes represent times without responses; dashed boxes represent states of engagement and disengagement. BERM stipulates that every response is followed by a refractory period δ, after which the subject either remains in a state of engagement with probability p, or exits to a state of disengagement with probability 1 − p. While in the state of engagement, responses are emitted at a fast rate w; while in the state of disengagement, responses (re-engagements) are emitted at a slow rate b. As a result, performance is organized into bouts, which are consecutive responses within the engagement state.

This microscopic analysis of reinforced operant performance has allowed researchers to begin mapping psychological processes to behavioral components. For example, bout-initiation rate (b) is sensitive to changes in rate of reinforcement and level of deprivation (Brackney et al. 2011; Podlesnik et al. 2006; Reed 2011; Shull 2004; Shull et al. 2001; Shull et al. 2002), supporting the notion that changes in b can reflect changes in incentive motivation (Bindra 1978). Within-bout response rate (w) and bout length (L) are sensitive to the type of reinforcement schedule (ratio vs. interval vs. compound) (Brackney et al. 2011; Reed 2011; Shull et al. 2001; Shull and Grimes 2003; Shull et al. 2004), supporting the interpretation that changes in w and L can reflect changes in response-outcome association, or coupling (Killeen 1994; Killeen and Sitomer 2003). The refractory period (δ) is sensitive to changes in motoric demand (Brackney et al. 2011), supporting the notion that changes in δ can reflect changes in motoric capacity. It is important to note that b is also sensitive to the type of reinforcement schedule and motoric demand (Brackney et al. 2011; Reed 2011), raising the possibility that, along with incentives, schedule and motoric variables also modulate motivation to engage the operant, perhaps by functioning as a response cost (Hursh and Silberberg 2008; Salamone et al. 2009; Weiner 1964). We anticipate that a similar microscopic examination of the structure of extinction performance will allow researchers to further uncover the relationships between experimental manipulations, psychological processes and overt behaviors.

3. Extending BERM to Extinction Performance

Within the framework of BERM, the decrease of overall response rate during extinction may be due to decreases in p, w, and/or b as a function of time without reinforcement (Brackney et al. 2011). Eq. 1 is generalized to allow these parameters to change as a function of time. Let p_t, w_t, and b_t be, respectively, the proportion of within-bout IRTs, the within-bout response rate, and the bout-initiation rate, at time t in extinction. Because these parameters change as a function of time in extinction, we call p_t, w_t, and b_t the dynamic parameters. If a response was emitted at time t in extinction, then the probability that an IRT that starts at extinction time t (IRT_t) will be of duration τ can be expressed as

$$\begin{array}{l}Pr({\text{IRT}}_t=\tau \mid \tau <\delta )=0,\\ Pr({\text{IRT}}_t=\tau \mid \tau \ge \delta )=p_t{w}_t{e}^{-w_t(\tau -\delta )}+(1-p_t)b_t{e}^{-b_t(\tau -\delta )}.\end{array}$$ (2)

It is important to note that t and τ refer to two different times: t is the time in extinction at which the IRT under consideration starts, and τ is the duration of the IRT under consideration. (Note also that the time between the last response and the end of the session should also be accounted for by the model; see Appendix B).

A reasonably simple model of extinction may assume that p_t, w_t and b_t decay exponentially to zero as a function of time in extinction. This was the assumption of Brackney et al. (2011). Alternatively, L (the mean bout length) instead of p could decay exponentially. Whether L or p decays exponentially yields subtle differences in response rate that may be validated empirically in the future. For the purpose of this paper we assume that L decays exponentially, because unlike p, which has a range between 0 and 1, L has the same range as w and b, allowing us to use the same group distribution to model parameter variability between subjects (see Section 6 below). Specifically, let L₀ be the mean bout length at the beginning of the extinction, let w₀ be the within-bout response rate, and let b₀ be the bout-initiation rate. Then,

$$\begin{array}{l}{L}_t=L_0{e}^{-\gamma t}\hfill \\ w_t=w_0{e}^{-\alpha t}\hfill \\ b_t=b_0{e}^{-\beta t}\hfill \end{array}\},\begin{array}{l}0<b_0<w_0\hfill \\ 0\le \alpha \le \beta \hfill \\ L_0,\gamma \ge 0\hfill \end{array},$$ (3)

where L_t is the mean bout length at time t in extinction, and γ, α, and β are the decay rates of L₀, w₀ and b₀, respectively. We call L₀, w₀ and b₀ the baseline parameters. α is constrained to be lower than β to ensure that w remain higher than b throughout extinction. Note that the exponential function in Eq. 3 is used to describe the decay of parameters as a function of time in extinction, and not to describe the probability distribution of IRTs (cf. Eqs. 1 and 2). For simplicity, it is assumed that if a response occurs at time t and the next response occurs at t + d, then the parameters L_t, w_t, and b_t remain constant between t and t + d.

Eqs. 2 and 3 are similar to BERM (Eq. 1), except that parameter values change over time. We therefore call Eqs. 2 and 3 the dynamic bi-exponential refractory model (DBERM) of extinction performance. Note that setting the decay parameters γ, α, and β at zero would mean that L_t, w_t and b_t remain constant during extinction, and DBERM would reduce to BERM.

4. Generalizing DBERM: Initial Steady-State (c) and Asymptotic Rate (Ω)

Eq. 3 (and Brackney et al. 2011) assumes that the decline in responding starts immediately upon the implementation of the extinction contingency, and that response rates approach zero at the limit. Alternatively, it may be assumed that L_t, w_t, and b_t remain stable at their baseline levels until time c during the extinction session, at which point they begin decaying exponentially. This model can be interpreted as the animal initially responding at steady-state during extinction until it detects the change in contingency at time c. It may also be assumed that w and b decay exponentially to an asymptotic rate, Ω, that is greater than zero. Asymptotic response rate Ω is akin to the notion of operant level (Margulies 1961). These two features, c and Ω, are incorporated into Eq. 3 as follows:

$$\begin{array}{l}\begin{array}{c}{L}_t=L_0\\ w_t=w_0\\ b_t=b_0\end{array}\},\text{if}t\le c\\ \begin{array}{l}{L}_t=L_0{e}^{-\gamma (t-c)}\hfill \\ w_t=(w_0-\mathrm{\Omega })e^{-\alpha (t-c)}+\mathrm{\Omega }\hfill \\ b_t=(b_0-\mathrm{\Omega })e^{-\beta (t-c)}+\mathrm{\Omega }\hfill \end{array}\},\begin{array}{l}0\le \mathrm{\Omega }<b_0<w_0\hfill \\ 0\le \alpha \le \beta \hfill \\ L_0,\gamma ,c\ge 0\hfill \end{array},\text{if}t>c.\end{array}$$ (4)

Note that if c and Ω are set at zero, Eq. 4 reduces to Eq. 3.

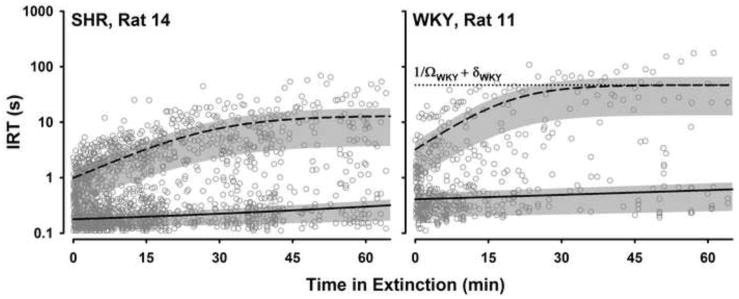
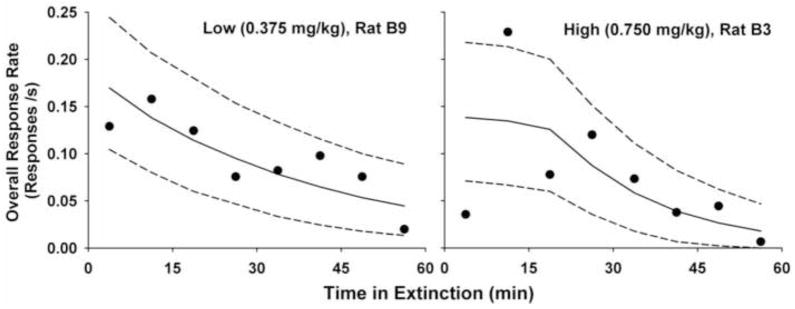
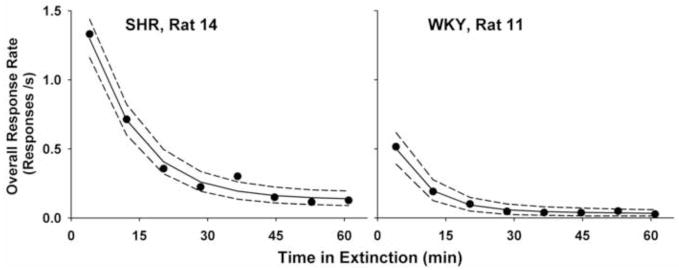
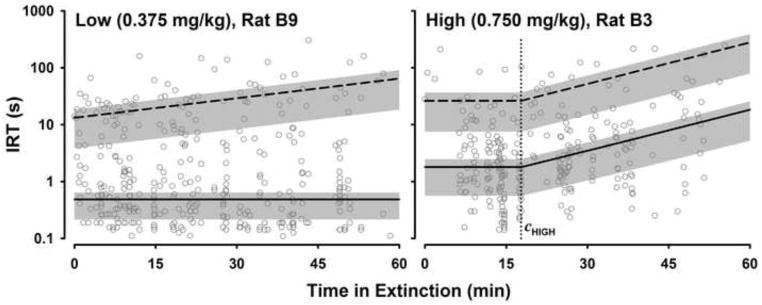
Table 1 lists all of the parameters of DBERM and their meaning. In order to illustrate the utility of DBERM in describing extinction performance, Figs. 2 to 5 present unpublished data of individual rats during the first session of extinction from two experiments. Figs. 2 and 3 are based on data from an experiment that compared extinction performance of two strains of rats: the Spontaneously Hypertensive Rat (SHR), an animal model of Attention Deficit Hyperactivity Disorder (Sagvolden 2000; Sanabria and Killeen 2008), and the normoactive Wistar Kyoto strain (WKY). In this experiment, which we call the SHR example, both groups of rats were trained on a multiple variable interval (VI) schedule of food reinforcement ranging between VI 12 s to VI 192 s. Fifty-four 65-min training sessions were conducted prior to extinction (for details see Hill et al., in press). In a different experiment, which we call the Cocaine example, two groups of rats were trained to self-administer cocaine intravenously on a simple variable interval (VI) 300-s schedule. The cocaine dose for one group was 0.75 mg/kg/infusion (high dose group); for the other group it was 0.375 mg/kg/infusion (low dose group). A minimum of thirty four 2-hr training sessions were conducted prior to extinction. Figs. 4 and 5 show performance of two rats from this experiment. Figs. 2 and 4, respectively, illustrate the utility of incorporating into DBERM a non-zero asymptotic response rate (Ω) and an initial steady-state of duration c. These two experiments (SHR and Cocaine examples) will be used to illustrate the application of DBERM to empirical data in the following sections.

Table 1.

List of model parameters and their meaning

Parameter	Unit	Meaning
δ	s	Refractory period
L0	Response	Baseline mean bout length
w0	Response/s	Baseline within-bout response rate
b0	Response/s	Baseline bout-initiation rate
γ	×10−3/s	Rate of decay of L0
α	×10−3/s	Rate of decay of w0
β	×10−3/s	Rate of decay of b0
c	s	Initial steady-state period
Ω	Response/s	Asymptote of w and b after decay

Fig. 2.

Inter-response times (IRTs) as a function of time in extinction for two rats from the SHR example, one from each group. The broken and solid lines are, respectively, traces of average bout initiation IRT (1/b_t + δ) and average within-bout IRT (1/w_t + δ) calculated using DBERM with individual parameters estimated using maximum likelihood. Bands around each line represent the interquartile range of each IRT distribution according to DBERM estimates. The dotted line shows the asymptotic IRT, (1/Ω + δ), for the WKY rat.

Fig. 5.

Overall response rate as a function of time in extinction for the two rats shown in Fig. 4 from the Cocaine example. Figure conventions are as in Fig. 3.

Fig. 3.

Overall response rate (dots) as a function of time in extinction for the two rats from the SHR example shown in Fig. 2. Overall response rate was calculated for each of the 8 equally-sized bins in the session. The solid and broken lines are, respectively, the predicted mean overall response rate and its 95% confidence interval, based on maximally-likely DBERM parameters used to generate the lines in Fig. 2. The prediction was calculated using 10000 runs of a Monte Carlo simulation. The MATLAB script used for this simulation is available for download².

Fig. 4.

Inter-response times (IRTs) as a function of time in extinction for two rats from the Cocaine example, one from each group. Figure conventions are as in Fig. 2. The dotted line shows the duration of the initial steady-state period, c, for the high-dose rat.

5. Identifying Underlying Behavioral Processes using Model Selection

DBERM has five free parameters that describe the change in response rate during extinction: γ, α, β, c, and Ω. It is possible that some of these parameters are not needed, in that they can be set at zero without decreasing goodness-of-fit substantially. For example, if response rates immediately decline at the onset of extinction, then c is not needed. If mean bout length remains constant throughout extinction, then γ is not needed. When a model has more parameters than are needed, overfitting occurs: excessive parameters describe noise rather than underlying processes, causing the model to have poor predictive properties (Babyak 2004; Hawkins 2004). One way of avoiding overfitting is to formally compare models using Akaike Information Criterion (AIC) or, preferably, its small-sample-size corrected variant, AICc (Anderson 2008; Burnham and Anderson 2002). AICc selects between models by balancing the maximized likelihood of each model (a measure of goodness-of-fit; Myung 2003) against its number of free parameters (model complexity). Higher likelihood and fewer free parameters yield lower AICc. A model’s AICc is often expressed in terms of Δ, which is its AICc minus the lowest AICc among the models compared. Δ of a model is a measure of its unlikelihood (deviance) relative to the most likely model; it is more probable that data are generated by models with lower than with higher Δ (Anderson 2008; Burnham and Anderson 2002). Δ is in a way similar to the coefficient of determination (R²) in linear regression: like Δ, R² is a measure of the goodness of fit of a more complex model (whose slope is free to vary) relative to that of a simpler model (whose slope is constrained to zero). Appendix C provides instructions for the computation of Δ. Excel spreadsheets demonstrating how to implement maximum likelihood and AICc in DBERM, together with instructions, are also available for download². For a demonstration of the application of AIC and Δ to DBERM see Brackney et al. (2011)³.

The utility of Δ in selecting between models of extinction is illustrated using our two working examples, SHR (N = 12) and Cocaine (N = 20). It was first assumed that each rat had its own set of DBERM parameters, independent from those of other rats. Model comparison was then carried out, for each example, in two phases. Phase 1 tested whether c and/or Ω were needed. This was done by comparing models that set various combinations of c and Ω to zero for all rats, while letting decay rates (γ, α, β) vary freely. Using the model selected in Phase 1, Phase 2 tested whether γ and/or α were needed and if both were equal to β. All models assumed that β was needed because there is substantial evidence that bout-initiation rate declines during extinction (Brackney et al. 2011; Podlesnik et al. 2006; Shull et al. 2002).

Table 2 shows the results of model comparison for the SHR example. Phase 1 found that the model that allowed only Ω to be free (c = 0) had the lowest Δ and was therefore selected. This means that response rate for these rats leveled out at the end of the session without completely ceasing. Moreover, allowing c to be free did not improve the fit enough to justify the increase in model complexity. This suggests that responding started to decline immediately upon extinction. In Phase 2, setting γ or α to zero led to substantially higher Δ, suggesting that L_t and w_t decayed during extinction. Also, setting γ = α = β increased Δ, suggesting that L_t, w_t, and b_t did not decay at the same rate. Therefore, only c was set at zero when estimating the group parameters for the SHR example in the next section.

Table 2.

Model comparison for the SHR example

	Model	Number of free parameters/rat	k	log(ML)	AICc	Δ
Phase 1	Default (unconstrained)	9	108	−15810	31839	22
	c = 0	8	96	−15812	31817	0
	Ω = 0	8	96	−15903	32000	183
	c, Ω = 0	7	84	−15903	31976	159
Phase 2	Default (c = 0)	8	96	−15812	31817	0
	γ = 0	7	84	−15891	31952	135
	α = 0	7	84	−15895	31960	143
	γ, α = 0	6	72	−16127	32399	582
	γ = α = β	6	72	−16084	32313	496

Note. Each model is identified by its constraints (Model column). The default model for Phase 2 is the model selected (lowest Δ) in Phase 1. The total number of observations, n, was 9542. The number of rats, N, was 12.

Table 3 shows the results of model comparison for the Cocaine example. Phase 1 found an opposite pattern to that of the SHR example: the model that allowed c, but not Ω, to be free had the lowest Δ. This suggests that it took some time before responding began to decline during extinction, and that responding would eventually cease altogether. In Phase 2, setting γ at zero gave the lowest Δ, suggesting that L_t (and thus p_t) did not decay during extinction. In contrast, setting γ = α = β increased Δ, suggesting that L_t, w_t, and b_t did not decay at the same rate. Therefore, Ω and γ were set at zero when estimating the group parameters for the Cocaine example.

Table 3.

Model comparison for the Cocaine example

	Model	Number of free parameters/rat	k	log(ML)	AICc	Δ
Phase 1	Default (unconstrained)	9	180	−10359	21097	26
	c = 0	8	160	−10440	21216	145
	Ω = 0	8	160	−10368	21071	0
	c, Ω = 0	7	140	−10445	21183	112
Phase 2	Default (Ω = 0)	8	160	−10368	21071	35
	γ = 0	7	140	−10372	21036	0
	α = 0	7	140	−10389	21070	34
	γ, α = 0	6	120	−10411	21071	36
	γ = α = β	6	120	−10418	21085	49

Note. Each model is identified by its constraints (Model column). The default model for Phase 2 is the model selected (lowest Δ) in Phase 1. The total number of observations, n, was 3521. The number of rats, N, was 20.

It should be emphasized that AICc was used in the present context to establish which free parameters were needed (i.e., could not be constrained to zero), in order to prevent overfitting. Overfitting can lead to biased parameter estimates. For example, consider a group of rats whose “true” values of Ω are zero, i.e., their response rates extinguish asymptotically to zero. Evens so, because of variability inherent to parameter estimation, a model that allows Ω to be free may fit some rats’ IRT data. Because Ω must be greater than zero, the resultant estimates of Ω will be biased upwards. Using AICc helps mitigate this problem: if a parameter is indeed spurious, then constraining it to zero will likely have little effect on data likelihood (barring model selection bias, see Anderson 2008; Burnham and Anderson 2002; Freedman 1983).

Moreover, it should be noted that not needing a parameter under one experimental condition does not imply that it is not needed under other experimental conditions. It was shown, for instance, that c could be set to zero in the SHR example but not in the Cocaine example, and vice versa for Ω. This suggests that the best estimates of c and/or Ω may be zero under particular circumstances, but not in general.

6. Comparing DBERM Parameters between Groups

Model comparison allowed the isolation of processes that are important contributors to extinction performance, which may vary from experiment to experiment. Nevertheless, this analysis did not assess experimental effects (e.g., of strain, cocaine dose) on the isolated processes. In between-group designs, effect sizes are often estimated on the basis of the difference between the means of two groups (Nakagawa and Cuthill 2007). Therefore, to assess experimental effects on model parameters, the distribution of individual parameters within each group must be described. We call this distribution the group distribution, and its parameters the group parameters. Therefore, on the first level of this two-level model, the distribution of IRTs for each animal is governed by DBERM and the animal’s individual parameters (L₀, w₀, etc.). On the second level, the distribution of individual parameters within a group is governed by the group distribution and group parameters. The group parameters are the group mean and standard deviation.

We will describe two different methods for estimating group parameters and effect sizes in DBERM. The first method, detailed in section 6.1, uses maximum likelihood and is easier to implement. It is suitable for most cases where there are plenty of IRTs from both within- and between-bout states (i.e., when p₀ is not very close to 0 or 1 and does not decay very rapidly). It is also suitable for researchers whose focus is in estimating parameters for individual rats but not for the group. The second method, detailed in section 6.2, uses Bayesian hierarchical modeling and is more complex than the first. It is suitable when some rats have very few IRTs from one of the two states, potentially causing its maximally-likely parameter estimates to be at extreme values. Hierarchical modeling allows information from other subjects in the same group to “pull” uncertain outliers back towards the group mean. Researchers using DBERM can choose between the two methods depending on the purpose of the analysis.

6.1. Parameter estimation using maximum likelihood

This method estimates individual and group parameters separately in two stages. The rationale behind this approach is that, because the maximum likelihood estimate (MLE, Myung 2003) is the best guess of the individual parameters given the selected model⁴, the MLEs of individual parameters should be treated as if they were observed data. The lines and bands in Figs. 2 and 4 were drawn using individual parameters estimated by maximum likelihood given the selected models; visual inspection suggests that MLE fitted extinction performance adequately. Figs. 3 and 5 graph the overall response rate, blocked into 8 bins, during extinction. The lines are the predicted overall response rate (± 95% confidence interval) using the same MLEs of individual parameters. For the SHR example (Fig. 3), where there were many responses, the prediction matches data very well. The data was scarcer and less orderly for the Cocaine example (Fig. 5). Visual inspection suggests, however, that DBERM predictions capture the dynamic changes in overall response rate adequately.

After individual parameters have been estimated using maximum likelihood, group parameters and effect sizes can be estimated in a subsequent stage. Assuming independence between model parameters, inferences can then be made on each of the parameters of interest using standard techniques such as t-tests, ANOVA, or p-rep (Killeen 2005; Sanabria and Killeen 2007). This two-stage approach has been implemented in previous studies (Brackney et al. 2011; Johnson et al. 2011; Johnson et al. 2009). Independence between DBERM parameters is assumed for simplicity, because the estimation of the group mean of each DBERM parameter does not depend on its covariance with other parameters.

Although it is conventional to use the normal distribution to describe between-subject variability, the parameters in DBERM are bounded below by zero, whereas the normal distribution is not. Because of this, the distribution of individual parameters is often positively skewed, violating the assumption of normality. We therefore recommend log-transforming individual parameter estimates before assuming normality and conducting inferential statistical analyses. This approach implies that the non-transformed parameters are log-normally distributed (Limpert et al. 2001). See Appendix D for details about the implications of using the log-normal distribution.

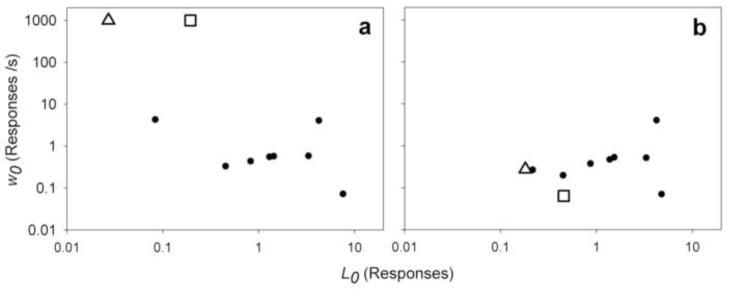
The maximum likelihood method outlined above is a simple and effective way of estimating both individual and group parameters when there are many IRTs from each of the two exponential mixtures (i.e., within- and between-bout IRTs). Nonetheless, this method can break down when one of the exponential mixtures has very few data points. This is because the maximum likelihood method treats estimated individual parameters as observed data points, although they were inferred from observed IRT data. This method therefore ignores the inherent uncertainty associated with estimating the individual parameters. For example, if a rat produces short bouts (low L₀), the estimates of parameters related to within-bout responding (i.e., w₀ and α) for this rat would be based on very few data points, because most of the IRTs separate bouts, not responses within bouts. The MLE of these parameters can sometimes be at extreme values, but this can be misleading: because these estimates are based on few data points, their uncertainty can be large (e.g., Kessel and Lucke 2008; Langton et al. 1995). These extreme estimates of individual parameters can result in unreliable estimates of group parameters. Fig. 6a, from the Cocaine example, shows the occurrence of two extreme values of w₀ due to this problem. One way to avoid this problem is to increase the bout length during training by imposing a tandem ratio requirement after the VI schedule (Brackney et al. 2011; Reed 2011; Shull et al. 2001; Shull and Grimes 2003; Shull et al. 2004). The method outlined below offers another way of estimating parameters that is more robust against uncertain outliers.

Fig. 6.

Demonstration of shrinkage by Bayesian hierarchical modeling. Rats are from the high dose group of the Cocaine example. L₀: mean bout length. w₀: within-bout response rate. a) Point estimates of individual parameters using maximum likelihood. Estimates of w₀ are capped above at 1000 responses/s. b) Point estimates of individual parameters using Bayesian hierarchical modeling. Two outliers (white triangle and white square) are highlighted. Note that data are plotted on log-log scale due to the assumption of log-normal variability for L₀ and w₀.

6.2. Parameter estimation using Bayesian hierarchical modeling

This method uses hierarchical modeling (Gelman et al. 2004) to reduce the impact of extreme and uncertain individual parameter estimates. In this approach, for each model parameter (e.g., L₀), the corresponding individual parameters (e.g., L₀ for rat 1, L₀ for rat 2, etc.) are modeled as latent variables sampled from a log-normal group distribution. Using a hierarchical model structure implies that the estimation of a rat’s individual parameters is no longer influenced only by its own IRTs, but also by the parameter estimates of other members of the group and its distribution. Because the estimation of group parameters uses data from every rat in the group, this allows partial sharing (pooling) of data across rats. For example, if a rat’s L₀ is very low, its estimate of w₀ from its data alone would be imprecise. But if other rats in the group have more precise estimates of w₀, then it is more probable that the original rat’s w₀ is close to the group mean than at some extreme value. Hierarchical modeling is a formalization of this intuition. Fig. 6b shows that imposing a hierarchical model structure allowed the two extreme unreliable estimates to be pulled towards the group mean, thereby reducing the uncertainties of the group parameter estimates (this technique is known as shrinkage; see Gelman et al. 2004).

Despite this advantage, parameter estimation in hierarchical models is not a simple undertaking. It requires ones to calculate the likelihood of data (i.e., IRTs) averaged (marginalized) over all possible combinations of individual parameters. This is achieved by first calculating data likelihood for each combination of individual parameters and then weighting it by the likelihood of those individual parameters given group parameters. This involves the calculation of a high-dimensional integral that is usually difficult to solve analytically. A popular technique to estimate parameters in hierarchical modeling is to use Markov Chain Monte Carlo methods (MCMC) combined with Bayesian inference (Gelman et al. 2004). A brief overview of Bayesian hierarchical methods follows, but for an in-depth treatment of Bayesian methods, see Gelman et al. (2004); for an account focused on Bayesian hierarchical modeling aimed at psychologists, see Griffiths et al. (2008), Shiffrin et al. (2008) and Rouder et al. (2005)⁵.

Within the Bayesian hierarchical modeling framework, each group parameter is treated as a random variable, initially distributed according to a prior distribution. In this paper, flat (uniform) prior distributions were used, due to the lack of information about group parameters before the experiment. The posterior distributions of the group parameters were then computed by updating their prior distributions with observed data using Bayes’ theorem (Gelman et al. 2004). Because the computation involves a high-dimensional integral, MCMC was used to generate samples from the posterior distribution of every parameter: at each iteration of MCMC sampling, a value for each group and individual parameter was generated. It can be shown that with enough samples, the empirical posterior distribution of the MCMC samples converges to the theoretical posterior distribution (MacKay 2003; Robert and Casella 1999). Appendix E gives the posterior probability function of DBERM used for MCMC sampling.

The generation of MCMC samples is computationally intensive and requires the use of specialized software. We have written a MATLAB script that performs group parameter estimation for DBERM that is available for download², and its details can be found in Appendix E⁶.

Once enough MCMC samples from the posterior distribution have been collected, parameters are estimated. For example, suppose we want to estimate the group mean of log-transformed b₀, denoted as μ(b₀), and its precision. First, marginalization of μ(b₀) over other parameters (i.e., individual parameters and other group parameters) is carried out by focusing on the posterior distribution of μ(b₀) alone, ignoring the joint distribution of other parameters. For the point estimate of μ(b₀), the mean of the MCMC samples of μ(b₀) is used. The precision of this point estimate can be quantified by the 95% credible interval, also known as the posterior interval. Credible intervals are the Bayesian analogue of confidence intervals (Gelman et al. 2004). The 95% credible interval of μ(b₀) can be estimated by taking the central 2.5^th and 97.5^th percentile of the MCMC samples of μ(b₀).

The next step is the estimation of effect sizes and their precisions. For example, suppose we want to quantify the effect of strain on b₀ in the SHR example. The unstandardized effect size of b₀, denoted E(b₀), is μ_SHR(b₀) − μ_WKY(b₀). In order to estimate E(b₀) and its precision, MCMC samples from its posterior distribution is first generated by calculating μ_SHR(b₀) − μ_WKY(b₀) for each MCMC sample. The point estimate of E(b₀) and its 95% credible interval can then be estimated as previously described. For the purpose of statistical inference, an effect is deemed significant if the 95% credible interval of the effect size does not envelop zero.

It is usually easier to interpret data on its original (linear) scale than on the log scale. Parameters, effect sizes, and their credible intervals can be back-transformed from the log scale to the linear scale by exponentiation. For example, if the log-transformed group mean is μ, then its back-transformed counterpart is μ′ = exp(μ). Table 4 shows the back-transformed group means μ′ and effect sizes E′ for the SHR example. μ′ is an estimate of the median of the group distribution on the linear scale; E′ is an estimate of the ratio between the group medians (see Appendix D). The credible interval of E′ is expected to include 1 if an experimental manipulation has no effect. Table 4 identifies 2 significant effects of strain on model parameters. First, the median b₀ of SHR rats was 3.2 times higher than that of WKY rats, which suggests that SHR rats initiated bouts at a higher rate at the beginning of extinction. Second, the median γ for SHR rats was 0.053 times that of WKY rats. To aid interpretation, decay rate parameters were converted to half-lives. The translation of γ into half-life shows that the half-life of L₀ for SHR rats was 350 min, 19 times longer than that of WKY (18 min), suggesting that the bout lengths of SHR rats decayed more slowly during the extinction session.

Table 4.

Group median estimates (μ′) for the SHR example.

Parameter	WKY	SHR	Effect size, E′ (ratio of SHR/WKY)
μ′ (δ)	0.12 (0.098—0.15)	0.11 (0.11—0.11)	0.90 (0.72—1.1)
μ′ (L0)	2.9 (2.0—4.2)	0.96 (0.29—3.2)	0.33 (0.093—1.2)
μ′ (w0)	2.9 (1.6—5.2)	4.1 (1.4—11)	1.4 (0.43—4.6)
μ′ (b0)	0.23 (0.13—0.40)	0.72 (0.45—1.1)	3.2 (1.5—6.6) *
μ′ (Ω)	0.028 (0.018—0.044)	0.033 (0.0065—0.12)	1.2 (0.22—4.4)
μ′ (γ)	0.63 (0.22—1.4)	0.033 (0.0011—0.20)	0.053 (0.0016—0.47) *
μ′ (α)	0.53 (0.12—1.8)	0.23 (0.033—1.0)	0.43 (0.044—3.8)
μ′ (β)	2.2 (1.1—5.6)	1.4 (0.74—2.8)	0.64 (0.21—1.67)
H(L0) (min)	18 (8.3—52)	350 (56—10000)	19 (2.1—630) *
H(w0) (min)	22 (6.6—97)	51 (11—350)	2.3 (0.27—23)
H(b0) (min)	5.1 (2.1—10)	8.0 (4.2—15)	1.6 (0.60—4.7)

Note. Estimates are rounded to 2 significant figures. The units of μ′ are in Table 1. Estimates of c were not needed, i.e., they were set to zero for all rats (see Table 2). Values in parenthesis indicate the 95% credible intervals (CI). The right-most column shows the multiplicative effect size, E′. The decay rate parameters have also been converted into half-lives (H) to help interpretation.

^*95% CI of E′ does not envelop 1.

Table 5 shows back-transformed μ′ and E′ for the Cocaine example. It identifies 3 significant effects of cocaine dose on model parameters. First, the median b₀ of the high dose group was nearly a third of that of the low dose group, suggesting that rats in the high dose group initiated bouts at a lower rate at the beginning of extinction. Second, both low and high dose group’s c were much greater than zero, suggesting that responding in both groups persisted for at least 10 min before beginning to decline. Moreover, the median c was twice as long for the high dose group relative to the low dose group, suggesting that responding for rats in the high dose group remained at baseline levels for longer before decaying. Third, the median β of the high dose group was 3.7 times that of the low dose group, which suggests that once bout initiation rate began to decline for the high dose group, it did so more quickly. Translating into half-life, this meant that once b_t started declining, its half-life was 4.7 min for the high-dose group, about a quarter of that of the low-dose group (18 min).

Table 5.

Group median estimates (μ′) for the Cocaine example.

Parameter	Low dose	High dose	Effect size, E′ (ratio of Low/High)
μ′ (δ)	0.10 (0.070—0.15)	0.11 (0.051—0.32)	1.1 (0.46—3.3)
μ′ (L0)	1.1 (0.54—2.0)	1.0 (0.28—3.1)	0.97 (0.24—3.6)
μ′ (w0)	0.60 (0.31—1.1)	0.31 (0.084—0.98)	0.51 (0.12—1.9)
μ′ (b0)	0.038 (0.022—0.064)	0.013 (0.0052—0.032)	0.35(0.12—0.99)*
μ′ (c)	1100 (600—1600)	2100(1500—2900)	2.0 (1.2—3.8)*
μ′ (α)	0.14 (0.019—0.40)	0.59(0.060—1.6)	4.1 (0.30—44)
μ′ (β)	0.65 (0.41—1.0)	2.4(0.78—8.6)	3.7 (1.1—14)*
H(w0) (min)	80 (29—640)	20 (7.4—190)	0.25 (0.023—3.3)
H(b0) (min)	18 (11—28)	4.7 (1.3—15)	0.27 (0.069—0.92)*

Note. Notations are as in Table 4. Estimates of γ and Ω were not needed, i.e., they were set to zero for all rats (see Table 3).

Finally, posterior estimates of individual parameters can be calculated from MCMC samples using the procedures already described. The data points in Fig. 6b are the posterior means of log-transformed individual parameters that have been back-transformed to the linear scale.

7. Implications for Theories of Extinction

The two examples above illustrate how DBERM can capture behavioral components of extinction performance that are not visible by inspecting overall response rate alone. The organization of operant behavior into bouts appears to be a robust phenomenon in rodents (Brackney et al. 2011; Conover et al. 2001; Johnson et al. 2011; Johnson et al. 2009; Reed 2011; Shull and Grimes 2003; Shull et al. 2004), and evidence suggests that this microstructure persists into extinction (Brackney et al. 2011; Mellgren and Elsmore 1991; Shull et al. 2002). DBERM allows the quantification of this microstructure by establishing the rate at which each the dynamic parameters (L_t, w_t, and b_t) decay during extinction. This in turn allows extinction to be studied in much closer detail.

In this section we will use the SHR and Cocaine examples to illustrate how DBERM may be utilized by researchers to gain insight into putative psychological constructs that can contribute to extinction performance and to generate novel predictions. For example, L has previously been interpreted as being related to the strength of the response-outcome association (Brackney et al. 2011; Reed 2011; Shull et al. 2004). If L remained constant throughout extinction, this may imply that the response-outcome association remained intact during the extinction session. This appeared to be the case for the SHR group and for both groups in the Cocaine example, but not for the WKY group. The parameter c, which estimates the duration of the steady-state period at the beginning of extinction, may be influenced by the time at which an animal detects the extinction contingency. If this were the case, one would predict that training under a leaner VI schedule would lead to a longer c, and this might contribute to the well-known partial reinforcement extinction effect (Nevin 1988; Shull and Grimes 2006). Another account of extinction, behavioral momentum theory (Nevin and Grace 2000; Nevin et al. 2001), posits that the magnitude and quality of a reinforcer is positively related to the resistance to extinction (see also Dulaney and Bell 2008; Shull and Grimes 2006). To the extent that this can be generalized to within-session extinction, it may be expected that training using a higher-valued reinforcer would increase c and/or decrease the rate of decay of one or more of the baseline parameters. The Cocaine example provides some evidence that the complete picture may be more complex: a higher dose of cocaine increased c but also increased the rate at which bout initiations decayed afterwards.

Interestingly, the Cocaine example suggests that baseline bout initiation rate, b₀, was lower for rats trained on a higher dose of cocaine. Previous experiments found that bout initiation rate decreases with reduced motivation or reinforcement rate (Shull 2004; Shull and Grimes 2003; Shull et al. 2004), raising the possibility that rats trained on the high dose of cocaine may be less motivated for cocaine at the beginning of the session. This might have been due to increased exposure to chronic cocaine in the high dose group causing decrease in general motivation when off-drugs. Alternatively the high dose group could have been engaging in more competing behavior at the beginning of the session (e.g., greater conditioned locomotor activity). Again, novel predictions can be generated that can test these competing hypotheses. If the high dose group had a lower b₀ due to greater chronic cocaine exposure reducing general motivation, then one may predict the following: if cocaine exposure was equalized between groups, for example by i) training rats to perform response 1 for a high dose of cocaine and response 2 for a low dose of cocaine, and ii) during extinction exposing the animals to only one of the two response operanda, then the baseline bout initiation rate for the rats extinguishing the high-dose response would no longer be slower than that of the other group (indeed it may even be faster). Alternatively if the lower b₀ of the high dose group was caused by increased competing conditioned locomotor activity, the corresponding difference in locomotor activity between dose groups should be observed.

Although the focus of analysis of the two illustrative examples was the differences in parameters due to experimental manipulations within each experiment, the analysis also revealed some differences between experiments. For instance, c was not needed in the SHR example, whereas γ and Ω were not needed in the Cocaine example. There are multiple potential reasons for this difference: the two experiments differed in terms of schedules of reinforcement (multiple vs. simple), types of reinforcer (food vs. cocaine), and strains of rat. However, it should be noted that DBERM was expanded to include Ω and c after visual inspection of data suggested that 1) the overall response rate in the SHR example did not decay asymptotically to zero; and 2) the overall response rate in the Cocaine example remained roughly steady at the beginning of extinction for a period before declining. This means that inferences about Ω and c were made post hoc. Although a previous report that response rate does not decline immediately at the beginning of an extinction session provides a priori reasons to consider c (Tonneau et al. 2000), future replication experiments would increase our confidence that c and Ω are indeed features of extinction performance. Furthermore, if the effect of a high cocaine dose on c and β was indeed due to a high dose of cocaine being more valued, then one would predict that similar effects will be found when the value of a natural reinforcer such as food is manipulated by altering the reinforcer magnitude.

It is important to note that DBERM is, at this stage, primarily a descriptive model. Despite that, DBERM is already showing potential utility in linking meaningful aspects of extinction performance to experimental manipulations and psychological processes, as illustrated by the two examples. Indeed, the systematic manipulation of experimental conditions is often interpreted in terms of psychological processes. For instance, the effect of food deprivation is often interpreted as increasing the motivation for food incentives (Hodos 1961). By examining the effects of experimental manipulations on DBERM parameters, the latter may be ultimately linked to meaningful psychological processes (cf. Brackney et al. 2011). Such mapping may further our understanding of the psychological effects of neurobiological treatments. For example, when it is found that a pharmacological treatment reduces drug-seeking behavior in the extinction/reinstatement paradigm, it is important to establish that the behavioral effect is at least in part due to the treatment reducing the motivation to seek the drug instead of through therapeutically less interesting mechanisms such as impairing motoric capacity. If, for instance, future experiments demonstrate that c is positively and uniquely related to reinforcer magnitude, then pharmacological treatments that reduce c may be interpreted as making the reinforcer subjectively smaller.

Microscopes allowed the subcomponents of a cell—e.g., cell membrane, nucleus, organelles—to be identified, and the function of a cell has since been understood in terms of the functions of the subcomponents and their interactions. Similarly, a microscopic analysis of behavior allows the subcomponents of behavior—its “natural lines of fracture” (Skinner 1935) —to be identified. The current challenge is to identify the psychological processes underlying each behavioral component, and how the components interact to give orderly behavior on a macroscopic scale (Herrnstein 1970; Killeen 1994; Nevin and Grace 2000). The microscopic analysis of extinction performance outlined in this paper, together with macroscopic analyses of extinction that examine overall response rate across time-blocks and sessions (Dulaney and Bell 2008; Podlesnik and Shahan 2010), are two complementary approaches for understanding the causes of extinction.

Highlights.

• A novel model separating extinction performance into its behavioral components.

• We illustrate the use of the model with two working examples.

• We describe procedures to identify underlying behavioral processes.

• We describe procedures to estimate model parameters for inferences.

• We provide examples of potential mappings of psychological processes to behavior.

Appendix A

Relating L (mean bout length) to p (proportion of within-bout IRTs)

Let us assume that the rat emitted m responses during extinction, i.e., there are m − 1 IRTs that ended with a response. Because p is the proportion of within-bout IRTs, there are p × (m − 1) within-bout responses and (1 − p) × (m − 1) bout initiations. The ratio of within-bout responses to bout initiations is therefore p/(1 − p) to 1. In other words, there are on average p/(1 − p) within-bout responses for every bout initiation. Therefore the mean bout length, L, is also p/(1 − p). Note that L ranges from 0 to +8. If L_t is the mean bout length and p_t is the proportion of within-bout responses at time t in extinction, then solving for p_t, we obtain

$$p_t=\frac{L_t}{L_t+1}.$$ (A.1)

Appendix B

Probability of intervals that do not end with a response

The very last interval in extinction sessions typically does not end with a response. The probability of observing this interval must also be accounted for by an accurate model of extinction. If, for example, a rat responds at a steady pace for the first half of the session and then ceases responding completely for the second half, neglecting the last interval would erroneously suggest steady responding for the entire session.

Given a response at time t during extinction, the probability that another response is not emitted after a duration τ is the same as the probability that the duration of the eventual IRT that would have ended with a response is greater than τ:

$$\begin{array}{l}Pr({\text{IRT}}_t>\tau \mid \tau <\delta )=1,\\ Pr({\text{IRT}}_t>\tau \mid \tau \ge \delta )=p_t{e}^{-w_t(\tau -\delta )}+(1-p_t)e^{-b_t(\tau -\delta )}.\end{array}$$ (A.2)

Appendix C

Calculation of AICc

AICc first requires the maximum likelihood of each model to be estimated. Maximum likelihood (Myung 2003) entails calculating the probability of the data given the model—i.e., model likelihood—and then adjusting model parameters until likelihood is maximized. Because every IRT is assumed to be independent of every other IRT, the probability of the data given the model is the product of: i) the probability of every IRT produced by every rat (Eqs. 2–4), and ii) the probability of every interval not ending with a response at the end of the session (Eq. A.2), given each rat’s model parameters. For this paper, the calculation of likelihood for AIC_c was done using spreadsheets from Microsoft Office Excel 2007. The solver add-in was used to estimate maximally likely parameters. A spreadsheet template that allows the user to carry out MLE for DBERM, as well as the Excel spreadsheets used for the two working examples, are available for download².

AICc is calculated as follows (Anderson 2008; Burnham and Anderson 2002):

$$\text{AICc}=-2log(ML)+2k+\frac{2k(k+1)}{n-k-1},$$ (A.3)

where ML is the maximized likelihood of the model, and n is the total number of observations (i.e., total number of IRTs plus intervals not ending with a response, summed across rats). k is calculated as the number of free model parameters for each rat multiplied by the number of rats. For example, if the model allowed p₀, w₀, b₀, α, β, Ω and δ to vary freely for 12 rats, then k = 7 × 12 = 84.

When selecting among a set of models, the model with the lowest AICc (AICc_min) represents the best balance between likelihood (high ML) and parsimony (low k). Furthermore, the AICc difference for model i, denoted as Δ_i = AICc_i − AICc_min, provides a measure of empirical support relative to the “best” model. The likelihood of the best model relative to model i can be calculated as exp(½ Δ_i). Because the estimate of Δ_i is meaningful, the use of cutoff values analogous to that of significance levels is not recommended (Anderson 2008; Burnham and Anderson 2002). However, as a rough rule of thumb, we may consider models with Δ_i > 4 to have weak empirical support, models with Δ_i > 10 to have little support, and models with Δ_i > 15 to be very implausible, relative to the best model (Anderson 2008; Burnham and Anderson 2002).

Appendix D

Log-normal distribution of parameters among rats

There are several advantages of assuming that parameters are log-normally distributed among rats within each group: 1) a log-normal distribution can closely mimic the shape of a normal distribution when data are symmetric, but it can also fit data that are positively skewed, 2) the support of a log-normal distribution mirrors that of the model parameters (i.e., positive numbers), and 3) the reciprocal of a log-normal distribution is also a log-normal distribution. The latter advantage implies that parameter variability will be log-normal regardless of whether rates (e.g., bout-initiation rate, decay rate) or time constants (e.g., mean pause time between bouts, half-life of decay) serve as dependent variables. Because the log-normal distribution requires the variable to be nonzero, all parameters estimates were capped below at e⁻¹⁵, which for practical purposes can be treated as zero (a decay rate of e⁻¹⁵ per second equates to a half-life of 26 days).

The group distribution of any parameter (e.g., w₀) may be characterized by two group parameters, its mean, μ(w₀), and its standard deviation, σ(w₀). μ may then be back-transformed onto the linear scale by exponentiation: μ′ = exp(μ). μ′ is the estimate of the median, not the mean, of the group distribution on the linear scale (Limpert et al. 2001). The advantage of using the median as a summary statistic instead of the mean is that, if the distribution is symmetric, it equals the mean, but if the distribution is positively skewed, it is a more representative statistic than the mean because the probability density around the median would be higher. The confidence interval of μ′ should be calculated by first estimating the confidence interval of μ on the log-scale before back-transforming to the linear scale.

For any two groups of animals, e.g., SHR vs. WKY, the unstandardized effect size on the log scale is E = μ_SHR − μ_WKY. The null hypothesis assumes that E = 0. Hypothesis testing should be carried out on the log-scale because it is on the log-scale that parameters are assumed to be normally distributed. However, it is worth noting that the back-transformed effect size, E′ = exp(E) = exp(μ_SHR)/exp(μ_WKY), is a measurement of the ratio of the two medians. The null hypothesis assumes that E′ = exp(0) = 1. The confidence interval of E′ should also be calculated by first estimating the confidence interval of E on the log scale before back-transforming.

The standard deviation on the log scale, σ, can also be back-transformed into σ′ = exp(σ). σ′ determines the skewness of the log-normal distribution, and is known as the multiplicative standard deviation: one can expect 95% of the parameters on the linear scale to fall between μ′/(σ′)^1.96 and μ′×(σ′)^1.96, analogous to the 95% of parameters on the log scale that fall between μ±1.96σ (Limpert et al. 2001). However, neither σ nor σ′ is the focus of our working examples, and for the sake of brevity their estimates are not reported in this paper.

Appendix E

Posterior density function for MCMC sampling

In order to calculate the posterior density function of the group and individual parameters, several pieces of information are needed. Let us assume that there are N subjects in the group:

1. We will use the vector θ_j to denote the individual parameters of rat j, where θ_j contains the entire set of the rat’s parameters (L₀, w₀, etc.). We will use f(D_j|θ_j) to denote the probability density function of rat j’s data (D_j) given θ_j. f(D_j|θ_j) is the product of the probability of every IRT of rat j given θ_j, and is calculated by substituting Eq. 4 into Eqs. 2 and A.2.

2. We will use the vector y to denote the entire set of group parameters (y contains μ(L₀), μ(w₀),…, σ(L₀), σ(w₀),…). We will use h(θ_j|y) to denote the probability function of an individual’s parameters given the group parameters. In our model, we assume the log-transformed individual parameters to be normally distributed, and that they are independent from each other. If we use η(x|μ, σ) to denote the probability function of x given that it is normally distributed with mean μ and standard deviation σ, then:

   $$h({\mathit{\theta }}_j\mid \mathit{y})=\prod _x\eta \left(log(x_j)\mid \mu (x),\sigma (x)\right),$$ (A.4)

   where x is a placeholder for model parameters, μ(x) and σ(x) are the mean and standard deviation of x. The product is taken over all x that are needed, as determined by model comparison. For parameters that are not needed (e.g., c for the SHR example, γ and Ω for the Cocaine example), there is no variability because individual parameters are all fixed at zero. We therefore treat the group distribution for those parameters as having a point mass at log(−∞) = 0, and η(x|μ, σ) for those parameters is 1.

3. We will use q(y) to denote the prior probability function of group parameters. Because we assume uniform prior distributions for each of the group parameter, the prior parameters simply consists of a lower bound (B_l) and an upper bound (B_u) for group parameters. The prior probability function of group parameters is therefore:

   $$\begin{array}{ll}q(\mathit{y})=k,\hfill & \text{if}{\mathit{B}}_l\le \mathit{y}\le {\mathit{B}}_u\hfill \\ q(\mathit{y})=0,\hfill & \text{otherwise}\hfill \end{array}$$ (A.5)

   where k is a constant greater than zero, and it does not depend on y.

The posterior probability of all individual parameters (θ) and group parameters (y), given observed data (D), Pr(θ, y|D), can be obtained using Bayes’ theorem:

$$Pr(\mathit{\theta },\mathit{y}\mid D)=\frac{Pr(D,\mathit{\theta },\mathit{y})}{Pr(D)}.$$ (A.6)

Because Pr(D)—the marginal probability of data given model—does not depend on the specific values of θ and y, we can ignore it and rewrite Eq. A.6 as:

$$Pr(\mathit{\theta },\mathit{y}\mid D)\propto Pr(D,\mathit{\theta },\mathit{y}).$$ (A.7)

Thus information about the shape of the posterior distribution is completely contained in Pr(D, θ, y), which is the joint probability of data and parameters, and can be calculated using the following identity:

$$\begin{array}{l}Pr(D,\mathit{\theta },\mathit{y})=Pr(D\mid \mathit{\theta },\mathit{y})·Pr(\mathit{\theta }\mid \mathit{y})·Pr(\mathit{y})\\ =\left(\prod _{j=1}^{N}f(D_j\mid {\mathit{\theta }}_j)h({\mathit{\theta }}_j\mid \mathit{y})\right)·q(\mathit{y}),\end{array}$$ (A.8)

Note that the expression on the second line utilizes the fact that the probability of data given individual parameters is conditionally independent of group parameters, i.e., Pr(D|θ, y) = Pr(D|θ).

Eq. A.8 is used by MCMC to generate samples of θ_j (for each rat) and y from the joint posterior density. At each iteration of MCMC sampling, a value for each of the parameter in θ and y is generated, and it can be shown that with enough samples the empirical posterior distribution of the MCMC samples converges to the theoretical posterior distribution (MacKay 2003; Robert and Casella 1999).

Note that as long as the group parameters are within the upper and lower bounds set by the prior, q(y) is flat and therefore does not affect the shape of the posterior distribution. The priors (B_l and B_u) used in the SHR and Cocaine examples are shown in Table A.1. c (duration of initial steady state, used only in the Cocaine example) was upper-bounded by the session length, 3600 s. Decay rates were upper-bounded by 1/s, which equates to a half-life of 0.7 second, and were lower-bounded by exp(−15)_/s, which equates to a half-life of 3.8 × 10⁴ min. In a subsequent analysis of the SHR example (Brackney et al. in submission) this bound was lowered to exp(−20)/s, which equates to a half-life of 5.6 × 10⁶ min. It should be noted that despite the differences in priors, the two analyses of the SHR example reached the same conclusion.

Table A.1.

Upper and lower bounds for group parameters

Group Parameter	Lower bound (Bl)	Upper bound (Bu)
μ(L0), μ(w0), μ(b0), μ(δ), μ(Ω)	−15	15
μ(γ), μ(α), μ(β)	−15	log(1)
μ(c)	−15	log(3600)
σ(all parameters)	10−10	105

Note. B_l and B_u also served as prior parameters. Note that B_l and B_u are in log units. Individual parameters were constrained between exp(B_l) and exp(B_u) for their respective μ parameters, with the exception of δ, which was upper-bounded by each rat’s minimum observed IRT.

MCMC protocol

The MCMC sampler used in this paper was a single-chain single-variable slice sampler (Neal 2003) programmed in MATLAB. Parameter expansion (Gelman 2006; Gelman et al. 2008) was used when sampling the standard deviation parameter σ of the group distribution for each model parameter. The following MCMC protocol was used for the SHR and Cocaine examples. A burn-in of 1000 samples was first generated and discarded. 20000 samples were then generated. Geweke’s (Geweke 1992) test was then used to verify MCMC convergence (see also Cowles and Carlin 1996; Ntzoufras 2009). If the samples failed the convergence test, the initial 250 MCMC samples were discarded, and another 500 samples were generated, and the samples were re-tested for convergence. This continued until convergence was reached. MCMC variance (required for Geweke’s test) was calculated using overlapping batch means method, with a batch length factor of 0.5 (Flegal and Jones 2010). The final number of MCMC samples generated was 22750 (SHR example) and 20000 (Cocaine example).