CEST phase mapping using a Length and Offset VARied Saturation (LOVARS) scheme

Abstract

Chemical exchange saturation transfer (CEST) MRI is a promising new technique for cellular and molecular imaging. This contrast allows the detection of tumors and ischemia without the use of gadolinium as well as the design of microenvironment-sensitive probes that can be discriminated based on their exchange contrast properties and saturation frequency. Current acquisition schemes to detect and analyze this contrast suffer from sensitivity to spatial B₀ inhomogeneity and low contrast-to-noise-ratio (CNR), which is an obstacle to widespread adoption of the technology. A new method to detect CEST contrast is proposed here, termed “Length and Offset VARied Saturation” or “LOVARS”, which acquires a set of images with the saturation parameters varied so as to modulate the exchange contrast. Either fast fourier transform or the general linear model can be employed to decompose the modulation patterns into separate sources of water signal loss. After transformation, a LOVARS phase map is generated, which is insensitive to B₀ inhomogeneity. When collected on live mice bearing 9L gliosarcomas, and compared to the conventional MTR_asym map using offset increment correction, the results show that LOVARS phase mapping obtains about four times higher CNR and exhibits less B₀ artifacts.

INTRODUCTION

Since the first report of Chemical Exchange Saturation Transfer (CEST) contrast in 2000(1), this imaging technology has attracted many new research studies (2–5), resulting in a number of pre-clinical (6–13) and now also clinical applications (13,14). Endogenous CEST contrast has been applied to charaterizing acute ischemia (7,15) and brain tumors (8,14,16), visualizing the concentration of tissue amide protons and their chemical exchange rate. CEST contrast has been found to relate to tumor grade (14), and allows separation of recurrent tumor from the effects of treatment (8). This contrast is also used in musculoskeletal imaging for monitoring glycosaminoglycan concentrations in cartilage (13). In addition, CEST reporter genes are being developed allowing detection of cells expressing this gene (6). An important advantage of CEST is the capability to design agents with protons at different frequencies, allowing simultaneous detection of probes with different functions (17,18). CEST probes have been designed to label virus particles (10,19), allow imaging of the kidneys (9,11), and allow the detection of peptides (17,20), drug delivery particles (4,21–23), changes in temperature (24), pH (9,25,26), and metabolite concentrations (27,28). Ultimately, for both endogenous and exogenous CEST contrast agent studies, improved detection technologies will be important to speed up the transition to widespread pre-clinical and clinical use.

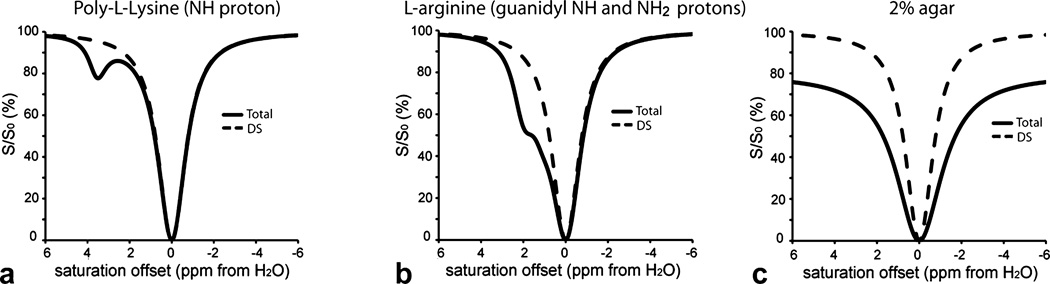
CEST contrast is produced through the application of a radiofrequency (RF) saturation pulse at the resonance frequency of the exchangeable protons, after which the resulting saturation is transferred via chemical exchange to bulk water leading to a loss in signal that yields contrast. However, the application of this pulse results in other sources of water signal loss such as due to conventional magnetization transfer contrast (MTC, mainly from solid-like macromolecules in tissue) (29,30) and direct saturation (DS) (31), complicating image analysis. In order to analyze the sources of water signal loss, it is widespread practice to plot the saturated water signal intensity (S) normalized with the intensity without saturation (S₀) as a function of saturation offset with respect to water, termed a Z-spectrum (32). As shown in Fig.1, the symmetries of the DS and MTC signals with respect to the water frequency (assigned to 0 ppm) differ from CEST. Because CEST contrast is asymmetric with respect to the water frequency, the conventional way to detect and quantify CEST contrast has been by calculating the asymmetry in the magnetization transfer ratio (MTR_asym) at the frequency of the exchangeable protons(Δ ω) :

$${\mathit{\text{MTR}}}_{\mathit{\text{asym}}}=\frac{(S(-\mathrm{\Delta }\omega )-S(+\mathrm{\Delta }\omega ))}{S_0}$$ [1]

The proton transfer ratio (PTR) (33) is a metric used to describe CEST contrast for a certain proton type in a given agent. Unfortunately the standard assumption that the experimentally determined MTR_asym equals PTR is not valid as MTC may have an inherent asymmetric component (${\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{inherent}}}$) (34,35). Moreover, the spatial inhomogeneity of magnetic field results in water frequency variations and produces artifacts (${\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{field}}}$). Therefore, the experimentally measured asymmetry is given by:

$${\mathit{\text{MTR}}}_{\mathit{\text{asym}}}=\mathit{\text{PTR}}+{\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{field}}}+{\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{inherent}}}$$ [2]

Errors in MTR_asym due to ${\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{field}}}$ contributions can be reduced by mapping the field and performing a voxel-based offset correction, which we categorized as Offset Incrementation Correction (OIC) methods. Mapping the field can be accomplished through fitting the Z-spectrum (36,37) for each pixel or through gradient echo based methods or fitting Z-spectra acquired using short, weak saturation pulses (38–40). The corrected contrast map is generated by acquiring a reduced number of images with frequencies around the proton of interest. Such types of either partial or whole Z-spectra acquisition require relatively long scan times and have the disadvantage that the CNR of the contrast map doesn’t increase as the number of offsets and the scan time increase. To partially compensate for this, CEST contrast can also be calculated by integrating over the width of the CEST peak (41,42) or using a Lorentzian line-fitting (43), but still require sweeping the offset over a wide range. Recently an additional method has been proposed (44) which utilizes two saturation frequency alternating to cancel out the ${\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{field}}}\text{ and }{\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{inherent}}}$.

Figure 1.

Simulations of the Z-spectra produced by solutions containing either CEST (PLL or L-arginine) or conventional MTC agents (Agar) to display the symmetries of the various contributions to saturation signal loss. a) Z-spectrum of PLL (solid line) in PBS and second without contrast agent (dash line). b) Z-spectrum for L-arginine (solid line) in PBS and second without contrast agent (dash line). c) Z-spectrum for 2% Agar (solid line) in PBS and second without contrast agent (dash line).

We propose here a different approach, termed Length and Offset VARied Saturation (LOVARS), in which the length (t_sat) and offset (Δω) of the saturation pulse is varied to cosine modulate the water signal loss and impart differential phases on the three different components of the asymmetric MTR contributions (PTR, ${\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{inherent}}},\text{ and }{\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{field}}}$). This allows their separation using post-processing techniques similar to those for analyzing time-varying signals in fMRI (45–51), such as the general linear model (GLM) to identify modulation patterns or fast fourier transform (FFT) to separate different frequency components. We tested the LOVARS scheme in vivo on mice bearing 9L gliosarcomas, which is known to produce a well-characterized endogenous CEST (amide proton transfer, APT) contrast (52).

THEORY

The sources of water signal loss upon application of a saturation pulse (MTC, PTR, DS) can be described using modified Bloch equations (29,33,53–55). The t_sat-dependence of CEST contrast (PTR) can be modeled using (33):

$$\text{PTR}(t_{\text{sat}})=\frac{k_{\mathit{\text{sw}}}·\alpha ·{\mathit{X}}_S}{{\mathit{R}}_{1w}+k_{\mathit{\text{sw}}}·X_S}\times [1-e^{-(R_{1w}+k_{\mathit{\text{sw}}}·X_s)t_{\mathit{\text{sat}}}}]$$ [3]

with k_sw the unidirectional exchange rate from solute protons to water protons, X_S the concentration of the solute exchangeable protons, R_1w the spin-lattice relaxation rate of water, α the saturation efficiency. This expression has been used to measure k_sw for poly-L-lysine (PLL), dendrimers, and other CEST agents in vitro (17,56) based on this exponential buildup as a function of t_sat (56).

Saturation pulses also produce a direct loss in water magnetization due to saturation of water protons. The longitudinal magnetization after applying an RF pulse in the absence of CEST agent can be modeled (54,57):

$${\mathrm{M}}_{\mathrm{z}}({\mathrm{t}}_{\text{sat}})=\frac{[{(R_2+{\mathrm{\alpha }}_1)}^2+\mathrm{\Delta }{\mathrm{\omega }}^2](R_1+{\mathrm{\alpha }}_1)}{{\mathrm{\alpha }}_1({\mathrm{\alpha }}_1-{\mathrm{\alpha }}_{\mathrm{2}})({\mathrm{\alpha }}_{\mathrm{1}}-{\mathrm{\alpha }}_3)}{e}^{{\mathrm{\alpha }}_1·t_{\mathit{\text{sat}}}}+\text{cos}(\frac{\sqrt{3}}{2}(A-B))\frac{[{(R_2+{\mathrm{\alpha }}_2)}^2+\mathrm{\Delta }{\mathrm{\omega }}^2](R_1+{\mathrm{\alpha }}_2)}{{\mathrm{\alpha }}_2({\mathrm{\alpha }}_2-{\mathrm{\alpha }}_1)({\mathrm{\alpha }}_2-{\mathrm{\alpha }}_3)}{e}^{[\frac{-(2R_2+R_1)}{3}-\frac{A+B}{2}]t_{\mathit{\text{sat}}}}$$ [4]

where ${\alpha }_1=\frac{-(2R_2+R_1)}{3}+A+B,{\alpha }_2=[\frac{-(2R_2+R_1)}{3}-\frac{A+B}{2}]+i\frac{\sqrt{3}}{2}(A-B)\text{and},{\mathrm{\alpha }}_3={\mathrm{\alpha }}_2^{*}$ in which $A=[-\frac{\mathrm{b}}{2}+{\sqrt{\mathrm{c}]}}^{\frac{1}{3}},B=[-\frac{\mathrm{b}}{2}-{\sqrt{\mathrm{c}]}}^{\frac{1}{3}},b=\frac{1}{27}(R_1-R_2)[2{(R_1-R_2)}^2+18{(\mathrm{\Delta }\omega )}^2-9{\omega }_1^2],c=\frac{1}{27}\{{[{(\mathrm{\Delta }\omega )}^2+{\omega }_1^2]}^3+{(R_1-R_2)}^2(2{(\mathrm{\Delta }\omega )}^2[2{(\mathrm{\Delta }\omega )}^2+{(R_1-R_2)}^2]-{\omega }_1^2[\frac{{\omega }_1^2}{4}+5{(\mathrm{\Delta }\omega )}^2])\}$. Eq.[4] shows that the buildup of DS with t_sat is related to the relaxation rates for water (R₁, R₂), Δω, and ω₁. As shown in Eqs.[3,4], the PTR and DS contrast dependencies on t_sat are different and we will show later using both simulations and experiments that MTC also possesses a different dependence on t_sat.

Design of LOVARS Scheme

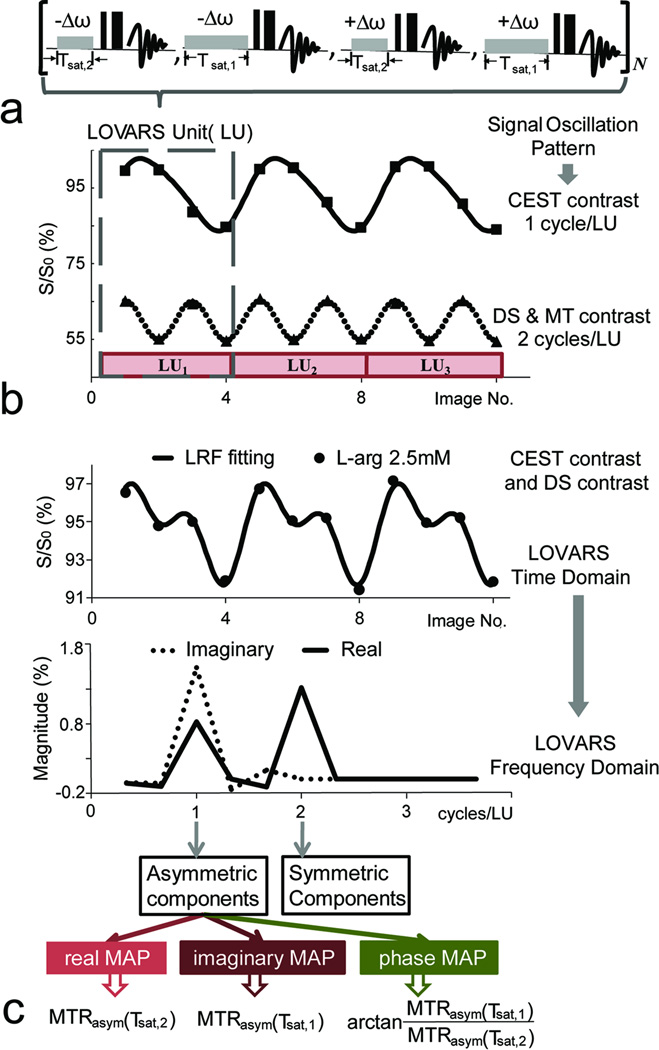
Based on the knowledge that CEST, DS and MTC behave differently as a function of t_sat and using the symmetry properties of DS and MTC (predominantly symmetric) and CEST (asymmetric) around the water resonance, the LOVARS imaging scheme was designed (Fig. 2). For this scheme, we acquire a series of images using N LOVARS’ Units (LUs) with four images within each LU (Fig.2a):

$$[{\mathrm{S}}_1,{\mathrm{S}}_2,{\mathrm{S}}_3,{\mathrm{S}}_4]=[\mathrm{S}(-\mathrm{\Delta }\mathrm{\omega },{\mathrm{T}}_{\text{sat},2}),\mathrm{S}(-\mathrm{\Delta }\mathrm{\omega },{\mathrm{T}}_{\text{sat},1}),\mathrm{S}(+\mathrm{\Delta }\mathrm{\omega },{\mathrm{T}}_{\text{sat},2}),\mathrm{S}(+\mathrm{\Delta }\mathrm{\omega },{\mathrm{T}}_{\text{sat},1})]$$ [5]

where S(−Δω, T_sat,2) represents the image signal with a saturation pulse with offset −Δω and length T_sat,2. Two different offsets are used: 1) +Δω, on resonance with the exchangeable protons and 2) −Δω, on the opposite side of water from the exchangeable protons, and two different t_sat values, a longer one (T_sat,1) and a shorter one (T_sat,2). Assuming no B₀ inhomogeneity (Fig.1), DS and MTC are mostly symmetric and therefore the signal loss for +Δω and −Δω are the same for a given t_sat resulting in 2 oscillations/LU as shown in Fig.2b. In contrast, for CEST agents such as PLL, signal loss occurs when the saturation pulse is on resonance with the protons (+Δω) and not when the pulse is on the opposite side of water (−Δω), leading to only 1 oscillation/LU (Fig.2b).

Figure 2.

Illustration of the LOVARS acquisition scheme depicting the oscillation patterns produced in water signal. a) The variation in saturation image LOVARS collection pattern is displayed, with both saturation offset (Δω), and length (t_sat) manipulated in a LU, with N total units collected (either 3 or 4 in this study). b) The resulting signal patterns produced on either 5 mg/mL PLL (upper, solid squares) or 4% agar (lower, solid triangles) with the data fit using Eq.[6]. CEST contrast oscillates at 1 cycle/LU and DS and MTC oscillate at 2 cycles/LU. c) The LOVARS signal patterns for L-arginine (2.5mM), Δω = 1.8 ppm, containing both CEST and DS contrast, with the data fit using Eq.[6]. The time domain data is transformed to the LOVARS frequency domain, generating the new LOVARS parameters for each voxel: real, imaginary and phase values.

Considering the combined contributions of CEST, DS, and MTC, the pattern of water signal can be represented by the LOVARS Response Function (LRF):

$${\mathrm{S}}_{\text{LRF}}={\mathrm{A}}_0+{\mathrm{A}}_1·\text{cos}[\mathrm{\pi }/2(\mathrm{m}-1)+\mathrm{\phi }]+{\mathrm{A}}_2·\text{cos}[\mathrm{\pi }(\mathrm{m}-1)]$$ [6]

where ‘m’ is the image number in the LOVARS time series (m=1,2,…,4XN) after acquiring N LUs, cos (π/2(m−1)+φ) represents the asymmetric components of the contrast (Eq.[1]) and cos(π (m−1)) represents the symmetric components of the contrast (Fig.1c) with respect to frequency offset. In addition, A₀ represents the mean water signal (DC bias), A₁, A₂ are amplitudes of the two cosine functions with different frequencies, and φ is the phase of the cosine modulation at the frequency of 1 cycle/LU. These parameters can be determined using either GLM or FFT. Figs.2b&c show the LOVARS signal pattern for PLL and L-arginine respectively, with both fit to Eq.[6]. The pattern for PLL is predominantly due to CEST contrast. For L-arginine the pattern contains both CEST and DS effects due to the closeness of the exchangeable protons chemical shift to water (1.8 ppm).

LOVARS Post-Processing

The LOVARS scheme creates modulations in the water signal that can be analyzed in multiple ways. One possibility is to FFT the signal intensity in the LOVARS time series to determine the contributions of CEST contrast (Fig.2c). According to the Discrete Fourier Transform of the acquisition pattern in Eq.[5] (normalized by S₀), for the nth LU (n=1,2,…,N), the transformed signal in LOVARS frequency domain is:

$$\mathrm{L}(k)=\frac{1}{S_0}{\displaystyle {\sum }_{l=1}^4}{S}_{l,n}·e^{(-\frac{2\pi i}{4})·(l-1)k}$$ [7]

where k is in units of cycles/LU and l is the image index within one LU. For k = 1 cycle/LU, expanding Eq.[7] using $e^{(-\frac{2\pi i}{4})·(l-1)}=\text{cos}(-\frac{2\pi i}{4})·(l-1)+i·\text{sin}(-\frac{2\pi i}{4})·(l-1)$ gives:

$$\begin{array}{cc}\mathrm{L}(1\text{cycle}/\text{LU})\hfill & =\frac{1}{S_0}[(S_{1,n}-S_{3,n})-i(S_{2,n}-S_{4,n})]=\frac{1}{S_0}[S(-\mathrm{\Delta }\omega ,T_{\mathit{\text{sat}},2})-S(+\mathrm{\Delta }\omega ,T_{\mathit{\text{sat}},2})]-i[S(-\mathrm{\Delta }\omega ,T_{\mathit{\text{sat}},1})-S(+\mathrm{\Delta }\omega ,T_{\mathit{\text{sat}},1})]={\mathit{\text{MTR}}}_{\mathit{\text{asym}}}(T_{\mathit{\text{sat}},2})-{\mathit{\text{iMTR}}}_{\mathit{\text{asym}}}(T_{\mathit{\text{sat}},1}).\hfill \end{array}$$ [8]

L(1 cycle/LU) relates in a straightforward manner to MTR_asym. The imaginary part of L(1 cycle/LU) corresponds to the MTR_asym produced using the longer saturation pulse, MTR_asym (T_sat,1), while the real part corresponds to the MTR_asym using a shorter saturation pulse, MTR_asym (T_sat,2). The relative phase between these two amplitudes (φ) is determined by tan(φ) = MTR_asym(T_sat,1)/MTR_asym(T_sat,2). When the two saturation lengths are chosen such that for CEST contrast: PTR(T_sat,1) > PTR(T_sat,2), while for MTC or DS: ${\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{field}}}({\mathrm{T}}_{\text{sat},1})\le {\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{field}}}({\mathrm{T}}_{\text{sat},2})$, the phase can be considered a new CEST contrast parameter that accounts for differences in the t_sat-dependence between PTR, ${\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{inherent}}}\text{ and }{\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{field}}}$ (Eq.[2]). Alternatively, GLM (commonly applied in fMRI) can be used to process the images using Eq.[6] as a model.

MATERIALS AND METHODS

Simulations

To estimate the optimal saturation parameters for LOVARS, we performed simulations on two different CEST contrast agents: PLL and L-arginine, using the numerical solutions for 2-pool and 3-pool models, respectively (55,56). The PLL simulations were performed as described previously (56). The L-arginine simulations were performed using two solute pools ’a’, chemical shift difference = 1.1 ppm (amine), and ‘b’, chemical shift difference = 2 ppm (guanidyl amine) and a water pool ‘w’. The Bloch equations were written in the general form dY/dt = A*Y + b (17,55,56) and solved using MATLAB (The MathWorks, Inc., Natick, MA, USA). Based on fitting the three pools in L-arginine at 11.7T, the relaxation rates are: R_1w=0.3sec⁻¹, R_1a=R_1b=0.71sec⁻¹, R_2w=1sec⁻¹, R_2a=32sec⁻¹ and R_2b=50sec⁻¹, and the exchange rates are k_aw=150sec⁻¹, k_bw=800sec⁻¹ and k_ab=100sec⁻¹ with the saturation B₁=3.8µT. For 10mM L-arginine the relative molar concentration of exchangeable protons to water protons ([H^exch]_solute/[H]_H2O) is 0.27*10⁻³ for pool ‘a’ and 0.36*10⁻³ for pool ‘b’. For the simulations including noise, 1%, 2%, 3% Gaussian white noise with mean of zero was added to the L-arginine simulations using MATLAB function ‘randn’.

Additionally simulations were carried out to model the t_sat dependence of MTC. We simulated data acquired on agar, a model of tissue magnetization transfer, by numerically solving the Bloch equations using a 2-pool model (29,58). The Z-spectra were first simulated at several different concentrations (2%, 3% and 4%) of agar using the relaxation and exchange rates: R_1s = 1sec⁻¹, R_2s = 2.23*10⁵sec⁻¹, R_1w = 0.35sec⁻¹, R_2w = 1.3sec⁻¹, and k_sw = 176sec⁻¹. To determine the t_sat dependence of ${\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{inherent}}}\text{ and }{\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{field}}}$, we shifted the offset of the saturation pulse and calculated the difference in water signal resulting from the saturation pulse (e.g., if the water frequency is shifted by 0.1 ppm, then the original offsets +Δω and −Δω would shift to +Δω − 0.1ppm and −Δω − 0.1 ppm, respectively) as a function of t_sat.

Phantom Preparation

We prepared a phantom that includes 4 types of samples: a CEST contrast agent (L-arginine), two MTC molecular models (cross-linked bovine serum albumin(BSA) and agar) and 0.01M phosphate-buffered saline (PBS), pH = 7.4, which should only show direct saturation. All samples were dissolved in PBS and placed into 1mm capillary tubes. L-arginine (Sigma, St Louis, MO) samples were prepared at four concentrations (10mM, 5mM, 2.5mM and 1.25mM) to produce a range of CEST contrast. Crosslinked BSA samples (2.5% and 5%) were prepared using bovine serum albumin(Sigma, St Louis, MO) by heating this for 8min in a water bath at 80°C. Agar samples were prepared at concentrations of 2%, 3% and 4% w/v.

Brain Tumor Studies

Rat gliosarcoma cells (9L) were grown in standard medium, collected by trypsinization, washed, and suspended in medium at a concentration of 1×10⁵ cells/µL. Balb/c NOD/SCID male mice (6–8 weeks old; n=7, ~25g weight) were initially anesthetized in a chamber containing 4~5% isoflurane. The animals were positioned in a stereotactic device (Stoelting Lab Standard), a small midline skin incision was made to expose the skull, and a 1mm² hole was drilled 2mm to the right of the bregma. Cells (2×10⁵/2 µL) were injected into the striatum, 2.5mm ventral to the surface of the brain, slowly over a period of 3min with the syringe removed 30sec after completion to minimize back flow.

For MRI, mice were anesthetized using 0.5–2% isoflurane. Immediately following the last MRI, mice were perfused with PBS followed by 4% paraformaldehyde(PFA), brains were removed, preserved in 4% PFA at 4°C for a week, cryosectioned (25µm thick), and stained using hematoxylin and eosin (H&E).

MRI Acquisition

In vitro (phantoms)

All experiments were performed on an 11.7 T vertical bore Bruker Avance system (Bruker Biospin, Billerica, MA) with a 15mm birdcage RF coil. The imaging sequence consists of a continuous-wave (CW) saturation pulse and a rapid acquisition with relaxation enhancement (RARE) sequence (RARE factor=8). Other imaging parameters were: field of view (FOV) = 1.15×1.15cm, acquisition matrix size = 64×64, slice thickness = 0.5 mm. The scanning protocol is similar to that described previously(40). At the beginning of the session, a group of images were acquired with Δω incremented from −0.6 ppm to 0.6 ppm (0.1 ppm step), t_sat = 500 msec, B₁ = 0.5 µT, and repetition time (TR) / echo time (TE) = 2200 msec / 4.9 msec to generate the B₀ map using water saturation shift referencing (WASSR) (39). Then a second set of saturation images was collected with Δω from −5 to 5 ppm (0.3 ppm step), t_sat = 4.0 sec, B₁ = 3.8 µT, TR/TE = 6000 msec / 4.9 msec, and number of averages (NA) equals 1 to generate the Z-spectrum. Another three pairs of saturation images (NA=2), with saturation offsets of ± 1.55 ppm, ± 1.8 ppm and ± 2.05 ppm for L-arginine are collected for the contrast map using OIC. For optimizing LOVARS, images were first acquired with t_sat varied from 0.5 sec to 5 sec. The final LOVARS images used two LUs, Δω = +1.8 ppm or −1.8 ppm, T_sat,2 = 1.5 sec, and T_sat,1 = 4 sec. An image without saturation pulse (S₀) was collected as intensity reference.

In vivo

All experiments were performed on a 9.4 T horizontal bore animal Bruker Avance system with a 25 mm sawtooth coil. After acquiring T₂-weighted scout images, a 1 mm thick coronal slice at the center of the tumor was chosen for collection of both OIC and LOVARS images. The pulse sequences were kept similar to the phantom studies with the following modifications. First, WASSR B₀ map images were collected with Δω incremented from −0.5 ppm to 0.5 ppm (0.1 ppm step), t_sat = 500 msec, B₁ = 0.5 µT, TR/TE_effective = 1500 msec / 14.6 msec and NA = 2, which was used for Scheme 2 OIC maps. After this, a Z-spectrum with Δω incremented from −4 ppm to +4 ppm (0.25 ppm step or use the scheme in Table 2 of (14)) was collected using t_sat = 3000 msec, B₁ = 3 µT, TR/TE = 5000ms / 14.6 ms, NA = 1. Another 3 pairs of the saturation images (NA = 2) were collected with offsets at ± 3.25 ppm, ± 3.5 ppm and ± 3.75 ppm respectively to generate the MTR_asym map using Scheme 1 for OIC as described previously(14,36). For optimizing LOVARS, images were acquired with t_sat varied from 0.8 sec to 4 sec. The final LOVARS images used 2 LUs, Δω = +3.5 ppm or −3.5 ppm, T_sat,2 = 0.8 sec, and T_sat,1 = 3 sec. An image without saturation pulse (S₀) was collected as a reference. The remaining imaging parameters were matrix size = 128 × 64, FOV = 1.65 × 1.5 cm.

For 3 mice, for tumor identification, additional T₁-weighted (T₁-w) Gd-DTPA images were collected after tail vein injection of 0.4 mmol/kg mouse body weight Gd-DTPA (Magnevist®). T₁-w images with the same FOV and resolution were acquired prior to injection and every 30sec until 15 minutes after injection. The imaging parameters were: TR/TE = 1000msec/7msec, RARE factor = 2, and NA = 1.

MRI Post-processing

All processing was performed using custom-written scripts in Matlab as described in the supplemental information.

RESULTS

Simulations and phantom study

All simulations and phantom experiments were performed at 11. 7T.

T_sat-Dependence Features

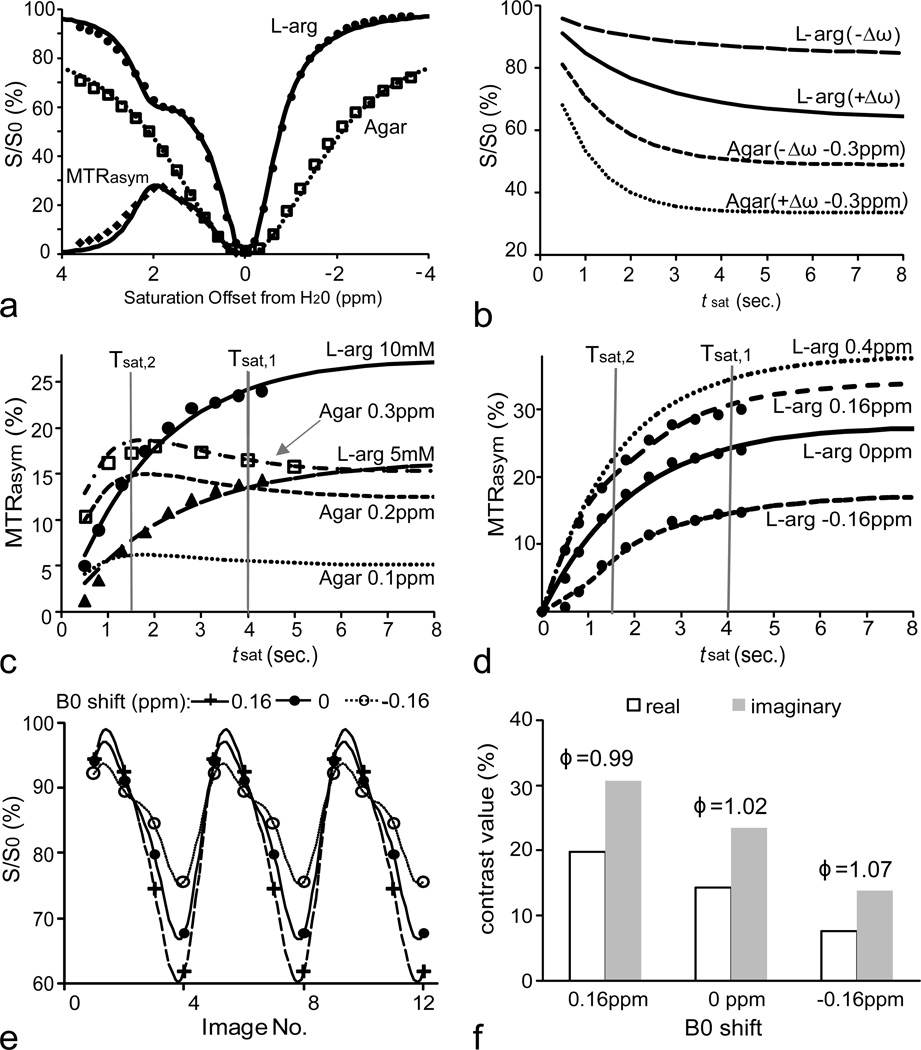
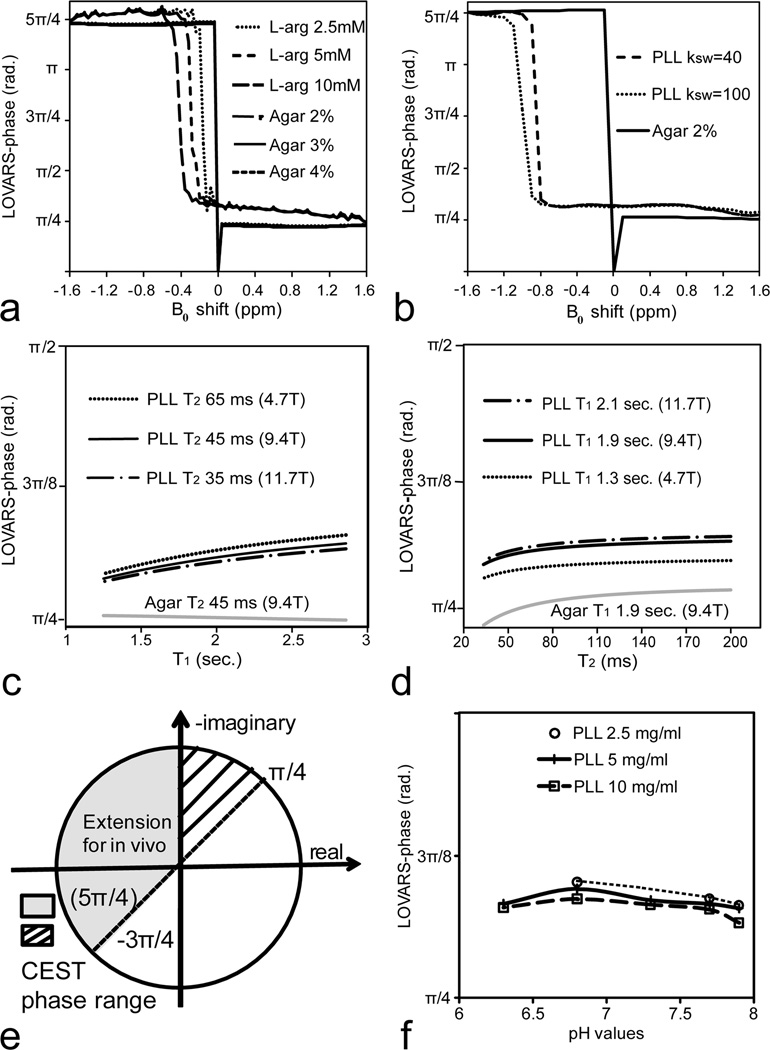
To design the LOVARS scheme (Fig.2), we collected experimental data from a phantom consisting of 1mm capillaries containing L-arginine (CEST agent) or agar (MTC agent). The simulated Z-spectra and MTR_asym (for L-arginine) curves were fit to the experimental data (Fig.3a). Additional simulations were performed to model the t_sat-dependence of the CEST and MTC agents. The simulations in Fig.3b demonstrate that for L-arginine the difference between the water signals S(+Δω)/S₀ and S(−Δω)/S₀ continue to increase with increasing t_sat. In contrast, for agar with a B₀ shift = 0.3 ppm, after t_sat exceeds 1.5sec~2sec, the separation between S(+Δω−0.3 ppm)/S₀ and S(−Δω−0.3 ppm)/S₀ no longer increases. If there is no B₀ inhomogeneity, the overall MTR_asym = 0 for agar, with B₀ inhomogeneity ${\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{field}}}$ is non-zero (Eq.[2]) leading to the overall MTR_asym ≠ 0. To determine the optimal T_sat,1 and T_sat,2 for LOVARS, we plotted the MTR_asym as a function of t_sat. After 1.5sec, the t_sat-dependence curves for agar plateau regardless of the shift in B₀ (Fig.3c). However, as shown for two different concentrations of L-arginine, the MTR_asym continues to increase. Therefore, 1.5sec was selected as T_sat,2. At T_sat = 4sec, the MTR_asym curves almost reach a maximum for L-arginine and therefore 4sec was chosen as T_sat,1. For L-arginine (10mM) with B₀ shifts 0.4 ppm, 0.16 ppm, 0 ppm, and −0.16 ppm, the curves maintain the feature of MTR_asym(T_sat,1)> MTR_asym(T_sat,2) (Fig.3d). If the LOVARS oscillation patterns are plotted and fit to Eq.[6] (Fig.3e), the phase varies <5%, (Fig. 3f), while the uncorrected MTR_asym (Imaginary component) varies 30% (+ 0.16 ppm) or 41.7% (−0.16 ppm).

Figure 3.

Comparison between 10 mM L-arginine and 2% agar phantoms at 11.7T using both experiments (symbols) and simulations (lines). a) Experimental Z-spectra (agar and L-arginine) and MTR_asym (L-arginine only) curves (symbols) and fitted (line); b) Simulations of water signal changes as function of t_sat for saturation offsets of +Δω or −Δω for 10mM L-arginine. For 2% agar the signal was plotted with saturation at +Δω −0.3 ppm and −Δω −0.3 ppm due to a water frequency shift of 0.3 ppm. c) t_sat-dependence of MTR_asym for L-arginine (10 mM and 5 mM, saturation at ±Δω) and for 2% agar with the water frequency shifted by 0.1 ppm, 0.2 ppm and 0.3 ppm. d) MTR_asym as a function of t_sat for L-arginine (10 mM) with the water frequency shifted by −0.16 ppm, 0 ppm, 0.16 ppm, and 0.4 ppm. e) LOVARS oscillation patterns and LRF fit for B₀ shifts of −0.16 ppm, 0 ppm and 0.16 ppm. f) FFT transform of patterns in e, showing real and imaginary components (and phase on top).

LOVARS phase map

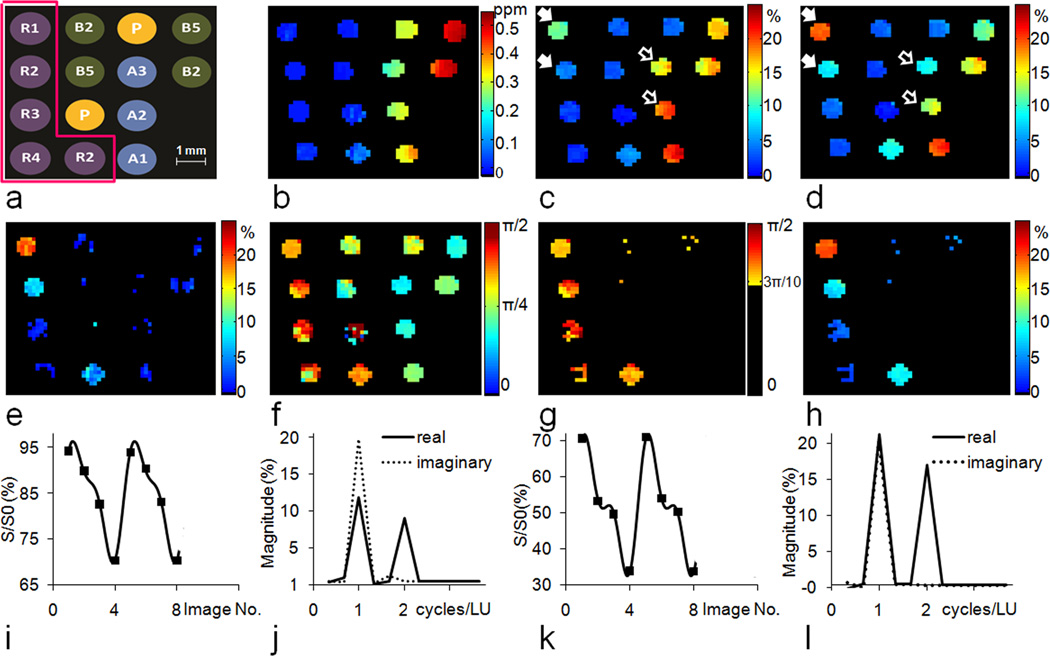
Fig.4a shows the distribution of samples in the phantom designed to test the capabilities of LOVARS, including four concentrations of L-arginine, three concentrations of agar, two concentrations of crosslinked BSA, and PBS. Fig.4b displays the WASSR B₀ map, with the B₀ shift varying from 0 to 0.5 ppm. Fig.4c and d display the MTR_asym maps at ±1.8 ppm for t_sat = 1.5sec and 4sec, respectively. L-arginine tubes are highlighted through CEST contrast (PTR) that increases from t_sat = 1.5sec to 4sec. MTC tubes also display contrast when their B₀ shift > 0.2 ppm, however this contrast (${\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{field}}}$) is either the same or smaller as t_sat increases. The OIC MTR_asym map is displayed in Fig.4e, with the high-concentration L-arginine tubes highlighted. It is difficult to detect tubes containing lower concentrations of L-arginine or to discriminate these from agar or BSA. Figs.4i&k display how the pattern of water signal can be manipulated with the LOVARS scheme for tubes containing L-arginine and agar when 2 LUs are collected. The signal patterns can be Fourier-transformed or fit to Eq.[6] (GLM), with the FFT results shown in Figs. 4j and l. After FFT, the magnitude of the real and imaginary components at 1 cycle/LU is nearly the same in the agar tubes (Fig.4l), whereas the imaginary component dominates in L-arginine tubes (Fig.4j) indicating that the LOVARS phase (φ in Eq.[6]) can be used to detect the presence of CEST contrast (PTR). Here we constrained the phase range to −π <φ<π The experimental LOVARS phase map is shown in Fig.4f. The phase for all but one of the BSA, agar and PBS tubes ≤ 3π/10, even with a B₀ inhomogeneity offset of up to 0.5 ppm, while the phase for the L-arginine tubes is >3π/10. For one PBS tube (3^rd row, 2^nd column), the phase varies widely due to MTR_asym almost equaling 0 and the noise dominates. To avoid this, the phase range of [3π/4, π] was unwrapped to [−5π/4, −π]. Fig. 4g shows only CEST tubes possess a phase within π/2>φ>3π/10, eliminating all the MTC and PBS tubes regardless of the B₀ inhomogeneity. In addition, the LOVARS contrast maps (Fig.4f–h) appear less noisy than the OIC-based MTR_asym map (Fig.4e). For quantitative comparison, Table 1 shows the number of scans, the total scan time, and the CNR for both LOVARS and OIC methods. The “CNR efficiency”, which equals the CNR divided by square root of the scan time (59), is used to evaluate the performance of the 2 methods. From the table we can see that LOVARS phase has about 2 times the CNR efficiency of the OIC method.

Figure 4.

In vitro test of the performance of the LOVARS phase mapping scheme. a) Configuration of the phantom (R1–R4: Arginine 10 mM, 5 mM, 2.5 mM and 1.25 mM at pH = 7.4, A1–A3: Agar 2%, 3% and 4%, B2: 2.5% heat crosslinked BSA, B5: 5% heat crosslinked BSA, P: 10 mM PBS; b) is the B₀ shift map obtained using WASSR; c) Uncorrected MTR_asym map, Δω = ±1.8 ppm, t_sat = 1.5 sec, which corresponds to a LOVARS real component map; d) Uncorrected MTR_asym map, Δω = ±1.8 ppm, t_sat = 4 sec, which corresponds to a LOVARS imaginary component map; The highest concentrations of L-arginine are marked by the solid white arrows, which clearly show that the CEST contrast (PTR) increases from t_sat = 1.5 sec to 4 sec. MTC tubes also highlight when the B₀ shift are larger than 100 Hz, however this contrast (${\mathit{\text{MTR}}}_{\mathit{\text{asym}}}^{\mathit{\text{field}}}$) is either the same or smaller as t_sat increases from 1.5sec to 4sec.(open white arrows) e) OIC MTR_asym map, Δω = ±1.8 ppm, t_sat = 4s; f) LOVARS phase map; g) LOVARS phase map using the thresholds described in Supplementary Material; h) LOVARS imaginary component map using the thresholds described in Supplementary Material; i) Plot of the water signal pattern produced for 8 LOVARS images (2 LUs) in the 10 mM L-arginine tube and j) Real and imaginary components after FFT for 10 mM L-arginine, with imaginary (1 cycle/LU) > real (1 cycle/LU); k) Plot of the water signal pattern produced for 8 LOVARS images (2 LUs) in a 2% agar tube with B₀ shift = 0.3–0.4 ppm and l) the corresponding real and imaginary components after FFT, with imaginary (1 cycle/LU) = real (1 cycle/LU).

Table 1.

Experimental Comparison Between LOVARS and OIC: L-arginine 10mM

	No. of scans	Scan time (sec)	aCNR		bCNR efficiency (sec−1/2)
LOVARS			phase	imaginary	phase	imaginary
	1 LU (4 scans) + 1 S0	480	28.5	23.1	1.3	1.1
	2 LUs (8 scans) + 1 S0	864	38.1	35.7	1.3	1.2
	3 LUs (12 scans) + 1 S0	1248	56.9	42.9	1.6	1.2
OIC			MTRasym		MTRasym
	B0 field map(WASSR)	221
	6 scans + 1 S0	672	21.4		0.71
	Total	893

^aCNR_contrast for a specific contrast is calculated by $\sqrt{2}\mathit{\text{mean}}(S_{\mathit{\text{contrast}}})/\mathit{\text{std}}(S_{\mathit{\text{contrast}},1}-S_{\mathit{\text{contrast}},2})$, where S_contrast,1 and S_contrast,2 are the signal intensity of two contrast maps acquired consecutively.

^b${\text{CNR efficiency}}_{\text{contrast}}={\text{CNR}}_{\text{contrast}}/\sqrt{\mathit{\text{scan time}}}$

Tolerance to B₀-shift and noise

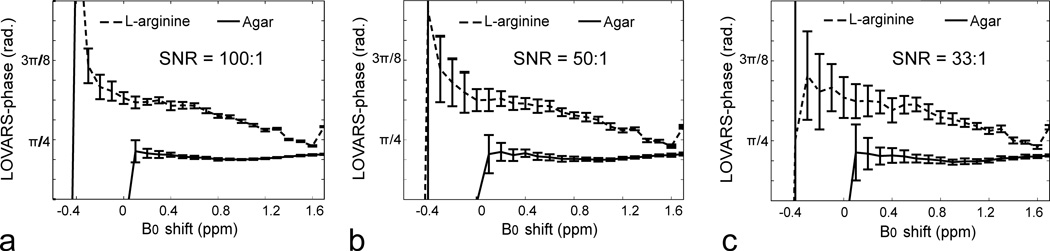
We further performed a series of simulations to test the limits of LOVARS phase mapping scheme in the presence of B₀ shifts and noise (Fig.5). Two different CEST agents were used: L-arginine and PLL, which possess exchangeable protons at 1.8 ppm and 3.6ppm separated from water, and compared with the phase value produced by the MTC agent agar. Fig.5a displays how the phase changes for three different concentrations of L-arginine and agar. The phase varies slightly with concentration and B₀ shift for L-arginine, and provided the B₀ shift is between −0.2 to +1.2 ppm, this phase can be used to discriminate L-arginine from agar using the criterium π/2>φ>3π/10. For shifts ranging from −0.2 to −1.2 ppm, L-arginine can be discriminated using the criterion φ>5π/4. Next, we determined how this scheme would perform for PLL, which has exchangeable protons twice the resonance frequency of L-arginine (Figs.1a&b) with the center at 3.6 ppm. Fig.5b shows how the LOVARS phase varies for PLL and agar using the LOVARS scheme when the saturation pulse is set at 3.6 ppm, where the LOVARS phase criterium π/2>φ>π/4 can be used to discriminate PLL from agar for a wide range of B₀ shifts (−0.8 to +1ppm). Figs.5c&d display how the phase depends on the water relaxation times, with the variation shown covering most brain tissues at field strengths of 4.7T, 9.4T and 11.7T (60). The criteria of LOVARS phase mapping are shown schematically in Fig.5e, owing to the feature of PTR(T_sat,1)>PTR(T_sat,2) >0 for phantoms and extending to PTR(T_sat,1)>PTR(T_sat,2) for in vivo imaging. We also investigated how the phase changes as a function of concentration and exchange rate through titrating three different concentrations of PLL (10 mg/ml, 5 mg/ml and 2.5 mg/ml) from pH 6.4 to 7.9 (Fig.5f). To determine how LOVARS performs as the SNR of the images change, simulations were performed at 11.7T using 2.5 mM L-arginine and 2% agar (Fig.6). Reduced SNR introduced an uncertainty in the measurement of the phase, however even with 3% noise (Fig.6c) there is a clear separation between L-arginine and agar for B₀ shifts varying up to 1.2 ppm, with a trend very similar for PBS. The phase for agar has a maximum of ~3π/10.

Figure 5.

a) Simulations of LOVARS phase as a function of B0 shift for L-arginine (10 mM, 5 mM, 2.5 mM) and agar (1%, 2%, 4%), Δω = ±1.8 ppm, with the resulting phase for all agar samples nearly identical. b) Simulation of LOVARS phase as a function of B0 shift for PLL (k_sw = 40, 100) and 2% agar, Δω = ±3.6 ppm; c) Simulation of LOVARS phase as a function of water T₁ for PLL (k_sw = 40) and 2% Agar, with T₂ set to the average rodent brain value found at 4.7T, 9.4T and 11.7T. d) Simulation of LOVARS phase as a function of T₂ relaxation for PLL (k_sw=40) and Agar 2%, with T₁ set to the average rodent brain value found at 4.7T, 9.4T and 11.7T. e) Illustration of phase range restrictions suitable for determining which pixels display CEST contrast; f) LOVARS phase as a function of pH for three different concentrations of PLL(10mg/ml, 5mg/ml and 2.5mg/ml). The exchange rates varied from ~70 Hz (pH 6.4) to ~1200 Hz (pH 7.9) for these samples.

Figure 6.

LOVARS phase as a function of B₀ shift with SNR = 100:1 (a), 50:1 (b) and 33:1 (c) respectively. The error bars indicate the SD values of LOVARS phase based on 20 different synthetic datasets using random noise.

In Vivo Imaging

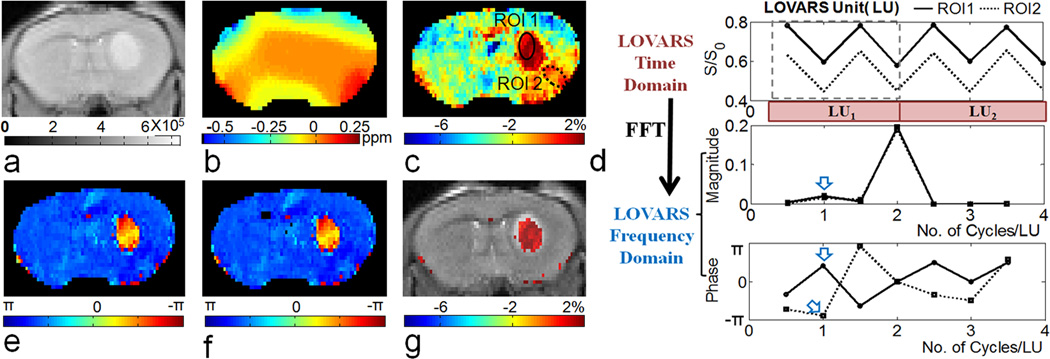
To test the performance of the scheme in vivo, we acquired LOVARS images on mice bearing 9L gliosarcomas, which are expected to show amide proton transfer contrast at an offset of 3.5 ppm. Similar to the phantom experiments, T_sat,1 and T_sat,2 were chosen based on examination of the t_sat-dependence of MTR_asym in tumor and contralateral control tissue. The average MTR_asym in tumors plateaued at a t_sat = 3 sec which we used for T_sat,1. T_sat,2 was set to 0.8sec to satisfy MTR_asym(T_sat,2) ~ 0.5 * MTR_asym(T_sat,1). Fig.7 displays images of a mouse 8 days after tumor inoculation. The WASSR map (Fig.7b) shows a typical range in B₀ shift from −0.4 ppm to 0.2 ppm across voxels in the brain slice, which distorts the MTR_asym map (Fig.7c) generated using only two images with Δω= +3.5 ppm and −3.5 ppm. The artifacts are especially prominent in the lower right hemisphere where there is normal brain tissue but water is shifted +0.2 ppm. However, when 2 LUs are acquired (8 scans) and the signal is followed for ROIs enclosing either the tumor (ROI1) or poorly shimmed control brain tissue (ROI2), as was the case for the phantoms, the LOVARS phases show a large difference between the two ROIs (Fig.7d) despite the fact that the MTR_asym (magnitude) is very similar in the uncorrected CEST map (Fig.7c). The LOVARS phase images produced using either FFT or GLM are shown in Figs.7e and f respectively. Alternatively, we can exclude the pixels with π/4>φ>− 3π/4 to threshold the imaginary component map (uncorrected MTR_asym(T_sat,1) map as in Fig.7c), displays the same information as the MTR_asym map obtained by OIC, but with all 8 images contributing to the CNR of the contrast map.

Figure 7.

In vivo demonstration of the LOVARS scheme as applied to the imaging of 9L gliosarcomas in mice. a) T2-w scout image; b) B₀ shift map (WASSR); c) uncorrected MTR_asym map; d) LOVARS time domain data (top) with phase (middle) and magnitude (bottom) traces determined through FFT with ROIs as marked in c, ROI1 = tumor region and ROI2 = control tissue with large B₀ shift. The arrows point to the average phase (middle) and magnitude (bottom) in ROI1 and ROI2 at 1cycle/LU based on FFT; e) LOVARS phase map calculated using FFT; f) LOVARS phase map calculated using GLM; g) thresholded LOVARS imaginary component map.

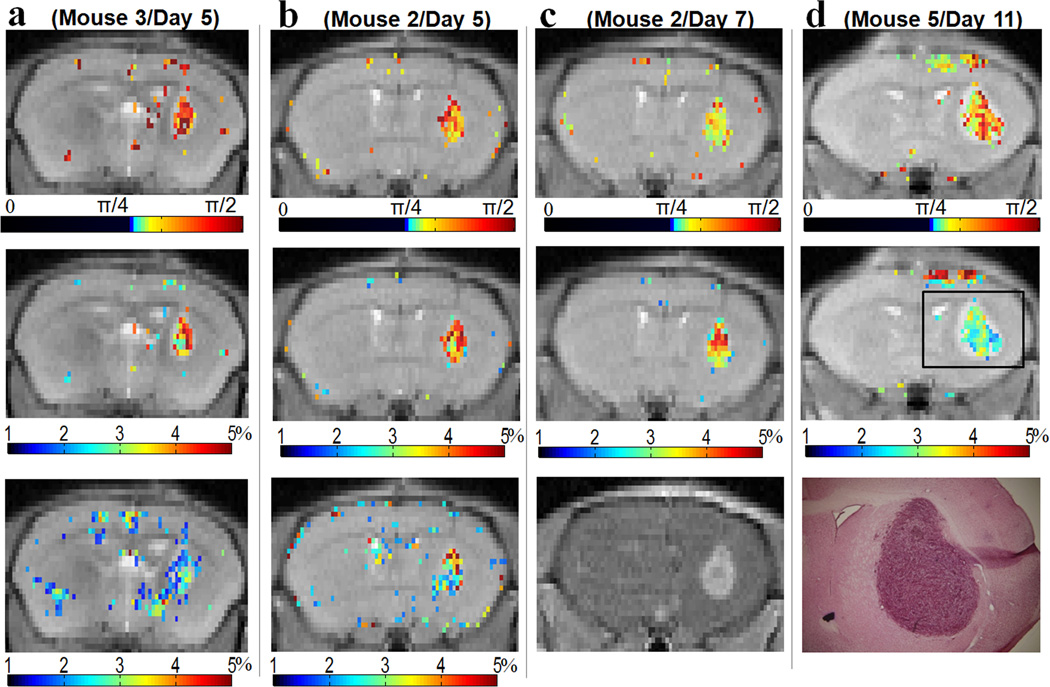
Next, we examined the variation in the LOVARS phase maps from day 5 to day 11 after cell engraftment. Tumors could clearly be detected in these LOVARS phase (Figs.8a–d: top) and filtered imaginary maps (Figs.8a–d: middle), which compared favorably to those collected using OIC (Fig.8a,b: bottom) and after administration of Gd-DTPA (Fig.8c: bottom), as validated with H&E staining (Fig.8d : bottom). As shown in Table2, LOVARS phase provides dramatic contrast for tumors (average φ = 1.12 radians or ~π/3) over normal brain tissue (average φ = −2.47 radians or ~ −4π/5), with a p-value of less than 0.001. The LOVARS contrast maps possess a higher CNR than the OIC maps, with the average CNR for the phase maps ~26.7 (2 LUs) vs. ~8.8 for OIC over the total 11 images on 7 mice and multiple days (Table 2). Table 2 also lists the scan times for LOVARS and the two OIC methods, showing that LOVARS achieves ~ 3.2 times CNR efficiency of that for OIC Scheme 2.

Figure 8.

Four representative LOVARS phase and imaginary component maps acquired 5, 7, and 11 days after tumor engraftment compared with other methods. a & b, top: LOVARS phase maps; middle: LOVARS imaginary component maps; bottom: OIC MTR_asym map obtained using 6 offsets; c)&d), top: LOVARS phase maps; middle: LOVARS imaginary component maps; bottom c: T₁-w image collected 30s after administration of Gd-DTPA; bottom d: H&E stain after tissue sectioning.

Table 2.

In vivo comparison of LOVARS and OIC for 9L tumors and control tissue

	LOVARS		OIC
	Phase (tumor)	Phase (control)	MTRasym(tumor, %)	MTRasym(control, %)
Day5/M2	1.20 ± 0.17	−2.34 ± 0.13	3.6 ± 0.8	−3.0 ± 0.6
Day5/M3	1.30 ± 0.20	−2.61 ± 0.16	2.8 ± 1.0	−3.9 ± 1.0
Day7/M2	1.12 ± 0.14	−2.01 ± 0.14	4.8 ± 0.9	−2.4 ± 0.8
Day8/ M1	1.01 ± 0.17	−2.71 ± 0.11	3.0 ± 0.4	−1.0 ± 0.4
Day8/ M3	1.10 ± 0.29	−2.23 ± 0.09	1.3 ± 0.7	−4.4 ± 0.5
Day10/M7	1.08 ± 0.22	−2.65 ± 0.13	4.8 ± 1.0	−2.0 ± 0.8
Day10/M1	0.97 ± 0.20	−2.65 ± 0.13	2.5 ± 0.7	−2.7 ± 0.6
Day11/M2	1.08 ± 0.13	−2.59 ± 0.14	5.2 ± 0.6	−1.4 ± 0.7
Day11/M4	1.06 ± 0.12	−2.48 ± 0.14	6.4 ± 0.9	−2.7 ± 0.9
Day11/M5	1.20 ± 0.25	−2.23 ± 0.15	2.1 ± 0.8	−4.5 ± 0.9
Day11/M6	1.16 ± 0.14	−2.68 ± 0.16	3.8 ± 0.7	−1.3 ± 0.9
Average value	1.12	−2.47	3.7	−2.7
aAverage CNR	26.7		8.8
Scan time (Tscan)	2 LUs		Scheme 1b	Scheme 2
	9 scans X 80 sec/scan		Zspectrum	WASSR
			25 scans X 40sec/scan	11 scans X 24sec/scan
			APT map	APT map
			7 scans X 80sec/scan	7 scans X 80sec/scan
	12 min		26 min (total)	13.7 min (total)
cCNR efficiency (sec−1/2)	1.00		0.22	0.31

^a$\mathit{\text{CNR}}=\sqrt{2}(S^{\mathit{\text{tumor}}}-S^{\mathit{\text{control}}})/\delta$, where the noise δ is the standard deviation of a 4 pixel by 4 pixel control ROI for the subtraction of 2 consecutively acquired contrast maps;

^bThe optimized offsets for the Z-spectrum were chosen according to Table 2, Reference 14.

^cCNR efficiency equals to ${\text{CNR}}_{\text{contrast}}/\sqrt{{\mathrm{T}}_{\text{scan}}};$

DISCUSSION

A new imaging scheme was constructed with the purposes of allowing the use of time domain analysis techniques to correct for B₀ inhomogeneity and achieve a higher CNR. Another time domain analysis technique for CEST has been proposed recently (61). The LOVARS scheme (Fig.2) takes advantage of the simulations we performed previously using t_sat to quantify exchange rates (56), and the large difference in symmetry with respect to the water proton frequency between CEST and MTC, DS. Alternative patterns can be chosen which produce more oscillations of MTC and DS per LU. However we decided to use this 4-point pattern based on its simplicity and efficiency (4 images produce 1 oscillation of CEST contrast and 2 oscillations of MTC and DS). We chose to test this sequence first using L-arginine, because at 1.8 ppm (L-arginine’s main chemical shift) there is a significant amount of DS (~15%), which is similar to in-vivo brain tumor studies (Figs.1b and 3a) where both MTC and CEST are present within one voxel.

For determining appropriate t_sat values for the LOVARS scheme, we used both simulations and experimental phantom data on multiple concentrations of L-arginine and agar (Figs.3b–d). In order to cosine modulate the water signal, we chose T_sat,1 = 4 sec and T_sat,2 = 1.5 sec which allowed us to produce the patterns in Figs.4i&k. As mentioned above, several LOVARS maps can be created using this imaging scheme: a real component map, an imaginary component map and a phase map. The phase map was found to be the least sensitive to B₀ inhomogeneity, and can be used to differentiate CEST from MT and DS. B₀ variation distorts the magnitude of the oscillations in LOVARS (Fig.3e) but produces very slight changes in the phase (Fig.3f). For voxels with only MT and/or DS, the phase remains nearly the same as B₀ varies from −1.6 ppm to 1.6 ppm for Agar (Fig.5a&b). For voxels possessing CEST contrast the phase remains within the CEST phase range, provided the offset of the saturation pulse is such that the pulse at least partially saturates the exchangeable protons. As such, the width at half height of the CEST contrast peak determines the tolerance to B₀ shifts. For our phantom using B₁ = 3.8 µT, the width was ~0.8 ppm (Fig.3a). Provided the B₀ variation over the image is less than this, the images produced were very clean (Fig.4g).

Another benefit of the LOVARS method is that it significantly reduces the Specific Absorption Rate (SAR) compared to OIC by decreasing the duty cycle. For our phantom experiments, the duty cycle for 1 LU (4 scans) is 45% less than for OIC, and for in vivo the duty cycle of LOVARS is 58% less than the OIC duty cycle.

One feature of the LOVARS phase map is that the phase is insensitive to concentration and exchange rate, as is shown for the 4 different L-arginine concentrations in Fig.4 and for the PLL data in Fig.5f. Here fourfold changes in concentration and sixteenfold changes in the exchange rate result in relative small changes in the LOVARS phase (φ) which are very small (<10%). For the same samples, the MTR_asym varies from 4% to 40% as shown in Fig. S2 (>90% change). This is because of the relationship of phase to PTR, with tan(φ) = MTR_asym(T_sat,1)/MTR_asym(T_sat,2) which results in removal of the prefactor $\frac{k_{\mathit{\text{sw}}}·\alpha ·X_S}{R_{1w}+k_{\mathit{\text{sw}}}·X_S}$ (in Eq.[3]). This leads to the phase being less sensitive to the exchange rate (k_sw), concentration (X_s) and water relaxation times, although the absolute value of the phase may still exhibit small changes in particular with water T₂ (Figs. 5c, d, f). In addition, the projection from tan(φ) to φ also diminishes the sensitivity. If this insensitivity is undesirable, the LOVARS phase filtered imaginary map can be displayed and this is sensitive to concentration and exchange rate.

Based on the robustness of this scheme in vitro, we moved on to testing this in mice. We chose to test this for APT imaging of 9L brain tumors as the APT contrast is well characterized (52), (~5% CEST contrast between tumor and normal tissue) and also because APT imaging of brain tumors is the first clinical application of CEST imaging, having been applied to more than 12 patients (14). We optimized this scheme on 3 mice, with several representative images shown (Figs.7 and 8). The LOVARS phase is significantly different between tumor and control tissue (Table2), and the phase map is less sensitive to B₀ than the standard MTR_asym map (Figs.7c,e,f). The LOVARS phase threshold had to be modified to exclude pixels with −3π/4<φ<π/4, because normal white and gray matter produced a negative MTR_asym at the power levels used and thus in tumors the total MTR_asym is either less negative or slightly positive. Based on all the images we have obtained, the B₀ correction range within LOVARS images was ~±0.35 ppm in vivo, above which normal brain tissue started to show contrast, compared to the ~0.8 ppm for the phantom. As a result, LOVARS is well suited for brain imaging as B₀ shifts are expected to not exceed this range for mouse brains at this field and for human brains at fields of 7T or lower. The LOVARS phase maps compared favorably to both the conventional APT image obtained using OIC and the Gd-enhanced image. We have not found meaningful differences between the FFT or GLM methods (Figs.7e&f) although this might change for other applications. In addition, the maps produced by this scheme possess a much higher CNR (Fig.8, Table 1) than conventional MTR_asym maps due to the acquisition of more LUs and the time domain post-processing, allowing each pair of images to contribute to the total CNR of the maps. We are currently investigating alternative LOVARS schemes to reduce scanning time, B₀ sensitivity, and improve the quantitative capabilities (61).

CONCLUSION

We have developed a new scheme for collecting CEST images based on saturation length and offset variations (LOVARS). Based on our results, the LOVARS phase maps showed some useful properties: 1) CEST contrast regions can be more readily identified in LOVARS phase maps as compared to conventional OIC MTR_asym maps while collecting either the same or a smaller number of images. 2) they are less sensitive to B₀ inhomogeneity than conventional approaches; and 3) every pair of images acquired contributes to the CNR of the LOVARS phase maps. When testing this method for detection of 9L gliosarcomas, the resulting images allowed a clear separation of tumor and normal tissue with a CNR four times better than conventional imaging under equivalent acquisition times. The LOVARS scheme appears well suited for use in a wide variety of in vivo CEST imaging applications.