Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2012 Mar 28;134(14):6409–6415. doi: 10.1021/ja300654t

Dispersion Energy Enforced Dimerization of a Cyclic Disilylated Plumbylene

Henning Arp 1, Judith Baumgartner 1,✉, Christoph Marschner 1,✉, Patrick Zark 2, Thomas Müller 2,✉
PMCID: PMC3336735  PMID: 22455750

Abstract

graphic file with name ja-2012-00654t_0009.jpg

By reaction of 1,4-dipotassio-1,1,4,4-tetrakis(trimethylsilyl)tetramethyltetrasilane with PbBr2 in the presence of triethylphosphine a base adduct of a cyclic disilylated plumbylene could be obtained. Phosphine abstraction with B(C6F5)3 led to formation of a base-free plumbylene dimer, which features an unexpected single donor–acceptor PbPb bond. The results of density functional computations at the M06-2X and B3LYP level of theory indicate that the dominating interactions which hold the plumbylene subunits together and which define its actual molecular structure are attracting van der Waals forces between the two large and polarizable plumbylene subunits.

Introduction

The isolation of the first stable germylenes and stannylenes was accomplished by Lappert and co-workers1,2 approximately 35 years ago, and still the chemistry of these heavier carbene analogues continues to attract the attention of both experimentally and theoretically oriented chemists.3,4

One major reason for this interest is the fundamental differences in electronic ground states, structures, and reactivities between carbenes and their dimers, i.e. alkenes, and their heavier counterparts the metallylenes and dimetallenes. Heavy metallylenes exhibit singlet ground states with an increasing singlet–triplet gap with rising atomic number.5 This is caused by the increasing energy difference between their s- and p-orbital levels and the consequential lack of orbital mixing. However, by attaching large electropositive substituents to the divalent group 14 atom to some extent they can be forced into mixing their s- and p-orbitals and thus significantly lower the singlet–triplet gap. This behavior is illustrated by Sekiguchi’s distannene (tBu2MeSi)2Sn=Sn(SiMetBu2)2 that despite bearing bulky groups on the tin atoms does not dissociate into monomers in solution.6

The tendency to form monomeric compounds is even more pronounced on descending group 14 to lead. This is well exemplified by the difference between bis[tris(trimethylsilyl)silyl]tin and -lead.7 Both compounds exist as monomers in solution, but the tin compound crystallizes as a distannene type dimer while the lead compound retains the monomeric plumbylene structure in the solid state.7,8 After our recent synthesis9 of a bicyclic distannene, utilizing the dimerization of a bidentate oligosilanylene ligated stannylene, we wanted to extend this study to lead.

Results and Discussion

Synthesis

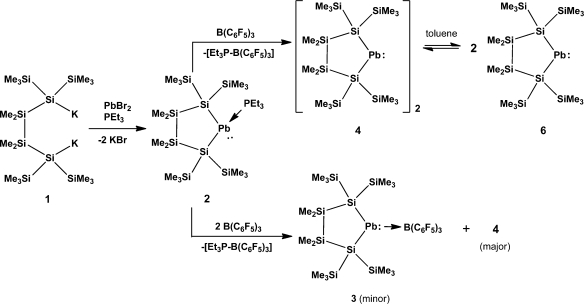
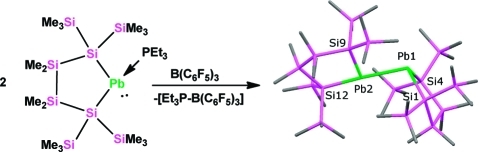
The synthesis of the plumbylene phosphine adduct 2 was accomplished by addition of 1,4-dipotassiotetrasilane 1(10,11) to a suspension of PbBr2 and PEt3 (Scheme 1). Generation of the “base free” plumbylene dimer 4 could then be achieved by abstraction of triethylphosphine from 2 with the strong Lewis acid B(C6F5)3 (Scheme 1). The thus formed phosphine adduct of the borane12 could be separated by fractional crystallization, but nevertheless several attempts of recrystallization from pentane were required to grow crystals of plumbylene dimer 4 suitable for X-ray diffraction (XRD). On one occasion together with much amorphous black material (shown by NMR spectroscopy to be 4) a few green symmetrically shaped crystals were found. By X-ray crystal structure analysis these were found to correspond to the plumbylene-B(C6F5)3 adduct 3 (Figure 2). However, even when 2 equiv of B(C6F5)3 were used in the reaction with 2 only trace amounts of 3 below the NMR detection limit were formed. This behavior toward B(C6F5)3 differs from our recently published results of the same reaction sequence applied to the corresponding stannylene phosphine adduct.9 In the tin case the stannylene borane adduct could be formed selectively suppressing a competing dimerization process. The dimeric structure of compound 4 was proven by XRD (Figure 3). While the phosphine complex 2 was found to be infinitely stable in solution as well as in the solid state under exclusion of moisture and air, plumbylene dimer 4 decomposed in solution at room temperature to elemental lead and the corresponding cyclotetrasilane, resulting from the reductive elimination of lead.

Scheme 1. Synthesis of Plumbylene Adducts 2 and 3 and Plumbylene Dimer 4 Which Dissociates to Plumbylene 6 in Solution.

Scheme 1

Open in a new tab

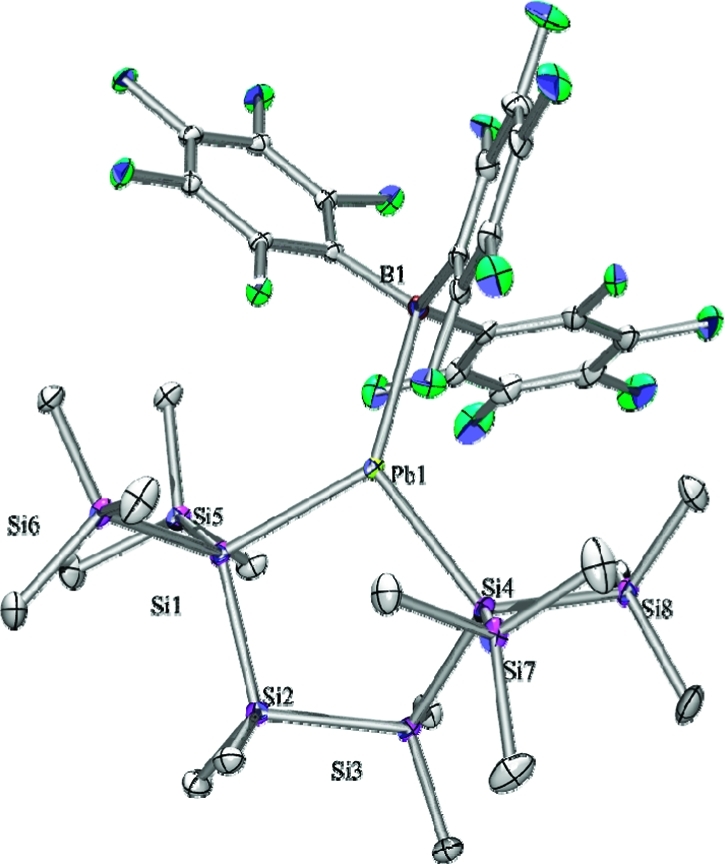
Figure 2.

Figure 2

Open in a new tab

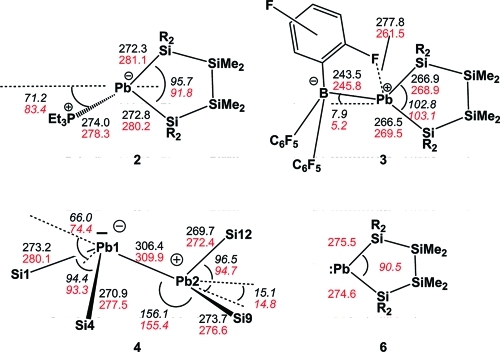
Molecular structure of 3 (thermal ellipsoid plot drawn at the 30% probability level). Hydrogen atoms omitted for clarity (bond lengths in pm, angles in deg). Pb(1)–B(1) 243.4(7), Pb(1)–Si(1) 266.54(17), Pb(1)–Si(4) 266.91(18), B(1)–Pb(1)–Si(1) 131.06(16), B(1)–Pb(1)–Si(4) 125.26(16), Si(1)–Pb(1)–Si(4) 102.80(6).

Figure 3.

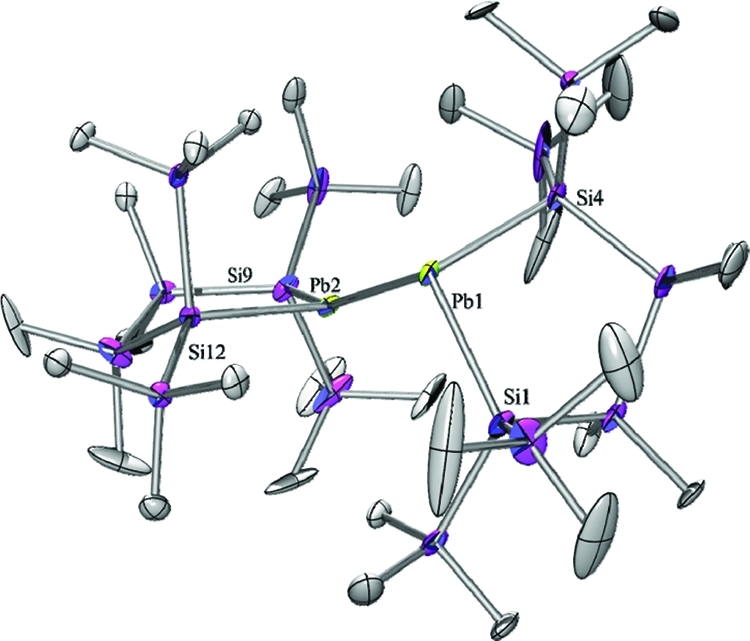
Figure 3

Open in a new tab

Molecular structure of 4 (thermal ellipsoid plot drawn at the 30% probability level). Hydrogen atoms omitted for clarity (bond lengths in pm, angles in deg). Pb(1)–Si(4) 270.9(4), Pb(1)–Si(1) 273.2(3), Pb(1)–Pb(2) 306.40(8), Pb(2)–Si(12) 269.7(3), Pb(2)–Si(9) 273.7(3), Si(1)–Si(2) 233.4(6), Si(2)–C(1) 187.5(13), Si(4)–Pb(1)–Si(1) 94.38(12), Si(4)–Pb(1)–Pb(2) 109.54(11), Si(1)–Pb(1)–Pb(2) 101.83(7), Si(12)–Pb(2)–Si(9) 96.49(10), Si(12)–Pb(2)–Pb(1) 101.80(7), Si(9)–Pb(2)–Pb(1) 156.09(9).

NMR Spectroscopy

For plumbylene phosphine adduct 2 at rt, no 207Pb NMR signal could be detected. This is probably due to a dissociation–association process of the phosphine. This is also indicated by the 31P NMR spectrum, where a broad signal at δ = −60.0 ppm without resolved coupling to 207Pb is observed. In the 29Si NMR spectrum sharp signals for the SiMe2 units at δ = −10.7 and the quaternary silicon atoms at δ = −87.3 ppm were found as expected while the SiMe3 resonances appeared as a badly resolved broad signal at δ = −1.5 ppm. This can also be rationalized by the said dissociation–association process of the phosphine. In the 1H and 13C NMR spectra the expected pattern of signals was found. Cooling to −60 °C allows the observation of a 207Pb resonance at δ = +1139 ppm as a doublet with a coupling constant of 1J(PbP) = 3083 Hz which was also observed in the 31P NMR spectrum at the same temperature. This chemical shift agrees fairly well with an expected value of δ = +1595 ppm based on Wrackmeyer’s empirical correlation13 of NMR chemical shifts of Sn(II) compounds to analogous Pb(II) compounds.13

For the plumbylene dimer 4 again no 207Pb NMR signals could be observed at rt, as decomposition of 4 in solution proved to be faster than acquisition of the 207Pb NMR spectrum. The decomposition takes place in an analogous way to bis[tris(trimethylsilyl)silyl]lead (5),7 but with a shorter lifetime. After 30 min in a benzene solution, complete decomposition to 1,1,2,2-tetrakis(trimethylsilyl)tetramethylcyclotetrasilane14 and elemental lead occurred. Nevertheless, acquisition of spectra at −40 °C allowed observation of a 207Pb resonance with a chemical shift of δ = +19516 ppm, which to the best of our knowledge is by far the most downfield shifted resonance of a lead compound ever recorded. This strong paramagnetically deshielded resonance is typical for tetrylenes which have small energy separations between occupied and virtual molecular orbitals with large coefficients at the magnetic active nuclei.15 Furthermore, the strongly deshielded 207Pb NMR signal clearly indicates that dimer 4 exists as plumbylene monomer, 6, in solution (see Scheme 1). When the 207Pb shifts of related plumbylenes such as PbAr*[Si(SiMe3)3] (Ar* = C6H3-2,6-Mes2) (δ = +10510 ppm)16 and Pb{(Me3Si)2(CSiMe2CH2)}2 (δ = +10050 ppm) are considered,17 a chemical shift of this order of magnitude seems reasonable. With respect to the 29Si chemical shift for the silicon atom attached to lead Klinkhammer and co-workers reported resonances of δ = +198.6 for Pb[Si(SiMe3)3]27,16 and δ = +156.5 for PbAr*[Si(SiMe3)3].16 However, we did not find any signal in this area. Comparison with the 29Si NMR chemical shifts of related stannylene derivatives18 suggests a 29Si NMR chemical shift for this silicon atom in plumbylene 6 close to δ = 0 ppm. This assumption was further supported by theoretical investigations, which predict for the α-silicon atom in plumbylene 6 a chemical shift of δ = −35 ppm.19 Our measurement at −40 °C eventually led to the observation of a signal at δ = −8.5 ppm which we tentatively assign to the α-Si resonance.

X-ray Crystallography

Compounds 2, 3, and 4 were subjected to single-crystal X-ray diffraction analysis, and the structural features are listed in Table S1. The structure of 2 (Figure 1) is the first plumba-cyclopentasilane to be structurally characterized. Similar to the recently published cyclopentasilanyl stannylene phosphine adduct9 it adopts an envelope conformation with one of the quaternary Si atoms on the flap. The donor–acceptor interaction with the phosphine is clearly indicated by the strong pyramidalization of the Pb atom in 2 [pyramidalization angle β(Pb) = 71.2°]20 and by the Pb–P bond (274.0 pm) which is significantly longer than the sum of the covalent radii (255 pm).21

Figure 1.

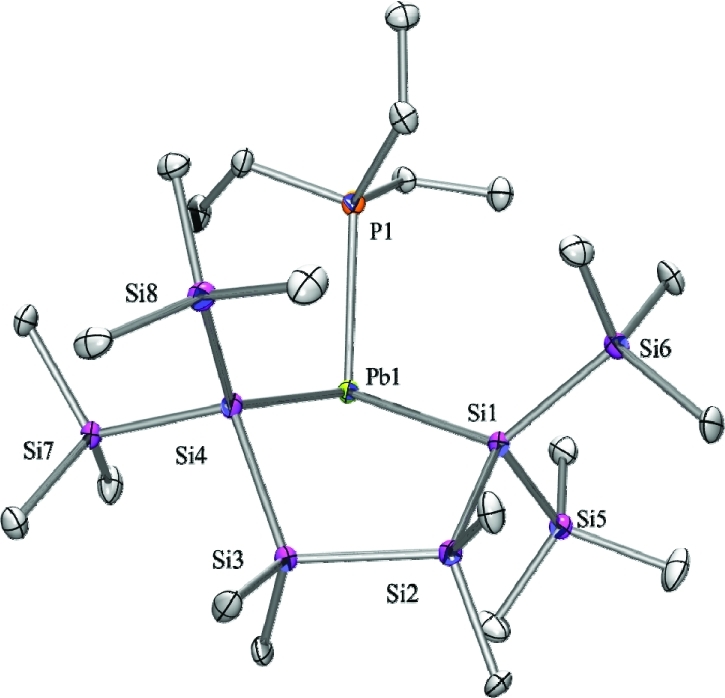
Figure 1

Open in a new tab

Molecular structure of 2 (thermal ellipsoid plot drawn at the 30% probability level). Hydrogen atoms omitted for clarity (bond lengths in pm, angles in deg). Pb(1)–Si(4) 272.3(2), Pb(1)–Si(1) 272.8(2), Pb(1)–P(1) 274.0(2), Si(1)–Si(2) 237.1(3), P(1)–C(19) 182.9(10), Si(2)–C(2) 189.8(9), Si(4)–Pb(1)–Si(1) 95.67(8), Si(4)–Pb(1)–P(1) 97.86(7), Si(1)–Pb(1)–P(1) 106.01(7).

The plumbylene borane adduct 3 (Figure 2) is an analogue to the stannylene borane adduct reported by us earlier.9 The lead atom in compound 3 is in an approximate trigonal planar coordination environment with only a small deviation from planarity [β(Pb) = 7.9°] and a relatively long B–Pb bond [243.5 pm (3) vs 229 pm (sum of the covalent radii)].21 Both features are in agreement with the predominant plumbylene/borane donor/acceptor interaction. In addition, the plumbylene is also acting as a Lewis acid by accepting electron donation from one of the ortho-fluorines of the BArf moiety. This is indicated in the solid state by a relative close F···Pb contact of 277.8 pm, halfway between the sum of the covalent and van der Waals radii (208 and 349 pm).21,22

In contrast to Klinkhammer’s disilylated monomeric plumbylene ([(Me3Si)3Si]2Pb) (5) the crystal structure analysis of 4 (Figure 3) revealed a dimeric arrangement with a Pb–Pb separation of 306.4 pm. This is substantially longer than a typical Pb–Pb single bond of 284 pm such as found for hexaphenyldiplumbane,23 but well within the range of 284–354 pm covered by Klinkhammer’s heteroleptic plumbylene dimers of the type {[(Me3Si)3Si]ArPb}2.8 The two plumbylene units of 4 show different arrangements around the lead atoms. The Pb(1) atom in Figure 3 shows some stereochemical activity of the lone pair, and it is therefore highly pyramidalized with both SiPb(1)Pb(2) bond angles being close to the tetrahedral angle of 109.5° and a pyramidalization angle β(Pb(1)) = 66.0°.20 Pb(2) to the contrary shows a distorted planar geometry, the sum of bond angles around Pb(2) being 354.3° concomitant by a pyramidalization angle β of 15.1°. This very unusual structural arrangement can be rationalized by assuming a single donor–acceptor interaction in the solid state between the two plumbylene units with the planar Pb(2) being the donor and the pyramidalized Pb(1) acting as the acceptor. A somewhat similar situation is found in distannene (Mebp2Sn)2 (Mebp = 2,3,4-methyl-6-tert-butylphenyl)24 and, in particular, in Weidenbruch’s cyclotriplumbane (Tep2Pb)3 (Tep =2,4,6-triethylphenyl), where each lead atom acts as an electron pair acceptor for one of its neighbors and as a donor to the other one.25 As the geometry of the core in Weidenbruch’s compounds depends on subtle changes in the steric bulk of the ligands, plumbylene 6 might adopt an intermediate position.25−27 The electronic situation would favor trimerization, while the silyl ligands employed do not allow higher aggregates than a dimer for steric reasons.

Computational Study

Quantum mechanical calculations at the M06-2X/SDD(Pb) 6-31G(d)(P, Si, F, C, B, H) level, here denoted as M06-2X/A, provided a more detailed picture of the bonding in 4, the dimeric form of plumbylene 6, and the related plumbylene complexes with PEt3 (2) and B(C6F5)3 (3).28,29 The molecular structures, which were predicted by the calculations for compounds 2–4, are in good qualitative agreement with the data obtained from XRD measurements (Figure 4). In addition, the results of the calculations reveal for the free plumbylene 6 a half-chair conformation of the plumbacyclopentasilane ring with an endocyclic SiPbSi bond angle α = 90.5° and Pb(II)Si(IV) bonds which are by 4–5 pm longer than reported for Pb–Si linkages in other plumbylenes (Figure 4).30 The substitution with the electropositive silyl groups decreases markedly the computed singlet–triplet energy difference, ΔE(ST), for tetrylene 6 compared to the parent plumbylene PbH2 [ΔE(ST) = −215.4 kJ mol–1 (PbH2), ΔE(ST) = −145.4 kJ mol–1 (6)]. Due to the small endocyclic SiPbSi bond angle α, ΔE(ST) is however larger than that predicted for Klinkhammer’s plumbylene 5 [ΔE(ST) = −128.9 kJ mol–1 (5)]. According to an NBO analysis29 the donor–acceptor interaction between plumbylene 6 and the phosphine molecule in complex 2 is accompanied by an electron transfer of 0.25 au from the phosphine to the plumbylene and results in a calculated donor–acceptor bond strength BE of −76.0 kJ mol–1.29,31 Both distinct features which are found in the experimental solid state structure of the plumbylene/borane Lewis base/acid complex 3, the almost trigonal planar coordination of the Pb atom and the close contact between the ortho-fluorine and the Pb-atom, are also present in the calculated gas phase structure of 3. This finding excludes the possibility that the close F···Pb contact found in the solid state structure is a consequence of crystal packing effects, and it suggests the presence of a structure shapening C–F→ Pb donor–acceptor interaction. The results of the NBO analysis reveal an overall electron donation from the plumbylene to the borane in 3 of 0.95 au, and the donor–acceptor bond strength BE of the Pb–B bond is calculated to be −65.1 kJ mol–1.29,31

Figure 4.

Figure 4

Open in a new tab

Comparison between experimental (XRD, black) and calculated [M06-2X/A, red] structural parameter of compounds 2, 3, the central part of dimer 4 and computed structural data of 6. Bond angles α and pyramidalization angles β in deg (italic), bond lengths in pm (R = SiMe3).

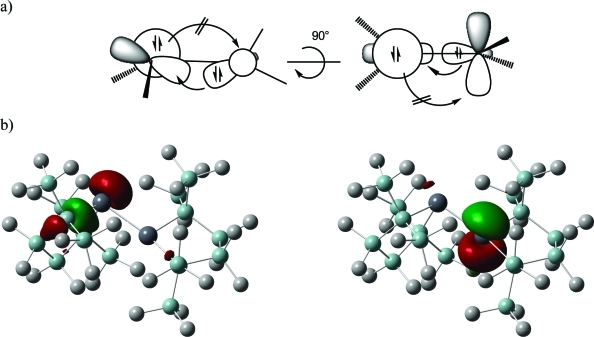
According to the results of the computations the overall molecular structure of the plumbacyclopentsilane ring of plumbylene 6 is conserved nearly unchanged in the acceptor complex 2 and in the donor adduct 3 and also in the plumbylene dimer 4. In agreement with the experimental data Pb atoms with two significantly different coordination environments were found in the computed structure of dimer 4 (Figures 3 and 4). The structural data suggest a single donor–acceptor interaction between the plumbylene subunits with a distorted trigonal planar Pb(2) atom (β(Pb(2)) = 14.8°),20 acting as the donor and a strongly pyramidalized second Pb(1) atom (β(Pb(1)) = 74.4°)20 (see Figures 4, 5). This interaction results in a relative long Pb(2)Pb(1) bond (d(Pb(1)Pb(2) = 309.9 pm). The conformation around this bond with a dihedral angle of 74.5° between the planes spanned by the Pb atoms and their adjacent Si atoms excludes a second donor–acceptor interaction (Figure 5a). Consequently, the frontier orbitals of dimer 4 are the stereochemically active electron pair at Pb(1) (HOMO) and the vacant p-type orbital at Pb(2) (LUMO) (Figure 5b). The NBO analysis suggests a significant electron transfer from the donor plumbylene to the acceptor plumbylene of 0.24 au which results in a calculated Wiberg bond index (WBI) for the donor–acceptor bond in dimer 4 of 0.70. This value is smaller than those computed for the Pb–Pb single bond in staggered Pb2H6 [point group (PG): D3d, d(PbPb) = 288.8 pm, WBI = 0.88] and in trans bent Pb2H4 [PG: C2h, d(PbPb) = 290.9 pm, WBI = 0.87]. According to the NBO analysis the Pb–Pb linkage in dimer 4 is supported by negative hyperconjugation which involves the lone pair at Pb(1) and the σ* orbital of the Pb(2)–Si(9) bond (see Scheme 2). As a result from this interaction the bond angle α(Pb(1), Pb(2)Si(9)) is significantly widened [α(Pb(1)Pb(2)Si(9)) = 155.4°] and the Pb(2)Si(9) (276.6 pm) bond is longer than the comparable Pb(2)Si(12) bond (272.4 pm). Consequently, also the computed WBIs of these two bonds differ markedly [WBI (Pb(2)Si(9)) = 0.64) and WBI (Pb(2)Si(12)) = 0.71].32

Figure 5.

Figure 5

Open in a new tab

(a) Schematic view of the donor–acceptor bond in plumbylene dimer 4. Left: View in the direction orthogonal to the Pb(2)Si(9)Si(12) plane. Right: After rotation by 90° around the Pb(1)Pb(2) bond. (b) Calculated surface diagrams of HOMO (left) and LUMO (right) of dimer 4 (isodensity value: 0.05; color code: dark gray: Pb; blue gray: Si; light gray: C; H-atoms omitted).

Scheme 2. Canonical Structures Which Describe the Negative Hyperconjugation in Dimer 4.

Scheme 2

Open in a new tab

The overall binding energy BE between both plumbylene subunits in dimer 4 is computed to be −110.8 kJ mol–1.31,33 Therefore, the PbPb linkage in 4 is considerably stronger than the PbPb bond in the parent diplumbene Pb2H4 in its trans bent conformation [BE(Pb2H4) = −62.4 kJ mol–1], although on the basis of the computed WBIs (see above) a stronger PbPb bond in Pb2H4 is expected. In addition, on the basis of the computed singlet/triplet separations E(ST) for plumbylenes 5 and 6 (see above) and the nonexistence of a dimer of plumbylene 5, the formation of dimer 4 is completely unexpected. This suggests that it is not the conventional donor–acceptor bonding interaction that ties both plumbylene subunits in dimer 4 together. A qualitative assessment of the attractive coulomb potential, EC, between the two Pb-atoms which results from charge transfer between both plumbylene subunits indicates that this factor is of only minor importance as it accounts for less than 25% of the computed BE (EC = −25.8 kJ mol–1).34 This leaves the attractive dispersion potential between the large and polarizable substituents of plumbylene 6 as the decisive force for an understanding of the bonding situation. A related situation is found in the sterically overloaded disilane tBu3Si–SitBu3 which is marked by an extremely long Si–Si bond but shows a comparatively high thermostability.35,36 Recently, dispersion forces were also recognized as important factors that explain the high stability of organometallic compounds37 and that of hydrocarbons with extremely long alkane C–C bonds.38 The here applied M06-2X functional properly accounts for noncovalent van der Waals interactions, while the most prominent deficit of the popular B3LYP functional is the nearly complete negligence of dispersion.39 Therefore, the difference in the calculated bond energies using these two functionals allows estimating the contribution of noncovalent bonding in dimer 4.37,38 As expected for the parent Pb2H4 nearly the same Pb–Pb bond energy BE is computed using the two different functionals [M06-2X/A//M06-2X/A: BE(Pb2H4) = −62.4 kJ mol–1; B3LYP/A//M06-2X/A: BE(Pb2H4) = −54.4 kJ mol–1]29 indicating that attracting dispersion forces are not significant. In sharp contrast in the case of dimer 4 dispersion forces are decisive as the B3LYP functional predicts an even positive Pb–Pb bond energy BE [M06-2X/A//M06-2X/A: BE(4) = −110.8 kJ mol–1; B3LYP/A//M06-2X/A: BE(4) = +1.0 kJ mol–1]. In addition free optimization of the molecular structure of dimer 4 using the B3LYP/A method results in a Pb(1)–Pb(2) bond, which is by 19.7 pm longer than determined by XRD. Furthermore, the computed binding energy BE for the free optimized dimer 4 at B3LYP/A is considerably decreased compared to the M06-2X value [B3LYP/A//B3LYP/A: BE(4) = −26.5 kJ mol–1].

A rotational isomer of dimer 4, the diplumbylene 7, with an approximate trans bent configuration of the constituent plumbylenes 6 and a slightly smaller Pb–Pb separation was located on the potential energy surface [Pb–Pb = 298.2 pm, β(Pb) = 52.2° and 36.9°]. In this conformer both plumbylenes are connected by a conventional double donor–acceptor interaction. The binding energy for trans bent dimer 7 is however significantly smaller than calculated for dimer 4 [BE = −76.4 kJ mol–1 (7) vs −110.8 kJ mol–1 (4) at M06-2X/A]. Interestingly, B3LYP computations applied at both plumbylene dimers at their M06-2X equilibrium structures predict both dimers to be nearly equal in energy with dimer 7 being slightly more stable by 0.5 kJ mol–1. The results of these model calculations suggest that it is solely the optimization of the dispersion energy as interplay between attracting and repelling forces between the plumbylene subunits which determines the actual shape of the plumbylene dimer 4.

The analysis of the computational results indicates that the dominant attracting force that holds together dimer 4 in its inmost folds40 is van der Waals interaction, which is supported by a comparatively weak donor–acceptor interaction. In addition, it is the stronger dispersion energy contribution that prefers the single donor–acceptor dimer 4 over the trans bent dimer 7 with an double donor–acceptor interaction between the constituent plumbylenes. At this stage of the discussion we feel that it is appropriate to point out that in the past many elaborate analyses of bonding in organometallic compounds,41 in particular in systems with important donor–acceptor interactions, the contributions of the attractive dispersion interactions between the experimentally often unavoidable large substituents are neglected although they might be decisive. This realization calls for a computational reinvestigation of these systems.

Experimental Section

General Remarks

All reactions involving air-sensitive compounds were carried out under an atmosphere of dry nitrogen or argon using either Schlenk techniques or a glovebox. All solvents were dried using a column based solvent purification system.42 Potassium tert-butanolate was purchased from Merck. All other chemicals were obtained from different suppliers and used without further purification.

1H (300 MHz), 13C (75.4 MHz), 31P (124.4 MHz), 207Pb (62.8 MHz), and 29Si (59.3 MHz) NMR spectra were recorded on a Varian INOVA 300 spectrometer. For all samples C6D6 was used as solvent if not stated otherwise. To compensate for the low isotopic abundance of 29Si the INEPT pulse sequence43,44 was used for the amplification of the signal.

X-ray Structure Determination

For X-ray structure analyses the crystals were mounted onto the tip of glass fibers, and data collection was performed with a BRUKER-AXS SMART APEX CCD diffractometer using graphite-monochromated Mo Kα radiation (0.71073 Å). The data were reduced to F2o and corrected for absorption effects with SAINT45 and SADABS,46,47 respectively. The structures were solved by direct methods and refined by the full-matrix least-squares method (SHELXL97).48 If not noted otherwise all non-hydrogen atoms were refined with anisotropic displacement parameters. All hydrogen atoms were located in calculated positions to correspond to standard bond lengths and angles. All diagrams were drawn with 30% probability thermal ellipsoids, and all hydrogen atoms were omitted for clarity.

Crystallographic data (excluding structure factors) for the structures of compounds 2, 3, and 4 reported in this paper have been deposited with the Cambridge Crystallographic Data Center as supplementary publication no. CCDC-831746 (2), 831750 (3), and 831749 (4). Copies of data can be obtained free of charge at http://www.ccdc.cam.ac.uk/products/csd/request/.

1,1,1,4,4,4-Hexakis(trimethylsilyl)tetramethyltetrasilane11 and B(C6F5)349 were prepared according to literature procedures.

Plumbylene Phosphine Adduct 2

After stirring a solution of 1,1,1,4,4,4-hexakis(trimethylsilyl)tetramethyltetrasilane (612 mg, 1.0 mmol) and KOtBu (236 mg, 2.1 mmol) in THF (5 mL) for 18 h at 60 °C the solution was cooled to rt and added dropwise to a stirred suspension of PbBr2 (367 mg, 1.0 mmol) and PEt3 (120 mg, 1.0 mmol) in THF (5 mL). On addition a color change from green to red appeared, and the resulting red suspension was stirred for 2 h. All volatiles were removed under reduced pressure, and the residue was extracted three times with pentane (5 mL each). The red solution was concentrated to 4 mL and stored at −60 °C for 36 h. Red crystals of 2 (569 mg, 72%) were isolated by filtration and dried in vacuo. 1H NMR (δ in ppm): 1.24 (pseudo quintet, J(apparent): 7.5 Hz, 6H, P(CH2CH3)3, 0.59 (td, 3JHH = 7.6 Hz, 3JPH = 15.1 Hz, P(CH2CH3)3, 0.50 (s, 12 H, SiMe2), 0.46 (s, 36H, SiMe3). 13C NMR (δ in ppm): 19.6 (d, 2JPC = 4.5 Hz, P(CH2CH3)3, 9.9 (s, P(CH2CH3)3), 5.1 (SiMe3), 2.3 (SiMe2). 29Si NMR (δ in ppm): −1.7 (br, SiMe3), −10.7 (SiMe2), −87.3 (quart. Si). 31P NMR (δ in ppm): −60.0 (br, PEt3); (solution in THF-d8, −60 °C): −53.9 (d, 1JPbP = 3087 Hz). 207Pb NMR (δ in ppm, solution in THF-d8, −60 °C): 1139 (d, 1JPbP = 3083 Hz); no signal at rt.

Plumbylene Dimer 4

A mixture of 2 (100 mg, 0.13 mmol) and B(C6F5)3 (67 mg, 0.13 mmol) was dissolved in pentane (10 mL) and stirred for 5 min. The color changed from red to black during this period. The dark reaction mixture was centrifuged and stored at −30 °C for 12 h. Colorless (C6F5)3B–PEt3 was removed by filtration at −30 °C. The remaining black solution was concentrated to 5 mL and stored at −60 °C for 24 h. The obtained material contained small impurities of 3. Compound 4 (84 mg, 96%) was isolated after several recrystallization steps with pentane as black plates. NMR data for the monomeric plumbylene 6: 1H NMR (δ in ppm, rt): 0.47 (s, 12H, SiMe2), 0.24 (s, 36H, SiMe3); (solution in toluene-d8, −40 °C): 0.62 (s, 12H, SiMe2), 0.42 (s, 36H, SiMe3). 13C: (δ in ppm, solution in toluene-d8, −40 °C): 6.4 (SiMe3), 5.0 (SiMe2). 29Si (δ in ppm, solution in toluene-d8, −40 °C): 3.2 (SiMe2), 1.5 (SiMe3), −8.5 (PbSi). 207Pb (δ in ppm, solution in toluene-d8, −40 °C): 19516; no signal at rt.

Acknowledgments

This work is dedicated to Prof. Akira Sekiguchi on the occasion of his 60th birthday. Support of the study was provided by the Austrian Fonds zur Förderung der Wissenschaften (FWF) via the project P-21346 (J.B.). P. Zark thanks the Fonds der Chemischen Industrie (FCI) for a scholarship (No.183191) and the High-Performance Computing centre of CvO university is thanked for computer time.

Supporting Information Available

Details for the calculated structures of compounds 2–7, as well as X-ray crystallographic information for compounds 2, 3, and 4 in CIF format. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Supplementary Material

ja300654t_si_001.pdf (1.5MB, pdf)
ja300654t_si_002.cif (74.8KB, cif)

References

  1. Goldberg D. E.; Harris D. H.; Lappert M. F.; Thomas K. M. J. Chem. Soc., Chem. Commun. 1976, 261–262. [Google Scholar]
  2. Goldberg D. E.; Hitchcock P. B.; Lappert M. F.; Thomas K. M.; Thorne A. J.; Fjeldberg T.; Haaland A.; Schilling B. E. R. J. Chem. Soc., Dalton Trans. 1986, 2387–2394. [Google Scholar]
  3. Ganzer I.; Hartmann M.; Frenking G. In The Chemistry of Organic Germanium, Tin and Lead Compounds Vol. 2; Rappoport Z., Ed.; John Wiley & Sons, Ltd.: 2002; pp 169–282. [Google Scholar]
  4. Fischer R. C.; Power P. P. Chem. Rev. 2010, 110, 3877–3923. [DOI] [PubMed] [Google Scholar]
  5. Mizuhata Y.; Sasamori T.; Tokitoh N. Chem. Rev. 2009, 109, 3479–3511. [DOI] [PubMed] [Google Scholar]
  6. Lee V. Y.; Fukawa T.; Nakamoto M.; Sekiguchi A.; Tumanskii B. L.; Karni M.; Apeloig Y. J. Am. Chem. Soc. 2006, 128, 11643–11651. [DOI] [PubMed] [Google Scholar]
  7. Klinkhammer K. W.; Schwarz W. Angew. Chem., Int. Ed. Engl. 1995, 34, 1334–1336. [Google Scholar]
  8. Klinkhammer K. Polyhedron 2002, 21, 587–598. [Google Scholar]
  9. Arp H.; Baumgartner J.; Marschner C.; Müller T. J. Am. Chem. Soc. 2011, 133, 5632–5635. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Kayser C.; Kickelbick G.; Marschner C. Angew. Chem., Int. Ed. 2002, 41, 989–992. [DOI] [PubMed] [Google Scholar]
  11. Fischer R.; Frank D.; Gaderbauer W.; Kayser C.; Mechtler C.; Baumgartner J.; Marschner C. Organometallics 2003, 22, 3723–3731. [Google Scholar]
  12. Welch G. C.; Prieto R.; Dureen M. A.; Lough A. J.; Labeodan O. A.; Holtrichter-Rossmann T.; Stephan D. W. Dalton Trans. 2009, 1559–1570. [DOI] [PubMed] [Google Scholar]
  13. Wrackmeyer B.; Stader C.; Horchler K. J. Magn. Reson. 1989, 83, 601–607. [Google Scholar]
  14. Fischer R.; Konopa T.; Baumgartner J.; Marschner C. Organometallics 2004, 23, 1899–1907. [Google Scholar]
  15. Müller T. J. Organomet. Chem. 2003, 686, 251–256. [Google Scholar]
  16. Klett J.; Klinkhammer K. W.; Niemeyer M. Chem.—Eur. J. 1999, 5, 2531–2536. [Google Scholar]
  17. Eaborn C.; Ganicz T.; Hitchcock P. B.; Smith J. D.; Sözerli S. E. Organometallics 1997, 16, 5621–5622. [Google Scholar]
  18. Klinkhammer K.Silylderivate der schweren Alkalimetalle in der Synthese niedervalenter Hauptgruppenelementverbindungen, habilitation thesis, Universität Stuttgart, 1998. [Google Scholar]
  19. Mean value from δ 29Si = −33 and δ 29Si = −37 predicted for the two nonequivalent α-Si-atoms in the optimized structure of plumbylene 6 at the GIAO/B3LYP/6-311+G(2d,p)(Si,C,H, def2TZVP(Pb)//M06-2X/A level of theory; see Supporting Information for further details.
  20. The pyramidalization angle β is defined as the angle between the vector of the exocyclic E–Pb bond and the plane spanned by the Pb atom and the two adjacent Si atoms.
  21. Pyykkö P.; Atsumi M. Chem.—Eur. J. 2009, 15, 12770–12779. [DOI] [PubMed] [Google Scholar]
  22. Mantina M.; Chamberlin A. C.; Valero R.; Cramer C. J.; Truhlar D. G. J. Phys. Chem. A 2009, 113, 5806–5812. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Preut H.; Huber F. Z. Anorg. Allg. Chem. 1976, 419, 92–96. [Google Scholar]
  24. Weidenbruch M.; Kilian H.; Peters K.; Schnering H. G. V.; Marsmann H. Chem. Ber. 1995, 128, 983–985. [Google Scholar]
  25. Stabenow F.; Saak W.; Marsmann H.; Weidenbruch M. J. Am. Chem. Soc. 2003, 125, 10172–10173. [DOI] [PubMed] [Google Scholar]
  26. Stürmann M.; Weidenbruch M.; Klinkhammer K. W.; Lissner F.; Marsmann H. Organometallics 1998, 17, 4425–4428. [Google Scholar]
  27. Stürmann M.; Saak W.; Marsmann H.; Weidenbruch M. Angew. Chem., Int. Ed. 1999, 38, 187–189. [DOI] [PubMed] [Google Scholar]
  28. The Gaussian 09 program was used. Gaussian 09 Revision B. 01; Gaussian, Inc.: Wallingford, 2010. [Google Scholar]
  29. For detailed description of the computations, see the Supporting Information.
  30. Pb(II)Si(IV) bonds in plumbylene 270–271 pm, see:Klinkhammer K. In The Chemistry of Organic Germanium, Tin and Lead Compounds Vol. 2; Rappoport, Z., Ed.; John Wiley & Sons, Ltd.: 2002; pp 283–357. [Google Scholar]
  31. The donor–acceptor bond strengths or binding energies, BE, were computed using the computed total energy of the complex and subtracting the computed total energies of its constituent molecules. Therefore, a more negative BE means a stronger bond.
  32. For a detailed description of the NBO analyses with respect to the negative hyperconjugation, see Supporting Information.
  33. Entropy and solvation effects favor the dissociation of dimer 4 into the two constituent plumbylenes 6. This is detailed and quantified in the Supporting Information (Figure S8). Therefore, the here reported BE for dimer 4 is in agreement with detection of the monomer 6 in toluene solution.
  34. Computed for charges of opposite sign of 0.24 au (resulting from the NBO analysis) in a distance of 309.9 pm (calculated d(Pb(1)Pb(2)) in dimer 4).
  35. Wiberg N.; Schuster H.; Simon A.; Peters K. Angew. Chem. 1986, 98, 100–101. [Google Scholar]
  36. a Masters (née Hinchley) S. L.; Grassie D. A.; Robertson H. E.; Hölbling M.; Hassler K. Chem. Commun. 2007, 2618–2620. [DOI] [PubMed] [Google Scholar]; b Bock H.; Solouki B. In The Chemistry of Organic Silicon Compounds, Vol. 3; Apeloig Y, Rappoport Z, Eds.; Wiley: Chichester, 2001; p 187. [Google Scholar]
  37. Sieffert N.; Bühl M. Inorg. Chem. 2009, 48, 4622–4624. [DOI] [PubMed] [Google Scholar]
  38. a Schreiner P. R.; Chernish L. V.; Gunchenko P. A.; Tikhonchuk E. Y.; Hausmann H.; Serafin M.; Schlecht S.; Dahl J. E. P.; Carlson R. M. K.; Fokin A. A. Nature 2011, 477, 308–311. [DOI] [PubMed] [Google Scholar]; b Grimme S.; Schreiner P. R. Angew. Chem., Int. Ed. 2011, 50, 12639–12642. [DOI] [PubMed] [Google Scholar]
  39. Zhao Y.; Truhlar D. G. Theor. Chem. Acc. 2007, 120, 215–241. [Google Scholar]
  40. Adapted from Goethe J. W. “Faust”, J. G. Cotta’schen Buchhandlung Tübingen 1808, translated by Priest G. M.Princeton University, 1932. [Google Scholar]
  41. Takahashi M.; Tsutsui S.; Sakamoto K.; Kira M.; Müller T.; Apeloig Y. J. Am. Chem. Soc. 2000, 123, 347–348. [DOI] [PubMed] [Google Scholar]
  42. Pangborn A. B.; Giardello M. A.; Grubbs R. H.; Rosen R. K.; Timmers F. J. Organometallics 1996, 15, 1518–1520. [Google Scholar]
  43. Morris G. A.; Freeman R. J. Am. Chem. Soc. 1979, 101, 760–762. [Google Scholar]
  44. Helmer B. J.; West R. Organometallics 1982, 1, 877–879. [Google Scholar]
  45. SAINTPLUS: Software Reference Manual, Version 6.45: Bruker-AXS: Madison, WI, 1997–2003. [Google Scholar]
  46. Blessing R. H. Acta Crystallogr., Ser. A 1995, 51, 33–38. [DOI] [PubMed] [Google Scholar]
  47. SADABS: Version 2.1; Bruker-AXS: Madison, WI, 1998. [Google Scholar]
  48. Sheldrick G. M. Acta Crystallogr., Ser. A 2008, 64, 112–122. [DOI] [PubMed] [Google Scholar]
  49. Lancaster S. Alkylation of boron trifluoride with pentafluorophenyl Grignard reagent; Tris(pentafluorophenyl)boron. http://cssp.chemspider.com/215 (accessed Nov 21, 2011).

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja300654t_si_001.pdf (1.5MB, pdf)
ja300654t_si_002.cif (74.8KB, cif)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES