Multilayer DNA Origami Packed on Hexagonal and Hybrid Lattices

Abstract

“Scaffolded DNA origami” has been proven to be a powerful and efficient approach to construct two-dimensional or three-dimensional objects with great complexity. Multilayer DNA origami has been demonstrated with helices packing along either honeycomb-lattice geometry or square-lattice geometry. Here we report successful folding of multilayer DNA origami with helices arranged on a close-packed hexagonal lattice. This arrangement yields a higher density of helical packing and therefore higher resolution of spatial addressing than has been shown previously. We also demonstrate hybrid multilayer DNA origami with honeycomb-lattice, square-lattice, and hexagonal lattice packing of helices all in one design. The availability of hexagonal close packing of helices extends our ability to build complex structures using DNA nanotechnology.

Introduction

The past two decades have witnessed the rapid growth of structural DNA nanotechnology as a field. A variety of one-dimensional (1D), two-dimensional (2D) and three-dimensional (3D) DNA nanostructures have been developed.^{1, 2, 3} These versatile DNA nanostructures offer unique advantages for nano-scale patterning.^4-8 and construction of nanoscale devices^9-13 with applications such as tools for molecular biophysics.^14-17 Nonetheless, rational design of complicated 3D DNA objects with high accuracy still poses great challenges. Recently, great progress has been achieved in this realm by using strategies based on scaffolded DNA origami.¹⁸ For example, two origami boxes^{19, 20} and a hollow tetrahedral shape²¹ have been demonstrated by linking discrete 2D origami assembled on a single scaffold. More generalized methods to construct 3D DNA origami packed on honeycomb-lattice geometry²² or square-lattice geometry²³ also have been reported. Seven helices in a close-packed hexagonal lattice have been demonstrated for a non-origami DNA system.²⁴ Here we generalize hexagonal-lattice close packing for helices in 3D DNA origami, and also demonstrate hybrid 3D DNA origami packed on mixed geometries of honeycomb lattice, square lattice, and hexagonal lattice.

Design

Hexagonal-Lattice Origami

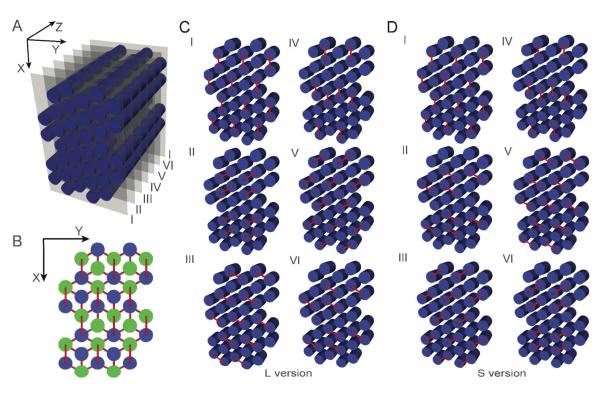
The design strategy used in this study for multilayer hexagonal-lattice DNA origami is illustrated in Figure 1. DNA origami conventionally are designed with a long single “scaffold” strand, typically the 7-kilobase genome of the M13 bacteriophage, that is folded with hundreds of short “staple” strands into a parallel array of double helices. Viewed down the axis parallel to the helices of the bundle (i.e. Z-axis), every double helix can be conceived as of two strands that each are characterized by a polarity (i.e. 5′ to 3′ away from the viewer versus towards the viewer) and a parity (made of scaffold DNA versus staple DNA). In the honeycomb- or square-lattice designs, like-parity strands on nearest-neighbor helices all are arranged with antiparallel polarity. As a result, adjacent helices are held together by antiparallel scaffold crossovers and antiparallel staple crossovers. In contrast, it is impossible to arrange helices in a hexagonal-lattice design such that like-parity strands on nearest-neighbor helices all are antiparallel. For example, if the six nearest neighbor scaffold-type strands are all antiparallel to the central strand, then they must all be parallel to each other.

Figure 1.

For our design, we chose to arrange strand polarity in the pattern shown in Figure 1B. Each double helix is connected by staple-strand antiparallel crossovers to three, four, or five of its six potential neighbors. Alternative crossover patterns are possible, although near equal representation of polarity for scaffold-parity strands has to be present to enable a single scaffold to traverse back and forth through the entire structure. Two versions of hexagonal-lattice origami were designed: Long (L) with staple crossovers occurring at 13 base-pair intervals (every 7/6 helical turns), and Short (S) with staple crossovers occurring at 9 base-pair intervals (every 5/6 helical turns). At each of these intervals (repeating slices I to VI in Figures 1C, 1D), one-sixth of neighboring helical pairs have staple bases that are positioned at the interhelix junction for antiparallel cross over. However, in our design, we only allowed like-parity crossovers, thus fewer than one-sixth of helical pairings have actual staple crossovers at any given interval slice.

Both L (11.1 bp/turn) and S (10.8 bp/turn) were designed with underwinding stress, compared to the naturally occurring B-form DNA double helix (10.5 bp per turn). We expected this underwinding would lead to a compensatory global right-handed twist, as previous studies suggested.^23-25 Two L origami (12HB-L and 24HB-L) and two S origami (24HB-S and 60HB-S) were designed and tested experimentally. Detailed descriptions of the designs can be found in the Supporting Materials (Figures S9 – S12).

Hybrid-Lattice Origami

We modified the S design to test the construction of multilayer DNA origami that combine honeycomb-, square-, and hexagonal-lattice packing of helices. Reciprocal twist and crossover densities were aligned throughout each design to minimize strain at the interfaces where helical packing was made to switch. For our 56HB honeycomb/hexagonal lattice design, we adjusted reciprocal twist densities to 10.8 bp/turn, and adjusted crossover densities to one every 54 bp. For our 52HB honeycomb/square/hexagonal lattice design, we adjusted reciprocal twist densities to 10.4 bp/turn, and adjusted crossover densities to one every 52 bp. Detailed descriptions of the designs can be found in the Supporting Materials (figure S13-S14).

Results

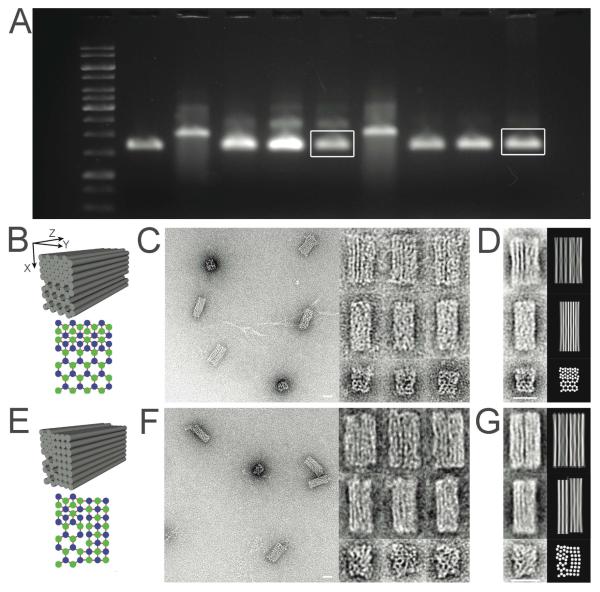
To form each designed DNA origami, the staple strands were mixed with 10 nM scaffold strands (p3024 for 12HB-L and 24HB-S; p7560 for 24HB-L, 60HB-S, 56HB, 52HB) at 50 nM each strand. A one-pot reaction allowed assembly of target structures by using the following thermal annealing conditions: 5 mM Tris + 1 mM EDTA at pH 8.0, a ramp from 80 to 60 °C over the course of 80 minutes, followed by a ramp from 60 to 24 °C over the course of 72 hours. The annealed mixtures were subjected to agarose-gel electrophoresis. Four different MgCl₂ concentrations (2, 6, 10, 14 mM) were tested for annealing each structure. Successful folding of all designs was observed at the 14 mM MgCl₂ annealing condition. Next, rapidly migrating bands corresponding to monomeric, well-folded species were excised from the gel and recovered by physical extraction using a Freeze-N-Squeeze column (see experimental details in the Supporting Information). The purified structures were imaged by transmission electron microscopy (TEM) after negative staining by uranyl formate.

Hexagonal-lattice Origami

The results of agarose-gel electrophoresis and TEM images for 12HB-L, 24HB-L, 24HB-S and 60HB-S hexagonal-lattices are shown in Figure 2. Folding with lower concentrations of MgCl₂ yielded slowly migrating bands on agarose-gel electrophoresis while folding with higher concentrations of MgCl₂ yielded fast-migrating bands, along with aggregated objects that barely moved into the agarose gel. Similar effects of divalent-cation concentration on multilayer DNA-origami folding had been observed previously for honeycomb and square-lattice origami.^{22, 23} TEM images revealed mostly views perpendicular to the Z axis of each shape; however, due to the large number of DNA double helices per cross section (i.e. large XY surface area), some particles of 60HB-S landed on the TEM grids to reveal an XY-projection view. For the 12HB-L and 60HB-S shapes, the YZ projection is predicted to be much thinner than the XZ projection, and correspondingly the experimental TEM views of these objects are easy to classify into these two types. For the 24HB-L and 24HB-S, the YZ projection is more modestly thinner, nevertheless classification still appears to be possible. We measured particle sizes of the four hexagonal-lattice structures (12HB-L, 24HB-L, 24HB-S and 60HB-S) and the two hybrid-lattice (56HB and 52HB) based on TEM images. Histograms of these measurements are shown in Figure S7. We also examined incorporation efficiency of twelve staple strands in 60HB-S using a gel-mobility shift assay (Figure S8). Both inside and outside staple strands had lower incorporation efficiencies if the strands were shorter; for strands of similar length, inside staple strands exhibited 20% lower incorporation efficiency than outside staple strands (see Figure S8 for further discussion).

Figure 2.

Table 1 compares the experimentally measured particle dimensions to the theoretical values. Comparing L-version objects to S-version objects, TEM images and results from Table 1 and Figure S7 revealed that the L-version shapes appear more disordered, while the S-version objects appear more compact and well-defined. Presumably the higher density of crossovers in the S-version hexagonal-lattices results in a stronger constraint on DNA double helix positional fluctuation. A distinctive feature of these well-defined S version hexagonal-lattices is that they do not exhibit profound stripes parallel to DNA double helices in the TEM images, while images of both the honeycomb-lattices and square-lattices show clear stripes when they land on TEM grids in certain orientations. These stripes originate from patterns of integrated transmission intensity that is directly related to the geometry of the structures. A detailed explanation of this phenomenon is included in Figure S15.

Table 1.

	X (nm)		Y (nm)		Z (nm)
	Theoretical	Experimental	Theoretical	Experimental	Theoretical	Experimental
12HB-L	13.5	15.4 ± 2.0	7.8	9.0 ± 1.7	79.6	76.6 ± 3.2
24HB-L	13.5	18.0 ± 1.3	11.7	13.0 ± 1.8	53.0	58.6 ± 4.5
24HB-S	13.5	13.5 ± 1.2	11.7	10.8 ± 1.2	36.7	41.0 ± 1.7
60HB-S	27.3	29.0 ± 1.8	13.5	13.7 ± 1.3	36.7	40.4 ± 2.2
56HB	23.4	21.6 ± 2.3	18	15.6 ± 1.6	36.7	38.5 ± 2.0
52HB	23.4	22.2 ± 1.7	19.4	17.1 ± 1.3	36.7	39.8 ± 1.7

For S version hexagonal-lattice structures, an effective diameter of 2.60 nm (SD ± 0.17 nm) for each DNA double helix was calculated from experimental measurements of X-dimension width (27.3nm ± 1.8nm) of 60HB-S (Table 1). The 2.60 nm effective diameter of S version hexagonal-lattice structures is the same as the effective DNA diameter reported earlier for square-lattice origami,²³ and significantly larger than the 2.4 nm effective DNA diameter reported earlier for honeycomb-lattice origami.²² This trend is roughly consistent with the lower crossover density employed (every 9 bp in hexagonal lattice versus every 8 bp in square lattice versus every 7 bp in honeycomb lattice).

Hybrid-Lattice Origami

Figure 3 shows experimental results of the two hybrid-lattice origami - 56HB (honeycomb-lattice / hexagonal-lattice) and 52HB (honeycomb-lattice / square-lattice / hexagonal-lattice). Despite their more complex geometries, both hybrid-lattice origami successfully assembled with high yields, as indicated by agarose-gel electrophoresis and TEM analysis. Three types of TEM images were observed for each design; to aid in interpretation, a toy model of the DNA bundles was evaluated computationally and used to generate simulated XY, XZ, and YZ projections. Each base pair was represented by a sphere, where the Z-position was fixed, and the XY position was determined as the minimum in a potential composed of attractive terms representing the effect of crossovers and repulsive terms representing electrostatics. Each attractive term was modeled as a pulling force exerted from a crossover between the base pair’s helix and a neighboring helix, with a magnitude that decays exponentially according to distance between the base pair and the crossover point on its helix. Each repulsive term was modeled as an electrostatic pushing force from another base pair in the same XY-plane.²⁶ The model was implemented in the Python programming language (http://python.org/) and all the base pairs were allowed to relax iteratively. Subsequently, the final relaxed structures could be projected onto XY, XZ, and YZ planes to generate approximations representing expected TEM-images.

Figure 3.

Comparisons of the simulated TEM images and actual data can be seen in Figures 3D and 3G. For the 56HB honeycomb/hexagonal lattice hybrid structure, the XZ projection is expected to consist of one section of pure honeycomb lattice with a striking pattern of stripes and one section of pure hexagonal lattice with a pattern of stripes that is not resolvable. Frequent examples of this easily identified projection can be found in the experimental images. For the YZ projection, on the other hand, no clear stripes and a more pronounced aspect ratio are expected; many examples of this type of image are seen experimentally as well. For the experimental images corresponding to the XY projection, it is clearly seen that the honeycomb-lattice section is significantly smaller than the hexagonal-lattice section, in good agreement with the simulations.

For the 52HB (honeycomb/square/hexagonal lattice) structure, a good match also was found between predicted and experimentally observed projection images. In the center of the structure exists a cavity without crossovers. For the XZ and YZ projections, the predicted stripe patterns can clearly be seen. For the YZ projection, a central dark strong line can be seen at the boundary between the honeycomb/hexagonal-lattice section and the square-lattice section; this boundary is especially pronounced due to the crossovers left out between helices along this interface. Viewed down the Z-axis, the hexagonal- and honeycomb-lattice side of the structures generally came out larger than the square-lattice part, as expected. However, the structures in Figure 3G did not exhibit a significant bulging as could have been expected given the large central interface without crossovers in the design. Other preparations of the sample did, however, show a stronger bulging, suggesting that it could be dependent on salt concentration or staining conditions.

Given that the toy model assumed a lack of defects, the strong correspondence between the simulated and experimental data indicates that the assembled origami structures are actually folding as expected.

Discussion

Here we have designed and realized a new family of three-dimensional DNA origami where parallel DNA double helices are packed on the highly compact hexagonal-lattice geometry. Taking advantage of all three available geometries of regular-packing helices in multilayer DNA origami—honeycomb, square, and hexagonal lattice—we also demonstrated that more complicated hybrid three-dimensional DNA origami could be constructed. A designer with some knowledge and experience of structural DNA nanotechnology could design a multilayer hexagonal-lattice origami or hybrid origami with desired geometry in a few hours, using computer programs such as caDNAno.²⁷ Currently, all crossovers need to be manually implemented in caDNAno for hexagonal-lattice or hybrid origami. We anticipate an updated version of caDNAno that can accommodate designs of all three geometries and even hybrid origami, which will make the process more automated and less time-consuming (Shawn Douglas, personal communication).

Two-dimensional and three-dimensional DNA-origami structures have been utilized or proposed for positioning guest macromolecules with precise orientational and spatial control in three-dimensional space. Such applications often will demand high-level control over overall shape and density as well as over the precise positions of each double helix of the DNA-origami structures. The hexagonal-lattice and hybrid-lattice origami design paradigms presented here will expand our capability to achieve such versatile and detailed control. For instance, since hexagonal-lattice 3D origami have the highest material density among all three architectures (honeycomb-lattice, square-lattice, and hexagonal-lattice), they should exhibit the strongest resistance to twist or compression per unit volume. Further systematic studies will be needed to better understand the mechanical properties of these 3D DNA lattices and thereby bring us closer to realizing the full potential of DNA-origami-directed self-assembly.