Convergence of Free Energy Profile of Coumarin in Lipid Bilayer

Abstract

Atomistic molecular dynamics (MD) simulations of druglike molecules embedded in lipid bilayers are of considerable interest as models for drug penetration and positioning in biological membranes. Here we analyze partitioning of coumarin in dioleoylphosphatidylcholine (DOPC) bilayer, based on both multiple, unbiased 3 μs MD simulations (total length) and free energy profiles along the bilayer normal calculated by biased MD simulations (∼7 μs in total). The convergences in time of free energy profiles calculated by both umbrella sampling and z-constraint techniques are thoroughly analyzed. Two sets of starting structures are also considered, one from unbiased MD simulation and the other from “pulling” coumarin along the bilayer normal. The structures obtained by pulling simulation contain water defects on the lipid bilayer surface, while those acquired from unbiased simulation have no membrane defects. The free energy profiles converge more rapidly when starting frames from unbiased simulations are used. In addition, z-constraint simulation leads to more rapid convergence than umbrella sampling, due to quicker relaxation of membrane defects. Furthermore, we show that the choice of RESP, PRODRG, or Mulliken charges considerably affects the resulting free energy profile of our model drug along the bilayer normal. We recommend using z-constraint biased MD simulations based on starting geometries acquired from unbiased MD simulations for efficient calculation of convergent free energy profiles of druglike molecules along bilayer normals. The calculation of free energy profile should start with an unbiased simulation, though the polar molecules might need a slow pulling afterward. Results obtained with the recommended simulation protocol agree well with available experimental data for two coumarin derivatives.

Introduction

Passive transport of drugs through membranes is the main process limiting their penetration into cells (in the absence of a specific active transporter) and thus a key step in their administration to the bodies of humans (and animals). Diffusion through membrane and partitioning between water and membrane phases are the key properties for this passive transport affecting kinetics and thermodynamics of permeation process,^1,2 respectively. Further, the equilibrium position of specific drugs in target membranes also affects their metabolism and transport (both active and passive).³⁻⁵

The composition of biological membranes is complex and diverse, varying substantially among the outer and inner leaflets of both organelles and organs.^6,7 They consist of proteins and lipids, in approximately equal mass proportions.⁸ While proteins are responsible for active transport and signaling, lipids pose the main barrier to passive membrane transport. The most important membrane for drug administration is the plasma membrane, through which drugs must penetrate to reach the internal milieu of target cells. However, mitochondrial and endoplasmic reticulum membranes are also involved in drug metabolism because they accommodate various drug-metabolizing enzymes (e.g., cytochromes P450 and UDP-glucuronosyltransferases).^5,9,10 The most abundant lipids in mammalian membranes are phosphatidylcholines (PC), although phosphatidylserines, phophatidylethanolamines, sphingomyelins, and cholesterol are also present,¹¹ thus PC bilayers are commonly used as simple membrane models. However, it must be remembered that in vivo membranes are much more complex, so results obtained using such simple models should be interpreted cautiously.

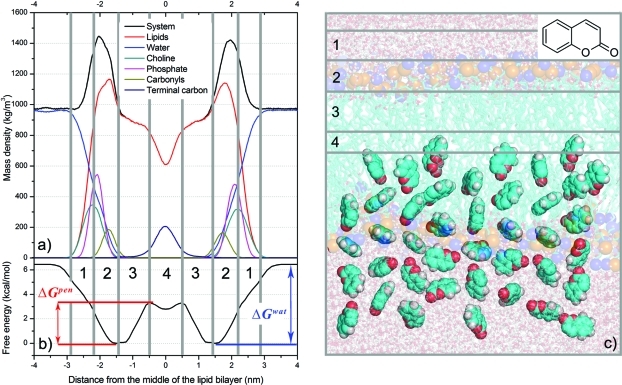
Several structural frameworks of lipid bilayers have been proposed, including the four-region model of Marrink and Berendsen¹² and others presented by Neale et al.¹³ and Orsi et al.¹⁴ The four-region model, applied in the study presented here, describes the physicochemical properties and densities of lipids in the following four regions along a bilayer’s normal axis (Figure 1):

• (i)The low headgroup density region (hereafter region 1), a polar zone with similar transport conditions to water, from the point where head groups are first encountered (at minimal density) and ending where the densities of head groups and water are comparable.
• (ii)The highly structured high headgroup density region (region 2), from the point where region 1 ends to the point closer to the bilayer center where the density of water decreases to below 1% and bulklike water disappears. Strong Coulombic interactions between polar groups keep polar molecules in the first two regions.¹⁵
• (iii)The high density of acyl chains region (region 3) is hydrophobic. Double bonds of unsaturated lipids are typically localized in this region.
• (iv)The fourth, low density of acyl chains region (region 4), resides in the middle of the bilayer and terminal methyl groups are primarily located in this region. Here, movement of all molecules is faster due to its low density. The two hydrophobic acyl chain regions are believed to form the main barrier for most druglike molecules, which are often water-soluble.^4,16

Figure 1.

Upper left panel (a): density profile of DOPC bilayer along the normal to the lipid bilayer plane showing densities of the complete system (black), water (blue), DOPC (red), phosphates (magenta), cholines (cyan), carbonyls (green), and terminal carbons (dark blue). Lower left panel (b): free energy profile of coumarin along the DOPC bilayer normal calculated from constraint simulation with initial structures obtained by free simulation (CF). The calculated bilayer center penetration barrier, ΔG^pen, and water/lipids barrier, ΔG^wat, are labeled. The free energy profile was calculated for one bilayer leaflet and was symmetrized to the other one, the densities of the system were symmetrized along the middle of the bilayer. The vertical bins labeled by numbers denote four bilayer regions: 1 – low density of head groups (2.2–2.9 nm), 2 – high density of head groups (1.45–2.2 nm), 3 – high density of acyl chains (0.5–1.45 nm), and 4 – low density of acyl chains (0–0.5 nm). Right panel (c): structure of DOPC bilayer, together with snapshots of coumarin initial structures. Carbons are colored in cyan, oxygens red, and hydrogens white. The olive and blue balls represent DOPC phosphate and nitrogen atoms.

Molecular dynamics (MD) simulations can be used to estimate the equilibrium position of a drug in a lipid bilayer, its partition coefficients and diffusion coefficients simultaneously at subpicosecond and atomic resolution.^4,15,17,18 The partitioning and mean position can be well described by a free energy (ΔG) profile along the normal to the lipid bilayer,^5,13,18,19 also known as a potential of mean force (PMF). In principle, such free energy profiles can be calculated from partitioning values obtained by long unbiased simulation. However, this approach only provides reliable free energy profiles when all states along the ΔG profile are thoroughly sampled. This is challenging for unbiased MD simulations, because they usually do not sample adequately at the available simulation time scales. The sampling problem is based on the dependence of probability of drug crossing a membrane on the energy barrier for this phenomenon. The probability of membrane crossing decreases exponentially with the energy barrier (Eq. S1 in the Supporting Information). If a barrier for a drug crossing a membrane is higher than ∼10 kcal/mol, the statistical probability of spontaneous membrane crossing is very low within typical time scales (hundreds of nanoseconds) accessible by unbiased atomistic MD simulations. Therefore during unbiased MD simulations, the polar molecules do not usually enter freely the deeper parts of bilayer and the nonpolar molecules do not sample enough of the area of bulk water.

Free energy profiles can also be calculated by biased MD simulations. Great advances have been made in this field in recent years, and numerous methods for obtaining free energy profiles have been developed, including umbrella sampling,^18,19 z-constraint method,^{12,14,15,17,18,22,23} metadynamics,^24,25 adaptive biasing force,^26,27 particle insertion,²² and others.^28,29 However, although these techniques undoubtedly enhance sampling, all of them have drawbacks for estimating free energy profiles along bilayer normals. For example, in an analysis of interactions between charged and neutral forms of ibuprofen and aspirin with a dipalmitoylphosphatidylcholine (DPPC) bilayer, Boggara and Krishnamoorti¹⁸ noted that the drugs (especially charged forms) caused deformations of the lipid bilayer in z-constraint simulations. Similarly, MacCallum et al.³⁰ observed “water defects” at the water–lipid interface in umbrella simulations applied for calculating free energy profiles of amino acids along the normal of a dioleoylphosphatidylcholine (DOPC) bilayer. Such deformation of lipid bilayer in simulations was recently analyzed by Neale et al., who identified it as a systematic sampling error of considerable interest. Neale and co-workers stressed that this systematic sampling error complicated the convergence of free energy profiles of druglike molecules along lipid bilayer normals, especially for charged molecules.

As this systematic error may also originate during the generation of starting structure sets used for biased MD simulations, this issue has been addressed in several previous studies using various strategies. Neale et al.¹³ used an inflategro procedure,³¹ in which (briefly) a pre-equilibrated bilayer is expanded, a molecule of interest is inserted, and the bilayer is compressed and re-equilibrated. Boggara and Krishnamoorti¹⁸ inserted molecules into a lipid bilayer manually using the VMD visualization program.³² Other approaches for generating starting structures have included growing the molecule inside the bilayer from zero size,¹⁴ pulling simulation,⁵ snapshots from unbiased simulation,³³ and estimation of reaction coordinates using metadynamics.²⁴ However, no methodological analyses of this problem have been previously published.

Here, based on an examination of the embedding of a nonpolar druglike molecule (coumarin; 1,2-benzopyrone) in DOPC bilayer, we show that systematic sampling error is difficult to avoid, but it can be reduced by using appropriate biased simulation and initial structure set generation method. Coumarin naturally occurs in diverse plants, including tonka beans (Dipteryx odorata), vanilla grass (Anthoxanthum odoratum), sweet woodruff (Galium odoratum), sweet clover (Meliotus L.), sweet grass (Hierochloe odorata), and cassia cinnamon (Cinnamomum aromaticum). It is absorbed by humans both orally from food and through the skin from perfumes. Further, it is a valuable test substance because it is a small, planar, rather rigid, nonpolar (logP_oct/wat 1.39³⁴), biologically significant druglike molecule, as its skeleton can be recognized in many drugs (e.g., the anticoagulant warfarin and antispasmodic/insecticide hymecromone³⁵) and other biologically active compounds (e.g., scopoletin). Therefore, coumarin is an ideal model for assessing the quality of various methods for calculating ΔG profiles of small low-polar druglike molecules along normals of lipid bilayers. DOPC bilayer has been previously used as a model of endoplasmic reticulum membrane, in which coumarin is metabolized by membrane-anchored Cytochrome P450 2A6.^36,37

The main aim of the study was to identify the mean position of coumarin in DOPC bilayer from calculations of free energy profiles using different biased MD simulations and different sets of initial structures. We also discuss convergence, advantages and disadvantages of z-constraint, and umbrella sampling methods using starting structures obtained by pulling and unbiased simulations. We focus on the systematic bias caused by choice of the initial structure set and the possibilities of avoiding this bias. The effect of choice of partial charges is also analyzed and results of biased and unbiased MD simulations (3 μs in total) are compared. Finally, a robust simulation protocol for obtaining a convergent free energy profile along a bilayer normal is suggested and tested against available experimental data for two coumarin derivatives embedded in dimyristoylphosphatidylcholine (DMPC) bilayer.

Methods

The structure and topology of coumarin (1,2-benzopyrone; CAS number 91-64-5) was generated by the PRODRG2 Beta server³⁸ using the GROMOS 53a6 forcefield.³⁹ However, partial charges assigned by PRODRG have been found to lead to unrealistic partitioning between water and cyclohexane phases.⁴⁰ As the partial charges used can introduce another systematic error into free energy calculations, we addressed this problem by also using Mulliken partial charges and restrained fit of electrostatic potential (RESP) partial charges. The RESP partial charges were successfully adopted by the second generation of AMBER family force fields. The electrostatic potential (ESP) and ESP partial charges were calculated by applying B3LYP/cc-pVDZ method to coumarin geometry optimized at the same level of theory in Gaussian 03.⁴¹ RESP fit⁴² was implemented by Antechamber from the AMBER 11 software package.⁴³ Mulliken partial charges, that were adopted by Berger lipid force field,⁴⁴ were calculated at the HF/6-31G* level in gas phase. Hereafter, all mentioned coumarin charges are RESP charges, except those explicitly named as PRODRG or Mulliken charges.

The lipid bilayer, as prepared and equilibrated by Siu et al.,⁴⁵ contained 128 DOPC molecules, 64 in each leaflet, with a structure generated by the Lipidbook server.⁴⁶ The bilayer was oriented perpendicularly to the z-axis of the simulation box and equilibrated for another 10 ns by a free MD simulation. Water and salt (NaCl) were added to give a physiological concentration, of 0.154 M, of salt in the aqueous phase (excluding the lipid bilayer from the volume calculation). The equilibrated box contained 5,188 molecules of Flexible Simple Point Charge (SPC) water,⁴⁷ 19 Na⁺ and 19 Cl^– ions. The equilibrated surface area per lipid was 0.638 nm², and the start of the z-axis was set in the middle of the bilayer.

The GROMACS 4.0.7 package⁴⁸ and united atom Berger lipid force field⁴⁴ were used for MD simulations. The latter reduces the number of atoms in simulations, as it merges nonaromatic and nonpolar hydrogens with their carbons. This simplification likely results in higher diffusion coefficients than those observed in all-atom model simulations.⁴⁹ Berger lipid force field⁴⁴ uses the Mulliken partial charges calculated at the HF/6-31G* level (in gas phase).⁵⁰ Simulations were taken with 2-fs integration time steps under periodic boundary conditions in all directions, with particle-mesh Ewald (PME) electrostatics,⁵¹ a van der Waals cutoff at 1 nm, bond constraints determined by the LINCS algorithm,⁵² V-rescale temperature coupling⁵³ to 310 K, and Berendsen anisotropic pressure coupling⁵⁴ to 1 bar with 10 ps time constant and compressibility of 4.5 × 10^–5 bar^–1.

A coumarin molecule was placed at the top of the simulation box, a 0.5 ns MD simulation was executed to pre-equilibrate the system, then five independent MD simulations with a total time of 3 μs were generated. From the pre-equilibrated simulation two sets of starting frames for biased MD simulations were generated: one by pulling coumarin to the bilayer center and the other from unbiased MD simulation. The first set of starting frames for biased MD simulations was obtained by pulling the center-of-mass (COM) of coumarin against that of the lipid bilayer (in its center). Coumarin was pulled along the bilayer normal (the z-axis) for 6 ns using a pulling force constant of 10,000 kJ·mol^–1·nm^–2 (2,390 kcal·mol^–1·nm^–2) and pulling rate of 1 nm·ns^–1. Pulling applies a harmonic potential on molecule and moves the center of this potential with a given pull rate. Starting positions were collected as snapshots from the pulling simulation, spaced 0.1 ± 0.02 nm apart along the z-axis from the area of bulk water (4 nm from the bilayer center) to the middle of the bilayer. From the structures at one distance bin, the structure with the lowest potential energy was chosen as the starting frame for biased MD simulations at a given distance from the center of the lipid bilayer. Hereafter, constraint and umbrella simulations with initial structures generated by pulling simulations are referred to as constraint-pulling (CP) and umbrella-pulling (UP), respectively.

In the other approach for generating starting frames, in which free unbiased simulation (20 ns long) was applied, spontaneous coumarin penetration through the DOPC bilayer was observed. Starting frames (spaced 0.1 ± 0.02 nm apart along the z-axis with the lowest potential energy of the structure at the respective points) for umbrella and constraint simulations were chosen as described above. Simulations with these starting structures are henceforth referred to as umbrella-free (UF) and constraint-free (CF), respectively.

With both sets of starting frames, umbrella sampling and constraint simulations (164 simulation windows in total) were carried out as described below for 30 ns per simulation window, except for simulation bins in the 1.0–2.5 nm z-axis region (for which simulation was prolonged for 50 ns, or up to 100 ns for CP and CF simulations, giving in the latter cases up to 6.9 μs of biased simulation in total).

In umbrella sampling a harmonic potential is applied between COMs of two groups of molecules, here the drug coumarin and DOPC lipid bilayer. The distance between COMs of coumarin and DOPC was restrained by a harmonic force constant of 2,000 kJ·mol^–1·nm^–2 (477.9 kcal·mol^–1·nm^–2). The force applied on coumarin was proportional to the square of the displacement from its original position, and a free energy profile was calculated from eq 1(4,55)

1

where P(z) and U(z) are the coumarin distribution and biasing potential along the bilayer normal, respectively. The force constant and distance between simulation windows were chosen to achieve equal sampling, as the presence of regions with low sampling density increases the error of umbrella sampling. Forces acting on coumarin were analyzed, and the free energy profile was reconstructed by the weighted histogram analysis method (WHAM)²⁰ using the g_wham program.⁵⁶

We also calculated a free energy profile from constraint simulations.^14,15,18 In this approach, the distance between COMs of the drug and lipid bilayer was constrained, and the constraint force was monitored. Free energy was then calculated from eq 2(4,16,17,57)

2

where the mean force applied on the molecule ⟨F⃗(z′)⟩_t in certain bilayer depth z′ is integrated along the bilayer normal axis beginning in water until the certain bilayer depth z.

Part of the free energy profile was also calculated from the partitioning displayed in an unbiased simulation using eq 3(15)

3

where K(z) is a partition coefficient estimated for a 0.02 nm bin in bilayer depth z, symmetrized for both leaflets. The partition coefficient is calculated from average mass density of coumarin in certain bin and by normalizing this density – the reference state is set to have K(z) = 1.

The minimum free energy (ΔG = 0 kcal/mol) of coumarin along the bilayer normal was considered the reference state in all profiles. All free energy profiles were calculated for one lipid leaflet and have been symmetrized for the other one. Error estimates of free energy were calculated as integrated standard deviations of the mean calculated either over the bins of 100 bootstraps generated by Bayessian bootstrap analysis by the g_wham program⁵⁶ in umbrella sampling or over the force distribution in 0.1 nm-spaced positions along the z-axis in constraint simulations.

For comparison with experimental data (see later) free energy profiles of 7-acetoxy-4-methylcoumarin and 7-acetoxycoumarin along the normal of a DMPC bilayer were calculated (using a DMPC bilayer structure with 128 DMPC molecules and 3,655 water molecules taken from Tieleman’s Web site,⁵⁸ after replacing 20 molecules of water by 10 Na⁺ and 10 Cl^– ions). The lipid bilayer was equilibrated for 200 ns. 7-Acetoxy-4-methylcoumarin topology was prepared by the simulation protocol described above for coumarin (including the use of RESP partial charges). Initial structure was generated from a 20 ns unbiased free simulation. During this simulation, 7-acetoxy-4-methylcoumarin penetrated to 1.8 nm from the middle of the bilayer and was then pulled into the bilayer for 4 ns with a pulling rate of 1 nm·ns^–1 and a pulling force constant of 500 kJ·mol^–1·nm^–2 (119.5 kcal·mol^–1·nm^–2). The mild force constant was chosen to avoid water artifacts, as the molecule did not penetrate into region 3 freely during the unbiased simulation and was still in touch with water molecules. A 10 ns constraint simulation was performed with the same simulation protocol as applied in the coumarin CF simulation, but the simulation near the equilibrium position (0.8–1.7 nm) was prolonged to 15 ns per simulation bin.

A free energy profile of 7-acetoxycoumarin was obtained by the same protocol as for 7-acetoxy-4-methylcoumarin, except the free simulation lasted 60 ns and during this time 7-acetoxycoumarin penetrated to 0.5 nm from the center of the lipid bilayer, then the molecule was pulled further into the bilayer for 1 ns with a pulling rate of 1 nm·ns^–1 and force constant of 2,000 kJ·mol^–1·nm^–2 (477.9 kcal·mol^–1·nm^–2). The molecule freely penetrated close to the bilayer center and thus was pulled with a higher force constant than in the previous case. A free energy profile was obtained by z-constraint simulation, which yielded a very large minimum energy zone, with substantial variation in mean forces, so the simulation was prolonged to 15 ns in the interval between 1.0 and 2.0 nm and more frames were added (so the distance between simulation windows was 0.05 nm in the zone between 1.0 and 2.0 nm).

Results

Unbiased MD Simulations

Five independent unbiased simulations starting from coumarin in water, 3 μs long in total (2 × 1 μs, 600 ns, 2 × 200 ns), showed a tendency for coumarin to stay at the boundary between regions 2 and 3, as coumarin was most frequently located 1.4 ± 0.1 nm from the bilayer center (see Supporting Information, Figure S1). Once a coumarin molecule entered the bilayer during the first 10 ns of the simulation, it did not leave the lipid bilayer during the rest of simulation (Figure S1). Coumarin occurred in both leaflets because it can transverse the bilayer center spontaneously. Twelve successful (and ten unsuccessful) transitions between leaflets were observed during the 3 μs of simulations (Figure S1). The transition between both leaflets took place on a 100+ ns time scale, but the transition process itself was rapid and lasted several nanoseconds. The unbiased simulations also identified a metastable state of coumarin in the bilayer center (Figure 2), where coumarin stayed up to 10 ns. The transition between the bilayer center and one leaflet occurred on time scales of ps up to ns (Figure S1). The bilayer center penetration barrier calculated from the partition coefficient profile (cf. Equation 3) was 2.1 kcal/mol, but the water/lipids barrier could not be calculated, as the distribution of coumarin in water was not properly sampled (Figure S1 and Figure 2).

Figure 2.

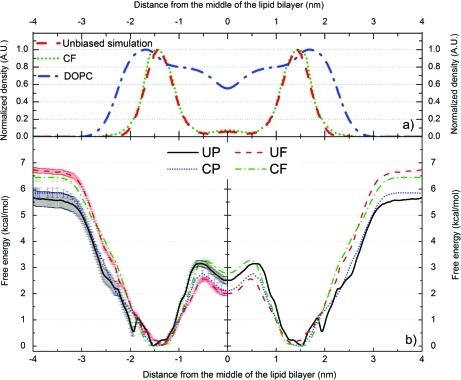
Density profiles of DOPC (blue dash-dotted curves) and coumarin calculated from unbiased MD simulations (3 μs in total; red dashed curves) and from the free energy profile acquired by the CF method (green dotted curve). The density profiles of coumarin obtained from both methods match each other well (upper panel – a). Free energy profiles obtained from biased simulations (lower panel – b). Both umbrella (UP – black curve and UF – red curve) and constraint (CP – dotted blue curve and CF – dotted green curve) simulations provide free energy minima positions for coumarin that overlap well with the maximum density calculated from the free simulation (cf. upper panel – a). The free energy profiles were calculated for one bilayer leaflet and were symmetrized to the other one; the density was symmetrized along the middle of the bilayer. UP and UF refer to umbrella simulations with initial structures obtained by pulling and free unbiased simulation, respectively; CP and CF refer to constraint simulation with pulling and free initial structures, respectively.

Biased Simulations

The free energy profiles of coumarin in DOPC lipid bilayer reconstructed from four types of biased (UP, CP, UF, and CF) simulations showed similar trends (Figure 2). Typically, the free energy dropped as coumarin entered region 1 (cf. Figure 1). As it moved deeper into the bilayer, the free energy decreased and the global free energy minimum was reached at the border between regions 2 and 3. When coumarin moved deeper into the bilayer center, the free energy rose. A small local minimum was located in the bilayer center (region 4). So, one global minimum at 1.35–1.53 nm (with a thermally accessible region within 1.05–1.95 nm at 310 K – by thermally accessible region we mean an area with energy barrier of RT (0.616 kcal/mol at 310 K) from the energy minimum) and one local minimum in the middle of the lipid bilayer were common features of all free energy profiles (Figure 2).

The bilayer center penetration barriers (ΔG^pen) obtained from the free energy profiles fitted a narrow interval, varying between 2.6–3.3 kcal/mol (Table 1, Figure 2). The water/lipids barrier (ΔG^wat) fitted an interval of 5.7–6.7 kcal/mol, and the values calculated with pulling initial structures were lower than those calculated in simulations with initial structures from unbiased simulations (ΔG^wat values derived from UP, CP, UF, and CF simulations were 5.7 ± 0.3, 5.9 ± 0.2, 6.7 ± 0.1, and 6.4 ± 0.2 kcal/mol, respectively; Table 1 and Figure 2). The UP free energy profile also showed a very shallow local minimum at 1.95 nm with an energy barrier of 0.5 kcal/mol (Figure 2). The free energy barrier of this minimum was higher than the free energy error bar estimated by statistical bootstrap analysis (0.1 kcal/mol), but the error seemed to be underestimated. As the depth of the shallow minimum declined with increasing duration of simulation windows (see the following paragraph “Convergence of Biased Simulations”) and no state corresponding to this minimum was observed in the unbiased simulation (Figure S1 in the Supporting Information), we considered this minimum to be an artifact and called it “the artificial minimum”.

Table 1. Properties Extracted from the Free Energy Profiles Calculated by Four Different Simulation Protocols with 50 ns of Biased Simulation Per Window^a.

simulation protocol	position of minimum (nm)	area within a reach of a thermal motion at 310 K (nm)		ΔGwat(kcal/mol)	ΔGpen(kcal/mol)
UP	1.53	1.15	1.95	5.7 ± 0.3	3.2 ± 0.2
UF	1.35	1.09	1.75	6.7 ± 0.1	2.6 ± 0.1
CP	1.47	1.20	1.71	5.9 ± 0.2	2.8 ± 0.1
CF	1.49	1.10	1.80	6.4 ± 0.2	3.3 ± 0.1

^aUP and UF refer to umbrella simulations with initial structures obtained by pulling and free unbiased simulation, respectively; CP and CF refer to constraint simulation with pulling and free initial structures, respectively. ΔG^wat and ΔG^pen are water/lipid and bilayer center penetration barriers, respectively. Area within reach of a thermal motion is considered to be the area surrounded by an energy barrier of RT (0.616 kcal/mol, T = 310 K).

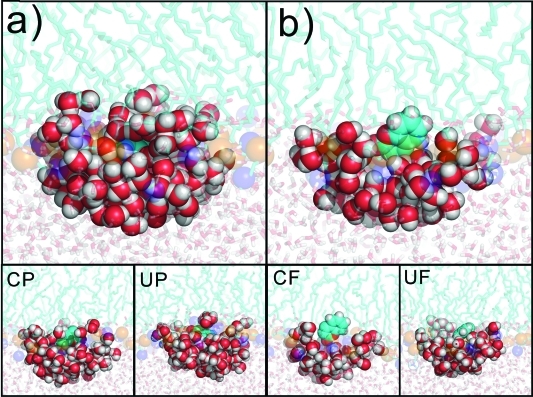
As such “artificial minima” may be due to systematic sampling errors, it was of considerable interest to determine the reasons for such behavior. The primary reason lay in the starting structures, which were generated by pulling coumarin along the bilayer normal in the UP and CP simulations. The pulling caused deformation of the lipid bilayer,^13,18 leading to a funnel-shaped bilayer surface depression (see Supporting Information, Figure S2) induced by solvated coumarin (Figure 3a). In other words, the pulling procedure produced structures in which coumarin embedded in the bilayer was hydrated by a few water molecules. The defects, namely these which were deeper in lipid bilayer, were eliminated during biased MD simulations, as water was expelled from the hydrophobic bilayer interior and bilayer relaxed rapidly on hundreds of picoseconds time scale. The relaxation time grew with increasing distance from the bilayer center. In the area of the artificial minimum (∼1.7–2.0 nm), close to the bilayer surface, the water defects were eliminated on a tens of nanoseconds time scale. It is of considerable interest that relaxation occurred significantly more rapidly in the CP than in UP simulations, and thus the membrane deformation was eliminated more rapidly (Figure 3 and Figure 4). The lipid bilayer depression was not observed during a spontaneous embedment of coumarin in the lipid bilayer in the unbiased simulations, hence the starting structures for biased simulations based on the snapshots from the unbiased simulation were free of this artifact (Figure 3b).

Figure 3.

Initial structures (at 1.9 nm from the bilayer center) obtained by pulling (a) and free simulation (b) show a difference in coumarin hydration. The structure generated by pulling simulations indicates that coumarin is pulled to the lipid bilayer with its solvation shell, which causes funnel-like bilayer deformation. Snapshots taken at 10 ns indicate that CP eliminates coumarin hydration more rapidly than UP. Both CF and UF simulations lead to similarly solvated coumarin structures. Carbons are colored in cyan, oxygens red, and hydrogens white. The olive and blue balls represent DOPC phosphate and nitrogen atoms, respectively. Waters surrounding coumarin are colored as red/white balls.UP and UF refer to umbrella simulations with initial structures obtained by pulling and free unbiased simulation, respectively; CP and CF refer to constraint simulation with pulling and free initial structures, respectively.

Figure 4.

Convergence of free energy profiles, positions of energy minima and energy barriers. The simulation windows within 1.0–2.5 nm have been simulated for 50 and 100 ns in case of UP and UF simulations of CP and CF simulations, respectively; the rest of each profile is calculated from 30 ns of simulation. Free energy profiles calculated from short simulation times (<5 ns) are biased by high error, because of small data set and nonequilibrium starting structures. Free energy profiles obtained by UP and CP simulations (left) show slow elimination of an artificial minimum (∼2.0 nm) and deepening of the global minimum (∼1.5 nm). Free energy profiles obtained from UF and CF simulation are consistent in coumarin positioning and have deeper energy minima than those obtained from UP and CP simulations. The global minimum energy is considered as reference. UP and UF refer to umbrella simulations with initial structures obtained by pulling and free unbiased simulation, respectively; CP and CF refer to constraint simulation with pulling and free initial structures, respectively.

Convergence of Biased Simulations

The position of the global minimum converged more rapidly in biased simulations starting from free (unbiased) simulations (UF and CF) than in simulations starting from pulling (UP and CP) simulations (Figure 4). The free energy profile obtained from UP simulation depended strongly on the length of the simulation windows, and two energetically similar minima in region 2 (one at ∼1.5 and the other at ∼2.0 nm) were observed during the beginning of this simulation (Figure 4). After 10 ns the minimum at ∼1.5 nm became the global minimum and its position converged to 1.53 nm, while the energy barrier of the artificial minimum decreased to 0.5 kcal/mol. During the first 16 ns of UP simulation the area accessible by thermal motion (ΔG_min+RT) gradually widened from 0.90 nm after 5 ns to 1.10 nm, and the region accessible by thermal motion thereafter declined to 0.80 nm. ΔG^wat gradually rose throughout the simulation, to a final value (at 50 ns) of 5.7 ± 0.3 kcal/mol, while ΔG^pen dropped within the first 16 ns of simulation, slowly rose until 30 ns, and then fluctuated around a final value of 3.2 ± 0.2 kcal/mol (cf. Figure 4).

The free energy profile obtained from CP simulation also displayed two minima initially, while the artificial minimum (at ∼2.0 nm) quickly vanished, and after ∼15 ns there was no sign of this minimum. The area within reach of thermal motion gradually narrowed from 1.38 nm after 5 ns of simulation to 0.51 nm after 40 ns and thereafter remained constant. ΔG^wat gradually rose throughout the simulation, to 5.9 ± 0.2 kcal/mol, while ΔG^pen grew during the first 11 ns of simulation, until 20 ns of simulation it gradually declined to 2.8 ± 0.1 kcal/mol and then fluctuated around this value. In the last 50 ns of the simulation prolonged to 100 ns the position of the energy minimum remained constant; ΔG^pen fluctuated around 2.8 ± 0.1 kcal/mol and ΔG^wat continued to rise, to 6.2 ± 0.2 kcal/mol.

The position of the minimum in the UF free energy profile was almost constant (within 1.29–1.35 nm) during the whole simulation time, with the area accessible by thermal motion slowly widening from 0.44 to 0.66 nm. ΔG^wat slowly decreased during the first 19 ns of simulation, then very slowly increased, and after 30 ns ΔG^wat converged to 6.7 ± 0.1 kcal/mol, while ΔG^pen became convergent after 20 ns, fluctuating within 2.6 ± 0.1 kcal/mol.

The CF free energy profile showed a minimum position within 1.29–1.49 nm, and the area of thermal motion slowly widened from 0.41 to 0.70 nm. ΔG^wat fluctuated around 6.4–7.0 kcal/mol during the whole simulation time, while ΔG^pen decreased during the first 10 ns of simulation and then fluctuated around 2.9–3.3 kcal/mol. The prolonged simulation to 100 ns showed similar trends – a free energy minimum at 1.29 nm, thermal motion within 0.6 nm, a constant ΔG^wat value of 7.0 kcal/mol after 80 ns, and ΔG^pen already convergent with a final value of 3.1 ± 0.1 kcal/mol.

Effect of Coumarin Partial Charges

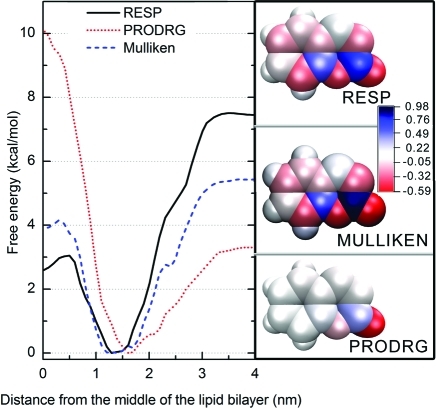
As assignment of partial charges might introduce another systematic sampling error into free energy calculations, we carried out 10 ns long CF simulations with PRODRG and Mulliken charges (assigned partial charges are listed in Supporting Information Table S1), to assess the extent to which the partial charges affected the free energy profiles. Coumarin with partial charges assigned by PRODRG bore a dipole moment of 9.5 D, assignment of Mulliken partial charges led to 6.0 D, and RESP partial charges resulted in a dipole moment of 4.9 D (Figure 5). The dipole moment based on RESP charges was close to that of coumarin in the gas phase calculated by the hybrid DFT method (B3LYP/cc-pvDZ) of 4.6 D, Mulliken partial charges represent a compromise between the dipole moment in water (represented by continuum dielectrics with ε_r = 78.39) and heptane (ε_r = 1.92), which we calculated by the CPCM/B3LYP/cc-pVDZ method and that resulted in 6.7 and 5.4 D, respectively. Considering these values, the dipole moment stemming from PRODRG charges seemed to be unreliably overestimated, which could systematically bias free energy profiles based on PRODRG charges. The global minimum of the ΔG profile of coumarin bearing RESP partial charges was located at 1.29 nm (CF with a 10 ns sampling window), energy minimum of coumarin bearing Mulliken partial charges was localized at 1.20 nm, and the minimum for PRODRG-charged coumarin was shifted toward the bilayer/water interface, at 1.62 nm. The global free energy minimum for RESP-charged coumarin was also considerably deeper than for Mulliken-charged or PRODRG-charged coumarin (ΔG^wat: 7.5, 5.6, and 3.3 kcal/mol, respectively), and the bilayer center penetration barriers of the systems also differed (ΔG^pen: 3.1, 4.6, and 10.1 kcal/mol, respectively) (Figure 5). As expected, the energy cost of bilayer center penetration grows with the increasing dipole moment, and reversely the energy barrier between lipid bilayer and water decreases with the growing dipole moment.

Figure 5.

Left panel: free energy profiles calculated for coumarin with PRODRG (red dotted curve), Mulliken (blue dashed curve), and RESP charges (black curve) by constraint simulation (CF) with initial structures obtained by free simulation using 10 ns windows. Coumarin with PRODRG partial charges is shifted to the outer part of the lipid bilayer. The bilayer center penetration barriers grow and the water/lipids barriers decrease with increasing dipole moment. The right panel shows that the partial charges (mapped on the vdW surface) calculated by RESP (upper part) and Mulliken population analysis (middle) are spread along the whole molecule, while partial charges assigned by PRODRG (lower part) are localized close to coumarin oxygens.

Comparison with Experimental Data

To our knowledge, the precise positioning of bare coumarin in a DOPC bilayer has not yet been studied experimentally; therefore, we compared the results of our theoretical calculations to data obtained in experiments with coumarin derivatives. Depths of several coumarin derivatives in dimyristoylphosphatidylcholine (DMPC) bilayer have been studied in NMR investigations,^2,46,47 in which chemical shifts of ¹³C-labeled derivatives were used to assess the polarity of the surroundings of ¹³C atoms and hence estimate their depth in the lipid bilayer. Results of the cited experiments indicate that the mean position of 7-acetoxy-4-methylcoumarin is at the border of regions 2 and 3 in DMPC lipid bilayer (0.7 nm from the DMPC choline nitrogens, corresponding to 1.2 nm from the center of the bilayer); ¹³C-labeled carbons of the derivative (C2 and C4, see Figure 6) appeared to be located 0.72 and 0.70 nm from the choline nitrogens, corresponding to 1.18 and 1.20 nm from the bilayer center, respectively. Another coumarin derivative, 7-acetoxycoumarin, was apparently located closer to the bilayer interface in region 2, with its ¹³C-labeled (C2 and C4) carbons 0.44 and 0.59 nm from the choline nitrogen, corresponding to 1.46 and 1.31 nm from the bilayer center, respectively. We recalculated the experimental positions (originally expressed as distances from the bilayer surface) as distances from the bilayer center to facilitate direct comparison with results of this study. In this recalculation, the distance between the DMPC bilayer surface and center was set at 1.9 nm: the mean distance between the bilayer center and maximum density of nitrogens (regarded as the membrane surface in the cited NMR experiments) in corresponding MD simulations.

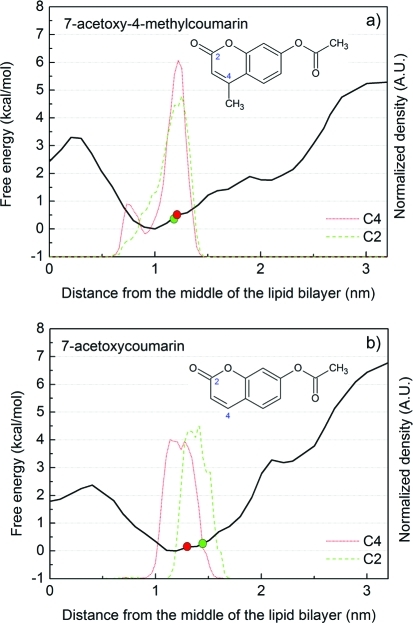
Figure 6.

Free energy profiles and structures of coumarin derivatives (7-acetoxy-4-methylcoumarin, upper panel (a), and 7-acetoxycoumarin, lower panel (b)) along a DMPC lipid bilayer normal calculated from constraint simulation with initial structures obtained by free simulation (CF). NMR-observed positions of ¹³C-labeled carbons (C2 and C4) are displayed as red and green circles, respectively, and the positions of C2 and C4 carbons calculated from simulation are depicted as green and red curves, respectively. The positions of marked carbons of both coumarin derivatives are in good agreement with the positions observed by NMR.

For the comparison we employed the most effective simulation protocol of those considered here to calculate the free energy profiles of the coumarin derivatives described above, briefly comprising unbiased simulation followed by constraint simulation with 10 ns simulation bins (see Methods for details). The profile obtained for 7-acetoxy-4-methylcoumarin indicated the free energy minimum position of its COM to be 1.0 nm from the center of the DMPC bilayer (Figure 6), with a thermally accessible region between 0.8 and 1.3 nm. The thermally accessible region estimated from the simulation (0.8–1.3 nm) matched that acquired from NMR experiments, where 7-acetoxy-4-methylcoumarin was located 1.2 ± 0.1 nm from the bilayer center. In addition, the positions of its C2 and C4 carbons calculated from simulations (1.25 and 1.21 nm, respectively) agreed well with those estimated from experiments (1.18 and 1.20 nm, respectively), although the C4 carbon seems to flip-flop between two positions in the bilayer (the other at 0.76 nm, with ca. 14% population, see Figure 6 up).

The free energy minimum position of the COM of 7-acetoxycoumarin in the simulation was located 1.2 nm from the bilayer center, with a thermally accessible region between 0.75 and 1.35 nm. The simulated distances of the C2 and C4 carbons from the bilayer center at this point (1.34 and 1.19 nm, respectively) again matched those obtained from the NMR data reasonably well (1.46 and 1.31 nm, respectively, see Figure 6 down).

In summary, the MD results for both coumarin derivatives agreed reasonably well with the experimental results, notably 7-acetoxy-4-methylcoumarin was located deeper in the bilayer than 7-acetoxycoumarin, and the carbon atoms’ positions calculated from simulations matched those deduced from experiments.

Discussion

Coumarin Preferentially Stays in Bilayer Regions 2 and 3 in Unbiased Simulations

During the five independent unbiased simulations (3 μs long in total) coumarin preferred the lipid bilayer phase rather than the aqueous phase, because it quickly (within <10 ns) entered the lipid bilayer and remained there for the rest of the simulation time (Figure S1 in the Supporting Information). The preferentially occupied position was at 1.4 ± 0.1 nm, at the border of regions 2 and 3, and the molecule was oriented mainly with its oxygens pointing toward the water phase (data not shown). In addition, coumarin penetrated the lipid bilayer spontaneously, i.e., moved from one leaflet to the other, remaining at the preferentially occupied positions in both leaflets for several hundreds of nanoseconds between brief (a few ns) visits to the lipid bilayer center (Figure S1 in the Supporting Information). Similarly, the transition movements were quite rapid, generally occurring within several nanoseconds.

Some key penetration properties were identified from the unbiased simulations, namely positions of local and global free energy minima and qualitative estimates of the height of energy barriers (Figure 2). The water/lipids barrier, ΔG^wat, seemed to be higher than the bilayer center penetration barrier, ΔG^pen. The number of penetration events allowed us to roughly estimate the absolute value of the bilayer center penetration barrier, at 2.1 kcal/mol (eq 3). However, the estimated ΔG^pen value should be interpreted with care, due to the limited sampling as only a small number of transitions between the minima were observed, and ΔG^wat could not be calculated as the water phase was not sampled adequately (Figure 2). Nevertheless, the spontaneous embedding of coumarin in DOPC bilayer strongly indicates that this is a barrierless process and that coumarin prefers the bilayer phase, in accordance with expectations based on coumarin’s logP_oct/wat value.

Free Energy Profiles Obtained by Biased and Unbiased Simulation Agree

The final free energy profiles obtained by all simulation protocols (UP, CP, UF, and CF) were in accord (Figure 2), but those obtained from the unbiased simulations provided more accurate information. The global energy minimum was found at 1.44 ± 0.09 nm, while a local energy minimum was localized in the membrane center. The presence of a local energy minimum in the lipid bilayer center agrees with previous findings presented by Bemporad et al.,²³ of such local minima for some other small solutes, e.g. water and acetamide. In our case, the bilayer center penetration barrier (ΔG^pen) of coumarin spanned 2.6–3.3 kcal/mol (Table 1, Figure 2), close to the ΔG^pen estimated roughly from the unbiased simulation (2.1 kcal/mol). In contrast, the water/lipids barrier (ΔG^wat) varied significantly with time and method used (see below). The estimated ΔG^wat from CF simulation (which is taken as reference, as constraint biasing eliminates possible artificial errors quicker) was 6.4 ± 0.2 kcal/mol (Figure 2). The free energy profiles therefore confirmed that coumarin more readily penetrates the bilayer than escapes to the water phase.

Partial Charges – The Force Field Issue

Neither accurate unbiased simulation, nor accurate free energy profile calculation, is possible without a careful choice of force field. The Berger force field (using Mulliken partial charges calculated at HF/6-31G* level (in gas phase)⁵⁰) used for lipids^39,44 was tested and shown to provide area per lipid and volume per lipid values that correspond well with experimental values.⁴⁴

Further, as coumarin parameters were not available in standard data sets for lipid simulations, they had to be acquired separately. Generally, atom types and corresponding parameters can be adopted for a nonlipid molecule from the standard data sets quite safely, but the set of partial charges had to be carefully considered, as it may introduce a serious systematic sampling error in lipid bilayer-guest molecule simulations. We addressed this issue by using three sets of partial charges (Figure 5, Table S1 in the Supporting Information): one generated by the PRODRG server, one assigned by Mulliken population analysis, and the third generated by applying the RESP procedure in B3LYP/cc-pVDZ calculations of electrostatic potential in gas phase. Generally, increasing the dipole moment of a molecule (by use of PRODRG or Mulliken partial charges) resulted in a lower ΔG^wat and higher ΔG^pen, in accordance with expectations, given the higher polarity of coumarin bearing PRODRG or Mulliken charges in comparison with RESP partial charges (Figure 5). With only these profiles it would be difficult to decide which partial charges provided more reliable results. However, PRODRG charges led to overestimation of the dipole moment of coumarin and (as mentioned above) partial charges assigned by the PRODRG server lead to unrealistically strong partitioning in water in cyclohexane/water systems as found by Lemkul et al.⁴⁰ The latter finding agrees with the trends observed in our lipid bilayer simulations. In summary, RESP charges seem to provide more accurate models for simulations of lipid bilayer-guest molecule systems than PRODRG charges (although whether the RESP charges should ideally be based on gas phase or solvent-polarized ESP, and if they can be robustly combined with the Berger force field for lipids, remains to be determined).

Convergence of Free Energy Profiles – The Artificial Minimum Issue

We have shown here that the convergence of free energy profiles was significantly influenced by the generation of initial structures when followed by the biasing method. The biased simulations starting from the pulling simulations (UP and CP) suffered from bilayer deformation induced by pulling coumarin from the water phase toward the bilayer center (Figure 3). Similar bilayer deformations have been repeatedly previously observed^13,18,30 and identified as a systematic sampling artifact in biased lipid bilayer simulations. For example, Neale et al.¹³ observed bilayer deformations when a charged molecule was embedded in the bilayer. We observed a funnel-shape bilayer surface depression (Figure S2 in the Supporting Information), caused by water hydrating the polar parts of coumarin penetrating the lipid bilayer more deeply and thereby exacerbating bilayer deformation during the pulling simulations. The bilayer deformation caused an artificial minimum (∼2.0 nm) in the free energy profiles in region 2 (Figure 2), whereas in unbiased simulation coumarin never stayed longer in this position, and its behavior showed no sign of reaching a local energy minimum.

This artificial minimum was most profound when short simulation times (<5 ns) for each sampling bin were applied, and it slowly disappeared when the simulation time was prolonged (Figure 4). The main reason for the slow convergence and need for longer simulation times was the slow coumarin water shell elimination in region 2. Furthermore, the presence of the artificial minimum led to underestimation of ΔG^wat in simulations using the initial structure set generated by pulling simulation (CP and UP). While ΔG^wat values obtained by CF and UF simulations seemed to reach convergence, they did not reach convergence in UP and CP simulations during 50 ns of simulation (or even during 100 ns of CP simulation), although both UP and CP yielded ΔG^wat values close to those obtained from CF and UF simulations.

In this respect, constraint biasing was more effective, as the artificial minimum was eliminated within 15 ns per bin (in CP), while there were signs of the artificial minimum in UP simulation even after 50 ns per bin (Figure 4). Even longer times may be needed in simulations of polar or charged residues, as previously shown by MacCallum et al.³⁰ and Neale et al.,¹³ who found that 80 to 205 ns per bin may be required to achieve convergence in umbrella simulations with charged solutes. In contrast, for nonpolar solutes Neale et al. achieved convergence more rapidly (in some cases after 20 ns per bin).^, These water artifacts seem to be present when nonequilibrated initial structures are used for biased simulation. The higher efficiency of constraint over umbrella biasing is also consistent with the recent observation by Gunsteren et al.,⁶¹ that constraint-biased simulation using force averaging is the most effective method for calculating potential of mean force with respect to a distance from a given reference point.

Convergence of the free energy profiles was clearly achieved more rapidly when using starting structures acquired from unbiased (UF and CF) simulations in comparison with the pulling simulation (UP and CP), since in cases of UF and CF simulation the free energy profiles changed only marginally with increases in the length of the simulation bins (Figure 4). Therefore we recommend starting the calculation of free energy profile with an unbiased simulation for all molecules, in a case of more polar molecules a slow pulling simulation (pulling force constant <500 kJ·mol^-1·nm^-2 (119.5 kcal·mol^-1·nm^-2) and a pulling rate <1 nm·ns^-1) from the deepest position in the lipid bilayer should follow. Thus, this approach was used for comparing the calculated results with experimental data, and the calculated positions of 7-acetoxy-4-methylcoumarin and 7-acetoxycoumarin in DMPC bilayer agreed well with positions derived from NMR experiments (Figure 6). In summary, whenever possible biased simulations should start from geometries acquired from unbiased MD simulations, and constraint biasing is the recommended and quickly converging method.

Conclusion

The convergence in time of free energy profiles of coumarin along a DOPC bilayer normal, calculated by both umbrella sampling and z-constraint techniques, was thoroughly analyzed. Two sets of starting structures were also considered: one based on unbiased MD simulation and the other on “pulling” coumarin along the bilayer normal. Water defects on the lipid bilayer surface were identified in the structures obtained by pulling simulation but not in structures acquired from unbiased simulation. Consequently, the free energy profiles converged more rapidly when starting frames from unbiased simulations were used. The used methods for free energy profile calculation (umbrella and constraint simulation) are quite equivalent when applied on an error-free set of starting structures. However, if the membrane defects are present, the z-constraint simulation leads to more rapid convergence than umbrella sampling. In summary, for efficient calculation of convergent free energy profiles of druglike molecules along bilayer normals, we recommend using z-constraint biased MD simulations based on as much starting geometries acquired from unbiased MD simulations as possible, otherwise when pulling simulation is employed, the biased simulation might need far longer time to reach convergence.

Supporting Information Available

Details of the recommended simulation protocol, used partial charges, four supplemental figures, and one equation. Table S1: Partial charges on coumarin atoms used in the paper. Figure S1: Position of coumarin in unbiased simulations. Figure S2: Funnel shape water defect caused by pulling coumarin into the membrane. Figure S3: Effect of window spacing in constraint and umbrella simulations. Figure S4: Atom labels as used in Table S1. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.