osDesign: An R Package for the Analysis, Evaluation, and Design of Two-Phase and Case-Control Studies

Abstract

The two-phase design has recently received attention in the statistical literature as an extension to the traditional case-control study for settings where a predictor of interest is rare or subject to missclassification. Despite a thorough methodological treatment and the potential for substantial efficiency gains, the two-phase design has not been widely adopted. This may be due, in part, to a lack of general-purpose, readily-available software. The osDesign package for R provides a suite of functions for analyzing data from a two-phase and/or case-control design, as well as evaluating operating characteristics, including bias, efficiency and power. The evaluation is simulation-based, permitting flexible application of the package to a broad range of scientific settings. Using lung cancer mortality data from Ohio, the package is illustrated with a detailed case-study in which two statistical goals are considered: (i) the evaluation of small-sample operating characteristics for two-phase and case-control designs and (ii) the planning and design of a future two-phase study.

1. Introduction

Researchers have at their disposal a wide variety of study designs with which to identify and assess associations between predictors and outcomes. In epidemiology, the case-control design is a mainstay of observational research for binary outcomes (Prentice and Pyke 1979; Breslow and Day 1980). While the design provides an efficient framework for investigating a rare outcome, gains over simple random sampling may be lost if the predictor or exposure of interest is also rare. For the setting where the exposure is binary, White (1982) proposed using the two-phase design as a means to improving efficiency (Neyman 1938). In this context, the design stratifies the population jointly on the outcome and exposure, resulting in four phase I strata. From each of these, a sample is drawn with additional exposure/confounder information retrospectively ascertained. Similar to the case-control design, efficiency gains arise due to the over-sampling of a rare sub-population (particularly exposed cases). Over the past 25 years the statistical literature has built on this (and other) work, to provide a comprehensive methodological treatment of the two-phase design; key recent references include Breslow and Holubkov (1997a), Scott and Wild (1997) and Breslow and Chatterjee (1999).

Despite the potential for substantial efficiency gains relative to a case-control design, the two-phase design has not been widely adopted. To illustrate this, and motivated by our work in epidemiologic applications, we recently conducted a survey of five top-line epidemiological/medical journals (American Journal of Epidemiology, Epidemiology, International Journal of Epidemiology, New England Journal of Medicine and Journal of the American Medical Association). Of the 4,792 studies published between 2002 and 2007, 816 used the case-control design; only one specifically employed the two-phase design. The lack of uptake may be due, in part, to a paucity of general-purpose, readily-available software for (i) the analysis of two-phase designs and (ii) the evaluation of small-sample operating characteristics, such as bias and power.

In this article we introduce and provide an overview of a new R (R Development Core Team 2011) package, osDesign, that contains a suite of functions useful when designing and analyzing two-phase and case-control studies. The package is available from the Comprehensive R Archive Network at http://CRAN.R-project.org/package=osDesign. In Section 2 we provide a brief review of the two-phase design including notation, an overview of estimation/inference techniques and a summary of the published literature on design considerations. Section 3 outlines a proposed simulation-based algorithm for evaluating small-sample operating characteristics of two-phase and case-control designs, implemented in the osDesign package. Sections 4, 5, and 6 illustrate the package with a detailed case-study using lung cancer mortality data from Ohio. Section 7 briefly discusses the trade-off between computing time and accuracy inherent to simulation-based estimation. Finally, Section 8 concludes with a brief summary and areas for further work.

2. The two-phase design

Let Y be the binary outcome under investigation and X a vector of explanatory variables which will generally include the exposure of interest as well as confounders and effect modifiers. Suppose the relationship between Y and X is characterized via the logistic regression model:

$$P(Y=1\mid \mathbf{X}=\mathbf{x})=\frac{\exp \{{\beta }_0+{\mathbf{x}}^{\top }{\beta }_{\mathbf{x}}\}}{1+\exp \{{\beta }_0+{\mathbf{x}}^{\top }{\beta }_{\mathbf{x}}\}}$$ (1)

In the context of this work, the primary statistical task is to perform estimation and inference with respect to the vector of exposure-specific log odds ratios, β_x. The rest of this section outlines the general two-phase sampling scheme and corresponding likelihood, presents an overview of estimation and inference techniques, and reviews the literature and available software for designing two-phase studies.

2.1. Data collection scheme

Initially, suppose N individuals from the population of interest are observed. These data can either be a complete enumeration of the observable population or a large sample drawn cross-sectionally, prospectively or retrospectively (Breslow and Holubkov 1997b). In addition to outcome status, some additional information is available for all N observed individuals; using this information a stratification variable, denoted by S and taking on one of K levels is constructed. For example if sex and age information is available, S could be constructed by either taking sex alone or categorizing age or some combination of both.

The cross-classification by Y and S is referred to as the phase I data and yields N_0k controls and N_1k cases in the k-th stratum of S, k = 1,…, K; Table 1 summarizes the notation.

Table 1.

Notation for the phase I data.

	S = 1	S = 2	…	5 = K	S = K
Y = 0	N10	N02	…	N0K	N0
Y = 1	N11	N12	…	N1K	N1

Given the phase I cross-classification in Table 1, phase II involves drawing n_yk individuals at random from the N_yk in each of the 2K outcome by stratum combinations. Note, when there is no stratification (or, equivalently, K = 1) Table 1 is analogous to a case-control sampling frame for the phase I population/sample.

For each individual sampled at phase II, detailed exposure/confounder information is (restro-spectively) obtained resulting in the covariate vectors x_yki, for i = 1,…, n_yk. The set of n = Σ_y Σ_k n_yk covariate vectors are collectively referred to as the phase II data.

2.2. Two-phase likelihood

The observed data in a two-phase study consist of two sets of random quantities: the 2K phase I counts, {N_yk; y = 0, 1, k = 1,…, K}, and the n phase II covariate vectors, {x_yki; y = 0, 1, k = 1,…, K, i = 1,…, n_yk}. When the phase I data arise via a prospective sample from the underlying population Scott and Wild (1991) showed that the likelihood for the two-phase design consists of two sets of contributions, for the phase I counts and phase II data:

$$\prod _{y=0}^1\prod _{k=1}^{K}P{(Y=y\mid S=k)}^{N_{yk}}\times \prod _{y=0}^1\prod _{k=1}^K\prod _{i=1}^{n_{yk}}P(\mathbf{X}={\mathbf{x}}_{yki}\mid Y=y,S=k).$$ (2)

The primary challenge in performing estimation and inference based on (2) is accounting for the retrospective nature of the data collection at phase II. Following similar arguments to those developed for the analysis of case-control studies (Prentice and Pyke 1979), the retrospective phase II contribution can be re-parameterized to give two components: a parametric prospective component for the outcome data and a non-parametric component for the marginal exposure distribution (Holubkov 1995). This induces a series of constraints on the β_x parameter space, however, which must be accounted for when performing estimation and inference. When the phase I data are obtained retrospectively, via a case-control scheme, Holubkov (1995) showed that the two-phase likelihood takes on a similar form as (2) but with the prospective P(Y = y|S = k) terms in the phase I contribution replaced by retrospective P(S = k|Y = y) terms. Re-parameterization of these latter terms induces a second series of constraints, although estimation and inference for the two types of two-phase designs is asymptotically equivalent (Breslow and Holubkov 1997a; Breslow and Chatterjee 1999).

2.3. Estimation and inference

The key advantage of re-parameterizing the two-phase likelihood is that it is then directly expressed in terms of the prospective model (1), the model of scientific interest. However, as noted, the re-parameterization induces a series of constraints on the parameter space for the regression coefficients {β₀, β_x}; one set for each phase of data collection that is retrospective. Three estimators have been proposed for the analysis of two-phase data: weighted likelihood (WL), pseudo- or profile likelihood (PL) and maximum likelihood (ML). While each is consistent and asymptotically normally distributed, the estimators differ in the extent to which the phase I and phase II constraints are satisfied: ML satisfies both, PL satisfies the phase I constraints and WL ignores both. A consequence is that the estimators differ in their efficiency properties (Breslow and Chatterjee 1999). Throughout, we assume the following conditional independence assumption holds: P(Y = 1|X = x, S = k) = P(Y = 1|X = x). This will hold, for example, when S is an element of X or a surrogate for one or more of the elements in X, with accuracy that does not depend on Y. We note that, while consistency and asymptotic normality of the PL and ML estimators require this assumption, it is not required by the WL estimator.

In the literature, two approaches to standard error estimation have appeared. In both approaches $\text{cov}\left(\widehat{\beta }\right)$ is decomposed into phase I and phase II contributions. The phase I contribution estimates the variance in $\widehat{\beta }$ if full data were available for all N subjects. The phase II contribution is the variance added by incomplete measurement of X. The phase II contribution is always estimated by a `sandwich' formula based on the Horvitz-Thompson variance estimator (Horvitz and Thompson 1952). Approaches for the phase I contribution differ in whether they assume model (1) is correctly specified. When model (1) is correct, the second derivative of the weighted log-likelihood estimates the Fisher information for $\widehat{\beta }$ with complete data, so its inverse estimates the variance of $\widehat{\beta }$. If model (1) is not assumed to be correct, an empirical weighted sandwich estimator can be used for the phase I contribution. Breslow and Holubkov (1997b) provide a detailed description of each estimator, expressions for estimators of their standard errors, as well as algorithms for their implementation.

As is well known, the sandwich and information-based standard error estimators for logistic regression tend to be very similar unless the data set is very small or the model is grossly misspecified. As such, the choice between model-based and model-robust standard error estimators tends not to be of practical importance. Based, in part, on the work of Breslow and Holubkov (1997b), the osDesign evaluates operating characteristics using empirical standard error estimates for the WL estimator and model-based standard error estimates for the PL and ML estimators.

2.4. Design considerations

While methods for estimation and inference are well-developed, to date there is a paucity of published literature specifically on design considerations for two-phase studies. As such, there is little in the literature to provide guidance to the practicing researcher on settings where a two-phase study would be useful and on how to design such a study. In the setting of a binary outcome and binary exposure, White (1982) noted that efficiency may be optimized by making all phase two sample sizes, n_yk, as equal as possible. Reilly (1996) considered optimal sampling strategies for two-stage methods using the mean-score method (equivalent to WL; Reilly and Pepe 1995), while, in the setting of categorical exposure/confounder variables, Schaubel, Hanley, Collet, Bolvin, Sharpe, Morrison, and Mao (1997) presented methods for determining the phase II sample size based on PL estimation. More recently, Hanley, Csizmadi, and Collet (2005) exploited a rearrangement of the variance for the PL estimator to permit an investigation of sample size requirements when confounders are qualitative.

Outside the context of regression problems, Jinn, Sedransk, and Smith (1987) consider optimal phase I and II sample sizes when one is interested in estimating the age distribution of a population, while Shrout and Newman (1989) and Erkanli, Soyer, and Angold (1998) consider estimation of the prevalence of a rare outcome.

Breslow and Chatterjee (1999) considered design issues in the two-phase studies framework, with an application to Wilms tumor prognosis, focusing on choosing the phase I sampling fractions. As with White (1982), they found that choosing the sampling fractions to achieve approximate equal numbers within each of the phase I strata (referred to as a balanced design) yielded efficiency gains over stratification based on outcome or phase I covariates alone. In the setting of binary exposure for which an error-prone surrogate is observed at phase I, McNamee (2005) compared a balanced design to the theoretically optimal design, and found the former to perform well in a broad range of settings. However, in more general settings (i.e., outside a binary exposure), it is unclear that the `one-size-fits-all' approach of a balanced design will be optimal. Further, deciding how to choose the phase I stratification variable, important when faced with several options, has not been adequately addressed.

2.5. Software

Beyond the lack of practical guidance on how to design a two-phase study, there is also a lack of convenient, general-purpose software for analyzing data arising from a two-phase design as well as for evaluating small-sample operating characteristics, such as power. Two notable exceptions are reported by Reilly and Salim (2005) and Schill, Wild, and Pigeot (2007). The former facilitates optimal design when the mean-score method is taken as the analytic approach and is implemented in several statistical packages including R, S-PLUS and Stata. The latter is implemented as a stand-alone application and permits the use of ML, although is restricted to settings with categorical covariates.

3. Evaluating operating characteristics via simulation

Approaches to evaluating operating characteristics of statistical procedures/methods, such as bias, efficiency/uncertainty and power, can broadly be grouped into two classes: formula-based and Monte Carlo or simulation-based. Formula-based approaches rely on closed form expressions for an estimator or a hypothesis test and have been developed in a broad range of settings (e.g., van Belle 2008). Unfortunately, however, formulae are unavailable in many settings that are common to statistical practice. In the context of two-phase studies, general closed-form expressions are unavailable for any of the estimators outlined in Section 2.3. Further, standard error estimators are generally complex, particularly as functions of the key elements for design consideration (the phase I stratification variable, S, and the phase II sample size, n). Finally, formulae-based evaluation of operating characteristics typically rely on asymptotic approximations to some sampling distribution, which may not work well in small-sample situations.

Monte Carlo or simulation-based methods provide a flexible, all-purpose approach to investigating small- and large-sample properties of statistical procedures (e.g., Robert and Casella 2004). In principle, one can implement a simulation in any setting, with the challenge being the proper accounting of all the necessary details. The key purpose, and contribution, of the osDesign package is to provide a convenient, easy-to-use framework for conducting simulation-based investigations of case-control and two-phase designs.

3.1. Algorithm

Both case-control and two-phase designs employ retrospective, outcome-dependent sampling schemes. As such, the explanatory variables X, or some subset, are the random quantities generated by each design. This is in contrast to the typical prospective model specification, where the outcome Y is viewed as the random quantity (see model (1), for example, which conditions on X). Simulating a retrospective, outcome-dependent sampling scheme while accommodating a prospective model specification requires care. Additionally ensuring that the simulation adequately reflects the two sources of uncertainty (i.e., sampling variability at phase I and at phase II) also requires care. One approach is to derive the induced retrospective likelihood, given by (2), and sample directly. This requires accurate accounting of the phase I and II constraints (see Section 2.2), which is complex. The approach we take is conceptually far simpler, as outlined in the following algorithm:

• (i)For the population of interest (i.e., the population to which the research will generalize), specify the marginal exposure distribution, P (X = x).
• (ii)Specify values for the regression coefficients in model (1), β₀ and β_x.
• (iii)Apply model (1) to a `population' of size N with a marginal exposure distribution specified in step (i). Specifically, for each of the N individuals generate a random Bernoulli outcome with their exposure-specific outcome probability (1).
• (iv)Stratify the simulated population according to the case-control or two-phase design under consideration, yielding the phase I data (as in Table 1).
• (v)For each of the resulting 2K strata, `sample' n_yk individuals by drawing (without replacement) from the N_yk individuals previously generated. Since each of the N individuals in the population were initially characterized on the basis of their vector of explanatory variables (steps (i) and (iii)) one can then retrospectively `observe' their value for X. These collectively form the phase II data.
• (vi)Evaluate and record the WL, PL and ML estimators as well as the corresponding estimated standard errors, denoted $\widehat{\beta }$ and $\widehat{\text{se}}\left(\widehat{\beta }\right)$, respectively.
• (vii)Repeat steps (iii) to (vi) B times.

While we believe this algorithm to be conceptually simpler than characterizing and sampling from the retrospective sampling distribution, we note that steps (i) and (ii) will, in general, not be trivial, requiring careful thought and consultation with the subject-matter experts.

3.2. Simulation functions

The core functions for evaluating operating characteristics and estimating statistical power under the two-phase design are tpsSim() and tpsPower(); analogous functions for the case-control design are ccSim() and ccPower(). For each function, a detailed help file is provided as part of the osDesign package. Briefly, a simulation is conducted using the algorithm outlined in Section 3.1. For each of B simulated datasets, five estimators of β_x are evaluated: the complete data ML estimate (i.e., based on complete information on all covariates for all N individuals and denoted CD), the case-control ML estimate (denoted CC) and the three two-phase estimators of Section 2.3 (WL, PL and ML). Evaluation of the CD and CC estimators is via the glm() function within R. The three two-phase estimators are implemented via a function tps(), originally written by Chatterjee and Breslow for S-PLUS, adapted for R and included as part of the osDesign package. Finally, while users can extract output directly from objects created by function in the osDesign package, plotPower() provides functionality for graphically presenting estimates of power from tpsPower() and ccPower().

The core functions automatically compute a series of operating characteristics for each of the five estimators (CD, CC, WL, PL and ML). Some of the simulated datasets may result in a failure to converge, particularly when the phase II sample size is small and/or the choice of phase I stratification variable yields sparse cells (e.g., when K is large). If there are such failures, output from each of the functions additionally returns the number of failures, with the evaluation of the operating characteristics based solely on the subset of B simulated datasets that converged.

4. Example: Lung cancer in Ohio

To illustrate the functionality of the osDesign package, we present a detailed case study using a dataset on lung cancer mortality. Specifically, we (i) estimate small-sample operating characteristics of the WL, PL and ML estimators, under various two-phase designs and (ii) examine design considerations in the context of planning a future two-phase study. Prior to doing so, we provide a brief description of the data and discuss how one specifies the underlying model/design of interest.

4.1. Marginal exposure distribution

The case study examines data on lung cancer mortality from the US state of Ohio. Specifically, the data consist of aggregated population estimates and lung cancer death counts for 55–84 year olds in 1988. The counts are available by 10-year age bands, sex and race and were obtained from the National Center for Health Statistics Compressed Mortality File. A more comprehensive dataset, providing counts further stratified by county as well as for the years 1968 to 1988, is described by Xia and Carlin (1998). The data for this case study are provided as part of the osDesign package:

• R> library(“osDesign”)

• R> data(“Ohio”)

• R> Ohio

	Age	Sex	Race	N	Death
1	0	0	0	429617	1025
2	0	0	1	48382	172
3	0	1	0	476170	507
4	0	1	1	54662	81
5	1	0	0	319387	1477
6	1	0	1	29972	182
7	1	1	0	408229	733
8	1	1	1	38767	62
9	2	0	0	139050	768
10	2	0	1	11610	100
11	2	1	0	244965	391
12	2	1	1	19366	35

Age is coded as 0/1/2 for the 55–64/65–74/75–84 year groups, Sex is coded as 0/1 for male/female and Race is coded as 0/1 for white/non-white. The columns labelled N and Death provide the population counts and number of lung cancer deaths, respectively. Jointly, the first four columns of the Ohio dataset form the marginal exposure distribution (across N = 2,220,177 individuals), required in step (i) of the simulation algorithm outlined in Section 3.1.

4.2. Model specification

For both the two-phase and case-control designs, the target of estimation and inference is some logistic regression model for the binary outcome Y. Let A₁ be a binary indicator of whether or not an individual's age is between 65 and 74 years, and A₂ a binary indicator of whether or not the age is between 75 and 84 years. Further, let S be a binary indicator of sex and R a binary indicator of race (both coded as in the Ohio data). Finally, let Y = 0/1 be a binary indicator of lung cancer mortality status. We consider the following two logistic models for π = P(Y = 1| A₁, A₂, S, R):

$$\mathrm{logit}\left(\pi \right)={\beta }_0+{\beta }_{\mathrm{A}1}{A}_1+{\beta }_{\mathrm{A}2}{A}_2+{\beta }_{\mathrm{S}}S+{\beta }_{\mathrm{R}}R,$$ (3)

$$\mathrm{logit}\left(\pi \right)={\beta }_0+{\beta }_{\mathrm{A}1}{A}_1+{\beta }_{\mathrm{A}2}{A}_2+{\beta }_{\mathrm{S}}S+{\beta }_{\mathrm{R}}R+{\beta }_{\mathrm{SR}}S\times R.$$ (4)

Model (3) consists solely of main effects for each of the three explanatory variables while model (4) further incorporates an interaction term between sex and race.

Specification of a logistic model within the osDesign package is achieved via a `design matrix', denoted by the generic argument X. The first column of the design matrix consist of 1's (specifically for the intercept parameter) while each subsequent column represents an individual predictor. The coding of each predictor column follows the same convention of having a referent group coded as 0 and subsequent categories as increasing integers. The induced model specification is then obtained via an application of the factor() function to each column of X and concatenated to construct an R formula object for use in either the glm() or tps() functions. This process can be reversed to construct the appropriate design matrix for any given model. For example, the specifications corresponding to models (3) and (4) are

• R> XM <- cbind(Int = 1, Ohio[, 1:3])

• R> XI <- cbind(XM, SbyR = XM[, 3] * XM[, 4])

• R> XM

	Int	Age	Sex	Race
1	1	0	0	0
2	1	0	0	1
3	1	0	1	0
4	1	0	1	1
5	1	1	0	0
6	1	1	0	1
7	1	1	1	0
8	1	1	1	1
9	1	2	0	0
10	1	2	0	1
11	1	2	1	0
12	1	2	1	1

It is important to note that XM and XI do not correspond to the standard definition of a design matrix. In both models (3) and (4), for example, the age variable is included via two dummy variables (with corresponding regression coefficients, β_A1 and β_A2); in a standard design matrix these would be represented by two separate columns as follows:

• R> cbind(Int = 1, Age1 = as.numeric(Ohio[, 1] == 1), + Age2 = as.numeric(Ohio[, 1] == 2), Ohio[, 2:3])

While the osDesign package currently allows arbitrary categorical variables in the specification of the underlying logistic model, continuous predictors are not accommodated at this time. As we expand upon below, the approach taken for the osDesign package permits the straightforward specification of the phase I stratification variable, S, in terms of the columns of X. An additional advantage is the representation of data as aggregated counts (i.e., binomial outcomes); accommodating continuous explanatory variables precludes aggregation and, for large phase I datasets such as the Ohio data, could dramatically increase the computational burden for each repetition of the simulation. We do note, however, that the tps() function, used for the analysis of data arising from a two-phase design, does accommodate continuous exposures in the model of interest.

Given a model of interest, step (ii) of the algorithm in Section 3.1 requires specification of the `true' values for regression coefficients. For both models (3) and (4), we take these from fits to the complete data:

• R> fitM <- glm(cbind(Death, N – Death) ^~ factor(Age) + Sex + Race, + data = Ohio, family = binomial)

• R> summary(fitM)

…

Coefficients:

	Estimate	Std. Error	z value	Pr(>|z|)
(Intercept)	−5.96210	0.02572	−231.769	< 2e-16	***
factor(Age)1	0.59538	0.03118	19.097	< 2e-16	***
factor(Age)2	0.68796	0.03671	18.738	< 2e-16	***
Sex	−1.00412	0.02879	−34.878	< 2e-16	***
Race	0.28303	0.04238	6.678	2.42e-11	***

• R> fitI <- glm(cbind(Death, N – Death) ^~ factor(Age) + Sex * Race, + data = Ohio, family = binomial)

• R> summary(fitI)

…

Coefficients:

	Estimate	Std. Error	z value	Pr(>|z|)
(Intercept)	−5.97008	0.02599	−229.722	< 2e-16	***
factor(Age)1	0.59547	0.03118	19.099	< 2e-16	***
factor(Age)2	0.68752	0.03672	18.724	< 2e-16	***
Sex	−0.97979	0.03045	−32.182	< 2e-16	***
Race	0.35097	0.05024	6.986	2.84e-12	***
Sex:Race	−0.22213	0.09362	−2.373	0.0177	*

4.3. Design choice

A key defining feature of the two-phase design is that one has access to complete data on a subset of data elements for all individuals in the phase I population/sample (see Section 2.1). Additional data collection efforts are required to obtain complete information on all data elements from a sub-sample; hence the phase II data. Of course, the nature of the available phase I information dictates which elements require collection at phase II. For the Ohio lung cancer data, given three predictors, Table 2 provides the 8 potential designs. Note design #1 has complete information on all individuals at phase I and is, therefore, referred to as the `complete data' design. Design #2 only has access to outcome information at phase I and is consequently the traditional case-control study. Designs #3 to #8 denote the 6 remaining potential two-phase designs. For each design, the third and fourth columns provide the number of phase I strata and the data elements requiring collection at phase II, respectively.

Table 2.

Data availability scenarios for hypothetical two-phase studies of the Ohio lung cancer mortality example

Design	Elements available at phase I	Number of phase I strata	Elements requiring collection at phase II
1a	Y, Age, Sex, Race	24	NA
2b	Y	2	Age, Sex, Race
3	Y, Age	6	Sex, Race
4	Y, Sex	4	Age, Race
5	Y, Race	4	Age, Sex
6	Y, Age, Sex	12	Race
7	Y, Age, Race	12	Sex
8	Y, Sex, Race	8	Age

^aequivalent to a complete data design

^bequivalent to a case-control design

5. Small-sample operating characteristics

Section 4 illustrated the how to specify key quantities, required by the core functions in the osDesign package. In this section we continue the case study and illustrate the use of the package to estimate small-sample operating characteristics for the two-phase and case-control designs.

5.1. A single two-phase design

To illustrate the evaluation of small-sample operating characteristics, consider the two-phase design for which age information is available at phase I (i.e., design #3 in Table 2). Table 3 provides the phase I stratification for the Ohio data.

Table 3.

Phase I data for the Ohio lung cancer mortality data, where S represents the three-level age variable described in Section 4.1.

	S = 1	S = 2	S = 3
Y = 0	1,007,046	793,901	413,697	2,220,177
Y = 1	1,785	2,454	1,294	5,533

Given these phase I data, additional data collection efforts are required to obtain information on sex and race. To this end, suppose sufficient resources exist to obtain such information on n = 300 individuals at phase II; allocating these equally across the 6 strata yields a balanced design for which n_yk = 50, for y = 0, 1 and k = 1, 2, 3.

As outlined in Section 3.2, the core function for evaluating operating characteristics of estimators for such a two-phase design is tpsSim(). In the present context, the basic command for running the simulation is:

• R> ocAge <- tpsSim(B = 10000, betaTruth = fitM$coef, X = XM, N = Ohio$N, + strata = 2, nII0 = c(50, 50, 50), nII1 = c(50, 50, 50), + betaNames = c(“Int”, “Age1”, “Age2”, “Sex”, “Race”), monitor = 100)

While greater detail on the usage of the tpsSim() function is provided by the corresponding help file, we briefly highlight three of the arguments. Firstly, the `strata' argument specifies the choice of the phase I stratification variable by referring to the columns of the design matrix X. For example, in the above sample code, `strata = 2' refers to the second column of XM (i.e., the column representing the three-level age variable). One could similarly stratify on sex or race by specifying `strata = 3' or `strata = 4', respectively. In some settings, information may be available at phase I on more than one exposure variable. For example, suppose sex and race information were available on all 2,220,177 individuals, with age requiring collection at phase II (design #8 in Table 2). Taking S to be sex and race jointly, the appropriate argument would be `strata = c(3, 4)', indicating the third and fourth columns of XM.

Secondly, the `nII0' and `nII1' arguments provide the phase II control and case sample sizes, respectively. While the above code corresponds to a balanced design (i.e., the same number of phase II samples drawn from the 6 phase I strata), these arguments can be easily modified to specify any phase II design with the caveat that each of the n_yk > 0. For example, one could specify an unbalanced design that over-samples individuals who are 75–84 years of age by setting `nII0 = c(25, 25, 100)' and `nII1 = c(25, 25, 100)'.

Finally, the `monitor' argument can be used to provide an update of the progress of the simulation, as the B datasets are generated and evaluated. In the above example a brief message is printed every 100 repetitions. The default is monitor = NULL; in this case no output is provided as the simulation progresses.

Once the simulation is completed, various operating characteristics are automatically evaluated and stored in an object of class `tpsSim()'. Many of the operating characteristics, such as bias, power, coverage probability are standard; the help files provide a detailed list. One operating characteristic we highlight here is the ratio of the standard error for a particular estimator, relative to the standard error of some referent estimator, multiplied by 100:

$$\frac{\mathrm{se}\left(\widehat{\beta }\right)}{\mathrm{se}\left({\widehat{\beta }}^{\mathit{REF}}\right)}\times 100$$

This quantity is closely related to the usual relative efficiency (a ratio of variances, rather than standard errors) and is referred to as the relative uncertainty. The appeal of this operating characteristic arises from its' interpretability in terms of the expected width of Wald-based confidence intervals. For example, suppose the relative uncertainty is estimated to be 82.3: Wald-based confidence intervals are expected to be approximately 82.3% tighter than those for the referent estimator, indicating lower uncertainty (or, equivalently, greater statistical efficiency) and greater power to detect a non-zero association. While the default in the osDesign package is to calculate the relative uncertainty with respect to the case-control estimator, an alternative choice can be made using the referent argument.

The following provides the basic output from the ocAge object (using a generic print function):

• R> ocAge

Number of simulations, B: 10000

Phase I stratification variable(s): Age

Sample size at Phase I: 2220177

Sample size at Phase II sample size:

controls, nII0: 50 50 50

cases, nII1: 50 50 50

Sample size for the case-control design, nCC: 150 150

'True' regession coefficients, betaTruth:

Int	−5.9620986
Age1	0.5953782
Age2	0.6879627
Sex	−1.0041234
Race	0.2830300

Mean percent bias

	Int	Age1	Age2	Sex	Race
CD	0.0	−0.1	−0.1	0.1	0.0
CC	NA	2.6	3.0	2.3	7.1
TPS-WL	−0.1	1.3	0.3	3.4	13.4
TPS-PL	−0.1	0.0	0.5	2.0	6.3
TPS-ML	−0.1	0.0	0.5	2.0	6.3

95% coverage probability

	Int	Age1	Age2	Sex	Race
CD	95.0	94.7	95.1	94.8	95.1
CC	NA	94.5	94.7	94.5	95.1
TPS-WL	95.1	96.9	96.2	94.5	94.9
TPS-PL	94.8	97.0	95.6	94.5	95.5
TPS-ML	94.8	97.0	95.6	94.5	95.5

Relative uncertainty

	Int	Age1	Age2	Sex	Race
CD	NA	11.0	10.8	11.6	10.0
CC	NA	100.0	100.0	100.0	100.0
TPS-WL	NA	42.9	37.0	104.0	110.7
TPS-PL	NA	30.3	27.3	98.3	99.3
TPS-ML	NA	30.3	27.3	98.3	99.3

From a substantive perspective, both the PL and ML estimators for the two-phase design generally exhibit reduced small-sample bias compared to both the case-control and two-phase WL estimators. For example, based on a phase II sample size of n = 300, the mean percent bias for the estimator of the race effect β_R is approximately 6.3% for both the PL and ML estimators; the corresponding small-sample percent biases for the CC and WL estimators are approximately 7.1% and 13.4%, respectively. That the coverage probabilities are all close to their nominal levels, together with the relatively small bias, indicates that standard errors are well estimated across all five estimators. Finally, compared to a standard case-control design, all three two-phase estimators for the intercept and two age coefficients (β₀, β_A1, and β_A2) exhibit substantially reduced uncertainty illustrating the fundamental utility of exploiting the phase I age information. While the two-phase WL estimator exhibits somewhat increased uncertainty for both the sex and race main effects (approximately 104% for β_S and 111% for β_R) there appear to be no trade-offs for PL and ML two-phase estimators.

5.2. Comparing specific designs

In some settings, researchers may have access to information on multiple covariates at phase I. For example, suppose sex and race information is available and the purpose of phase II is to facilitate collection of age information. In this setting, there are three potential phase I stratification schemes: (i) sex alone, (ii) race alone and (iii) sex and race jointly (designs #4, #5 and #8 in Table 2, respectively). The following commands can be used to investigate these three designs when interest lies in model (4) and sufficient resources exist to collect n = 200 samples at Phase II sample size:

• R> ocInterS <- tpsSim(B = 50000, betaTruth = fitI$coef, X = XI, N = Ohio$N, + strata = 3, nII0 = c(50, 50), nII1 = c(50, 50))

• R> ocInterR <- tpsSim(B = 50000, betaTruth = fitI$coef, X= XI, N = Ohio$N, + strata = 4, nII0 = c(50, 50), nII1 = c(50, 50))

• R> ocInterSR <- tpsSim(B = 50000, betaTruth = fitI$coef, X = XI, N = Ohio$N, + strata = c(3, 4), nII0 = c(25, 25, 25, 25), nII1 = c(25, 25, 25, 25))

Table 4 provides estimates of small sample percent median bias for the main effect for sex, β_S, and the interaction term, β_SR. We see that, in terms of small-sample bias, estimation of β_S under either two-phase design that stratifies on sex (either alone or jointly with race) is superior to that under the case-control design. Interestingly, estimation of β_S under the two-phase design that stratifies solely on race is no better in terms of bias than the case-control design. Small-sample estimation of both parameters is generally superior under each of the two-phase designs than under the case-control design. This is particularly the case for the β_SR parameter; compare 38.7% bias to 1.1%, 1.4% and 0.6% under the ML estimator for the three two-phase designs.

Table 4.

Percent median bias for estimation of β_S and β_SR in model (4), under various design/estimator combinations. Estimates are based on B = 10,000 simulated datasets.

Design	Sex main effect, βS			Interaction, βSR
	WL	PL	ML	WL	PL	ML
Complete data	-	-	0.0	-	-	0.6
Case-control designa	-	-	1.7	-	-	38.7
Two-phase design
Sexb	1.4	0.1	0.1	5.7	2.7	1.1
Raceb	6.3	2.9	2.9	−15.5	1.4	1.4
Sex and Race jointlyc	0.9	−0.4	−0.4	−5.7	0.6	0.6

^abalanced case-control design with n₀ = n₁ = 100,

^bBalanced two-phase design with n_yk = 50 for y = 0,1 and k = 0,1,

^cBalanced two-phase design with n_yk = 25 for y = 0,1 and k = 0,1, 2, 3

5.3. All two-phase designs

Beyond comparing specific two-phase designs, it may be of interest to investigate the relative performance of all possible designs based on the X argument. This is achieved by specifying `strata = 0'. Since the number of phase I strata will differ across the designs (see Table 2), an exhaustive comparison is restricted to balanced designs and hence only requires specification of the overall phase II sample sizes (n₀, n₁), via the nII argument. Note, researchers interested in investigating unbalanced designs can do so using the tpsSim() function and modifying the nII0 and nII1 arguments.

The following provides the basic command for running the simulation, taking n₀ = n₁ = 250, along with abbreviated output restricted to relative uncertainty:

• R> ocAll <- tpsSim(B = 10000, betaTruth = fitM$coef, X = XM, N = Ohio$N, + strata = 0, nII = c(250, 250), monitor = 100)

• R> ocAll

Number of simulations, B: 10000

Phase I stratification variable(s):

• All combinations of

  • 2 : Age
  • 3 : Sex
  • 4 : Race

Sample size at Phase I: 2220177

Sample size at Phase II, nII=c(nII0, nII1): 250 250

Sample size for the case-control design, nCC: 250 250

…

Relative uncertainty

		Int	Age1	Age2	Sex	Race
CD		NA	14.7	14.2	14.7	13.4
CC		NA	100.0	100.0	100.0	100.0
TPS-WL	2	NA	42.3	36.5	102.7	109.4
	3	NA	103.7	104.6	31.8	107.2
	4	NA	128.3	134.5	132.2	29.7
	23	NA	19.8	17.6	18.6	108.5
	24	NA	49.8	43.6	128.8	25.4
	34	NA	130.9	132.0	37.8	20.3
TPS-PL	2	NA	31.2	28.5	98.4	101.0
	3	NA	96.4	96.5	23.5	98.4
	4	NA	98.7	101.7	100.6	22.1
	23	NA	17.4	16.2	16.0	96.8
	24	NA	34.9	32.9	98.0	20.3
	34	NA	95.8	98.6	29.2	17.6
TPS-ML	2	NA	31.2	28.5	98.4	101.0
	3	NA	96.4	96.5	23.5	98.4
	4	NA	98.7	101.7	100.6	22.1
	23	NA	16.5	15.7	15.8	101.1
	24	NA	33.0	30.1	98.9	20.0
	34	NA	96.5	99.5	25.2	17.1

As the phase I stratification schemes for each of the two-phase designs are identified in terms of the columns of the design matrix XM (see the left-hand most column of the output above), a key is provided to remind the user of the variables to which they correspond (see the top of the table). So, for example, the two-phase design that jointly stratified on age and race corresponds to the results for the `24' design.

From the output, it is clear that efficiency gains for any given coefficient depend heavily on the choice of phase I stratification variable. While it is well-known that stratification schemes that involve a specific explanatory variable result in efficiency gains (i.e., reduced uncertainty relative to a balanced case-control design) for the corresponding coefficient (e.g., Breslow and Chatterjee 1999), the output from tpsSim() provides a direct quantitative assessment of these gains in small-sample settings.

5.4. Case-control sampling at phase I

As mentioned in Section 2.1, the phase I sample may arise via one of several different sampling schemes. The `cohort' argument in the tpsSim() function indicates the sampling scheme for the phase I data: `cohort = TRUE' is the default and is appropriate if the phase I data are a complete enumeration or a large prospective sample; `cohort = FALSE' indicates the phase I data were collected via a case-control scheme. When the phase I data are taken to arise from a case-control scheme, the `NI' = {N₀, N₁} argument is used to specify the number of controls and cases observed at phase I, respectively. Note, the N argument is still required, in that it specifies the underlying population from which the phase I case-control sample is drawn (i.e., the phase I sample may not be a complete enumeration of the population). The following provides an example of code where the phase I data arise from a case-control study with N₀ = N₁ = 5,000:

• R> ocAge <− tpsSim(B = 10000, betaTruth = fitM$coef, X = XM, N = Ohio$N, + strata = 2, cohort = FALSE, NI = c(5000, 5000), nII0 = c(50, 50, 50), + nII1 = c(50, 50, 50), betaNames = c(“Int”, “Age1”, “Age2”, “Sex”, + “Race”), monitor = 100)

5.5. Traditional case-control designs

Researchers may not always have access to suffcient information to consider a two-phase design or may solely be interested in the case-control design. osDesign also provides functionality for evaluating the operating characteristics of the traditional case-control design, via the ccSim() function. One key difference between the ccSim() and tpsSim() functions is that the former does not require specification of the stratification variable. To provide some flexibility in the range of case-control designs considered, ccSim() permits the investigation of alternative balances between the number controls and number of cases sampled. Specifically, an additional argument `r' represents the control-to-case ratio from the nCC sampled. The following illustrates the use of the the function along with abbreviated output:

• R> resultsCC <- ccSim(B = 10000, betaTruth = fitM$coef, X = XM, N = Ohio$N, + nCC = 500, r = c(0.67, 1.5), betaNames = c(“Int”, “Age1”, “Age2”, + “Sex”, “Race”), monitor = 100)

• R> resultsCC

…

Mean percent bias

		Int	Age1	Age2	Sex	Race
CD		0	0.0	0.0	0.0	−0.3
CC	r = 1	NA	1.4	1.5	0.9	1.3
CC	r = 0.67	NA	1.0	1.6	1.1	4.7
CC	r = 1.5	NA	1.3	1.2	1.3	−1.5

…

Relative uncertainty

		Int	Age1	Age2	Sex	Race
CD		NA	14.7	14.3	15.1	13.2
CC	r = 1	NA	100.0	100.0	100.0	100.0
CC	r = 0.67	NA	101.6	100.2	103.2	102.8
CC	r = 1.5	NA	101.2	102.1	104.2	100.2

As with the tpsSim() function, ccSim() automatically includes a balanced case-control design (r = 1) in the list of designs for which operating characteristics are estimated. This balanced design is used as the referent in evaluation of relative uncertainty.

6. Power calculations for study design

Section 5 focused on evaluating general small-sample operating characteristics. Another important task, for which the osDesign package provides practical assistance, is the planning and designing of future studies. In this section we illustrate the use of osDesign to examine the impact of alternative phase I stratification schemes, estimate and present power for both the two-phase and case-control designs, and modify the anticipated effect size to be detected.

6.1. Expected phase I strata

In most practical settings, the focus of study design considerations will be on the anticipated effect sizes, β_x, and phase II sample size, n. Depending on the nature of the availability of phase I information, researchers may also have options with respect to the phase I stratification. Each of these choices have ramifications for the power of the design and will require detailed communication between the statistician and collaborators. To aid this communication, the phaseI() function provides the expected phase I counts based on the assumed marginal exposure distribution, logistic model, overall sample size and stratification variable. For example, taking S to be race for the main effects only model yields:

• R> phaseI(betaTruth = fitM$coef, X = XM, N = Ohio$N, strata = 4)

Expected Phase I counts:

	N0k	N1k
Race = 0	2012517	4901
Race = 1	202127	632

Additionally stratifying on age yields:

• R> phaseI(betaTruth = fitM$coef, X = XM, N = Ohio$N, strata = c(2, 4))

Expected Phase I counts:

		N0k	N1k
Age = 0	Race = 0	904235	1552
Age = 0	Race = 1	102811	233
Age = 1	Race = 0	725434	2182
Age = 1	Race = 1	68467	272
Age = 2	Race = 0	382848	1167
Age = 2	Race = 1	30849	127

Given phase II sample sizes, the phaseI() function also calculates the expected sampling probabilities for each of the 2K phase I stratum. For example, stratifying on age alone and sampling n_yk = 100 from each of the 6 phase I strata, yields:

• R> phaseI(betaTruth = fitM$coef, X = XM, N = Ohio$N, strata = 2, + nII0 = rep(100, 3), nII1 = rep(100, 3)

Expected Phase I counts:

	N0k	N1k
Age = 0	1007046	1785
Age = 1	793901	2454
Age = 2	413697	1294

Phase II sample size:

	nII0k	nII1k
Age = 0	100	100
Age = 1	100	100
Age = 2	100	100

Expected Phase II sampling probabilities:

	p0k	p1k
Age = 0	0.000099	0.056022
Age = 1	0.000126	0.040750
Age = 2	0.000242	0.077280

Finally, phaseI() also permits the calculation expected counts under a case-control sampling scheme for the phase I data via the cohort and NI arguments:

• R> phaseI(betaTruth = fitM$coef, X = XM, N = Ohio$N, strata = 4, + cohort = FALSE, NI = c(5000, 5000))

Expected Phase I counts:

	N0k	N1k
Race = 0	4544	4429
Race = 1	456	571

6.2. Power for a two-phase study

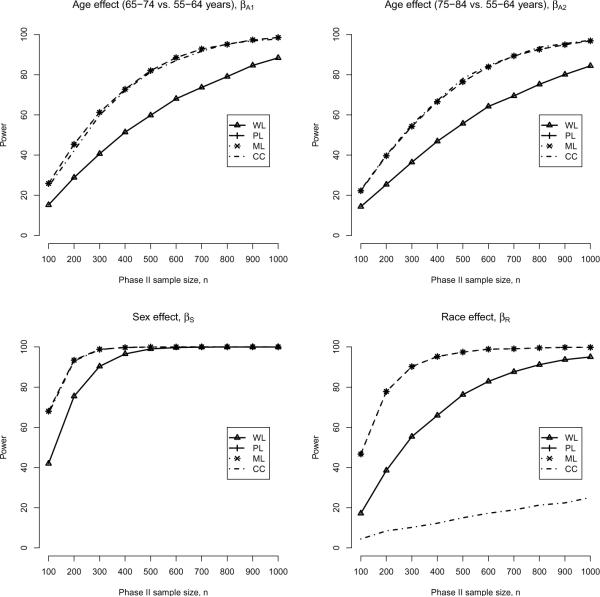
When planning a study, the two-phase design is a useful option when additional information, beyond outcome status, is available on all members of the population or a large cross-sectional, cohort or case-control sub-sample (see Section 2.1). For a hypothetical study of lung cancer mortality in Ohio, suppose the only information available at phase I is outcome and race; further data collection efforts are required to obtain information on age and sex. In this specific setting, one could consider planning a case-control study that ignores the available race information or incorporate race into the sampling scheme via a two-phase design; Figure 1 quantifies the differences in power between the two designs. Each sub-plot provides estimated power curves for one of the log-odds ratio coefficients in Model (3), as a function of the phase II sample size n. Shown are curves for the case-control ML estimator and three two-phase estimators for a balanced design with S taken to be race. The calculations and figure were produced using the tpsPower() and plotPower() functions:

• R> powerRaceTPS <- tpsPower(B = 10000, betaTruth = fitM$coef, X = XM, + N = Ohio$N, strata = 4, nII = seq(from = 100, to = 1000, by = 100))

• R> par(mfrow = c(2, 2))

• R> plotPower(powerRaceTPS, coefNum = 2, + xAxis = seq(from = 100, to = 1000, by = 100), + main = expression(“Age effect (65–74 vs. 55–64 years), ” * beta[A1]), + legendXY = c(800, 60))

• R> plotPower(powerRaceTPS, coefNum = 3, + xAxis = seq(from = 100, to = 1000, by = 100), + main = expression(“Age effect (75–84 vs. 55–64 years), ” * beta[A2]), + legendXY = c(800, 60))

• R> plotPower(powerRaceTPS, coefNum = 4, + xAxis = seq(from = 100, to = 1000, by = 100), + main = expression(“Sex effect, ” * beta[S]), legendXY = c(800, 60))

• R> plotPower(powerRaceTPS, coefNum = 5, + xAxis = seq(from = 100, to = 1000, by = 100), + main = expression(“Race effect, ” * beta[R]), legendXY = c(800, 60))

Figure 1.

Power for each of the four main-effects regression coefficients in Model (3), under a case-control design and a balanced two-phase design where the phase I stratification variable, S, is taken to be race. Power estimates are based on B = 10,000 simulated datasets.

From Figure 1 there are clear, substantial power gains for the race effect when one adopts the two-phase design compared to a case-control design. When n = 200, the power to detect β_R = 0.283 is approximately 8% under the case-control design and increases to approximately 78% for the PL and ML estimators under the two-phase design. Doubling the sample size increases the power for the two-phase estimators to 95%, while the case-control estimator increases to 12%.

Interestingly, there appears to be a trade-off with the two-phase WL estimator. For example, when n = 400, the WL estimator exhibits approximately 68% power for the race effect. While this is considerably higher than the case-control estimator, the power for the two age effects is lower than under the case-control design. This phenomenon is likely dependent on the interplay between the outcome and the joint marginal exposure/confounder distribution. While beyond the scope of this paper, the osDesign could be be used to investigate this phenomenon. Specifically, a simulation study could be designed that examines differing structures for the joint marginal exposure/confounder distribution and the extent to which specific choices of phase I stratification variable(s) reproduce the phenomenon.

6.3. Comparing two-phase designs

While Figure 1 presents power estimates for the case-control ML estimator and the three two-phase estimators for a single two-phase design, it may also be of interest to compare different designs. Figure 2 provides estimates of power for each of the four main effects in Model (3) based on ML estimation for three designs: (i) a two-phase design with S taken to be race, (ii) a two-phase design with S taken to be sex and (iii) a case-control design. We find that, at least for these examples, power gains under a two-phase design are primarily obtained for the coefficient corresponding to the covariate that is stratified upon. That is, for the age coefficients, β_A1 and β_A2, there is little to be gained (in terms of power) by employing a two-phase design that stratifies either on race or sex.

Figure 2.

Power for each of the four main-effects regression coefficients in Model (3) based on ML estimation for three designs: (i) a two-phase design with S taken to be race, (ii) a two-phase design with S taken to be sex and (iii) a case-control design. Power estimates are based on B = 10,000 simulated datasets.

The following provides the code used to generate the upper-left-hand sub-figure of Figure 2.

• R> powerSexTPS <- tpsPower(B = 10000, betaTruth = fitM$coef, X = XM, + N = Ohio$N, strata = 3, nII = seq(from = 100, to = 1000, by = 100))

• R> nLvls <- length(powerSexTPS$nII)

• R> plotPower(powerRaceTPS, coefNum = 2, include = “ML”, + xAxis = seq(from = 100, to = 1000, by = 100), + main = expression(“Age effect (65–74 vs. 55–64 years), ” * beta[A1]))

• R> lines(powerSexTPS$nII, powerSexTPS$power[(5 + c(0:(nLvls − 1)) * 4), 2], + lwd = 2, lty = 2, pch = 2, type = “o”)

• R> lines(powerSexTPS$nII, powerSexTPS$power[(2 + c(0:(nLvls − 1)) * 4), 2], + lwd = 2, lty = 3, pch = 3, type = “o”)

• R> legend(650, 65, c(“TPS: Race”, “TPS: Sex”, “Case-control”), + lwd = c(2, 2, 2), lty = c(1, 2, 3), pch = c(1, 2, 3))

6.4. Power for case-control studies

Just as the osDesign package provides a function dedicated to estimating operating characteristics of the traditional case-control design, the package also provides functionality for planning a case-control study via the ccPower() function. The following sample code examines the impact of the sample size on power for the components of Model (3) based on a balanced case-control design (i.e., r = 1).

• R> powerCC <- ccPower(B = 10000, betaTruth = fitM$coef, X = XM, N = Ohio$N, + r = 1, nCC = seq(from = 100, to = 500, by = 50))

• R> par(mfrow = c(2, 2))

• R> plotPower(powerCC, coefNum = 2, + xAxis = seq(from = 100, to = 500, by = 100), + main = expression(“Age effect (65–74 vs. 55–64 years), ” * beta[A1]))

• R> plotPower(powerCC, coefNum = 3, + xAxis = seq(from = 100, to = 500, by = 100), + main = expression(“Age effect (75–84 vs. 55–64 years), ” * beta[A2]))

• R> plotPower(powerCC, coefNum = 4, + xAxis = seq(from = 100, to = 500, by = 100), + main = expression(“Sex effect, ” * beta[S]))

• R> plotPower(powerCC, coefNum = 5, + xAxis = seq(from = 100, to = 500, by = 100), + main = expression(“Race effect, ” * beta[R]))

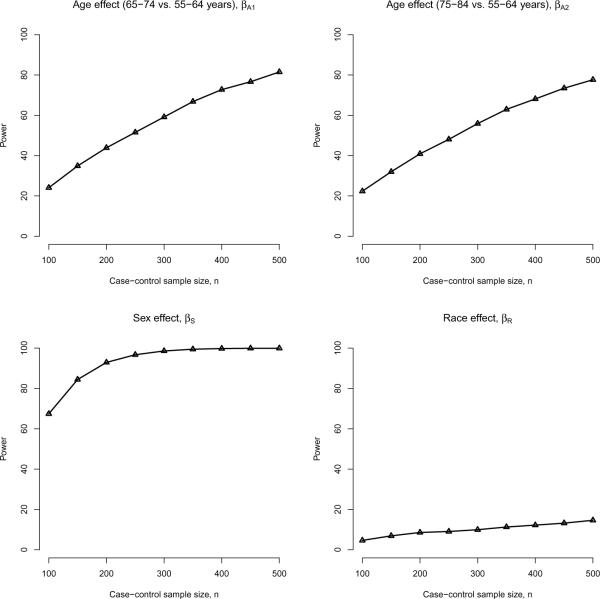
Figure 3 provides the resulting power curve estimates. Note these are the same estimates of power indicated by the `CC' curves in Figure 1; in situations where solely case-control designs are being considered, such plots may be useful. In addition to investigating the impact of increasing the overall sample size, n, researchers may be interested in investigating the benefits of sampling additional controls. Figure 4 provides estimates of power for case-control designs where the number cases is fixed at n₁ = 100 and the number of controls is set to be n₀ = n₁ × r for r between 1 and 5. The following provides sample code used to generate the power estimates as well as Figure 4.

Figure 3.

Power for each of the four main-effects regression coefficients in Model (3), under a traditional balanced case-control design. Power estimates are based on B = 10,000 simulated datasets.

Figure 4.

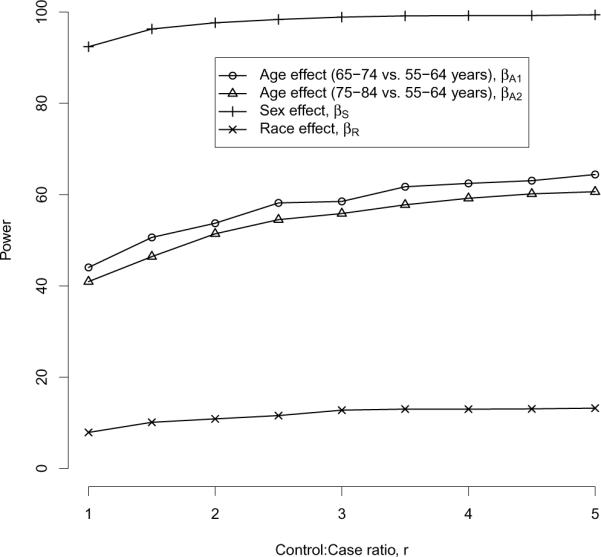
Power for each of the four main-effects regression coefficients in Model (3), under a case-control design with r:1 matching. For each setting, the number of cases is fixed at n₁ = 100. Power estimates are based on B = 10,000 simulated datasets.

• R> powerCC100 <- ccPower(B = 10000, betaTruth = fitM$coef, X = XM, + N = Ohio$N, r = 1, nCC = 200)

• R> powerCC150 <- ccPower(B = 10000, betaTruth = fitM$coef, X = XM, + N = Ohio$N, r = 1.5, nCC = 250)

• R> powerCC200 <- ccPower(B = 10000, betaTruth = fitM$coef, X = XM, + N = Ohio$N, r = 2, nCC = 300) …

• R> powerCC450 <- ccPower(B = 10000, betaTruth = fitM$coef, X = XM, + N = Ohio$N, r = 4.5, nCC = 550)

• R> powerCC500 <- ccPower(B = 10000, betaTruth = fitM$coef, X = XM, + N = Ohio$N, r = 5, nCC = 600)

• R> powerCCr <- rbind( + powerCC100$power[2, -1], … + powerCC500$power[2, -1])

• R> plot(c(1, 5), c(0, 100), xlab = “Control:Case ratio, r”, ylab = “Power”, + axes = FALSE, type = “n”)

• R> axis(1, at = seq(from = 1, to = 5, by = 1))

• R> axis(2, at = seq(from = 0, to = 100, by = 20))

• R> lines(seq(from = 1, to = 5, by = 0.5), powerCCr[, 1], lwd = 2, + type = “o”, pch = 1)

• R> lines(seq(from = 1, to = 5, by = 0.5), powerCCr[, 2], lwd = 2, + type = “o”, pch = 2)

• R> lines(seq(from = 1, to = 5, by = 0.5), powerCCr[, 3], lwd = 2, + type = “o”, pch = 3)

• R> lines(seq(from = 1, to = 5, by = 0.5), powerCCr[, 4], lwd = 2, + type = “o”, pch = 4)

• R> legend(2, 90, c( + expression(”Age effect (65–74 vs. 55–64 years), ” * beta[A1]), + expression(”Age effect (75–84 vs. 55–64 years), ” * beta[A2]), + expression(”Sex effect, ” * beta[S]), + expression(”Race effect, ” * beta[R])), lwd = rep(2, 4), pch = 1:4)

Finally, as a reminder, we note that power for unbalanced case-control studies can be investigated by modifying the `r' argument in either the ccSim() or ccPower() functions.

6.5. Modifying anticipated effect sizes

The power calculations presented in Figures 1 and 3 are for effect sizes equal to the `true' coefficient values obtained from a fit of the complete data (see Section 4.2). When conducting sample size/power calculations it is often of interest to characterize power at alternative levels of the strength of the anticipated association. This is achieved by modifying the betaTruth argument, which represents the vector (β₀, β_x) in the notation of model (1). Modifying any of the components of β_x, however, will have consequences for the expected number of cases. For example, suppose the two age coefficients were reduced in magnitude by 50%, to give:

• R> newBetaM <- fitM$coef

• R> newBetaM[2:3] <- newBetaM[2:3] * 0.5

• R> phaseI(betaTruth = newBetaM, X = XM, N = Ohio$N, strata = c(2, 4))

Expected Phase I counts:

		Y=0	Y=1
Age = 0	Race = 0	904235	1552
Age = 0	Race = 1	102811	233
Age = 1	Race = 0	725995	1621
Age = 1	Race = 1	68536	203
Age = 2	Race = 0	383186	829
Age = 2	Race = 1	30886	90

Compared with the expected counts based on `betaTruth=fitM$beta', there are 1,006 fewer expected cases or, equivalently, a decrease in the outcome prevalence from 2.49 to 2.04 per 1,000. In most applied settings, the overall outcome prevalence in the population will be well-known and, in particular, fixed. Hence, it is important to ensure that the outcome prevalence is held constant across various scenarios for β_x. One approach to achieving this is to fix β₀ so that the overall (expected) prevalence is held at some specified level; the function beta0() calculates the appropriate value of β₀ given β_x, the marginal exposure distribution and outcome prevalence (represented by the rhoY argument):

• R> fitM$coef1]

(Intercept) −5.962099

• R> newBetaM[1] <- beta0(betaX = newBetaM[-1], X = XM, N = Ohio$N, + rhoY = sum(Ohio$Death)/sum(Ohio$N))

• R> newBetaM[1]

(Intercept) −5.760943

Using the modified `newBetaM' in the tpsSim() and tpsPower() functions (as well as the ccSim() and ccPower() functions) permits the investigation of operating characteristics under various alternative effect sizes, while retaining comparability in terms of the underlying overall outcome prevalence.

7. Run times and Monte Carlo error

As outlined in Section 3, osDesign estimates operating characteristics of both two-phase and case-control designs via simulation. In practice, the use of simulation involves a trade-off between the time the simulation takes to run and the uncertainty of the estimates. The latter arises from sampling variability due to the finite choice of B and is often referred to as Monte Carlo error (MCE, Metropolis and Ulam 1949). This form of uncertainty is analogous to the usual form of sampling variability measured by standard errors; as one increases B (the `simulation sample size'), the longer it takes to run the simulation but the more accurate the results will be. Each of the examples in this manuscript, as well as those in the osDesign package, use B = 10,000. Table 5 provides run times for selected function calls presented in this manuscript, for several common choices of B. Each are based on an Apple iMac with dual core 3.6 GHz Intel Core i5 processors and 8Gb of memory, running Mac OS X 10.6.7. Further, throughout, version 1.3 of the osDesign package was used in R version 12.2.2.

Table 5.

Run times, in minutes, for select calls presented in the manuscript.

Function call	Manuscript sub-section	Distinct designsa			Simulation sample size, B
		TP	CC	CD	500	1,000	10,000
ocAge <- tpsSim()	5.1	1	1	1	0.28	0.58	5.95
ocAll <- tpsSim()	5.3	6	1	1	1.45	2.93	27.92
powerRaceTPS <- tpsPower()	6.2	9	9	1	2.48	4.87	49.83
powerCC <- ccPower()	6.3	0	9	1	0.38	0.77	7.60

^aNumber of distinct two-phase (TP), case-control (CC) and complete data (CD) designs evaluated during each repetition.

Clearly, as B increases the time taken to run the simulation increases and since the underlying functions are based on a loop, they increase somewhat linearly with B. A simple strategy could be to run a small number of repetitions, say B = 500, to help choose the details of the broader simulation and then present final based on a larger value (as we have done). More generally, Koehler, Brown, and Haneuse (2009) provide an overview of MCE as well as simple approaches to estimating MCE in a broad range of settings. Further, given a desired level of accuracy (or uncertainty), they develop a graphical technique for determining the value of B. Their methods have been implemented in the MCE package (Koehler and Haneuse 2010) for R.

8. Summary

Although the two-phase design is well-established in the statistical literature, researchers have been slow to adopt the design as an efficient alternative to the traditional case-control design. A key factor in the lack of uptake may be the paucity of flexible, convenient software for (i) analyzing data that arises from a two-phase design, (ii) estimating small-sample operating characteristics of various designs and (iii) planning a two-phase study. The osDesign package for R provides a suite of functions that help fill this gap. The focus of this paper is the functionality of the osDesign package and we have not sought to provide general guidelines to researchers. We believe, however, that the Ohio lung cancer example may serve as a useful template to researchers as they plan their own studies (both for design purposes and the investigation of small-sample operating characteristics).

Compared to existing software, the strengths of the package include the ability to simultaneously investigate case-control and two-phase designs that vary in terms of the variable(s) determining the phase I stratification and case-control/phase II sample size; user-friendly output (both tabular and graphical) is returned for a broad range of small-sample operating characteristics. Further, functions tpsSim() and ccSim() both permit the investigation of unbalanced two-phase and case-control designs, respectively.

As outlined in Section 4.2, osDesign uses a design matrix, denoted X, for the specification of the underlying logistic model and the phase I stratification. While easy-to-use and flexible, in terms of being able to specify arbitrary design matrixes that involve categorical covariates, an important limitation is that continuous covariates are currently not accommodated. Although such covariates could not be directly used for the phase I stratification, they are often collected at phase II and included in models. However, we note that this limitation is specific to the evaluation of operating characteristics. For the analysis of data arising from a two-phase design, osDesign includes the tps() function for which there is no restriction on the covariates. While large-sample properties of the WL, PL and ML estimators are well-established in the literature, a number of real life data scenarios and design issues deserve further investigation. Within the contexts of their own scientific studies, for example, researchers may be interested in understanding small-sample properties of the various estimators. These may include characterizing the performance of the estimators when the stratification variable is subject to varying degrees of non-differential error (i.e., the conditional independence assumption of Section 2.3 does not hold) or when the model is misspecified (e.g., Breslow and Chatterjee 1999). We are currently working on extending the osDesign package to permit the investigation of these scenarios. Other avenues for extending the package that we are currently pursing include accommodating continuous exposures as well as providing functions for a broader range of outcome-dependent designs: case-control studies where all cases are sampled and controls are sampled until some pre-determined threshold for power is achieved; nested case-control designs (Oakes 1981; Langholz and Borgan 1995); and case-cohort designs (Prentice 1986).