Cross-simulation between two pharmacokinetic models for the target-controlled infusion of propofol

Abstract

Background

We investigated how one pharmacokinetic (PK) model differed in prediction of plasma (C_p) and effect-site concentration (C_eff) using a reproducing simulation of target-controlled infusion (TCI) with another PK model of propofol.

Methods

Sixty female patients were randomly assigned to TCI using Marsh PK (Group M) and TCI using Schnider PK (Group S) targeting 6.0 µg/ml of C_p of propofol for induction of anesthesia, and loss of responsiveness (LOR) was evaluated. Total and separate cross-simulation were investigated using the 2 hr TCI data (Marsh TCI and Schnider TCI), and we investigated the reproduced predicted concentrations (MARSH_SCH and SCHNIDER_MAR) using the other model. The correlation of the difference with covariates, and the influence of the PK parameters on the difference of prediction were investigated.

Results

Group M had a shorter time to LOR compared to Group S (P < 0.001), but C_eff at LOR was not different between groups. Reproduced simulations showed different time courses of C_p. MARSH_SCH predicted a higher concentration during the early phase, whereas SCHNIDER_MAR was maintained at a higher concentration. Volume and clearance of the central compartment were relevant to the difference of prediction, respectively. Body weight correlated well with differences in prediction between models (R_sqr = 0.9821, P < 0.001).

Conclusions

We compared two PK models to determine the different infusion behaviors during TCI, which resulted from the different parameter sets for each PK model.

Introduction

Pharmacokinetic (PK) models of propofol have been used in target controlled infusion (TCI) for the rapid achievement and maintenance of a stable plasma concentration (C_p) within a clinically acceptable range of performance errors [1-3]. However, each PK model has different parameter values, even though the parent drug is the same. Recent reports using a non-linear mixed effect model present complex parameter sets that are expressed with complex equations of covariates. Commercially available TCI devices and PK software programs have various PK models for one drug. Therefore, we have faced some difficulties in choosing the appropriate PK model for routine clinical settings. Furthermore, time courses of predicted C_p and effect-site concentration (C_eff) of propofol were different when the manual bolus and continuous infusion were simulated using different PK models. Likewise, the amounts of propofol administered for maintenance of a stable C_p were also different between the PK models [4]. Therefore, we compared the PK models of propofol to investigate different infusion patterns using the reproducing simulation of TCI data of one PK model using another PK model.

Materials and Methods

With approval of the Institutional Review Board and signed informed consent, a total of 60 female patients, American Society of Anesthesiologists physical status I, age 20-50 years, and scheduled for gynecologic surgery under general anesthesia were enrolled in this study. Exclusion criteria included body weight of over 150% of ideal body weight, medications for the central nervous system, patients with chronic pain, or neurological and endocrine disorders. Patients received glycopyrrolate 0.2 mg intravenously for premedication; however, no other sedatives were administrated before and during the period of this study. Electrocardiograph, pulse oximeter, noninvasive blood pressure monitor, and capnogram were applied. Heart rate and blood pressure were monitored and recorded every 30 s during the study and thereafter every 3 min. After pre-oxygenation, lidocaine 30 mg was given and propofol TCI was started.

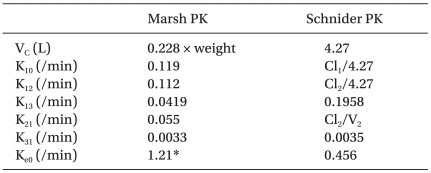
Patients were randomfly assigned to one of two groups. The three compartment mammillary pharmacokinetic model of Marsh PK [5] and 1.21/min of K_e0 [6] were used for Group M, and the multiple covariate-adjusted model of Schnider et al. [7,8] was used for Group S. The PK parameters and their equations with covariates and the K_e0 are illustrated in Table 1. Propofol (1% Fresofol®, Fresenius Kabi, Graz, Austria) was administrated using a syringe pump (Graseby 3500, Sims Graseby Ltd., Herts, England) targeting at 6.0 µg/ml of C_p for induction of anesthesia. The syringe pump was controlled using pharmacokinetic/pharmacodynamic (PK/PD) software (STANPUMP©, written by Steven L. Shafer, Palo Alto, CA, USA) through RS232 serial communication. The propofol-filled syringe was connected to the 3-channel extension tube with a unidirectional valve preventing the back flow to the intravenous bag. In the case of any alarm triggered from the TCI device during the study, the patient was also excluded from the study.

Table 1.

Pharmacokinetic/Pharmacodynamic Parameters and Associated Equations with Covariates for Target-Controlled Infusion of Propofol

V₂: 18.9 - 0.391 × (age - 53), Cl₁: 1.89 + 0.0456 × (weight - 77) - 0.0681 × (lbm - 59) + 0.0264 × (height - 177), Cl₂: 1.29 - 0.024 × (age - 53), Age: age in years, Weight: body weight in kilograms, Height: height in centimeters, Lbm (lean body mass) for women: 1.07 × weight - 148 × (weight / height)². ^*K_e0 from the study of Struys et al. [6].

Assessment of loss of responsiveness

About the time the patients became drowsy, a blind investigator assessed the loss of responsiveness (LOR), asking them to open their eyes with mild prodding of their shoulder every 10 s. Any responses to these stimuli, such as opening their eyes, nodding their head, and any kind of behavior showing an attempt to respond, were defined as 'responsiveness', and no response was defined as 'LOR'. We have chosen the 10-s interval because the interval for pump control update and data saving was set at 10 s. Time to LOR, the predicted C_eff and the amount of propofol infused until LOR were recorded. Interventions were terminated when subjects had shown LOR. During the study, patients received oxygen via a facemask. If oxygen saturation decreased below 95%, they were encouraged to breathe deeply if they responded to verbal commands, and if not, then manual breathing was supported using an anesthetic breathing circuit system with oxygen, while maintaining the end-tidal CO₂ partial pressure between 30 and 35 mmHg. After LOR, opioid or neuromuscular blocking agents were administered, and tracheal intubation was done according to scheduled surgery.

Total cross-simulation of the predicted plasma and effect-site concentrations

After surgery, two kinds of TCI regimen were simulated for every patient. (1) Regimen I: Two hour TCI was virtually performed targeting 6.0 µg/ml of C_p. (2) Regimen II: TCI was provided targeting 6.0 µg/ml of C_p (0 min to 10 min), then decreased to 4.0 µg/ml (10 min to 2 hr). The cumulative amounts of propofol infused until 1, 5, 10, 30, 60, 90, and 120 min were compared between models. Total cross-simulation was performed using the reproducing function of STANPUMP©; the TCI using Marsh PK (Marsh TCI) was analyzed using Schnider PK (MARSH_SCH), and the TCI using Schnider PK (Schnider TCI) was analyzed using Marsh PK (SCHNIDER_MAR). The analysis was performed using the command line arguments with a patient-specific external parameter PK/PD file (e.g. Stanpump kinetics marsh.kin rep patient1.dat). In addition, the reproduced C_p (C_p-rep) and C_eff (C_eff-rep) were saved on a hard disk. We also investigated the correlation between the patient's covariates (age, body weight, height, and LBM) and the percentage differences after 2 hr infusion. The percentage difference was calculated as follows:

Percentage difference (%) = 100 × (C_p-rep - C_p-prior) / C_p-prior

Time courses of C_p-rep and C_eff-rep were evaluated with the prior target plasma (C_p-prior) and effect-site concentration (C_eff-prior). Peak deviation from the prior target, time to intercept the prior predicted concentration, and C_p-rep and C_eff-rep at 30 min and 2 hr were compared.

Separate cross-simulation of the predicted plasma concentrations

Separate cross-simulation was performed in order to determine the effect of one PK parameter on the overall differences. We replaced only one PK parameter of one model with the corresponding value of the other PK model, and performed simulations with the infusion data that targeted 6.0 µg/ml of C_p. Each simulation was separately investigated for six PK parameters (V_C, V₂, V₃, Cl₁, Cl₂, and Cl₃), and time courses of the percentage difference were evaluated. The percentage difference was calculated as follows:

Percentage difference (%) = 100 × (C_p-rep - C_p-prior) / C_p-prior

Statistics

Comparisons of demographic and hemodynamic variables, observations of LOR, total propofol infused, differences of C_p-rep and C_eff-rep were performed with the Student t-test (SPSS©, version 10.0.1, SPSS Inc.) at a P < 0.05 level of significance. Data were presented as mean ± SD, unless stated otherwise. Regression between the covariates and the discrepancy observed in the predicted concentrations were performed with linear regression (SigmaPlot© 2004 for Windows Version 9.0, Systat Software, Inc., USA).

Results

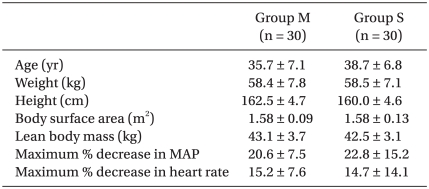
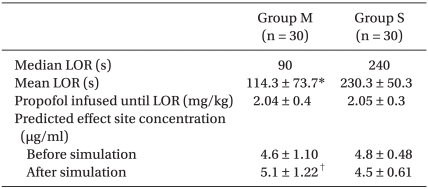
There were no significant differences in the demographic data and hemodynamic variables between groups (Table 2). Group M showed shorter time to LOR compared to Group S (P < 0.001). However, the amount of propofol infused until LOR did not differ significantly between the groups (Table 3 and Fig. 1). C_eff at LOR did not differ between groups, but after cross-simulation using the other PK/PD model, C_eff at LOR were significantly different between groups (P = 0.009) (Table 3).

Table 2.

Demographic and Hemodynamic Variables of the Patients in this Study

Data are reported as mean ± SD. There were no significances in patient groups.

Table 3.

Observations at Loss of Responsiveness (LOR) and Predicted Effect Site Concentrations before and after Cross-Simulation

Data are reported as mean ± SD. ^*P < 0.001 vs. Group S , ^†P = 0.009 vs. Group S.

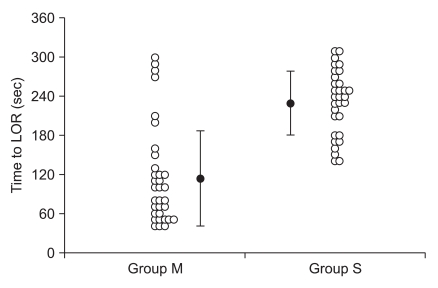
Fig. 1.

Scatter plots and error bars show the time to loss of responsiveness during target-controlled infusion of propofol using the pharmacokinetic model of Marsh et al. (Group M) and Schnider et al. (Group S).

Total cross-simulation

Regimen I

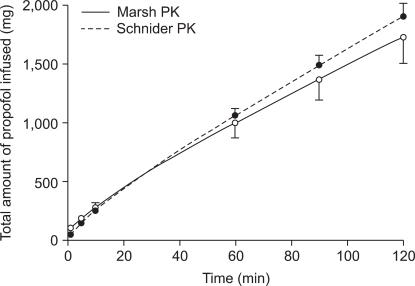
Marsh TCI infused more propofol than Schnider TCI until 1, 5, and 10 min (P < 0.001); in particular, nearly twice the amount of propofol was infused during Marsh TCI (98.6 ± 11.9 mg) compared to Schnider TCI (48.4 ± 1.3 mg) during the first 1 min after the start of infusion. However, Marsh TCI infused less propofol until 60 min (P = 0.009), 90 min (P = 0.01), and 120 min (P < 0.001) compared to Schnider TCI (Fig. 2).

Fig. 2.

Cumulative amounts of infused propofol targeting 6.0 µg/ml of plasma concentration during 2 hr of target controlled infusion with the pharmacokinetic (PK) model of Marsh (solid line) and Schnider et al. (dotted line). Error bars show the amount of propofol infused until 1, 5, 10, 60, 90, and 120 min.

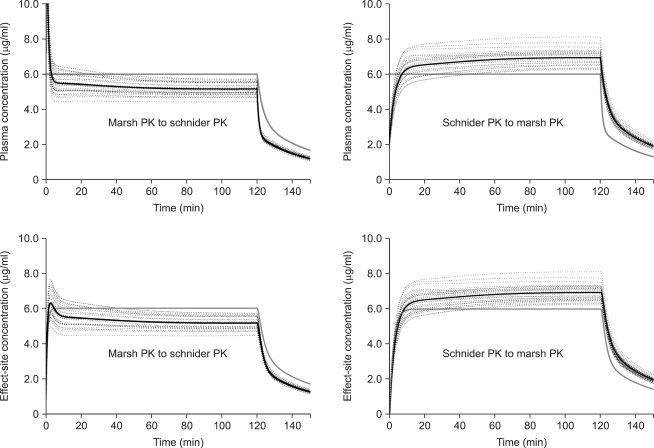
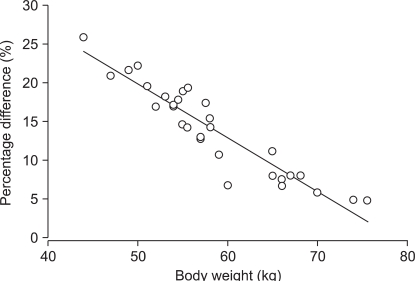
MARSH_SCH showed that C_p-rep was over-predicted up to 15.4 ± 1.86 µg/ml, and decreased to C_p-prior at 3.3 min after the start of infusion (Fig. 3, left upper graph). Thereafter, it gradually decreased to 5.4 ± 0.44 µg/ml at 30 min (P < 0.001) and 5.1 ± 0.35 µg/ml at 2 hr (P < 0.001). C_eff-rep was also over-predicted up to 6.3 ± 0.71 µg/ml at 2.9 min (P < 0.001) (Fig. 3, left lower graph). Thereafter, it gradually decreased to 5.4 ± 0.45 µg/ml at 30 min (P < 0.001) and 5.2 ± 0.35 µg/ml at 2 hr (P < 0.001). The percentage of difference of prediction at the end of the 2 hr infusion correlated well with body weight (R_sqr = 0.9821, P < 0.001) (Fig. 4), and LBM also correlated well (R_sqr = 0.9603, P < 0.001).

Fig. 3.

The time courses of the reproduced individual (dotted line) and mean (black solid line) predicted plasma (upper graphs) and effect-site (lower graphs) concentrations of propofol targeting 6.0 µg/ml of plasma concentration (gray line). The infusion data file of the pharmacokinetic (PK) model of Marsh et al. (Marsh PK) was analyzed using that of Schnider et al. (Schnider PK) (left graphs), and the infusion data file of Schnider PK was analyzed using Marsh PK (right graphs).

Fig. 4.

Regression of the body weight with the percentage difference of predicted plasma concentrations after 2 hr of infusion targeting 6.0 µg/ml of plasma concentration (R_sqr = 0.9821, P < 0.001). The infusion data file of the pharmacokinetic model of Marsh et al. was analyzed using that of Schnider.

SCHNIDER_MAR showed that C_p-rep was under-predicted during the initial period of infusion and while it reached C_p-prior at 7.5 min. It then increased to 6.61 ± 0.51 µg/ml at 30 min (P < 0.001) and 6.94 ± 0.45 µg/ml at 2 hr (P < 0.001). C_eff-rep increased more slowly than C_eff-prior during the early period of infusion and became C_eff-prior at 8.7 min. It then increased to 6.61 ± 0.51 µg/ml at 30 min (P < 0.001) and 6.9 ± 0.45 µg/ml at 2 hr (P < 0.001).

Regimen II

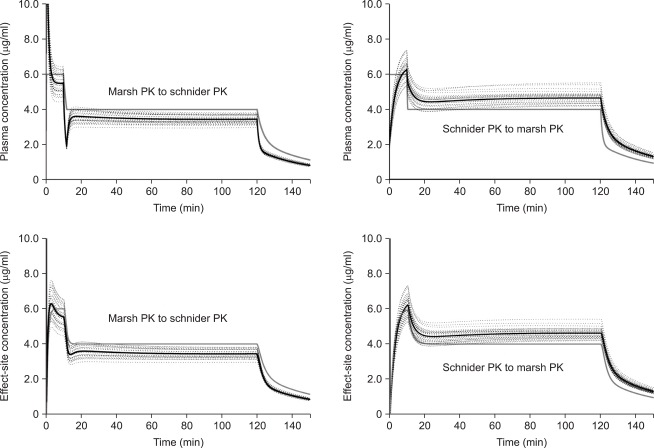
Patterns of discrepancy during the first 10 min were similar to those of Regimen I. After the target concentration decreased to 4 µg/ml, MARSH_SCH showed that C_p-rep decreased to 2.0 ± 0.13 µg/ml, and increased to 3.6 ± 0.28 µg/ml at 30 min (P < 0.001), then decreased to 3.4 ± 0.23 µg/ml at the end of the 2 hr infusion (P < 0.001) (Fig. 5, left upper graph). After the target concentration decreased to 4 µg/ml, C_eff-rep decreased to 3.4 ± 0.30 µg/ml at 14.3 min, and became 3.6 ± 0.29 µg/ml at 30 min (P < 0.001). It finally decreased to 3.4 ± 0.23 µg/ml at the end of the 2 hr infusion (P < 0.001) (Fig. 4, left lower graph).

Fig. 5.

Total cross-simulation shows the time courses of the reproduced individual (dotted line) and mean (black solid line) predicted plasma (upper graphs) and effect-site (lower graphs) concentrations of propofol. Targeting 6.0 µg/ml of plasma concentration (0 to 10 min), and 4.0 µg/ml (10 min to 2 hr) (gray line). The infusion data file of the pharmacokinetic (PK) model of Marsh et al. (Marsh PK) was analyzed using the file of Schnider et al. (Schnider PK) (left graphs), and the infusion data file of Schnider PK was analyzed using Marsh PK (right graphs).

After the target decreased to 4 µg/ml, SCHNIDER_MAR showed that C_p-rep decreased, but remained higher than C_p-prior and increased to 4.5 ± 0.36 µg/ml at 30 min (P < 0.001) and 4.7 ± 0.34 µg/ml at 2 hr (P < 0.001) (Fig. 4, right upper graph). After the target concentration decreased to 4 µg/ml, C_eff-rep showed a much slower decrease, but remained higher than C_eff-prior, and showed a maximal decrease to 4.4 ± 0.35 µg/ml at 24.3 min, and increased to 4.4 ± 0.34 µg/ml at 30 min (P < 0.001) and 4.6 ± 0.29 µg/ml at 2 hr (P < 0.001) (Fig. 4, right lower graph).

Separate cross-simulation

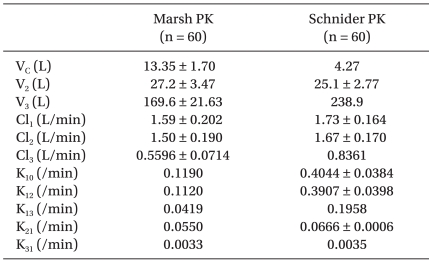
The mean ± SD or fixed values of PK parameters for separate cross-simulation are illustrated in Table 4. Fig. 6 shows the time course of the percentage difference of each parameter. V_C appeared to be relevant to the initial large difference. Thereafter, Cl₁ and V₃ increasingly contributed to the difference until 2 hr of infusion. The upper and lower graphs show a mirror image, and the summation curve of the percentage differences of each parameter appeared to be similar with MARSH_SCH and SCHNIDER_MAR of Regimen I.

Table 4.

Values for Pharmacokinetic Parameters of Propofol

Data are reported as mean ± SD or fixed values.

Fig. 6.

Simulation was separately investigated with one pharmacokinetic (PK) parameter (V_C, V₂, V₃, Cl₁, Cl₂, and Cl₃) replaced of the PK model with the corresponding value of the other model and each curve shows the time course of the percentage differences of predictions. Each parameter of Marsh PK was replaced with that of Schnider PK (upper curves), and each parameter of Schider PK was replaced with that of Marsh PK (lower curves).

Discussion

During TCI of propofol, the infusion data files that were supposed to maintain a stable C_p did not produce identical results when played back to a different PK model. The differences were greater during the early period of infusion, whereas later a relatively stable range of differences was maintained, but with a continual increase during long-term infusion. These discrepancies highly correlated with the body weight of the subject.

Using simulations, we attempted to perform a straightforward comparison of the integrated difference of the two PK models. Apparently, the volume of the central compartment of Marsh PK was nearly triple that of Schnider PK. Therefore, Marsh PK required a larger amount of propofol to fill up the central compartment when there was no drug in the body, and, as a result, showed a more rapid loss of responsiveness than Schnider PK. However, the clearance of the central compartment of Marsh PK was smaller than that of Schnider PK. Therefore; we could deduce that Marsh TCI requires less propofol than Schnider TCI. These differences appeared to be distinct when we simply compared the cumulative amounts of propofol and the PK parameters (3 volumes and 3 clearances). However, the degree of discrepancy during TCI and time course of the predicted concentration could not be determined.

Therefore, we performed total and separate cross-simulation. During the early phase of infusion, the difference of C_p was significant. Thereafter, overall differences were shown to be roughly 10% (at 30 min) and 15% (at 2 hr) under- or overprediction of C_p, and the differences showed a gradual increase with time. However, total cross-simulations could not explain the impact of each parameter on the overall difference of prediction. Therefore, we performed separate cross-simulations. Young and Shafer [9] also demonstrated the changes of C_p and decrement time of three opioids by independently changing the volumes and clearance of the three compartments. They used simulations that were similar to our method, while predicting the change in C_p of opioid after a bolus if each pharmacokinetic parameter were independently increased by 5%. Our separate cross-simulation showed that V_C mainly contributed to the initial differences, and Cl₁ and V₃ to the difference of long-term infusion. The difference of Cl₃ also seemed to be an important factor during the initial period, but contributed less during long term infusion.

Even though Marsh TCI showed a more rapid loss of responsiveness than Schnider TCI, the amount of propofol infused until LOR and C_eff at LOR did not differ between the groups (Table 3). The k_e0 used for Marsh PK was 1.21/min [6], whereas 0.456/min was used for Schnider PK. The volume of distribution of Schnider PK was small and time to LOR was long during Schnider TCI, but the predicted C_eff slowly increased because of its smaller k_e0 than Marsh PK. Therefore, C_eff at LOR appeared to be insignificant between groups. However, the reproduced C_eff at LOR after simulation was significantly different between groups. During TCI, C_eff is calculated using the k_e0 and C_p. However, the value of k_e0 is highly influenced by the PK model and it was reported that it is unwise to use the k_e0 from one PK model with another PK model from a different study [6,10,11].

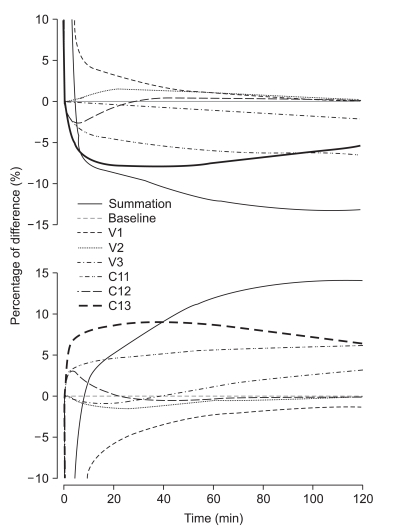
Body weight and LBM correlated well with the discrepancies of prediction. LBM is calculated using body weight and height. In Marsh PK, body weight influences V_C, V₂, V₃, Cl₁, Cl₂, and Cl₃. As a result, decreasing body weight leads to a smaller volume and clearance of each compartment. In addition, the relationship between Cl₁ and height-body weight showed a flat mesh (Fig. 7, left graph, gray mesh). In Schnider PK, only Cl₁ is influenced by body weight and height. Decreasing body weight and height leads to smaller Cl₁, and increasing height with lower body weight or decreasing height with higher body weight leads to a higher Cl₁ (Fig. 7, left graph, transparent mesh). Therefore, a taller patient with a lower body weight or a shorter obese patient showed a larger difference of clearance between the two models (Fig. 7, Right graph). Accordingly, there could be a large difference in the level of hypnosis between models during the TCI to these types of patients.

Fig. 7.

Clearances of the central compartment of Marsh PK (gray mesh, left graph) and Schnider PK (transparent mesh, right graph), and the difference of the clearances between the models of propofol (lower graph) according to patient body weight and height.

In our study, the mean Cl₁ of Schnider PK was 8.8% higher than that of Marsh PK. Wietasch et al. reported that they found a smaller V_C (3.55 L) than Marsh PK, and Cl₁ was reduced to 1.31 L/min in comparison with that of Marsh PK (2.04 L/min) and Schnider PK (1.89 L/min) [3]. In this study, contrary to our study, Cl₁ of Marsh PK was greater than Schnider PK, and mean body weights of subjects were around 75 kg, which was the heaviest body weight in our study. Kim et al. [12] reported that the V_C of lipid emulsion of propofol was 3.9 L and Cl₁ was 1.53 L/min. Jung et al. [13] reported that V_C of lipid emulsion of propofol was 6.78 L and Cl₁ was 1.46 L/min. The populations of these two reports were similar overall to those of our study. Marsh PK and Schnider PK are known to under-predict C_p [3,14]. White et al. [15] also suggested the use of the parameters of Marsh PK adjusted with the covariates, such as age and gender. Therefore, the possibility of overdose of propofol using Schnider PK could increase during long term infusion, especially for patients with low body weight.

There are some caveats that need to be taken into consideration. First, our study evaluated the PD difference between the models, only for the period of induction of anesthesia. Further study on the PD differences during maintenance of anesthesia and recovery period will be helpful in differentiation of the characteristics between the models. Second, the population of this study was limited to females. TCI using Marsh PK administers propofol irrelevant to gender. However, Schnider PK estimates different Cl₁ according to gender. The covariate, LBM, used for calculation of Cl₁, is differently calculated according to gender; men, LBM = 1.1 × weight - 128 × (weight / height)²; women, LBM = 1.07 × weight - 148 × (weight / height)² [16]. Cl₁ for women is calculated higher than that of men when other covariates are equal. Therefore, the results of this study could be different if investigated for both genders. Third, it took nearly 4 min to induce LOR using Schnider PK. The longest time to LOR was 310 s in Group S, which is considered to be inadequate for the routine induction of anesthesia. Therefore, other modalities, such as higher target of C_p or targeting C_eff, are indicated.

The primary goal of this study was to increase our understanding between the different PK models and the influence of PK parameters on the infusion patterns during TCI. This comparison method between PK models would be helpful in selection of an appropriate PK model of a certain drug in clinical settings and research fields.