Abstract
Purpose: To evaluate how a more flexible and thorough multiobjective search of feasible IMRT plans affects performance in IMRT optimization.
Methods: A multiobjective evolutionary algorithm (MOEA) was used as a tool to investigate how expanding the search space to include a wider range of penalty functions affects the quality of the set of IMRT plans produced. The MOEA uses a population of IMRT plans to generate new IMRT plans through deterministic minimization of recombined penalty functions that are weighted sums of multiple, tissue-specific objective functions. The quality of the generated plans are judged by an independent set of nonconvex, clinically relevant decision criteria, and all dominated plans are eliminated. As this process repeats itself, better plans are produced so that the population of IMRT plans will approach the Pareto front. Three different approaches were used to explore the effects of expanding the search space. First, the evolutionary algorithm used genetic optimization principles to search by simultaneously optimizing both the weights and tissue-specific dose parameters in penalty functions. Second, penalty function parameters were individually optimized for each voxel in all organs at risk (OARs) in the MOEA. Finally, a heuristic voxel-specific improvement (VSI) algorithm that can be used on any IMRT plan was developed that incrementally improves voxel-specific penalty function parameters for all structures (OARs and targets). Different approaches were compared using the concept of domination comparison applied to the sets of plans obtained by multiobjective optimization.
Results: MOEA optimizations that simultaneously searched both importance weights and dose parameters generated sets of IMRT plans that were superior to sets of plans produced when either type of parameter was fixed for four example prostate plans. The amount of improvement increased with greater overlap between OARs and targets. Allowing the MOEA to search for voxel-specific penalty functions improved results for simple cases with three structures but did not improve results for a more complex case with seven structures. For this modification, the amount of improvement increased with less overlap between OARs and targets. The voxel-specific improvement algorithm improved results for all cases, and its clinical relevance was demonstrated in a complex prostate and a very complex head and neck case.
Conclusions: Using an evolutionary algorithm as a tool, it was found that allowing more flexibility in the search space enhanced performance. The two strategies of (a) varying the weights and reference doses in the objective function and (b) removing the constraint of equal penalties for all voxels in a structure both generated sets of plans that dominated sets of plans considered to be “Pareto optimal” within the conventional, more limited search space. When considering voxel-specific objectives, the very large search space can lead to convergence problems in the MOEA for complex cases, but this is not an issue for the VSI algorithm.
Keywords: multiobjective optimization, intensity modulated radiation therapy (IMRT), evolutionary algorithm
INTRODUCTION
Inverse planning was intended to be a simple clinically based approach to treatment planning in which the physician defined the desired dosimetric goals of the plan and the optimization algorithm would calculate the necessary set of beam intensities. However, it is rarely the case that such a simple process actually produces a desirable plan. Except in the rare case of easily achievable objectives, it usually takes several iterations. In each iteration, the number or type of objectives, the parameters in the objectives, and the weights of the objectives are changed, and the resulting penalty function is minimized to generate one IMRT plan. All of these strategies, except for adjusting objective weights, change the optimization process in unpredictable ways and make the inverse planning process tedious and somewhat arbitrary.
In a typical IMRT plan, there are several hundred separate beamlets, each with its own intensity. Even if we consider the fact that the intensity of each beamlet can be constrained somewhat by the neighboring intensities, there is still an enormous number of possible intensity maps, which we denote as the feasible space. In conventional inverse planning algorithms, a single penalty function is constructed as a weighted sum of multiple organ-specific objective functions and then optimized. Each optimization returns the set of beamlet intensities that minimizes that particular function. While the optimization of a single-objective function simplifies the problem by mapping the n individual beamlet intensities to a single number, this number does not accurately reflect the diversity of clinical variables that go into selecting a plan. Those decisions are made in a separate multidimensional space defined by decision criteria. The planning process proceeds by making adjustments to the penalty function based on examination of decision criteria resulting from individual optimizations. Multiple plans are compared with respect to each decision criterion, but more importantly, they are examined with respect to the trade offs between the criteria. For each of the inverse planning strategies described above, a certain region of feasible space is explored. By varying the numbers and types of objectives and the objective function parameters, different regions can be explored. We use the term search space to denote the feasible space of possible objective functions and weights used to generate the penalty function for individual IMRT optimization. By varying the weights for a given set of penalty objectives, a set of optimal plans within the corresponding region in decision space are obtained (known as the Pareto optimal set or Pareto front).
Much has been written with respect to the optimality of IMRT plans. A multiobjective optimization using convex objective functions can generate plans that are indeed optimal in terms of these objective functions; however, these plans are unlikely to be optimal in terms of the decision criteria used for clinical determinations and only explore a limited space that does not include all possible IMRT plans. While that issue has been acknowledged, there has been little discussion regarding the means by which a more complete search can be accomplished. One of the manifestations of this problem is how to determine the optimal dose parameters to use in the organ-specific objective functions. It is recognized that there is no good way of finding optimal values in the clinical setting. Most often, planners settle for a plan that is “good enough,” either with respect to historical plans or a set of protocol-defined dosimetric criteria.
A key element in IMRT is that typical optimizers perform single-objective optimization whereas the actual problem is multiobjective. Thus, the search for improved plans is time consuming since an optimization needs to be performed, analyzed, and the optimization parameters adjusted without guidance or automation. Multiobjective optimization algorithms can search a greater space without external interaction and provide a set of plans that embody the trade offs between multiple decision criteria.
Multiobjective optimization (MOO) is a more comprehensive approach to inverse planning since the search is performed automatically. In some methods, the algorithm returns all the Pareto plans; in others an element in the optimization algorithm selects a plan based on an a priori ranking of objectives. Lahanas et al.1, 2 used a methodical incremental approach to exploring the Pareto front by varying the weights. Craft et al.3, 4, 5, 6, 7 have developed a method that reduces the computational effort by calculating a representative surface to the Pareto front and then interpolating between the calculated points when needed. In both of these methods, the region searched is restricted by the initial choices of the functional parameters. Other MOO algorithms perform constrained optimization8, 9 in which the individual objectives are ranked by importance. They start by optimizing the top level objectives, converting those objectives into constraints, optimizing with the next level, and so on. Methods are implemented to relax lower level constraints when not all can be met. Breedveld et al.9 achieve this by an iterative method in which voxel weights are modified, then if constraints are not met, some are relaxed by changing their values. In this way, a larger search space is explored until all the constraints are met.
In this paper, we use a multiobjective evolutionary algorithm (MOEA) to study the ways in which the current inverse planning paradigm limits the types of solutions that are obtained. In particular, we study the effects of allowing weighting parameters and reference doses to be optimized simultaneously and allowing each voxel considered in the optimization to have an individualized contribution to the penalty function.
MATERIALS AND METHODS
Definition of objective spaces
Conventional IMRT optimization finds a single plan that optimizes the set of beamlet intensities by minimizing a single penalty function that combines the individual, structure-specific penalty objectives using importance weighting factors. For example, the optimization process might find the beamlet weights or MLC configurations that minimize the function: , where k is the number of structures, F is called the penalty function, is the contribution from the ith objective, is the importance weight of the ith objective, and is the dose distribution of the ith structure. Boldface variables represent vectors. To simplify the notation, we assume a single-objective per structure, but in general, there is no restriction on the number of objectives per structure. A quadratic form of the structure-specific objective function is common, i.e., , where is the number of voxels in the ith structure, is the dose parameter penalty input for the ith structure, and is the dose in the jth voxel in the ith structure. If the reference dose is identical for all voxels in a structure, then equals a constant for all j. In the MOEA used in this paper, the beam intensities were optimized using the objective function
| (1) |
where H is a function that acts like a Heaviside function (0 when and 1 otherwise) for all OAR voxels and is always one for all target voxels.
Optimizing F(d) finds a point on the Pareto front in the space defined by the vector of individual functions, f. By varying the weights, other Pareto optimal solutions on the front are obtained. However, the optimal values of the penalty function parameters, , are not known a priori. In conventional IMRT planning, the weights and function parameters are varied in an ad hoc fashion. Changing even one of the parameters changes the objective space so that comparisons of the penalty function values of plans obtained before and after the changes are invalid. We define search space as that part of the feasible plan space that is mapped to the space of penalty objectives. Our MOEA expands the search space by varying penalty objectives and weights to iteratively reformulate the IMRT optimization problem as described below.
Plan comparisons obtained from different objective spaces need to be performed in a separate, constant space. We define a separate set of objective functions designed solely to be clinical relevant, which we call decision criteria, for such comparisons. For any patient, a set of decision criteria specifically relevant to the details of the treatment can be defined. The mathematical form of the decision criteria can be whatever is most closely related to clinical outcomes so long as they are functions of the 3D dose distribution. The efficiency of the algorithm is not affected by the choice of decision criteria since their calculation is insignificant compared to the individual deterministic IMRT optimizations that take 99% of the computation time. In summary, we find individual plans by optimizing a weighted sum of penalty objectives, and we search the feasible plan space by varying both reference dose parameters and weights. Plan quality is evaluated in a separate space defined by the decision criteria.
Domination and Pareto optimality
The IMRT problem is inherently multiobjective, thereby requiring that trade offs must be considered when selecting the most suitable IMRT plan to be used for patient treatment. In multiobjective optimization, domination occurs when at least one objective is strictly better than the others and the rest can be equal or better. If all the objectives are better, it is called strong domination; otherwise, it is termed weak domination. In this work, we use weak domination. For example, consider the minimization of three decision criteria used to characterize a plan, and plan A has values (1, 1, 3), plan B has values (2, 1, 2), and plan C has values (3, 2, 3). Neither plan A nor B dominates the other, but both plans A (weakly) and B (strongly) dominate C.
For a given set of criteria, a plan is Pareto optimal if there is no other feasible plan that dominates it. This means that it would also be impossible to improve any one criterion of this plan without making at least one other criterion worse. In our MOEA, the deterministic IMRT optimizations do achieve Pareto optimality in the space defined by the penalty function optimized; however, these plans are unlikely to be Pareto optimal as defined by the decision criteria. The evolutionary (stochastic) algorithm will generate more and more superior plans and will eventually approach (but never reach) the Pareto front in decision criteria space, if it runs for a sufficient number of iterations.
In order to compare different sets of plans produced using one multiobjective optimization method versus a second method, we have defined the concept domination comparison.10, 11 Domination comparison, , is defined to be the percent of comparisons between plans from sets A and B that result in the plan from set A dominating the plan from set B. can also be thought of as the probability for a plan randomly selected from set A to dominate a plan randomly selected from set B. If , it is likely that set A more closely approaches Pareto optimality better than set B. Note that this metric can be applied regardless of whether any of the plans are on the Pareto front and provides a statistical measure of the relative merit of one method versus the other.
Multiobjective evolutionary algorithm
MOEA has been developed for IMRT planning.10, 12 This stochastic optimization algorithm has the advantages of being able to optimize any form of decision criteria, is effective at searching a large space, and incorporates various methods designed to improve its efficiency and performance. The drawbacks include the fact that it does not guarantee convergence to the Pareto front and is typically slower than deterministic optimization algorithms. In order to improve convergence and to respond to clinical demands, the MOEA’s speed has been increased by using an accelerated deterministic algorithm to find the beamlet intensities for a given set of penalty objectives.10 Using evolutionary optimization principles, an individual’s genes consist of the importance weighting values, w, and the parameters of the penalty functions, . Methods for reproduction and mutation are used to generate new penalty functions from genes of the current population. These penalty functions are minimized to generate plans that are Pareto optimal in terms of these objective functions; however, in the selection process the plan quality is judged by more clinically relevant decision criteria, and plans are eliminated if and only if they are dominated. After multiple iterations, the population will converge to a set of plans that approach Pareto optimality in decision criteria space in a reasonably short amount of time.10
The dose calculations for the optimization and final dose distributions were performed using the macropencil beam model which has been demonstrated to provide accurate 3D dose calculations for IMRT-type fields.13 Optimizations were performed using fluence maps but a smoothing term was included in the penalty function to insure that dose gradients were deliverable with Elekta linacs using the step-and-shoot technique.
Expanding the Search Space
The search for plans within the feasible plan space was accomplished by using the MOEA to vary w and/or through the evolutionary optimization mechanisms. Varying w searched a region defined by the penalty objective functions and . Varying defined a new region within the plan space.
A second method for expanding the search space was introduced by dividing organs at risk (OARs) into voxels (0.25 × 0.25 × 0.25 cm3) and assigning individual weights and reference doses to each voxel. This corresponds to replacing with and pulling within the voxel-specific summation in Eq. 1. Thus a single organ was characterized by large sets of weights and reference doses (genes in the MOEA); however, the decision space was not altered, and only one decision criterion was used for each OAR or target. This can potentially have a large impact on the time to convergence since the number of genes increased from the order of 5–10 to several thousand.
Incrementally improving voxel-specific penalty objectives
Splitting up the genes of structures considered in the IMRT optimizations results in a rapid increase in the number of genes which may slow the convergence of the evolutionary algorithm especially for complex cases with many structures. To ameliorate this effect, a quick deterministic algorithm that automatically adjusts the penalty function parameters of individual voxels was introduced. The starting point for the voxel-specific improvement (VSI) algorithm was the set of plans in the final population generated with the MOEA using structure-specific penalty objectives. For each plan in that population, all structures (targets and OARs) were subdivided into m voxels and the matricies w and for each voxel was initialized to the values of the corresponding structure for that plan. Then the following incremental adjustments were made: the dose parameters were lowered in target voxels with higher than prescription dose, the weights were raised in target voxels with lower than prescription dose, and the penalties were raised in certain voxels of OARs by either increasing weight or lowering the reference dose when necessary to either flatten the target distribution or to maintain OAR decision criteria values. Every plan went through 20–40 additional iterations, and only changes that improved plans were accepted, i.e., the variance in each target’s dose distribution was reduced while either maintaining or decreasing the OAR decision criteria corresponding to lower overall OAR dose.
Comparison of Methods
Five different cases were studied: three simple prostate cancer treatments (cases 1, 2, and 3), a complex prostate cancer treatment (case 4), and a complex head and neck treatment (case 5). Case 1 was a simple plan that had two OARs: rectum and bladder wall, and a small PTV (72 Gy) with no overlap amongst structures. Case 2 was a simple plan with two OARs: rectal wall and bladder wall, and a PTV with a 69.6 Gy prescription dose with a typical amount of overlap between structures. Case 3 was designed to be a simple but challenging plan with two OARs: rectal wall and bladder, a PTV with a 66.6 Gy prescription dose, and high degree of overlap between structures. Case 4 was complex prostate plan with five OARs: rectal wall, bladder wall, left femoral head, right femoral head, and unspecified normal tissue, and both a GTV and PTV with a prescription dose of 81 Gy. Case 5 was a very complex head and neck plan with a primary GTV and a primary PTV with prescription doses of 70 Gy. It also had two secondary PTVs with prescription doses of 62.7 and 56.9 Gy and ten OARs: left cochlea, right cochlea, left parotid, right parotid, oral cavity, spinal cord, brainstem, epiglottis, unspecified brain, and a submandibular region. All plans used seven equally spaced 6 MV photon beams.
All dose distributions were scaled to meet minimum target dose requirements that 95% of the target volume receive at least the prescription dose. The same type of decision criteria was used in all of the optimizations: mean dose (after scaling) for OARs and dose range, , for targets. Since doses are scaled to meet target minimum DVH requirements, these decision criteria are nonconvex. OAR voxels inside the PTV were excluded from calculation of the OAR decision criteria functions. Some comparisons were also made between MOEA plans after they had been translated into deliverable beams and plans generated using a commercial IMRT optimization algorithm with our current clinical planning procedures (Pinnacle, Philips Medical Systems, Andover, MA).
The performance of the following methods was compared to demonstrate the effects of expanding the search space:
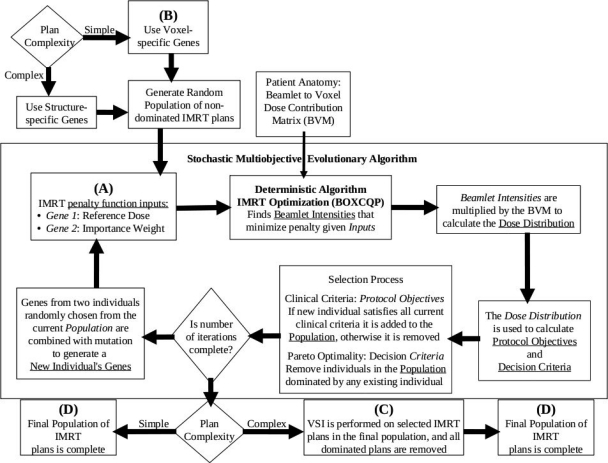
From label (A) in Fig. 1: Comparing the performance of MOEA optimizations implementing either one dose reference gene per OAR, one weighting gene per OAR, or both genes (Sec. 3A);
From label (B) in Fig. 1: Comparing MOEA optimizations using individual penalty objectives for each voxel with MOEA optimizations that use structure-specific penalty objectives (Sec. 3B);
From label (C) in Fig. 1: Evaluating a versatile algorithm (VSI) that can be used to incrementally improve voxel-specific genes in any IMRT plan (Sec. 3C);
From label (D) in Fig. 1: DVH comparison using the complex head and neck case of structure-specific MOEA IMRT plans that had been further optimized using VSI with a clinically generated plan (Sec. 3D).
Figure 1.
A block diagram summarizing the process of each iteration of the MOEA. Boldface letters (A), (B), (C), and (D) refer to individual steps that are the subject of specific comparisons as referred to in Sec 2F.
RESULTS
Multiobjective optimization of objective function parameters
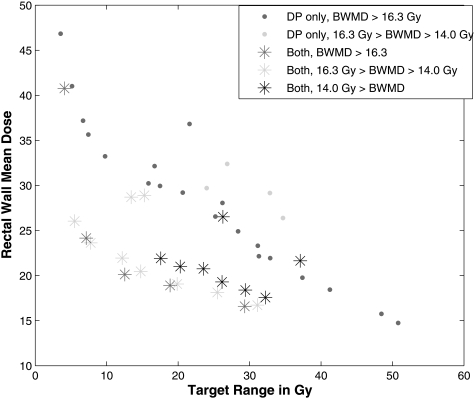
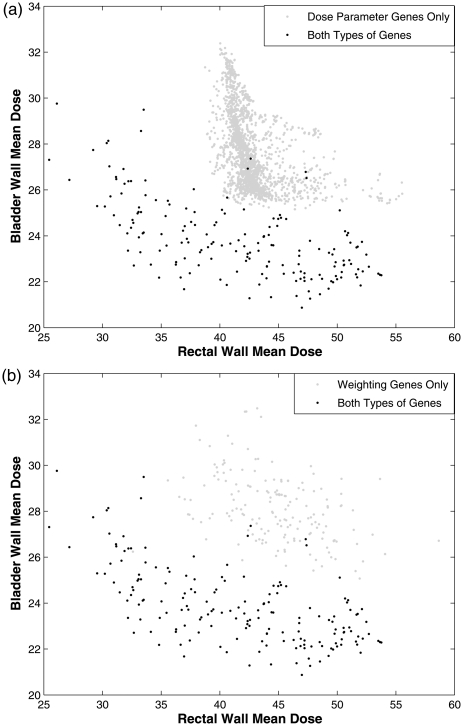
Figure 2 shows the results of two optimizations for case 1. One optimization was performed with just the reference doses as genes, and the second was performed with both the reference doses and weights as genes. When one type of input parameter is not optimized, the fixed value used for the optimization may impact performance. For this demonstration, all structures were given equal weighting. This was a short optimization and the number of solutions was limited to allow for easier decision analysis.10 Note that the figure is a 2D projection of a three-dimensional surface which complicates the visual interpretation of the points in the plot. The population generated using both gene sets dominated an average of the population generated with using only importance weighting genes and of dominations occurred in reverse. Figure 2 illustrates the shapes of the two populations are somewhat similar, but all objectives values improved when both genes were used. The inferior results suggest that the fixed weight used for the OARs was improperly chosen and should have been much less than the fixed weight used for the target.
Figure 2.
Comparison of optimizations for a prostate case (case 1) with two OARs and one target in which both weights and reference doses were genes (“both,” asterisks) and with only the reference doses as genes (“DP only,” diamonds). The bladder wall mean dose (BWMD) is plotted by binning the plans by mean dose value and identifying the values by color-coding.
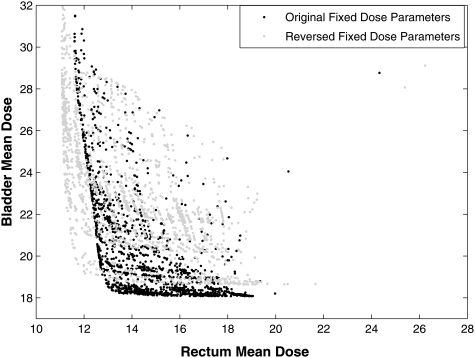
A demonstration of the importance of the selection for the fixed reference doses has on the final solution set when only weights are optimized is shown in Fig. 2. The MOEA that only optimized weights searched a restricted, inferior region of the feasible space resulting in poor IMRT plans . A 3000-iteration MOEA optimization was performed with no a priori knowledge using both reference dose and weighting genes to approximate the Pareto front for this allowed gene set for case 1. From this set of solutions, average dose parameters of 4 Gy for bladder and 12 Gy for rectum were found. They were used as the fixed values in an optimization using the same number of iterations but with only the importance weighting as genes. For the demonstration of the effect, another optimization was performed with two different values of the reference doses (12 Gy for bladder and 4 Gy for rectum), both values of which were among the solutions found in the comprehensive optimization. Figure 3 illustrates that these two different optimizations searched different regions within decision space. The best IMRT plans from all other possible values of the reference doses would result in the filling in of the concave region near the “knees” of the surfaces in Fig. 3. Note that the third decision criterion, target variance, is not plotted on this graph. The MOEA selection process removes all dominated plans, so the IMRT plans that appear to be dominated (have higher doses in both OARs) in this figure have lower target variances.
Figure 3.
Two OAR decision criteria of populations that approached the Pareto front for two different optimization problems by optimizing only the weights for case 1 are plotted. The third decision criterion, target variance, is not shown and all plans are nondominated. In the first optimization, fixed “optimal” dose parameter values of 4 Gy for the bladder and 12 Gy for the rectum were used. A second optimization was performed using a 12 Gy fixed dose parameter for the bladder and a 4 Gy dose parameter for the rectum.
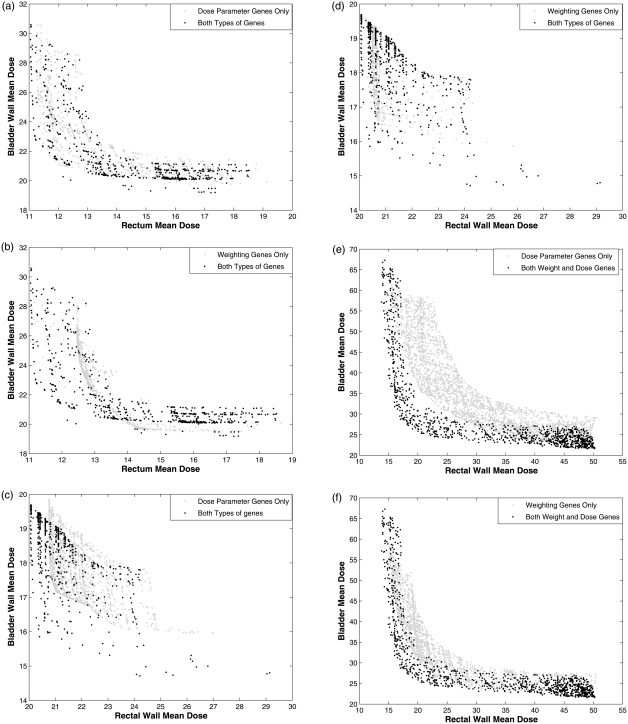
This effect was investigated more systematically for all four example prostate patients. First, a long single 3000-iteration (9000-iteration for case 3) MOEA optimization was performed to approximate the Pareto front with no a priori knowledge using both reference dose genes and weighting genes. Mean values of the weights obtained from these sets of plans were used as the fixed weight values in a second run using the same number of iterations but with only the dose parameters as genes. Complementary experiments were also performed using weights as genes and with the dose parameters fixed to their mean values from the long optimization. Figure 4 shows the results of optimizing the reference doses alone [Figs. 4a, 4c, and 4e] and weighting alone [Figs. 4b, 4d, and 4f]. In both cases, comparisons are made to optimizations using both sets of parameters. To better show the shape of optimal sets of plans in these 2D plots of OAR decision criteria, the third dimension was restricted so that only IMRT plans with target decision criteria within a specific range were plotted on the graph: (case 1) ; (case 2) ; (case 3) ; (case 4) , left femur: , right femur: , and unspecified tissue: . These ranges were chosen to be near the knee of the Pareto front where trade offs between objectives are reasonable.
Figure 4.
Populations that approached the Pareto front were generated with the MOEA using both dose parameter genes and importance weighting genes for the three simple prostate example cases. On the left side, plots (a), (c), and (e) compare them to results when only the reference dose genes were varied for cases 1, 2, and 3, respectively. On the right side, plots (b), (d), and (f) compare them to results when only the weighting genes were considered in the MOEA. Rectal wall (or rectum) and bladder wall (or bladder) objectives are plotted for each set of plans over specific ranges of target variance.
A similar comparison was made for the complex prostate case 4 and results are shown in Figs. 5a, 5b.
Figure 5.
Case 4 results obtained in the same manner as Fig. 4.
The increased degrees of freedom of varying w and produced sets of plans that dominated more single gene plans than vice versa (Table Table I.). The improvement is less than for Fig. 2, since appropriately optimum fixed values of weights or reference doses were used in these optimizations. Results were considerably worse for the optimizations that used only dose parameter genes, suggesting that being able to individually optimize importance weighting for each plan is particularly important.
Table I.
Domination comparison values with respect to decision criteria between plans obtained by varying weights, references doses and both sets of parameters. Each cell in the table represents the domination comparison values for one set versus the other and the reverse domination. For example in the top left cell, “both” plans dominated “ only” plans in 1.22% of possible comparisons, and 0.00% of “” plans dominated “both only” plans.
| Both vs dref only | Both vs w only | |
|---|---|---|
| Case 1 | ||
| Case 2 | ||
| Case 3 | ||
| Case 4 |
Splitting up OAR penalty objectives
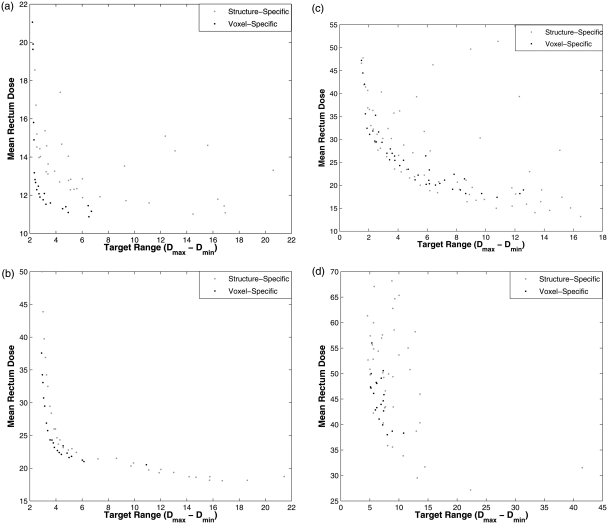
The previous optimizations all operated under the constraint that every voxel within a structure had the same weight and reference dose. To explore the effects of removing that constraint, the MOEA search space was expanded so that each voxel in each OAR had its own pair of genes ( ) while still using only one decision criteria for each OAR (mean dose after scaling to meet minimum target requirements). MOEA optimizations were performed with 9000 iterations. Figure 6 shows the comparisons between voxel-specific and structure-specific optimizations for cases 1–4. The decision criteria values for mean rectal wall dose were plotted versus the dose range () in the target structure.
Figure 6.
Sets of IMRT plans were generated using 9000-iteration MOEA optimizations with structure-specific and voxel-specific genes. Mean rectal wall dose values are plotted versus the range of target doses. Plots (a)–(d) represent the optimizations for cases 1–4, respectively.
The large number of genes in the voxel-specific optimization raises questions regarding convergence toward the Pareto optimal surface. To explore that effect and to quantify the results, domination comparison values were calculated for 900-iteration MOEA optimizations and 9000-iteration MOEA optimizations using voxel-specific and structure-specific genes, and the results are shown in Table Table II..
Table II.
Values of domination comparison between sets of IMRT plans obtained with 900 and 9000-iteration MOEA optimizations using either structure-specific or voxel-specific penalty objectives. In all cases, both w and were varied. Each cell in the table represents the domination comparison values for one set versus the other and the reverse domination.
| Voxel-specific versus structure-specific | Voxel-specific versus structure-specific | |
|---|---|---|
| (900 iterations) | (9000 iterations) | |
| Case 1 | ||
| Case 2 | ||
| Case 3 | ||
| Case 4 |
For the three simple cases, using voxel-specific genes improves performance for MOEA optimizations. The more difficult cases with a high degree of overlap between OARs and PTV demonstrate more modest improvements. For the complex prostate case, using voxel-specific genes did not improve and even degraded results. The fact that more iterations increased the separation between the voxel-specific and structure-specific optimizations suggests that convergence takes longer when voxel-specific genes are used. Although the optimization potential is greater, it is challenging to realize this potential when clinically feasible computation times are necessary, especially in complex cases.
Use of voxel-specific improvement (VSI) algorithm
As illustrated by Sec. 3B, increasing the search space by using voxel-specific penalty objectives can lead to poor results for complex cases when computation time is limited. To avoid this problem, an independent algorithm that can act on any IMRT plan was developed that deterministically adjusted the weights and dose parameters for each voxel to simultaneously reduce target variance and OAR dose (see Sec. 2E). This VSI was used to systematically improve sets of plans generated with the MOEA algorithm using structure-specific genes.
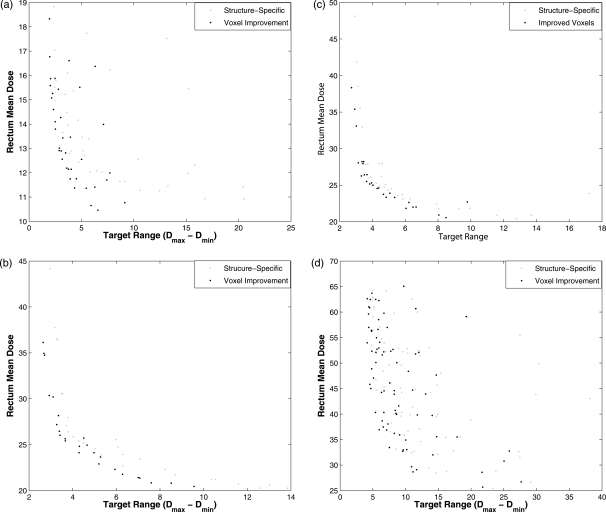
To see if the proposed algorithm could improve sets of MOEA plans, 900-iteration MOEA optimizations for each example case were performed with and without voxel-specific improvement (Fig. 7). In this figure, structure-specific optimizations were performed. The plans obtained were then operated on by the VSI algorithm to see the degree to which the plans, on the whole, were improved.
Figure 7.
Sets of IMRT plans were generated using 900-iteration MOEA optimizations with structure-specific genes. These sets of plans were compared to sets of plans that subsequently used the deterministic VSI algorithm. Target range and mean rectal wall dose (or rectum dose) are plotted for cases 1–4 [plots (a)–(d), respectively].
The first column in (Table Table III.) compares domination comparison values for the plots represented in Fig. 7. This same set of IMRT plans using VSI was also compared to the set of plans resulting from a long structure-specific optimization (9000 iterations). The reduced domination comparison of VSI plans to the long MOEA optimizations illustrates the fact that the additional iterations brought the optimized set of plans closer to the Pareto front. For the most complex case (case 4), the improvement was more noticeable in that the structure-specific optimization after 9000 iterations showed more dominations compared to the VSI plans after 900 iterations.
Table III.
Values of domination comparison of (900-iteration) structure-specific MOEA IMRT plans with voxel-specific improvement (VSI) with various other methods without VSI. The first column compares the VSI plans with a similar structure-specific MOEA optimization (900 iterations), the second column compares the VSI plans to long structure-specific optimizations (9000 iterations), and the third column compares the VSI plans to voxel-specific MOEA optimizations (900 iterations). Each cell in the table represents the domination comparison values for one set versus the other and the reverse domination.
| VSI versus structure-specific | VSI versus structure-specific | VSI versus voxel-specific | |
|---|---|---|---|
| (900 iterations) | (9000 iterations) | (900 iterations) | |
| Case 1 | |||
| Case 2 | |||
| Case 3 | |||
| Case 4 |
Finally, the third column of Table Table III. shows the results of comparing the same set of plans resulting from 900 iteration structure-specific MOEA optimizations with VSI to a 900 iteration optimization using voxel-specific genes. The large improvement of the MOEA voxel-specific optimization for the simpler cases illustrates how quickly this search found plans that were better than structure-specific optimization even after being improved by the VSI. For the more complex case, VSI was very effective whereas the MOEA using voxel-specific genes was detrimental due to search times needed in this high-dimensional space. It should be kept in mind that as the number of decision criteria increases, the more difficult it is for any given plan to dominate another, which is part of the reason for the decreased values of the complex cases.
Complex head and neck case clinical example
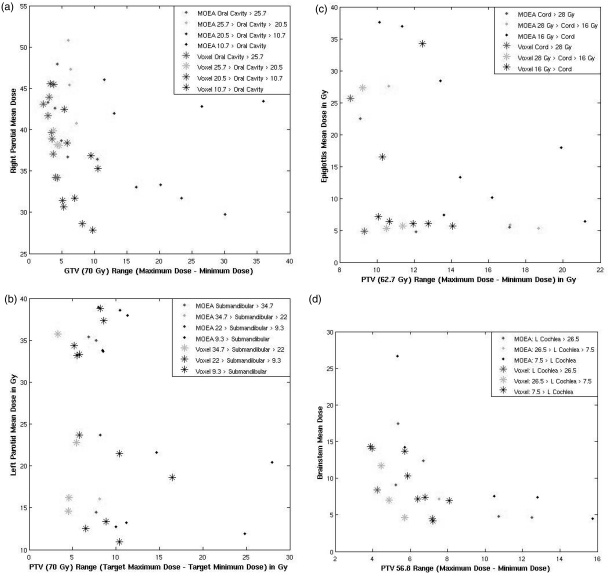
To demonstrate a clinically feasible example, a 900-iteration IMRT MOEA optimization was performed for the very complex head and neck case (case 5, 14 decision criteria) using only two genes per OAR. The VSI algorithm was then applied to all of the plans. Due to the greater complexity of the case, each individual deterministic optimization took ∼20 s, so each MOEA optimization took ∼5 h (∼7 h with further voxel-specific improvement) on an eight core workstation with 2.00 GHz Intel processors. This compares to approximately 1 h (90 min with VSI) for 900-iteration MOEA optimizations for the prostate cases. Decision criteria values before and after the voxel-specific improvement are shown in Fig. 8. Each plot shows the values of three decision criteria for each plan. The third value is binned according to its value and plotted in different colors.
Figure 8.
All four figures compare the results of a 900-iteration optimization using organ-specific genes with the results obtained after voxel-specific-improvement. Three of the 14 decision criteria are plotted on each graph for every plan in each population. The target range is plotted on the x-axis; an OAR mean dose is plotted on the y-axis, and the fitness objective value for a different OAR is shown using color-coding.
The decision criteria in the plans obtained with MOEA + VSI are superior to the plans generated using only the MOEA. with no dominations occurring in reverse. This rate of domination is significant when 14 fitness objectives are used given that the probability of a random domination is 1 in 16 384. The voxel-specific algorithm focuses on reducing target variance and adjusting the scaling factor among multiple targets. This method appears to be more effective in complex cases.
Dose volume histograms for multiple OARs and targets were compared between a MOEA IMRT plan and a clinical plan. The clinical plan was generated by an experienced dosimetrist using Pinnacle’s standard IMRT interface. This optimization was performed so that the total number of segments for seven beams in the Pinnacle plan and the MOEA plan matched (77 segments). The fluence maps of MOEA plans were translated to a step-and-shoot delivery using the algorithm of Bortfeld et al.21 during optimization prior to evaluating decision criteria. The MOEA generated the entire Pareto front so the comparison was performed by selecting one plan that had target coverage comparable to the Pinnacle plan. The different translation algorithms had different effects on target distributions. The Pinnacle translator results in targets with lower minimum dose and higher maximum dose in most cases, but had steeper fall off in the intermediate region than the basic translator we used for the MOEA plan.
Dose volume histograms for each target and OAR in this plan were compared to a plan generated using standard clinical methods in Fig. 9.
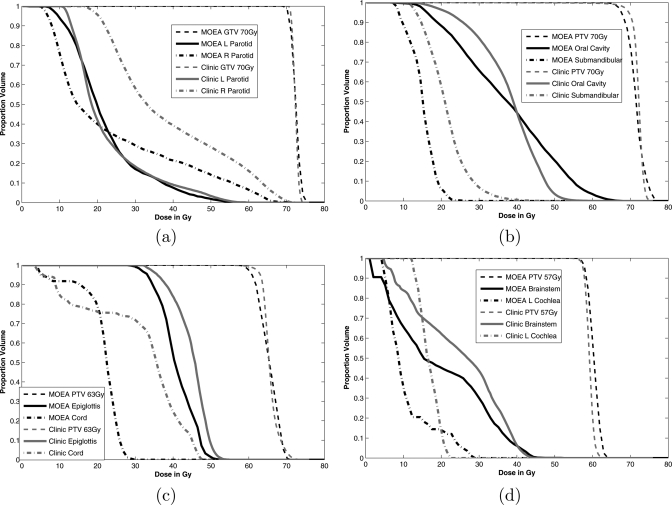
Figure 9.
Dose volume histograms comparing a head and neck IMRT plan generated using a 900-iteration MOEA optimization with the voxel-specific improvement method (MOEA) and a plan generated using standard clinical methods (Clinic) for case 5.
When comparing the translated MOEA using VSI with the clinical plan, dose distributions in most OARs were much lower in the MOEA plan. Only the oral cavity and left parotid did not have superior dose distributions. These OARs were close to at least one PTV, and hence, there were physical limitations to lowering these doses while maintaining acceptable target uniformity. The translated MOEA plan using VSI also resulted in PTV dose distributions that better met maximum and minimum clinical requirements although the fall off was steeper in the intermediate region for the Pinnacle plan. The GTV dose distributions were similar for both methods.
DISCUSSION
The search for the “optimal” plan in IMRT has been the subject of much study. In this paper, we have been concerned with a more comprehensive view that includes the issues of (a) how to define optimality when considering competing objectives, (b) how to define the objective space which defines the allowed penalty functions minimized in individual IMRT optimization, and (c) how to compare different optimizations. Critical to all of these issues is the space of feasible plans that are available to be searched during the optimization process. This search is accomplished by adding a stochastic optimization that can explore a large range of different penalty objectives and weights used in Eq. 1. Even though we have focused on some of the more abstract aspects of optimization, we have kept a close eye on clinical constraints of time and effort. This consideration has led to the use of a multiobjective optimization algorithm that can search through the space of possible IMRT plans without need of human intervention.
Pareto optimality is the appropriate method of comparing solutions with multiple attributes. The Pareto front consists of all the Pareto optimal plans that cannot be dominated by any other possible plan. Deterministic optimization algorithms can be shown to yield the theoretically optimal solutions in the space defined by the penalty objectives; however, these objectives are designed to be mathematically easy to be optimized. Decision criteria can be designed solely to reflect what is best for the patient. In order to explore a greater region of decision criteria space, we have used a stochastic algorithm, MOEA, which does not guarantee Pareto optimality in this space. The true Pareto front in this space is unknown to us, and the MOEA can only provide an approximation. To determine how close a given set of plans is to the true Pareto front, we can observe the rate of change in the solution set, and we can explore this by changing the number of individual plans created. Thus, we have used large numbers of plans (up to 9000) to judge how close we were and then reduced that number for the sake of efficiency. The issue of convergence for stochastic optimization also presents a problem in the very high-dimensional space of voxel-specific genes. In these cases, a reasonable optimization time does not provide a close enough approximation to the true Pareto front when a large number of decision criteria (>4) are used. To improve the performance of our algorithm, we have added a heuristic deterministic search which has been shown to produce a better approximation to the true Pareto front in a reasonable amount of time.
Figure 2 illustrates an important point regarding the limitations of either fixing or randomly searching for values of the reference doses. Fixing the values of the penalty function reference doses, which is commonly done in clinical inverse planning, limits the plans that are available to the optimizer and, ultimately, to the planner. In this simple example, a different set of plans was achieved by changing the reference doses, and a number of those plans dominated the plans from the original search. By limiting the search by fixing those values, the decision maker is denied the opportunity to evaluate some better alternatives.
If only one set of objective parameters (either w or ) is optimized, an inferior set of IMRT plans can result, especially if the fixed penalty objectives (or weights) are inappropriately chosen. The results can be improved by doing an initial optimization to find effective values for the OAR reference doses and then fixing the penalty objectives to those values. Once this set of reference doses has been found, reasonable changes in the fixed values have little effect on performance;3 however, this is different from simultaneously searching all possible reference doses and weights. The optimal set of weights found for a particular set of OAR references doses will change for different sets of reference doses and vice versa. If both types of penalty inputs are allowed to vary and are optimized relative to each other, improvements in overall performance are possible.
We found that by optimizing both the weights and reference dose parameters used in the penalty function, the MOEA was able to better approximate the Pareto front with respect to clinically relevant decision criteria. The poorest results occurred when importance weighting was fixed. For each optimal set of dose parameters, the optimal set of weights specific to that set could be found, thereby creating a composite search space that contains some dominant plans that would be difficult to find without a systematic search.
When structures were divided so that each voxel in all OARs was allowed to have its own penalty objective and weight, results improved for simple example cases as judged by the same decision criteria. This did not hold true for more complex cases where using voxel-specific genes significantly increased the number of iterations it took to converge to the Pareto front. In the voxel-specific MOEA, the dimensionality of the search space increased by three or four orders of magnitude, but the number of decision criteria remained unchanged. This corresponds to a significant difference between the complexity of the search space (10 000 to 100 000 degrees of freedom) and the decision space (<20 variables). This allows a more thorough search for nonintuitive optimal sets of penalty objectives while simultaneously maintaining a tractable decision space. This would not be possible using multiobjective optimization methods where the decision space and the search space were the same.
To avoid the disadvantages of dimensional overload when using a voxelized search space in an evolutionary optimization, a set of IMRT plans was first generated using MOEA optimizations with organ-specific genes and then further optimized by incrementally adjusting voxel-specific genes. This method takes advantage of the increased search space without the disadvantage of slower convergence. This technique resulted in significant improvement in the final set of IMRT plans for both complex and simple situations and was able to improve upon the organ-specific “Pareto front” by exploring the expanded allowable search space. Dose in OARs close to targets were lowered, and PTV dose distributions were more uniform and clinically desirable. This demonstrates that using organ-specific doses and weights limited the search within decision criteria space. The voxel-specific genes allowed a broader search and hence, a closer approximation to the true Pareto front. Some plans were significantly improved in all decision criteria by expanding the search space by means of voxel-specific genes.
Voxel-specific factors have been used to improve dosimetric metrics of IMRT plans with the assumption that more weight should be given to voxels that receive higher dose.14 This method used only a priori knowledge and relied on an assumption that may not always hold. A related method used an interactive approach in which isodose contours and DVH’s were used to identify voxels whose weight needed to be modified.15 Voxel-specific genes adjustments have also been made to effectively meet specific OAR clinical dose volume constraints a posteriori,16 but this method did not take full advantage of greater search space provided by voxel-specific penalty parameters. Originally, in our algorithm voxel-specific parameters were used to calculate penalties only for those OAR voxels with dose greater than the dose parameter for greater speed,10 but in the current work, a posteriori knowledge was used to adjust voxel-specific penalty parameters with the goal of improving plan quality. The algorithm is analogous to treatment planners drawing new structures and adjusting objectives to make IMRT plans more clinically desirable, but this method is automated and can make modifications at the detail of each voxel.
The fact that the organ-specific objective functions play a role in the quality of the optimized plan has received less attention than has voxel-specific weighting. However, there is still the issue of how to find the best parameters given a particular type of objective function. Wu et al.17 developed a method for modifying either the weighting factors or the functional parameters, i.e., reference doses. They state that the two different modifications are identical, but this is only with respect to their implementation of an interactive optimization algorithm, not with respect to the optimization itself. Yan et al.18 and Stieler et al.19 have used fuzzy logic inference to find better dose parameters. This is mainly a method for speeding up the planning process by eliminating the manual trial-and-error of conventional inverse planning. However, the results are only as good as the input which came from the manual planning method. Krause et al.20 used a Lagrange multiplier method to determine the elasticity and specificity of objective function parameters, thereby providing a planner with quantitative feedback as to the most promising modifications to be made to the parameters.
Comparing the quality of plans that are optimized using different penalty functions is challenging. Without an independent set of clinically relevant criteria for judging a plan’s merit that falls outside the optimization process, it is impossible to compare two plans. In the single-objective optimization problem, varying any of the parameters changes the problem so that the solutions obtained are optimal to that particular problem. Multiobjective optimization that only varies the weights can get around that problem by presenting the entire Pareto optimal set with respect to the organ-specific objectives. However, once the individual function parameters are altered, there is no common space in which to compare the plans. Therefore, we have explicitly kept our decision criteria constant and separate from the optimization objectives. Another aspect is how to compare two optimization methods that produce sets of plans, when not all the plans from one method are demonstrably superior (or inferior). The use of domination comparison is our response, with more details of such comparisons being described in Phillips and Holdsworth.11
CONCLUSIONS
The two strategies of (a) varying both the weights and reference doses in the objective function and (b) removing the constraint of using the same penalty functions and weights for all voxels in a structure improved the quality of the set of IMRT plans produced as determined by clinically relevant decision criteria. This demonstrates that sets of plans considered to be “Pareto optimal” within the conventional, more limited search space can be dominated by sets of plans resulting from a multiobjective search of a larger, less constrained space. Using voxel-specific objectives greatly increases the size of the search space which can lead to convergence problems in the MOEA for complex cases, but this was not a problem for a voxel-specific heuristic algorithm that was developed and applied. The use of a stochastic multiobjective optimization algorithm had the flexibility to explore the effects of expanding the available search space independent of the decision space. The results presented in this paper show that the form of the search space used in IMRT optimization has an important impact on the quality of the plans that are produced.
ACKNOWLEDGMENTS
This work was supported in part by NIH Grant No. 1-R01-CA112505.
References
- Lahanas M., Schreibmann E., and Baltas D., “Multiobjective inverse planning for intensity modulated radiotherapy with constraint-free gradient-based optimization algorithms,” Phys. Med. Biol. 48, 2843–2871 (2003). 10.1088/0031-9155/48/17/308 [DOI] [PubMed] [Google Scholar]
- Lahanas M., Schreibmann E., and Baltas D., “Intensity modulated beam radiation therapy dose optimization with multiobjective evolutionary algorithms,” Fonseca C. M., editor, Proceedings of 2nd International Conference Evolutionary Multi-Criterion Optimization, EMO 2003, Faro, Portugal, April 8–11, 2003, pp. 439–447.
- Craft D. L., Halabi T. F., Shih H. A., and Bortfeld T. R., “Approximating convex Pareto surfaces in multiobjective radiotherapy planning,” Med Phys. 33, 3399–3407 (2006). 10.1118/1.2335486 [DOI] [PubMed] [Google Scholar]
- Craft D., Halabi T., Shih H. A., and Bortfeld T., “An approach for practical multiobjective IMRT treatment planning,” Int. J. Radiat. Oncol., Biol., Phys. 69, 1600–1607 (2007). 10.1016/j.ijrobp.2007.08.019 [DOI] [PubMed] [Google Scholar]
- Hong T. S., Craft D. L., Carlsson F., and Bortfeld T. R., “Multicriteria optimization in intensity-modulated radiation therapy treatment planning for locally advanced cancer of the pancreatic head,” Int. J. Radiat. Oncol., Biol., Phys. 72, 1208–1214 (2008). 10.1016/j.ijrobp.2008.07.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monz M., Küfer K. H., Bortfeld T. R., and Thieke C., “Pareto navigation,” Phys. Med. Biol. 53, 985–998 (2008). 10.1088/0031-9155/53/4/011 [DOI] [PubMed] [Google Scholar]
- Thieke C., Kufer K. H., Monz M., Scherrer A., Alonso F., Oelfke U., Huber P. E., Debus J., and Bortfeld T., “A new concept for interactive radiotherapy planning with multicriteria optimization: First clinical evaluation,” Radiother. Oncol. 85, 292–298 (2007). 10.1016/j.radonc.2007.06.020 [DOI] [PubMed] [Google Scholar]
- Jee K. W., McShan D. L., and Fraass B., “Lexicographic ordering: Intuitive multicriteria optimization for IMRT,” Phys. Med. Biol. 52, 1845–1861 (2007). 10.1088/0031-9155/52/7/006 [DOI] [PubMed] [Google Scholar]
- Breedveld S., Storchi P. R. M., Keijzer M., Heemink A. W., and Heijmen B. J. M., “A novel approach to mulit-criteria inverse planning for IMRT,” Phys. Med. Biol. 52, 6339–6353 (2007). 10.1088/0031-9155/52/20/016 [DOI] [PubMed] [Google Scholar]
- Holdsworth C., Kim M., Liao J. J., and Phillips M. H., “A hierarchical approach to multiobjective optimization in IMRT,” Med. Phys. 37, 4986–4997 (2010). 10.1118/1.3478276 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips M. H. and Holdsworth C., “When is better best? A multiobjective perspective,” Med. Phys. 38, 1635–1640 (2011). 10.1118/1.3553404 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holdsworth C., Stewart R., Kim M., Liao J. J., and Phillips M. H., “Investigation of effective decision criteria for multiobjective optimization in IMRT,” Med. Phys. 38, 2964–2974 (2011). 10.1118/1.3589128 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips M. H., Singer K. M., and Hounsell A. R., “A macropencil beam model: Clinical implementation for conformal and intensity modulated radiation therapy,” Phys. Med. Biol. 44, 1067–1088 (1999). 10.1088/0031-9155/44/4/018 [DOI] [PubMed] [Google Scholar]
- Yang Y. and Xing L., “Clinical knowledge based inverse treatment planning,” Phys. Med. Biol. 49, 5101–5117 (2004). 10.1088/0031-9155/49/22/006 [DOI] [PubMed] [Google Scholar]
- Cotrutz C. and Xing L., “IMRT dose shaping with regionally variable penalty scheme,”Med. Phys. 30, 544–541 (2003). 10.1118/1.1556610 [DOI] [PubMed] [Google Scholar]
- Breedveld S., Storchi P. R. M., Keijzer M., and Heijmen B. J. M., “Fast, multiple optimization of quadratic dose objective functions in IMRT,” Phys. Med. Biol. 51, 3569–3579 (2006). 10.1088/0031-9155/51/14/019 [DOI] [PubMed] [Google Scholar]
- Wu C., Olivera G. H., Jeraj R., Keller H., and Mackie T. R., “Treatment plan modification using voxel-based weighting factors/dose prescription,” Phys. Med. Biol. 48, 2479–2491 (2003). 10.1088/0031-9155/48/15/315 [DOI] [PubMed] [Google Scholar]
- Yan H., Yin F. F., Guan H., and Kim J. H., “AI-guided parameter optimization in inverse treatment planning,” Phys. Med. Biol. 48, 3565–3580 (2003). 10.1088/0031-9155/48/21/008 [DOI] [PubMed] [Google Scholar]
- Stieler F., Yan H., Lohr F., Wenz F., and Yin F. F., “Development of a neuro-fuzzy technique for automated parameter optimization of inverse treatment planning,” Radiat. Oncol. 4, 1–16 (2009). 10.1186/1748-717X-4-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krause M., Scherrer A., and Thieke C., “On the role of modeling parameters in IMRT plan optimization,” Phys. Med. Biol. 53, 4907–4926 (2008). 10.1088/0031-9155/53/18/004 [DOI] [PubMed] [Google Scholar]
- Bortfeld T. R., Kahler D. L., Waldron T. J., and Boyer A. L., “X-ray field compensation with multileaf collimators,” Int. J. Radiat. Oncol., Biol., Phys. 28, 723–730 (1994). 10.1016/0360-3016(94)90200-3 [DOI] [PubMed] [Google Scholar]