Comparative analysis of nonlinear dimensionality reduction techniques for breast MRI segmentation

Abstract

Purpose: Visualization of anatomical structures using radiological imaging methods is an important tool in medicine to differentiate normal from pathological tissue and can generate large amounts of data for a radiologist to read. Integrating these large data sets is difficult and time-consuming. A new approach uses both supervised and unsupervised advanced machine learning techniques to visualize and segment radiological data. This study describes the application of a novel hybrid scheme, based on combining wavelet transform and nonlinear dimensionality reduction (NLDR) methods, to breast magnetic resonance imaging (MRI) data using three well-established NLDR techniques, namely, ISOMAP, local linear embedding (LLE), and diffusion maps (DfM), to perform a comparative performance analysis.

Methods: Twenty-five breast lesion subjects were scanned using a 3T scanner. MRI sequences used were T1-weighted, T2-weighted, diffusion-weighted imaging (DWI), and dynamic contrast-enhanced (DCE) imaging. The hybrid scheme consisted of two steps: preprocessing and postprocessing of the data. The preprocessing step was applied for B₁ inhomogeneity correction, image registration, and wavelet-based image compression to match and denoise the data. In the postprocessing step, MRI parameters were considered data dimensions and the NLDR-based hybrid approach was applied to integrate the MRI parameters into a single image, termed the embedded image. This was achieved by mapping all pixel intensities from the higher dimension to a lower dimensional (embedded) space. For validation, the authors compared the hybrid NLDR with linear methods of principal component analysis (PCA) and multidimensional scaling (MDS) using synthetic data. For the clinical application, the authors used breast MRI data, comparison was performed using the postcontrast DCE MRI image and evaluating the congruence of the segmented lesions.

Results: The NLDR-based hybrid approach was able to define and segment both synthetic and clinical data. In the synthetic data, the authors demonstrated the performance of the NLDR method compared with conventional linear DR methods. The NLDR approach enabled successful segmentation of the structures, whereas, in most cases, PCA and MDS failed. The NLDR approach was able to segment different breast tissue types with a high accuracy and the embedded image of the breast MRI data demonstrated fuzzy boundaries between the different types of breast tissue, i.e., fatty, glandular, and tissue with lesions (>86%).

Conclusions: The proposed hybrid NLDR methods were able to segment clinical breast data with a high accuracy and construct an embedded image that visualized the contribution of different radiological parameters.

INTRODUCTION

Diagnostic radiological imaging techniques are powerful noninvasive tools with which to identify normal and suspicious regions within the body. The use of multiparametric imaging methods, which can incorporate different functional radiological parameters for quantitative diagnosis, has been steadily increasing.^{1, 2, 3} Current methods of lesion detection include dynamic contrast-enhanced (DCE) magnetic resonance imaging (MRI) and/or positron emission tomography/computed tomography (PET/CT) images, which generate large amounts of data. Therefore, image-processing algorithms are required to analyze these images and play a key role in helping radiologists to differentiate normal from abnormal tissue. In multiparametric functional radiological imaging, each image sequence or type provides different information about a tissue of interest and its adjacent boundaries.^{4, 5, 6, 7} For example, in multiparametric breast MRI, diffusion-weighted imaging (DWI) and Dynamic Contrast Imaging (DCE) MRI provide information about cellularity and the vascular profile of normal tissue and tissue with lesions.^{8, 9, 10} Similarly, PET/CT data provide information on the metabolic state of tissue.^{11, 12} However, combining these data sets can be challenging, and because of the multidimensional structure of the data, methods are needed to extract a meaningful representation of the underlying radiopathological interpretation.

Currently, most computer-aided diagnosis (CAD) can act as a second reader in numerous applications, such as breast imaging,^{13, 14, 15} Most CAD systems are based on pattern recognition and use Euclidean distances, correlation, or similar methods to compute similarity between structures in the data segmentation procedure.^{13, 16} It has been shown that methods based on Euclidean distance and other similarity measures cannot fully preserve data structure, which will negatively affect the performance of a CAD system.^{17, 18} To overcome this limitation, we propose a new hybrid methodology, based on advanced machine learning techniques, and called “dimensionality reduction” (DR), which preserves the prominent data structures and may be useful for quantitatively integrating multimodal and multiparametric radiological images. Dimensionality reduction methods are a class of algorithms that use mathematically defined manifolds for statistical sampling of multidimensional classes to generate a discrimination rule of guaranteed statistical accuracy.^{19, 20, 21, 22, 23} Moreover, DR can generate a two- or three-dimensional map, which represents the prominent structures of the data and provides an embedded image of meaningful low-dimensional structures hidden in the high-dimensional information.¹⁹ Pixel values in the embedded image are obtained based on distances over the manifold of pixel intensities in the higher dimension, and could have higher accuracy in detecting soft and hard boundaries between tissues, compared to the pixel intensities of a single image modality. To investigate the potential of DR methods for medical image segmentation, we developed and compared the performance of DR methods using ISOMAP, local linear embedding (LLE), and Diffusion Maps (DfM) on high-dimensional synthetic data sets and on a group of patients with breast cancer.

METHODS AND MATERIALS

Dimensionality reduction

To detect the underlying structure of high-dimensional data, such as that resulting from multiparametric MRI, we used dimensionality reduction methods. Dimensionality reduction (DR) is the mathematical mapping of high-dimensional data into a meaningful representation of the intrinsic dimensionality (lower dimensional representation) using either linear or nonlinear methods (described below). The intrinsic dimensionality of a data set is the lowest number of images or variables that can represent the true structure of the data. For example, T1-weighted imaging (T1WI) and T2-weighted imaging (T2WI) are the lowest-dimension set of images that can represent anatomical tissue in the breast. Mathematically, a data set, X ⊂ R^{D(x₁,x₂,…x_n)=D(Images)} where, x₁,x₂,…,x_n = T1WI, T2WI, DWI, DCE MRI or others and the data set has an intrinsic dimensionality, d < D, if X can be defined by d points or parameters that lie on a manifold. R^D refers to D dimensional space with real numbers. Typically, we use a manifold learning method to determine points or locations within a dataset X (e.g., MRI, PET, etc.) lying on or near a manifold with intrinsic (lower) dimensionality, d, that is embedded in the higher dimensional space (D). By definition, a manifold is a topological space that is locally Euclidean, i.e., around every point, there exists a neighborhood that is topologically the same as the open unit ball in Euclidian space. Indeed, any object that can be “charted” is a manifold.²⁴

Dimensionality reduction methods map dataset X = {x₁, x₂,…,x_n} ⊂ R^D(images) into a new dataset, Y= {y₁, y₂,…, y_n} ⊂ R^d, with dimensionality d, while retaining the geometry of the data as much as possible. Generally, the geometry of the manifold and the intrinsic dimensionality d of the dataset X are not known. In recent years, a large number of methods for DR have been proposed, which belong to two groups: linear and nonlinear and are briefly discussed in this paper.

Linear DR

Linear DR methods assume that the data lie on or near a linear subspace of some high-dimensional topological space. Some examples of linear DR methods are: Principal components analysis (PCA),²⁵ linear discriminant analysis (LDA),²⁶ and multidimensional scaling (MDS).²⁷

PCA

Principal component analysis finds a lower dimensional subspace that best preserves the data variance, and where the variance in the data is maximal. In mathematical terms, PCA attempts to find a linear mapping, M, which maximizes the sum of the diagonal elements (trace) of the following matrix:

$$M^T*\Sigma *M,$$ (1)

under the constraint that |M| = 1, where Σ is the covariance matrix of the D dimensional data and $X=[x_1,x_2,...,x_N]$ is zeroed mean. “*” represents the multiplication of two matrices. Reports have shown that the linear map M could be estimated using d eigenvectors, i.e., PCA, of the covariance matrix of the data

$$\Sigma *V=\lambda V,$$ (2)

λ is the eigenvalue corresponding to the eigenvector V. The data X now can be mapped to an embedding space by

$$Y=M*X,$$ (3)

where the first d largest PCAs are stored in the columns of matrix M. If the size of the Σ is high, the computation of the eigenvectors would be very time consuming. To solve this problem, Partridge et al. propsed an approximation method, termed “Simple PCA,” which uses an iterative Hebbian approach to estimate the principal eigenvectors of Σ.²⁸ PCA has been applied in several applications for pattern recognition and the intrinsic dimension of the data is distributed on a linear manifold; however, if the data are not linear, then an overestimation of the dimensionality could occur or PCA could fail.^{29, 30}

Multidimensional scaling (MDS)

Classical MDS determines the subspace (Y ⊂ R^d) that best preserves the interpoint distances by minimizing the cost function of error between the pair-wise Euclidean distances in the low-dimensional and high-dimensional representation of the data. That is, given X ⊂ R^D(images), MDS attempts to preserve the distances into lower dimensional space, Y ⊂ R^d, so that inner products are optimally preserved.

The cost function is defined as

$$E(X,Y)=\sum _{\mathit{ij}}{(\Vert x_i-x_j\Vert -\Vert y_i-y_j\Vert )}^2,$$ (4)

where $\Vert x_i-x_j\Vert$ and $\Vert y_i-y_j\Vert$ are Euclidean distances between data points in the higher and lower dimensional space, respectively. Similar to PCA, the minimization can be performed using the eigen decomposition of a pairwise distance matrix as shown below

$$B=\tau (D)=X^T*X,B*V=\lambda V,M=[V_1,V_2,...V_d],Y=M*X,$$ (5)

where B is the pair-wise distance matrix, V is the eigenvectors, M is the eigenvalues, and Y, the first d largest eigenvectors stored in the columns of matrix M, and the embedded data in the reduced dimension, respectively.

MDS has been applied in several applications in pattern recognition and data visualization.^{19, 20, 21, 22, 31, 32} We selected the most frequently used linear DR methods (PCA and MDS) to compare with nonlinear DR techniques in our application.

Nonlinear dimension reduction

Nonlinear techniques for DR do not rely on the linearity assumption for segmentation and, as a result, more complex embedding of high-dimensional data can be identified where linear methods often fail. There are a number of nonlinear techniques, such as Isomap,^{21, 33} locally linear embedding,^{22, 34} Kernel PCA,³⁵ diffusion maps,^{36, 37} Laplacian Eigenmaps,³² and other techniques.^{38, 39}

Isometric feature mapping (Isomap)

As mentioned before, DR technique map dataset X into a new dataset, Y, with dimensionality d, while retaining the geometry of the data as much as possible. If the high-dimensional data lies on or near a curved smooth manifold, Euclidean distance does not take into account the distribution of the neighboring data points and might consider two data points as close, whereas their distance over the manifold is much larger than the typical interpoint distance. Isomap overcomes this problem by preserving pairwise geodesic (or curvilinear) distances between data points using a neighborhood graph.²¹ By definition, Geodesic distance (GD) is the distance between two points measured over the manifold and generally estimated using Dijkstra’s shortest-path algorithm.⁴⁰

GDs between the data points are computed by constructing a neighborhood graph, G (every data point x_i is connected to its k nearest neighbors, x_ij), where, the GDs between all data points form a pair-wise GD matrix. The low-dimensional space Y is then computed by applying multidimensional scaling (MDS) while retaining the GD pair-wise distances between the data points as much as possible. To accomplish this, the error between the pair-wise distances in the low-dimensional and high-dimensional representation of the data are minimized using the equation below

$$\sum {(\Vert x_i-x_{\mathit{ij}}\Vert -\Vert y_i-y_{\mathit{ij}}\Vert )}^2.$$ (6)

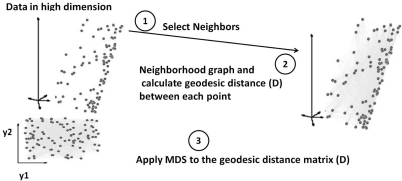
This minimization is performed using various methods, such as the eigen-decomposition of the pair-wise distance matrix, the conjugate gradient method, or a pseudo-Newton method.⁴¹ We used the eigen decomposition for our implementation and Fig. 1 demonstrates the steps used to create the Isomap embedding.

Figure 1.

The steps of Isomap algorithm used for mapping data into lower dimension d: (1) find K nearest neighbors for each data point X_i; (2) calculate pair-wise geodesic distance matrix and reconstruct neighborhood graph using Dijkstra search algorithm; (3) apply Multidimensional scaling (MDS) on the reconstructed neighborhood graph (matrix D) to compute the low-dimensional embedding vectors.

Locally linear embedding (LLE)

In contrast to Isomap, LLE preserves the local properties of the data, which allow for successful embedding of nonconvex manifolds. LLE assumes that the global manifold can be reconstructed by “local” or small connecting regions (manifolds) that are overlapped. That is, if the neighborhoods are small, the manifolds are approximately linear. LEE performs linearization to reconstruct the local properties of the data by using a weighted summation of the k nearest neighbors for each data point. This approach of linear mapping of the hyperplane to a space of lower dimensionality preserves the reconstruction weights. Thus, this allows the reconstruction weights, W_i, to reconstruct data point y_i from its neighbors in the reduced dimension.

Therefore, to find the reduced (d) dimensional data representation Y, the following cost function is minimized for each point x_i:

$$\varepsilon (W)=\sum _{i=1}^n\Vert x_i-\sum _{j=1}^k{w}_{\mathit{ij}}{x}_{\mathit{ij}}{\Vert }^2,$$ (7)

subject to two constraints, ${\displaystyle \sum _{j=1}^k}{w}_{\mathit{ij}}=1$ and w_ij = 0 when x_j ∉ R^D(images). Where X is input data, n is the number of points, and k is the neighborhood size. The optimal weights matrix W (n × k), subject to these constraints, is found by solving a least-squares problem.²²

Then, we compute the embedding data (Y) by calculating the eigenvectors corresponding to the smallest d nonzero eigenvalues of the matrix

$$E={(I-W)}^T*(I-W),E*V=\lambda V,M=[V_1,V_2,...V_d],Y=M*X,$$ (8)

where I is the identity matrix and W is the weights matrix (n × k). Figure 2 shows the steps for LLE.

Figure 2.

Steps of Locally Linear Embedding (LLE) algorithm used for mapping data into lower dimension d (1) search for K nearest neighbors for each data point X_i; (2) solve the constrained least-squares problem in Eq. 7 to obtain weights W_ij that best linearly reconstruct data point X_i from its K neighbors, (3) Compute the low-dimensional embedding vectors Y_i best reconstructed by W_ij.

Diffusion maps (DfM)

Diffusion maps find the subspace that best preserves the diffusion interpoint distances based on defining a Markov random walk on a graph of the data called a Laplacian graph.^{36, 37} These maps use a Gaussian kernel function to estimate the weights (K) of the edges in the graph

$$K_{\mathit{ij}}=e^{-\frac{\Vert x_i-x_i{\Vert }^2}{2{\sigma }^2}}\begin{array}{cc}\multicolumn{1}{c}{}& \hfill 1\le i,j\le L\hfill \end{array},$$ (9)

where L equals the number of multidimensional points and σ is the free parameter, sigma. In the next step, the matrix K is normalized such that its rows add up to 1

$$p_{\mathit{ij}}^{(t)}=\frac{K_{\mathit{ij}}}{{\displaystyle \sum _{n=1}^L}{K}_{\mathit{in}}},$$ (10)

where P represents the forward transition probability of t-time steps of a random walk from one data point to another data point. Finally, the diffusion distance is defined as

$$D_{\mathit{ij}}^{(2)}=\sum _{r=1}^L\frac{{(p_{\mathit{ir}}^{(t)}-p_{\mathit{jr}}^{(t)})}^2}{\Psi (x_r)},\Psi (x_m)=\frac{{\displaystyle \sum _{j=1}^L}{p}_{\mathit{jm}}}{{\displaystyle \sum _{k=1}^L}{\displaystyle \sum _{j=1}^L}{p}_{\mathit{jk}}},$$ (11)

Here, the high density portions of the graph defined by the diffusion distance have more weight, and pairs of data points with a high forward transition probability have a smaller diffusion distance. The diffusion distance is more robust to noise than the geodesic distance because it uses several paths throughout the graph to obtain the embedded image. Based on spectral theory about the random walk, the embedded image of the intrinsic dimensional representation Y can be obtained using the d nontrivial eigenvectors of the distance matrix D

$$Y:x\to \{{\lambda }_2{V}_2,...{\lambda }_d{V}_d\}.$$ (12)

The DfM graph is a fully connected, eigenvector v₁ of the largest eigenvalue (${\lambda }_1=1$) that is discarded, and the remaining eigenvectors are normalized by their corresponding eigenvalues.

DR-based manifold unfolding

As mentioned above, the DR methods map high-dimensional data to a lower dimension while preserving data structure. This property of DR can be used to unfold N-dimensional manifolds into a lower dimension. To illustrate DR capabilities, the advantages and disadvantages of each linear and nonlinear DR method for manifold unfolding, three well-known synthetic datasets—the Swiss-roll, 3D-clusters, and sparse data sets—were used to test each of the methods and determine which one(s) to use on the clinical data.

DR-based multidimensional image data integration

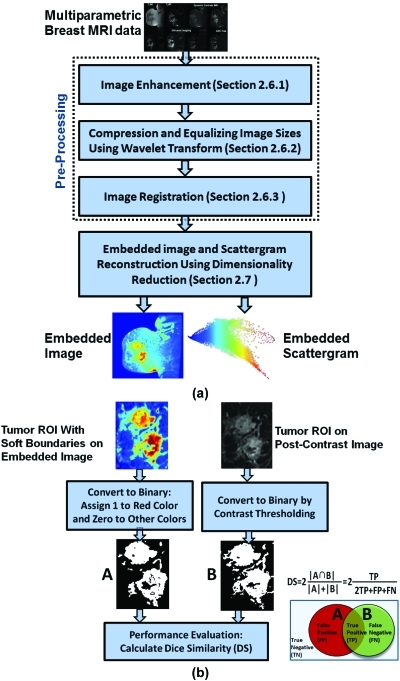
By using DR and its manifold unfolding ability, we can integrate multidimensional image data for visualization. Our proposed DR scheme is shown in Fig. 3a and includes two stages: (1) preprocessing (enhancement, coregistration, and image resizing); and (2) dimensionality reduction to obtain an embedded image for soft tissue segmentation. Figure 3b shows the steps for automated extraction of tumor boundaries [A and B in Fig. 3b] from the embedded and postcontrast images. The same procedure is used for fatty and glandular breast tissue. To test for overlap and similarity, we used the Dice similarity (DS) metric.⁴² The DS measure is defined as

$$\mathrm{DS}=2\frac{\mathrm{A}\mathrm{\cap }\mathrm{B}}{\mathrm{A}\mathrm{+}\mathrm{B}}=2\frac{\mathrm{TP}}{2\mathrm{TP}\mathrm{+}\mathrm{FP}\mathrm{+}\mathrm{FN}},$$ (13)

where A is the tissue boundary in the embedded image, B is the tissue boundary in the postcontrast image, TP is the true positive, FP is the false positive, and FN is the false negative.

Figure 3.

(a) Proposed schema for multidimensional image data integration using the Non Linear Dimensional Reduction (NLDR) methods to construct the embedded image and soft tissue segmentation; (b) Proposed schema for extraction of tumor hard boundaries for direct comparison with the postcontrast image as the current standard technique. The same procedure is used for the other breast tissue (fatty and glandular).

Preprocessing steps

Image enhancement

Since artifacts and noise can degrade radiological images and may make identification and diagnosis difficult. In particular, MRI images can have large B₁ inhomogeneities that can obscure anatomical structures. To estimate true signal and correct B₁-inhomogeneity effects, we used a modified version of the “local entropy minimization with a bicubic spline model (LEMS),” developed by Salvado et al.⁴³ LEMS is based on modeling the bias field, β, as a bicubic spline and the RF coil geometry as a sufficiently close rectangular grid of knots scattered across the image (X). Initialization of LEMS begins with a fourth-order polynomial function estimation of the tissue voxel, where the background is excluded. Optimization of the bicubic spline model is performed in piecewise manner. LEMS first identifies a region within the image with the highest SNR and assigns it to Knot K₁ to ensure that a good local estimate of the field β is obtained. LEMS then adjusts the signal at K₁, based on an 8 × 8 neighborhood of knots, to locally minimize the entropy of X in K₁ and its neighbors. LEMS repeats the same routine for other knots with high SNR and minimizes the entropy within the corresponding knot (K_t) neighbor, as well as in prior knots (${\{K_j\}}_{1\le j<t}$) until either the maximum number of iterations are reached or the knot entropies do not change significantly.

Equalizing image sizes using wavelet transform

As image sizes can vary, there is a need for a method to equalize image sizes with less loss of spatial and textural information. If any image is smaller than the desired size (N), data interpolation should be used to upsize the image to N. There are several well-known interpolation methods, such as nearest-neighbor, bilinear, and bicubic. However, if any of the images are larger than the desired size (N), the image should be downsized, which causes loss of spatial and textural information. To avoid this problem, a powerful multiresolution analysis using wavelet transforms can be used.^{44, 45}

Wavelets are mathematical functions that decompose data into different frequency components, thereby facilitating the study of each component with a resolution matched to its scale.⁴⁴ The continuous wavelet transform of a square-integrable function, f(t), is defined as

$$\mathit{wf}(s,t)={\int }_{-\infty }^{\infty }f(t)\frac{1}{\sqrt{s}}\psi (\frac{t-\tau }{s}),$$ (14)

where s and t are the scale (or frequency) and time variable, respectively. The function $\psi (t)$, is called a wavelet and must satisfy the admissibility condition, that is, it must be a zero-meaned and square-integrable function.

In practical applications, the parameters s and t must be discretized. The simplest method is dyadic. By using this method, the fast wavelet transform (FWT) is defined as

$$\mathit{wf}[n,2^j]=\sum _{m=0}^{N-1}f[m]{\psi }_j[m-n]=f[n]*{\psi }_j[n],$$ (15)

where ${\psi }_j[n]=\psi (\frac{n}{2^j})$ and f [n] is a sequence with a length of N (discrete time function), and the * sign represents a circular convolution.

To implement a fast-computing transform, the FWT algorithm was used. At each level of decomposition, the FWT algorithm filters data with two filters, called h[n] and g[n]. The filter h[n], a conjugate mirror filter, is a low-pass filter, and thus, only low-frequency (coarse) components can pass through it; conversely, g[n] is a high-pass filter to pass high frequency (detail) components. The dyadic wavelet representation of signal a₀ is defined as the set of wavelet coefficients up to a scale J (=log₂N), plus the remaining low-frequency information [1 ≤ j ≤ J].^{44, 45}

For image processing, we first applied the 1D FWT to the rows of the image. Then, we applied the same transform to the columns and diagonals of each component. Therefore, we obtained three high-pass (detail) components corresponding to vertical, horizontal, and diagonal, and one approximation (coarse) component. Figure 4 outlines with block diagrams the procedure using the 1D and 2D FWT. By using the inverse FWT (IFWT), we could reconstruct the original image in a different scale and resolution (see Fig. 4) and when we reformatted, there was no loss of resolution.

Figure 4.

Signal (a) and image (b) decomposition using Fast Wavelet Transform (FWT); Signal (c) and Image (d) reconstruction using Inverse FWT (IFWT). a₀ is original signal (image). a_j and d_j, respectively, are the approximation (coarse or low pass) and detail (high pass) components corresponding to vertical, horizontal, and diagonal at decomposition level j.

Coregistration methods

For coregistration of the different modalities/parameters, we used a modified nonrigid registration technique developed by Periaswamy and Farid.⁴⁶ The method is based on both geometric (motion) and intensity (contrast and brightness) transformations. The geometric model assumes a locally affine and globally smooth transformation. The local affine model is based on motion estimation. Model parameters are estimated using an iterative scheme that uses nonlinear least-squares optimization to compute model parameters.⁴⁷ In order to deal with the large amount of motion and capture both large and small-scale transformations, a Gaussian pyramid was built for both source and target images. Model parameters were initially estimated at the coarsest level and were used to warp the source image at the next level of the pyramid and update the model parameters at each level of the pyramid. This multiscale approach enabled registration of different images, such as T1WI, T2WI, and DWI. A set of derivative filters designed for multidimensional differentiation was used to decrease noise and to improve the resultant registration.

Embedded image and scattergram reconstruction

After the preprocessing (e.g., image enhancement, wavelet-based compression, and image registration), the radiological images were used as inputs for DR methods. The embedded image was constructed by projecting the features (image intensities) from N-dimensional space to a one-dimensional embedding space, using the results from the DR methods [see Fig. 3a]. The resultant embedding points then reconstructed the embedded image by reforming the embedded data matrix from the size $L\times 1$ to $\frac{L}{2}\times \frac{L}{2}$. If we map data from N-dimensional space into two-dimensional space, we will obtain an unfolded version of the data manifold with different clusters.^{21, 22}

Multiparametric breast MRI segmentation

Clinical subjects

Twenty-five women were scanned as part of a breast research study. All subjects signed written, informed consent, and the study was approved by the local IRB. Twenty-three patients had breast tumors (19 malignant and 4 benign) and two patients had no masses.

Multiparametric MRI imaging protocol

MRI scans were performed on a 3T magnet, using a dedicated phased array breast coil with the patient lying prone with the breast in a holder to reduce motion. MRI sequences were: fat suppressed (FS) T2WI spin echo (TR/TE = 5700/102) and fast spoiled gradient echo (FSPGR) T1WI (TR/TE = 200/4.4, 2562, slice thickness, 4 mm, 1 mm gap); diffusion-weighted (TR/TE = 5000/90 ms, b = 0,500–1000,1282,ST = 6 mm); and finally, precontrast and postcontrast images FSPGR T1WI (TR/TE = 20/4, matrix = 5122, slice thickness, 3 mm) were obtained after intravenous administration of a GdDTPA contrast agent [0.2 ml/kg(0.1 mmol/kg)]. The contrast agent was injected over 10 s, with MRI imaging beginning immediately after completion of the injection and the acquisition of at least 14 phases. The contrast bolus was followed by a 20cc saline flush. The DCE protocol included 2 min of high temporal resolution (15 s per acquisition) imaging to capture the wash-in phase of contrast enhancement. A high spatial resolution scan for 2 min then followed, with additional high temporal resolution images (15 s per acquisition) for an additional 2 min to characterize the wash-out slope of the kinetic curve. Total scan time for the entire protocol was less than 45 min.

Multiparametric breast MRI segmentation and Comparison

The nonlinear dimensionality reduction (NLDR) methods and the embedded image and scattergram were applied to the breast MRI data. To differentiate tissue types and soft boundaries between them, a continuous RGB color code can be assigned to the embedded image. To perform a quantitative comparison between the embedded image and ground-truth, we used similarity measures based on regional overlap between hard boundaries. Ground truth was based on the current clinical standard in breast imaging, which is the post contrast MRI. We used the Dice similarity index, designed to find the overlapping regions between two objects (see Fig. 3). In our application, A and B are lesion areas obtained by ground truth (postcontrast image) and the embedded image, respectively. The lesion area for the postcontrast was obtained by thresholding of the contrast image. The threshold was obtained by evaluating the postcontrast MR image histogram, and using the mean and a 95% confidence interval. However, the embedded image returned a fuzzy boundary with an RGB color code and the hard boundary was obtained by converting the embedded image to a binary image and assigning a “1” to the red color-coded pixels and a zero to the pixels with other colors. If A and B have full overlap, then the DS = 1.0. But if A and B do not intersect, then the DS = 0. To evaluate the DR methods, we applied them to segment and visualize breast tumors using multiparametric MRI data in a small series of patients and volunteers to discern the properties of each MR sequence in breast lesion identification, no classification was performed and under investigation.

RESULTS

Synthetic data

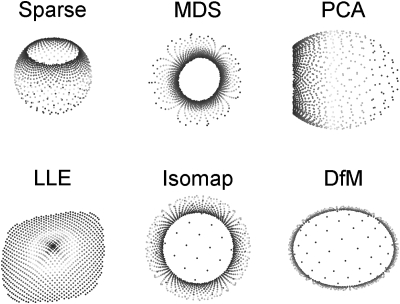
Figure 5 shows typical results for DR methods applied to the Swiss Roll manifold. Both linear methods (PCA and MDS) failed to unfold the manifold and preserve structure when mapping from 3 to 2 dimensions. The nonlinear method, Isomap, was able to unfold the Swiss roll with good results: but, both LEE and DfM methods were able, in part, to unfold the Swiss roll with most of the structure retained. In the 3D point cluster model, most of the linear and nonlinear DR methods, with the exception of LLE, were able to maintain the 3D cluster structure when mapped to the lower dimension, as demonstrated in Fig. 6. Notably, LLE converted each cluster to points. Finally, the sparse (nonuniform) manifold data revealed the main difference and the power of nonlinear DR methods compared to linear methods, as shown in Fig. 7. The linear methods failed to unfold the sparse data set, whereas, the nonlinear DR methods were able to preserve, in most cases, the structure of the sparse manifold. In particular, LLE performed the best, but Isomap and DfM were able to partially preserve the structure.

Figure 5.

Dimension reduction of the Swiss Roll (a) from 3 to 2 dimensions using MDS, PCA, LLE, Isomap and diffusion maps (DfM). Neighborhood size for LLE and Isomap, respectively, were 5 and 10. Sigma for DfM was 0.2. The linear methods (MDS and PCA) both failed to unfold the Swiss Roll in the reduced dimension, while all nonlinear methods (LLE, Isomap, and DfM) were able to unfold the data and preserve structure. The best result was obtained by Isomap.

Figure 6.

Demonstration of dimension reduction of 3D clusters (a) from 3 to 2 dimensions using Multidimensional Scaling (MDS), Principal Component Analysis (PCA), Locally Linear Embedding (LLE), Isomap and diffusion maps (DfM). Sigma for DfM was 0.2. Neighborhood size for LLE and Isomap, respectively, were 5 and 10. In this example, all methods except LLE were able to preserve clusters in the reduced dimension. Isomap was not able to fully preserve structure of for the cyan color cluster in the embedding space. LLE was not able to preserve structure of all three clusters and converted the clusters to points in the embedding space.

Figure 7.

Embedding of sparse data (a) from 3 to 2 dimensions using MDS, PCA, LLE, Isomap and diffusion maps (DfM). Neighborhood size for LLE and Isomap, respectively, were 5 and 10. Sigma for DfM was 0.2. Both linear methods (MDS and PCA) failed to preserve the sparse data structure in the reduced dimension. DfM was able to fully preserve the sparse data pattern in the embedding space. LLE successfully mapped the sparse data structure to the embedded space. Isomap also was able to preserve most of the data structure but was unable to correctly map the all the blue color to the embedding space.

Multiparametric breast MRI preprocessing steps

Based on our encouraging results from the synthetic data, we applied the nonlinear methods to the multiparametric breast data using our hybrid integration scheme outlined in Fig. 3. The preprocessing of the T1WI (sagittal and axial) before and after B1 inhomogeneity correction is shown in Fig. 8. The coefficients of variation (COV) for fatty tissue, as an example, before applying LEMS, were 98.6 and 67.2, respectively, for T1WI and precontrast MRI images. The COV improved to 49.3 and 39.2, after correction.

Figure 8.

Correction of B₁ inhomogeneity in the MRI data with the local entropy minimization with a bicubic spline model (LEMS) method: Shown are original and corrected images, respectively, for T1-weighted images. After correction, better visualization of breast tissues is noted and they isointense across the image, compared with the images on the left.

Figure 9 demonstrates the wavelet compression and decompression methods applied to a DWI (b = 500) image. The original size was 256 × 256, and was resized (compressed and decompressed) to 64 × 64. The reconstructed image was identical to the original image with no errors. Finally, registration of the breast MRI was achieved using a locally affine model, and typical results are shown in Fig. 10. The mean square error between the predicted intensity map of the reference image and original reference image was 0.0567.

Figure 9.

Typical diffusion-weighted image (b = 500) in the original size 256 × 256, after compression (64 × 64) and decompression (reconstructed image: 256 × 256). For compression, 2D biorthogonal spline wavelets were used. $d_{j,}^{(h)}{d}_j^{(v)}\mathrm{and}{d}_j^{(d)}$, respectively, are detail components corresponding to vertical, horizontal, and diagonal. a_j, is the approximation (coarse) component at decomposition level j.

Figure 10.

Demonstration of the coregistration of the MRI data using a locally affine model: (a) the T2WI source image; (b) the T1WI reference image; (c) warping map; (d) the final coregistered image and (e) the difference image obtained from subtracting the reference image from the registered image.

Multiparametric breast MRI segmentation

Figures 1112 demonstrate the power of using nonlinear embedding of multiparametric breast MRI in several dimensions, for example, in Fig. 11, there are nine dimensions: T1WI; T2WI; precontrast; postcontrast; DWI (4-b values) and ADC maps into a single image that provided a quantitative map of the different tissue types for abnormal (malignant) and normal tissue. All images were resized to 256 × 256 using the methods outlined in Fig. 4. After scaling the intensity of the embedded images (range of 0–1000), the lesion tissue appeared red, with normal fatty tissue appearing blue. The embedded scattergram was useful in classifying the different tissue types (see Figs. 1112). The Dice similarity index between the lesion contours defined by the embedded image demonstrated excellent overlap (>80%) with the DCE-MRI-defined lesion. Table TABLE I. summarizes the Dice similarity index on 25 patients (19 malignant and four benign cases, and two cases with no masses).

Figure 11.

(a) Typical multiparametric MRI data and (b) resulting embedded images and scattergrams for a malignant breast case from three NLDR algorithms Diffusion Maps (DfM), Isometric feature mapping (ISOMAP), Locally Linear Embedding (LLE). The lower scattergram shown is derived from Isomap. Clear demarcation of the lesion and surrounding breast are shown.

Figure 12.

(a) Typical axial multiparametric MRI data from a patient with no breast lesion. (b) resulting embedded images and scattergrams demonstrating the separation of fatty and glandular tissue in the embedded image, the scattergram shown is derived from Isometric feature mapping (ISOMAP).

TABLE I.

Dice similarity metric.

	Benign (4 cases)			Malignant (19 cases)
	DfM (%)	Isomap (%)	LLE (%)	DfM (%)	Isomap (%)	LLE (%)
Mean	81.18	80.61	81.49	87.40	86.70	85.50
Median	82.08	79.97	82.74	86.72	86.15	86.31
SD	6.35	8.51	6.91	5.81	6.83	8.57

Note: 2 cases did not have masses and are not shown. Isometric feature mapping (ISOMAP), Locally Linear Embedding (LEE) Diffusion Mapping (DfM).

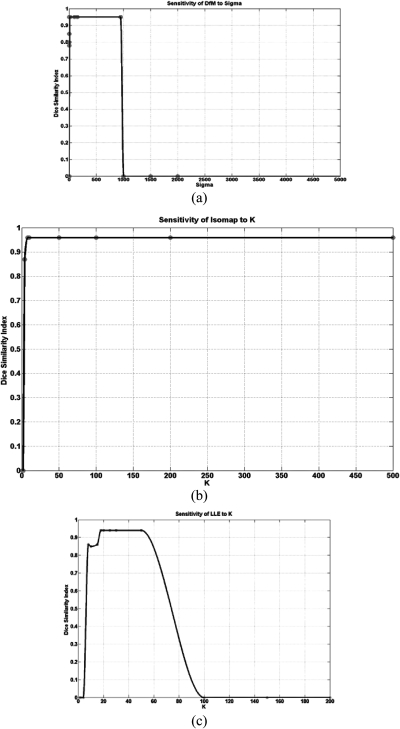
Comparison of the computational loads for the NLDR methods indicated that the load for Isomap was very high compared to DfM and LLE. For example, for breast MRI images with a matrix size of 256 × 256, the computation times for DfM, Isomap, and LLE were 19.2, 508.4, and 78.6 s, respectively, using an Intel quad-core with 8 Gb RAM and a Nvidia Quadro 4000 (256 cores, 2 GB) video card. To determine the robustness of the NLDR methods to their input parameters, we varied the different input parameters. These parameters are defined in Isomap and LLE as the neighborhood size [K], and defined in DfM as the sigma parameter. Figure 13 shows how the Dice similarity index changed with each of the NLDR parameter [neighborhood size [K] in Isomap and LLE; sigma in DfM] variations. As shown, the neighborhood size K for Isomap should be chosen to be greater than 10, and, for LLE, it should vary from 20 to 60. However, the DfM is very sensitive to sigma in the Gaussian kernel, and, based on our investigations, sigma should range between 100 and 1000, but a sigma of at least 100 would be sufficient for complex data, such as MRI.

Figure 13.

Demonstration of the sensitivity of NLDR methods to control parameters: (a) effects of Sigma value on the dice similarity index between Diffusion Maps (DfM) based embedded image and the postcontrast; (b) and (c) effects of neighborhood size (K) on the dice similarity index between the embedded image and the postcontrast, respectively, for Isomap and LLE. Example input MRI data for the NLDR methods are shown in Fig. 11.

DISCUSSION

In this paper, we developed a novel hybrid scheme using NLDR methods to integrate multiple breast MRI data into a single embedded image. The resultant embedded image enabled the visualization and segmentation of breast lesions from the adjacent normal breast tissue with excellent overlap and similarity. To determine which DR method to use, we compared the performance of both linear and nonlinear DR methods using synthetic and multiparametric breast MRI. In the synthetic data, the three nonlinear DR methods, namely DfM, Isomap, and LLE, outperformed the linear methods (PCA and MDS) in all categories. The NLDR methods, in general, were able to segment and visualize the underlying structure of the Swiss Roll, point clouds, and, more importantly, sparse data. This is important because the sparse data represents a real-world scenario and the NLDR methods were able to unfold the underlying structure. This led us to choose the NLDR methods for the breast data. Multiparametric breast data represent complex high-dimensional data, and no single parameter conveys all the necessary information. Integration of the breast parameters is required and our methods provide an opportunity to achieve such integration. Our results demonstrate that when the NLDR methods are applied to breast MRI data, the DR methods were able segment the lesion and provide excellent visualization of the tissue structure.

This mapping of high-dimensional data to a lower dimension provides a mechanism by which to explore the underlying contribution of each MR parameter to the final output image. Indeed, each one of these methods is designed to preserve different data structures when mapping from higher dimensions to lower dimensions. In particular, DfM and Isomap primarily emphasize the global structure within the multidimensional feature space and are less sensitive to variations in local structure. However, LLE has greater sensitivity to the variations in local structure and is less sensitive to variations in global structure. In general, DfM and Isomap returned images similar to the embedded images from LEE, using the breast MRI data. Therefore, each of the methods was able to differentiate the breast lesion cluster within the scattergram, suggesting that, for computer-assisted diagnosis, either of the three DR methods (DfM and Isomap for global structures and LLE for local structures) could be applied to better assist the radiologist in decision-making. This was confirmed by the congruence between each embedded image and breast DCE MRI with the Dice similarity metric. The Dice similarity metric showed excellent results with a little variation in the segmented lesion areas between the embedded and DCE MRI. One potential advantage of using an embedded image created from the breast MRI would be to create tissue masks for automatic overlay onto functional MRI parameters, such as ADC or sodium maps to develop an automatic quantification system that could be used to monitor treatment response.¹²

Other applications for DR methods with MRI data that have been published include the differentiation of benign and malignant tissue on magnetic resonance spectroscopy (MRS) data. Tiwari et al.⁴⁸ used DR methods to separate the different peaks of metabolites (choline, citrate, etc.) into different classes and then overlaid the results onto the T2WI of the prostate with increased sensitivity and specificity. However, these investigators only utilized the frequency domain of the spectra and not the entire dimensionality of the prostate data set, that is, combined MRI and MRS. Nevertheless, they did demonstrate the power of DR methods consistent with our results. Other recent applications for DR methods include use on diffusion tensor magnetic resonance images (DT-MRI). DT-MRI cannot be analyzed by commonly used linear methods, due to the inherent nonlinearity of tensors, which are restricted to a nonlinear submanifold of the space in which they are defined. To overcome this problem, Verma et al.⁵⁰ and Hamarneh et al.⁴⁹ calculated the geodesic distance using Isomap to perform tensor calculations and colorize the DTI tensor data. DT-MRI represents tensor data and step 3 of the Isomap and other NLDR algorithms (embedded space reconstruction) cannot be applied to integrate diffusion tensor images. Therefore, the full use of any DR techniques on DTI data is not feasible. Compared to previous work, in this manuscript, we compared six types of DR techniques (three linear and three nonlinear techniques) using both real and synthetic data and use the power of the DR methods to segment breast tissue and create an embedding image of each parameter. Future work is ongoing to discern the importance of each parameter in the MRI data space. In another report, Richards et al.,⁵¹ demonstrated that DfM outperformed PCA (linear DR) in the classification of galaxy red-shift spectra when used as input in a regression risk model. In addition, DfM gave better visualization of the reparameterized red-shift separation in the embedded image, but both methods were able to separate the first few components to identify the different subgroups, which are consistent with our results. Similarly, we have demonstrated a method by which to reconstruct an embedded image from the higher-dimension MRI data space into a reduced (embedded) dimension to use for tumor segmentation and visualization. Moreover, to deal with the high computational load of DR, we tested the stability of each method in relation to the input parameters to determine the optimal range for correct segmentation as defined by the current clinical imaging standard and found ranges that can be utilized for as starting points for other applications using breast MRI or other related data sets. In summary, by combining different MRI sequences, using dimensionality reduction and manifold learning techniques, we developed a robust and fully automated tumor segmentation and visualization method. This approach can be extended to facilitate large-scale multiparametric/ multimodal medical imaging studies designed to visualize and quantify different pathologies.⁵²