Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2012 Apr 12;134(16):7001–7008. doi: 10.1021/ja210856v

Direct Observation of Cooperative Protein Structural Dynamics of Homodimeric Hemoglobin from 100 ps to 10 ms with Pump–Probe X-ray Solution Scattering

Kyung Hwan Kim †,#, Srinivasan Muniyappan †,#, Key Young Oang †,#, Jong Goo Kim †,#, Shunsuke Nozawa ‡, Tokushi Sato ‡, Shin-ya Koshihara §, Robert Henning ∥, Irina Kosheleva ∥, Hosung Ki †, Youngmin Kim †, Tae Wu Kim †, Jeongho Kim †, Shin-ichi Adachi ‡,⊥, Hyotcherl Ihee †,✉
PMCID: PMC3337689  PMID: 22494177

Abstract

graphic file with name ja-2011-10856v_0007.jpg

Proteins serve as molecular machines in performing their biological functions, but the detailed structural transitions are difficult to observe in their native aqueous environments in real time. For example, despite extensive studies, the solution-phase structures of the intermediates along the allosteric pathways for the transitions between the relaxed (R) and tense (T) forms have been elusive. In this work, we employed picosecond X-ray solution scattering and novel structural analysis to track the details of the structural dynamics of wild-type homodimeric hemoglobin (HbI) from the clam Scapharca inaequivalvis and its F97Y mutant over a wide time range from 100 ps to 56.2 ms. From kinetic analysis of the measured time-resolved X-ray solution scattering data, we identified three structurally distinct intermediates (I1, I2, and I3) and their kinetic pathways common for both the wild type and the mutant. The data revealed that the singly liganded and unliganded forms of each intermediate share the same structure, providing direct evidence that the ligand photolysis of only a single subunit induces the same structural change as the complete photolysis of both subunits does. In addition, by applying novel structural analysis to the scattering data, we elucidated the detailed structural changes in the protein, including changes in the heme–heme distance, the quaternary rotation angle of subunits, and interfacial water gain/loss. The earliest, R-like I1 intermediate is generated within 100 ps and transforms to the R-like I2 intermediate with a time constant of 3.2 ± 0.2 ns. Subsequently, the late, T-like I3 intermediate is formed via subunit rotation, a decrease in the heme–heme distance, and substantial gain of interfacial water and exhibits ligation-dependent formation kinetics with time constants of 730 ± 120 ns for the fully photolyzed form and 5.6 ± 0.8 μs for the partially photolyzed form. For the mutant, the overall kinetics are accelerated, and the formation of the T-like I3 intermediate involves interfacial water loss (instead of water entry) and lacks the contraction of the heme–heme distance, thus underscoring the dramatic effect of the F97Y mutation. The ability to keep track of the detailed movements of the protein in aqueous solution in real time provides new insights into the protein structural dynamics.

Introduction

The allosteric structural transition of hemoglobin induced by ligand binding is an important process that is directly related to the function and reactivity of the protein.1−7 Because of the heteromeric nature of human tetrameric hemoglobin, the structural propagation between allosteric sites involving cooperative ligand binding and subsequent tertiary and quaternary structural changes is complex. As a result, it has been difficult to characterize the structure and kinetics of singly, doubly, or multiply liganded species that are transiently formed along the allosteric pathways. In this regard, HbI has a simpler homodimeric structure and thus is a convenient model system for studying allosteric structural changes.8−10 However, even for this simpler system, the allosteric process involving cooperative ligand binding and subsequent tertiary and quaternary structural changes is complex, and its detailed structural dynamics has yet to be understood completely.

Static crystal structures of the oxygenated (relaxed, R) and deoxygenated (tense, T) forms of HbI11−15 may provide the starting and end structures of the R–T transition, allowing theoretical prediction of the reaction pathways and associated protein motions between the two end states.16−21 However, such static structures cannot provide information on the detailed motions and the existence of any intermediates involved in the allosteric structural transitions. Dynamical information is often accessible via time-resolved measurements,9,22−29 but optical spectroscopy techniques are generally not sensitive to global quaternary structural changes.30−32 As an alternative approach to circumvent the limitation in the structural sensitivity of optical spectroscopies, time-resolved X-ray crystallography33−38 can be used to track structural transitions in the crystal. It has been shown that the positive cooperativity of HbI is maintained in the crystal,10 but recent time-resolved X-ray crystallography studies of HbI showed a quaternary subunit rotation of only 0.6° instead of the 3.3° rotation expected on the basis of static R and T crystal structures.36,37

In this work, to investigate directly the structural dynamics of HbI in the solution phase instead of the crystalline phase, we applied pump–probe X-ray solution scattering (which is globally sensitive to secondary, tertiary, and quaternary structural changes of proteins in solution) to visualize the detailed allosteric structural transition of HbI in solution in real time. Although pump–probe X-ray solution scattering has previously been applied to proteins,39−44 detailed structural information on transient intermediates could not be obtained in those studies because of the lack of a proper structural analysis tool, which is well-established for small molecules.45−49 Here, by applying to the measured X-ray solution scattering data a novel structural analysis using Monte Carlo simulations, we report a detailed description of the structural dynamics involved in the allosteric structural transitions of wild-type HbI and its F97Y mutant, whose structures are shown in Figure 1. Details of the experimental methods and data analysis are provided in Materials and Methods and in the Supporting Information (SI). In general, small-angle X-ray scattering (SAXS) can provide global structural information such as the radius of gyration and molecular shape.50−62 In this work, we used wide-angle X-ray scattering (WAXS) data as well as SAXS data to extract additional higher-resolution structural information such as the subunit rotation angle and the heme–heme distance as a function of time.

Figure 1.

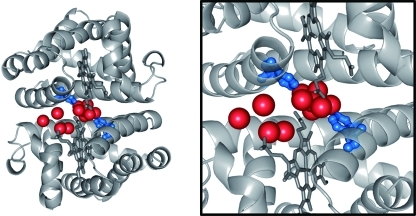
Figure 1

Open in a new tab

Crystal structure of HbI(CO)2.11 (left) Crystal structure of wild-type HbI(CO)2 (PDB entry 3sdh); (right) close-up view of the subunit interface. In the F97Y mutant, the Phe97 residue in each subunit of the wild type (shown in blue) is replaced by Tyr. Water molecules (shown in red) are well-organized at the interface of the two subunits. Static crystallography shows that the R–T transition induces a change in the number of interfacial water molecules. The hemes are directly in contact with each other through the hydrogen-bonding network.

Materials and Methods

Data Acquisition

Time-resolved X-ray solution scattering data were acquired using the pump–probe method at the 14IDB beamline at the Advanced Photon Source and beamline NW14A at KEK (see the SI for details). Aqueous solution samples of HbI ligated with CO ligands [HbI(CO)2] and its F97Y mutant were prepared using a previously established protocol.63 The samples contained in a capillary of 1 mm thickness were excited with ∼35 ps laser pulses at 532 nm. Time-resolved scattering curves were collected at 40–70 pump–probe time delays between the laser pump pulse and the X-ray probe pulse in the range from 100 ps to 56.2 ms as well as at a reference time delay of −5 μs. To attain a signal-to-noise ratio good enough for data analysis, about 20 images were acquired and averaged at each time delay. The measured time delays were spread evenly on a logarithmic time scale as follows: −5 μs, 108 ps, 167 ps, 246 ps, 352 ps, 492 ps, 680 ps, 930 ps, 1.26 ns, 1.71 ns, 2.30 ns, 3.09 ns, 4.15 ns, 5.55 ns, 7.43 ns, 10 ns, 13.3 ns, 17.8 ns, 23.7 ns, 31.6 ns, 42.2 ns, 56.2 ns, 75 ns, 100 ns, 133 ns, 178 ns, 237 ns, 316 ns, 422 ns, 562 ns, 750 ns, 1 μs, 1.33 μs, 1.78 μs, 2.37 μs, 3.16 μs, 4.22 μs, 5.62 μs, 7.5 μs, 10 μs, 13.3 μs, 17.8 μs, 23.7 μs, 31.6 μs, 42.2 μs, 56.2 μs, 75 μs, 100 μs, 133 μs, 178 μs, 237 μs, 316 μs, 422 μs, 562 μs, 750 μs, 1 ms, 1.33 ms, 1.78 ms, 2.37 ms, 3.16 ms, 4.22 ms, 5.62 ms, 7.5 ms, 10 ms, 13.3 ms, 17.8 ms, 23.7 ms, 31.6 ms, 42.2 ms, and 56.2 ms. To check the power dependence (and thus the ligation dependence) of the structural transition of HbI after ligand photolysis, three sets of data were collected using laser fluences of 0.25 (“low”), 0.5 (“mid”), and 1.0 (“high”) mJ/mm2. Taking the difference between the scattering curve measured at each time delay point and the reference scattering curve measured at −5 μs yielded the difference scattering curve ΔS(q,t). The contribution from laser-induced solvent heating was removed from the measured scattering curves (see the SI for details).

Kinetic Analysis

The measured data were analyzed by applying singular value decomposition (SVD) and kinetic analysis to extract the kinetics of the allosteric structural transition of HbI. From SVD of the experimental data in the q range 0.15–1.0 Å–1, three singular components of significant amplitudes were identified. The relaxation times were determined by simultaneously fitting the three principal time-dependent components (right singular vectors) multiplied by singular values with a sum of seven exponentials sharing common relaxation times. From the fitting, we obtained relaxation times of 3.2 ± 0.2 ns, 93 ± 20 ns, 730 ± 120 ns, 5.6 ± 0.8 μs, 15.2 ± 8 μs, 1.8 ± 0.3 ms, and 9.1 ± 0.9 ms for wild-type HbI excited at the mid laser fluence. The same fitting procedure was performed for F97Y mutant HbI excited at the mid laser fluence, and relaxation times of 3.0 ± 0.3 ns, 40 ± 20 ns, 370 ± 100 ns, 4.7 ± 3.1 μs, 26 ± 14 μs, and 330 ± 40 μs were obtained. These relaxation times were used in the subsequent kinetic analysis based on a kinetic model. In this step, the theoretical time-resolved difference scattering curve at each time delay was generated as a linear combination of the species-associated difference scattering curves obeying the kinetics determined by the kinetic model. By minimizing the discrepancy between the experimental and theoretical time-resolved difference scattering curves, the species-associated scattering curves for three intermediates were extracted and used for further structure refinement. This procedure is basically identical to principal component analysis (PCA) except that the species-associated difference scattering curves are constructed from a linear combination of the principal time-independent left singular vectors. Details are provided in the SI.

Structure Refinement Aided by Monte Carlo Simulations

To obtain more detailed structural insight into the tertiary and quaternary structural changes of HbI, we developed a structure refinement procedure aided by Monte Carlo simulations using the species-associated difference curves obtained from the kinetic analysis. Each subunit of the HbI intermediate was divided into nine rigid bodies, namely, eight helices and one heme group, giving a total of 18 rigid bodies in the entire HbI protein. To prevent the simulation from being trapped in local energy minima, we generated many starting structures for the structure refinement (instead of using only one crystal structure) by randomly moving the rigid bodies in known crystal structures of HbI using the Monte Carlo simulation. As a result, hundreds of random structures with symmetric subunits were generated with a root-mean-square deviation (rmsd) of 1.2 Å, which is twice as large as the rmsd between the mono-CO- and deoxy-HbI crystal structures (0.6 Å). The goal of the structure refinement was to find a structure that minimized the value of the target function, E, which consisted of Edata, the difference between the experimental and theoretical curves, and Echem, the penalty proportional to the chemical interactions of the nonbonded short-range repulsion and symmetry restraints between two subunits. The Edata term was represented by a χ2 value determined from the difference between the theoretical curve from the simulation and a time-independent species-associated curve. The Echem term contained the components of collision and symmetry restraints. The rigid bodies could be moved randomly until the lowest target function value was found, but this approach was rather slow in minimizing the target function value. To speed up the convergence, in our approach the rigid bodies were moved according to the three potential terms (the chemical, χ2, and symmetry force fields). Details are provided in the SI.

Results and Discussion

Kinetic Analysis of Difference Solution Scattering Curves

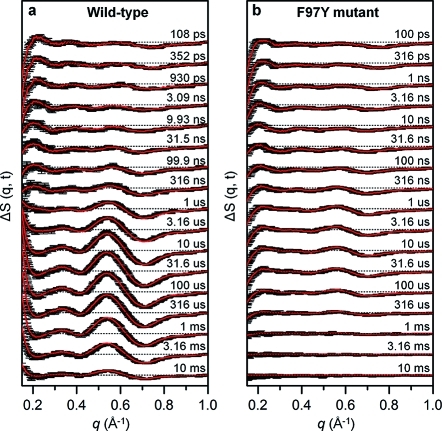
Time-resolved difference X-ray solution scattering curves, ΔS(q,t), following photoexcitation of a wild-type HbI solution at the mid laser fluence (0.5 mJ/mm2) are shown in Figure 2a. The corresponding data for the F97Y mutant, in which the Phe97 residue in each subunit of the wild type is replaced by Tyr, are shown in Figure 2b. Even a simple comparison indicates that the structural dynamics are greatly altered by the mutation.

Figure 2.

Figure 2

Open in a new tab

Picosecond pump–probe X-ray solution scattering for wild-type HbI(CO)2 and its F97Y mutant. Time-resolved difference X-ray solution scattering curves, ΔS(q,t), measured for solution samples of (a) wild-type and (b) F97Y mutant HbI are shown. The time delay after photoexcitation is indicated above each curve. For clarity, only data at selected time delays are shown (see the SI for data at all time delays). Experimental curves (black) are compared with theoretical curves (red) that were generated from linear combinations of three time-independent species-associated scattering curves extracted from the kinetic analysis using the model shown in Figure 3a.

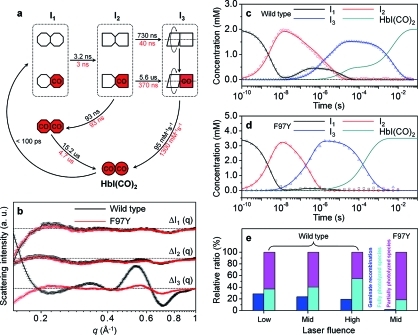
To extract the structure and formation kinetics of intermediates involved in the photocycle of HbI, we applied SVD-aided kinetic analysis to the data measured at time delays from 100 ps to 56.2 ms (see the SI for details). Regardless of the laser fluence, the SVD analysis identified three significant singular components. The three time-independent left singular vectors could be converted into the three time-independent species-associated scattering curves shown in Figure 3b, suggesting the existence of three structurally distinct intermediates, termed as I1, I2, and I3 in the order of their appearance in time. Careful kinetic analysis revealed that the data of for both the wild type and the F97Y mutant can be satisfactorily explained by the common kinetic model described in Figure 3a involving biphasic kinetics, geminate recombination, and bimolecular CO recombination (see the SI for details). The associated kinetic parameters were optimized to make the linear combination of the species-associated scattering curves give a satisfactory match (red curves in Figure 2) with the experimental time-dependent difference scattering curve for each of the data sets measured at the three different laser fluence levels.

Figure 3.

Figure 3

Open in a new tab

Kinetic model, species-associated X-ray scattering curves for the three intermediates and their time-dependent population changes, and dependence of the fully and partially photolyzed species on laser fluence. (a) Kinetic model compatible with the data for both the wild type and mutant. The time constants in black and red correspond to the wild type and mutant, respectively. The kinetics of the mutant is accelerated relative to that of the wild type. Each intermediate species can have both fully photolyzed and partially photolyzed forms. The red (with “CO”) and white symbols indicate the liganded and photolyzed subunits, respectively. On the basis of our structural analysis, the subunits of each intermediate are represented with differently shaped symbols to indicate the change in the tertiary structure. In intermediate I3, one subunit is described as rotating with respect to the other, reflecting the quaternary structural change in the transition from I2 to I3. For the wild type, intermediate I1 is generated within 100 ps and transformed into intermediate I2 with a time constant of 3.2 ± 0.2 ns. Subsequently, intermediate I3 is formed, exhibiting ligation-dependent formation kinetics with time constants of 730 ± 120 ns for the fully photolyzed form and 5.6 ± 0.8 μs for the partially photolyzed form. Intermediate I3 returns to HbI(CO)2 with a bimolecular nongeminate CO recombination rate constant of 95 ± 0.27 mM–1 s–1. Some of intermediate I2 returns to the nonphotolyzed form of intermediate I1 via geminate recombination with a time constant of 93 ± 20 ns. This nonphotolyzed form of I1 returns to HbI(CO)2 with a time constant of 15.2 ± 8 μs. For the F97Y mutant, the overall kinetics is accelerated, except for the transition of I1 to I2 and the geminate recombination. (b) Species-associated scattering curves for the earliest intermediate I1, the early intermediate I2, and the late intermediate I3. These curves correspond to the constituents of the matrix B described in the SI. The curves for the wild type (black) and F97Y mutant (red) are shown together. (c, d) Population changes of the three intermediates (mid laser fluence) as functions of time for (c) the wild type and (d) the mutant. The lines correspond to the populations obtained from the kinetic analysis of the experimental scattering data, and the symbols correspond to the optimized populations at the time delay points where experimental data were measured. (e) Relative ratios of the fully photolyzed species (cyan), the partially photolyzed species (magenta), and the geminately recombined species (blue) as functions of laser fluence.

Figure 3c,d shows the population changes of the three intermediates at the mid laser fluence as functions of time for the wild type and the mutant, respectively. For the wild type, the earliest intermediate, I1, which was determined to be R-like via structural analysis as shown later, is formed within 100 ps and transformed into the I2 intermediate with a time constant of 3.2 ± 0.2 ns. Some of intermediate I2 undergoes geminate recombination with CO with a time constant of 93 ± 20 ns, returning to the nonphotolyzed form of intermediate I1, which then ultimately decays to the initial HbI(CO)2 structure with a time constant of 15.2 ± 8 μs. The rest of I2 is converted to intermediate I3 biphasically with time constants of 730 ± 120 ns and 5.6 ± 0.8 μs. Subsequently, intermediate I3, which corresponds to the T state, returns to the initial HbI(CO)2 via bimolecular CO recombination with a bimolecular rate constant of 95 ± 0.27 mM–1 s–1. For the F97Y mutant, the overall kinetics is accelerated, except for the transition of I1 to I2 (3.0 ± 0.3 ns) and the geminate recombination. The R–T transition from I2 to I3 (with time constants of 40 ± 20 ns for the fully photolyzed form and 370 ± 100 ns for the partially photolyzed form) is accelerated and becomes faster than the geminate recombination from I2 to I1. As shown in Figure 3d,e, the geminate recombination pathway is practically quenched. The bimolecular recovery of HbI(CO)2 from I3 is accelerated (1310 ± 20 and 95 ± 0.27 mM–1 s–1 for the mutant and wild type, respectively), and the ratio of the fully photolyzed species becomes much smaller, as shown in Figure 3e. These observations are consistent with a stronger CO binding affinity for the F97Y mutant than for the wild type.

Since the slower component of the I2 population decay decreases at the high laser fluence and the relative ratio of the fully photolyzed form increases with laser fluence as shown in Figure 3e, the fast and slow components are associated with the fully and partially photolyzed forms of intermediate I2, respectively. Here we note that the biphasic kinetics associated with only a single (structurally distinct) species indicates that both the partially and fully photolyzed variants of I2 (and thus I3) have the same structure. This finding is direct structural evidence that CO photolysis of a single subunit of HbI effectively induces the same structural change as photolysis of both subunits does. Recently, a mechanistic model for transmitting the motion of one subunit to the other subunit was proposed based on a meta-analysis of a large collection of various crystal structures of HbI.64 Our observation is consistent with this structural mechanism that keeps the two subunits in symmetry.

Structural Analysis of Intermediates

The species-associated scattering curves of the three intermediates for the wild type and the mutant (Figure 3b) reveal important structural information. The wild type and the mutant have identical scattering curves for I1 and I2, indicating that the structures of I1 and I2 are not affected by the mutation, in contrast to the much accelerated kinetics in the mutant. However, the wild type and the mutant exhibit significantly different scattering curves for I3. To distinguish the two different intermediates, the I3 intermediates of the wild type and the F97Y mutant are named I3(WT) and I3(F97Y), respectively, where necessary. Especially, the signals for I3(WT) and I3(F97Y) show opposite signs at small angles (<0.2 Å–1), positive for the wild type and negative for the mutant. As the small-angle signal is sensitive to the overall number of electrons belonging to the scattering particle, the small-angle region of the I3 intermediate data may serve as the signature of major entry or exit of interfacial water molecules. Our observation is consistent with the previously reported water entry for the wild type12 and water loss for the F97Y mutant.15

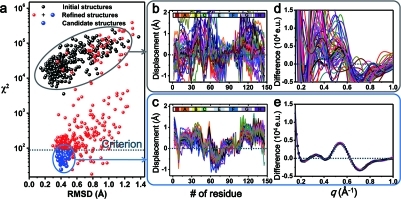
To extract detailed structural changes such as subunit rotation and movements of hemes and helices, we performed structure refinement aided by Monte Carlo simulations for the time-independent, species-associated scattering curves of I1, I2, I3(WT), and I3(F97Y) (see the SI for details). Each subunit of an HbI intermediate was divided into nine rigid bodies (eight helices and one heme group), giving a total of 18 rigid bodies in the entire HbI protein. Recently, slight bending of the E helix was proposed on the basis of an inspection of various crystal structures of HbI,64 but the extent of the bending is not substantial enough to deviate from the rigid-body approximation. Starting from a crystal structure, Monte Carlo simulation was employed to generate many random structures by moving the rigid bodies. On the basis of the aforementioned correlation between the small-angle signal and the known entry/exit of interfacial water molecules, the numbers of interfacial water molecules were fixed as those of the crystal structures (Table 1). Figure 4 shows the results for the I3(WT) intermediate as an example. For each intermediate, 360 random structures were generated. For each of the initial random structures, we refined the structure by minimizing the χ2 value (i.e., the degree of discrepancy between the experimental curve and the theoretical curve calculated from the structure). To do so, we explored the structural space using Monte Carlo simulations guided by molecular dynamics (MD) force fields and simulated annealing. In Figure 4a, the χ2 values for the initial structure (black circles) and the refined structures (red and blue circles) are plotted as functions of the rmsd with respect to an arbitrary reference structure (in this case deoxy-HbI, PDB entry 4sdh). The wide range of the structural space consisting of these random structures is evident in the widespread distribution of the displacement plots shown in Figure 4b. A displacement plot of a structure shows the displacement of amino acid residues in comparison with a reference structure as a function of the amino acid sequence and thus displays the difference in tertiary structure between a structure of interest and a reference structure. Here the position of a residue is defined by the distance between the Cα atom in the residue and the iron atom of the heme, and the displacement of the residue is the difference in this distance for the two compared structures. As expected from the variety and high χ2 values of the initial random structures, the theoretical scattering curves calculated from those structures (Figure 4d) show a wide range of variations and do not match at all with the species-associated curve obtained from the experiment.

Table 1. Rmsd Values for the Whole Protein, Fe–Fe Distances between the Two Hemes, Numbers of Interfacial Water Molecules, and Subunit Rotation Angles for the Averaged Refined Structures of the Intermediates (I1, I2, and I3) and the Deoxy-HbI Crystal Structure (PDB Entry 4sdh(11)) with Respect to the HbI(CO)2 Crystal Structure (PDB Entry 3sdh(11))a.

  rmsd (Å) Fe–Fe distance (Å) number of interface water molecules rotation angle (deg)
HbI(CO)2(3sdh) – 18.4 11 –
deoxy-HbI (4sdh) 0.6 16.6 17 3.5
deoxy-HbI F97Y mutant (2aup) 0.6 17.2 6 3.4b
I1 0.4 (±0.05) 18.0 (±0.2) 9 (fixed) –0.1 (±0.5)
I2 0.4 (±0.06) 17.9 (±0.3) 9 (fixed) 0.1 (±0.5)
I3(WT) 0.7 (±0.05) 16.6 (±0.2) 17 (fixed) 3.5 (±0.6)
I3(F97Y) 0.8 (±0.04) 18.0 (±0.2) 6 (fixed) 3.0 (±0.6)
Open in a new tab
a

Values in parentheses are standard deviations among the candidate structures.

b

The subunit rotation angle for the deoxy-HbI F97Y mutant crystal structure (PDB entry 2aup)15 was calculated with respect to the HbI(CO)2 F97Y mutant crystal structure (PDB entry 2auo).15

Figure 4.

Figure 4

Open in a new tab

Structure refinement aided by Monte Carlo simulations. The case of the wild-type I3 intermediate is shown as an example. Starting from 360 random initial structures generated from Monte Carlo simulations, we minimized the χ2 value (i.e., the degree of discrepancy between the experimental curve and the theoretical curve calculated from one of the starting structures) by exploring the structural space via Monte Carlo simulations guided by MD force fields and simulated annealing. (a) The χ2 values between the experimental curve and the theoretical curve for the initial structure (black circles) and the refined structures (red and blue circles) are plotted as functions of the rmsd vs an arbitrary reference structure (4sdh). Those corresponding to the best structures are circled in blue. (b, c) Displacement plots for (b) 50 arbitrary structures chosen from among the 360 initial structures and (c) the 76 best refined structures. The displacement was calculated with respect to the 3sdh structure of HbI(CO)2. Helices are labeled at the top of the plots. (d, e) Comparison of the experimental species-associated scattering curve with the theoretical scattering curves of (d) the 50 arbitrary structures and (e) the 76 best refined structures.

Among 106 refined structures that had substantially reduced χ2 values, we selected the representative structures by applying the clustering method, in which the structures were categorized according to their structural similarities by comparing the rmsd values. As a result, 76 structures (out of 106) were classified as the first cluster and proposed as the candidate structures (blue circles). A structure having an average rmsd among the first cluster was selected as a representative structure for the wild-type I3 intermediate. The convergence to the optimized structure was confirmed by inspecting the displacement plots for all 76 candidate structures included in the first cluster. As shown in Figure 4c, the displacement plots for the candidate structures were well-matched with each other, confirming the convergence. Naturally, the theoretical scattering curves from the best structures converged to the experimental species-associated scattering curve, as shown in Figure 4e.

The rmsd values of the overall protein structures, the heme–heme distances, the subunit rotation angles, and the comparison with static structure of deoxy-HbI for the averaged refined structures of the intermediates are summarized in Table 1.

Changes in Structural Parameters and the Effect of F97Y Mutation

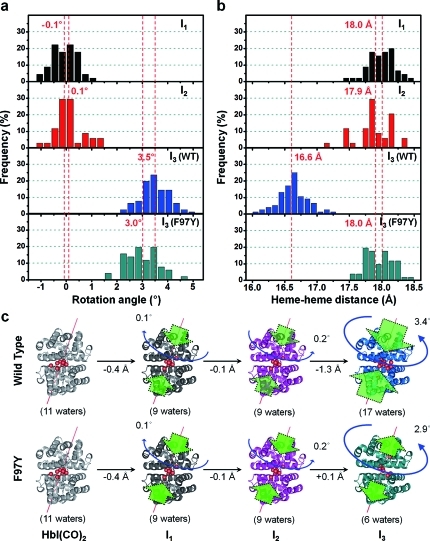
Inspection of the structural parameters of the best structures for the four structurally distinct intermediates [I1, I2, I3(WT), and I3(F97Y)] reveals detailed structural transitions between the intermediates. The subunit rotation angle is the key structural parameter for a quaternary structural transition. In addition, it is relevant to compare the distance between the iron atoms of the hemes that are directly in contact with each other through the hydrogen-bonding network and thus modulate the ligand affinity drastically.13,23 Figure 5 shows the occurrence distributions of the subunit rotation angle and the heme–heme distance for I1, I2, I3(WT), and I3(F97Y). The transitions from HbI(CO)2 to I1 and I2 involve only negligible amounts of rotation, with rotation angles of −0.1 ± 0.5 and 0.1 ± 0.5°, respectively, and the distance between iron atoms of the two hemes remains essentially identical (18.0 ± 0.2 and 17.9 ± 0.3 Å for I1 and I2, respectively). The deviation value represents the variation only among the best structures. The major rotation occurs in the transition from I2 to I3(WT), with a rotation angle of 3.5 ± 0.6°. The F97Y mutant also undergoes a similar degree of major rotation (3.0 ± 0.6°) as the wild type in the transition from I2 to I3(F97Y). The subunit rotation angles and the heme–heme distances determined for I1, I2, and I3 in solution reveal that I1 and I2 are in R states and I3 is in the T state.

Figure 5.

Figure 5

Open in a new tab

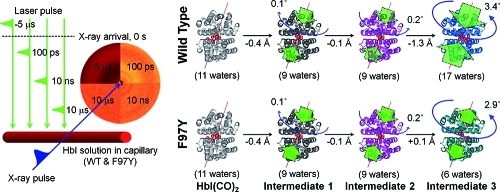
Structural dynamics of HbI extracted from the species-associated scattering curves using structure refinement. (a, b) Distributions of (a) the subunit rotation angles and (b) the heme–heme distances for the best-fit structures. Those corresponding to I1, I2, I3(WT), and I3(F97Y) are colored in black, red, blue, and green, respectively. (c) Schematic summary of the structural transitions for the wild type and the mutant. The structural transitions from HbI(CO)2 to I2 via I1 are identical for the wild type and the mutant. In contrast, for the transition from I2 to I3, interfacial water molecules enter in the wild type and exit in the mutant, and the extent of the structural change is smaller for the mutant. Especially, the heme–heme distance of I3(F97Y) is not reduced relative to that of I2, whereas I3(WT) exhibits a smaller heme–heme distance than I2. The green and blue arrows in (c) are used to indicate the relative magnitudes and directions of the changes in the heme–heme distance and subunit rotation angle relative to HbI(CO)2.

However, the heme–heme distance shows a dramatic contrast between I3(WT) and I3(F97Y). As can be seen in the occurrence distribution of the iron–iron distance in Figure 5b, the transition from I2 to I3(WT) further reduces the heme–heme distance to 16.6 ± 0.2 Å, whereas I3(F97Y) has a heme–heme distance of 18.0 ± 0.2 Å, which is nearly identical to the distance in I2. The unchanged heme–heme distance in I3(F97Y) relative to I2 can be linked to the absence of flipping of Phe97 in the mutant. In the wild type, the Phe97 residue is flipped from the interface to the inside of the subunit as a result of the transition from I2 to I3(WT), while Tyr97 of I3(F97Y) remains in the interface between the subunits and thus hinders the contraction of the heme–heme distance.15 The larger distance between the hemes of I3(F97Y) also leads to the acceleration of bimolecular CO recombination in the mutant by a factor of 14. For the CO recombination to occur in I3(WT), the two hemes at a reduced distance must move away to allow the CO ligands to come in. However, I3(F97Y) can easily accept the CO ligands without a large movement of the hemes because the heme–heme distance in I3(F97Y) is already similar to that of HbI(CO)2. Therefore, it takes less time for the bimolecular CO recombination to occur in the F97Y mutant than in the wild type.

Conclusion

In this work, by applying pump–probe X-ray solution scattering, we visualized the structural transition of a protein in solution in real time. Although time-resolved X-ray solution scattering has been previously applied to proteins, detailed structural information on transient intermediates could not be obtained from those studies because of the lack of a proper structural analysis tool. By taking advantage of a novel structural analysis using Monte Carlo simulations, we have elucidated the unprecedented structural details of transient intermediates involved in the solution-phase protein structural transition on picosecond and nanosecond time scales. From the extensive analysis of both the kinetics and structure of the transient intermediates, we have revealed that the singly liganded and unliganded forms of the intermediates formed in the HbI allosteric transition share the same structure. Application of our approach combining time-resolved X-ray solution scattering and structural analysis aided by Monte Carlo simulations to other systems should provide new insights into protein structural dynamics.

Acknowledgments

We thank V. Šrajer (University of Chicago) for support and helpful discussions. This work was supported by Creative Research Initiatives (Center for Time-Resolved Diffraction) of MEST/NRF and PRESTO/JST. K.H.K., S.M., K.Y.O., and J.G.K. acknowledge the support from the WCU Program (R31-2008-000-10071-0). Use of the BioCARS Sector 14 was supported by the National Institutes of Health, National Center for Research Resources, under Grant RR007707. This work was carried out with the approval of the Photon Factory Program Advisory Committee (Proposals 2009S2-001 and 2010G553).

Supporting Information Available

Sample preparation; data collection; data processing; data analysis, including SVD, kinetic analysis, and the kinetic model; calculation of theoretical X-ray scattering curves; structure refinement aided by Monte Carlo simulations of rigid-body movement; constraints to maintain the coordination; description of loop movement; checking of the mother structures; dependence on the choice of the HbI(CO)2 structure; clustering method; example of structure refinement for the I3(WT) intermediate; calculation of the scaling factor between the experimental and theoretical difference scattering curves; comparison of data measured at APS and KEK; and related figures, tables, and materials. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Author Contributions

# These authors contributed equally.

Funding Statement

National Institutes of Health, United States

Supplementary Material

ja210856v_si_001.pdf (2.1MB, pdf)

References

  1. Perutz M. F. Nature 1970, 228, 726. [DOI] [PubMed] [Google Scholar]
  2. Baldwin J.; Chothia C. J. Mol. Biol. 1979, 129, 175. [DOI] [PubMed] [Google Scholar]
  3. Shaanan B. J. Mol. Biol. 1983, 171, 31. [DOI] [PubMed] [Google Scholar]
  4. Fermi G.; Perutz M. F.; Shaanan B.; Fourme R. J. Mol. Biol. 1984, 175, 159. [DOI] [PubMed] [Google Scholar]
  5. Perutz M. F. Q. Rev. Biophys. 1989, 22, 139. [DOI] [PubMed] [Google Scholar]
  6. Eaton W. A.; Henry E. R.; Hofrichter J.; Mozzarelli A. Nat. Struct. Biol. 1999, 6, 351. [DOI] [PubMed] [Google Scholar]
  7. Adachi S.; Park S. Y.; Tame J. R.; Shiro Y.; Shibayama N. Proc. Natl. Acad. Sci. U.S.A. 2003, 100, 7039. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chiancone E.; Vecchini P.; Verzili D.; Ascoli F.; Antonini E. J. Mol. Biol. 1981, 152, 577. [DOI] [PubMed] [Google Scholar]
  9. Antonini E.; Ascoli F.; Brunori M.; Chiancone E.; Verzili D.; Morris R. J.; Gibson Q. H. J. Biol. Chem. 1984, 259, 6730. [PubMed] [Google Scholar]
  10. Mozzarelli A.; Bettati S.; Rivetti C.; Rossi G. L.; Colotti G.; Chiancone E. J. Biol. Chem. 1996, 271, 3627. [DOI] [PubMed] [Google Scholar]
  11. Royer W. E. Jr.; Hendrickson W. A.; Chiancone E. Science 1990, 249, 518. [DOI] [PubMed] [Google Scholar]
  12. Royer W. E. Jr.; Pardanani A.; Gibson Q. H.; Peterson E. S.; Friedman J. M. Proc. Natl. Acad. Sci. U.S.A. 1996, 93, 14526. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Knapp J. E.; Gibson Q. H.; Cushing L.; Royer W. E. Jr. Biochemistry 2001, 40, 14795. [DOI] [PubMed] [Google Scholar]
  14. Knapp J. E.; Royer W. E. Jr. Biochemistry 2003, 42, 4640. [DOI] [PubMed] [Google Scholar]
  15. Knapp J. E.; Bonham M. A.; Gibson Q. H.; Nichols J. C.; Royer W. E. Jr. Biochemistry 2005, 44, 14419. [DOI] [PubMed] [Google Scholar]
  16. Zhou Y. Q.; Zhou H. Y.; Karplus M. J. Mol. Biol. 2003, 326, 593. [DOI] [PubMed] [Google Scholar]
  17. Seno Y. J. Comput. Chem. 2006, 27, 701. [DOI] [PubMed] [Google Scholar]
  18. Kiyota Y.; Hiraoka R.; Yoshida N.; Maruyama Y.; Imai T.; Hirata F. J. Am. Chem. Soc. 2009, 131, 3852. [DOI] [PubMed] [Google Scholar]
  19. Hub J. S.; Kubitzki M. B.; de Groot B. L. PLoS Comput. Biol. 2010, 6, e1000774. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Fischer S.; Olsen K. W.; Nam K.; Karplus M. Proc. Natl. Acad. Sci. U.S.A. 2011, 108, 5608. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Yoshida N.; Imai T.; Phongphanphanee S.; Kovalenko A.; Hirata F. J. Phys. Chem. B 2009, 113, 873. [DOI] [PubMed] [Google Scholar]
  22. Chiancone E.; Elber R.; Royer W. E. Jr.; Regan R.; Gibson Q. H. J. Biol. Chem. 1993, 268, 5711. [PubMed] [Google Scholar]
  23. Rousseau D. L.; Song S.; Friedman J. M.; Boffi A.; Chiancone E. J. Biol. Chem. 1993, 268, 5719. [PubMed] [Google Scholar]
  24. Nichols J. C.; Royer W. E. Jr.; Gibson Q. H. Biochemistry 2006, 45, 15748. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Nienhaus K.; Knapp J. E.; Palladino P.; Royer W. E. Jr.; Nienhaus G. U. Biochemistry 2007, 46, 14018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Choi J.; Muniyappan S.; Wallis J. T.; Royer W. E. Jr.; Ihee H. ChemPhysChem 2010, 11, 109. [DOI] [PubMed] [Google Scholar]
  27. Mizutani Y.; Kitagawa T. Science 1997, 278, 443. [DOI] [PubMed] [Google Scholar]
  28. Sakakura M.; Yamaguchi S.; Hitota N.; Terazima M. J. Am. Chem. Soc. 2001, 123, 4286. [DOI] [PubMed] [Google Scholar]
  29. Zhang L.; Wang L.; Kao Y.-T.; Qiu W.; Yang Y.; Okobiah O.; Zhong D. Proc. Natl. Acad. Sci. U.S.A. 2007, 104, 18461. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Rodgers K. R.; Spiro T. G. Science 1994, 265, 1697. [DOI] [PubMed] [Google Scholar]
  31. Jayaraman V.; Rodgers K. R.; Mukerji I.; Spiro T. G. Science 1995, 269, 1843. [DOI] [PubMed] [Google Scholar]
  32. Balakrishnan G.; Case M. A.; Pevsner A.; Zhao X.; Tengroth C.; McLendon G. L.; Spiro T. G. J. Mol. Biol. 2004, 340, 843. [DOI] [PubMed] [Google Scholar]
  33. Šrajer V.; Teng T.-y.; Ursby T.; Pradervand C.; Ren Z.; Adachi S.; Schildkamp W.; Bourgeois D.; Wulff M.; Moffat K. Science 1996, 274, 1726. [DOI] [PubMed] [Google Scholar]
  34. Moffat K. Chem. Rev. 2001, 101, 1569. [DOI] [PubMed] [Google Scholar]
  35. Bourgeois D.; Vallone B.; Schotte F.; Arcovito A.; Miele A. E.; Sciara G.; Wulff M.; Anfinrud P.; Brunori M. Proc. Natl. Acad. Sci. U.S.A. 2003, 100, 8704. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Knapp J. E.; Pahl R.; Cohen J.; Nichols J. C.; Schulten K.; Gibson Q. H.; Šrajer V.; Royer W. E. Jr. Structure 2009, 17, 1494. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Knapp J. E.; Pahl R.; Šrajer V.; Royer W. E. Jr. Proc. Natl. Acad. Sci. U.S.A. 2006, 103, 7649. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Ihee H.; Rajagopal S.; Šrajer V.; Pahl R.; Anderson S.; Schmidt M.; Schotte F.; Anfinrud P. A.; Wulff M.; Moffat K. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 7145. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Cammarata M.; Levantino M.; Schotte F.; Anfinrud P. A.; Ewald F.; Choi J.; Cupane A.; Wulff M.; Ihee H. Nat. Methods 2008, 5, 881. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Ahn S.; Kim K. H.; Kim Y.; Kim J.; Ihee H. J. Phys. Chem. B 2009, 113, 13131. [DOI] [PubMed] [Google Scholar]
  41. Andersson M.; Malmerberg E.; Westenhoff S.; Katona G.; Cammarata M.; Wohri A. B.; Johansson L. C.; Ewald F.; Eklund M.; Wulff M.; Davidsson J.; Neutze R. Structure 2009, 17, 1265. [DOI] [PubMed] [Google Scholar]
  42. Cho H. S.; Dashdorj N.; Schotte F.; Graber T.; Henning R.; Anfinrud P. Proc. Natl. Acad. Sci. U.S.A. 2010, 107, 7281. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Cammarata M.; Levantino M.; Wulff M.; Cupane A. J. Mol. Biol. 2010, 400, 951. [DOI] [PubMed] [Google Scholar]
  44. Kim K. H.; Oang K. Y.; Kim J.; Lee J. H.; Kim Y.; Ihee H. Chem. Commun. 2011, 47, 289. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Ihee H. Acc. Chem. Res. 2009, 42, 356. [DOI] [PubMed] [Google Scholar]
  46. Vincent J.; Andersson M.; Eklund M.; Wöhri A. B.; Odelius M.; Malmerberg E.; Kong Q.; Wulff M.; Neutze R.; Davidsson J. J. Chem. Phys. 2009, 130, 154502. [DOI] [PubMed] [Google Scholar]
  47. Christensen M.; Haldrup K.; Bechgaard K.; Feidenhans’l R.; Kong Q. Y.; Cammarata M.; Lo Russo M.; Wulff M.; Harrit N.; Nielsen M. M. J. Am. Chem. Soc. 2009, 131, 502. [DOI] [PubMed] [Google Scholar]
  48. Ihee H.; Lorenc M.; Kim T. K.; Kong Q. Y.; Cammarata M.; Lee J. H.; Bratos S.; Wulff M. Science 2005, 309, 1223. [DOI] [PubMed] [Google Scholar]
  49. Kong Q.; Lee J. H.; Kim K. H.; Kim J.; Wulff M.; Ihee H.; Koch M. H. J. Am. Chem. Soc. 2010, 132, 2600. [DOI] [PubMed] [Google Scholar]
  50. Hura G. L.; Menon A. L.; Hammel M.; Rambo R. P.; Poole F. L. II; Tsutakawa S. E.; Jenney F. E. Jr.; Classen S.; Frankel K. A.; Hopkins R. C.; Yang S.-j.; Scott J. W.; Dillard B. D.; Adams M. W. W.; Tainer J. A. Nat. Methods 2009, 6, 606. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Tsuruta H.; Irving T. C. Curr. Opin. Struct. Biol. 2008, 18, 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Lamb J. S.; Zoltowski B. D.; Pabit S. A.; Crane B. R.; Pollack L. J. Am. Chem. Soc. 2008, 130, 12226. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Doniach S. Chem. Rev. 2001, 101, 1763. [DOI] [PubMed] [Google Scholar]
  54. Konuma T.; Kimura T.; Matsumoto S.; Got Y.; Fujisawa T.; Fersht A. R.; Takahashi S. J. Mol. Biol. 2011, 405, 1284. [DOI] [PubMed] [Google Scholar]
  55. Kathuria S. V.; Guo L.; Graceffa R.; Barrea R.; Nobrega R. P.; Matthews C. R.; Irving T. C.; Bilsel O. Biopolymers 2011, 95, 550. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Roux B.; Yang S. C.; Blachowicz L.; Makowski L. Proc. Natl. Acad. Sci. U.S.A. 2010, 107, 15757. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Roh J. H.; Guo L.; Kilburn J. D.; Briber R. M.; Irving T.; Woodson S. A. J. Am. Chem. Soc. 2010, 132, 10148. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Zuo X.; Wang J.; Foster T. R.; Schwieters C. D.; Tiede D. M.; Butcher S. E.; Wang Y. J. Am. Chem. Soc. 2008, 130, 3292. [DOI] [PubMed] [Google Scholar]
  59. Forster F.; Webb B.; Krukenberg K. A.; Tsuruta H.; Agard D. A.; Sali A. J. Mol. Biol. 2008, 382, 1089. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Akiyama S.; Takahashi S.; Kimura T.; Ishimori K.; Morishima I.; Nishikawa Y.; Fujisawa T. Proc. Natl. Acad. Sci. U.S.A. 2002, 99, 1329. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Koch M. H. J.; Vachette P.; Svergun D. I. Q. Rev. Biophys. 2003, 36, 147. [DOI] [PubMed] [Google Scholar]
  62. Makowski L.; Gore D.; Mandava S.; Minh D.; Park S.; Rodi D. J.; Fischetti R. F. Biopolymers 2011, 95, 531. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Summerford C. M.; Pardanani A.; Betts A. H.; Poteete A. R.; Colotti G.; Royer W. E. Jr. Protein Eng. 1995, 8, 593. [DOI] [PubMed] [Google Scholar]
  64. Ren Z.; Šrajer V.; Knapp J. E.; Royer W. E. Jr. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 107. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja210856v_si_001.pdf (2.1MB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES